Site-specific hydrogen-atom elimination in photoexcited ethyl radical

Abstract

The photochemistry of the ethyl radical following excitation to the 3p Rydberg state is investigated in a joint experimental and theoretical study. Velocity map images for hydrogen atoms detected from photoexcited isotopologues CH₃CH₂, CH₃CD₂ and CD₃CH₂ at ∼201 nm, are discussed along with high-level ab initio electronic structure calculations of potential energy curves and non-adiabatic coupling matrix elements (NACME). A novel mechanism governed by a conical intersection allowing prompt site-specific hydrogen-atom elimination is presented and discussed. For this mechanism to occur, an initial ro-vibrational excitation is allocated to the radical permitting to access this reaction pathway and thus to control the ethyl photochemistry. While hydrogen-atom elimination from cold ethyl radicals occurs through internal conversion into lower electronic states followed by slow statistical dissociation, prompt site-specific C_α elimination into CH₃CH + H, occurring through a fast non-adiabatic crossing to a valence bound state followed by dissociation through a conical intersection, is accessed by means of an initial ro-vibrational energy content into the radical. The role of a particularly effective vibrational promoting mode in this prompt photochemical reaction pathway is discussed.

---

1 Introduction

Conical intersections play a remarkable role governing and controlling photochemistry in molecules and radicals. Their significant role and characteristics have been largely reported over the years in theoretical and experimental investigations.^1,2 Conical intersections often act, for instance, as funnels in radiationless deactivation of amino-acids or other biologically-relevant molecules, while they are crucial in a variety of photochemical reactions such as in electrocyclic ring-opening or cis–trans photoisomerization reactions.^3,4 In the present work, a novel mechanism governed by a conical intersection is reported following photoexcitation of the ethyl radical and allowing site-specific hydrogen-atom elimination. The photoreactivity of this radical is indeed controlled by means of an initial ro-vibrational excitation in the parent molecule permitting to access the reported pathway.

Radicals, and in particular alkyl radicals, are crucial intermediate species in photoinduced chemical reactions in different areas including atmospheric and interstellar chemistry (see, for instance, ref. 5–7), as well as in combustion chemistry.⁸ Among them, the ethyl radical, one of the simplest hydrocarbon radicals, constitute a prototype of alkyl radical. Numerous investigations have been performed on its thermal decomposition^9–13 as well as on its UV-VUV excitation and photodissociation dynamics, from both experimental^14–19 and theoretical approaches.^20,21

Koplitz's group carried out in the early 1990's a series of experiments bringing out site-specific bond cleavage following ethyl radical excitation based on measured intensity of hydrogen and deuterium atom Doppler profiles for different isotopologues (i.e. CH₃CH₂, CH₃CD₂ and CD₃CH₂).^14,15 A clear preference for C–H bond dissociation from the methyl moiety (C_β) was indeed observed following excitation around 248 nm, while at shorter wavelengths (193 nm), H–D isotope scrambling was found to mask any site-specific process. Later experimental studies on ethyl photodissociation following excitation into the 3s Rydberg state (first absorption band around 250 nm), produced by both photolysis and pyrolysis of a precursor, confirmed the H-atom loss from the C_β.^18,19 H-Atom Rydberg tagging time-of-flight spectroscopy¹⁸ and velocity map imaging¹⁹ experiments pointed out two dissociation processes: slow H atoms assigned to unimolecular dissociation from the ground state in highly excited levels and fast H atoms assigned to direct dissociation forming ethylene in its ground state. H-Atom elimination was assigned to the initial formation of the bridged C_2v structure, i.e., one H atom from the methyl moiety rotates being then located at 90° with respect to the C–C bond. In this C_2v geometry, the 3s Rydberg state correlates adiabatically to the H + C₂H₄ dissociation limit with both species in their ground state. The dynamics is mediated by a conical intersection between the 3s Rydberg state and the X̃²A′ ground state, which adiabatically leads to the H + C₂H₄ (ã³B_1u) limit. Fast H atoms are thus produced by direct dissociation on the 3s state, while some population goes into the ground state forming slow H atoms. Theoretical studies including ab initio molecular dynamics employing surface hopping have also been performed supporting the existence of these two mechanisms although some small discrepancies exist concerning the unimolecular dissociation leading to slow H atoms.^20,21 Besides, Matsugi²² performed a classical trajectory study revealing in particular the existence of a minor roaming pathway in ground state ethyl leading to C₂H₃ + H₂ followed by secondary dissociation of C₂H₃ into C₂H₂ + H.

Bersohn and co-workers¹⁶ published a first experimental study on the photodissociation dynamics of the ethyl 3p Rydberg state by excitation at 205 nm. The averaged translational energy of H fragment atoms deduced from the Doppler broadened fluorescence detection lines were reported and discussed. A curve crossing between the 3p state and a valence state was proposed to lead to fast H-atom loss; besides, complete H–D isotope scrambling was observed and envisaged as hydrogen exchange in the 3p excited state. In the proposed picture, this last state would present two minima with a small barrier, vibrational excitation allowing the molecule to go back and forth above the two minima.

Here, we report a novel mechanism for site-specific H-atom elimination following excitation of the ethyl radical to the 3p Rydberg state at around 201 nm. A fast H-atom loss occurs from C–H cleavage precisely in the methylene moiety (C_α), leading to H + CH₃CH, in contrast to all previously reported selectivity. As shown in Fig. 1, ethyl radicals generated in situ are photoexcited into 3p Rydberg states using a first laser pulse centered around ∼201 nm. The subsequent H(²S) atoms formed by dissociation of the populated Rydberg states are detected by (3 + 1) resonance enhanced multiphoton ionization (REMPI) at ∼364 nm. As mentioned above, an internal energy of about 1.27 eV characterizes the initial ethyl radical produced by in situ photolysis of the precursor molecule ethyl iodide at the same wavelength.²³ Velocity map images of the H(²S) fragments are recorded for different ethyl isotopologues, i.e. CH₃CH₂, CH₃CD₂ and CD₃CH₂, and then Abel inverted to extract the corresponding fragment translational and angular distributions. The experimental findings are complemented by high level ab initio calculations employing multireference configuration interaction of potential energy curves for the first six electronic states and the calculation of non-adiabatic coupling matrix elements (NACMEs), exploring different reaction pathways.

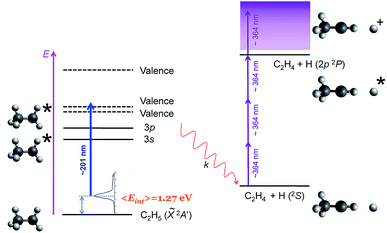Fig. 1 Scheme of the experimental procedure. A first nanosecond laser pulse centered at ∼201 nm is used to excite the ethyl radicals into the 3p Rydberg state. The H(²S) atoms following dissociation are detected using a (3 + 1) resonance enhanced multiphoton ionization (REMPI) scheme at ∼364 nm. Ethyl radicals are produced with an internal energy distribution depicted in the figure with 〈E_int〉 = 1.27 eV from the in situ photolysis of C₂H₅I at ∼201 nm.²³

2 Methods

2.1 Experimental

The main characteristics of the experimental setup have been already described in detail^24,25 and only a brief summary will be reported here. Ethyl iodide, which is employed as a precursor of hot ethyl radicals, was seeded in helium (10%, 1 atm backing pressure) and expanded into vacuum using a pulsed nozzle (General Valve Series 9, 0.5 mm orifice). The gas pulse passes through a skimmer (Beam Dynamics, Standard Model 2, 0.5 mm diameter orifice) and reaches the ionization chamber. A sum-frequency mixing nonlinear crystal is used to combine the fundamental and the second harmonic radiation of a Nd:YAG (Quanta Ray Pro 230) pumped frequency doubled dye laser (Sirah Cobra-Stretch). The radiation produced around 201 nm (0.15 mJ per pulse) is employed for in situ photolysis of ethyl iodide forming ethyl radicals with a characteristic internal energy of about 1.27 eV,²³ as well as for excitation of the radicals into the 3p Rydberg states (see Fig. 1). This pump wavelength is tuned at 201.2, 200.8, 200.3 and 200.15 nm for each isotopologue, so that the 0⁰₀ origin of the B-band of the corresponding precursor, i.e. CH₃CH₂I, CH₃CD₂I, CD₃CH₂I and CD₃CD₂I, respectively, is excited ensuring a maximal formation of ethyl radicals of characterized internal energy. H- and D-atom action spectra as a function of the excitation wavelength have been recorded and are reported in the ESI (Fig. S1†).

The produced H(²S) (or D(²S)) atoms are ionized 10 ns later using the 2p(²P_1/2) ← 1s(²S_1/2) (3 + 1) REMPI scheme at 364.8 nm (or 364.5 nm) of a second Nd:YAG (Quanta Ray Pro 190) pumped dye laser. The generated H⁺ ions are accelerated by a 6 kV applied to the repeller plate and pass through a field-free time-of-flight (TOF) region (45 mm) before hitting the impedance matched microchannel plates (Chevron configuration, 40 mm diameter) of our velocity map imaging (VMI) apparatus set in the single-field configuration.²⁶ The resulting electron avalanche strikes a phosphor screen (P47), thereby creating the ion image, which is recorded by a CCD camera (SONY 1024 × 768 pixel) controlled using National Instrument (NI) LabView 7.1 and IMAQ VISION software.

2.2 Theoretical

The potential energy curves (PECs) of the different electronic states were obtained using state-averaged complete active space self-consistent field (SA-CASSCF) calculations followed by the internally contracted multi-reference configuration interaction (MRCI) treatment available in the MOLPRO package.²⁷ For this system, it has been found that Davidson correction becomes unstable for the excited states probably due to strong couplings between them, therefore no correction to the size inconsistency of MRCI has been included. The active space used for these calculations consists of 13 electrons in 10 orbitals, the two first orbitals being kept closed (those associated with the 1s orbitals of the two carbon atoms). Ideally, the ethyl radical can be described in the C_s symmetry group. However, in order to characterize the dissociation pathways to the different asymptotes corresponding to H-atom elimination, two possible symmetry planes may arise for torsion angles ϕ = 0° and ϕ = 90°. Since the description of the electronic wavefunction calculated with multi-reference methods is very sensitive to the orbitals included in the active space, it is important to use the same active space for the different PECs leading to the different fragments in both the Franck–Condon and the long range regions. To avoid mismatches between the symmetries of the different electronic states (the ground state switches from A′ to A′′ under a torsion of 90°) and to ensure that the active space always includes the same orbitals, the calculations were performed without symmetry.

The ethyl radical is composed of 7 atoms and thus possesses 15 degrees of freedom. The purpose of the calculations is to obtain a simple (one dimensional) representation of the energetics of the involved electronic states as a function of R_CH, the distance between the dissociating hydrogen atom and its corresponding carbon atom. A partial relaxation of the ground state of the system has been performed at CASPT2 level at each R_CH distance between 0.6 and 5 Å for all the dissociation channels considered. This presents the advantage to match the dissociation energy of the ground state, always keeping in mind that the calculated path is not necessarily the most favorable of the excited states were then performed over the ground state geometries obtained.

The diabatization was later carried out using the model presented in ref. 25 and 28. This method consists of estimating geometrically the mixing angles between the different states along the reaction coordinate that allow to pass from the adiabatic to the diabatic representation. The non-adiabatic coupling matrix elements (NACMEs) between the different states are then obtained as the derivative of the corresponding mixing angle as a function of the chosen coordinate, in this case, the C–H bond.

In addition, in order to get an estimate of the internal energy of the system, anharmonic zero-point energies were calculated for the ethyl CH₃CH₂ radical, the carbene CH₃CH radical and ethylene CH₂CH₂ and the corresponding isotopologues. Vibrational anharmonic fundamentals were computed using vibrational second order perturbation theory (VPT2)²⁹ as implemented in Gaussian,³⁰ to estimate the zero-point vibrational energies. The corresponding full-dimensional anharmonic force field was computed using second order Möller–Plesset theory (MP2).³¹ For all the calculations, the aug-cc-pVTC basis set of Dunning were used for C and H atoms. The harmonic and anharmonic corrected vibrational energies for CH₃CH₂, CH₃CH and CH₂CH₂ are summarized in Tables S1, S2 and S3 of the ESI.† The harmonic and anharmonic zero point energies of those species are listed in Table S4† and the harmonic zero point energies and dissociation energies of all isotopomers are shown in Table S5 of the ESI.†

3 Results and discussion

Recorded H-atom inverted images obtained from photoexcited CH₃CH₂, CH₃CD₂ and CD₃CH₂ at 201.2, 200.8 and 200.3 nm, respectively (see ESI†), into the 3p Rydberg states are depicted in Fig. 2 along with the corresponding total translational energy distributions (TED). A central blot leading to a Boltzmann-type energy distribution is similarly observed for the three isotopomers while an additional narrow quasi-isotropic ring associated with a sharp peak in the TED is exclusively recovered for CH₃CH₂ and CD₃CH₂. This last peak highlights thus a site-specific hydrogen-atom fast elimination channel leading to H + CH₃CH. As reflected by the results for CH₃CD₂, H-atom elimination from the methyl moiety (C_β) is characterized by a Boltzmann-type distribution, which reflects a high ro-vibrational energy of the co-fragment. Such transfer of energy from translational to internal modes usually reflects either a statistical dissociation or a slow process with a long-lifetime transition state. This latter case was similarly reported for methyl radical dissociation where several conical intersections control the dynamics.²⁵ In contrast, the H-atom loss channel from the methylene moiety (C_α) arises from two different mechanisms: one contributing to the measured Boltzmann-type distribution, and a more favourable prompt direct dissociation process, as reflected by the higher intensity of the sharp peak for CD₃CH₂.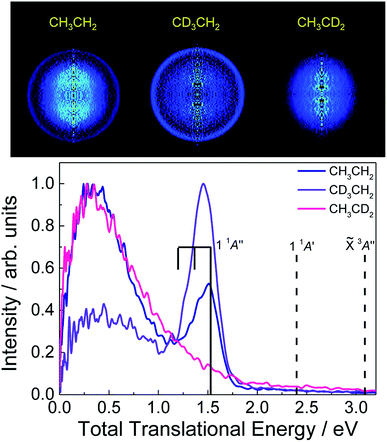

Fig. 2 Top: H-atom Abel-inverted velocity map images for the three isotopologues CH₃CH₂, CH₃CD₂ and CD₃CH₂, excited at 201.2, 200.8 and 200.3 nm, respectively (see ESI†). Bottom: Total translational energy distributions (TED) extracted from the images. Vertical bars specify the available energy for the three first C_α dissociation limits, i.e. H(²S) + CH₃CH(X̃³A′′), H(²S) + CH₃CH(1 ¹A′) and H(²S) + CH₃CH(1 ¹A′′) (see the text for more details). The comb represents the position of the two first excited vibrational levels of CH₃CH(1 ¹A′′) in the methyl deformation mode. The TEDs have been normalized independently with respect to their corresponding intensity maximum.

Similar experiments have been carried out detecting D-atoms from the three corresponding isotopologues, i.e. CD₃CD₂, CD₃CH₂ and CH₃CD₂, and the results are reported in the ESI.† Indeed, the site-specific prompt dissociation process is also observed although the ring in the images and corresponding peak in the TEDs present a remarkably lower intensity (see Fig. S2†). Experiments performed at a higher excitation energy, i.e. 193 nm, have shown, however, a similar intensity characterizing the D- and H-atoms from the prompt dissociation process. The results obtained at the excitation wavelength of 193 nm will be reported and discussed separately. The present results reveal that prompt D-atom formation requires a somewhat higher excitation energy when compared to H-atom formation. Ab initio calculations have been carried out to evaluate the zero-point energies for all isotopomers (CH₃CH₂, CH₃CD₂, CD₃CH₂ and CD₃CD₂) and the corresponding D₀ dissociation energies (see Table S5 of the ESI†). The latter D₀ values are indeed higher for the photofragmentation channels yielding D-atoms.

Vertical bars displayed in the TEDs correspond to the available energy for the first three dissociation channels: H(²S) + CH₃CH(X̃³A′′), H(²S) + CH₃CH(1 ¹A′) and H(²S) + CH₃CH(1 ¹A′′), which can contribute to the measured narrow peak, deduced from:

E_av = hν + E_int(parent) − D₀ (1)

where E_av is the available energy for dissociation, hν is the photon energy, E_int(parent) is the ethyl initial internal energy, and D₀ is the dissociation energy, i.e. 4.35, 5.04 and 5.91 eV, respectively, as obtained from the calculations preformed in the present work taking into account the difference in zero-point energy (ZPE) between the initial C₂H₅ radical and the CH₃CH product in its electronic ground state, although the ZPE for the excited states of CH₃CH might slightly change (see ESI†).

The narrow peak in the TED can indeed be assigned to the H(²S) + CH₃CH(1 ¹A′′) limit, where CH₃CH is produced in its second excited electronic state, as observed in Fig. 2. The width characterizing this peak can besides reflect some ro-vibrational excitation of the CH₃CH co-fragment, taking into account the Gaussian symmetric shape of the peak and the position of the maximum intensity. Some structure can indeed be guessed, in particular for CH₃CH₂. The corresponding vibrational frequencies of the CH₃CH fragment in its electronic ground state have been computed and are summarized in the ESI.† Among the large number of vibrational modes, we select the methyl deformation to highlight the probable vibrational excitation in ν = 1, as shown by a vertical bar in Fig. 2, although such vibrational excitation may be in another modes, in particular, the H deformation or the C–C stretch.

Similar experiments have been carried out using pyrolysis of n-propyl nitrite to produce cold ethyl radicals, as described by Fischer and co-workers,¹⁹ instead of in situ photolysis of ethyl iodide. In this case, only the central blot leading to a Boltzmann-type distribution in the TED was recovered while the narrow peak was not observed (not shown). The main difference between these two methods lies on the internal energy distribution of the radicals produced. While CH₃CH₂ radicals produced by pyrolysis are vibrationally cold, those formed by in situ photolysis of ethyl iodide are characterized by a significant internal energy, i.e. 〈E_int〉 = 1.27 eV,²³ as mentioned above. The initial ro-vibrational excitation of CH₃CH₂ in the present experiments favors indeed the appearance of the site-specific prompt H-atom elimination channel. Worth to mention at this point is the fact that, since H-atom distribution in Fig. 2 peaks at a total translational energy of ∼1.5 eV, the observation of the site-specific mechanism obeys to a threshold effect. The parent initial energy content added to the energy provided by the photolysis photon is barely enough to surpass the barrier to dissociate. Furthermore, due to the thermalizing effect of the non-adiabatic crossings – the available energy is transferred preferentially into the product internal degrees of freedom – little additional kinetic energy is expected to be communicated to the H and C₂H₄ products.

The angular distributions obtained by radial integration of the images are given by

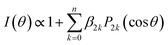where θ represents the angle between the photolysis laser and the fragment recoil velocity, β_2k are anisotropy parameters that reflect the dissociation dynamics and the photofragment polarization, and P_2k(cos θ) are 2k^th order Legendre polynomials. The number of necessary β_2k anisotropy parameters depends on both the number of photons involved in the multiphoton ionization detection step of the H-atoms, and the angular momentum of the species detected. In the present case, the H-atom images correspond to a secondary process in which ethyl radicals are photoexcited after dissociation of the ethyl iodide precursor. For all molecules, the central blot is characterized by a single β₂ parameter slightly positive, ranging around 0.2–0.4, while a β₂ around −0.1 describes the prompt dissociation process. In agreement with previous investigations,²³ the in situ photolysis of ethyl iodide produces ethyl radicals with an almost isotropic distribution, slightly perpendicular, as reflected by a reported β₂ around −0.1, due to an electronic predissociation mechanism. The angular distribution for the narrow peak seems then to mainly reflect the ethyl radical distribution arising from the initially excited ethyl iodide precursor. The small values of β₂ obtained reflect often the contribution of transitions to excited states of different symmetries, i.e., the measured β₂ is the convolution of several parallel and perpendicular transitions with different weights, or a long reaction time, the rotational motion of the molecule leading to a loss of angular information. This second effect may indeed explain the low values found for the central blot.

The experimental results presented here clearly highlight a prompt H-atom elimination channel which is site-specific from the C_α. In order to further understand the mechanism leading to this channel, high-level ab initio calculations have been performed. The computed excited states characterizing the UV absorption of ethyl radical are listed in Table 1. Vertical excitation energies (VEE) at the equilibrium geometry along with total transition dipole moments (TDM) for the absorption from the ground state are specified. Theoretical vertical excitations are compared as first approximation to the experimental transition energies,³² showing a reasonable agreement considering that vibrational zero point energy are not taken in account in the VEE. We note that to ensure homogeneity in the description of the excited states involved in all dissociation channels, all calculations have been carried out without taking into account any symmetry (see computational details). As observed in Table 1, three valence excited states, from now on valence-2A′, valence-1A′ and valence-1A′′ in order of increasing energy, lie above the 3p Rydberg state. In particular, two of them could be energetically populated following ∼201 nm excitation after in situ photolysis, although this is unlikely considering the particularly small TDMs characterizing these states.

Table 1 Computed vertical excitation energies (VEE) and transition dipole moments (TDM) for the first excited states in ethyl radical (from the ground state) compared to reported experimental values (ref. 32)

	VEE (eV)	TE (eV)	VEE (nm)	TE (nm)	TDM (debye)
	Theo.	Exp.	Theo.	Exp.	Theo.
X̃	0	0	0	0	—
Rydberg 3s	4.97	5.04	249	246.49	0.858
Rydberg 3p	5.75	6.05	216	204.93	0.697
Valence-2A′	6.81	—	182	—	0.125
Valence-1A′	7.15	—	173	—	0.002
Valence-1A′′	9.61	—	129	—	0.320

---

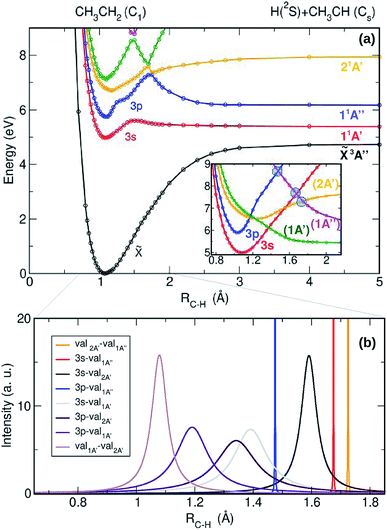
The adiabatic potential energy curves (PECs) computed as a function of the C–H bond distance leading to the H + CH₃CH dissociation limit, are presented in Fig. 3(a). In order to shed light on the intrinsic character of the electronic wavefunctions of the excited states and to estimate the intensities of the couplings between them, the adiabatic PECs have been diabatized following the scheme presented in ref. 25 and 28. The result of the diabatization of the computed PECs (inset in Fig. 3(a)) and the non-adiabatic coupling matrix elements (NACMEs) associated with the kinetic (derivative) couplings (Fig. 3(b)) are also depicted. In Fig. 3(a), the first excited state – the 3s Rydberg state (red curve) – presents a slightly bound shape with an exit barrier. Predissociation from this state would require to overcome a 0.7 eV energy barrier, similarly to the methyl radical,²⁵ although this predissociative channel has never been experimentally reported following ethyl radical photoexcitation. A similar bound shape is observed for the 3p Rydberg state (blue curve), characterized by an energy barrier around ∼1.2 eV. Taking into account the ≃1.3 eV of ro-vibrational initial energy of the ethyl radical in the present experiment, the total energy (∼7.4 eV) would allow to overcome this adiabatic energy barrier leading to prompt H-atom elimination into H + CH₃CH. In contrast, for cold ethyl radicals photoexcited at ∼201 nm, this prompt dissociation may be highly unfavoured. CH₃CH₂ would then preferentially undergo internal conversion to lower states (to the 3s Rydberg or to the ground state) followed by statistical dissociation.

Fig. 3 (a) Adiabatic potential energy curves as a function of the C–H distance leading to CH₃CH + H. Inset: Corresponding diabatic curves in the Franck–Condon region. Ground state: black line, 3s Rydberg state: red line, 3p Rydberg state: blue line, and valence states: yellow, green and magenta lines. The grey circles in the inset represent the conical intersections found between the indicated excited states. (b) Non-adiabatic coupling matrix elements (NACMEs) associated with the kinetics couplings, obtained from the diabatization procedure. The narrow NACMES 3p-1A′′ (blue), 3s-1A′′ (red) and 2A′-1A′′ (yellow) correspond to the conical intersections represented by the blue circles in the inset of panel (a) from left to right.

The adiabatic barrier for the 3p Rydberg state is nevertheless located in a region of strong interaction with two valence states, so that the diabatic picture along with the NACMEs may be more appropriate. In the diabatic representation, depicted in the inset of Fig. 3(a), the valence-1A′ state (green line) presents a repulsive character while the valence-2A′ state (yellow line) is still bound. These two valence states overlap now with the 3p Rydberg state and several curve crossings are observed. In Fig. 3(b), the NACMEs allow us to identify the presence of conical intersections versus non-adiabatic crossings. The latter are attributed to couplings, which are generally broad in the depicted adiabatic picture, associated with strong electronic couplings for a large number of geometries. In contrast, kinetic couplings (NACMEs) are very intense near conical intersections although very narrow, leading to very small electronic couplings. Three conical intersections have been identified and they are depicted in the inset of Fig. 3(a) by blue circles. In addition, non-adiabatic couplings are present between the 3p Rydberg state and the valence-2A′ and valence-1A′ states. It is well known that conical intersections are not a single point but rather a multidimensional seam.³³ Our 1D model allows us to spot only 1 point of this multidimensional seam. In order to confirm their existence and find their lower energy geometry at ab initio level (i.e., the geometry where the minimal energy of the seam is found) the three conical intersections have been optimized at CASSCF level and the obtained geometries are presented in the ESI (see Fig. S3†).

As noted above, the two valence states are not initially populated considering the low values of the computed TDMs. The bound valence-2A′ state (yellow line) and the valence-1A′ state (green line) may nevertheless be populated by fast non-adiabatic crossings at a total energy of ∼6.5 eV from the 3p Rydberg state. According to the Landau–Zener model,^34,35 the diabatic transition probability is proportional to the V/ΔE ratio, where V is the (electronic) potential coupling intensity and ΔE is the adiabatic potential energy difference. Although for such diabatic transition the electronic coupling is strong, its efficiency depends then on the shape of the adiabatic curves and how fast ΔE varies with R_C–H. Taking into account the remarkable distortion of the 3p state in the adiabatic representation (see Fig. 3(a)), where the 3p (blue), 2A′ (yellow) and 1A′ (green) curves are involved in a relatively large region of R_C–H distances, along with the width of the kinetic coupling (see Fig. 3(b), 3p-val_2A′ purple line and 3p-val_1A′ violet line), which is usually a good indicator of the range of efficiency, we can assume that the diabatic transition probabilities from the 3p state into the valence-2A′ and valence-1A′ states are significant. Further dissociation on this valence-2A′ state (yellow line) via the conical intersection lying at ∼7.3 eV and R_C–H ∼ 1.7 Å, would then lead to H-atom prompt elimination into CH₃CH + H, visualized as a narrow isotropic ring in the image depicted in Fig. 2. In contrast, internal conversion to lower electronic states and statistical dissociation would be expected from the populated valence-1A′ state (green line), contributing to the Boltzmann-type distribution observed as a central blot in the image.

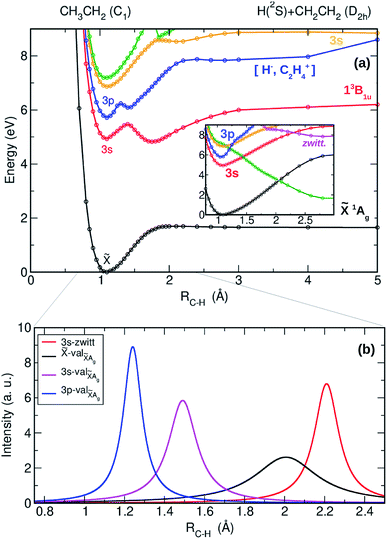
The adiabatic PECs have also been computed as a function of the C–H distance leading to H + CH₂CH₂ and are presented in Fig. 4(a) along with the result of the diabatization (see inset) and with the NACMEs (Fig. 4(b)). A complex interplay between the Rydberg states of the ethyl radical with the valence states converging to the first electronic state of ethylene, and with ion pair states leading to zwitterionic excited states of ethylene³⁶ characterizes the photochemistry leading to the H + CH₂CH₂ channel. All the electronic states, including the 3s and 3p Rydberg states, and the two lowest valence states present a pronounced bound shape. Based on the adiabatic representation, a prompt dissociation appears highly unlikely. Internal conversion to highly ro-vibrationally excited levels of lower electronic states and slow dissociation is more probable in this case.

Fig. 4 (a) Adiabatic potential energy curves as a function of the C–H distance leading to CH₂CH₂ + H. Inset: Corresponding diabatic curves. Ground state: black line, 3s Rydberg state: red line, 3p Rydberg state: blue line and valence states: yellow and green lines. Ion-pair state correlating with zwitterion state: magenta line. (b) Non-adiabatic coupling matrix elements (NACMEs) associated with the kinetics couplings obtained from the diabatization procedure. NACMEs are shown for 3s-zwitt (red-magenta crossing in inset of panel (a)), X̃-val_X̃Ag (black-green crossing), 3s-val_X̃Ag (red-green crossing) and 3p-val_X̃Ag (blue-green crossing).

The result of the diabatization, depicted in the inset of Fig. 4(a), shows nevertheless a first probable diabatic transition from the 3p state into the second excited valence state (green line). This will certainly lead to some transfer of population from the 3p state into the 3s state and by no means to fast dissociation into CH₂CH₂ + H. Taking into account the Landau–Zenner model, the diabatic transition from the 3p into 3s seems indeed favoured by a small ΔE, while the gap between the 3s and the ground state – high ΔE – impede the diabatic transition. These results demonstrate that dissociation into H + CH₂CH₂ occurs only via slow internal conversion and statistical dissociation, contributing thus to the Boltzmann distribution observed in the experiments.

Further dissociation of the ethylidene (CH₃CH) co-fragment formed from the C_α H-atom elimination of the ethyl radical has been evaluated. Its PECs have been computed as a function of the C–H distance correlating to CH₃C + H and CH₂CH + H as well as for the C–C cleavage leading to CH₃ + CH. The first electronic states of CH₃CH, X̃³A′, 1 ¹A′ and 1 ¹A′′, are noticeably bounded and non-dissociative. The secondary formation of H-atoms is thus certainly improbable while an isomerization process of ethylidene may occur in agreement with literature, suggesting a rapid rearrangement into CH₂CH₂.^37,38

On the other hand, the possible dynamics of the photoexcited ethyl radical involving a bridged C_2v geometry and subsequent dissociation has been also considered. The calculations performed demonstrate a slight stabilization of the 3p Rydberg state in C_2v, but the absence of dissociation from this latter, highlighting indeed favorable H-atom scrambling; the molecule going back and forth from C_s symmetry to C_2v symmetry, allowing H-atom exchange from CH₃CH₂ to CH₂CH₃ prior to slow dissociation. This results will be nevertheless further discussed elsewhere.

The present results demonstrate that while one ∼201 nm photon excitation of cold ethyl radicals leads to a complete scrambling and to slow unimolecular dissociation, the initial internal energy provided by in situ photolysis of the ethyl iodide precursor operates as a doorway to a site-specific prompt H-atom elimination channel. The former, i.e., unimolecular dissociation, takes place through internal conversion to lower electronic states in ro-vibrationally highly excited levels. The available energy is hence randomly distributed among the internal degrees of freedom while the system attempts to reach a convenient reaction coordinate to dissociate, leading thus to a complete intramolecular vibrational energy redistribution (IVR) and to Boltzmann-type fragment translational distributions. In contrast, the latter arises from a prompt predissociation mechanism involving a first fast internal conversion and a conical intersection mediating the dissociation.

Such prompt predissociation mechanism would usually produce recoiled H-atom distributions characterized by a highly averaged translational energy and a broad distribution due to the significant transfer of the available energy into internal energy of the polyatomic co-fragment. The presence of a conical intersection may nevertheless favour a certain degree of vibrational selectivity reflected in the measured translational energy distribution, which shows for instance a progression in a certain preferred vibrational mode. Investigations by Ashfold and co-workers demonstrated indeed a remarkably high vibrational selectivity in the photodissociation of phenol, where specific vibrational modes channel the reaction through the conical intersection yielding dissociation.³⁹ Such vibrational promoting modes, skeletal modes of the parent molecule for instance, enable the absorption process and are largely preserved during the parent to product evolution, acting as spectators with respect to the reaction coordinate.

Strikingly, the observed H atom velocity distribution is not smeared by the spread of initial velocities and it only partially reflects the spread of internal energies of the C₂H₅ precursors. The sharp peak observed in the TED (associated with the narrow ring in the image) for the C_α H-atom elimination channel in the present case (see Fig. 2) reflects the high vibrational selectivity which is attained during the reaction pathway and the role of a vibrational promoting mode. The conical intersection mediating the reaction is closely related to this mode and dictates the dynamics occurring before, during and after the passage. During the absorption step, such vibrational promoting mode is indeed characterized by larger Franck–Condon factors, while it presents the appropriate configuration for passing the conical intersection. It is particularly interesting and somewhat unexpected that such information survives during the 3p-2A′ non-adiabatic transition, where some IVR of the available energy would have been predicted. Bar and co-workers have previously reported mode-dependent enhancement of the photodissociation and photoionization of methylamine (CH₃NH₂).⁴⁰ The methyl umbrella (bending) mode, acting as a vibrational promoting mode, was shown to survive IVR on a considerably long time scale (nanoseconds). In our case, the initial internal energy of the ethyl radical leads, during the photon absorption, to an enhanced excitation on a specific vibrational mode which survives during the electronic relaxation after predissociation, and guides efficiently the radical into dissociation through the conical intersection. Considering the strong distortion of CH₂ in the optimized geometry of the third conical intersection (C3 in ESI†), where the CCH angles are found to be 162.3 and 106.6 degrees, we can propose the CH₂ rock mode as a likely promoting mode that favoured the transition through the C3 conical intersection.

4 Conclusions

Velocity map images for hydrogen atoms detected in the photodissociation of the isotopologues CH₃CH₂, CH₃CD₂ and CD₃CH₂ from the 3p Rydberg state at ∼201 nm, and the corresponding translational energy and angular distributions, have been presented and discussed along with ab initio high-level calculations of potential energy curves and non-adiabatic coupling matrix elements (NACMEs) describing the different possible hydrogen-atom eliminations channels. Remarkably, we have demonstrated that the photoreactivity of the ethyl radical is controlled by means of an initial ro-vibrational energy content of the generated parent radical arising from the in situ photodissociation of the precursor molecule (ethyl iodide). The photoexcited ro-vibrationally hot radicals lead to a surprisingly prompt site-specific (carbon α) hydrogen-atom elimination, which is characterized by a relatively narrow translational energy distribution, occurring through a fast and efficient predissociation from the 3p Rydberg state to a valence bound state, followed by dissociation via a conical intersection. This novel site-specific hydrogen-atom elimination photochemical mechanism reveals the role of an effective promoting vibrational mode of the parent radical, which is certainly responsible for an efficient vibrationally selective crossing through the conical intersection, leading unexpectedly to a narrow distribution of speeds of the hydrogen atoms. More experiments on similar hydrocarbon radicals would be necessary to confirm the universal character of this novel prompt site- and vibrationally-specific hydrogen-atom elimination photochemistry.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. V. C. and S. M. P. contributed equally to the paper. D. V. C. thanks a contract from Spanish MINECO under the FPI predoctoral program. S. M. P. acknowledges financial support from a postdoctoral contract of the Regional Government of Madrid (Spain) (Grant PEJD-2016/IND-3217). A. B. acknowledges the financial support of the Tunisian Ministry of Higher Education, Scientific Research, and Technology, of the Short Term Scientific Mission (STSM) program of the COST Action CM1401, and of LSAMA at the Université de Tunis El Manar, that made possible research visits to the Instituto de Física Fundamental (CSIC, Spain). This work has been financed by the Spanish MINECO (Grants No. CTQ2015-65033-P, FIS2016-76418-P and FIS-2016-77889-R) and EU COST Action CM1401. This research has been carried out within the Unidad Asociada Química Física Molecular between the Departamento de Química Física of Universidad Complutense de Madrid and CSIC. The facilities provided by the Centro de Láseres Ultrarrápidos at Universidad Complutense de Madrid are gratefully acknowledged. The Centro de Supercomputación de Galicia (CESGA, Spain) and CTI (CSIC) are acknowledged for the use of their resources.

Notes and references

1. G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158.
2. W. Domcke, D. R. Yarkony and H. Köppel, Conical intersections: theory, computation and experiment, World Scientific, 2011, vol. 17.
3. B. G. Levine and T. J. Martínez, Annu. Rev. Phys. Chem., 2007, 58, 613–634.
4. D. Polli, P. Altoe, O. Weingart, K. M. Spillane, C. Manzoni, D. Brida, G. Tomasello, G. Orlandi, P. Kukura, R. A. Mathies, M. Garavelli and G. Cerullo, Nature, 2010, 467, 440.
5. Y. L. Yung, M. Allen and J. P. Pinto, Astrophys. J., Suppl. Ser., 1984, 55, 465–506.
6. E. H. Wilson and S. K. Atreya, J. Geophys. Res.: Planets, 2004, 109, E6.
7. C. J. Bennett, C. S. Jamieson, Y. Osamura and R. I. Kaiser, Astrophys. J., 2006, 653, 792.
8. J. Warnatz, Combustion Chemistry, Springer, New York, NY, 1984, pp. 197–360.
9. W. L. Hase and H. B. Schlegel, J. Phys. Chem., 1982, 86, 3901–3904.
10. W. L. Hase, H. B. Schlegel, V. Balbyshev and M. Page, J. Phys. Chem., 1996, 100, 5354–5361.
11. M. A. Hanning-Lee, N. J. B. Green, M. J. Pilling and S. H. Robertson, J. Phys. Chem., 1993, 97, 860–870.
12. Y. Feng, J. T. Niiranen, A. Bencsura, V. D. Knyazev, D. Gutman and W. Tsang, J. Phys. Chem., 1993, 97, 871–880.
13. J. A. Miller and S. J. Klippenstein, Phys. Chem. Chem. Phys., 2004, 6, 1192–1202.
14. J. L. Brum, S. Deshmukh and B. Koplitz, J. Chem. Phys., 1990, 93, 7504–7505.
15. J. L. Brum, S. Deshmukh, Z. Wang and B. Koplitz, J. Chem. Phys., 1993, 98, 1178–1192.
16. Z. Min, R. Quandt and R. Bersohn, Chem. Phys. Lett., 1998, 296, 372–376.
17. T. Gilbert, T. L. Grebner, I. Fischer and P. Chen, J. Chem. Phys., 1999, 110, 5485–5488.
18. G. Amaral, K. Xu and J. Zhang, J. Chem. Phys., 2001, 114, 5164–5169.
19. M. Steinbauer, J. Giegerich, K. H. Fischer and I. Fischer, J. Chem. Phys., 2012, 137, 014303.
20. J. M. Hostettler, A. Bach and P. Chen, J. Chem. Phys., 2009, 130, 034303.
21. A. F. Wagner, L. A. Rivera-Rivera, D. Bachellerie, J. W. Perry and D. L. Thompson, J. Phys. Chem. A, 2013, 117, 11624–11639.
22. A. Matsugi, J. Phys. Chem. Lett., 2013, 4, 4237–4240.
23. S. Marggi Poullain, P. Recio, D. V. Chicharro, L. Rubio-Lago, J. González-Vázquez and L. Bañares, Phys. Chem. Chem. Phys., 2019 10.1039/C8CP06482B.
24. L. Rubio-Lago, A. García-Vela, A. Arregui, G. A. Amaral and L. Bañares, J. Chem. Phys., 2009, 131, 174309.
25. S. Marggi Poullain, D. V. Chicharro, A. Zanchet, M. G. González, L. Rubio-Lago, M. L. Senent, A. García-Vela and L. Bañares, Phys. Chem. Chem. Phys., 2016, 18, 17054–17061.
26. V. Papadakis and T. N. Kitsopoulos, Rev. Sci. Instrum., 2006, 77, 083101.
27. H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz, P. Celani, T. Korona, R. Lindh, A. Mitrushenkov, G. Rauhut, K. R. Shamasundar, T. B. Adler, R. D. Amos, A. Bernhardsson, A. Berning, D. L. Cooper, M. J. O. Deegan, A. J. Dobbyn, F. Eckert, E. Goll, C. Hampel, A. Hesselmann, G. Hetzer, T. Hrenar, G. Jansen, C. Köppl, Y. Liu, A. W. Lloyd, R. A. Mata, A. J. May, S. J. McNicholas, W. Meyer, M. E. Mura, A. Nicklass, D. P. O'Neill, P. Palmieri, D. Peng, K. Pflüger, R. Pitzer, M. Reiher, T. Shiozaki, H. Stoll, A. J. Stone, R. Tarroni, T. Thorsteinsson and M. Wang, MOLPRO, version 2015.1, a package of ab initio programs, 2015.
28. A. Zanchet, L. Bañares, M. L. Senent and A. García-Vela, Phys. Chem. Chem. Phys., 2016, 18, 33195–33203.
29. V. Barone, J. Chem. Phys., 2005, 122, 014108.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, revision A 1, Gaussian, 2010.
31. C. Möller and M. Plesset, Phys. Rev., 1934, 46, 618.
32. H. R. Wendt and H. E. Hunziker, J. Chem. Phys., 1984, 81, 717–723.
33. A. Toniolo, M. Ben-Nun and T. J. Martínez, J. Phys. Chem. A, 2002, 106, 4679–4689.
34. C. Zener, Proc. R. Soc. London, Ser. A, 1932, 137, 696–702.
35. L. D. Landau, Phys. Z. Sowjet., 1932, 2, 46.
36. K. Alnama, S. Boyé-Péronne, A.-L. Roche and D. Gauyacq, Mol. Phys., 2007, 105, 1743–1756.
37. J. J. Lin, C. C. Wang, Y. T. Lee and X. Yang, J. Chem. Phys., 2000, 113, 9668–9677.
38. M. Barbatti, J. Paier and H. Lischka, J. Chem. Phys., 2004, 121, 11614–11624.
39. M. N. R. Ashfold, B. Cronin, A. L. Devine, R. N. Dixon and M. G. D. Nix, Science, 2006, 312, 1637–1640.
40. A. Golan, S. Rosenwaks and I. Bar, J. Chem. Phys., 2006, 125, 151103.

---

Footnotes

† Electronic supplementary information (ESI) available: H-Atom action spectra from the CH₃CH₂I, CH₃CD₂I and CD₃CH₂I precursors photodissociation as a function of the excitation wavelength as well as the D-atom action spectrum for CD₃CD₂I, computed harmonic and anharmonic corrected vibrational frequencies for CH₃CH₂, CH₂CH₂ and CH₃CH in their respective ground electronic states and zero-point energies and dissociation energies for all isotopomers, and geometries characterizing the conical intersections found. See DOI: 10.1039/c9sc02140j

‡ These authors contributed equally to this work.

---