Open Access Article
Open Access ArticleStructure and effective charge characterization of proteins by a mobility capillary electrophoresis based method
Wenjing
Zhang
 a,
Haimei
Wu
a,
Rongkai
Zhang
a,
Xiang
Fang
b and
Wei
Xu
a,
Haimei
Wu
a,
Rongkai
Zhang
a,
Xiang
Fang
b and
Wei
Xu
 *a
*a
aSchool of Life Science, Beijing Institute of Technology, No. 5 South Zhongguancun Street, Haidian Dist, Beijing, China. E-mail: weixu@bit.edu.cn
bNational Institute of Metrology, No. 18, Bei San Huan Dong Lu, Chaoyang Dist, Beijing, China
First published on 3rd July 2019
Abstract
Measuring the conformations and effective charges of proteins in solution is critical for investigating protein bioactivity, but their rapid analysis remains a challenging problem. Here we report a mobility capillary electrophoresis (MCE) based method for the rapid analysis of protein stereo-structures and effective charges in different solution environments. With the capability of mixture separation, MCE measures the hydrodynamic radius of a protein through Taylor dispersion analysis and its effective charge through ion mobility analysis. The experimental results acquired from MCE are then utilized to restrain molecular dynamics simulations, so that the most probable conformation of that protein can be obtained. As proof-of-concept demonstrations, the charge states and structures of five proteins were analyzed under close to native environments. The conformation transitions and charge state variations of bovine serum albumin and lysozyme under different pH conditions were also investigated. This method is promising for high-throughput protein analysis, which could potentially be coupled with mass spectrometry for investigating protein stereo-structures and functions in top-down proteomics.
Introduction
Proteins perform a vast number of biological functions in living organisms.1,2 Besides its primary sequence, the function of a protein greatly depends on its stereo-structure,3–5 as well as its effective charge in solution.6,7 The protein conformation and effective charge could also influence each other. To understand the working mechanism of a biosystem or the physiological functions of proteins,8,9 it is essential to identify not only the expression level of proteins, but also their structures. High-resolution protein structure analytical techniques, such as X-ray diffraction,10 nuclear magnetic resonance (NMR)11 and electron microscopy,12 are available. To obtain a high-resolution protein structure, high abundance samples are typically required and the whole process is time-consuming, which limits these techniques from use in large-scale protein analysis.13,14 On the other hand, large-scale protein analysis has been carried out in proteomics, in which the entire set of proteins in an organism or biosystem are studied typically through the combination of liquid chromatography (LC) or capillary electrophoresis (CE) with mass spectrometry (MS).15–17 Protein primary sequences and post-translational modifications (PTMs) could be resolved through tandem MS.18 However, protein stereo-structure information,19 as well as its effective charge in solution, are mostly missing. As a result, biological phenotypic variances caused by protein stereo-structural differences would be masked.To distinguish and separate molecular isoforms, ion mobility spectrometry (IMS) is increasingly integrated into MS instruments.20 Collision cross sections (CCSs) of ions21 after gasification and ionization could be obtained. Ion CCSs22 could reflect ion structures in the gas phase,23,24 which may not have a direct relationship with their corresponding structures in solution.25 Protein charge states in the gas phase26 also have no correlation with its effective charge in solution.7 Taylor dispersion analysis (TDA) is a liquid-phase structural analysis technique, through which the diffusion coefficient and hydrodynamic radius of a particle or molecule can be measured.27 In TDA experiments, a constant pressure was applied to drive analytes in a laminar flow, which could easily be realized on a CE instrument.28 Since electroosmotic flow (EOF) in a CE experiment would destroy the laminar flow field distribution,29 no electric field was applied in conventional TDA methods. Therefore, conventional TDA methods do not have mixture separation/analysis capabilities.30 To address this problem, a time-sharing technique was proposed by Billy A. Williams and Gyula Vigh, in which analytes were first separated by operating a CE instrument in a conventional CE mode and then structure analyzed by tuning the instrument into the TDA mode. With this two-step operation, the hydrodynamic radiuses of different molecules in a mixture could be measured.31
Recently, mobility capillary electrophoresis (MCE) was proposed to achieve ion separation and hydrodynamic radius measurement simultaneously.32,33 In MCE experiments, ions were driven in a constant flow34,35 and separated by an electric field, making MCE a liquid-phase analogue of IMS. With minimized EOF,36–38 ion electrophoresis migration could be precisely determined, and the ion hydrodynamic radius was calculated from ion migration time. After the spheroidal approximation, the ion hydrodynamic radius of a protein obtained from MCE defines a mathematical relationship between the length and diameter of this spheroid, which could then be applied to select the most probable protein conformation in solution from molecular dynamics (MD) simulation results. However, in previous studies, the ion effective charge state needed to be estimated from theoretical analysis, which limited its application in terms of both solution and analyte categories. Specifically, only proteins in a solution with no or very low salt concentrations can be analyzed. However, salts are present in many practical biosystems, and their presence may help in maintaining the native conformations of proteins. Furthermore, the accuracy of protein charge state estimation also limits the accuracy of ion hydrodynamic radius calculation.32,33 In fact, the protein charge state is an important factor affecting its activity and solubility,39 and it may affect the protein conformation in turn.40–42 Its measurement in solution is a challenging problem in itself.43 Through chemical modifications, the protein charge ladder method has been developed to study the effective charge of each protein.6,44 The capillary isotachophoresis (ITP) method was also developed to determine the effective charges of polymers and polycationic peptides.45–47 In summary, although the established structural biology technologies could provide high resolution protein structure information, they have relatively low throughput. High throughput proteomic methods could provide little protein stereo-structure information.48 Additional methods are essential for bridging this gap.
To overcome these limitations, a new MCE based method was proposed in this work. As the first attempt to integrate TDA into MCE experiments, this method allows ion separation, hydrodynamic radius and effective charge measurements in different solution environments to be achieved in a single experiment. Without the need for any chemical modification, ion dispersion analysis was first performed on the shape of a peak to obtain the ion hydrodynamic radius; ion mobility analysis was then carried out on peak retention time to acquire the ion effective charge. As proof-of-concept demonstrations, peptide and protein mixtures were studied. The ion hydrodynamic radiuses obtained using this method were first confirmed with conventional TDA results. The isoelectric point of a protein estimated using this MCE based method also agrees with that in the literature. Next, by coupling with MD simulations, the native conformations49 of three proteins were first analyzed with results confirmed by protein data bank (PDB) results. Unfolding and structural variations of two other proteins induced by pH changes were also explored.50
Theory
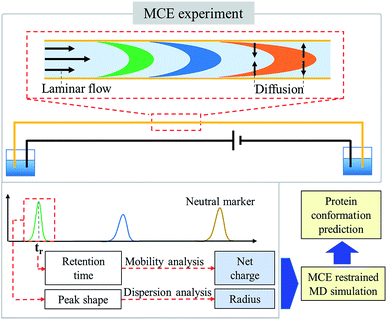
In an MCE experiment as shown in Fig. 1, ions in a constant liquid flow will experience an electric field force.32 The constant liquid flow is maintained by applying a constant pressure over the separation channel. Coated silica capillaries were used as the separation channel, so that electroosmotic flow (EOF) was minimized and not considered.38 As a result, a stable laminar flow is formed within the separation channel, which is the same as that in a TDA experiment.51,52 Different from a TDA experiment, a separation voltage was also applied during an MCE experiment. In the presence of both the electric field and the laminar flow field, analyte ions could be separated based on their charge states and hydrodynamic radiuses.53–55 To accurately measure the hydrodynamic radius and effective charge of an ion,56 four steps were carried out, including ion velocity distribution analysis, diffusion coefficient calculation, temperature and viscosity correction, and ion effective charge calculation, in which the TDA57–59 and electrokinetic dispersion (EKD) theories54,55 were applied.Ion velocity distribution analysis
By applying a constant pressure, a laminar flow is expected within the silica capillary. The velocity profile (v(r)) has a parabolic shape over the cross section of the capillary.60,61| v(r) = vm(1 − r2/Rc2) | (1) |
| u(r) = v(r) + qU/(Lξ) | (2) |
The second term in eqn (2) is a constant for the same ion species. Eqn (2) shows that different ion species would have different velocity profiles, and thus they could be separated. Furthermore, for each type of ion, its velocity distribution in MCE experiments also has a parabolic shape, which is the same as the velocity profile in TDA experiments. Therefore, ion dispersion in the radial direction in an MCE experiment is also the same as that in a TDA experiment.
Diffusion coefficient calculation in MCE
With the same ion velocity profile, similar derivation procedures as in TDA could be applied in the dispersion coefficient calculation in MCE experiments. Developed by Westhaver,62,63 Taylor,64 and Aris,65 the TDA approach was further studied by Datta and Kotamarthi (1990) to obtain the following electrokinetic dispersion coefficient (Ki) expression54,55 for the general case involving both pressure driven and electroosmotic flows:| Ki = D + Rc2(vp2 + ∂2vpveo + ∂3veo2)/(48D) | (3) |
| Ki = D + Rc2vp2/(48D) | (4) |
Under the same assumption as in TDA that the ion dispersion along the capillary axis is negligible, which is D ≪ Rc2vp2/(48D),57
| Ki = Rc2vp2/(48D) | (5) |
Utilizing the fact that the ion dispersion in the radial direction in an MCE experiment is the same as that in a TDA experiment, the recorded peak should have a Gaussian distribution. The peak arrival time (or retention time, tr) and temporal standard deviation (σ) of the peak55 could be used to calculate its electrokinetic dispersion coefficient (Ki):
| σ2 = 2Kitr/u2 | (6) |
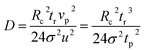 | (7) |
As shown in eqn (7), the ion diffusion coefficient could be obtained by measuring its peak retention time and temporal standard deviation of the peak, but it also requires introducing a neutral marker and measuring its retention time. Subsequently, the protein hydrodynamic radius (Rh) could be calculated from the Stokes equation:
| Rh = kBT/(6πηD) | (8) |
Temperature and viscosity correction
With the introduction of a separation voltage into the MCE system, the effects of thermal heating68,69 need to be considered and corrected for before we can accurately calculate the ion hydrodynamic radius. Although most commercial CE instruments have temperature control, the heat generated inside the capillary may not be conducted instantaneously, and a higher temperature may be present inside the capillary.70 In turn, temperature also affects the viscosity of the solvent, which is another important parameter when calculating the ion hydrodynamic radius. Since a neutral marker is present in the system in every MCE run, temperature over viscosity in every MCE run was corrected for as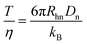 | (9) |
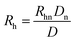 | (10) |
It should be noticed that the average thermal effect was corrected for using the neutral marker in this study. Spatially varying temperature fields were not considered.
Ion effective charge calculation
After determining the hydrodynamic radius of an ion, the effective charge of that ion could then be obtained by performing mobility analysis of ion retention time (tr) as shown in Fig. 1. Ion retention time is determined from the ion effective charge (q) and the ion hydrodynamic radius,| Lt = (vp + qU/(Lξ))tr | (11) |
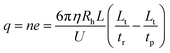 | (12) |
MCE restrained protein structure modelling
As demonstrated in previous publications,32,33 MCE based experimental results could be used as a selection rule for MD simulations to predict the most probable protein structures in solution. However, the previous method requires the estimation of ion charge states before the ion hydrodynamic radius could be obtained. Charge states of proteins were estimated through pKa calculations. Theoretical charge state calculation was heavily limited to solvents with no salt or very low salt concentrations. Nevertheless, an appropriate salt concentration is essential in terms of maintaining the native structures of biomolecules. The method proposed in this study could measure both the hydrodynamic radius and effective charge of a biomolecule, and it could work under different salt and pH conditions. After obtaining the ion hydrodynamic radius, similar procedures could be carried out, including spheroid approximation and matching with MD simulations, so that the most probable protein conformations under different solvent conditions could be obtained.Experimental section
Chemicals
Peptides bradykinin and VEALYL (pentapeptide) were synthesized by SBS Genetech Co. Ltd. (Beijing, China). All proteins including insulin, cytochrome C, ribonuclease A (RNase A), lysozyme and bovine serum albumin (BSA) were purchased from Sigma Aldrich (St. Louis, MO, USA). Sodium dihydrogen phosphate dihydrate (NaH2PO4·2H2O), di-sodium hydrogen phosphate (Na2HPO4·12H2O), sodium chloride (NaCl), citric acid monohydrate (C6H8O7·H2O) and phenol were purchased from Aldrich Chemical Co. (Milwaukee, WI). Pure water used in this work was purchased from Wahaha company (Hangzhou, China).The above chemicals were used for the preparation of sample and buffers. Phosphate buffer with pH 7 was prepared by mixing 6.1 mL of 0.2 mol L−1 Na2HPO4 and 3.9 mL of 0.2 mol L−1 NaH2PO4. Disodium hydrogen-phosphate citric acid buffers were also prepared to set the pH values at 2.2, 3.4, 5, 6 and 7. The disodium hydrogen-phosphate citric acid buffers with pH 2.2, 3.4, 5, 6, and 7 were prepared by the mixing of 0.40 mL, 5.70 mL, 10.30 mL, 12.63 mL and 16.47 mL of 0.2 mol L−1 Na2HPO4 with 10.60 mL, 14.30 mL, 9.70 mL, 7.37 mL and 3.53 mL of 0.1 mol L−1 C6H8O7, respectively. These buffers were diluted 10 times to dissolve peptides and proteins to their final concentrations. Phenol was selected as the neutral marker to calculate the retention time driven by pressure, and it was also used to correct for temperature and viscosity variations. 1/1000 (volume ratio) phenol was added in every sample solution, unless otherwise specified.
MCE experiment
A commercial Lumex CE system equipped with a UV detector (model Capel 105M, St. Petersburg, Russia) was used to perform MCE experiments. All capillaries used in the MCE experiment were coated capillaries obtained from Sino Suntech (Hebei, China), which have stable neutral polymer coatings (poly N-isopropyl-acrylamide, PAM). Capillaries with 75 μm id, 60 cm total length, and 50 cm effective length were used. Before each working day, the capillary should be rinsed with water for 10 min, and then rinsed with the buffer solution for 10 min. The capillary was flushed with the buffer for 5 min between all of the runs. Sample injection was performed using a pressure of 50 mbar for 5 s. Most experiments in this paper use 50 mbar to maintain laminar flow in the separation channel and 10 kV to separate ions, unless otherwise specified. The UV detector works at a wavelength of 214 nm. 25 °C was set for the capillary during experiments.MD simulation
MD simulations were performed using the GROMOS54A7 force field72 in GROMACS 2016.1.73 The initial structure of a protein was obtained from the RCSB Protein Data Bank (PDB ID: 1APH; 1AKK; 1RUN; 4F5S; 1GXV). pKa calculations were performed with PROPKA.74,75 The systems were placed in a cubic box, solvated with explicit simple point charge (SPC) model water molecules.76 The counter ions (chloride at pH 7, formate at pH 3) were added as necessary to ensure system neutrality. The model was then energetically stabilized by the steepest descent algorithm, followed by an equilibration for at least 1 ns in water at 300 K. Periodic boundary conditions were used with a 1.4 nm cut off for non-bonded interactions. Long-range electrostatic corrections were taken into account by the particle mesh Ewald method.77 The overall simulation window was 100 ns. The root-mean-square deviation (RMSD) of the radius of gyration was monitored throughout all simulations.Results and discussion
Method validation
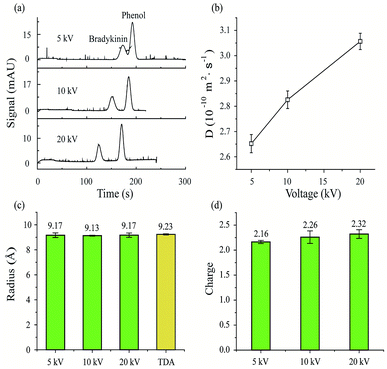
First, MCE experiments were carried out for a peptide (bradykinin, 0.24 μmol mL−1) by applying different separation voltages (5, 10 and 20 kV). The phosphate buffer was used as the running buffer (20 mM, pH 7). After sample injection (50 mbar, 5 s), a pressure of 50 mbar was then applied to generate the constant liquid flow during MCE separation processes. Phenol (1/4000, volume ratio) was used as the neutral marker. As shown in Fig. 2a, the bradykinin peak would separate further away from the phenol peak with increased separation voltages. Retention time variation also exists for phenol peaks among experiments. Theoretically, the retention time of the phenol peak should remain the same in all experiments, because phenol molecules are not affected by electric fields. Since EOF was minimized in this study, voltage induced thermal heating is believed to be the predominant reason for this neutral marker retention time variation. At higher temperatures, the viscosity of the solvent decreases, which would result in an increased solvent flow rate. In turn, the results suggest that temperature and viscosity corrections are important in MCE experiments.Eqn (7) was then applied to calculate the diffusion coefficients of bradykinin in these three experiments. As plotted in Fig. 2b, bradykinin has larger diffusion coefficients at elevated voltages, which agrees with the fact that bradykinin ions would have stronger dispersion at higher temperatures in a solvent with lower viscosity.69 After the temperature and viscosity correction, Fig. 2c and d plot the hydrodynamic radius and effective charge of bradykinin, which were calculated using eqn (10) and (12), respectively. Although the diffusion coefficient of bradykinin varies under different experimental conditions, the hydrodynamic radius (Rh) and its effective charge number (n) remain relatively unchanged. The calculated Rh and n are 9.17 ± 0.18 Å and 2.16 ± 0.03, 9.13 ± 0.04 Å and 2.26 ± 0.13, and 9.17 ± 0.17 Å and 2.32 ± 0.09 with an applied separation voltage of 5, 10 and 20 kV, respectively. Conventional TDA experiments were also carried out with the measured hydrodynamic radius of bradykinin plotted in Fig. 2c for comparison. An Rh of 9.23 ± 0.05 Å was obtained using the TDA method. The agreement between TDA and MCE results confirms the validity of this MCE based ion hydrodynamic radius measurement.
Mixture analyses
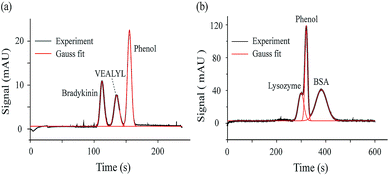
As one type of CE method, MCE could achieve mixture separation, which allows measuring the ion hydrodynamic radius and effective charge of each peak presented in the electropherogram. As proof-of-concept demonstrations, MCE analyses were performed for a two-peptide mixture and a two-protein mixture. Fig. 3a shows the separated electropherogram of bradykinin (0.24 μmol mL−1), VEALYL (pentapeptide, 0.71 μmol mL−1) and the neutral marker, phenol (1/4000, volume ratio). The phosphate buffer (20 mM, pH 7) was used as the running buffer. 50 mbar and 20 kV were applied as the driving and separation forces, respectively. Using eqn (10) and (12) in the theory section, Rh and n could be obtained as 9.10 ± 0.03 Å and 2.45 ± 0.02 for bradykinin, and 7.33 ± 0.23 Å and 0.84 ± 0.02 for VEALYL.For the mixture of lysozyme (0.36 μmol mL−1), BSA (0.07 μmol mL−1) and phenol (1/500, volume ratio), the same running buffer was used as in the previous case (phosphate buffer, 20 mM, pH 7), and 30 mbar and 10 kV were applied to drive and separate those molecules. As shown in Fig. 3b, the lysozyme peak appears before phenol, while the BSA peak appears after phenol. Since a positive voltage is applied and the electric field drives cations towards the UV detector, lysozyme is positively charged, while BSA is negatively charged under the experimental solvent conditions. After performing the peak fitting and ion retention time calculations (eqn (12)), it was found that lysozyme and BSA have an effective charge of 0.91 ± 0.04 and −4.38 ± 0.02, respectively. The calculated hydrodynamic radiuses of lysozyme and BSA are 19.01 ± 0.74 Å and 38.26 ± 0.86 Å, which agrees well with those acquired using TDA methods from the literature.78
Coupling with MD simulations for protein structure analyses
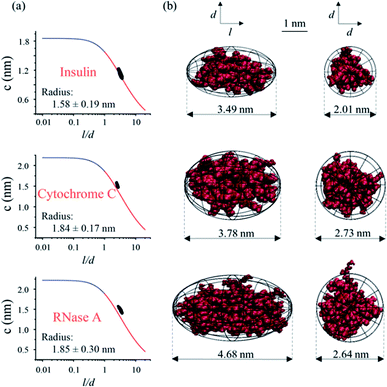
As depicted in Fig. 1, the hydrodynamic radius obtained from MCE experiments could be further utilized as a selection rule for MD simulations, so that the most probable protein conformation under experimental solvent conditions could be obtained.32,33 Briefly, a lot of possible conformations of a protein could be acquired from the MD simulation, and a selection rule is needed to pick out the most probable protein conformation. By assuming that this protein has a spheroidal shape and applying the Stokes flow equation at low Reynolds numbers, the ion hydrodynamic radius of this protein obtained from the MCE experiment defines a mathematical relationship between the spheroid length to diameter ratio (l/d) and its radius (c and d = 2c). This mathematical relationship (named as the shape restrain curve as shown in Fig. 4a) could then be used as the selection rule to find the most probable protein conformation from MD simulation results.As described earlier, the current method is applicable over a wide range of salt concentrations and pHs, which could cover the biological environments of most proteins. First, MCE experiments were performed for three proteins: insulin, cytochrome C and RNase A, respectively. Cytochrome C (2.26 μmol mL−1) was prepared in the sodium chloride solution (22 mmol L−1, pH 7); insulin (0.52 μmol mL−1) and RNase A (0.22 μmol mL−1) were prepared in the disodium hydrogen-phosphate citric acid buffers (∼10 mM, pH 2.2). 50 mbar and 10 kV were applied as the driving and separation forces with the addition of 1/1000 (volume ratio) phenol as the neutral marker. The hydrodynamic radiuses measured from MCE experiments of these three proteins are shown in Fig. 4a insets, and the effective charge of insulin, cytochrome C and RNase A was 3.92 ± 0.06, 3.91 ± 0.53 and 4.76 ± 0.09, respectively. MD simulations were also performed in parallel. The spheroid approximation was applied on both MCE results and simulation results as shown in Fig. 1. Fig. 4a plots the shape restrain curves obtained from MCE experiments, and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 simulated possible conformations for each protein (after spheroid approximation) were also plotted as black dots in these figures. The most probable protein conformation was selected if its corresponding dot has the closest distance from the shape restrain curve. Details about this spheroid approximation and matching processes could also be found in the literature.32,33,79 As shown in Fig. 4b, we described the conformations of these three proteins from side and top views respectively, and all of these three proteins have spheroid shapes but with different l and d values. The most probable conformations of these three proteins obtained using this MCE based method agree well with those from PDB.
000 simulated possible conformations for each protein (after spheroid approximation) were also plotted as black dots in these figures. The most probable protein conformation was selected if its corresponding dot has the closest distance from the shape restrain curve. Details about this spheroid approximation and matching processes could also be found in the literature.32,33,79 As shown in Fig. 4b, we described the conformations of these three proteins from side and top views respectively, and all of these three proteins have spheroid shapes but with different l and d values. The most probable conformations of these three proteins obtained using this MCE based method agree well with those from PDB.
Protein charge and conformation variations at different pHs
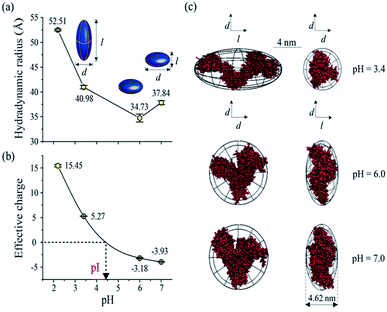
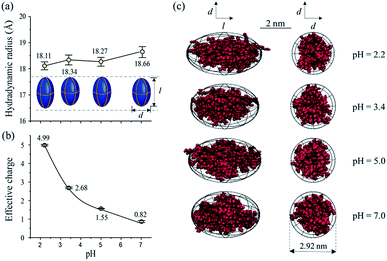
As one of the most important bio-environment parameters, pH has large effects on both charge states and conformations of proteins. As a result, proteins would show very distinct characteristics under different pH conditions, such as solubility and bio-activity. In reality, different proteins may have distinct tolerances to pH changes in solution. As a demonstration, the conformations and charge states of two proteins, BSA and lysozyme, were analyzed and compared under different pH conditions. BSA and lysozyme were diluted in the disodium hydrogen-phosphate citric acid buffers at different pH values. Four different pH conditions were tested for both BSA and lysozyme, and the final concentrations of BSA and lysozyme were 0.05 μmol mL−1 and 0.14 μmol mL−1, respectively, for all cases. After performing MCE experiments, it was found that the hydrodynamic radius and charge state of BSA generally increase at lower pHs (Fig. 5a and b). Its radius increases from 37.84 to 52.51 Å, while its charge state varies from −3.93 to 15.45. The effective charge of BSA would change from negative to positive at a pH of ∼4.4, which agrees well with the isoelectric point (pI) value of BSA in the literature.80,81 By coupling with MD simulation, the most probable conformations of BSA under different pH conditions were also obtained and are shown in Fig. 5c. Under pH neutral or 6.0 conditions, BSA exhibits the “basic” conformation.82 An unfolding process of BSA under lower pH conditions could be well observed. First BSA is a “Y” shaped “dish” like protein at pH 6.0 and 7.0, and its two branches would spread further from each other at lower pHs. With decreased pH, the net charge of BSA increases dramatically from ∼−3.93 to ∼+15.45. The increased number of charged residues would induce intense electrostatic forces within a BSA molecule, causing the collapse and/or unfolding of the molecule.83 As the solvent pH decreases to 3.4, it is found that this “Y” shaped “dish” like BSA would transform into a “V” shaped “rugby” like spheroid. Disulfide bonds and hydrophobic interactions within BSA would break together with reduced helical content, which causes BSA unfolding into the “F” conformation.82Lysozyme is an important immune related enzyme present in many body secretions, and it is known to be thermally stable. The crystal structure of lysozyme was clarified by Phillips et al. through X-ray analysis,84 and it has a spheroid shape. As shown in Fig. 6, the hydrodynamic radius of lysozyme remains relatively stable over the whole measured pH range (Fig. 6a). Although the effective charge of lysozyme also increases, the absolute increment is much smaller (from +0.82 to +4.99, Fig. 6b) when compared to that of BSA. Protein conformation prediction results show that lysozyme is a “rugby” shaped protein, and its conformation only has very small variations in terms of pH changes. With reduced effective charge variation, less intense electrostatic forces exist within lysozyme, and the 4 disulfide bonds within lysozyme are retained, which in turn helps in maintaining its stereo-structure at different pHs. The conformations of BSA and lysozyme under different pH conditions match well with those in the literature,82,85 suggesting that this MCE based method is a reliable method in terms of protein structure analysis under different solvent conditions.
Conclusions
A new MCE based method was proposed in this work to measure the hydrodynamic radiuses and effective charges of proteins under different solvent conditions. Without the need for chemical modifications, proteins in mixtures could be separated and analyzed in a single experiment. Using MCE experimental results as a selection rule for MD simulations, the most probable protein conformations could be acquired. This method has been demonstrated to analyze peptide and protein mixtures. The structures and charges of three proteins were analyzed under conditions close to their native pH. The effects of pH changes on protein conformation transitions and charge state variations were also explored for BSA and lysozyme. BSA and lysozyme react significantly differently to pH changes. Besides the large charge state variations, BSA shows a significant conformation variation from a “Y” shaped “dish” like protein to a “V” shaped rugby like protein, while lysozyme maintains a relatively stable rugby like shape. By using pressure to drive the liquid flow and minimizing the EOF in separation capillaries, an ordinary CE instrument could be used to perform these MCE based experiments. Furthermore, besides proteins, radiuses and net charges of other molecules, such as drugs, glycans, lipids and even nanoparticles86,87 could also be analyzed using this method. Compared to conventional structural biology technologies, low-resolution protein shape information is mainly obtained from MCE experiments, and MD simulations are required for protein conformation predictions. However, as a liquid-phase analogue of IMS, this MCE based method is rapid in terms of speed and has low sample consumption rates (nanoliter level), which makes it potentially applicable in top-down proteomics for large-scale protein structure and function investigations. For instance, a small fraction of a biological sample could be subjected to this MCE-based analysis first to rapidly pick out structurally abnormal proteins. The rest of the sample could then be subjected to a conventional structural biology analysis process to resolve the high-resolution structures of abnormal proteins identified in the previous MCE experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NNSFC (201827810, 61635003), and National Key Research and Development Plan (2018YFF0212500).References
- L. Jia, L. Zhang, C. Shao, E. Song, W. Sun, M. Li and Y. Gao, PLoS One, 2009, 4, e5146 CrossRef
.
- R. S. Lee, L. Zhang, A. Berger, M. G. Lawrence, J. Song, B. Niranjan, R. G. Davies, N. L. Lister, S. K. Sandhu, M. A. Rubin, G. P. Risbridger, R. A. Taylor, D. S. Rickman, L. G. Horvath and R. J. Daly, Neoplasia, 2019, 21, 389–400 CrossRef CAS
.
-
W. Bode, P. Schwager and R. Huber, Proteolysis and Physiological Regulation, 1976, vol. 11, pp. 43–76 Search PubMed
.
- J. D. Watson, R. A. Laskowski and J. M. Thornton, Curr. Opin. Struct. Biol., 2005, 15, 275–284 CrossRef CAS
.
- B. Over, P. Matsson, C. Tyrchan, P. Artursson, B. C. Doak, M. A. Foley, C. Hilgendorf, S. E. Johnston, M. D. Lee IV and R. J. Lewis, Nat. Chem. Biol., 2016, 12, 1065 CrossRef CAS
.
- I. Gitlin, J. D. Carbeck and G. M. Whitesides, Angew. Chem., Int. Ed., 2006, 45, 3022–3060 CrossRef CAS
.
- C. T. Zahler and B. F. Shaw, Chem.–Eur. J., 2019, 25, 7581–7590 CrossRef CAS
.
- G. Pearson, F. Robinson, T. Beers Gibson, B.-e. Xu, M. Karandikar, K. Berman and M. H. Cobb, Endocr. Rev., 2001, 22, 153–183 CAS
.
- M. D. Brand and T. C. Esteves, Cell Metab., 2005, 2, 85–93 CrossRef CAS
.
- M. Sunde, L. C. Serpell, M. Bartlam, P. E. Fraser, M. B. Pepys and C. C. Blake, J. Mol. Biol., 1997, 273, 729–739 CrossRef CAS PubMed
.
- D. S. Wishart, B. D. Sykes and F. M. Richards, J. Mol. Biol., 1991, 222, 311–333 CrossRef CAS
.
- H. E. Huxley, J. Mol. Biol., 1963, 7, 281–308 CrossRef CAS
.
- C.-Y. Huang, V. Olieric, P. Ma, N. Howe, L. Vogeley, X. Liu, R. Warshamanage, T. Weinert, E. Panepucci and B. Kobilka, Acta Crystallogr., Sect. D: Struct. Biol., 2016, 72, 93–112 CrossRef CAS
.
- C. L. Moralesperez, C. M. Noviello and R. E. Hibbs, Nature, 2016, 538, 411–415 CrossRef CAS
.
- R. Ramautar, Adv. Clin. Chem., 2016, 74, 1–34 CAS
.
- R. Gahoual, E. Leizewagner, P. Houze and Y. Francois, Rapid Commun. Mass Spectrom., 2018, 33, 11–19 CrossRef
.
- M. Dams, J. L. Doressousa, R. Lamers, A. Treumann and S. Eeltink, Chromatographia, 2019, 82, 101–110 CrossRef CAS
.
- K. L. Ford, W. Zeng, J. L. Heazlewood and A. Bacic, Frontiers in Plant Science, 2015, 6, 674 CrossRef
.
- A. Leitner, Chem. Sci., 2016, 7, 4792–4803 RSC
.
- B. Schindler, A. D. Depland, G. Renoispredelus, G. Karras, B. Concina, G. Celep, J. Maurelli, V. Loriot, E. Constant and R. Bredy, Int. J. Ion Mobility Spectrom., 2017, 20, 119–124 CrossRef CAS
.
- S. M. Stow, T. J. Causon, X. Zheng, R. T. Kurulugama, T. Mairinger, J. C. May, E. E. Rennie, E. S. Baker, R. D. Smith and J. A. Mclean, Anal. Chem., 2017, 89, 9048–9055 CrossRef CAS
.
- T. Jiang, M. He, D. Guo, Y. Zhai and W. Xu, Phys. Chem. Chem. Phys., 2016, 18, 12058–12064 RSC
.
- C. Klein, S. M. Cologna, R. T. Kurulugama, P. S. Blank, E. Darland, A. Mordehai, P. S. Backlund and A. L. Yergey, Analyst, 2018, 143, 4147–4154 RSC
.
- T. Jiang, Y. Chen, L. Mao, A. G. Marshall and W. Xu, Phys. Chem. Chem. Phys., 2016, 18, 713–717 RSC
.
- H. Yang, S. Yang, J. Kong, A. Dong and S. Yu, Nat. Protoc., 2015, 10, 382 CrossRef CAS
.
- S. Prasad, I. Mandal, S. Singh, A. Paul, B. Mandal, R. Venkatramani and R. Swaminathan, Chem. Sci., 2017, 8, 5416–5433 RSC
.
- H. Cottet, M. Martin, A. Papillaud, E. Souaid, H. Collet and A. Commeyras, Biomacromolecules, 2007, 8, 3235–3243 CrossRef CAS
.
- A. Alizadeh, C. A. N. De Castro and W. A. Wakeham, Int. J. Thermophys., 1980, 1, 243–284 CrossRef CAS
.
- U. Tallarek, E. Rapp, T. W. J. Scheenen, B. Ernst and H. Van As, Anal. Chem., 2000, 72, 2292–2301 CrossRef CAS PubMed
.
- H. Cottet, J. Biron and M. Martin, Anal. Chem., 2007, 79, 9066–9073 CrossRef CAS
.
- B. A. Williams and G. Vigh, Anal. Chem., 1997, 69, 4410–4418 CrossRef CAS
.
- M. He, P. Luo, J. Hong, X. Wang, H. Wu, R. Zhang, F. Qu, Y. Xiang and W. Xu, ACS Omega, 2019, 4, 2377–2386 CrossRef CAS
.
- R. Zhang, H. Wu, M. He, W. Zhang and W. Xu, J. Phys. Chem. B, 2019, 123, 2335–2341 CrossRef CAS
.
- R. Johann and P. Renaud, Electrophoresis, 2004, 25, 3720–3729 CrossRef CAS
.
- A. Kamholz and P. Yager, Biophys. J., 2001, 80, 155–160 CrossRef CAS PubMed
.
- M. A. Hayes, I. Kheterpal and A. G. Ewing, Anal. Chem., 1993, 65, 2010–2013 CrossRef CAS
.
- J. E. Melanson, N. E. Baryla and C. A. Lucy, Trends Anal. Chem., 2001, 20, 365–374 CrossRef CAS
.
- W. Zhang, M. He, T. Yuan and W. Xu, Electrophoresis, 2017, 38, 3130–3135 CrossRef CAS
.
- Z. Hall and C. V. Robinson, J. Am. Soc. Mass Spectrom., 2012, 23, 1161–1168 CrossRef CAS
.
- Y. Shi, M. J. Acerson, A. Abdolvahabi, R. A. Mowery and B. F. Shaw, J. Am. Chem. Soc., 2016, 138, 5351 CrossRef CAS
.
- S. Rasouli, A. Abdolvahabi, C. M. Croom, D. L. Plewman, Y. Shi, J. I. Ayers and B. F. Shaw, J. Biol. Chem., 2017, 292, 19366–19380 CrossRef CAS
.
- G. Irina, J. D. Carbeck and G. M. Whitesides, Angew. Chem., 2010, 45, 3022–3060 Search PubMed
.
- E. Alexov and M. Gunner, Biophys. J., 1997, 72, 2075–2093 Search PubMed
.
- J. Gao, F. A. Gomez, R. Härter and G. M. Whitesides, Proc. Natl. Acad. Sci. U. S. A., 1994, 91, 12027–12030 CrossRef CAS
.
- A. Ibrahim, D. Koval, V. Kašička, C. Faye and H. Cottet, Macromolecules, 2013, 46, 533–540 CrossRef CAS
.
- J. Chamieh, D. Koval, A. Besson, V. Kašička and H. Cottet, J. Chromatogr. A, 2014, 1370, 255–262 CrossRef CAS PubMed
.
- T. Tůmová, L. Monincová, O. Nešuta, V. Čeřovský and V. Kašička, Electrophoresis, 2017, 38, 2018–2024 CrossRef
.
- M. B. Cammarata and J. S. Brodbelt, Chem. Sci., 2015, 6, 1324–1333 RSC
.
- N. A. Yewdall, T. M. Allison, F. G. Pearce, C. V. Robinson and J. A. Gerrard, Chem. Sci., 2018, 9, 6099–6106 RSC
.
- W. Chen, S. Li, X. Li, C. Zhang, X. Hu, F. Zhu, G. Shen and F. Feng, Chem. Sci., 2019, 10, 2179–2185 RSC
.
- H. Cottet, J.-P. Biron and M. Martin, Anal. Chem., 2007, 79, 9066–9073 CrossRef CAS
.
- T. Le Saux and H. Cottet, Anal. Chem., 2008, 80, 1829–1832 CrossRef CAS
.
- C. T. Culbertson and J. W. Jorgenson, Anal. Chem., 1994, 66, 955–962 CrossRef CAS
.
- R. Datta and V. R. Kotamarthi, AIChE J., 1990, 36, 916–926 CrossRef CAS
.
- R. Datta, Biotechnol. Prog., 2010, 6, 485–493 CrossRef
.
- A. Ibrahim, H. Ohshima, S. A. Allison and H. Cottet, J. Chromatogr. A, 2012, 1247, 154–164 CrossRef CAS
.
- J. Ostergaard and H. Jensen, Anal. Chem., 2009, 81, 8644–8648 CrossRef
.
- I. Frankel and H. Brenner, J. Fluid Mech., 1989, 204, 97–119 CrossRef CAS
.
-
R. Aris, Process Systems Engineering, 1999, vol. 1, pp. 109–120 Search PubMed
.
- S. Upma, N. J. Gleason and J. D. Carbeck, Anal. Chem., 2005, 77, 806–813 CrossRef
.
- M. Kahlen, A. Engel and C. Van den Broeck, Phys. Rev. E, 2017, 95, 012144 CrossRef
.
- C. Willingham, V. Sedlak, F. Rossini and J. Westhaver, Ind. Eng. Chem., 1947, 39, 706–712 CrossRef CAS
.
- J. W. Westhaver, J. Res. Natl. Bur. Stand., 1947, 38, 169–183 CrossRef CAS
.
- G. I. Taylor, Proc. Roy. Soc. Lond. Math. Phys. Sci., 1953, 219, 186–203 CrossRef CAS
.
- R. Aris, Proc. Roy. Soc. Lond. Math. Phys. Sci., 1956, 235, 67–77 CrossRef
.
- P. Gebauer and P. BočEk, Anal. Chem., 1998, 69, 1557–1563 CrossRef
.
- F. E. P. Mikkers, F. M. Everaerts and T. P. E. M. Verheggen, J. Chromatogr. A, 1979, 169, 1–10 CrossRef CAS
.
- Y. G. Tang, C. Yang, Q. H. Gong, C. J. Chai and C. Y. Lam, Anal. Chim. Acta, 2006, 561, 138–149 CrossRef
.
- J. Vlassakis and A. E. Herr, Anal. Chem., 2017, 89, 12787–12796 CrossRef CAS
.
- D. Dutta, Electrophoresis, 2018, 39, 760–769 CrossRef CAS
.
- Z. Min, Y. L. Han, Q. I. Li and C. Yi, Chin. Sci. Bull., 2007, 52, 3325–3332 CrossRef
.
- N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843 CrossRef CAS
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25 CrossRef
.
- M. Rostkowski, M. H. M. Olsson, C. R. Sondergaard and J. H. Jensen, BMC Struct. Biol., 2011, 11, 6 CrossRef CAS
.
- H. Li, A. D. Robertson and J. H. Jensen, Proteins, 2005, 61, 704–721 CrossRef CAS
.
- T. A. Soares, X. Daura, C. Oostenbrink, L. J. Smith and W. F. Van Gunsteren, J. Biomol. NMR, 2004, 30, 407–422 CrossRef CAS
.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS
.
- W. L. Hulse and R. T. Forbes, Int. J. Pharm., 2011, 411, 64–68 CrossRef CAS
.
- C. N. Davies, J. Aerosol Sci., 1975, 6, 273 Search PubMed
.
- U. Łapińska, K. L. Saar, E. V. Yates, T. W. Herling, T. Müller, P. K. Challa, C. M. Dobson and T. P. Knowles, Phys. Chem. Chem. Phys., 2017, 19, 23060–23067 RSC
.
- Z. Peng, K. Hidajat and M. Uddin, J. Colloid Interface Sci., 2004, 271, 277–283 CrossRef CAS
.
-
J. F. Foster, Albumin Structure Function & Uses, 1977, pp. 53–84 Search PubMed
.
- M. T. Donor, A. M. Mroz and J. S. Prell, Chem. Sci., 2019, 10, 4097–4106 RSC
.
- C. Blake, D. Koenig, G. Mair, A. North, D. Phillips and V. Sarma, Nature, 1965, 206, 757 CrossRef CAS
.
- Y. Yamagata, M. Kubota, Y. Sumikawa, J. Funahashi, K. Takano, S. Fujii and K. Yutani, Biochemistry, 1998, 37, 9355–9362 CrossRef CAS
.
- W. Ma, H. Ma, J.-F. Chen, Y.-Y. Peng, Z.-Y. Yang, H.-F. Wang, Y.-L. Ying, H. Tian and Y.-T. Long, Chem. Sci., 2017, 8, 1854–1861 RSC
.
- C. Jing, Z. Gu, T. Xie and Y.-T. Long, Chem. Sci., 2016, 7, 5347–5351 RSC
.
| This journal is © The Royal Society of Chemistry 2019 |