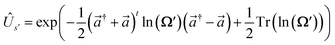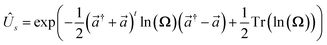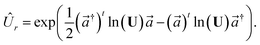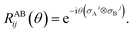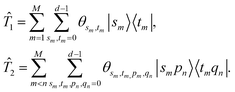DOI:
10.1039/C9SC01313J
(Edge Article)
Chem. Sci., 2019,
10, 5725-5735
Digital quantum simulation of molecular vibrations
Received
17th March 2019
, Accepted 23rd April 2019
First published on 25th April 2019
Abstract
Molecular vibrations underpin important phenomena such as spectral properties, energy transfer, and molecular bonding. However, obtaining a detailed understanding of the vibrational structure of even small molecules is computationally expensive. While several algorithms exist for efficiently solving the electronic structure problem on a quantum computer, there has been comparatively little attention devoted to solving the vibrational structure problem with quantum hardware. In this work, we discuss the use of quantum algorithms for investigating both the static and dynamic vibrational properties of molecules. We introduce a physically motivated unitary vibrational coupled cluster ansatz, which also makes our method accessible to noisy, near-term quantum hardware. We numerically test our proposals for the water and sulfur dioxide molecules.
I. Introduction
Simulating many-body physical systems enables us to study chemicals and materials without fabricating them, saving both time and resources. The most accurate simulations require a full quantum mechanical treatment—which is exponentially costly for classical computers. While many approximations have been developed to solve this problem, they are often not sufficiently accurate.1 One possible route to more accurate simulations is to use quantum computers. Quantum computation can enable us to solve certain problems asymptotically more quickly than with a ‘classical’ computer.2–4 While the quantum computers that we currently possess are small and error prone, it is hoped that we will one day be able to construct a universal, fault-tolerant quantum computer—widely expected to be capable of outperforming its classical counterparts on certain tasks. One example of such tasks is simulating quantum systems on quantum computers.5–7 In particular, simulating chemical systems, such as molecules,8 has received significant attention.84,85 This may stem from the commercial benefits of being able to investigate and design such systems in silico.9 The development of quantum computational chemistry has arguably echoed its classical counterpart. In both fields, the majority of investigations have focused on the electronic structure of molecules.10 This has resulted in a wealth of well established methods for solving problems of electrons. However, methods concerned with the nuclear degrees of freedom are comparatively less well established. Understanding vibrations is critical for obtaining the most accurate models of real physical systems.10 Unfortunately, the most detailed classical simulations of vibrations are limited to small molecules, consisting of a few atoms.11 While approximations can be used to treat larger systems, these tend to be less accurate than experiments.12 Although recently proposed analog quantum algorithms13–19 are capable of simulating molecular vibrations using resources which scale polynomially with the size of the molecule, the long term scalability of these approaches has yet to be established.
In this work, we discuss a general method for efficiently simulating molecular vibrations on a universal quantum computer. Our method targets the eigenfunctions of a vibrational Hamiltonian with potential terms beyond quadratic order (‘anharmonic potentials’). These wavefunctions can then be used to efficiently calculate properties of interest, such as absorption spectra at finite temperatures. We can also use our method to perform simulations of vibrational dynamics, enabling the investigation of properties such as vibrational relaxation.
II. Vibrations
A consequence of quantum mechanics is that molecules are never at rest, possessing at least the vibrational zero-point energy correction to the ground-state energy.20–22 As a result, vibrations affect all chemical calculations, to a greater or lesser extent. They are important in both time dependent and independent contexts. From a dynamics perspective, vibrational structure affects high frequency time-resolved laser experiments,23 reaction dynamics,24–26 and transport.27,28 In a static context, vibrations underpin spectral calculations, such as: infrared and Raman spectroscopy29 and fluorescence.30 These calculations determine the performance of solar cells31,32 and industrial dyes,33,34 as well as the susceptibility of molecules to photodamage.13,35
Despite their importance for accurate results, studying vibrations has proven difficult. There are several possible routes to obtaining an accurate description of vibrational behaviour. Real-space, grid based methods, which treat the electronic and nuclear degrees of freedom on an equal footing, are limited to systems of a few particles. While algorithms to efficiently solve this problem on a universal quantum computer exist,36,37 it will take many years to develop a quantum computer with the required number of qubits.38 Alternatively, one may separate the electronic and nuclear degrees of freedom. We can solve for the electronic energy levels of the system as a function of the nuclear positions, which enables us to map out potential energy surfaces for the system. A number of approximate classical methods have been developed to solve this problem,1,39 as well as several quantum algorithms.8,40–42 These electronic potential surfaces can then be viewed as the nuclear potential, determining the vibrational energy levels. This is known as the vibrational structure problem. The accuracy of the nuclear potential is determined by the accuracy of the electronic structure calculation, as well as the number of points obtained for the potential energy surface. Once this potential has been obtained, a number of classical methods can be used for solving both the time dependent and independent Schrödinger equations.
The most simple method uses the ‘harmonic approximation’. This treats the nuclear potential in the vicinity of the equilibrium geometry as a harmonic oscillator potential, resulting in energy eigenstates which are harmonic oscillator eigenfunctions.
Alternatively, one may consider higher order expansions of the nuclear potential, resulting in more accurate calculations.43 One common route towards obtaining the nuclear potential is to first carry out many electronic structure calculations on the system, in the vicinity of the minimum energy configuration. Each of these electronic structure calculations is approximate, and so the cost of each one scales polynomially with the system size. However, if one proceeds to obtain the nuclear potential using this simple grid based method, then a number of grid points scaling exponentially with the number of modes is required.44 In practice one can often instead construct an approximate nuclear potential by considering a reduced number of mode couplings, or using interpolation, or using adaptive methods. A review of these, and other state-of-the-art methods can be found in ref. 44. The requirement to first perform multiple electronic structure calculations to obtain the anharmonic nuclear potential makes calculating vibrational energy levels expensive,45 even if only mean-field vibrational calculations are then performed. If the correlation between different vibrational modes is included in the calculation, then the simulation becomes even more expensive. While most of the existing classical vibrational simulation methods scale polynomially with the number of modes in the system (e.g. vibrational self-consistent field methods,12 or vibrational coupled cluster theory46), and are sufficiently accurate for some systems, they only provide approximations to the true full configuration interaction vibrational wavefunction, which can be exponentially costly to obtain. A similar hierarchy of accuracy also exists for dynamics simulations.
The computational difficulties described above make accurate vibrational calculations on large systems very challenging for classical computers. To overcome these challenges, quantum solutions have been suggested for the vibrational structure problem.13–19,47 To date, the majority of suggestions have focused on analog quantum simulation of vibrations. In analog simulations, the simulator emulates a specific system of interest, but cannot in general be programmed to perform simulations of other, different systems. Huh et al. proposed using boson sampling circuits to determine the absorption spectra of molecules.13 These boson sampling circuits consist of photons passing through an optical network. This initial proposal relied on the harmonic oscillator approximation at zero temperature, but does take into account bosonic mode mixing due to nuclear structural changes that result from electronic excitation. This method has since been experimentally demonstrated,15,16 and extended to finite temperature spectra.14,19 The main limitation of these simulations is the use of the harmonic oscillator approximation for the vibrational wavefunction. It is in general difficult to engineer ground states of anharmonic Hamiltonians using an optical network, as non-linear operations, such as squeezing, are required. Optical networks have also been used for simulating vibrational dynamics.17 These simulations investigated vibrational transport, adaptive feedback control, and anharmonic effects.
The aforementioned schemes make use of the analogy between the vibrational energy levels in molecules in the Harmonic oscillator approximation, and the bosonic energy levels accessible to photons and ions. One advantage of this is that the bosonic modes are in principle able to store an arbitrary number of excitations. As these analog simulators are relatively simple to construct (when compared to a universal, fault-tolerant quantum computer), they will likely prove useful for small calculations in the near-term. However, it is not yet known how to suppress errors to an arbitrarily low rate in analog simulators. As a result, if we are to simulate the vibrational behaviour of larger quantum systems, we will likely require error corrected universal quantum computers. This motivates our work on methods for vibrational simulation on universal quantum computers.
The rest of this paper is organised as follows. In Section III, we introduce the vibrational structure problem for molecules and show how this problem can be mapped onto a quantum computer. In Section IV, we show how to solve both static and dynamic problems of molecular vibrations. Finally, in Section V, we present the results of numerical simulations of the H2O and SO2 molecules.
III. Encoding
A. Vibrational Hamiltonian
Under the Born–Oppenheimer approximation, nuclear variables are treated as parameters in the electronic structure problem and are restored as quantum nuclear variables at the level of the full problem. In the following, we neglect the rotational degrees of freedom from negligible rotational–vibrational couplings for rigid molecules (rigid rotator approximation). After diagonalising the electronic Hamiltonian and neglecting nonadiabatic couplings, the molecular Hamiltonian becomes| | 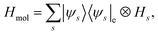 | (1) |
where |ψs〉e are the electronic energy eigenstates. The effective nuclear Hamiltonian Hs is| | 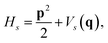 | (2) |
where q = (q1, q2…) are nuclear coordinates, p = −i∂/∂q are nuclear momenta with ħ = 1, and Vs(q) is the effective nuclear potential. This potential is determined by the corresponding electronic potential energy surface of |ψs〉e. As described in Appendix A, we work in mass-weighted normal coordinates and decouple the rotational and vibrational modes. The potential Vs(q) can be approximated as| | 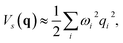 | (3) |
where ωi is the harmonic frequency of the ith vibrational normal mode. Thus, the nuclear Hamiltonian Hs can be approximated by a sum of independent harmonic oscillators,| | 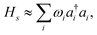 | (4) |
with a†i and ai being the creation and annihilation operators of the ith harmonic oscillator. This is the commonly used ‘harmonic approximation’. Even for accurate potentials and rigid molecules, the harmonic approximation is less accurate than modern spectroscopic techniques.12 This approximation becomes inadequate for large and ‘floppy’ molecules.12 Improved results can be obtained by including anharmonic effects which requires information of higher order potential terms in the Hamiltonian.44 For example, we can expand the potential as| | 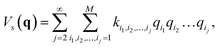 | (5) |
where M is the number of modes, ki1,i2,…,ij are the coefficients of the expansion qi1qi2…qij, and the harmonic frequencies are 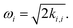 In general, the eigenstates of these Hamiltonians are entangled states, when working in a basis of harmonic oscillator eigenstates. Consequently, solving the higher order vibrational Hamiltonian is a hard problem for classical computers.
In general, the eigenstates of these Hamiltonians are entangled states, when working in a basis of harmonic oscillator eigenstates. Consequently, solving the higher order vibrational Hamiltonian is a hard problem for classical computers.
In contrast, we show below that it is possible to efficiently encode the kth order nuclear Hamiltonian into a Hamiltonian acting on qubits. We can then use quantum algorithms to efficiently calculate the static and dynamic properties of the nuclear Hamiltonian.
B. Mapping to qubits
We first discuss mapping the molecular Hamiltonian into qubits. We work in the basis of harmonic oscillator eigenstates, as these can be easily mapped to qubits. The direct mapping presented below was originally suggested in the context of simulating general bosonic systems by Somma et al.48 It has been used recently in the context of quantum simulation of nuclear physics to investigate the binding energy of a deuteron nucleus.49 The compact mapping discussed below was proposed by Veis et al., in the context of using quantum computers to simulate ‘nuclear orbital plus molecular orbital (NOMO)’ theory, which uses Gaussian orbitals for the nuclei, and treats them on an equal footing to the electrons.50 This differs from our work, which separates the nuclear and electronic degrees of freedom, and predominantly considers a harmonic oscillator basis for the vibrational modes. While this tailors our method for vibrational problems, it means we are limited to solving problems for which the Born–Oppenheimer approximation is valid, unlike ref. 50.
Focusing first on one harmonic oscillator, ĥ = ωa†a, we consider the truncated eigenstates with the lowest d energies, |s〉 with s = 0,1,…,d − 1. A direct mapping of the space {|s〉} is to encode it with d qubits as
| | | |s〉 = ⊗s−1j=0|0〉j|1〉s⊗d−1j=s+1|0〉j, | (6) |
with creation operator
| | 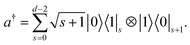 | (7) |
The annihilation operator can be obtained by taking the Hermitian conjugate of a†. As an alternative to the direct mapping, we can use a compact mapping, using K = [log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d]′ qubits,
d]′ qubits,
| | | |s〉 = |bK−1〉|bK−2〉…|b0〉, | (8) |
with binary representation
s =
bK−12
K−1 +
bK−22
K−2 + …
b02
0. The representation of the creation operator is
| | 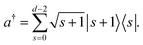 | (9) |
These binary projectors can then be mapped to Pauli operators;
| | 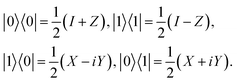 | (10) |
when decomposing
a† and
a into local Pauli matrices, there are
O(
d) and
O(
d2) terms for the direct and compact mapping, respectively. In
Fig. 1, we show the number of qubits required to describe the vibrational Hamiltonians of several molecules, for both mappings.
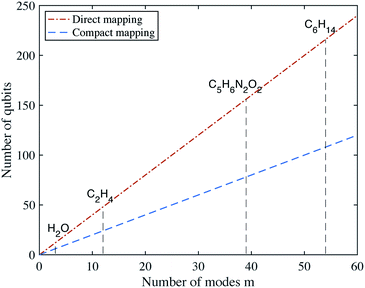 |
| | Fig. 1 Number of qubits required for the direct and compact mappings with d = 4 energy levels for each mode. | |
As p and q can both be represented by a linear combination of creation and annihilation operators, we can thus map the nuclear vibrational Hamiltonian to a qubit Hamiltonian. If the molecule has n atoms, it has M = 3n − 6 vibrational modes for a nonlinear molecule, and M = 3n − 5 for a linear molecule. The vibrational wavefunction can then be represented with Md (direct mapping) or M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(d) (compact mapping) qubits. This can be contrasted with the exponentially scaling classical memory required to store the wavefunction. If the potential is expanded to kth order (with M ≫ k), the Hamiltonian contains O(Mkdk) (direct) or O(Mkd2k) (compact) terms. These terms are strings of local Pauli matrices. In this work, we take d to be a small constant. This approximation constrains us to the low energy subspace of the Hamiltonian, which should be valid for calculations of ground and low-lying excited states. The applicability of this approximation to the simulation of dynamics is discussed in Section VI. We set k = 4 to investigate the Hamiltonian to quartic order. The resulting Hamiltonian has O(M4) terms.
log(d) (compact mapping) qubits. This can be contrasted with the exponentially scaling classical memory required to store the wavefunction. If the potential is expanded to kth order (with M ≫ k), the Hamiltonian contains O(Mkdk) (direct) or O(Mkd2k) (compact) terms. These terms are strings of local Pauli matrices. In this work, we take d to be a small constant. This approximation constrains us to the low energy subspace of the Hamiltonian, which should be valid for calculations of ground and low-lying excited states. The applicability of this approximation to the simulation of dynamics is discussed in Section VI. We set k = 4 to investigate the Hamiltonian to quartic order. The resulting Hamiltonian has O(M4) terms.
IV. Simulating molecular vibrations
Once the vibrational modes have been mapped to qubits, we can use quantum algorithms to obtain the static and dynamic properties of the system. We can write the qubit Hamiltonian as 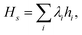 where λi are coefficients determining the strength of each term in the Hamiltonian.
where λi are coefficients determining the strength of each term in the Hamiltonian.
A. Vibrational energy levels
An important, but classically difficult problem, is to obtain accurate energy levels for the vibrational Hamiltonian. The spectrum of the vibrational Hamiltonian provides corrections to the electronic eigenstates used to predict reaction rates.22 Moreover, we will show how these energy levels can be used to calculate the absorption spectrum of molecules in Section IV.B. Of particular interest are the lowest lying energy levels at low temperature. Using a universal quantum computer, we can first prepare an initial state that has a large overlap with the ground state of the vibrational Hamiltonian. We can then use the phase estimation algorithm7,51 to probabilistically obtain the ground state and ground state energy. A possible initial ground state is the lowest energy product state of the harmonic oscillator basis states, |ψ0〉 = ⊗m|sm〉m. However, we note that the overlap between this state and the true ground state may decrease exponentially with the size of the molecule. This so-called ‘orthogonality catastrophe’ has been discussed previously in the context of electronic structure calculations on a quantum computer.52,53 As a result, for large systems it may be more efficient to use an initial state obtained from a classical vibrational self-consistent field (VSCF) calculation. VSCF is the vibrational analogue of the Hartree–Fock method in electronic structure theory. VSCF optimises the basis functions to minimise the energy of the Hamiltonian with a product state.
Another route to a state with a large overlap with the ground state, is to prepare the VSCF state, and then adiabatically evolve under a Hamiltonian that changes slowly from the VSCF Hamiltonian, to the full vibrational Hamiltonian H. This approach has received significant attention within quantum computing approaches to the electronic structure problem, since it was first proposed in the context of quantum computational chemistry in ref. 8. However, both adiabatic state preparation and phase estimation typically require long circuits, with a large number of gates. As a result, quantum error correction is required to suppress the effect of device imperfections. It is therefore helpful to introduce variational methods, which may make these calculations feasible for near-term, non-error corrected quantum computers. Variational methods replace the long gate sequences required by phase estimation with a polynomial number of shorter circuits.42,54 This dramatically reduces the coherence time required. As a result, quantum error correction may not be required, if the error rate is sufficiently low, in the context of the number of gates required. The circuits used consist of a number of parametrised gates which seek to create an accurate approximation of the desired state. The parameters are updated using a classical feedback loop, in order to produce better approximations of the desired state. The circuit used is known as the ‘ansatz’ circuit.
Inspired by classical methods for the vibrational structure problem, we introduce the unitary vibrational coupled cluster (UVCC) ansatz. This is a unitary analogue of the VCC ansatz introduced in ref. 12 and 46. We note that a similar pairing exists for the electronic structure problem, where the unitary coupled cluster (UCC) ansatz55,56 has been suggested as a quantum version of the classical coupled cluster method. The UVCC ansatz is given by
| | |Ψ(![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) )〉 = exp( )〉 = exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †)|Ψ0〉, †)|Ψ0〉, | (11) |
where the initial state |
Ψ0〉 can be either the ground state |
ψ0〉 of the harmonic oscillators or the VSCF state |
ΨVSCF〉,
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
is the sum of molecular excitation operators truncated at a specified excitation rank, and
![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif)
are the parameters defined below. Similar to the unitary coupled cluster ansatz in electronic structure problems, the single and double excitation operators are
with
| | 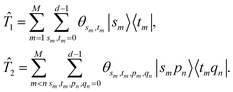 | (13) |
Here, we omit the subscript of modes for simplicity.
θsm,tm and
θsm,tm,pm,qn are real parameters, and
![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif)
= {
θsm,tm,
θsm,tm,pm,qn}. The
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
operators can be mapped to qubit operators
via either the direct or compact mapping.
The UVCC ansatz seeks to create a good approximation to the true ground state by considering excitations above a reference state. We note that the classical VCC ansatz is not a unitary operator. Correspondingly, the method is not variational, meaning that energies are not bounded from below. Moreover, we expect that the UVCC ansatz will deal better with problems of strong static correlation than the VCC ansatz, as the former can easily be used with multi-reference states. This echoes the way in which the UCC ansatz can be used with multi-reference states,56 while it is typically more difficult when using the canonical CC method.1
Once we have obtained the energy levels of the vibrational Hamiltonian using the methods discussed above, we can calculate the infrared and Raman frequencies, using the difference between the excited and ground-state energies.57
It is often also the case that one is interested in the properties of a system in thermal equilibrium, rather than a specific eigenstate. We can also use established quantum algorithms with the Hamiltonians described above to construct these thermal states. On error corrected quantum computers, we can use the heuristic algorithms presented in ref. 58 and 59 to construct these thermal states. Alternatively, we can use near-term devices to implement hybrid algorithms for imaginary time evolution.60–62
B. Franck–Condon factors
In addition to focusing on the eigenstates or thermal states of a single vibrational Hamiltonian, we can also consider vibronic (vibrational and electronic) transitions between the vibrational levels resulting from different electronic potential energy surfaces. Consider two electronic states, |i〉e and |f〉e. The molecular Hamiltonian is| | | Hmol = |i〉〈i|e⊗Hi + |f〉〈f|e⊗Hf, | (14) |
where Hi and Hf are vibrational Hamiltonians, with energy eigenstates |ψivib〉 and |ψfvib〉, respectively. Using Fermi's Golden rule, the probability of a photon-induced transition between two wavefunctions |ψi〉 = |i〉⊗|ψivib〉 and |ψf〉 = |f〉⊗|ψfvib〉 is proportional to the square of the transition dipole moment P2 = |〈ψf|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ψi〉|2, using first order time-dependent perturbation theory. Within the Condon approximation,
|ψi〉|2, using first order time-dependent perturbation theory. Within the Condon approximation, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) =
= ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) e +
e + ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) N, the transition probability becomes proportional to P2 = |〈ψfvib|ψivib〉|2·|〈f|
N, the transition probability becomes proportional to P2 = |〈ψfvib|ψivib〉|2·|〈f|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) e|i〉|2. Here |〈ψfvib|ψivib〉|2 are referred to as Franck–Condon integrals. Without the Condon approximation, the Franck–Condon integrals become |〈ψfvib|
e|i〉|2. Here |〈ψfvib|ψivib〉|2 are referred to as Franck–Condon integrals. Without the Condon approximation, the Franck–Condon integrals become |〈ψfvib|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (q)|ψivib〉|2, with
(q)|ψivib〉|2, with ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (q) = |〈f|
(q) = |〈f|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |i〉|2.
|i〉|2.
In practice, |ψivib〉 and |ψfvib〉 are eigenstates of Hamiltonians with different harmonic oscillator normal modes qf and qi. These modes are related by the Duschinsky transform qf = Uqi + d.45,63 According to the Doktorov unitary representation of the Duschinsky transform, the harmonic oscillator eigenstates are related by13,14,64
where |
si〉 and |
sf〉 are harmonic oscillator eigenstates in the initial and final coordinates
qi and
qf, respectively. The Doktorov unitary can be decomposed into a product of unitary operators
ÛDok =
ÛtÛ†s′ÛsÛr, which depend on the displacement vector
d, the rotation matrix
U, and matrices of the frequencies of the harmonic oscillators
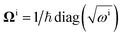
and
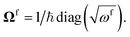
The definitions of the unitary operators are shown in Appendix C.
If |Ψivib〉 and |Ψfvib〉 are the qubit wavefunctions resulting from diagonalisation of Hi and Hf using a quantum computer, they will be obtained in different normal mode bases |si〉 and |sf〉, respectively. We cannot directly calculate the Franck–Condon integrals using |〈Ψfvib|Ψivib〉|2, as this does not take into account the different bases. Instead, we must implement the Doktorov unitary to get the Franck–Condon integrals
| | | |〈ψfvib|ψivib〉|2 = |〈Ψfvib|ÛDok|Ψivib〉|2. | (16) |
The Franck–Condon integrals without the Condon approximation can be efficiently calculated
via| | |〈ψfvib|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (q)|ψivib〉2 = |〈Ψfvib| (q)|ψivib〉2 = |〈Ψfvib|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (qf)ÛDok|Ψivib〉|2. (qf)ÛDok|Ψivib〉|2. | (17) |
They can be both efficiently calculated with the generalised SWAP-test circuit.
65
Alternatively, we can obtain the Franck–Condon integrals without realising the Doktorov transform. The qubit states |Ψivib〉 and |Ψfvib〉 are obtained from Hi(qi) and Hf(qf) with normal mode coordinates qi and qf, respectively. Instead, we can focus on one set of normal mode coordinates qi and represent the Hamiltonian Hf in qi, H′f(qi). By solving the energy eigenstates of H′f(qi), we can directly get 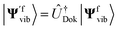 and calculate the Franck–Condon integrals without realising the Doktorov transform. However, as the Hamiltonian H′f(qi) is not encoded in the correct normal mode basis, the ground state of the harmonic oscillators or the VSCF state |ΨVSCF〉 may not be an ideal initial state to start with. However, this effect may be negligible if the overlap between |Ψivib〉 and
and calculate the Franck–Condon integrals without realising the Doktorov transform. However, as the Hamiltonian H′f(qi) is not encoded in the correct normal mode basis, the ground state of the harmonic oscillators or the VSCF state |ΨVSCF〉 may not be an ideal initial state to start with. However, this effect may be negligible if the overlap between |Ψivib〉 and 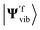 is suitably large. In this case, the initial state |Ψ0〉 for |Ψivib〉 should also be an ideal initial state for
is suitably large. In this case, the initial state |Ψ0〉 for |Ψivib〉 should also be an ideal initial state for 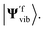 The aforementioned transformation can be implemented by transforming the normal mode coordinates qi as described in ref. 45.
The aforementioned transformation can be implemented by transforming the normal mode coordinates qi as described in ref. 45.
C. Vibrational dynamics
In this section, we consider methods to investigate the dynamic properties of vibrational Hamiltonians. Vibrational dynamics underpin phenomena including energy and electron transport27,28 and chemical reactions.24–26 Dynamical behaviour can be studied by transforming to a single-mode basis of spatially localised vibrational modes, as described in ref. 17. The spatially localised vibrational modes aLi, are related to the normal modes aivia a basis transformation| | 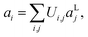 | (18) |
with real unitary matrix Ui,j. We can obtain the corresponding localised Hamiltonian HL, using the transformation of the normal coordinates and momenta| | 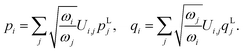 | (19) |
Given an initial state of the localised vibrations, the dynamics can be simulated by applying the time evolution operator e−iHLt. This can be achieved in a number of ways, using different Hamiltonian simulation algorithms, including: Trotterization (also referred to as product formulae),5,66 the Taylor series method,67–69 and qubitization70,71 in conjunction with quantum signal processing.72,73 The product formula method is the most simple to realise. If HL can be decomposed as 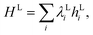 the time evolution operator e−iHLt can be realised using a product formula,
the time evolution operator e−iHLt can be realised using a product formula,| | 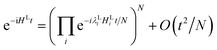 | (20) |
where N is chosen to be sufficiently large to suppress the error in the approximation.
Alternatively, the vibrational dynamics can be realised using a recently proposed variational algorithm.74 One could use either a UVCC ansatz, or a Trotterized ansatz.75,76
V. Numerical simulations
In this section, we demonstrate how the techniques described above can be used to calculate the vibrational energy levels of small molecules. We focus on the polyatomic molecules H2O and SO2, which both have three vibrational modes. The coefficients were computed at MP2/aug-cc-pVTZ level of theory using Gaussian09 software.83 in Appendix D. We consider the cases with two and four energy levels for each of the harmonic oscillator modes, yielding Hamiltonians acting on 6 and 12 qubits for the direct mapping, and 3 and 6 qubits for the compact mapping. We used the compact mapping in our numerical simulations, as it requires fewer qubits. There are 216 and 165 terms in the Hamiltonian for H2O and SO2, respectively.
Table 1 Coefficients of the potential energy surface of H2O and SO2. The coefficients are in atomic units, where the unit of length is a0 = 1 Bohr (0.529167 × 10−10 m), the unit of mass is the electron mass me, and the unit of energy is 1 Hartree (1 Hartree = e2/4πε0a0 = 27.2113 eV)
|
k
|
H2O |
SO2 |
|
k
1,1
|
0.275240 × 10−4 |
0.252559 × 10−5 |
|
k
2,2
|
0.151618 × 10−3 |
0.125410 × 10−4 |
|
K
3,3
|
0.161766 × 10−3 |
0.176908 × 10−4 |
|
K
1,1,1
|
0.121631 × 10−6 |
0.316![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 × 10−8 646 × 10−8 |
|
K
1,1,2
|
0.698476 × 10−6 |
0.575325 × 10−8 |
|
K
1,2,2
|
−0.266427 × 10−6 |
0.197771 × 10−7 |
|
k
2,2,2
|
−0.312538 × 10−5 |
−0.668689 × 10−7 |
|
K
1,3,3
|
−0.915428 × 10−6 |
−0.370850 × 10−9 |
|
k
2,3,3
|
−0.964649 × 10−5 |
−0.284244 × 10−6 |
|
K
1,1,1,1
|
−0.463748 × 10−9 |
0.330842 × 10−11 |
|
K
1,1,2,2
|
−0.449480 × 10−7 |
−0.172869 × 10−9 |
|
K
1,2,2,2
|
0.957558 × 10−8 |
−0.215928 × 10−9 |
|
k
2,2,2,2
|
0.433267 × 10−7 |
0.225400 × 10−9 |
|
K
1,1,3,3
|
−0.555026 × 10−7 |
−0.356155 × 10−9 |
|
K
1,2,3,3
|
0.563566 × 10−7 |
−0.128135 × 10−9 |
|
k
2,2,3,3
|
0.269239 × 10−6 |
−0.220168 × 10−8 |
|
K
3,3,3,3
|
0.462143 × 10−7 |
0.458046 × 10−9 |
|
k
2,3,3,3
|
0 |
−0.720760 × 10−11 |
We first calculate the energy levels under the harmonic approximation. We compare this to the energy levels obtained with a fourth order expansion of the potential. The results for H2O are shown in Fig. 2. We can see that although the ground state can be well approximated by the harmonic oscillators, the excited states deviate from the harmonic oscillators at higher energy levels. The results for SO2 can be found in the Appendix. These calculations highlight the importance of anharmonic terms in the potential for even small molecules.
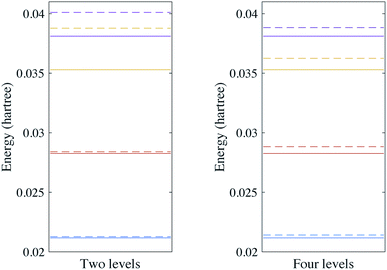 |
| | Fig. 2 Vibrational spectra of H2O with two and four energy levels for each mode. The solid lines are the energy levels of the harmonic oscillator eigenstates and the dashed lines are the vibrational spectra of the Hamiltonian with a fourth order expansion of the potential. | |
Next, we implemented the UVCC ansatz to obtain the vibrational energy levels of H2O using the variational quantum eigensolver.42 For simplicity, we considered two energy levels for each mode. To implement the UVCC ansatz, we first calculate the imaginary part of ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and encode it into a linear combination of local Pauli terms, i.e.,
and encode it into a linear combination of local Pauli terms, i.e.,
| | 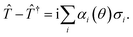 | (21) |
Then, as for the UCC ansatz, we realise exp(
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
−
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †
†) by a first order Trotterisation
via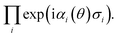
For example, the UVCC ansatz of H
2O with two energy levels can be prepared by the circuit in
Fig. 3.
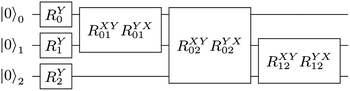 |
| | Fig. 3 The UVCC ansatz of three modes each with two energy levels. There are nine gates with six parameters (joined gates share the same parameters). The single qubit gate on the ith qubit is 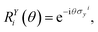 and the two qubit gate on the ith and jth is and the two qubit gate on the ith and jth is 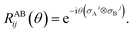 | |
Using the UVCC ansatz, we can obtain the vibrational ground state with a variational procedure. As the ground state is close to the initial state |0〉⊗3, we start with parameters slightly perturbed from zero. We then use gradient descent to find the minimum energy of the system. The results are shown in Fig. 4.
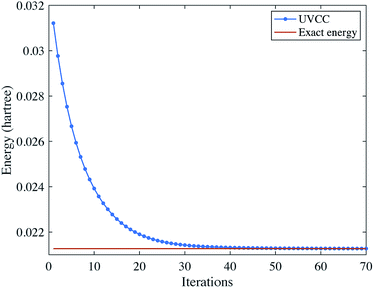 |
| | Fig. 4 Solving the vibrational ground state of H2O with the UVCC ansatz. Here, we consider two energy levels for each mode. | |
VI. Discussion
In this work, we have extended many of the techniques developed for quantum simulation to the problem of simulating vibrations. Understanding vibrations is an important problem for accurately modelling chemical systems, yet one that is difficult to solve classically.
We have discussed ways to map between vibrational modes and qubit states. This is only possible when we consider a restricted number of harmonic oscillator energy levels. This approximation is appropriate when investigating the low energy properties of the Hamiltonian, such as the ground state energy. However, it may not always be possible to use this approximation when considering time evolution, as this requires the exponentiation of our truncated Hamiltonian. One possible route to overcome this challenge is to repeat simulations which consider an increasing number of energy levels, and then to extrapolate to the infinite energy level result. This technique was used in a similar context to this work in ref. 49.
Once the vibrational Hamiltonian has been mapped to a qubit Hamiltonian, much of the existing machinery for quantum simulation can be applied. Static properties, such as energy levels, can be calculated using phase estimation or variational approaches. To aid variational state preparation, we proposed a unitary version of the powerful VCC method used in classical vibrational simulations. The resulting energy eigenstates can be used as an input for SWAP-test circuits. These calculate the Franck–Condon factors for the molecules, which are related to the absorption spectra. Alternatively, one may investigate dynamic properties, using methods for Hamiltonian simulation to time evolve a specified state.
Compared with analog algorithms,13,14,16,17 our method can easily take into account anharmonic terms in the nuclear Hamiltonian. Moreover, it could be used to simulate large systems by protecting the quantum computer with error correction. As our technique is tailored for simulating vibrational states, it makes it simple to investigate interesting vibrational properties, such as the Franck–Condon factors. However, as our approach uses the Born–Oppenheimer approximation, it is not suitable for all problems in chemistry, such as problems including relativistic effects77 or conical intersections.78–80 Future work will address whether restricting our vibrational modes to low-lying energy levels poses a significant challenge for problems of practical interest.
Appendix A: encoding vibrational Hamiltonians into qubits
The molecular Hamiltonian in atomic units is| | 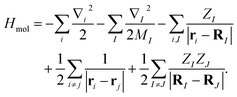 | (A1) |
where MI, RI, and ZI are the mass, position, and charge of nuclei I, and ri is the position of electron i. Given the location of the nucleus, the electronic Hamiltonian is| | 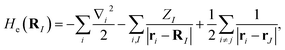 | (A2) |
and the total Hamiltonian is| | 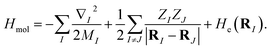 | (A3) |
Under the Born–Oppenheimer approximation, we assume the electrons and nuclei are in a product state,
To get the ground state of the Hamiltonian, one can thus separately minimise over |
ψ〉
n and |
ψ〉
e,
| | 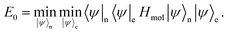 | (A5) |
As only
He(
RI) depends on |
ψ〉
e, the minimisation over |
ψ〉
e is equivalent to finding the ground state of
He(
RI). Denote
| | 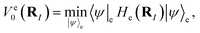 | (A6) |
then the ground state of
Hmol can be found by solving the ground state of
H0,
| | 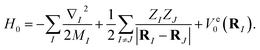 | (A7) |
In general, considering a spectral decomposition of 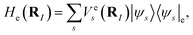 the molecular Hamiltonian is
the molecular Hamiltonian is
| | 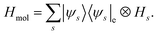 | (A8) |
Here, |
ψs〉
e are eigenstates of the electronic Hamiltonian and
| | 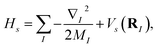 | (A9) |
and
| | 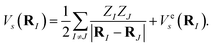 | (A10) |
Finding the spectra of He(RI) is called the electronic structure problem, which can be efficiently solved using a quantum computer.8 One approach is to consider a subspace that the ground state lies in and transform the Hamiltonian He(RI) into the second quantised formulation, with a basis determined by the subspace. As electrons are fermions, the obtained Hamiltonian is a fermionic Hamiltonian. By using the standard encoding methods, such as Jordan–Wigner and Bravyi–Kitaev,82 the fermionic Hamiltonian is converted into a qubit Hamiltonian, whose spectra can be efficiently computed.
Focusing on the ground state of the electronic structure Hamiltonian, we show how to redefine H0 in the mass-weighted basis and how to encode it with qubits. Denote 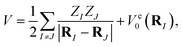 then one can obtain the mass-weighted normal coordinates qi by minimising the coupling between the rotational and vibrational degrees of freedom and diagonalising the Hessian matrix,
then one can obtain the mass-weighted normal coordinates qi by minimising the coupling between the rotational and vibrational degrees of freedom and diagonalising the Hessian matrix,
| | 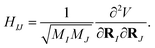 | (A11) |
In the mass-weighted basis, the potential can be expanded
via a Taylor series truncated at fourth order
| | 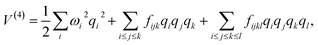 | (A12) |
and the total Hamiltonian becomes
| | 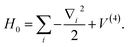 | (A13) |
If we consider the higher order terms as a perturbation, one can get the normal modes by solving the harmonic oscillator
| | 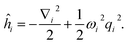 | (A14) |
We denote the eigenbasis for
ĥi as
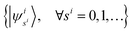
, then the nuclear wave function can be represented by
| | 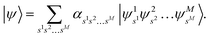 | (A15) |
The Hamiltonian under the normal mode basis becomes,
| | 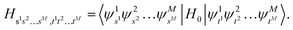 | (A16) |
Suppose the basis
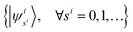
is truncated to the lowest
d energy levels, the space of
Hs1s2…sM,t1t2…tM is equivalent to the space of
M d-level systems, or equivalently
M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
log
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d
d qubits.
Appendix B: variational quantum simulation with the unitary vibrational coupled cluster ansatz
We can make use of variational methods to find the low energy spectra of the vibrational Hamiltonian. Inspired by classical computational chemistry, we introduce the unitary vibrational coupled cluster (UVCC) ansatz| | |VCC〉 = exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) − − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †)|Φ0〉 †)|Φ0〉 | (B1) |
where the reference state |Φ0〉 is a properly chosen initial state, and T is the sum of molecular excitation operators truncated at a specified excitation rank (often single and double excitations)56
with
The initial state can be the product of the ground-state of each mode
Or we can also run a vibrational self-consistent field (VSCF) to get the Hartree–Fock initial state
which is obtained by minimising the energy of the Hamiltonian
| | 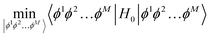 | (B4) |
by solving the self-consistent equation
with
Hi = 〈
ϕ1…
ϕi−1ϕi+1…
ϕM|
H0|
ϕ1…
ϕi−1ϕi+1…
ϕM〉.
Appendix C: Duschinsky transform
The relation between the initial coordinates q1 and final coordinates q2 iswhere U is the Duschinsky rotation matrix and d is the displacement vector. The harmonic oscillator Hamiltonian with unit mass is| | 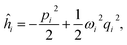 | (C2) |
with 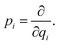 The operators q1 and p1 can be represented by the creation and annihilation operators
The operators q1 and p1 can be represented by the creation and annihilation operators| | 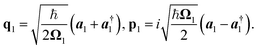 | (C3) |
The transformation for p is p1 = U†p2. The transformation for the creation operators are
| | 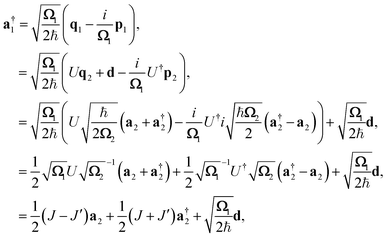 | (C4) |
where
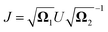
and
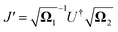
.
It was shown by Doktorov et al.64 that the Duschinsky transform can be implemented using a unitary transform inserted into the overlap integral
| | | 〈νf|νi〉 = 〈ν′f|ÛDok|νi〉 | (C5) |
where |
v〉 is a harmonic oscillator eigenstate in the initial coordinate
q and |
v′〉 is a harmonic oscillator eigenstate in the final coordinate
q′. The Doktorov unitary can be decomposed into a product of unitaries, which depend on the displacement vector
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
, the rotation matrix
U, and matrices of the eigenenergies of the harmonic oscillator states
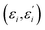
;

and
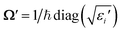
. It is given by
where
| | 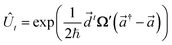 | (C7) |
where
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif)
= (
a0,…,
aM)
T, and
| | 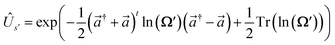 | (C8) |
and
| | 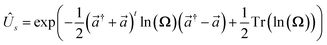 | (C9) |
and
| | 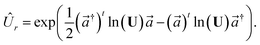 | (C10) |
These exponentials could be expanded into local qubit operators using Trotterization. It is important to note that these relations are only valid when the single-mode basis functions are chosen to be harmonic oscillator eigenstates.
Appendix D: numerical simulation
The simulation results of the vibrational energy levels of SO2 are shown in Fig. 5.
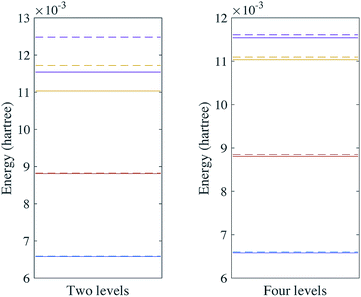 |
| | Fig. 5 Vibrational spectra of SO2 with two and four energy levels for each mode. The solid lines are the energy levels of the harmonic oscillator eigenstates and the dashed lines are the vibrational spectra of the Hamiltonian with a fourth order expansion of the potential. | |
Note added
After this work was released as a preprint, a notable related work was released online.81 That paper provides a quantum algorithm for efficiently calculating the entire converged Franck–Condon profile, as opposed to the method we present herein, which calculates a single Franck–Condon factor. However, the techniques we have discussed for finding vibrational ground states and thermal states provide a way to realise the crucial first step of their algorithm. As such, our two works are highly complementary, and can be compared.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We acknowledge insightful comments from Joonsuk Huh. This work was supported by BP plc and the EPSRC National Quantum Technology Hub in Networked Quantum Information Technology (EP/M013243/1). X. Shan acknowledges the use of the University of Oxford Advanced Research Computing (ARC) facility http://dx.doi.org/10.5281/zenodo.22558.
References
-
T. Helgaker, P. Jorgensen and J. Olsen, Molecular electronic-structure theory, John Wiley & Sons, 2014 Search PubMed.
- R. P. Feynman, Int. J. Theor. Phys., 1982, 21, 467–488 CrossRef.
-
P. W. Shor, 1994 Proceedings, 35th Annual Symposium on Foundations of Computer Science, 1994, pp. 124–134 Search PubMed.
-
L. K. Grover, Proceedings of the twenty-eighth annual ACM symposium on Theory of computing, 1996, pp. 212–219 Search PubMed.
- S. Lloyd, Science, 1996, 273, 1073–1078 CrossRef CAS PubMed.
- D. S. Abrams and S. Lloyd, Phys. Rev. Lett., 1997, 79, 2586–2589 CrossRef CAS.
- D. S. Abrams and S. Lloyd, Phys. Rev. Lett., 1999, 83, 5162–5165 CrossRef CAS.
- A. Aspuru-Guzik, A. D. Dutoi, P. J. Love and M. Head-Gordon, Science, 2005, 309, 1704–1707 CrossRef CAS PubMed.
- A. Aspuru-Guzik, R. Lindh and M. Reiher, ACS Cent. Sci., 2018, 4, 144–152 CrossRef CAS PubMed.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC.
- J. M. Bowman, T. Carrington and H.-D. Meyer, Mol. Phys., 2008, 106, 2145–2182 CrossRef CAS.
- O. Christiansen, J. Chem. Phys., 2004, 120, 2140–2148 CrossRef CAS PubMed.
- J. Huh, G. G. Guerreschi, B. Peropadre, J. R. McClean and A. Aspuru-Guzik, Nat. Photonics, 2015, 9, 615 CrossRef CAS.
- J. Huh and M.-H. Yung, Sci. Rep., 2017, 7, 7462 CrossRef PubMed.
-
W. R. Clements, J. J. Renema, A. Eckstein, A. A. Valido, A. Lita, T. Gerrits, S. W. Nam, W. S. Kolthammer, J. Huh and I. A. Walmsley, arXiv preprint arXiv:1710.08655, 2017.
- Y. Shen, Y. Lu, K. Zhang, J. Zhang, S. Zhang, J. Huh and K. Kim, Chem. Sci., 2018, 9, 836–840 RSC.
- C. Sparrow, E. Martín-López, N. Maraviglia, A. Neville, C. Harrold, J. Carolan, Y. N. Joglekar, T. Hashimoto, N. Matsuda and J. L. OBrien,
et al.
, Nature, 2018, 557, 660 CrossRef CAS PubMed.
-
S. Chin and J. Huh, arXiv preprint arXiv:1803.10002, 2018.
- L. Hu, Y.-C. Ma, Y. Xu, W.-T. Wang, Y.-W. Ma, K. Liu, H.-Y. Wang, Y.-P. Song, M.-H. Yung and L.-Y. Sun, Sci. Bull., 2018, 63, 293–299 CrossRef CAS.
- R. P. de Tudela, F. J. Aoiz, Y. V. Suleimanov and D. E. Manolopoulos, J. Phys. Chem. Lett., 2012, 3, 493–497 CrossRef PubMed.
- S. Karazhanov, M. Ganchenkova and E. Marstein, Chem. Phys. Lett., 2014, 601, 49–53 CrossRef CAS.
- A. Gross and M. Scheffler, J. Vac. Sci. Technol., A, 1997, 15, 1624–1629 CrossRef CAS.
-
T. Seideman, Forming Superposition States, in Computational Molecular Spectroscopy, Wiley, Chichester, 2000, pp. 589–624 Search PubMed.
- F. F. Crim, Proc. Natl. Acad. Sci., 2008, 105, 12654–12661 CrossRef CAS PubMed.
- D. Antoniou and S. D. Schwartz, J. Phys. Chem. B, 2001, 105, 5553–5558 CrossRef CAS.
- D. L. Proctor and H. F. Davis, Proc. Natl. Acad. Sci., 2008, 105, 12673–12677 CrossRef CAS PubMed.
- R. Borrelli, M. D. Donato and A. Peluso, Theor. Chem. Acc., 2006, 117, 957–967 Search PubMed.
- H. Hwang and P. J. Rossky, J. Phys. Chem. A, 2004, 108, 2607–2616 CrossRef CAS.
- C. Zhu, K. K. Liang, M. Hayashi and S. H. Lin, Chem. Phys., 2009, 358, 137–146 CrossRef CAS.
- T.-W. Huang, L. Yang, C. Zhu and S. H. Lin, Chem. Phys. Lett., 2012, 541, 110–116 CrossRef CAS.
- S.-Y. Yue, X. Zhang, G. Qin, J. Yang and M. Hu, Phys. Rev. B, 2016, 94, 115427 CrossRef.
- L. Debbichi, M. C. Marco de Lucas, J. F. Pierson and P. Krger, J. Phys. Chem. C, 2012, 116, 10232–10237 CrossRef CAS.
- S. Dhananasekaran, R. Palanivel and S. Pappu, J. Adv. Res., 2016, 7, 113–124 CrossRef CAS PubMed.
- N. Biswas and S. Umapathy, J. Phys. Chem. A, 1997, 101, 5555–5566 CrossRef CAS.
- K.-W. Choi, J.-H. Lee and S. K. Kim, J. Am. Chem. Soc., 2005, 127, 15674–15675 CrossRef CAS PubMed.
- I. Kassal, S. P. Jordan, P. J. Love, M. Mohseni and A. Aspuru-Guzik, Proc. Natl. Acad. Sci., 2008, 105, 18681–18686 CrossRef CAS PubMed.
- I. D. Kivlichan, N. Wiebe, R. Babbush and A. Aspuru-Guzik, J. Phys. A: Math. Theor., 2017, 50, 305301 CrossRef.
- N. C. Jones, J. D. Whitfield, P. L. McMahon, M.-H. Yung, R. Van Meter, A. Aspuru-Guzik and Y. Yamamoto, New J. Phys., 2012, 14, 115023 CrossRef.
-
A. Szabo and N. S. Ostlund, Modern quantum chemistry: introduction to advanced electronic structure theory, Courier Corporation, 2012 Search PubMed.
- R. Babbush, D. W. Berry, I. D. Kivlichan, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, New J. Phys., 2016, 18, 033032 CrossRef.
- R. Babbush, D. W. Berry, Y. R. Sanders, I. D. Kivlichan, A. Scherer, A. Y. Wei, P. J. Love and A. Aspuru-Guzik, Quantum Sci. Technol., 2017, 3, 015006 CrossRef.
- A. Peruzzo, J. McClean, P. Shadbolt, M.-H. Yung, X.-Q. Zhou, P. J. Love, A. Aspuru-Guzik and J. L. Obrien, Nat. Commun., 2014, 5, 4213 CrossRef CAS PubMed.
- O. Christiansen, Phys. Chem. Chem. Phys., 2007, 9, 2942–2953 RSC.
- O. Christiansen, Phys. Chem. Chem. Phys., 2012, 14, 6672–6687 RSC.
-
J. Huh, PhD thesis, Frankfurt institute for advanced studies, Johann Wolfang Goethe Universitat, Frankfurt, 2011.
- O. Christiansen, J. Chem. Phys., 2004, 120, 2149–2159 CrossRef CAS PubMed.
- S. Joshi, A. Shukla, H. Katiyar, A. Hazra and T. S. Mahesh, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 90, 022303 CrossRef.
- R. D. Somma, G. Ortiz, E. H. Knill and J. Gubernatis, Proc. SPIE, 2003, 5105 Search PubMed.
- E. F. Dumitrescu, A. J. McCaskey, G. Hagen, G. R. Jansen, T. D. Morris, T. Papenbrock, R. C. Pooser, D. J. Dean and P. Lougovski, Phys. Rev. Lett., 2018, 120, 210501 CrossRef CAS PubMed.
- L. Veis, J. Vik, H. Nishizawa, H. Nakai and J. Pittner, Int. J. Quantum Chem., 2016, 116, 1328–1336 CrossRef CAS.
-
A. Y. Kitaev, preprint at http://arxiv.org/abs/quant-ph/9511026, 1995.
- J. R. McClean, R. Babbush, P. J. Love and A. Aspuru-Guzik, J. Phys. Chem. Lett., 2014, 5, 4368–4380 CrossRef CAS PubMed.
-
N. M. Tubman, C. Mejuto-Zaera, J. M. Epstein, D. Hait, D. S. Levine, W. Huggins, Z. Jiang, J. R. McClean, R. Babbush, M. Head-Gordon and K. B. Whaley, arXiv:1809.05523, 2018.
- J. R. McClean, J. Romero, R. Babbush and A. Aspuru-Guzik, New J. Phys., 2016, 18, 023023 CrossRef.
- M.-H. Yung, J. Casanova, A. Mezzacapo, J. McClean, L. Lamata, A. Aspuru-Guzik and E. Solano, Sci. Rep., 2014, 4, 3589 CrossRef PubMed.
- J. Romero, R. Babbush, J. McClean, C. Hempel, P. Love and A. Aspuru-Guzik, Quantum Sci. Technol., 2018, 4, 014008 CrossRef.
-
E. B. Wilson, J. C. Decius and P. C. Cross, Molecular vibrations: the theory of infrared and Raman vibrational spectra, Courier Corporation, 1980 Search PubMed.
- K. Temme, T. J. Osborne, K. G. Vollbrecht, D. Poulin and F. Verstraete, Nature, 2011, 471, 87 CrossRef CAS PubMed.
- M.-H. Yung and A. Aspuru-Guzik, Proc. Natl. Acad. Sci., 2012, 109, 754–759 CrossRef CAS PubMed.
-
S. McArdle, T. Jones, S. Endo, Y. Li, S. Benjamin and X. Yuan, arXiv:1804.03023, 2018.
-
X. Yuan, S. Endo, Q. Zhao, S. Benjamin and Y. Li, 2018, arXiv:1812.08767.
-
M. Motta, C. Sun, A. T. K. Tan, M. J. O. Rourke, E. Ye, A. J. Minnich, F. G. S. L. Brandao and G. K.-L. Chan, 2019, arXiv:1901.07653.
- H. Kupka and P. H. Cribb, J. Chem. Phys., 1986, 85, 1303–1315 CrossRef CAS.
- E. Doktorov, I. Malkin and V. Man'ko, J. Mol. Spectrosc., 1977, 64, 302–326 CrossRef.
-
L. Cincio, Y. Suba, A. T. Sornborger and P. J. Coles, 2018, arXiv:1803.04114.
- H. F. Trotter, Proc. Am. Math. Soc., 1959, 10, 545–551 CrossRef.
- D. W. Berry and A. M. Childs, Quantum Inf. Comput., 2012, 12, 29–62 Search PubMed.
- D. W. Berry, A. M. Childs, R. Cleve, R. Kothari and R. D. Somma, Phys. Rev. Lett., 2015, 114, 090502 CrossRef PubMed.
-
D. W. Berry, A. M. Childs and R. Kothari, 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, 2015, pp. 792–809 Search PubMed.
-
G. H. Low and I. L. Chuang, arXiv:1610.06546, 2016.
-
G. H. Low, arXiv preprint arXiv:1807.03967, 2018.
- G. H. Low, T. J. Yoder and I. L. Chuang, Phys. Rev. X, 2016, 6, 041067 Search PubMed.
- G. H. Low and I. L. Chuang, Phys. Rev. Lett., 2017, 118, 010501 CrossRef PubMed.
- Y. Li and S. C. Benjamin, Phys. Rev. X, 2017, 7, 021050 Search PubMed.
- J. O'Gorman and E. T. Campbell, Phys. Rev. A, 2017, 95, 032338 CrossRef.
-
T. Jones and S. C. Benjamin, arXiv:1811.03147, 2018.
-
M. Reiher and A. Wolf, Relativistic quantum chemistry: the fundamental theory of molecular science, John Wiley & Sons, 2014 Search PubMed.
-
W. Domcke, D. R. Yarkony and H. Köppel, Conical Intersections, World Scientific, 2004 Search PubMed.
- W. Domcke and D. R. Yarkony, Annu. Rev. Phys. Chem., 2012, 63, 325–352 CrossRef CAS PubMed.
- I. G. Ryabinkin, L. Joubert-Doriol and A. F. Izmaylov, Acc. Chem. Res., 2017, 50, 1785–1793 CrossRef CAS PubMed.
-
N. P. D. Sawaya and J. Huh, 2018, arXiv:1812.10495.
- J. T. Seeley, M. J. Richard and P. J. Love, J. Chem. Phys., 2012, 137, 224109 CrossRef PubMed.
-
M. Frisch, http://www.gaussian.com/, 2009.
-
S. McArdle, S. Endo, A. Aspuru-Guzik, S. Benjamin and X. Yuan, 2018, arXiv:1808.10402.
-
Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson, M. Kieferová, I. D. Kivlichan, T. Menke, B. Peropadre, N. P. D. Sawaya, S. Sim, L. Veis and A. Aspuru-Guzik, 2018, arXiv:1812.09976.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
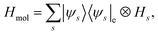
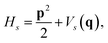
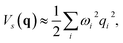
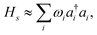
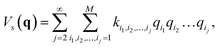
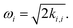 In general, the eigenstates of these Hamiltonians are entangled states, when working in a basis of harmonic oscillator eigenstates. Consequently, solving the higher order vibrational Hamiltonian is a hard problem for classical computers.
In general, the eigenstates of these Hamiltonians are entangled states, when working in a basis of harmonic oscillator eigenstates. Consequently, solving the higher order vibrational Hamiltonian is a hard problem for classical computers.
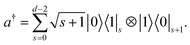
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d]′ qubits,
d]′ qubits,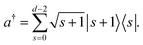
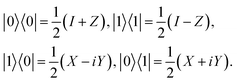

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(d) (compact mapping) qubits. This can be contrasted with the exponentially scaling classical memory required to store the wavefunction. If the potential is expanded to kth order (with M ≫ k), the Hamiltonian contains O(Mkdk) (direct) or O(Mkd2k) (compact) terms. These terms are strings of local Pauli matrices. In this work, we take d to be a small constant. This approximation constrains us to the low energy subspace of the Hamiltonian, which should be valid for calculations of ground and low-lying excited states. The applicability of this approximation to the simulation of dynamics is discussed in Section VI. We set k = 4 to investigate the Hamiltonian to quartic order. The resulting Hamiltonian has O(M4) terms.
log(d) (compact mapping) qubits. This can be contrasted with the exponentially scaling classical memory required to store the wavefunction. If the potential is expanded to kth order (with M ≫ k), the Hamiltonian contains O(Mkdk) (direct) or O(Mkd2k) (compact) terms. These terms are strings of local Pauli matrices. In this work, we take d to be a small constant. This approximation constrains us to the low energy subspace of the Hamiltonian, which should be valid for calculations of ground and low-lying excited states. The applicability of this approximation to the simulation of dynamics is discussed in Section VI. We set k = 4 to investigate the Hamiltonian to quartic order. The resulting Hamiltonian has O(M4) terms.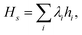 where λi are coefficients determining the strength of each term in the Hamiltonian.
where λi are coefficients determining the strength of each term in the Hamiltonian.
![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) )〉 = exp(
)〉 = exp(![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −
− ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †)|Ψ0〉,
†)|Ψ0〉,![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is the sum of molecular excitation operators truncated at a specified excitation rank, and
is the sum of molecular excitation operators truncated at a specified excitation rank, and ![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) are the parameters defined below. Similar to the unitary coupled cluster ansatz in electronic structure problems, the single and double excitation operators are
are the parameters defined below. Similar to the unitary coupled cluster ansatz in electronic structure problems, the single and double excitation operators are![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 +
1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 +…,
2 +…,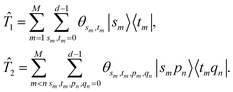
![[small theta, Greek, vector]](https://www.rsc.org/images/entities/i_char_e1c8.gif) = {θsm,tm,θsm,tm,pm,qn}. The
= {θsm,tm,θsm,tm,pm,qn}. The ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) operators can be mapped to qubit operators via either the direct or compact mapping.
operators can be mapped to qubit operators via either the direct or compact mapping.
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |ψi〉|2, using first order time-dependent perturbation theory. Within the Condon approximation,
|ψi〉|2, using first order time-dependent perturbation theory. Within the Condon approximation, ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) =
= ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) e +
e + ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) N, the transition probability becomes proportional to P2 = |〈ψfvib|ψivib〉|2·|〈f|
N, the transition probability becomes proportional to P2 = |〈ψfvib|ψivib〉|2·|〈f|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) e|i〉|2. Here |〈ψfvib|ψivib〉|2 are referred to as Franck–Condon integrals. Without the Condon approximation, the Franck–Condon integrals become |〈ψfvib|
e|i〉|2. Here |〈ψfvib|ψivib〉|2 are referred to as Franck–Condon integrals. Without the Condon approximation, the Franck–Condon integrals become |〈ψfvib|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (q)|ψivib〉|2, with
(q)|ψivib〉|2, with ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (q) = |〈f|
(q) = |〈f|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) |i〉|2.
|i〉|2.
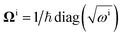 and
and 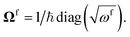 The definitions of the unitary operators are shown in Appendix C.
The definitions of the unitary operators are shown in Appendix C.
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (q)|ψivib〉2 = |〈Ψfvib|
(q)|ψivib〉2 = |〈Ψfvib|![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) (qf)ÛDok|Ψivib〉|2.
(qf)ÛDok|Ψivib〉|2.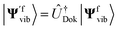 and calculate the Franck–Condon integrals without realising the Doktorov transform. However, as the Hamiltonian H′f(qi) is not encoded in the correct normal mode basis, the ground state of the harmonic oscillators or the VSCF state |ΨVSCF〉 may not be an ideal initial state to start with. However, this effect may be negligible if the overlap between |Ψivib〉 and
and calculate the Franck–Condon integrals without realising the Doktorov transform. However, as the Hamiltonian H′f(qi) is not encoded in the correct normal mode basis, the ground state of the harmonic oscillators or the VSCF state |ΨVSCF〉 may not be an ideal initial state to start with. However, this effect may be negligible if the overlap between |Ψivib〉 and 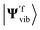 is suitably large. In this case, the initial state |Ψ0〉 for |Ψivib〉 should also be an ideal initial state for
is suitably large. In this case, the initial state |Ψ0〉 for |Ψivib〉 should also be an ideal initial state for 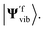 The aforementioned transformation can be implemented by transforming the normal mode coordinates qi as described in ref. 45.
The aforementioned transformation can be implemented by transforming the normal mode coordinates qi as described in ref. 45.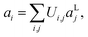
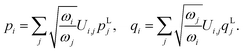
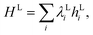 the time evolution operator e−iHLt can be realised using a product formula,
the time evolution operator e−iHLt can be realised using a product formula,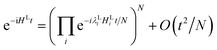
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 646 × 10−8
646 × 10−8![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and encode it into a linear combination of local Pauli terms, i.e.,
and encode it into a linear combination of local Pauli terms, i.e.,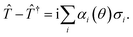
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −
− ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †) by a first order Trotterisation via
†) by a first order Trotterisation via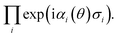 For example, the UVCC ansatz of H2O with two energy levels can be prepared by the circuit in Fig. 3.
For example, the UVCC ansatz of H2O with two energy levels can be prepared by the circuit in Fig. 3.

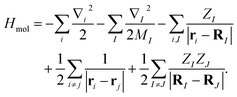
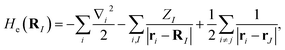
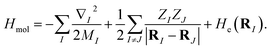
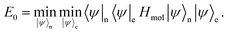
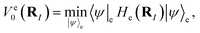
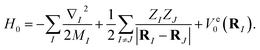
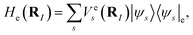 the molecular Hamiltonian is
the molecular Hamiltonian is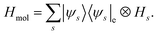
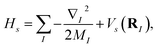
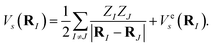
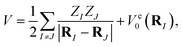 then one can obtain the mass-weighted normal coordinates qi by minimising the coupling between the rotational and vibrational degrees of freedom and diagonalising the Hessian matrix,
then one can obtain the mass-weighted normal coordinates qi by minimising the coupling between the rotational and vibrational degrees of freedom and diagonalising the Hessian matrix,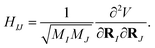
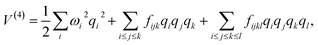
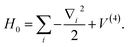
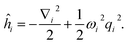
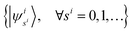 , then the nuclear wave function can be represented by
, then the nuclear wave function can be represented by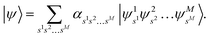
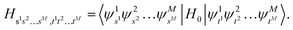
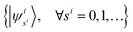 is truncated to the lowest d energy levels, the space of Hs1s2…sM,t1t2…tM is equivalent to the space of M d-level systems, or equivalently M
is truncated to the lowest d energy levels, the space of Hs1s2…sM,t1t2…tM is equivalent to the space of M d-level systems, or equivalently M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log2
log2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d qubits.
d qubits.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) −
− ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) †)|Φ0〉
†)|Φ0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) =
= ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 +
1 + ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 2 +…
2 +…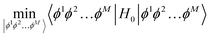
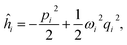
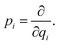 The operators q1 and p1 can be represented by the creation and annihilation operators
The operators q1 and p1 can be represented by the creation and annihilation operators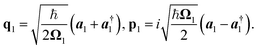
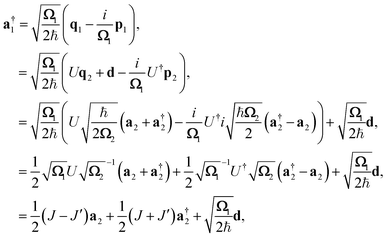
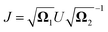 and
and 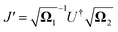 .
.
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) , the rotation matrix U, and matrices of the eigenenergies of the harmonic oscillator states
, the rotation matrix U, and matrices of the eigenenergies of the harmonic oscillator states 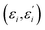 ;
;  and
and 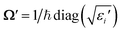 . It is given by
. It is given by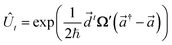
![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) = (a0,…,aM)T, and
= (a0,…,aM)T, and