Open Access Article
Open Access ArticleNucleophilic substitution reactions of cyclic thiosulfinates are accelerated by hyperconjugative interactions†
Daniel P.
Donnelly
 ab,
Jeffrey N.
Agar
ab,
Jeffrey N.
Agar
 ab and
Steven A.
Lopez
ab and
Steven A.
Lopez
 *a
*a
aDepartment of Chemistry and Chemical Biology, Northeastern University, 360 Huntington Avenue, Boston, Massachusetts 02115, USA
bBarnett Institute of Chemical and Biological Analysis, Northeastern University, 360 Huntington Avenue, Boston, Massachusetts 02115, USA
First published on 29th April 2019
Abstract
Cyclic thiosulfinates are a class of biocompatible molecules, currently expanding our in vivo toolkit. Agar and co-workers have shown that they are capable of efficient cross-linking reactions. While strain energy has been shown to promote the nucleophilic substitution reactions of cyclic disulfides, the reactivities of cyclic thiosulfinate nucleophilic substitution is unexplored. We used density functional theory calculations [M06-2X/6-311++G(d,p)] to determine the activation and reaction free energies for the reactions of 3–10-membered cyclic thiosulfinates and cyclic disulfides with methyl thiolate. The nucleophilic substitution reaction of cyclic thiosulfinates was found to be strain-promoted, similar to the strain-promoted nucleophilic substitution reactions of cyclic disulfides. The origin of the nearly 100-fold rate enhancement of cyclic thiosulfinates over cyclic disulfides was understood using the distortion/interaction model and natural bond order analysis. The cyclic thiosulfinates benefit from a hyperconjugative interaction between an oxygen lone pair and the  orbital
orbital  . This interaction generally lengthens the reactant S1–S2 bond, which pre-distorts cyclic thiosulfinates to resemble their corresponding transition structures. The inductive effect of the oxygen in cyclic thiosulfinates lowers the
. This interaction generally lengthens the reactant S1–S2 bond, which pre-distorts cyclic thiosulfinates to resemble their corresponding transition structures. The inductive effect of the oxygen in cyclic thiosulfinates lowers the  orbital energies relative to cyclic disulfides and results in more stabiliizing transition state frontier molecular orbital interactions with methyl thiolate.
orbital energies relative to cyclic disulfides and results in more stabiliizing transition state frontier molecular orbital interactions with methyl thiolate.
Introduction
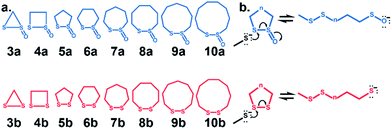
Cyclic disulfides are a privileged class of molecules that have long played important roles in energy metabolism and the modulation of cellular redox status.1–6 Recently, they have been used for in vivo applications in biochemistry and biomaterials as building blocks for self-healing, biocompatible polymers, and hydrogels.7,8 They can also serve as vehicles to shuttle large molecules and apoptosis-inducing substrates through cell membranes via the transferrin receptor.9–12 In many cases, α-lipoic acid, a cyclic disulfide, has been used in a variety of functional assemblies at the gold surface.13–15 Cyclic disulfides are one of the first known cross-linking-specific molecules; Agar and co-workers showed that they could selectively cross-link cysteine pairs while reversibly modifying lone cysteines in vivo.16 Our groups recently introduced a six-membered cyclic thiosulfinate (1,2-dithiane-1-oxide) capable of cross-linking free cysteine pairs up to 104-fold faster than a six-membered cyclic disulfide (1,2-dithiane), by circumventing the rate-determining oxidation step.16 A covalent cross-link is efficiently formed between the sulfenic acid intermediate and a second thiolate. Whitesides and coworkers augmented their experiments with MM2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 calculations to show that the reactivities of cyclic disulfides towards biological thiolate-based nucleophiles were strain-promoted.18,19 Bachrach and co-workers used DFT calculations to locate transition structures for the nucleophilic substitution reactions of a model thiolate to a series of cyclic disulfides.20 This computational study builds on the results of Whitesides and Bachrach to determine the origin of the increased nucleophilic substitution reactivities of 3–10-membered cyclic thiosulfinates relative to cyclic disulfides (Scheme 1). A rigorous conformational search was employed to identify the global minima of reactants, ring-opened intermediates, and the lowest-energy transition structures. The DFT calculations are used to predict the reactivities of 3–10-membered cyclic thiosulfinates (3–10)a towards a model thiolate (methyl thiolate) by locating transition structures and disulfide-exchange intermediates. The corresponding activation free energies and reaction energies (ΔG‡ and ΔGrxn, respectively) were compared to those of an analogous series of cyclic disulfides to understand why cyclic thiosulfinates are more reactive than cyclic disulfides towards thiolates.
17 calculations to show that the reactivities of cyclic disulfides towards biological thiolate-based nucleophiles were strain-promoted.18,19 Bachrach and co-workers used DFT calculations to locate transition structures for the nucleophilic substitution reactions of a model thiolate to a series of cyclic disulfides.20 This computational study builds on the results of Whitesides and Bachrach to determine the origin of the increased nucleophilic substitution reactivities of 3–10-membered cyclic thiosulfinates relative to cyclic disulfides (Scheme 1). A rigorous conformational search was employed to identify the global minima of reactants, ring-opened intermediates, and the lowest-energy transition structures. The DFT calculations are used to predict the reactivities of 3–10-membered cyclic thiosulfinates (3–10)a towards a model thiolate (methyl thiolate) by locating transition structures and disulfide-exchange intermediates. The corresponding activation free energies and reaction energies (ΔG‡ and ΔGrxn, respectively) were compared to those of an analogous series of cyclic disulfides to understand why cyclic thiosulfinates are more reactive than cyclic disulfides towards thiolates.
Results and discussion
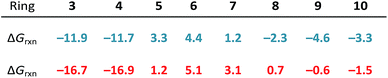
Ring strain is released upon nucleophilic addition of MeS−; as such, we defined strain energy as −ΔGrxn. We computed reaction energies (ΔGrxn) for the nucleophilic addition of MeS− to (3–10)a and (3–10)b to assess the reversibilities of the nucleophilic substitution reactions. These energies are summarized in Table 1.For the most strained reactants, (3–4)a and (3–4)b, the reaction energies for the nucleophilic addition of MeS− range from −11.9 to −11.7 and −16.9 to −16.7 kcal mol−1, respectively. These reactions are exergonic because ring strain is released upon ring-opening. (5–7)a and (5–7)b lead to endergonic reaction energies ranging from 1.2 to 4.4 kcal mol−1 and 1.2 to 5.1 kcal mol−1, respectively. The larger cyclic structures, (8–10)a and (8–10)b have reaction free energies that range from −2.3 to −4.6 kcal mol−1 and +0.7 to −1.5 kcal mol−1, respectively.
The reaction energies of these series follow a similar trend to cycloalkanes in which (3–4)a and (3–4)b are significantly strained, (5–7)a and (5–7)b are relatively unstrained, and (8–10)a and (8–10)b are moderately strained.20–22 The longer S1–S2 bond in the thiacycles relieves some strain compared the corresponding cycloalkanes (e.g., 1,2-dithiolane vs. cyclopentane).
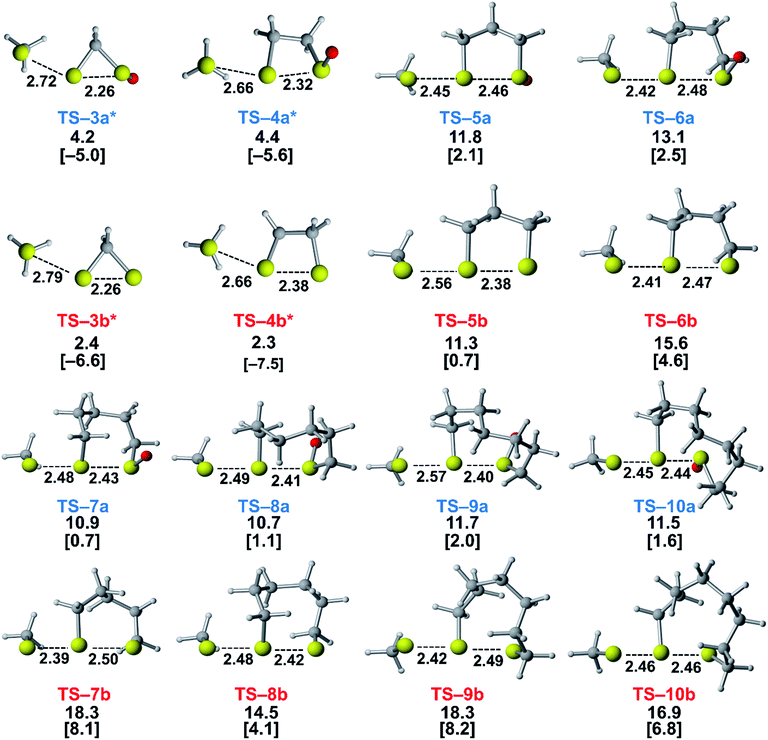
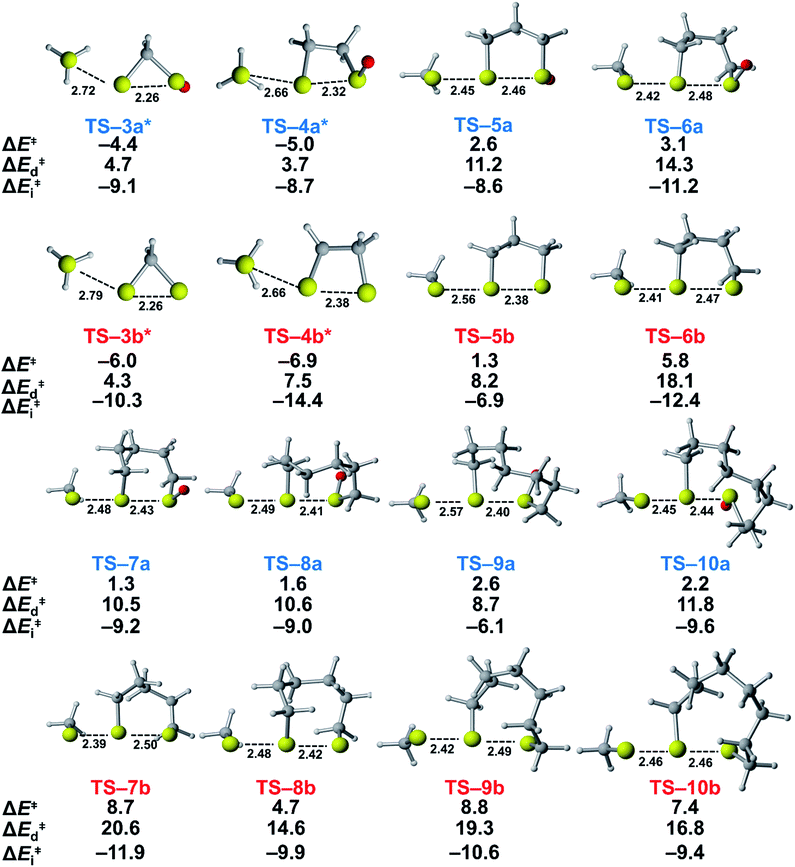
We assessed the reactivities of the cyclic thiosulfinates and cyclic disulfides towards methyl thiolate by locating transition structures and computing their corresponding activation free energies and enthalpies (Fig. 1). The transition structures shown in Fig. 1 generally have a nearly linear MeS−–S1–S2 angle; the transition states range from exactly synchronous to asynchronous. The breaking S1–S2 bonds of TS-(3–10)a and TS-(3–10)b range from 2.26–2.48 Å and 2.26–2.50 Å, respectively. The S–S1 distance in TS-(3–10)a and TS-(3–10)b ranges from 2.42–2.72 Å and 2.39–2.79 Å, respectively. TS-10b is exactly synchronous (2.46 Å), while TS-5b is the most asynchronous (2.56 and 2.38 Å). The C–C and C–S σ bonds of (3–4)a and (3–4)b are well-described by Walsh orbitals due to the nearly 60° and 90° bonding angles, respectively. As such, incipient nucleophiles will interact with bent S1–S2 σ* orbitals, which results in the non-linear transition state geometries of TS-(3–4)a and TS-(3–4)b. The activation free energies of the smallest rings TS-(3–4)a and TS-(3–4)b are the lowest (2.3–4.4 kcal mol−1). The low activation energies of (3–4)a and (3–4)b are consistent with the established strain-promoted reactions of cyclic disulfides. The activation free of energies of TS-(5–10)a are generally higher and range from 10.9 to 13.1 kcal mol−1. The activation free energies of TS-(6–10)a are substantially lower than those of TS-(6–10)b; ΔΔG‡ range from −2.5 to −7.4 kcal mol−1, which corresponds to a 102–105-fold rate enhancement for cyclic thiosulfinates relative to cyclic disulfides.
Are these reactions strain promoted?
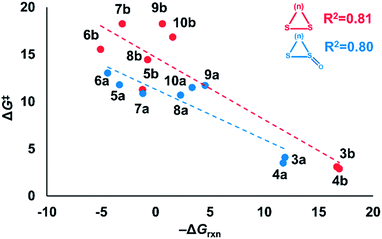
Nucleophilic substitution reactions of cyclic disulfides are often described as strain-promoted.18,20,23 We assessed the role of strain energy on the reactivities of (3–10)a and (3–10)b by plotting ΔG‡ against −ΔGrxn (Fig. 2).Fig. 2 shows a linear correlation between ΔG‡ and −ΔGrxn for the cyclic disulfide and cyclic thiosulfinate reactions (R2 = 0.81 and 0.80, respectively). This suggests that strain energy controls the reactivities for a broad set of cyclic disulfides and establishes that the reactivities of cyclic thiosulfinates are also controlled by strain energy. The activation free energies of cyclic thiosulfinates are generally lower than those of cyclic disulfides; the y-intercept values are 11.3 and 14.7 kcal mol−1, respectively.
Distortion/interaction model
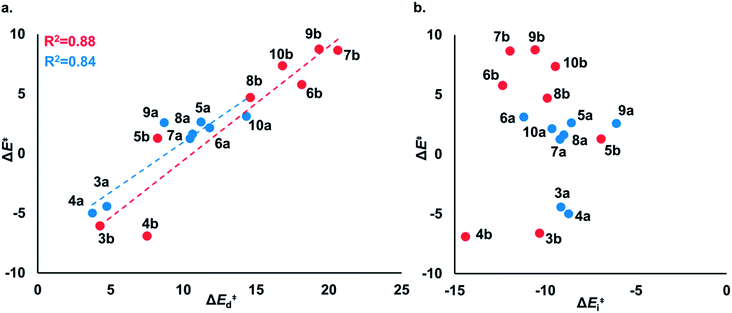
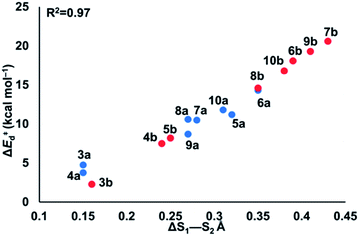
To understand the origin of generally lower activation barriers and strain energies of cyclic thiosulfinates relative to the cyclic disulfides, we turned to the distortion/interaction model.24–26 The distortion/interaction model dissects activation barriers for bimolecular reactions into two terms: distortion and interaction energy [ΔE‡ = ΔE‡d + ΔE‡i]. Distortion energy (ΔE‡d) is the energy required to deform reactants from their equilibrium structures to their distorted transition structure geometries without allowing them to interact. Interaction energy (ΔE‡i) results from the difference in ΔE‡ and ΔE‡d and has been attributed to favorable intermolecular electrostatic, dispersion, and charge transfer interactions. The distortion/interaction model has been used to explain the reactivities and selectivities of pericyclic27–30 and organometallic31–33 reactions. The computed distortion and interaction energies of TS-(3–10)a and TS-(3–10)b are summarized in Fig. 3.The distortion energies of cyclic thiosulfinates (3–10)a range from 3.7 to 14.3 kcal mol−1 and the distortion energies of cyclic disulfides (3–10)b range from 4.3 to 20.6 kcal mol−1. We plotted activation energies against distortion energies for the reactions of cyclic thiosulfinates (blue) and cyclic disulfides (red) in Fig. 4. These plots show that there is a linear relationship between ΔE‡ and ΔE‡d for cyclic disulfides (R2 = 0.88) and cyclic thiosulfinates (R2 = 0.84). This suggests that the reactivities are controlled by distortion energy. The interaction energies of cyclic thiosulfinates (3–10)a and cyclic disulfides (3–10)b range from −6.1 to −11.2 kcal mol−1 and −6.9 to −14.4 kcal mol−1, respectively. There is no correlation between ΔE‡ and ΔE‡i (R2 = 0.001 for cyclic thiosulfinates and R2 = 0.05 for cyclic disulfides), which implies that the interaction energies do not influence reactivities. We hypothesized that the strain energy would manifest itself as a structural pre-distortion of the reactants, an effect that results in distortion-accelerated reactions.34 To this end, we analyzed (3–10)a and (3–10)b in their equilibrium and distorted transition state geometries; strained cyclic thiosulfinates and disulfides require less distortion to achieve their transition state geometries. This is demonstrated in Fig. 5, where we show the relationship between distortion energy and the difference in S1–S2 bond lengths in the reactant and transition state (ΔS1–S2).
The reactions with the lowest activation energies resulted from reactants with the longest (pre-distorted) S1–S2 bonds at equilibrium. The linear relationship between ΔE‡d and ΔS1–S2 (R2 = 0.97) confirms that the S1–S2 pre-distortion of cyclic thiosulfinates results in lower activation energies.
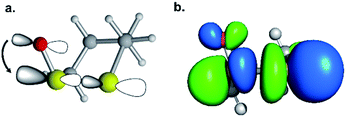
We then scrutinized the geometric and electronic structures of the cyclic thiosulfinates to understand why they are more pre-distorted than the cyclic disulfides. One of the oxygen lone pair orbitals adjacent to the S1–S2 bond is ideally positioned for a hyperconjugative interaction with the  orbital, via the general anomeric effect, which stabilizes the developing electron deficiency in the breaking S1–S2 bond. There is a rich literature on this effect from the experimental and theoretical communities.35–42Fig. 6 illustrates the possible
orbital, via the general anomeric effect, which stabilizes the developing electron deficiency in the breaking S1–S2 bond. There is a rich literature on this effect from the experimental and theoretical communities.35–42Fig. 6 illustrates the possible  orbital interaction.
orbital interaction.
We quantified this effect with natural bond order (NBO)43 calculations and second order perturbation theory analysis on the optimized structures of the cyclic thiosulfinates. Table 2 shows the hyperconjugative  interaction energies, and the effect on S1–S2 bond lengths.
interaction energies, and the effect on S1–S2 bond lengths.
 energies, and the interaction energies between the nO and
energies, and the interaction energies between the nO and  orbitals
orbitals
| S1–S2a | Energy, nOb | Energy, b | ||
|---|---|---|---|---|
a S1–S2 bond lengths are reported in Å.
b
 energies are reported in kcal mol−1. energies are reported in kcal mol−1.
|
||||
| 3a | 2.12 | −10.07 | −0.54 | −47.3 |
| 4a | 2.17 | −9.87 | −0.17 | −40.3 |
| 5a | 2.14 | −9.74 | 0.38 | −35.8 |
| 6a | 2.13 | −9.74 | 0.47 | −35.4 |
| 7a | 2.15 | −9.75 | 0.32 | −36.9 |
| 8a | 2.14 | −9.77 | 0.45 | −35.9 |
| 9a | 2.13 | −9.69 | 0.53 | −33.9 |
| 10a | 2.13 | −9.70 | 0.53 | −35.8 |
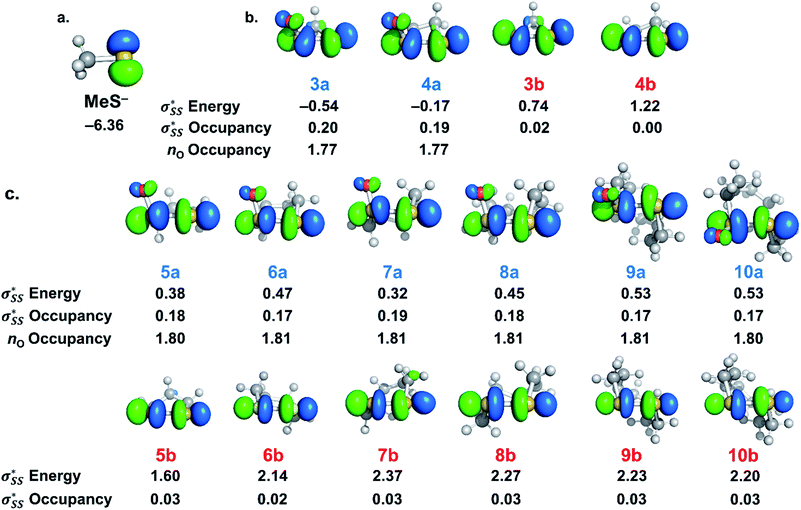
S1–S2 bond distances, energies for the nO and  orbitals participating in the hyperconjugative interaction, and the energies of the corresponding
orbitals participating in the hyperconjugative interaction, and the energies of the corresponding  interactions are given in Table 2. The σ framework of 3a and 4a have relatively high-lying σ orbitals because of the increased p-character associated with the so-called banana bonds.44 As such, 3a and 4a benefit from smaller energy gaps between the nO and
interactions are given in Table 2. The σ framework of 3a and 4a have relatively high-lying σ orbitals because of the increased p-character associated with the so-called banana bonds.44 As such, 3a and 4a benefit from smaller energy gaps between the nO and  orbitals, which results in
orbitals, which results in  interaction energies of −47.3 and −40.3 kcal mol−1, respectively. (5–10)a have smaller, but similar, orbital interaction energies (−33.9 to −36.9 kcal mol−1), because of the larger energy gap between the nO and
interaction energies of −47.3 and −40.3 kcal mol−1, respectively. (5–10)a have smaller, but similar, orbital interaction energies (−33.9 to −36.9 kcal mol−1), because of the larger energy gap between the nO and  orbitals and linear
orbitals and linear  orbitals.
orbitals.
We then compared the  orbital energies of cyclic thiosulfinates to those of cyclic disulfides to quantify the extent in which the
orbital energies of cyclic thiosulfinates to those of cyclic disulfides to quantify the extent in which the  hyperconjugative interaction contributes to nucleophilic substitution rate-enhancement. The HOMO energy of methyl thiolate, the
hyperconjugative interaction contributes to nucleophilic substitution rate-enhancement. The HOMO energy of methyl thiolate, the  orbital (LUMO) energies of (3–10)a and (3–10)b, and the occupancies of the
orbital (LUMO) energies of (3–10)a and (3–10)b, and the occupancies of the  and nO orbitals are shown in Fig. 7.
and nO orbitals are shown in Fig. 7.
The  energies of cyclic thiosulfinates range from −0.54 to 0.53 eV; the
energies of cyclic thiosulfinates range from −0.54 to 0.53 eV; the  energies of cyclic disulfides range from 0.74 to 2.37 eV. The
energies of cyclic disulfides range from 0.74 to 2.37 eV. The  orbitals of cyclic thiosulfinates are relatively low-lying because of the adjacent oxygen that is inductively electron withdrawing. The electron density of the sulfoxide oxygen disfavors nucleophilic attack of thiolates at S1 because of substantial closed-shell repulsions with the incipient thiolate lone pair orbitals. (3–4)a and (3–4)b feature bent
orbitals of cyclic thiosulfinates are relatively low-lying because of the adjacent oxygen that is inductively electron withdrawing. The electron density of the sulfoxide oxygen disfavors nucleophilic attack of thiolates at S1 because of substantial closed-shell repulsions with the incipient thiolate lone pair orbitals. (3–4)a and (3–4)b feature bent  orbitals because of the small C–S–S bond angles in the three- and four-membered rings (54° and 78°, respectively). The nO orbitals of cyclic thiosulfinates have reduced occupancies (1.77–1.81e) from the ideal value of 2.00e due to the hyperconjugative interaction; the
orbitals because of the small C–S–S bond angles in the three- and four-membered rings (54° and 78°, respectively). The nO orbitals of cyclic thiosulfinates have reduced occupancies (1.77–1.81e) from the ideal value of 2.00e due to the hyperconjugative interaction; the  orbitals of cyclic thiosulfinates have increased occupancies (0.17–0.20e) from the ideal value of 0.00e. The large stabilizing
orbitals of cyclic thiosulfinates have increased occupancies (0.17–0.20e) from the ideal value of 0.00e. The large stabilizing  energies corroborate the proposed hyperconjugation between the nO and the
energies corroborate the proposed hyperconjugation between the nO and the  orbitals. Cyclic disulfides have a significantly lower occupancy of the
orbitals. Cyclic disulfides have a significantly lower occupancy of the  orbitals ranging from 0.00–0.03e. The generally lower
orbitals ranging from 0.00–0.03e. The generally lower  orbital energies of cyclic thiosulfinates, resulting from the
orbital energies of cyclic thiosulfinates, resulting from the  interaction, lead to stronger frontier molecular orbital interactions with the MeS− lone pair orbitals in the transition state. These more favorable interactions contribute to the general rate-enhancement of nucleophilic substitution towards cyclic thiosulfinates.
interaction, lead to stronger frontier molecular orbital interactions with the MeS− lone pair orbitals in the transition state. These more favorable interactions contribute to the general rate-enhancement of nucleophilic substitution towards cyclic thiosulfinates.
Methods
Initial conformational searches of all structures studied were performed within Maestro 11 (ref. 45) using low-mode sampling with a maximum atom deviation cutoff of 0.5 Å within the OPLS3e force field in the dielectric constant of water (ε = 78).46 Each conformational search produced as maximum of 10 low energy conformations (energy cutoff = 100 kJ mol−1). Each of these OPLSe-minimized structures were subjected to geometrical optimization using the hybrid density functional M06-2X/6-311++G(d,p) and the polarizable continuum model using the integral equation formalism variant (IEF-PCM) with the parameters for water.47,48 Each stationary point was subjected to vibrational analysis from which exactly one negative frequency was identified for transition structures and an absence of negative frequencies for the minima. All DFT calculations were performed using the Gaussian 16 (ref. 49) program. All stationary points for (5–10)a and (5–10)b were optimized using M06-2X/6-311++G(d,p). Transition state scans of (3–4)a and (3–4)b were performed using the coupled cluster method (CCSD).50 The distance between methyl thiolate and the cyclic disulfide/thiosulfinate was scanned between 2.3–2.8 Å. 9 steps at 0.04 Å per step were taken. Each result from this scan was optimized by constraining the forming MeS−–S2 bond distance using the coupled cluster singles doubles method (CCSD) with the 6-31+G(d,p) basis set. Single point energy calculations were performed on the constrained transition structures with the same method and basis set [M06-2X/6-311++G(d,p)] as the unconstrained transition states to evaluate activation free energies. NBO analysis and second order perturbation theory analysis on the optimized cyclic thiosulfate reactants was performed to measure the interaction between the oxygen lone pair and the orbital and the corresponding orbital energies and occupancies. All chemical structures were prepared using CylView.51 The ESI† was prepared using ESIgen.52
orbital and the corresponding orbital energies and occupancies. All chemical structures were prepared using CylView.51 The ESI† was prepared using ESIgen.52
Conclusions
We used DFT calculations to predict the reactivities of a series of 3–10-membered cyclic thiosulfinates towards methyl thiolate for the first time. Similar to previous reports of cyclic disulfide reactivity, the reaction of thiolates towards cyclic thiosulfinates is strain-promoted. Our calculations suggest that the rate of nucleophilic substitution reactions of 6–10-membered cyclic thiosulfinates will be 102–105-fold faster than 6–10-membered cyclic disulfides. Our calculations show that (3–4)a and (3–4)b have bent orbitals that contribute to their significantly higher strain-dependence and lower activation barriers through increased p-character. The S1–S2 bonds in cyclic thiosulfinates (6–10)a are pre-distorted towards their transition structures and require less distortion energy (ΔE‡d) to deform reactants from their equilibrium geometries relative to corresponding cyclic disulfides (6–10)b. This results in generally lower activation barriers. A hyperconjugative interaction between the oxygen lone pair and the
orbitals that contribute to their significantly higher strain-dependence and lower activation barriers through increased p-character. The S1–S2 bonds in cyclic thiosulfinates (6–10)a are pre-distorted towards their transition structures and require less distortion energy (ΔE‡d) to deform reactants from their equilibrium geometries relative to corresponding cyclic disulfides (6–10)b. This results in generally lower activation barriers. A hyperconjugative interaction between the oxygen lone pair and the  orbitals
orbitals  is responsible for the pre-distortion of cyclic thiosulfinates and was verified by decreased occupancies of nO orbitals and increased occupancies of
is responsible for the pre-distortion of cyclic thiosulfinates and was verified by decreased occupancies of nO orbitals and increased occupancies of  orbitals. The activation barriers are further lowered because the
orbitals. The activation barriers are further lowered because the  orbital energies are decreased by an inductive effect of the adjacent oxygen, which improves transition state frontier molecular orbital interactions. This effect is not observed in cyclic disulfides which have higher energy
orbital energies are decreased by an inductive effect of the adjacent oxygen, which improves transition state frontier molecular orbital interactions. This effect is not observed in cyclic disulfides which have higher energy  orbitals. These theoretical insights have begun to guide our development of new cross-linking tools that avoid toxic dead-end modifications and increase reaction rates in vitro and in vivo. We predict that cyclic thiosulfinate 7a will make the best cross-linking scaffold. Its relatively low strain energy results in a reversible nucleophilic substitution reaction, which will prevent off-target (dead-end) modification of cysteine residues. Additionally, the nucleophilic substitution towards 7a is 7.4 kcal mol−1 lower in activation energy than 7b, resulting in a 105-fold increase in reaction rate.
orbitals. These theoretical insights have begun to guide our development of new cross-linking tools that avoid toxic dead-end modifications and increase reaction rates in vitro and in vivo. We predict that cyclic thiosulfinate 7a will make the best cross-linking scaffold. Its relatively low strain energy results in a reversible nucleophilic substitution reaction, which will prevent off-target (dead-end) modification of cysteine residues. Additionally, the nucleophilic substitution towards 7a is 7.4 kcal mol−1 lower in activation energy than 7b, resulting in a 105-fold increase in reaction rate.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. A. L. thanks the NSF through the Extreme Science and Engineering Discovery Environment (TG-CHE170074), the Discovery HPC Cluster for computational resources, and NEU for financial support. D. P. D is funded by in part by the NIH R01NS065263, the Robert Johnston Foundation, and ALSA 18-IIA-420.Notes and references
- L. J. Reed, B. G. DeBusk, I. C. Gunsalus and C. S. Hornberger, Science, 1951, 114, 93–94 CrossRef CAS PubMed.
- A. Solmonson and R. J. DeBerardinis, J. Biol. Chem., 2018, 293, 7522–7530 CrossRef CAS PubMed.
- K. P. Shay, R. F. Moreau, E. J. Smith, A. R. Smith and T. M. Hagen, Biochim. Biophys. Acta, 2009, 1790, 1149–1160 CrossRef CAS PubMed.
- H. R. Rosenberg and R. Culik, Arch. Biochem. Biophys., 1959, 80, 86–93 CrossRef CAS.
- P. Ou, H. J. Tritschler and S. P. Wolff, Biochem. Pharmacol., 1995, 50, 123–126 CrossRef CAS PubMed.
- E. L. Feldman, J. Clin. Invest., 2003, 111, 431–433 CrossRef CAS PubMed.
- H. Ishida, A. Kisanuki and K. Endo, Polym. J., 2008, 41, 110 CrossRef.
- H. Yu, Y. Wang, H. Yang, K. Peng and X. Zhang, J. Mater. Chem. B, 2017, 5, 4121–4127 RSC.
- D. Abegg, G. Gasparini, D. G. Hoch, A. Shuster, E. Bartolami, S. Matile and A. Adibekian, J. Am. Chem. Soc., 2017, 139, 231–238 CrossRef CAS PubMed.
- P. Morelli and S. Matile, Helv. Chim. Acta, 2017, 100, e1600370 CrossRef.
- L. Zong, E. Bartolami, D. Abegg, A. Adibekian, N. Sakai and S. Matile, ACS Cent. Sci., 2017, 3, 449–453 CrossRef CAS PubMed.
- N. Chuard, G. Gasparini, D. Moreau, S. Lorcher, C. Palivan, W. Meier, N. Sakai and S. Matile, Angew. Chem., Int. Ed. Engl., 2017, 56, 2947–2950 CrossRef CAS PubMed.
- Y. Dong, S. Abaci, C. Shannon and M. J. Bozack, Langmuir, 2003, 19, 8922–8926 CrossRef CAS.
- S. Roux, B. Garcia, J.-L. Bridot, M. Salomé, C. Marquette, L. Lemelle, P. Gillet, L. Blum, P. Perriat and O. Tillement, Langmuir, 2005, 21, 2526–2536 CrossRef CAS PubMed.
- J. M. Abad, S. F. L. Mertens, M. Pita, V. M. Fernández and D. J. Schiffrin, J. Am. Chem. Soc., 2005, 127, 5689–5694 CrossRef CAS PubMed.
- D. P. Donnelly, M. G. Dowgiallo, J. P. Salisbury, K. C. Aluri, S. Iyengar, M. Chaudhari, M. Mathew, I. Miele, J. R. Auclair, S. A. Lopez, R. Manetsch and J. N. Agar, J. Am. Chem. Soc., 2018, 140, 7377–7380 CrossRef CAS PubMed.
- N. L. Allinger, J. Am. Chem. Soc., 1977, 99, 8127–8134 CrossRef CAS.
- J. A. Burns and G. M. Whitesides, J. Am. Chem. Soc., 1990, 112, 6296–6303 CrossRef CAS.
- R. Singh and G. M. Whitesides, J. Am. Chem. Soc., 1990, 112, 6304–6309 CrossRef CAS.
- S. M. Bachrach, J. T. Woody and D. C. Mulhearn, J. Org. Chem., 2002, 67, 8983–8990 CrossRef CAS PubMed.
- P. Hanson, R. A. A. J. Hendrickx and J. R. Lindsay Smith, New J. Chem., 2010, 34, 65–84 RSC.
- J. A. Boatz, M. S. Gordon and R. L. Hilderbrandt, J. Am. Chem. Soc., 1988, 110, 352–358 CrossRef CAS.
- É. Dumont, P.-F. Loos and X. Assfeld, Chem. Phys. Lett., 2008, 458, 276–280 CrossRef.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10187–10198 CrossRef CAS PubMed.
- W.-J. van Zeist and F. M. Bickelhaupt, Org. Biomol. Chem., 2010, 8, 3118–3127 RSC.
- B. J. Levandowski, T. A. Hamlin, F. M. Bickelhaupt and K. N. Houk, J. Org. Chem., 2017, 82, 8668–8675 CrossRef CAS PubMed.
- P. H. Y. Cheong, R. S. Paton, S. M. Bronner, G. Y. J. Im, N. K. Garg and K. N. Houk, J. Am. Chem. Soc., 2010, 132, 1267–1269 CrossRef CAS PubMed.
- P. Yu, Z. Yang, Y. Liang, X. Hong, Y. Li and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 8247–8252 CrossRef CAS PubMed.
- F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642–15649 CrossRef CAS PubMed.
- A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583 CrossRef CAS PubMed.
- S. A. Lopez, M. Pourati, H.-J. Gais and K. N. Houk, J. Org. Chem., 2014, 79, 8304–8312 CrossRef CAS PubMed.
- T. Bura, S. Beaupré, M.-A. Légaré, J. Quinn, E. Rochette, J. T. Blaskovits, F.-G. Fontaine, A. Pron, Y. Li and M. Leclerc, Chem. Sci., 2017, 8, 3913–3925 RSC.
- S. A. Lopez and K. N. Houk, J. Org. Chem., 2013, 78, 1778–1783 CrossRef CAS PubMed.
- I. V. Alabugin, M. Manoharan and T. A. Zeidan, J. Am. Chem. Soc., 2003, 125, 14014–14031 CrossRef CAS PubMed.
- I. V. Alabugin, J. Org. Chem., 2000, 65, 3910–3919 CrossRef CAS PubMed.
- M. P. Freitas, Org. Biomol. Chem., 2013, 11, 2885–2890 RSC.
- C. J. Cramer, D. G. Truhlar and A. D. French, Carbohydr. Res., 1997, 298, 1–14 CrossRef CAS.
- Y. Mo, H. Jiao and P. von Rague Schleyer, J. Org. Chem., 2004, 69, 3493–3499 CrossRef CAS PubMed.
- I. V. Alabugin, J. Org. Chem., 2000, 65, 3910–3919 CrossRef CAS PubMed.
- E. Juaristi, G. dos Passos Gomes, A. O. Terent’ev, R. Notario and I. V. Alabugin, J. Am. Chem. Soc., 2017, 139, 10799–10813 CrossRef CAS PubMed.
- G. D. P. Gomes, V. Vil, A. Terent'ev and I. V. Alabugin, Chem. Sci., 2015, 6, 6783–6791 RSC.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- K. B. Wiberg, Acc. Chem. Res., 1996, 29, 229–234 CrossRef CAS.
- Schrödinger Release 2019-1: Maestro, Schrödinger, LLC, New York, NY, 2018 Search PubMed.
- E. Harder, W. Damm, J. Maple, C. Wu, M. Reboul, J. Y. Xiang, L. Wang, D. Lupyan, M. K. Dahlgren, J. L. Knight, J. W. Kaus, D. S. Cerutti, G. Krilov, W. L. Jorgensen, R. Abel and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 281–296 CrossRef CAS PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117–129 CrossRef.
- J. L. Pascual-ahuir, E. Silla and I. Tuñon, J. Comput. Chem., 1994, 15, 1127–1138 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, 2016 Search PubMed.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- C. Legault, CYLview User Manual, 2012 Search PubMed.
- J. Rodriguez-Guerra Pedregal, P. Gomez-Orellana and J. D. Marechal, J. Chem. Inf. Model., 2018, 58, 561–564 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01098j |
| This journal is © The Royal Society of Chemistry 2019 |