Open Access Article
Open Access ArticlePhoton upconversion utilizing energy beyond the band gap of crystalline silicon with a hybrid TES-ADT/PbS quantum dots system†‡
Naoyuki
Nishimura
 ab,
Jesse R.
Allardice
a,
James
Xiao
a,
Qifei
Gu
a,
Victor
Gray
ab,
Jesse R.
Allardice
a,
James
Xiao
a,
Qifei
Gu
a,
Victor
Gray
 ac and
Akshay
Rao
ac and
Akshay
Rao
 *a
*a
aCavendish Laboratory, University of Cambridge, J. J. Thomson Avenue, Cambridge, CB3 0HE, UK. E-mail: ar525@cam.ac.uk
bCorporate Research & Development, Asahi-Kasei Corporation, 2-1 Samejima, Fuji, Shizuoka, 416-8501, Japan
cDepartment of Chemistry, Ångström Laboratory, Uppsala University, Box 532, SE-751 20 Uppsala, Sweden
First published on 27th March 2019
Abstract
The recent introduction of inorganic semiconductor quantum dots (QDs) as triplet sensitizers for molecular semiconductors has led to significant interest in harvesting low energy photons, which can then be used for photon upconversion (PUC), via triplet–triplet annihilation (TTA). A key goal is the harvesting of photons from below the bandgap of crystalline silicon 1.12 eV (≈1100 nm) and their upconversion into the visible region. In practice, the systems demonstrated so far have been limited to harvesting photons with energies above 1.2 eV (≈1 μm), due to two reasons: firstly the need to use transmitter ligands which allow efficient energy harvesting from the QD but introduce an energy loss of larger than 200 meV in transmission from the QD to the annihilator, and secondly due to the use of molecules such as tetracene which cannot accept smaller energy than 1.2 eV. Here, we introduce a new strategy to overcome these difficulties by using a low energy triplet annihilator that also harvests excitations efficiently from QDs. Specifically, we show that 5,11-bis(triethylsilylethynyl)anthradithiophene (TES-ADT, triplet energy of 1.08 eV: ca. 1150 nm) functions as a triplet annihilator (20% TTA efficiency) while also rapidly extracting triplet excitons from lead sulfide (PbS) QDs with a rate constant of k = ca. 2 × 10−8 s−1 with an excitation at 1064 nm. This rate is consistent with an orbital overlap between TES-ADT and PbS QDs, which we propose is due to the thiophene group of TES-ADT, which enables a close association with the PbS surface, allowing this system to function both as annihilator and transmitter. Our results pave the way for the design of triplet annihilators that can closely associate with the QD surface and harvest low energy excitons with minute losses in energy during the TET process, with the ultimate goal of efficiently utilizing photon energy beyond the bandgap of crystalline silicon.
1. Introduction
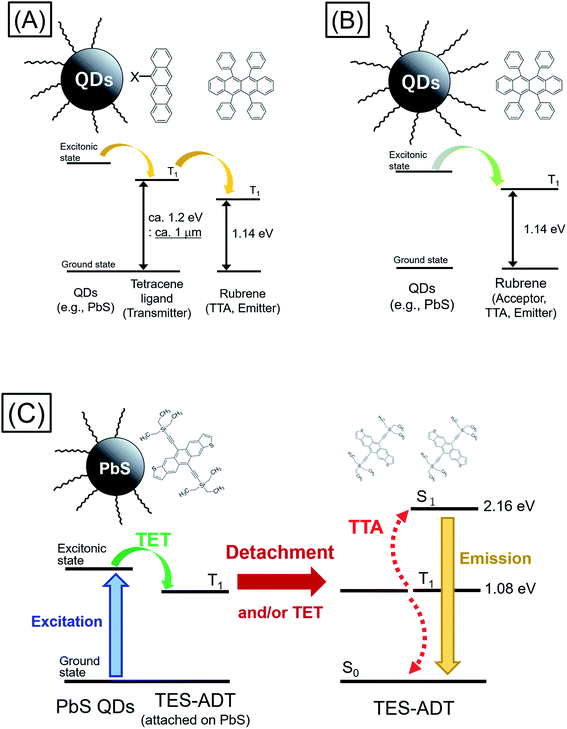
Triplet energy transfer (TET) between organic semiconductors and inorganic quantum dots (QDs) has recently emerged as a novel means of transferring energy in hybrid nanosystems,1–23 allowing the tuning of the excited state lifetime,3,9–11 the radiative harvesting of ‘dark’ triplet excitons and the sensitization of organic molecules for photon upconversion (PUC) via triplet–triplet annihilation (TTA).7,8 In comparison to traditional heavy-metal complexes used for triplet sensitization, QDs have almost no energy difference between singlet and triplet excited state configurations, allowing, in principle, for the sensitization of triplets with almost no energy loss with respect to the band gap of the QD. For PUC, this implies that a large anti-Stokes shift between the wavelengths of excitation and emission is possible.2,14 In addition, these systems allow for efficient harvesting of near infrared (NIR) photons1–8,18–24 for NIR to visible light (VIS) PUC, something which proves to be challenging with traditional heavy-metal based sensitizers.As TET from the QD to the organic material is based on Dexter transfer, which requires orbital overlap between donor and acceptor, there is an exponential dependence on the distance between the QD and the organic material.15–17 TET from QDs passivated with long-chain ligands, such as oleic acid, has been shown to result in low TET yields especially in solution.8,18–20 Thus, an important advance in the field was the introduction of triplet transmitter ligands on the QD surface, allowing for a short distance between QD and organic material and hence enabling efficient Dexter transfer. These ligands are commonly based on acenes functionalized with carboxylic acids to attach to the QD surface.1–6 Moreover, as opposed to free molecules and QDs in solution which must rely on collisions to undergo the bimolecular TET reaction, the ligands are permanently fixed on the QD, thus allowing much higher efficiency of transfer from the QD to free molecules in solution. Once on the triplet transmitter ligand, the lifetime of the triplet state can be on the order of ms, rather than the μs lifetime of the QDs.9 This provides sufficient time for the transfer of triplets to free-floating annihilator molecules, usually rubrene for PUC from NIR to VIS, in solution which can then undergo TTA. However, the introduction of the triplet transmitter ligands introduces an energy loss within the PUC process. There needs to be an energy gradient between the QD and the ligand to facilitate the TET process and a further driving energy from the ligand to the free-floating annihilator molecules in solution. In total (i.e., from the excitation energy or excitonic absorption peak of the QDs to the annihilator) this commonly requires an energy loss of around 230 meV, necessitating the use of higher energy QDs to sensitize the process. Thus so far, demonstrations of NIR to VIS upconversion have mostly been based on excitation at 808 nm.21–23
Moving forward, an important goal would be the utilization of longer wavelengths for PUC, especially the region beyond the bandgap of the crystalline silicon (c-Si), which at room temperature is 1.12 eV (≈1100 nm); an indirect gap with a very weak absorption edge.25,26 This could be of great interest for photodetection, sensing and energy materials applications.24 However, in current systems consisting of QDs as triplet sensitizers, acene derivatives (e.g., tetracene derivative) as triplet transmitters, and TTA materials (e.g., rubrene),22,23 displayed in Fig. 1A, the T1 energy of the triplet transmitter ligand (ca. 1.2 eV ≈ 1 μm for tetracene based systems) disallows this process. As shown in Fig. 1B, in principle a system via direct TET between QDs and TTA materials is advantageous for its simplicity, not requiring an energetic cascade from a triplet transmitter ligand to TTA materials,8,19,20 compared to the scheme of Fig. 1A. To employ rubrene as a TTA material, directly extracting triplet excitons from QDs as Fig. 1B, is beneficial to utilize a small energy in PUC since T1 of rubrene (1.14 eV: 1090 nm) is smaller than that of tetracene. Nevertheless, direct TET between rubrene and QDs is not efficient8,19,20 due to the poor orbital overlap. Therefore, it would be advantageous to develop novel TTA materials which have small T1 energy and can directly and efficiently accept triplet excitons from QDs.
Here we demonstrate a new strategy that overcomes both the energy loss to drive triplet transfer from transmitter ligand to free-floating molecules as well as the ability to harvest photons beyond the c-Si bandgap, upconverting to the visible. We show that the use of a thiophene containing moiety, here within 5,11-bis(triethylsilylethynyl)anthradithiophene (TES-ADT),27–29 allows for the close association of TES-ADT with the lead sulfide (PbS) surface, eliminating the need for separate transmitter ligand and free-floating triplet annihilator species and hence the energy loss between them (Fig. 1C). We demonstrate PUC for excitation wavelengths out to 1100 nm and use ultrafast spectroscopy to elucidate the energy transfer rates in this system. Our data indicates that after triplet energy transfer the TES-ADT may unbind from the PbS and go on to act as a free-floating triplet annihilator.
2. Results and discussion
2.1. Absorption and emission properties of TES-ADT
Thiophene possesses a weaker conjugation than benzene, hence in terms of controlling energy levels of acenes, conjugation with thiophenes is a prominent strategy. TES-ADT (Fig. 1C) and its derivatives are well known as organic transistor materials,27,28 and it has been reported that 2,8-difluoro-5,11-bis(triethylsilylethynyl)anthradithiophene (diF-TES-ADT) functions as a singlet fission material which splits one singlet exciton into two triplet excitons.29 TES-ADT has S1 and T1 energies of 2.16 eV and 1.08 eV (ca. 1150 nm),29 smaller than the corresponding values for the commonly used PUC material rubrene.We begin by characterizing the steady state properties of TES-ADT. Fig. 2A depicts absorption and emission spectra of 0.2 mM TES-ADT in toluene. The absorption edge corresponding to the S1 gap of TES-ADT was observed at around 575 nm (2.16 eV). The emission spectrum was measured with excitation by a 520 nm continuous wave (CW) laser. The solution gave an emission composed of (0–0), (0–1), and (0–2) peaks located at around 580, 610, and 660 nm, respectively.
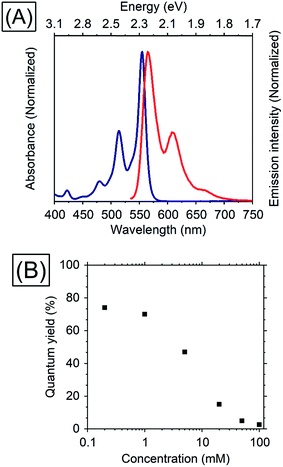 | ||
| Fig. 2 (A) Absorption (blue) and emission (red) spectra of 0.2 mM TES-ADT in toluene and (B) dependence of TES-ADT concentration in toluene on the QY with excitation at 520 nm. | ||
Dependence of the photoluminescence QY on the concentration of TES-ADT, was measured under excitation at 520 nm, as shown in Table 1 and Fig. 2. With an increase in concentration from 0.2 mM to 1 mM, the QY slightly decreased from 74 to 70%, beyond which it steeply dropped to 2.6% at 100 mM, suggesting that there is a loss process for singlet excitons in the highly concentrated TES-ADT. Fig. S1† displays time-resolved emission spectra of TES-ADT solutions with various concentrations. The decay life time of the emission at each concentration was less than 100 ns. With low concentrations (e.g., 0.2 mM), the shape of spectra does not change in time. With high concentrations however (e.g., 100 mM), a red-shifted and delayed emission was observed with a peak at around 660 nm after 10 ns, which is similar to emission from a diF-TES-ADT excimer formed with a pair of triplets (TT)1 converted from the S1 state.29 The contribution of (TT)1 state was also observed in steady state emission spectra with high concentration TES-ADT (Fig. S2†). Consequently, the low QY of the emission from TES-ADT at high concentration is mainly due to a conversion from S1 to the (TT)1 and T1 due to singlet fission. Any use of this materials for TTA thus needs to balance this potential loss channel.
| Concentration of TES-ADT (mM) | QY (%) |
|---|---|
| 0.2 | 74 |
| 1 | 70 |
| 5 | 47 |
| 20 | 15 |
| 50 | 4.9 |
| 100 | 2.6 |
2.2. TTA efficiency of TES-ADT
TTA properties (e.g., TTA efficiency) of a thiophene conjugated directly on the acene backbone have not yet been investigated, as far as we know. Therefore, we first characterize the performance of TES-ADT as a triplet annihilator material using conventional heavy-metal based sensitizers. Parameters of PUC are estimated with the following eqn (1)| ΦUC = 1/2ΦISC × ΦTET × ΦTTA × ΦFL | (1) |
Fig. 3 displays a PUC emission spectrum of a solution containing 1 mM TES-ADT and 20 μM PdTPBP with excitation at 647 nm which is beyond the S1 gap of TES-ADT. This system gives emission with peaks at 580 nm and 610 nm assigned as the (0–0) and the (0–1) emission from TES-ADT, respectively. Compared to emission with a direct S1 excitation, the (0–0) emission is suppressed due to reabsorption, resulting in the largest peak located at 610 nm (2.03 eV). Fig. S4† shows excitation power dependency on the intensity of PUC emission. A change from almost linear (slope = 1.15) to roughly square (slop = 1.52) was observed at a power density of 48 W cm−2, which is a characteristic of TTA PUC.1–8 These results reveal that TES-ADT functions as a TTA material. The ΦUC of this PUC was estimated to be 6.7% (relative rhodamine B in degassed ethanol (Φr = 0.97)31). ΦISC of PdTPBP is around 0.97 due to the fast ISC process.30 In addition, ΦTET is also estimated to be 1, as judged by the completely quenched phosphorescence from PdTPBP. From eqn (1) we obtain, the ΦTTA of TES-ADT as 20% which is comparable to the other TTA materials such as rubrene (33%)32 (Table 2).
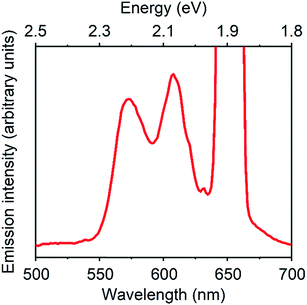 | ||
| Fig. 3 PUC emission spectrum of a system composed of 1 mM TES-ADT and 20 μM PdTPBP, excited at 647 nm. | ||
| Sample | Φ UC | Φ ISC | Φ TET | Φ FL | Φ TTA |
|---|---|---|---|---|---|
| 1 mM TES-ADT | 0.067 | 0.97 | 1.00 | 0.70 | 0.20 |
| 20 μM PdTPBP |
2.3. PUC properties of a system consisting of TES-ADT and PbS QDs
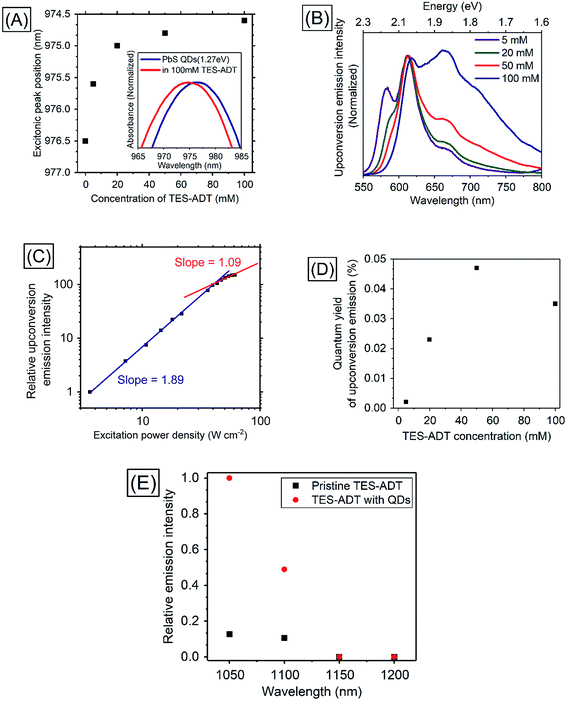
In order to utilize lower energies than conventional heavy metal complex sensitizers, PbS QDs were used as triplet sensitizers for TES-ADT. PbS QDs with excitonic peak energies of 1.27 ∓ 0.07, 1.19 ∓ 0.08, or 1.08 ∓ 0.07 eV were used in this work; their absorption spectra are shown in Fig. S5.† Energy of the absorption peak reflects average excitonic energy in each sample. The excitonic energies of QDs were controlled by the synthesis condition33 as described in the Experimental section. Excitonic peak positions and the zoomed in absorption spectra of PbS QDs (1.27 eV) in the presence of various concentration of TES-ADT are displayed in Fig. 4A. With an increase in the concentration of TES-ADT, the excitonic absorption peak of the PbS QDs gradually shifted to shorter wavelengths. Particularly with 100 mM TES-ADT, the magnitude in the shift was 2 nm. Small blue-shifts in an excitonic absorption peaks of lead chalcogenide QDs by modifications of the QDs with acene derivative ligands have been previously reported, due to an interaction between the QD and the chemically attached ligand on the QD.13,34 Accordingly, the small blue-shift in the presence of TES-ADT is assigned to a close association of the TES-ADT with the PbS, most likely due to the thiophene group of TES-ADT.PUC properties of a system comprised of TES-ADT and PbS QDs were investigated. Fig. 4B shows PUC emission spectra from a sample consisting of PbS QDs (1.27 eV) and various concentrations of TES-ADT, excited at 1064 nm. The concentration of PbS QDs was optimized at 2.5 mg mL−1 (O.D.: 0.04 at 1064 nm) as shown in Fig. S6.† The TES-ADT (0–0) emission almost disappeared due to strong reabsorption attributed to the deep penetration depth. With an increase in the concentration, the emission at around 660 nm showed a relative increase, matching the trend seen in the emission spectra with direct excitation (Fig. S2†). The small difference in the emission shape between the direct excitation (at 520 nm) and PUC (excited at 1064 nm) was likely due to the difference in the population of excited states, discussed in ESI (Fig. S7).† The anti-Stokes shift in this system was estimated to be 0.86 eV which was comparable to the highest number in PUC from over 800 nm to VIS so far.2Fig. 4C depicts the excitation power dependence for PUC emission intensity from a solution containing 50 mM TES-ADT and PbS QDs. The slope change between approximately linear (1.09) and about square (1.89) was observed at 43 W cm−2 which was a very similar value to the system consisting of TES-ADT and PdTPBP, proving that the observed PUC was also via TTA.
Fig. 4D shows PUC QY (ΦUC) dependence on the TES-ADT concentration. With an increase in TES-ADT concentration, ΦUC increased from 0.0021% at 5 mM to a peak of 0.047% at 50 mM and then decreased to 0.035% at 100 mM. Table 3 shows calculations of ΦTET for each TES-ADT concentration. Here, the ΦISC of PbS QDs was taken to be 1. In addition, ΦTTA was taken to be 20% as was determined from the ΦUC with PdTPBP sensitizer within the linear region in the excitation power dependence (Fig. S4†), since these measurements here were also done in the linear region, where ΦTTA is maximized, ΦTTA should be the same in both samples. Error bars of ΦFL are due to the changing population of excited states, discussed in ESI (Fig. S7),† these are also taken into account in Table 3. With an increase in TES-ADT concentration, ΦTET increased from 0.04 ± 0.01% at 5 mM to 12 ± 2% at 100 mM. ΦUC of the system was balanced between a decrease in ΦFL and an increase in ΦTET with a highly concentrated TES-ADT, consequently, the concentration dependence of TES-ADT PUC QY in Fig. 5D resulted in a peak at 50 mM. The increase in ΦTET with an increase in a TES-ADT concentration (in Table 3) coincides with a trend that the probability of collisions and attachments with TES-ADT to PbS QDs increases with increasing the concentration.
| TES-ADT concentration (mM) | Φ UC (%) | Φ ISC (%) | Φ TTA (%) | Φ FL (%) | Φ TET (%) |
|---|---|---|---|---|---|
| 5 | 0.0021 | 100 | 20 | 54 ± 5 | 0.04 ± 0.01 |
| 20 | 0.023 | 100 | 20 | 16 ± 1 | 1.4 ± 0.1 |
| 50 | 0.047 | 100 | 20 | 5.4 ± 0.5 | 8.8 ± 0.8 |
| 100 | 0.035 | 100 | 20 | 2.9 ± 0.3 | 12 ± 2 |
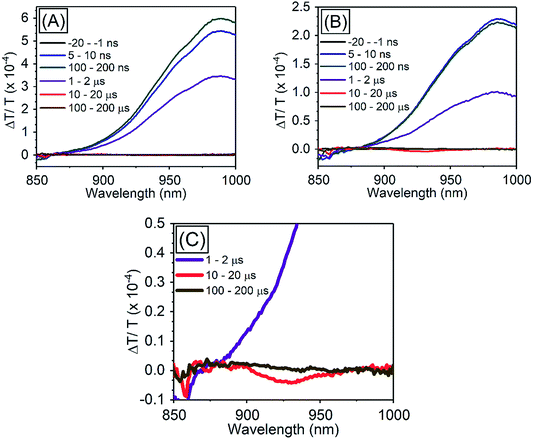 | ||
| Fig. 5 TA spectra of PbS QDs (1.27 eV) (A) in the absence of TES-ADT, (B) in the presence of 50 mM TES-ADT with excitation at 1064 nm, (C) zoom in of (B). | ||
Importantly, the obtained ΦTET in this system, 12 ± 2% at 100 mM, is orders of magnitude higher even with relative small driving force (smaller than 200 meV) than one shown in previous solution systems without the use of the triplet accepting ligand, for instance for direct transfer from PbS to rubrene ΦTET was found to be less than 0.02%.19,20 Thus, the use of the TES-ADT system with the thiophene moiety allows for a close association between the QD and the organic molecule, enabling efficient TET, which cannot be achieved with the conventional annihilator material (i.e., rubrene), while still allowing the use of a single chromophore as triplet acceptor and annihilator unlike conventional transmitter ligands with COOH functional group.
Table 4 shows the dependence of PUC QY on the band gap of the PbS QDs. With a decrease in the energy of the QDs, ΦUC deceased from 0.047% at 1.27 eV to 0.0004% at 1.08 eV, resulting in a decrease in ΦTET from 10% at 1.27 eV to 0.08% at 1.08 eV. T1 energy of TES-ADT has previously been measured to be 1.08 eV, therefore, the decrease in the driving force for TET from the excitonic state of PbS QDs to the T1 state of TES-ADT leads to less efficient TET. When the effective driving energy was reduced to zero (PbS QD at 1.08 eV to T1 of TES-ADT at 1.08 eV) ΦUC and ΦTET were both reduced, but still measurable.
| Φ UC (%) | Φ ISC (%) | Φ TTA (%) | Φ FL (%) | Φ TET (%) |
|---|---|---|---|---|
| 0.047 | 100 | 20 | 5.4 ± 0.5 | 8.8 ± 0.8 |
| 0.012 | 100 | 20 | 5.4 ± 0.5 | 2.3 ± 0.2 |
| 0.0004 | 100 | 20 | 5.4 ± 0.5 | 0.07 ± 0.01 |
In order to confirm the utilization of low-energy photons for PUC, excitation wavelength dependence of relative emission intensity was measured (Fig. 4E). Although a solution consisting only TES-ADT gave emission derived from two photon absorption due to the use of a pulsed laser system (<200 fs pulses), the presence of PbS QDs resulted in a large increase in visible emission (3–5 times), indicating that the difference in the emission intensities originated from PUC emission via QD sensitization. The PUC emission was obtained with an excitation up to 1100 nm, but it disappeared at 1150 nm. We note that the T1 energy of TES-ADT (1.08 eV: ca. 1150 nm) was assigned from a peak of phosphorescence from a film sample in a previous report,29 hence the estimated T1 energy may be affected by Stokes shift of the phosphorescence and/or conjugation of the film structure. Accordingly, the actual T1 energy of TES-ADT molecule is slightly larger than 1.08 eV (1150 nm), which would allow for a small driving for the TTA process (2T1–S1).
2.4. TET properties from PbS QDs to TES-ADT
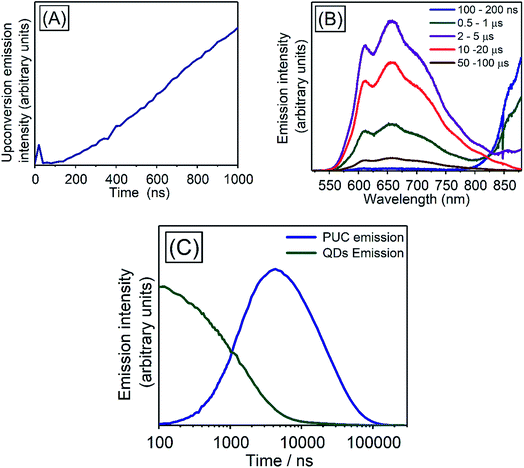
In order to investigate TET properties from PbS QDs to TES-ADT in more detail, pump–probe measurements were carried out. Transient absorption (TA) measurement is advantageous to detect features of triplet excitons because T1 → Tn transition which reflects existence of triplet exciton can be directly observed. The photoinduced triplet absorption spectra of TES-ADT molecules were measured as described in the ESI (Fig. S8).†Fig. 5 shows the TA spectra of PbS QDs (1.27 eV) in the absence or in the presence of TES-ADT (50 mM) with an excitation at 1064 nm. At early times, the sample without TES-ADT (Fig. 5A) shows photo induced absorption (PIA) up to 820 nm, beyond which a broad positive signal associated with the ground state bleach (GSB) was observed with a peak at ca. 980 nm. Subsequently, the intensity of the GSB gradually decreased, disappearing between 10–20 μs. These features are in good agreement with the TA features of PbS QDs in previous reports.34–39 In the case of PbS QDs with 50 mM TES-ADT (Fig. 5B (zoomed in: Fig. 5C)), initially, a similar spectrum to the one in the absence of TES-ADT is observed. Subsequently, a much faster decrease in the GSB was observed. In addition, an extra PIA peak assigned as triplet feature of TES-ADT was observed at 920–930 nm at 10–20 μs, which is evidence for the existence of triplet excitons in TES-ADT and TET from PbS QDs to TES-ADT. We note that there is no contribution of two photon absorption by TES-ADT within our experimental conditions, as confirmed by a measurement with pristine 100 mM TES-ADT solution as a reference. Fig. 6A shows kinetics of the TA signal at 920 nm for samples consisting of PbS QDs and various concentrations of TES-ADT. In the absence of TES-ADT, decay on μs timescales were observed, however, in the presence of TES-ADT, as extra fast decay on ns timescales was observed at early times. This fast decay channel became more significant with an increase in the concentration of TES-ADT. For 100 mM TES-ADT, the decay time (τ) was ca. 5 ns corresponding to a rate constant of k = ca. 2 × 10−8 s−1.
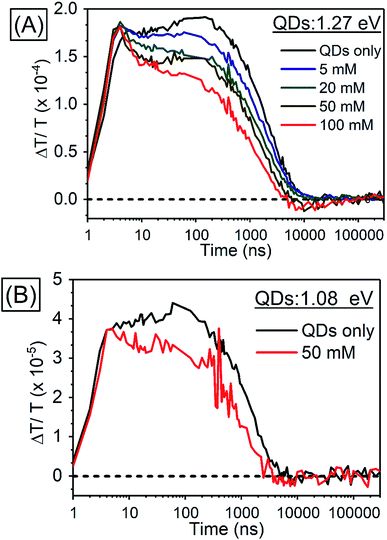 | ||
| Fig. 6 Kinetics of TA (A) in PbS QDs (1.27 eV) with various concentrations of TES-ADT at 920–930 nm, (B) in PbS QDs (1.08 eV) with 50 mM TES-ADT at 980–990 nm. | ||
As a control experiment, TA features with PbS QDs with as energy of 1.08 eV, which is degenerate with the T1 energy of TES-ADT were investigated. Fig. S9† displays TA spectra of PbS QDs (1.08 eV) with or without 50 mM TES-ADT. Fig. 6B depicts kinetics of TA at 980–990 nm with PbS QDs (1.08 eV) in the absence or in the presence of 50 mM TES-ADT. Only a μs timescale decay was observed in both samples, and the fast decay observed in the 1.27 eV dots was not observed. Furthermore, no triplet feature was observed in both kinetics.
Taken together, two timescales for the GSB decay of PbS QDs on ns and μs timescales were observed. For the 1.08 eV PbS QDs the efficiency of the TET was negligible, 0.07 ± 0.01%, as estimated from the PUC QY measurements (Table 4). Therefore, for this samples, we conclude that the observed difference between the kinetics of the 1.08 eV PbS with and without the TES-ADT (Fig. 6B) are not indicative of TET, but rather a change in the decay rate of the PbS with μs order, perhaps due to a change in surface passivation by attachment of TES-ADT. In contrast, for the 1.27 eV PbS QDs a TET efficiency of 12 ± 2% is estimated from the PUC QY measurements (Table 4). For these samples (Fig. 6A) a fast decay on sub-10 ns timescales are observed in the presence of TES-ADT and we assign this early time decay to TET from PbS to TES-ADT. We note that this timescale is not consistent with a diffusion mediated process, but would be consistent with a close interaction between the TES-ADT and PbS QDs contributing to orbital overlap between them, leading to the ns scale Dexter transfer.9,23,40–42 In the previous reports, for instance, TET from CdSe QDs to 9-carboxylic acid anthracene was k = 0.15–2.2 × 10−9 s−1,9,40 TET from CdS QDs to 2,5-diphenyloxazole was k = 1.5 × 10−10 s−1,41 TET from CdSe QDs to bis(pyridine) anthracenes was k = 0.96–1.28 × 10−9 s−1,42 or TET from PbS QDs to 5-carboxylic acid tetracene was k = 5.91 × 10−9 s−1.23 The rate constant obtained here (k = ca. 2 × 10−8 s−1) is in this range, verifying that orbital overlap between TES-ADT and PbS QDs must contribute to the observed fast TET. This is also in line with the blue-shift in the PbS absorption steady state absorption data, suggesting an interaction between the TES-ADT and PbS (Fig. 4A). These results thus show that the TES-ADT performs comparable to a directly chemically attached triplet acceptor group, while also functioning as the triplet annihilator species.
2.5. Kinetics of PUC emission from a system consisting of TES-ADT and PbS QDs
We investigated the kinetics of the PUC emission, for which there is a little reported data in the literature for systems using QDs triplet sensitizers. The kinetics of the PUC emission would provide information of the PUC mechanism especially about efficient energy transfer from the PbS QD to the free-floating TES-ADT with the small driving force (<200 meV). Fig. 7 shows spectra and kinetics of an emission from a solution containing 100 mM TES-ADT and PbS QDs (1.27 eV). At early times (∼20 ns) (Fig. 7A) there is a small contribution to the emission from two photon absorption,8 but the later time data is free from this effect which directly generated short lived singlet excitons on TES-ADT. Fig. 7B shows the emission spectra from the sample at each time. The spectra are divided into two features originated from a PUC emission in 550–850 nm and an emission from the QDs down to ca. 800 nm. In the early time at 100–200 ns, the emission intensity of PbS QDs was significant, after that, the intensity of emission from the PbS QDs gradually decreased and then disappeared after 10 μs. On the other hand, the PUC emission gradually increased from 100–200 ns to 10–20 μs, before decreasing and lasts over 100 μs. This trend observed in Fig. 7B as a decrease in the emission from PbS QDs and the simultaneous increase in PUC emission is good agreement with the TET from PbS QDs to TES-ADT. The kinetics at 600–610 nm and 870–880 nm shown in Fig. 7C describes features of PUC emission and an emission from the PbS QDs in more detail. The PUC emission begins from ca. 100 ns, with a rate constant of k = 5 × 105 s−1 (τ = 2.19 ± 0.13 μs). After the emission peaks at around 3 μs, corresponding to a disappearance of emission from the PbS QDs, the intensity slowly decreased with the decay constant of τ = 24.9 ± 0.6 μs.We note, that the above described kinetics appear to be slower than one would expect and slower than previous reports.7,43 As a comparison, we measure the PUC emission from a solution composed of TES-ADT and PdTPBP (Fig. S10†) (system previously described in Fig. 3). We find that in this case the PUC emission peaked and saturated within 100 ns. The comparison shows that the kinetics of the TES-ADT/PbS system is indeed slow. The estimated rate constant for the PUC emission k = 5 × 105 s−1 included various processes; (1) TET from PbS QDs to TES-ADT attaching to PbS QDs, (2a) TET from TES-ADT attached onto the PbS QDs to another TES-ADT or (2b) detachment of TES-ADT from PbS QDs following TET, (3) TTA, and (4) the emission from TES-ADT, is slow compared to the previous reports. This rate constant will be dominated by the rate determining step which could provide information on the underlying mechanism for the system. The emission process (process (4)) is fast and takes place on ns timescales, as observed in the time resolved emission with pristine TES-ADT solution (Fig. S1†). According to the control measurement on PUC emission from a solution composed of TES-ADT and PdTPBP (Fig. S10†), the rate constant of TTA is fast (intensity of the PUC emission was saturated within 100 ns), indicating that (3) TTA process was not rate determining step. In terms of the TET from the QDs to TES-ADT (process (1)), the TA results indicate that it is relatively fast with a rate constant of k = ca. 2 × 10−8 s−1 which is considerably faster than the rate constant for PUC. Nevertheless, the TA results also suggest that the coverage of attached TES-ADT on the PbS QDs is low and not enough to extract all excitons from the PbS QDs on fast timescales, as even with the larger gap QDs (1.27 eV) a slow decay on μs time scale remains (Fig. 6A). Once the T1 state of TES-ADT is occupied, it cannot accept another triplet until it transfers the triplet to a free-floating TES-ADT. Therefore, either process (2a) or (2b) should be the rate determining step.
Starting with case (2a), TET from TES-ADT attached onto the PbS QDs to free floating TES-ADT, the time scale is not consistent with the rate determining step (of μs order) since in the concentrated solution (100 mM) TES-ADT molecules including the ones attached on PbS QD should collide with each other in several ns.44 Turning to process (2b), detachment of TES-ADT from PbS QDs following TET, this could be compatible with the μs order time scale, as it might involve gradual detachment of the TES-ADT molecule from the surface of the PbS and as well as physical separation from the ligand shell surrounding the dots. This would also rationalize the slow decay of PUC emission, τ = 24.9 ± 0.6 μs, which is much slower than the decay of free triplets in 100 mM TES-ADT, τ = 10.6 μs (Fig. S8†), implying a much longer lifetime for the triplets in the TES-ADT/PbS QDs system than for free TES-ADT. This dynamic attach/detach mechanism would be advantageous, not requiring an energetic driving force from acceptor ligands to free TTA materials as is needed in conventional system, thus minimizing energy loss. Here this process could be driven by the weaker interaction between metal chalcogenide QDs and the thiophene moiety than ones in the conventional system like carboxylic acid while providing for a strong enough interaction to allow for efficient triplet harvesting. We note that the proposed detachment mechanism is speculative and further theoretical and experimental studies will be needed to confirm this model.
3. Conclusion
We have demonstrated a new strategy of materials combination for PUC systems which enables the harvesting of excitations from low band gap PbS QDs to molecular triplet excitons with minimal energy loss. Using the TES-ADT/PbS QDs system we were able to demonstrate upconversion to visible wavelengths with exciton energy as low as 1100 nm. Ultrafast spectroscopy measurements demonstrated fast TET from the QD to the TES-ADT, with a rate constant of k = ca. 2 × 108 s−1, indicating a close association and orbital overlap between the TES-ADT and the PbS QDs. The fast TET suggests that the TES-ADT is bound to the PbS which we presume occurs via the heterocyclic thiophene moiety, despite this not being a traditional ligand group such as carboxylic acid. Time-resolved measurements of the PUC indicate that the transfer of the triplets from the TES-ADT bound to the surface of the QDs to ‘free’ TES-ADT in solution is the rate limiting step in this system, which suggests that after accepting triplet excitons TES-ADT might be decoupling from the PbS and participating in the PUC process. Although further studies will be needed to explore this dynamic detachment mechanism, it is clear that the use of the same species acting as triplet transmitter and annihilator allows for less energy loss needed to drive TET than in conventional systems. Combined with the use of the low triplet-energy ADT unit, where S1 ≈ 2T1, very energy efficient upconversion is possible. The use of this strategy paves the way for the development of efficient PUC systems which harvest energy from below the bandgap of c-Si (ca. 1100 nm), which would find applications in energy generation and sensing.4. Experimental
4.1. Materials
All original chemicals were purchased from Sigma-Aldrich except PdTPBP which was from Frontier Science and used as delivered.4.2. Synthesis of PbS QDs
The synthesis of PbS QDs was carried out by the following method of the previous report with some modifications.33 PbO (0.625 g, 2.8 mmol), oleic acid (4 mL, 12.6 mmol) and 1-octadecene (25 mL, 78 mmol) were placed in a 3-necked round bottomed flask and degassed under vacuum (<10−2 mbar) at 383 K for 2 hours with stirring, forming a colourless solution. Subsequently, the flask was put under nitrogen flow and heated to the injection temperature. In a nitrogen glovebox, a syringe was prepared containing 1-octadecene (13.9 mL, 43 mmol), diphenylphosphine (144 μL, 0.83 mmol) and hexamethyldisilathiane (296 μL, 1.4 mmol). The syringe containing the sulfur precursor was rapidly injected into the reaction flask and allowed to cool. The bandgap was tuned by varying the oleic acid concentration and injection temperature between 3 mL and 398 K (1.27 eV) to 4 mL and 453 K (1.08 eV). Upon cooling to 333 K, the reaction mixture was transferred to an argon glovebox. The synthesized nanocrystals were twice purified through selective precipitation with ethanol/1-butanol and resuspension in hexane. The purified QDs were re-dispersed in toluene for storage at a concentration of 50 mg mL−1.4.3. Steady state absorption and emission measurement
Absorption spectra were measured on solutions containing TES-ADT and/or PbS QDs in a 1 mm path length quartz cuvette using a spectrometer (UV3600-Plus, Shimadzu). Emission spectra was measured using a spectrograph (Shamrock SR-303i, ANDOR) with CCD camera (Andor iDus DU420A Si CCD, ANDOR), calibrated for spectral sensitivity of the detector at each wavelength. The samples filled in a 1 mm path length quartz cuvette were excited by a 520 nm CW laser (Thorlabs) from the side facing the detector. The emitted light passed through a 500 nm long pass filter (Thorlabs) before the detector.4.4. QY measurement of TES-ADT solutions with a direct excitation
The QY of TES-ADT solution with an excitation at 520 nm CW laser (Thorlabs) was measured using the method of Mello et al.45 For this set up, an integrating sphere was fiber-coupled to the same spectrograph as described in Section 4.3, calibrated for spectral response of the entire system.4.5. QY measurement of PUC system
QY of PUC was measured with a detector constructed with a spectroscopy camera (Andor iDus DU420A Si detector, ANDOR) coupled to spectrograph (Shamrock SR303i, ANDOR) and samples consisting of TES-ADT and triplet sensitizers (i.e., PdTPBP or PbS QDs) filled in a 1 mm path length quartz cuvette excited by CW laser. The QY (ΦUC) was calculated with the following eqn (2),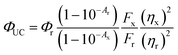 | (2) |
4.6. Dependency of PUC emission intensity on the excitation wavelength
Effects of the excitation wavelength on emission intensity from a solution from pristine 100 mM TES-ADT solution or a solution consisting of 100 mM TES-ADT and 25 mg mL−1 PbS QDs (1.27 eV) was investigated with excitation by a pulsed laser. The desired excitation wavelength was obtained using a Nd:YAG based laser system (PHAROS; Light Conversion, pulse duration < 200 fs) with a reputation rate of 38 kHz and a collinear optical parametric amplifier (ORPHEUS; Light Conversion). Each excitation power was adjusted to 200 nJ per pulse.4.7. Time resolved emission spectra
Time resolved emission spectra was carried out for pristine TES-ADT solution, PUC sample of 100 mM TES-ADT with PdTPBP, or 100 mM TES-ADT with PbS QDs (1.27 eV) with an excitation of 1 kHz pulsed laser at 400 nm with a power of 25 nJ per pulse from a second harmonic of Ti:sapphire amplifier system (Soltice; Spectra Physics, pulse duration: 100 fs), at 635 nm with a power of 30 nJ per pulse from a home built NOPA system using the Ti:sapphire amplifier system, or at 1064 nm with a power of 7 μJ per pulse from a Nd:YVO4 laser (AOT-YVO-25QSPX; Advanced Optical Technologies, pulse duration < 1.5 ns), respectively. The emission was recorded by an intensified CCD camera. The fitting of generation and decay in PUC emission was conducted by Origin with the following eqn (3) of mono exponential ascent and descent decay.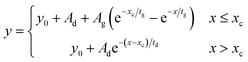 | (3) |
4.8. TA measurement
TA spectra were recorded over time delays from 1 ns to 300 μs with a pump of 50 nJ per pulse at 532 nm (for pristine TES-ADT solution) or 200 nJ per pulse at 1064 nm (for PbS QDs in the presence or in the absence of TES-ADT) and a probe pulse covering between 850 and 1000 nm. The pump triggered with the probe pulse and delayed with electrically control was generated from a Nd:YVO4 laser (AOT-YVO-25QSPX; Advanced Optical Technologies, pulse duration: < 1.5 ns). The probe pulse was generated from a home-built noncollinear optical parametric amplifier with BBO single crystal and pulsed laser from Ti:sapphire amplifier system (Soltice; Spectra Physics) operating at 1 kHz. The probe beam was split into two before the sample filled in a quartz cuvette with a path length of 1 mm, then a probe beam and the pump beam were overlapped on the sample adjacent to another probe beam passing through the sample as the reference. The beams after the sample were focused into as imaging spectrometer (Shamrock SR 303i; Andor) and detected by a pair of linear image sensors (G11608, Hamamatsu Photonics) driven and read out at full laser repetition rate by a custom-built board from Stresing Entwicklungsburo. In all measurements, every second pump shots were omitted electrically in order to obtain the fractional differential transmission (ΔT/T). The ΔT/T of the probe was calculated for each data point once 1000 shots had been collected. The estimation of fast quench in the kinetics of PbS QDs (1.27 eV) with 100 mM TES-ADT at 920–930 nm was used a fitting by Origin with a mono exponential decay.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Winton Programme for the Physics of Sustainability and the Engineering and Physical Sciences Research Council for funding. J. X. acknowledges EPSRC CDT in Nanoscience and Nanotechnology for financial support. V. G. acknowledges funding from the Swedish Research Council, Vetenskapsrådet 2018-00238.References
- Z. Huang and M. L. Tang, J. Am. Chem. Soc., 2017, 139, 9412–9418 CrossRef CAS PubMed.
- N. Yanai and N. Kimizuka, Acc. Chem. Res., 2017, 50, 2487–2495 CrossRef CAS PubMed.
- S. Garakyaraghi and F. N. Castellano, Inorg. Chem., 2018, 57, 2351–2359 CrossRef CAS PubMed.
- L. Nienhaus, M. Wu, V. Bulović, M. A. Baldo and M. G. Bawendi, Dalton Trans., 2018, 47, 8509–8516 RSC.
- V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71 CrossRef CAS.
- Z. Huang and M. L. Tang, J. Phys. Chem. Lett., 2018, 9, 6198–6206 CrossRef CAS PubMed.
- M. Wu, D. N. Congreve, M. W. B. Wilson, J. Jean, N. Geva, M. Welborn, T. V. Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Photonics, 2015, 10, 31–34 CrossRef.
- Z. Huang, X. Li, M. Mahboub, K. M. Hanson, V. M. Nichols, H. Le, M. L. Tang and C. J. Bardeen, Nano Lett., 2015, 15, 5552–5557 CrossRef CAS PubMed.
- C. Mongin, S. Garakyaraghi, N. Razgoniaeva, M. Zamkov and F. N. Castellano, Science, 2016, 351, 369–372 CrossRef CAS PubMed.
- C. Mongin, P. Moroz, M. Zamkov and F. N. Castellano, Nat. Chem., 2017, 10, 225–230 CrossRef PubMed.
- M. L. Rosa, S. A. Denisov, G. Jonusauskas, N. D. McClenaghan and A. Credi, Angew. Chem., Int. Ed., 2018, 57, 3104–3107 CrossRef PubMed.
- N. J. L. K. Davis, J. R. Allardice, J. Xiao, A. J. Petty, N. C. Greenham, J. E. Anthony and A. Rao, J. Phys. Chem. Lett., 2018, 9, 1454–1460 CrossRef CAS PubMed.
- D. M. Kroupa, D. H. Arias, G. M. Carroll, D. B. Granger, L. Blackburn, J. E. Anthony, M. C. Beard and J. C. Johnson, Nano Lett., 2018, 18, 865–873 CrossRef CAS PubMed.
- K. Okumura, K. Mase, N. Yanai and N. Kimizuka, Chem.–Eur. J., 2016, 22, 7721–7726 CrossRef CAS PubMed.
- N. J. Thompson, M. W. Wilson, D. N. Congreve, P. R. Brown, J. M. Scherer, T. S. Bischof, M. Wu, N. Geva, M. Welborn, T. V. Voorhis, V. Bulović, M. G. Bawendi and M. A. Baldo, Nat. Mater., 2014, 13, 1039–1043 CrossRef CAS PubMed.
- M. Tabachnyk, B. Ehrler, S. Gélinas, M. L. Böhm, B. J. Walker, K. P. Musselman, N. C. Greenham, R. H. Friend and A. Rao, Nat. Mater., 2014, 13, 1033–1038 CrossRef CAS PubMed.
- X. Li, Z. Huang, R. Zavala and M. L. Tang, J. Phys. Chem. Lett., 2016, 7, 1955–1959 CrossRef CAS PubMed.
- L. Nienhaus, M. Wu, N. Geva, J. J. Shepherd, M. W. B. Wilson, V. Bulović, T. V. Voorhis, M. A. Baldo and M. G. Bawendi, ACS Nano, 2017, 11, 7848–7857 CrossRef CAS PubMed.
- M. Mahboub, H. Maghsoudiganjeh, A. M. Pham, Z. Huang and M. L. Tang, Adv. Funct. Mater., 2016, 26, 6091–6097 CrossRef CAS.
- M. Mahboub, P. Xia, J. Van Baren, X. Li, C. H. Lui and M. L. Tang, ACS Energy Lett., 2018, 3, 767–772 CrossRef CAS.
- Z. Huang, D. E. Simpson, M. Mahboub, X. Li and M. L. Tang, Chem. Sci., 2016, 7, 4101–4104 RSC.
- M. Mahboub, Z. Huang and M. L. Tang, Nano Lett., 2016, 16, 7169–7175 CrossRef CAS PubMed.
- Z. Huang, Z. Xu, M. Mahboub, X. Li, J. W. Taylor, W. H. Harman, T. Lian and M. L. Tang, Angew. Chem., Int. Ed., 2017, 56, 16583–16587 CrossRef CAS PubMed.
- B. D. Ravetz, A. B. Pun, E. M. Churchill, D. N. Congreve, T. Rovis and L. M. Campos, Nature, 2019, 565, 343–346 CrossRef CAS PubMed.
- K. N. Kowk, Complete guide to semiconductor devices, 2nd edn, Wiley-IEEE Press, United States, 2002 Search PubMed.
- S. M. Sze and K. N. Kowk, Physics of semiconductor devices, 3rd edn, Wiley-IEEE Press, United States, 2006 Search PubMed.
- M. M. Payne, S. R. Parkin, J. E. Anthony, C. C. Kuo and T. N. Jackson, J. Am. Chem. Soc., 2005, 127, 4986–4987 CrossRef CAS PubMed.
- W. Jiang, Y. Li and Z. Wang, Chem. Soc. Rev., 2013, 42, 6113–6127 RSC.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Deljone, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- J. E. Rogers, K. A. Nguyen, D. C. Hufnagle, D. G. McLean, W. Su, K. M. Gossett, A. R. Burke, S. A. Vinogradov, R. Pachter and P. A. Fleitz, J. Phys. Chem. A, 2003, 107, 11331–11339 CrossRef CAS.
- G. Weber and F. W. J. Teale, Trans. Faraday Soc., 1957, 53, 646–655 RSC.
- Y. Y. Cheng, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, Phys. Chem. Chem. Phys., 2010, 12, 66–71 RSC.
- M. A. Hines and G. D. Scholes, Adv. Mater., 2003, 15, 1844–1849 CrossRef CAS.
- S. Garakyaraghi, C. Mongin, D. B. Granger, J. E. Anthony and F. N. Castellano, J. Phys. Chem. Lett., 2017, 8, 1458–1463 CrossRef CAS PubMed.
- Y. Yang, W. Rodriguez-Cordoba and T. Lian, J. Am. Chem. Soc., 2011, 133, 9246–9249 CrossRef CAS PubMed.
- K. E. Knowles, M. Malicki and E. A. Weiss, J. Am. Chem. Soc., 2012, 134, 12470–12473 CrossRef CAS PubMed.
- Y. Yang, W. Rodriguez-Cordoba and T. Lian, Nano Lett., 2012, 12, 4235–4241 CrossRef CAS PubMed.
- H. Chung, H. Choi, D. Kim, S. Jeong and J. Kim, J. Phys. Chem. C, 2015, 119, 7517–7524 CrossRef CAS.
- K. O. Aruda, M. Bohlmann Kunz, M. Tagliazucchi and E. A. Weiss, J. Phys. Chem. Lett., 2015, 6, 2841–2846 CrossRef CAS PubMed.
- G. B. Piland, Z. Huang, M. L. Tang and C. J. Bardeen, J. Phys. Chem. C, 2016, 120, 5883–5889 CrossRef CAS.
- V. Gray, P. Xia, Z. Huang, E. Moses, A. Fast, D. A. Fishman, V. I. Vullev, M. Abrahamsson, K. Moth-Poulsen and M. L. Tang, Chem. Sci., 2017, 8, 5488–5496 RSC.
- X. Li, A. Fast, Z. Huang, D. A. Fishman and M. L. Tang, Angew. Chem., Int. Ed., 2017, 56, 5598–5602 CrossRef CAS PubMed.
- V. Gray, D. Dzebo, A. Lundin, J. Alborzpour, M. Abrahamsson and B. Albinsson, J. Mater. Chem. C, 2015, 3, 11111–11121 RSC.
- B. J. Walker, A. J. Musser, D. Beljonne and R. H. Friend, Nat. Chem., 2013, 5, 1019–1024 CrossRef CAS PubMed.
- J. C. D. Mello, H. F. Wittmann and R. H. Friend, Adv. Mater., 1997, 9, 230–232 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc00821g |
| ‡ The data underlying this publication are available at https://www.repository.cam.ac.uk/. |
| This journal is © The Royal Society of Chemistry 2019 |