Molecular multifunctionality preservation upon surface deposition for a chiral single-molecule magnet

Abstract

The synthesis and characterization of a chiral, enneanuclear Mn(III)-based, Single-Molecule Magnet, [Mn₉O₄(Me-sao)₆(L)₃(MeO)₃(MeOH)₃]Cl (1; Me-saoH₂ = methylsalicylaldoxime, HL = lipoic acid) is reported. Compound 1 crystallizes in the orthorhombic P2₁2₁2₁ space group and consists of a metallic skeleton describing a defect super-tetrahedron missing one vertex. The chirality of the [Mn^III₉] core originates from the directional bridging of the Me-sao²⁻ ligands via the –N–O– oximate moieties, which define a clockwise (1ΔΔ) or counter-clockwise (1ΛΛ) rotation in both the upper [Mn^III₃] and lower [Mn^III₆] subunits. Structural integrity and retention of chirality upon dissolution and upon deposition on (a) gold nanoparticles, 1@AuNPs, (b) transparent Au(111) surfaces, 1ΛΛ@t-Au(111); 1ΔΔ@t-Au(111), and (c) epitaxial Au(111) on mica surfaces, 1@e-Au(111), was confirmed by CD and IR spectroscopies, mass spectrometry, TEM, XPS, XAS, and AFM. Magnetic susceptibility and magnetization measurements demonstrate the simultaneous retention of SMM behaviour and optical activity, from the solid state, via dissolution, to the surface deposited species.

---

Introduction

Modern information technology is based on the combined use of the charge and spin properties of electrons, exploited within devices incorporating magnetic nanomaterials.^1,2 The next generation of such devices will incorporate molecular magnetic materials that serve the purpose of miniaturization and allow the exploitation of the quantum properties that matter exhibits at this scale.³ The controlled deposition of such materials on substrates^4–7 and the subsequent addressing and manipulation of their magnetic moment at the molecular level^8–10 is a prerequisite for device realization. This can be achieved through the use of chiral magnetic molecular materials, since the absence of an inversion centre leads to efficient coupling of electric fields to the molecular magnetic moment,¹¹ and to magnetochirality,^12–14 a second order non-reciprocal effect that can be harnessed by unpolarised light.¹⁴ Thus, surface deposited chiral magnetic molecular materials are excellent candidates for the realization of spintronic devices operating on the basis of electric or optical control of molecular magnetic moments via spin-electric coupling or the magnetochiral effect. Single-Molecule Magnets^15,16 (SMMs) are a class of molecular materials currently considered for applications in molecular spintronics, such as quantum computing.^17–19 The unique potential of SMMs lies in their physics dominated by quantum effects such as quantum tunnelling of the magnetisation,²⁰ Berry phase²¹ and spin coherence.²² However, there still persists a crucial open question: how are the molecular properties affected by the drastic change in molecular environment that occurs upon surface deposition?

Until very recently, the few studies that addressed the spin dynamics of SMMs deposited on metallic surfaces showed serious alteration of the molecular properties after deposition on the surface and failed to observe magnetic hysteresis. It has been shown that Mn₁₂ is reduced when deposited at monolayer level on gold.²³ It has also been shown by several recent studies that the molecular magnetic properties of SMMs evolve upon dissolution^24,25 or deposition on surfaces.²⁶ It is only very recently that magnetic hysteresis from a tetranuclear Fe(III) SMM anchored on a gold surface by thiolate groups,^27–29 or on carbon-nanotubes (CNTs),³⁰ from Mn₁₂ on Au(111),²⁸ and from Ln-based SMMs anchored on CNTs,³¹ on gold,³² on magnesium oxide,³³ or on silicon,³⁴ was detected. The grafting of Cr₇Ni on gold and on highly oriented pyrolytic graphite was also reported.^35,36 Very recently, engineering of the magnetic coupling and anisotropy of a Co^II- and of a Ni^II-based SMM with the Fe₃O₄ (111) surface,³⁷ was demonstrated. Recent review articles present the main strategies for the attachment of SMMs on surfaces.^4–6 Chiral SMMs have been extensively studied in the bulk³⁸ but to the best of our knowledge simultaneous retention of chirality and SMM behaviour has never been demonstrated upon surface deposition.

Herein, we present the synthesis and characterization of a chiral, enneanuclear Mn(III)-based SMM, [Mn₉O₄(Me-sao)₆(L)₃ (MeO)₃(MeOH)₃]Cl (1), where LH is lipoic acid and Me-saoH₂ is methylsalicylaldoxime, functionalized for surface deposition and stable in solution. We demonstrate, for the first time, the simultaneous retention of superparamagnetism-like SMM behaviour and chirality, from the solid state, via dissolution, to the surface deposited species.

Results and discussion

Solid state

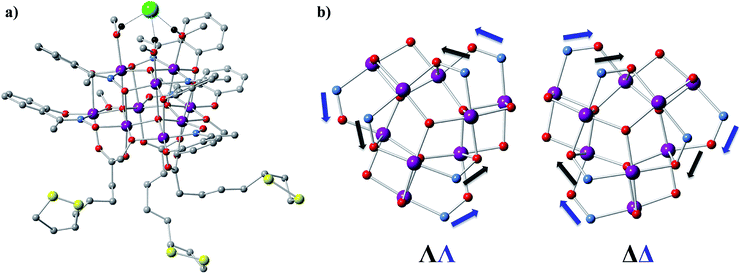
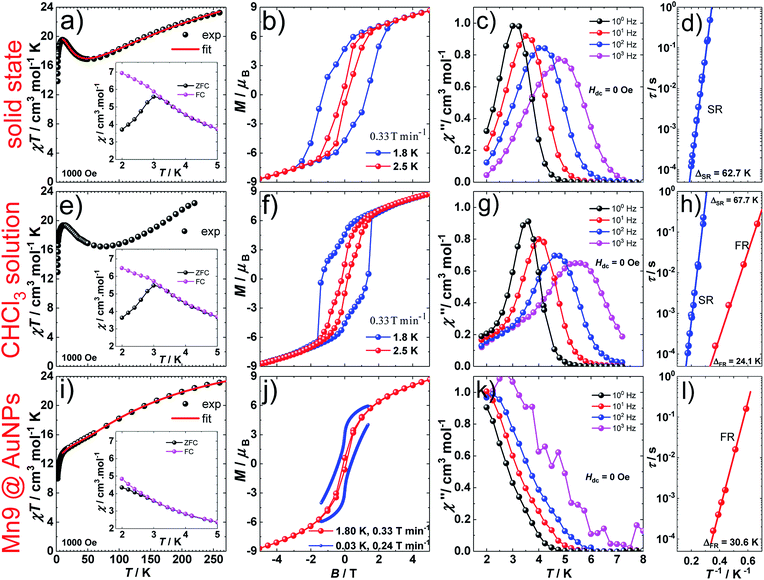
1 (Fig. 1a and S1a†) crystallizes in the orthorhombic P2₁2₁2₁ space group (Table S1†) which is one of the 65 Sohncke space groups that contain only symmetry operations of the first kind (rotations and translations) and can accommodate chiral molecules.³⁹ Only species of the same enantiomeric structure are present in a given crystal of 1. The chirality of the [Mn^III₉] core in 1 originates from the directional bridging of the Me-sao²⁻ ligands via the –N–O– oximate moieties, which define a clockwise (1ΔΔ) or counter-clockwise (1ΛΛ) rotation in both the upper [Mn^III₃] and lower [Mn^III₆] subunits (Fig. 1b), with respect to the axis normal to both planes. The metal-core of 1 consists of nine Mn(III) ions describing a defect super-tetrahedron missing one vertex (Fig. 1a). In the upper [Mn^III₃] subunit, the three Mn(III) ions are linked by a central μ₃-O²⁻ ion, while the edges of the [Mn^III₃] triangle consist of three bridging –N–O– oximates (Mn–N–O–Mn torsion angles: 38.0–39.5°, Tables S2 and S3†) from the Me-sao²⁻ ligands. The upper face of the [Mn^III₃] unit is capped by three MeOH molecules (Mn–O_MeOH = 2.180–2.206 Å Tables S4 and S5†) and the counter-anion (Cl⁻) that is H-bonded to the capping solvent (H_MeOH⋯Cl⁻ 2.190–2.200 Å). In the basal [Mn^III₆] subunit, the almost co-planar Mn(III) ions are alternately connected from the exterior by three oximates (Mn–N–O–Mn torsion angles: 8.6–13.7°, Tables S2 and S3†) and three methoxides (Mn–O_μ-MeO–Mn angles: 98.79–100.16°, Tables S6 and S7†), while from the interior the metal-ions are linked via three μ₄-O²⁻ bridges. Thus, the six Mn(III) ions form a triangle with three ions positioned at the vertices and the other three at the middle of the edges. The lower face of the [Mn^III₆] subunit is capped by three sulfur-containing carboxylates, bonding in a bidentate bridging fashion conferring tripodal ligand attributes to 1. The inner μ₄-O²⁻ ion from the basal [Mn^III₆] unit, the oximato O-atoms from the bridging aldoximes, the phenoxide O-atoms of Me-Sao²⁻ and the –N–O– oximate bridges from the upper [Mn^III₃] subunit link [Mn^III₃] and [Mn^III₆] to form the [Mn^III₉] defect super-tetrahedron. The Jahn–Teller axes of the Mn(III) ions are perpendicular to both the [Mn^III₃] and [Mn^III₆] planes and are approximately co-parallel to each other (Fig. S1†). The crystal packing and intermolecular interactions are shown in Fig. S2–S4.†

Fig. 1 Structure of [Mn₉O₄(Me-sao)₆(L)₃(MeO)₃(MeOH)₃]Cl. (a) Molecular structure of 1. Color scheme: Mn – purple, N – blue, O – red, C – gray, S – yellow, Cl – green. Hydrogen atoms have been omitted for clarity, except those of the methanol molecules (black) that form H-bonds with the Cl⁻counter-anion. (b) ΛΛ and ΔΔ configurations of the [Mn^III₉] core in 1.

Direct-current (d.c.) magnetic susceptibility studies in a magnetic field, B, of 0.1 T, were performed on polycrystalline 1, the purity of which was confirmed by powder X-ray diffraction (Fig. S5†). The χT versus T data, where χ = M/B, with M the magnetization, χ the molar magnetic susceptibility and T the temperature, are shown in Fig. 2. The χT product of 1 at 270 K is 23.2 cm³ K mol⁻¹, lower than that expected for the spin-only contributions of nine uncorrelated Mn(III) ions (27 cm³ K mol⁻¹, S_Mn = 2, g_Mn = 2). Upon cooling, the χT product decreases to reach 16.7 cm³ K mol⁻¹ at 50 K, indicative of dominant antiferromagnetic interactions in 1. Below 50 K, the χT product increases to 19.5 cm³ K mol⁻¹ at 10 K. Upon further cooling, χT decreases rapidly to 13.6 cm³ K mol⁻¹, most likely because of the anisotropy of Mn(III) ions. The nesting and the absence of magnetization saturation in the reduced magnetisation curves for polycrystalline 1 (Fig. S20†), confirms its magnetic anisotropy. A bifurcation between the zero-field-cooled (ZFC) and field-cooled (FC) susceptibilities (Fig. 2) indicates a blocking temperature, T_B, of 3 K. Below T_B, magnetic hysteresis (coercive field of 1.3 T at 1.8 K and 0.33 T min⁻¹) is observed (Fig. 2), which is the experimental manifestation of SMM (superparamagnetic-like) behavior.

Fig. 2 Magnetic properties of [Mn₉O₄(Me-sao)₆(L)₃(MeO)₃(MeOH)₃]Cl. Solid state (a–d), 19.6 mM CHCl₃ solution (e–h) and on AuNPs (i–l). a, e, i, χT versus T plots at 0.1 T, with χ = M/B the molar magnetic susceptibility of 1, inset: ZFC and FC susceptibility measurements in an applied d.c. field of 0.1 T; b, f, j, d.c. magnetization hysteresis loops at 1.8 and 2.5 K and 0.33 T min⁻¹ (b, f) and at 1.8 K and 0.33 T min⁻¹ and at 0.03 K and 0.24 T min⁻¹ (j); c, g, k, out-of-phase, χ′′, component of the a.c. susceptibility at 10⁰, 10¹, 10² and 10³ Hz at T < 8 K, in a 3.5 Oe a.c. field and in zero d.c. field. Solid lines are guides for the eye; d, h, l, Arrhenius τ vs. T⁻¹ plot in zero d.c. field for the fast-relaxing (FR) and slow-relaxing (SR) species. The solid lines represent the best fit to the Arrhenius law of the frequency and temperature dependent χ′′ data.

Modeling of the static magnetic properties of 1 on the basis of a spin-Hamiltonian is far from straightforward because of the large dimension (5⁹ = 1 953 125) of the associated spin-Hamiltonian matrix. Within an isotropic model, use of Irreducible Tensor Operator (ITO) algebra⁴⁰ allows blocking of the spin-Hamiltonian matrix into nineteen blocks (ESI §6.2†), each corresponding to a given value of the total spin, S. Thus, the 180 325 S multiplets of 1 (Table S8†), with S varying between 0 and 18, were grouped into nineteen blocks of dimensions ranging from 1 (S = 18) to 25 200 (S = 4). These were subsequently numerically diagonalized by use of standard techniques.⁴¹ The temperature dependence of the χT product of 1 was numerically fitted, down to 10 K, to an isotropic spin-Hamiltonian model by use of the Levenberg–Marquardt algorithm.⁴² To avoid overparameterization, we considered the simplest model of magnetic exchange in 1 (ESI §6.2†), where J₁, J₂ and J₃ are the isotropic exchange parameters within [Mn^III₆], [Mn^III₃] and between [Mn^III₆] and [Mn^III₃], respectively (Fig. S32†). This resulted in the best fit parameters: J₁ = −7.6 cm⁻¹, J₂ = 1.8 cm⁻¹ and J₃ = −1.6 cm⁻¹ (in the −2J convention). These results are in excellent agreement with previous magnetostructural correlations developed for similar oxime-bridged Mn(III)-based SMMs, where Mn–N–O–Mn torsion angles above or below 31° lead to ferromagnetic (J > 0) or antiferromagnetic (J < 0) interactions, respectively.^43,44 Within this highly symmetric isotropic model, the ground spin state of 1 is a doubly degenerate S = 5 with numerous excited multiplets lying very low in energy (Fig. S33a†). However, given the magnetically anisotropic nature of Mn(III), description of the low temperature magnetic properties of 1 in terms of S multiplets is meaningless, since the anisotropy-induced splitting of the m_s sublevels of these S-multiplets is much larger (Fig. S35, Table S9†) than the isotropic exchange induced splitting between S-multiplets (Fig. S33a†). Use of an iterative subspace approach, known as the Davidson algorithm,^45,46 that exploits the sparse nature of the spin-Hamiltonian matrix,^47,48 allowed exact determination of the 32 lowest lying eigenvalues and eigenvectors (ESI §6.2†). This subspace was subsequently used to model the low temperature magnetic properties of 1 (Fig. S34†) allowing estimation of the single-ion uniaxial anisotropy of Mn(III), D_Mn = −3.4 cm⁻¹.

The spin-dynamics of 1 was probed by alternating current (a.c.) magnetic susceptibility measurements, revealing frequency and temperature dependent in-phase (χ′) and out-of-phase (χ′′) components (Fig. 2, S21 and S22†). These were used to extract the energy barrier of the thermally activated process, Δ_eff, by fitting the relaxation time, τ, to the Arrhenius law τ = τ₀ exp(Δ_eff/k_BT), with k_B the Boltzmann constant and τ₀ a pre-exponential factor, resulting in: Δ_eff/k_B = 62.7 K and τ₀ = 4.0 × 10⁻¹⁰ s.

Solution

Since single crystals of 1 are very dark, preventing solid state optical activity measurements, we performed these on chloroform solutions of individual single-crystals of 1. Circular Dichroism (CD) spectra showed mirror-image Cotton effects at several wavelengths (Fig. 3). The higher intensity bands below 330 nm are attributed to charge-transfer²⁵ (CT) and/or internal ligand transitions⁴⁹ (Fig. S19†). The weaker bands observed above 330 nm are attributed to the seven possible d–d transitions for Mn(III) in a low-symmetry crystal field.²⁵ The solution CD spectra of the enantiomers of 1 show that it does not racemize or decompose in solution. Further evidence of the stability of 1 in solution was obtained by infrared (IR) spectroscopy (Fig. S6†) and mass spectrometry (Fig. S7†).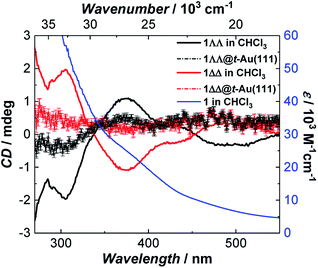

Fig. 3 Room temperature absorption spectrum of 1 (blue) and circular dichroism spectra of 1ΔΔ (red) and 1ΛΛ (black) in CHCl₃ (background corrected data, see ESI†) and as monolayers on Au(111) (raw data). The intensity of 1ΛΛ@t-Au(111) and 1ΔΔ@t-Au(111) was multiplied by a factor of 10 to increase its visibility.

D.c. magnetization measurements on 19.6 mM chloroform solutions of 1 revealed very similar behavior to that observed in the solid state (Fig. 2). The temperature dependence of the χT product, T_B, and the magnetic hysteresis of the frozen solution of 1 are very similar to the analogous measurements in the solid state (Fig. 2), reflecting the structural integrity of 1 in solution. A.c. susceptibility measurements on 19.6 mM chloroform solutions (Fig. 2, S23 and S24†) showed the presence of a slow-relaxing (SR) and a fast-relaxing (FR) process. Since the molecular spin-dynamics is extremely sensitive to the coordination sphere of the metal centres,^50,51 these are attributed to a SR and a FR species, for which we obtain: Δ_eff/k_B of 66.7 and 24.1 K and τ₀ = 8.2 × 10⁻¹⁰ and 1.6 × 10⁻⁸ s, respectively. Magnetization measurements on a 6.8 mM chloroform solution of 1 showed an increase in the FR species (Fig. S25 and S26†). This observation suggests the loss of terminal MeOH ligands upon dissolution, leading to the modification of the axial anisotropy of Mn(III) centres and/or to a change in the Mn(III) Jahn–Teller axis orientation at these centres.^52,53

Surface deposition

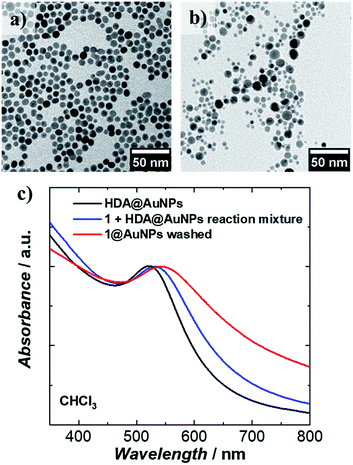
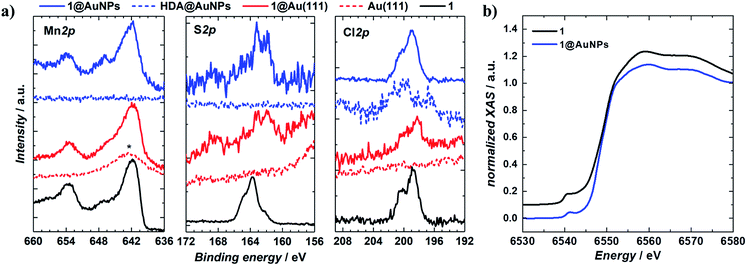
1 was chemically grafted on several metallic gold substrates by exploiting the high affinity of sulfur for gold^54,55 (40–50 kcal mol⁻¹, close to the Au–Au bond strength) and the tripodal ligand nature of 1. These were: (a) gold nanoparticles, AuNPs, used to increase the specific surface area of the substrate for the study of the magnetic properties of grafted 1 (1@AuNPs) by conventional magnetometry;⁵⁶ (b) transparent Au(111) surface,⁵⁷t-Au(111), to allow probing of the optical activity of grafted 1ΛΛ and 1ΔΔ (1ΛΛ@t-Au(111) and 1ΔΔ@t-Au(111), respectively); and (c) epitaxial Au(111) surface, e-Au(111), to study the organization of 1 on this substrate (1@e-Au(111)).

1@AuNPs were obtained from hexadecylamine (HDA) capped AuNPs (HDA@AuNPs) of 7.3 nm average size, as determined by Transmission Electron Microscopy (TEM, Fig. 4, S8 and S9†). Taking into account some simple geometric calculations,⁵⁶ a 10% by weight ratio of 1 is necessary to achieve full coverage. Upon grafting, the dark red color of HDA@AuNPs changed to red-violet for 1@AuNPs (plasmon resonances at 522 and 542 nm, respectively, Fig. 4), indicating a change of dielectric constant around the AuNPs.⁵⁸ To confirm grafting of 1 on AuNPs rather than adsorption, X-ray Photoelectron Spectroscopy (XPS) measurements of 1, HDA@AuNPs and 1@AuNPs were carried out on the Au4f, Au4p, Mn3s, Mn2p, S2p, Cl2p, N1s, O1s and C1s regions of binding energies (Fig. 5a, S10–S12 and Tables S8–S10†). The photoemission of 1@AuNPs allowed confirmation of the presence of Mn, S, and Cl. These elements are not present or have different binding energies in HDA@AuNPs when compared to 1. The S2p region is particularly interesting because S2p_3/2 peaks at 161.8–161.9 eV are assigned to thiols bound to the Au surface while S2p_3/2 peaks at 163.2–163.5 eV are consistent with unbound thiols/disulfides.⁵⁹ The observed shift of the S2p_3/2 bands from 163.5 eV (1) to 161.9 eV (1@AuNPs) of binding energy (and of the less intense S2p_1/2 bands from 164.7 eV (1) to 162.8 eV (1@AuNPs)) and the change of their intensity profile (Fig. 5a and S11†) shows that sulfur is reduced upon binding to Au,^59,60 confirming grafting of 1. Information on the surface stoichiometry (Tables S8 and S9†) was derived by quantitative analysis of the XPS spectra. The stability of 1 upon deposition on AuNPs can be confirmed by the Mn/S ratio values since these elements are not present in HDA@AuNPs. The measured Mn/S ratio in 1 and in 1@AuNPs fits well with the expected stoichiometric value (Table S9†), whereas S/N, Mn/N, and S/Cl ratios are lower than the expected ones in 1@AuNPs suggesting that elements such as N and Cl are present in excess likely due to their high content on the surface of HDA@AuNPs used as starting material in the preparation of 1@AuNPs. Mn(III)-based SMMs often undergo reduction to Mn(II)-containing species upon deposition on gold.⁶¹ The XPS-derived modified Auger parameter (Table S11†), insensitive to charging of non-conducting specimens, has the same value (within standard deviation) for 1, 1@AuNPs and 1@Au(111), suggesting a constant oxidation state in the three samples.^62,63 However, since in XPS, intense Au4f peaks totally cover the Mn3s signals, and Au4p partially interferes with the weak Mn2p signals (Fig. S12†), we performed X-ray absorption spectroscopy (XAS) to compare the oxidation state of Mn in 1 and in 1@AuNPs. The experimental X-ray absorption spectra (Fig. 5b) are dominated by the 1s to 4p transitions with a much weaker pre-edge feature, assigned to dipole-forbidden 1s to 3d transitions. This energetically low-lying pre-edge feature, being weakly dependent on the exact ligand field, is usually taken as a fingerprint of the oxidation state of a transition metal. The Mn K-edge spectra of 1 and of 1@AuNPs reveal a remarkable similarity, confirming that Mn is in the same oxidation state in both systems. By comparison to published Mn(III) K-edge absorption spectra,^64,65 we can conclude that the oxidation state of Mn in 1 and 1@AuNPs is +III. Furthermore, both 1 and 1@AuNPs display very weak X-ray Magnetic Circular Dichroism (XMCD) at the Mn K-edge (Fig. S13†). At the K-edge of a transition metal ion, the XMCD signal is due to the orbital magnetization of the 4p- and 3d-states, induced by the intra-atomic spin–orbit interaction. The XMCD spectrum of 1 (Fig. S13†) reveals several clear features in the pre-edge, at the edge and also characteristic super-Coster–Kronig multi-electron excitations at ∼47 eV above the edge.⁶⁶ However, the amplitude of the XMCD signal of 1 is found to be nearly 100 times weaker than the one detected in paramagnetic Mn³⁺ ions in GaN.⁶⁷ This observation indicates significant quenching of orbital moments in 1.

Fig. 4 Transmission Electron Microscopy (TEM) images of (a) HDA@AuNPs and (b) evenly distributed 1@AuNPs formed after the deposition of 1 on AuNPs; (c) plasmon resonance spectra of HDA@AuNPs and 1@AuNPs.

Fig. 5 XPS and XAS spectra of bulk and surface deposited [Mn₉O₄(Me-sao)₆(L)₃(MeO)₃(MeOH)₃]Cl. (a) XPS spectra of 1, 1@AuNPs, 1@Au(111), HDA@AuNPs, and blank Au(111) surface at Mn2p, S2p and Cl2p core levels. The Mn2p_3/2 core level line in 1@Au(111) is superimposed on the Au4p_1/2 feature, marked with *; (b) Normalised XAS spectra of 1 and 1@AuNPs, the intensity of the former is shifted by 0.1 a.u. for clarity of presentation.

1@AuNPs, HDA@AuNPs and HL@AuNPs were investigated in the solid state with SQUID magnetometry. AuNPs are known to display magnetic properties ranging from diamagnetism, through paramagnetism, to ferromagnetism, depending on the type of surface ligand and the degree of coverage.^68–75 The χT product of 1@AuNPs at 270 K is 22.2 cm³ K mol⁻¹, slightly lower than the 23.2 cm³ K mol⁻¹ seen for 1 (Fig. 2). Between 270 and 60 K the χT product decreases to a value of 15.7 cm³ K mol⁻¹, following the trend observed in 1. On further cooling, the χT product for 1@AuNPs continues to decrease, contrary to 1, until it reaches a plateau around 18.5 cm³ K mol⁻¹ between 25 and 10 K. Below 10 K, χT abruptly decreases, as in 1, to 9.6 cm³ K mol⁻¹ at 1.8 K. Fitting of the temperature dependence of the χT product for 1@AuNPs to the same spin-Hamiltonian model as for 1, resulted in the best-fit parameters: J₁ = −4.5 cm⁻¹, J₂ = 2.7 cm⁻¹ and J₃ = −2.8 cm⁻¹. Thus, the absence of a maximum in the χT product of 1@AuNPs at 10 K is mainly due to the modification of the magnetic exchange interactions within the [Mn₆] subunit (J₁) as a consequence of the distortion of the [Mn₉] core upon grafting to the AuNPs surface via the sulfur-containing carboxylates bound to the [Mn₆] subunit. This modification could be assigned to Mn–N–O–Mn torsion angles within the [Mn₆] subunit evolving from 7.9–13.3° (Tables S2 and S3†), corresponding to J₁ = −7.6 cm⁻¹, towards the 31° limit.^43,44 In fact, a previously reported [Mn₉] complex presenting a very similar temperature dependence of the χT product to 1@AuNPs displayed Mn–N–O–Mn torsion angles of 25° within the [Mn₆] subunit.⁶⁵ The reduced magnetization curves show no saturation and are not superimposable (Fig. S20†), again confirming the magnetically anisotropic nature of 1@AuNPs. The magnetization of 1@AuNPs at 1.8 K and at 5 T is 8.7 μ_B, similar to the solid state. A less well pronounced bifurcation between the ZFC and FC susceptibility curves was observed at 3 K for 1@AuNPs (Fig. 2). 1@AuNPs exhibits magnetic hysteresis (Fig. 2 and S29†) with a coercive field of 0.08 T at 1.8 K and 0.33 T min⁻¹ and of 0.38 T at 0.03 K and 0.24 T min⁻¹. The magnetization observed at low temperatures for 1@AuNPs was several orders of magnitude higher than for HDA@AuNPs or HL@AuNPs (Fig. S28 and S29†). Temperature and frequency dependent χ′ and χ′′ components of the a.c. susceptibility were observed (Fig. 2 and S27†) at zero d.c. field from where Δ_eff/k_B = 30.6 K and τ₀ = 2.4 × 10⁻⁹ s were determined. HDA@AuNPs and HL@AuNPs displayed no such features (Fig. S28–S30†). The values of Δ_eff, T_B, and of the coercive field for 1@AuNPs point towards grafting of the FR species on AuNPs. This is due to the loss of MeOH, and the possible ensuing reorientation of the Jahn–Teller axis, caused by the multiple washing cycles during the surface deposition of 1.

Monolayers of 1@e-Au(111), 1@t-Au(111), 1ΛΛ@t-Au(111) and 1ΔΔ@t-Au(111), hereafter collectively referred to as 1@Au(111), were prepared by soaking e-Au(111) or t-Au(111) films in 2 mM solutions of 1, 1ΛΛ or 1ΔΔ in chloroform, followed by extensive washing with chloroform. All monolayers were characterised by XPS. The observed binding energies and lineshapes of equivalent XPS bands are the same for 1@AuNPs and 1@Au(111) (Fig. 5 and S10–S12†), confirming the redox integrity of 1 and its grafting to form a monolayer. Stoichiometric analysis of the XPS spectra (Table S8†) showed that the Mn/S and Mn/N ratios measured for 1@Au(111) (Table S19†) are higher than the corresponding values for 1 or 1@AuNPs, suggesting a higher Mn content. The observed excess could be caused by the intense Au4f peaks totally superposing the Mn3s signals and Au4p partially interfering with the weak Mn2p signals (Fig. 5a and S12†). The measured value for the S/N ratio is in good agreement with the value measured in 1. Since S and N were not detected on the clean Au(111) surface, the value of S/N ratio for 1@Au(111) can be considered an indirect indication of the [Mn₉] stability during the deposition process.

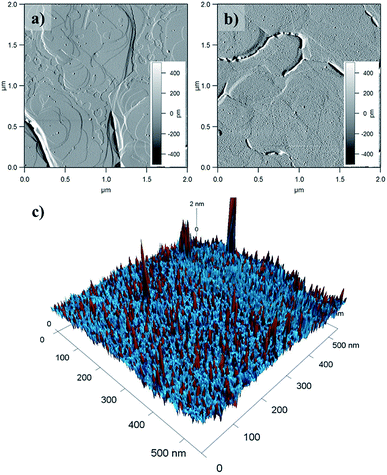
Surface coverage was imaged by Atomic Force Microscopy (AFM) of 1@e-Au(111) (Fig. 6 and S14–S16†). Comparison of the pristine e-Au(111) surface (Fig. 6a) with this of 1@e-Au(111) (Fig. 6b) shows monolayer coverage of the Au(111) facets with isolated protrusions being distributed across the surface. The heights of these individual protrusions range from 0.5 to 1.1 nm, with an average of 0.7 nm (Fig. S16†). This length distribution corresponds well to the length distribution obtained by considering a model where the three sulfur-containing carboxylate bridging ligands either “stand fully elongated” on the Au surface or “lie flat” on it (Fig. S17†). Such a distribution of topologies would create a difference of compressibility in the deposited monolayer since the [Mn₉] metal core is less compressible than the sulfur-containing carboxylates standing fully elongated on the Au(111) surface. This is confirmed by the phase of the AFM taping-mode image (color mapping in Fig. 6c) where individual protrusions also correspond to a change in the AFM phase. A more detailed insight over the organization of the molecules of 1 on the Au(111) surface, though could be offered by high resolution and low temperature scanning tunneling microscopy combined with angle dependent X-ray magneto-circular and/or linear dichroisms.^34,76

Fig. 6 AFM amplitude mode images of (a) e-Au(111) clean surface with visible atomic steps and (b) 1@e-Au(111). (c) 3D combined phase and height AFM taping-mode profiles of 1@e-Au(111). Red and blue taping-mode phases correspond to different compressibilities of the deposited material. Individual protrusions coincide with the red phase.

CD spectra of monolayers of 1ΛΛ@t-Au(111) and 1ΔΔ@t-Au(111) showed mirror-image Cotton effects below 450 nm (Fig. 3 and S19†) corresponding to d–d and CT bands in 1, in very close agreement to the CD spectra observed for solutions of single crystals of 1. These observations confirm both the deposition of enantiopure 1 on Au(111) and the structural stability of 1 upon surface deposition from solution. The structural integrity of 1 upon deposition on t-Au(111) was also confirmed with ATR FT-IR. The obtained IR spectrum of 1@t-Au(111) is superimposable on that of crystalline 1 (Fig. S18†) in the 2000–650 cm⁻¹ spectral region, with no stretching vibrations specific to the free ligands (Me-saoH₂ or HL, Fig. S6†).

Conclusions

We have demonstrated that, by exploiting the power of synthetic chemistry and by taking advantage of the chemical affinity of sulfur for gold, we were able to deposit a chiral SMM on a metallic surface, preserving its molecular multifunctionality (superparamagnetism-like behaviour and optical activity) from the solid state, via dissolution, to the surface deposited species. The observed magnetic properties of the enneannucler Mn(III)-based SMM are explained qualitatively on the basis of established magnetostructural correlations, and quantitatively within the spin-Hamiltonian formalism by use of ITO algebra and of an iterative subspace approach, known as the Davidson algorithm. Future efforts will focus on addressing these surface-deposited chiral SMMs by electric fields via spin-electric coupling, and by light via the magnetochiral effect. This will pave the way for the integration of molecular magnetic chiral materials in molecular quantum spintronics devices, the use of which will revolutionize the way we perceive and manipulate information.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

SP thanks VILLUM FONDEN for research grant 13376. EKB thanks the EPSRC (EP/P025986/1 and EP/N01331X/1) for funding. WW acknowledges ERC Advanced Grant Moquos No. 741276. The European Synchrotron Radiation Facility is acknowledged for measurements (CH-5014) on beamline ID12.

Notes and references

1. C. Chappert, A. Fert and F. N. Van Dau, Nat. Mater., 2007, 6, 813–823.
2. A. R. Rocha, V. M. Garcia-Suarez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335–339.
3. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
4. A. Cornia, M. Mannini, P. Sainctavit and R. Sessoli, Chem. Soc. Rev., 2011, 40, 3076–3091.
5. A. Cornia and M. Mannini, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, pp. 293–330.
6. A. Cornia and M. Mannini, Single-Molecule Magnets on Surfaces, Springer-Verlag, Berlin Heidelberg, 2014.
7. A. Cornia, D. R. Talham and M. Affronte, in Molecular Magnetic Materials: Concepts and Applications, ed. B. Sieklucka and D. Pinkowicz, Wiley - VCH Verlag GmbH & Co. KGaA, 2016, pp. 187–229.
8. S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135–1138.
9. M. Urdampilleta, S. Klyatskaya, J. P. Cleuziou, M. Ruben and W. Wernsdorfer, Nat. Mater., 2011, 10, 502–506.
10. R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357–360.
11. M. Trif, F. Troiani, D. Stepanenko and D. Loss, Phys. Rev. Lett., 2008, 101, 217201.
12. G. L. J. A. Rikken and E. Raupach, Nature, 1997, 390, 493–494.
13. C. Train, R. Gheorghe, V. Krstic, L. M. Chamoreau, N. S. Ovanesyan, G. L. J. A. Rikken, M. Gruselle and M. Verdaguer, Nat. Mater., 2008, 7, 729–734.
14. R. Sessoli, M. E. Boulon, A. Caneschi, M. Mannini, L. Poggini, F. Wilhelm and A. Rogalev, Nat. Phys., 2015, 11, 69–74.
15. D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2007.
16. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
17. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
18. F. Meier, J. Levy and D. Loss, Phys. Rev. Lett., 2003, 90, 047901.
19. F. Troiani, A. Ghirri, M. Affronte, S. Carretta, P. Santini, G. Amoretti, S. Piligkos, G. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2005, 94, 207208.
20. L. Thomas, F. Lionti, R. Ballou, D. Gatteschi, R. Sessoli and B. Barbara, Nature, 1996, 383, 145–147.
21. W. Wernsdorfer and R. Sessoli, Science, 1999, 284, 133–135.
22. K. Bader, D. Dengler, S. Lenz, B. Endeward, S. D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304.
23. M. Mannini, P. Sainctavit, R. Sessoli, C. C. D. Moulin, F. Pineider, M. A. Arrio, A. Cornia and D. Gatteschi, Chem. Eur. J., 2008, 14, 7530–7535.
24. R. Inglis, J. Bendix, T. Brock-Nannestad, H. Weihe, E. K. Brechin and S. Piligkos, Chem. Sci., 2010, 1, 631–636.
25. J. M. Bradley, A. J. Thomson, R. Inglis, C. J. Milios, E. K. Brechin and S. Piligkos, Dalton Trans., 2010, 39, 9904–9911.
26. L. Bogani, L. Cavigli, M. Gurioli, R. L. Novak, M. Mannini, A. Caneschi, F. Pineider, R. Sessoli, M. Clemente-Leon, E. Coronado, A. Cornia and D. Gatteschi, Adv. Mater., 2007, 19, 3906–3911.
27. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M. A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Nat. Mater., 2009, 8, 194–197.
28. M. Mannini, F. Pineider, P. Sainctavit, L. Joly, A. Fraile-Rodriguez, M. A. Arrio, C. C. D. Moulin, W. Wernsdorfer, A. Cornia, D. Gatteschi and R. Sessoli, Adv. Mater., 2009, 21, 167–171.
29. M. Mannini, F. Pineider, C. Danieli, F. Totti, L. Sorace, P. Sainctavit, M. A. Arrio, E. Otero, L. Joly, J. C. Cezar, A. Cornia and R. Sessoli, Nature, 2010, 468, 417–421.
30. L. Bogani, C. Danieli, E. Biavardi, N. Bendiab, A. L. Barra, E. Dalcanale, W. Wernsdorfer and A. Cornia, Angew. Chem., Int. Ed., 2009, 48, 746–750.
31. S. Kyatskaya, J. R. Galan-Mascaros, L. Bogani, F. Hennrich, M. Kappes, W. Wernsdorfer and M. Ruben, J. Am. Chem. Soc., 2009, 131, 15143–15151.
32. A. Hofmann, Z. Salman, M. Mannini, A. Amato, L. Malavolti, E. Morenzoni, T. Prokscha, R. Sessoli and A. Suter, ACS Nano, 2012, 6, 8390–8396.
33. C. Wäckerlin, F. Donati, A. Singha, R. Baltic, S. Rusponi, K. Diller, F. Patthey, M. Pivetta, Y. Lan, S. Klyatskaya, M. Ruben, H. Brune and J. Dreiser, Adv. Mater., 2016, 28, 5142.
34. M. Mannini, F. Bertani, C. Tudisco, L. Malavolti, L. Poggini, K. Misztal, D. Menozzi, A. Motta, E. Otero, P. Ohresser, P. Sainctavit, G. G. Condorelli, E. Dalcanale and R. Sessoli, Nat. Commun., 2014, 5, 4582.
35. V. Corradini, A. Ghirri, E. Garlatti, R. Biagi, V. De Renzi, U. del Pennino, V. Bellini, S. Carretta, P. Santini, G. Timco, R. E. P. Winpenny and M. Affronte, Adv. Funct. Mater., 2012, 22, 3706–3713.
36. A. Ghirri, V. Corradini, C. Cervetti, A. Candini, U. del Pennino, G. Timco, R. J. Pritchard, C. A. Muryn, R. E. P. Winpenny and M. Affronte, Adv. Funct. Mater., 2010, 20, 1552–1560.
37. V. E. Campbell, M. Tonelli, I. Cimatti, J. B. Moussy, L. Tortech, Y. J. Dappe, E. Riviere, R. Guillot, S. Delprat, R. Mattana, P. Seneor, P. Ohresser, F. Choueikani, E. Otero, F. Koprowiak, V. G. Chilkuri, N. Suaud, N. Guihery, A. Galtayries, F. Miserque, M. A. Arrio, P. Sainctavit and T. Mallah, Nat. Commun., 2016, 7, 13646.
38. C. Train, G. Rikken and M. Verdaguer, in Molecular Magnetic Materials: Concepts and Applications, ed. B. Sieklucka and D. Pinkowicz, Wiley - VCH Verlag GmbH & Co. KGaA, 2016, ch. 11, pp. 301–322.
39. H. D. Flack, Helv. Chim. Acta, 2003, 86, 905–921.
40. B. L. Silver, Irreducible tensor methods : an introduction for chemists, Academic, New York, 1976.
41. E. Anderson, LAPACK Users's Guide, Society for Industrial and Applied Mathematics, Philadelphia, 2nd edn, 1995.
42. W. H. Press, B. P. Flannery, S. A. Teukolsky and W. T. Vetterling, Numerical recipes: the art of scientific computing, Cambridge University Press, Cambridge, 1992.
43. C. J. Milios, R. Inglis, A. Vinslava, R. Bagai, W. Wernsdorfer, S. Parsons, S. P. Perlepes, G. Christou and E. K. Brechin, J. Am. Chem. Soc., 2007, 129, 12505–12511.
44. R. Inglis, C. J. Milios, L. F. Jones, S. Piligkos and E. K. Brechin, Chem. Commun., 2012, 48, 181–190.
45. E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94.
46. B. Liu, Numerical Algorithms in Chemistry: Algebraic Method, Lawrence Berkeley Laboratory, University of California, California, 1978, pp. 49–53.
47. S. Piligkos, E. Bill, D. Collison, E. J. L. McInnes, G. A. Timco, H. Weihe, R. E. P. Winpenny and F. Neese, J. Am. Chem. Soc., 2007, 129, 760–761.
48. S. Piligkos, H. Weihe, E. Bill, F. Neese, H. El Mkami, G. M. Smith, D. Collison, G. Rajaraman, G. A. Timco, R. E. P. Winpenny and E. J. L. McInnes, Chem. Eur. J., 2009, 15, 3152–3167.
49. E. K. Fields and S. Meyerson, Acc. Chem. Res., 1969, 2, 273–278.
50. R. Inglis, J. Bendix, T. Brock-Nannestad, H. Weihe, E. K. Brechin and S. Piligkos, Chem. Sci., 2010, 1, 631–636.
51. A. R. Tomsa, J. Martinez-Lillo, Y. L. Li, L. M. Chamoreau, K. Boubekeur, F. Farias, M. A. Novak, E. Cremades, E. Ruiz, A. Proust, M. Verdaguer and P. Gouzerh, Chem. Commun., 2010, 46, 5106–5108.
52. M. Soler, W. Wernsdorfer, Z. M. Sun, J. C. Huffman, D. N. Hendrickson and G. Christou, Chem. Commun., 2003, 2672–2673.
53. P. Parois, S. A. Moggach, J. Sanchez-Benitez, K. V. Kamenev, A. R. Lennie, J. E. Warren, E. K. Brechin, S. Parsons and M. Murrie, Chem. Commun., 2010, 46, 1881–1883.
54. H. Häkkinen, Nat. Chem., 2012, 4, 443.
55. E. Pensa, E. Cortés, G. Corthey, P. Carro, C. Vericat, M. H. Fonticelli, G. Benítez, A. A. Rubert and R. C. Salvarezza, Acc. Chem. Res., 2012, 45, 1183–1192.
56. M. Perfetti, F. Pineider, L. Poggini, E. Otero, M. Mannini, L. Sorace, C. Sangregorio, A. Cornia and R. Sessoli, Small, 2014, 10, 323–329.
57. I. Ashur, O. Schulz, C. L. McIntosh, I. Pinkas, R. Ros and A. K. Jones, Langmuir, 2012, 28, 5861–5871.
58. R. Bukasov and J. S. Shumaker-Parry, Nano Lett., 2007, 7, 1113–1118.
59. D. G. Castner, K. Hinds and D. W. Grainger, Langmuir, 1996, 12, 5083–5086.
60. T. M. Willey, A. L. Vance, C. Bostedt, T. van Buuren, R. W. Meulenberg, L. J. Terminello and C. S. Fadley, Langmuir, 2004, 20, 4939–4944.
61. J. Dreiser, A. M. Ako, C. Wäckerlin, J. Heidler, C. E. Anson, A. K. Powell, C. Piamonteze, F. Nolting, S. Rusponi and H. Brune, J. Phys. Chem. C, 2015, 119, 3550–3555.
62. M. Shima, K. Tsutsumi, A. Tanaka, H. Onodera and M. Tanemura, Surf. Interface Anal., 2018, 50, 1187–1190.
63. M. C. Biesinger, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Phys. Chem. Chem. Phys., 2012, 14, 2434–2442.
64. S. A. Pizarro, P. Glatzel, H. Visser, J. H. Robblee, G. Christou, U. Bergmann and V. K. Yachandra, Phys. Chem. Chem. Phys., 2004, 6, 4864–4870.
65. S. Wang, L. Kong, H. Yang, Z. He, Z. Jiang, D. Li, S. Zeng, M. Niu, Y. Song and J. Dou, Inorg. Chem., 2011, 50, 2705–2707.
66. N. Kawamura, T. Yamamoto, H. Maruyama, I. Harada, M. Suzuki and T. Ishikawa, J. Synchrotron Radiat., 2001, 8, 410–412.
67. E. Sarigiannidou, F. Wilhelm, E. Monroy, R. M. Galera, E. Bellet-Amalric, A. Rogalev, J. Goulon, J. Cibert and H. Mariette, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74.
68. G. L. Nealon, B. Donnio, R. Greget, J.-P. Kappler, E. Terazzi and J.-L. Gallani, Nanoscale, 2012, 4, 5244–5258.
69. I. Carmeli, G. Leitus, R. Naaman, S. Reich and Z. Vager, J. Chem. Phys., 2003, 118, 10372–10375.
70. P. Crespo, R. Litrán, T. C. Rojas, M. Multigner, J. M. de la Fuente, J. C. Sánchez-López, M. A. García, A. Hernando, S. Penadés and A. Fernández, Phys. Rev. Lett., 2004, 93, 087204.
71. S. Trudel, Gold Bull., 2011, 44, 3–13.
72. R. Singh, J. Magn. Magn. Mater., 2013, 346, 58–73.
73. F. Tassinari, D. R. Jayarathna, N. Kantor-Uriel, K. L. Davis, V. Varade, C. Achim and R. Naaman, Adv. Mater., 2018, 30, 1706423.
74. H. Al-Bustami, G. Koplovitz, D. Primc, S. Yochelis, E. Capua, D. Porath, R. Naaman and Y. Paltiel, Small, 2018, 14, 1801249.
75. J. S. Garitaonandia, M. Insausti, E. Goikolea, M. Suzuki, J. D. Cashion, N. Kawamura, H. Ohsawa, I. Gil de Muro, K. Suzuki, F. Plazaola and T. Rojo, Nano Lett., 2008, 8, 661–667.
76. J. Dreiser, G. E. Pacchioni, F. Donati, L. Gragnaniello, A. Cavallin, K. S. Pedersen, J. Bendix, B. Delley, M. Pivetta, S. Rusponi and H. Brune, ACS Nano, 2016, 10, 2887–2892.

---

Footnotes

† Electronic supplementary information (ESI) available: Full experimental details and additional data for all the characterizations presented in the main text. Crystallographic data (including structure factors) for 1ΔΔ and 1ΛΛ have been deposited with the Cambridge Crystallographic Data Centre (CCDC 1839660-1839661, respectively). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc04917c

‡ Present Address: Institute of Nanotechnology, Karlsruhe Institut für Technologie, 76344 Eggenstein-Leopoldshafen, Germany.

---