Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic synergism of pyridinic- and graphitic-nitrogen on N-doped carbons for the oxygen reduction reaction†
Xiaomei
Ning‡
ab,
Yuhang
Li‡
a,
Jingyan
Ming
a,
Qiang
Wang
 c,
Hongjuan
Wang
a,
Yonghai
Cao
c,
Hongjuan
Wang
a,
Yonghai
Cao
 a,
Feng
Peng
a,
Feng
Peng
 d,
Yanhui
Yang
d,
Yanhui
Yang
 c and
Hao
Yu
c and
Hao
Yu
 *a
*a
aSchool of Chemistry and Chemical Engineering, Guangdong Provincial Key Lab of Green Chemical Product Technology, South China University of Technology, Guangzhou 510640, China. E-mail: yuhao@scut.edu.cn; Fax: +86 20 8711 4916; Tel: +86 20 8711 4916
bSchool of Chemistry and Chemical Engineering, Lingnan Normal University, Zhanjiang 524048, China
cInstitute of Advanced Synthesis, School of Chemistry and Molecular Engineering, Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing Tech University, Nanjing 211816, China
dSchool of Chemistry and Chemical Engineering, Guangzhou University, Guangzhou, 510006, China
First published on 13th December 2018
Abstract
Nitrogen-doped carbon materials (NCs) are extensively studied for the oxygen reduction reaction (ORR). However, the nature of active sites of pyridinic nitrogen (NP) or graphitic nitrogen (NG) on NCs is still under debate. Herein, we demonstrated that the ORR activity of NCs in alkaline media depended on the electronic synergism between NP and NG, rather than any single type of N. We measured the transferable electrons of NCs by absorption spectroscopy using 7′7′8′8-tetracyanoquinodimethane as an electron acceptor. The transferable electron amount of NCs is relevant to either NP or NG, leading to the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio as an electron transfer descriptor of NCs in a reverse volcano curve manner across nineteen NCs. The similar dependence of ORR activity on the [NP]
[NG] ratio as an electron transfer descriptor of NCs in a reverse volcano curve manner across nineteen NCs. The similar dependence of ORR activity on the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio of NCs was also discovered, demonstrating the synergistic effect of NP and NG. These results provide a new angle to understand the nature of ORR activity of NCs and optimize the ORR catalyst.
[NG] ratio of NCs was also discovered, demonstrating the synergistic effect of NP and NG. These results provide a new angle to understand the nature of ORR activity of NCs and optimize the ORR catalyst.
Introduction
The oxygen reduction reaction (ORR) is essential for various cutting-edge energy conversion technologies, including metal–air batteries and fuel cells. However, the slow ORR kinetics requires a high dosage of cathodic Pt catalysts that consume two thirds of the over-potential and 90% of Pt in the whole fuel cell.1 Considerable efforts have been devoted to developing the low platinum group metal (PGM) or PGM-free catalysts for the ORR. Nitrogen-doped carbon materials (NCs) are promising candidates among the next generation ORR catalysts because of their low cost, high availability, and good and stable catalytic performance.2,3 N dopants modify the local electronic properties and surface chemistry of carbon materials, and therefore significantly enhance the oxygen adsorption and ORR rate.4,5 Moreover, the NCs enable the synergism with metals toward higher performance by forming M–N–C sites6,7 or metal-core@NC-shell structures.8–10Despite the numerous contributions in this field, the active sites on NCs for the ORR are still under debate. One of the key concerns is regarding which nitrogen component, including pyridinic (NP), pyrrolic, and graphitic (NG) nitrogen substituents and nitrile and amidogen groups, contributes to the enhanced ORR catalytic activity.11–13 NP and NG sites have attracted extensive attention among the nitrogen sites because of their high abundance in most NCs. It has been widely documented that the NP sites are responsible for the ORR activity.5,14 Yasuda et al.15 conducted the temperature-induced surface polymerization of pyridine and julolidine to produce NCs with 90% NP and 80% NG, respectively. It was revealed that NP sites are more active for the ORR than NG because the former site reduces oxygen via a four-electron pathway whereas the latter does it via a two-electron process. Recently, the higher activity of NP sites has been ascertained by investigating model catalysts dominated by NP or NG species on HOPG.5 Nonetheless, the NG site offers considerable activity for the ORR activity as well, leading to strong correlations between the number of NG sites and ORR activity in some literature studies.12,16
The controversial results imply undiscovered factors dominating the activity of NCs. It should be noted that most of the mechanistic studies employed a reductionism methodology, which attempts to correlate the activity with the amount of a single type of nitrogen to identify the so-called structure–activity relationship. To this end, model catalysts containing single N groups need to be synthesized with sophisticated routes, and it is a prerequisite to quantify their amounts via advanced spectroscopic technology (XPS, EELS, etc.) as well.17,18 However, theoretical calculations suggested that various nitrogen sites (pyridinic, pyrrolic and graphitic) are capable of adsorbing and activating oxygen, in spite of their different strengths.19,20 More importantly, the practical NCs inevitably consist of a polymorph of different nitrogen groups. They may either synergistically modulate the overall electronic structure of NCs because of the large delocalized electron distribution of the carbon matrix, or mutually affect the localized electronic properties around the NP or NG.21,22 In fact, the mutual impact between two different dopants has recently been recognized as a significant factor to determine the catalysis of N–S/N–B/N–P co-doped carbons.23–26 Taking into account the distinctly different electronic properties of NP and NG, it is natural to expect that the synergism between proximal NP and NG may lead to essentially different activity from the isolated ones, which only exist in the ideal case with extremely low site density.
Theoretical and experimental studies suggest that the carbon atom next to NP or NG adsorbs and activates the O2 in a different configuration.5,11,27 Zhang et al.4 have reported that the ORR activity of N-doped graphene is related to its electron spin density and atomic charge density due to the introduced N. An elaborate theoretical calculation study by Qiao and co-workers28 revealed that the structure of the dopant changes the density of states at the Fermi level of the carbon atoms, which modulates the capability of transferring electrons to facilitate the reduction reaction at interfaces. The differential configuration and charging of dioxygen on NG and NP sites have recently been proved by a DFT calculation.29 Similarly, the NG and vacant NP sites behave as electron donors and acceptors, respectively, by anchoring a platinum single metal atom, thereby the catalytic activity of the metal may be modified in redox reactions.30,31 The strong relevance of the catalysis of NCs with the electron transfer properties inspired the exploration of the dependence of electron affinity of NCs on the nitrogen dopants. Regarding NP and NG sites as moieties with different electron affinities, their amounts, distribution and synergism may be reflected by the overall electronic properties of NCs. By doing so, it is possible to establish a new descriptor for ORR activity of NCs, which allows for evaluation of the performance of NCs with practical compositions to understand the nature of activity of NCs.
In this work, a non-covalent conjugative interaction between NCs and 7′7′8′8-tetracyanoquinodimethane (TCNQ) was employed to investigate the electron transfer properties at the interfaces. TCNQ and its derivatives or analogues, e.g. tetracyanoethylene (TCNE), are commonly used as electron acceptors to study the electron donation of materials because of their small HOMO–LUMO gaps and high electron affinity.32,33 Due to the electron transfer via π–π interaction between TCNQ and the graphitic carbon matrix, TCNQ has been adopted as an effective molecular modifier to tune the electronic properties of graphene-based systems.32,34 More importantly, the well-developed TCNQ chemistry offers a powerful tool to quantitatively evaluate the electrons that are donated from host materials to TCNQ.
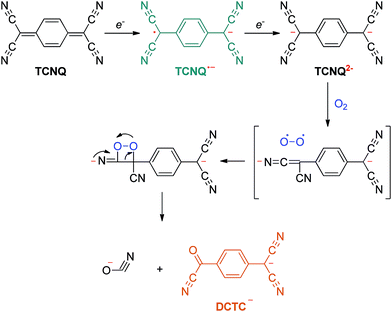
Suchanski and Van Duyne35 have reported the electrochemistry of TCNQ in acetonitrile solution in the 1970s. As shown in Scheme 1, TCNQ consecutively reacts with one and two electrons to form TCNQ˙− and a TCNQ2− dianion. When exposed to air, a rapid oxidation reaction of the TCNQ2− dianion occurs to produce an α,α-dicyano-p-toluoylcyanide anion (DCTC−), which shows a maximum at 477 nm in the absorption spectrum, leading to an orange DCTC− solution. Along these lines, the reactions between NCs and TCNQ may be employed to titrate the electrons that transfer from NCs to TCNQ via a facile optical spectroscopic method. A similar method has been applied by Wang et al.36 to probe the transferable electrons from molybdenum oxides to supported gold nanoparticles using TCNE as the electron-accepting molecule, elucidating the electronic improvement of the MoOx support to gold catalysis. So far, however, this approach has not been explored to quantitatively measure the electronic properties of NCs.
Herein, we demonstrate that NCs interact with TCNQ as an electron-acceptor, allowing for their transferable electrons to be counted quantitatively by absorption spectroscopy of TCNQ-derived anions. It is revealed that the transferable electron amount is highly relevant to either NP or NG, leading to the ratio [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] as a new descriptor of the electron transfer, which definitely suggests a synergism between NP and NG on the electronic properties of NCs. For the first time, it is clearly revealed that the ORR activity of NCs in alkaline media heavily depends on the ratio [NP]
[NG] as a new descriptor of the electron transfer, which definitely suggests a synergism between NP and NG on the electronic properties of NCs. For the first time, it is clearly revealed that the ORR activity of NCs in alkaline media heavily depends on the ratio [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] in a reverse volcano curve (V) manner, suggesting the synergistic effect of NP and NG on the ORR. Combined with DFT calculations, these results shed light on the dependence of ORR activity on the global electronic properties of NCs and afford a new insight into understanding the catalytic nature of NCs.
[NG] in a reverse volcano curve (V) manner, suggesting the synergistic effect of NP and NG on the ORR. Combined with DFT calculations, these results shed light on the dependence of ORR activity on the global electronic properties of NCs and afford a new insight into understanding the catalytic nature of NCs.
Results and discussion
A variety of NCs, with a wide spectrum of structures (graphene or carbon nanotubes) and synthesis methods, were investigated to unbiasedly reflect the effect of N dopants on electronic properties. One group of NCs investigated are N-doped carbon nanotubes (NCNTs) synthesized by a CVD method using aniline or xylene as feedstock in an argon or ammonia atmosphere.30,37 By changing the combination of feedstock and atmosphere, the amount of N dopants and thickness of CNT walls can be readily adjusted. Fig. 1(a–c) display the typical bamboo-like structure of the NCNTs.37 Depending on the synthesis conditions, the N content measured by XPS varied from 0.41 to 7.41 at%, as shown in Fig. S1 and Table S1.† The NCNTs prepared by the CVD method have N atoms doped in both outer and inner carbon layers.37,38 An alternative strategy was applied for the synthesis of N-doped CNTs with N dopants enriched on surfaces, denoted as N@CNTs, by a post thermolysis of pyridine on conventional CNTs.39Fig. 1(d) clearly shows the inner CNTs and the N-enriched surface carbon layer. By changing the duration and temperature of thermolysis, the content of N dopants can be facilely tuned (Fig. S1 and Table S1†). This approach can also be extended to other supports, e.g. graphene, to compare the one-dimensional and two-dimensional materials (N@RGO in Fig. 1(e)). In addition, N-doped mesoporous graphenes (NG) were also synthesized by a methane CVD method in ammonia using porous MgO as the template,40 and they feature a high specific surface area and N/(N + C) atomic ratio of 6.46% and 4.07% (see Fig. S1 and Table S1†), respectively. | ||
| Fig. 1 TEM images of (a) NCNTs(X–N), (b) NCNTs(A–N), (c) NCNTs(A–A), (d) N@CNTs(A-2.5), (e) N@RGO(A-2.5), and (f) NG. | ||
The N1s XPS spectra of the nineteen samples are displayed in Fig. S1.† Quantitative XPS analysis of nitrogen content, deconvoluted by NP, NG, pyrrolic nitrogen (NPy), N oxides (Nox), and chemisorbed nitrogen (Nads), as well as the ratio of [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] are summarized in Table S1.† For the NCNTs prepared by the CVD method, the NG percentage of NCNTs(A–A)-900 synthesized in Ar is higher than that for those synthesized in an NH3 atmosphere, NCNTs(A–N)-900 and NCNTs(X–N)-900. Because NG is more thermodynamically stable than NP at higher temperatures,41–43 annealing at 1100 °C led to the decrease of the [NP]
[NG] are summarized in Table S1.† For the NCNTs prepared by the CVD method, the NG percentage of NCNTs(A–A)-900 synthesized in Ar is higher than that for those synthesized in an NH3 atmosphere, NCNTs(A–N)-900 and NCNTs(X–N)-900. Because NG is more thermodynamically stable than NP at higher temperatures,41–43 annealing at 1100 °C led to the decrease of the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio of NCNTs(A–N) from 0.94 to 0.64. For N@CNT samples, the content of surface nitrogen increased with the pyrolysis duration, from 0.41% for 1.5 h to 7.41% for 4.5 h; meanwhile, the [NP]
[NG] ratio of NCNTs(A–N) from 0.94 to 0.64. For N@CNT samples, the content of surface nitrogen increased with the pyrolysis duration, from 0.41% for 1.5 h to 7.41% for 4.5 h; meanwhile, the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio decreased from 1.33 for 1.5 h to 0.55 for 4.5 h. Being similar to NCNTs, the [NP]
[NG] ratio decreased from 1.33 for 1.5 h to 0.55 for 4.5 h. Being similar to NCNTs, the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio of N@CNTs decreased with increasing pyrolysis temperature, accompanied by the decline of gross nitrogen content due to the decomposition and transition of N dopants. Besides, the distribution of N species can be further tuned by the atmosphere during the pyridine pyrolysis. The pyrolysis in NH3 considerably elevated the [NP]
[NG] ratio of N@CNTs decreased with increasing pyrolysis temperature, accompanied by the decline of gross nitrogen content due to the decomposition and transition of N dopants. Besides, the distribution of N species can be further tuned by the atmosphere during the pyridine pyrolysis. The pyrolysis in NH3 considerably elevated the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio of N@CNTs compared to that in Ar (entries 12 and 9 of Table S1†) at the cost of decreased total nitrogen content, probably due to the etching of hydrogen from NH3 decomposition.38 The similar flexibility of the distribution of N species, represented by the [NP]
[NG] ratio of N@CNTs compared to that in Ar (entries 12 and 9 of Table S1†) at the cost of decreased total nitrogen content, probably due to the etching of hydrogen from NH3 decomposition.38 The similar flexibility of the distribution of N species, represented by the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio, was demonstrated for graphene samples as well. Such a relatively large library of NCs covers two types of most popular nanocarbons, i.e. CNTs and graphene, and varies the N content from 0.41% to 7.41 at%, which may offer an opportunity to summarize the relationships between N doping and electronic properties and ORR catalytic activity.
[NG] ratio, was demonstrated for graphene samples as well. Such a relatively large library of NCs covers two types of most popular nanocarbons, i.e. CNTs and graphene, and varies the N content from 0.41% to 7.41 at%, which may offer an opportunity to summarize the relationships between N doping and electronic properties and ORR catalytic activity.
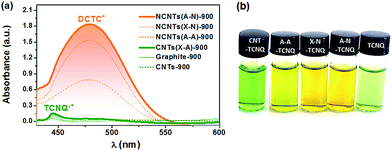
The electron transfer reaction between NCs and TCNQ was employed to probe the transferable electrons via tracking the anions derived from the reactions in Scheme 1. The TCNQ solution in acetonitrile has a greenish color (see Fig. 2(b)) because the free radicals of TCNQ ions in acetonitrile solution absorb infrared or near-infrared light.44 After being thoroughly exposed to un-doped carbon materials (CNTs and graphite), the solution turned dark green, giving a weak yet distinct absorption peak at ca. 445 nm as shown in Fig. 2(a). This is indicative of the formation of additional TCNQ˙− anions,44,45 suggesting the one-electron transfer reaction between carbon materials and TCNQ. Interestingly, the reaction between TCNQ and NCs generated completely different anionic products with a tawny color, as shown in Fig. 2(b). The optical study indicated a strong and broad absorption band centered at ca. 480 nm, which was absent or extremely weak in the case of un-doped carbons (Fig. 2a and S2†). The absorption can be assigned to DCTC− anions, resulting from the oxidation of dianion TCNQ2−.35 Namely, the peak at ca. 480 nm was caused by the two-electron transfer reaction, which was only noticeable in the presence of N dopants. Hence, it was the N dopants rather than other factors (e.g. carbon defects) that triggered the two-electron reaction pathway between TCNQ and NCs, rationalizing the ability of NCs as an excellent material for improving electron transfer for various applications, e.g. optoelectronics,46 solar cells,47 and (electro-)catalysts.48 The different reaction mechanism may stem from the stronger adsorption of the TCNQ˙− anion on NCs compared to un-doped carbons, as supported by a DFT calculation (Fig. S3†), which facilitates further electron transfer reaction of TCNQ˙−.
The distinct absorption peak at 480 nm enables the facile quantitation of transferable electrons on NCs through the Lambert–Beer law. Assuming that NCs are the exclusive source of electrons of DCTC− anions, the absorbance at 480 nm can be a measure of transferable electrons of NCs. Taking into account the different electron transfer reaction mechanisms between N-doped and un-doped carbons, the absorbance should be normalized by the mass of NCs, since only the deposited carbon layer wrapped on surfaces contains nitrogen in the cases of N@CNTs and N@RGO, which can be determined by weighing the samples after the pyridine pyrolysis. It is defined as the intensity of electron transfer, IET (m g−1), caused by N-doping. We firstly attempted to establish the relationship between IET and the content of nitrogen measured by XPS. Unfortunately, the scattering plots of IETvs. the gross nitrogen content, as well as any specific type of nitrogen (see Fig. S4†), indicate that the electron transfer reaction cannot be simply regarded as an interplay between TCNQ and isolated single N sites, and that the role of different N sites, including NP, NPy, and NG, may be diverse.
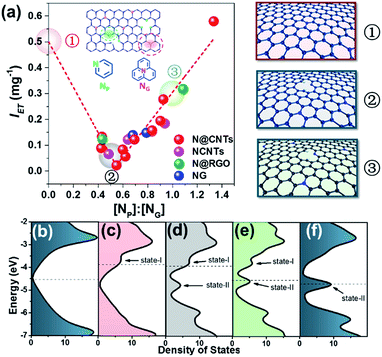
Surprisingly, a quite high relevance in a reverse volcano shape appeared when the content ratio of pyridinic to graphitic nitrogen ([NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG]) was used to correlate IET. As shown in Fig. 3, the IET value decreases with the increase of the [NP]
[NG]) was used to correlate IET. As shown in Fig. 3, the IET value decreases with the increase of the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio as it is smaller than 0.55. Further increasing the ratio leads to an opposite tendency. With increasing [NP]
[NG] ratio as it is smaller than 0.55. Further increasing the ratio leads to an opposite tendency. With increasing [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio from 0.55 to 1.3, the IET value increases linearly from 0.02 to 0.6 mg−1 by 30 fold. It affords a comprehensive insight into how N dopants affect the electron transfer on surfaces of NCs. When the [NP]
[NG] ratio from 0.55 to 1.3, the IET value increases linearly from 0.02 to 0.6 mg−1 by 30 fold. It affords a comprehensive insight into how N dopants affect the electron transfer on surfaces of NCs. When the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio is small (less than 0.55 in Fig. 3(a)), there will be more transferable electrons if the sample contains more graphitic nitrogen. The opposite is also true. However, their coexistence may reduce the transferable electrons. This result rationalizes well the controversial results in the literature as interpreted in the Introduction section, demonstrating that NP and NG sites can both improve the electron transfer.14,49 In addition, it is impressive that the dependence is irrelevant to the structure and synthesis method of NCs across the considerably large sample library containing nineteen samples, strongly suggesting that the transferable electron may be intrinsically determined by the synergism between pyridinic and graphitic nitrogen sites. This synergism may provide a new horizon to understand the nature of active sites on NCs.
[NG] ratio is small (less than 0.55 in Fig. 3(a)), there will be more transferable electrons if the sample contains more graphitic nitrogen. The opposite is also true. However, their coexistence may reduce the transferable electrons. This result rationalizes well the controversial results in the literature as interpreted in the Introduction section, demonstrating that NP and NG sites can both improve the electron transfer.14,49 In addition, it is impressive that the dependence is irrelevant to the structure and synthesis method of NCs across the considerably large sample library containing nineteen samples, strongly suggesting that the transferable electron may be intrinsically determined by the synergism between pyridinic and graphitic nitrogen sites. This synergism may provide a new horizon to understand the nature of active sites on NCs.
DFT calculations were employed to understand the unique allotropic synergistic effect on transferable electrons. We compared the transfer of the first electron from N-doped graphene to TCNQ, assuming that it is the rate-determining step. The calculation results suggest that the electronic interaction is stronger in the case of N-doped graphene (NG). It is revealed that the HOMO of the TCNQ-NG complex is primarily contributed by the defect carbon atom near NP. The valence electrons from NG redistribute to the defect carbon induced by the NP, and then transfer to TCNQ (see Fig. S3†).
The effect of the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio can be illustrated by density of states (DOS) analyses through varying the numbers of NP and NG atoms in the graphene sheet. Three [NP]
[NG] ratio can be illustrated by density of states (DOS) analyses through varying the numbers of NP and NG atoms in the graphene sheet. Three [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratios were selected to compare their electronic properties, i.e. 0, 0.5 and 1, as highlighted by the balloons in Fig. 3(a). Their structures are shown in the right panel of Fig. 3(a). As shown in Fig. 3(c), after introducing NG atoms into graphene, a new state (marked as state-I) appears distinctly ranging from −4 to −3.5 eV compared to the pristine graphene (Fig. 3(b)). Meanwhile, the Fermi level shifts toward a more positive energy level at −3.88 eV, locating at the newly introduced state-I.50 In comparison, doping NP atoms in graphene leads to the formation of a new energy state (marked as state-II, see Fig. 3(f)) ranging from −5 to −4.5 eV, associated with the Fermi level shifting toward a more negative energy level at −4.70 eV.50 Notably, despite the negative shift of the Fermi level, the electron transfer between NCs and TCNQ can also occur naturally because the calculated LUMO energy of TCNQ is −5.29 eV, meeting the requirement of orbital energy difference between NCs and TCNQ. In the presence of both NP and NG, it can be seen that state-I is attenuated gradually as the [NP]
[NG] ratios were selected to compare their electronic properties, i.e. 0, 0.5 and 1, as highlighted by the balloons in Fig. 3(a). Their structures are shown in the right panel of Fig. 3(a). As shown in Fig. 3(c), after introducing NG atoms into graphene, a new state (marked as state-I) appears distinctly ranging from −4 to −3.5 eV compared to the pristine graphene (Fig. 3(b)). Meanwhile, the Fermi level shifts toward a more positive energy level at −3.88 eV, locating at the newly introduced state-I.50 In comparison, doping NP atoms in graphene leads to the formation of a new energy state (marked as state-II, see Fig. 3(f)) ranging from −5 to −4.5 eV, associated with the Fermi level shifting toward a more negative energy level at −4.70 eV.50 Notably, despite the negative shift of the Fermi level, the electron transfer between NCs and TCNQ can also occur naturally because the calculated LUMO energy of TCNQ is −5.29 eV, meeting the requirement of orbital energy difference between NCs and TCNQ. In the presence of both NP and NG, it can be seen that state-I is attenuated gradually as the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio increases, and state-II is enhanced. Importantly, the Fermi level shifts between state-I and state-II upon varying the [NP]
[NG] ratio increases, and state-II is enhanced. Importantly, the Fermi level shifts between state-I and state-II upon varying the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio. When the ratio is less than 0.5, the Fermi level falls into state-I, indicating that the graphitic nitrogen doping contributes primarily to the electron transfer from NCs to TCNQ. Accordingly, when the ratio is greater than 1, the Fermi level locates in state-II, showing that the pyridinic nitrogen doping dominates the electron transfer. During this evolution, the DOS at the Fermi level would firstly decrease and then increase due to the transition from NG-dominated to NP-dominated electronic properties. It should be noted that this transition passes through a DOS at the Fermi level approaching zero at a specific [NP]
[NG] ratio. When the ratio is less than 0.5, the Fermi level falls into state-I, indicating that the graphitic nitrogen doping contributes primarily to the electron transfer from NCs to TCNQ. Accordingly, when the ratio is greater than 1, the Fermi level locates in state-II, showing that the pyridinic nitrogen doping dominates the electron transfer. During this evolution, the DOS at the Fermi level would firstly decrease and then increase due to the transition from NG-dominated to NP-dominated electronic properties. It should be noted that this transition passes through a DOS at the Fermi level approaching zero at a specific [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio, where the system has the lowest electron transfer ability. Although a precise determination of this point is still unavailable because of the limitation of computational ability, the lower DOS at an [NP]
[NG] ratio, where the system has the lowest electron transfer ability. Although a precise determination of this point is still unavailable because of the limitation of computational ability, the lower DOS at an [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio of 0.5 can be indeed observed as shown in Fig. 3(d). These results are well consistent with the experimental data showing the mutual influence between NG and NP on the transferable electrons of NCs. It is rationalized that NG and NP both favor the electron transfer as isolated dopants, as widely documented in the literature.21,22 Nonetheless, their blends are not necessarily beneficial, because of the interaction between NP and NG with different electronic properties. In other words, the electronic properties of a single NP may be different in the presence of neighboring NG, and vice versa. This circumstance may have been overlooked when investigating model catalysts previously, thus resulting in the controversial results.
[NG] ratio of 0.5 can be indeed observed as shown in Fig. 3(d). These results are well consistent with the experimental data showing the mutual influence between NG and NP on the transferable electrons of NCs. It is rationalized that NG and NP both favor the electron transfer as isolated dopants, as widely documented in the literature.21,22 Nonetheless, their blends are not necessarily beneficial, because of the interaction between NP and NG with different electronic properties. In other words, the electronic properties of a single NP may be different in the presence of neighboring NG, and vice versa. This circumstance may have been overlooked when investigating model catalysts previously, thus resulting in the controversial results.
Bearing this synergism between NP and NG in mind, the ORR performance of the NCs in alkaline media was revisited. Considering the complexity of the ORR involving multiple elementary steps, the catalytic investigation was restricted to the ten N@CNTs samples, in which the CNT inner core affords a conductive network while the surface N-doped carbon layer more efficiently catalyzes the ORR.39 By doing so, it is attempted to keep the structure, surface area, and porosity of electro-catalysts as constant as possible, since they have been widely documented to be potent to ORR activity.16,51,52 Linear sweep voltammetry (LSV) tests on an RDE at different rotating speeds were conducted for extracting the kinetic parameters of the ORR through the Koutecky–Levich (K–L) equation:
| j−1 = jl−1 + jk−1 = (0.62nFCD2/3ν−1/6ω1/2)−1 + jk−1. |
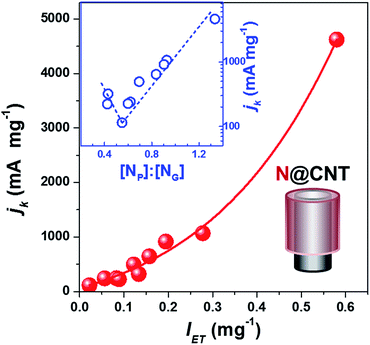
The kinetic current density (jk), which has been recommended as a descriptor of ORR activity,53,54 can be obtained by fitting the experimental data in the K–L plots (j−1vs. ω−1/2) as shown in Fig. S6.† The electron transfer number of N@CNTs determined by the Koutecky–Levich (K-L) equation is within the range from 4.2 to 2.2. As a simplified prediction, the ORR activity should benefit from the stronger electron donating ability of the catalyst because oxygen accepts electrons to produce OH− or H2O2. Fig. 4 displays the jk value at −0.7 V as a function of intensity of electron transfer (IET) defined by the absorption of TCNQ at 480 nm. Depending on the amount and type of N-dopant wrapped on CNTs, the jk varies in a wide range from 114.6 to 4623.5 mA mg−1 almost by 40 fold enhancement, demonstrating the improvement of ORR activity by the N-doping strategy. More importantly, we revealed the clear relationship between jk and IET. The jk at −0.7 V monotonically increases with IET as shown in Fig. 4, suggesting the crucial role of electron transfer on catalyst surfaces in the ORR activity. A similar dependence between jk and IET was obtained using the jk at −0.6 V and −0.5 V from the K–L plots (see Fig. S7†). In addition, the Tafel equation was applied to evaluate the ORR performance of N@CNTs (see Fig. S8† for the Tafel curves). The Tafel slope declines with increasing IET from 105 to 70 mV dec−1 (Fig. S9†). This result implies that the strong electron transfer may reduce the over-potential, as shown in Fig. S10.†
To understand the structure–activity relationship of NCs, we correlated jk with the gross nitrogen content, as well as any specific type of nitrogen, but scattering plots were obtained again (see Fig. S11†). However, a reverse volcano-type curve can be plotted when summarizing the structure–activity relationship using the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio as a descriptor, as displayed in the inset of Fig. 4 and S7.† The high content of either NG or NP can improve the activity. jk has a minimum at an NP
[NG] ratio as a descriptor, as displayed in the inset of Fig. 4 and S7.† The high content of either NG or NP can improve the activity. jk has a minimum at an NP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NG ratio of 0.55, where the N@CNTs have the lowest amount of transferable electrons as mentioned earlier. The highest ORR activity is reached over the sample with the highest [NP]
NG ratio of 0.55, where the N@CNTs have the lowest amount of transferable electrons as mentioned earlier. The highest ORR activity is reached over the sample with the highest [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio, which is consistent with the widely accepted conclusion that pyridinic nitrogen is the most active site for the ORR. However, our results indicate that the graphitic nitrogen can be alternative active sites when the content of pyridinic nitrogen or the [NP]
[NG] ratio, which is consistent with the widely accepted conclusion that pyridinic nitrogen is the most active site for the ORR. However, our results indicate that the graphitic nitrogen can be alternative active sites when the content of pyridinic nitrogen or the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio is low. Nevertheless, we emphasize that the dependence of ORR activity on the [NP]
[NG] ratio is low. Nevertheless, we emphasize that the dependence of ORR activity on the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio is confirmed for the NCs with a similar synthesis and structure, and other factors, such as micropores, nitrogen content, and conductivity, may influence the activity.
[NG] ratio is confirmed for the NCs with a similar synthesis and structure, and other factors, such as micropores, nitrogen content, and conductivity, may influence the activity.
The above results provide a new insight into the nature of the active sites of the ORR on NCs. Differing from conventional elucidation, our results emphasize the synergistic effect of different types of N-dopants on the electron transfer and ORR activity. The activity of nitrogen-containing active sites may be influenced by other N-dopants. Because of the different electronic properties of NP and NG, their co-existence may reduce the electron transfer and thus the ORR activity, as evidenced by the reverse volcano curve ascribed to the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio. This suggests that the content of NP and NG has to be synchronously controlled for the rational design of NCs as ORR catalysts. Moreover, the design, synthesis and characterization of the graphene-like unit containing different nitrogen configurations could be interesting, which may lead to a new paradigm for synthesizing metal-free electrocatalysts.
[NG] ratio. This suggests that the content of NP and NG has to be synchronously controlled for the rational design of NCs as ORR catalysts. Moreover, the design, synthesis and characterization of the graphene-like unit containing different nitrogen configurations could be interesting, which may lead to a new paradigm for synthesizing metal-free electrocatalysts.
Conclusions
In summary, we developed a method to measure the transferable electrons of NCs using TCNQ as an electron accepting molecule. It was found that the strong electronic interaction between NCs and TCNQ facilitated the two-electron reduction reaction of TCNQ to produce DCTC− anions, which can be quantitatively analyzed by absorption spectroscopy with a characteristic peak at 480 nm, allowing for the transferable electrons to be counted as a measure of the electron donating ability of NCs. By this facile technique, it was uncovered that the intensity of electron transfer on NCs depended on the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio in a reverse volcano curve across a wide spectrum of NCs. When these NCs were subjected to the ORR in alkaline media, a similar relationship between the kinetic current density and the [NP]
[NG] ratio in a reverse volcano curve across a wide spectrum of NCs. When these NCs were subjected to the ORR in alkaline media, a similar relationship between the kinetic current density and the [NP]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [NG] ratio was observed. This result sheds light on the roles of NP and NG in determining the electronic properties and ORR activity of NCs. Namely, isolated NP or NG can both improve the ORR activity, while their interaction results in lower electron donation and ORR activity, as revealed by experimental and theoretical data. Our results provide a new horizon to survey and optimize the activity of metal-free NC electrocatalysts. The insight into the synergistic effect of NP and NG on electronic properties also paves a new avenue to enhance other cutting-edge applications based on NCs, such as supports of metal catalysts, co-catalysts for photo-electro-catalysis, dye-sensitized solar cells, etc.
[NG] ratio was observed. This result sheds light on the roles of NP and NG in determining the electronic properties and ORR activity of NCs. Namely, isolated NP or NG can both improve the ORR activity, while their interaction results in lower electron donation and ORR activity, as revealed by experimental and theoretical data. Our results provide a new horizon to survey and optimize the activity of metal-free NC electrocatalysts. The insight into the synergistic effect of NP and NG on electronic properties also paves a new avenue to enhance other cutting-edge applications based on NCs, such as supports of metal catalysts, co-catalysts for photo-electro-catalysis, dye-sensitized solar cells, etc.
Experimental and computational methods
Catalyst preparation
The N-doped graphene (NG) was synthesized by a CVD method with CH4 as a carbon source and introduced NH3 as a nitrogen source over the MgO catalyst in a horizontal tube furnace.40,56 The NG was obtained after CH4 cracking at 700 °C for 20 min. The sample was further purified using HCl reflux, and then filtered, dried and ground.
Graphite oxide (GO) was synthesized through a modified Hummers' method, as detailed in ref. 57 and 58. The GO was further reduced in 10% H2/Ar at 700 °C for 2 h. The same pyridine pyrolysis was conducted on the reduced GO (RGO) in Ar or NH3 for 2.5 h. The resulting samples are denoted as N@RGO(A-2.5) and N@RGO(N-2.5), respectively.
NCs were further annealed at 800 °C, 900 °C, or 1100 °C in Ar gas at 100 N cm3 min−1 for 2 h, to vary the nitrogen content and distribution. The resulting samples are denoted as NCNTs-T, NG-T, or N@CNTs-T (T = 800/900/1100 °C).
Catalyst characterization
X-ray photoelectron spectroscopy (XPS) analysis was conducted using a Kratos Axis Ultra (DLD) spectrometer with an AlKα X-ray source. The calibration peak of C 1s was defined at 284.6 eV. The morphology of the samples was observed by transmission electron microscopy (TEM) with a JEOL JEM2010 microscope operating at 200 kV. UV-Vis absorption spectroscopy (SHIMADZU, UV-2450) measurement was performed using a TCNQ acetonitrile solution as a reference.Computational methods
The periodic pure graphene and nitrogen-doped graphene were initially optimized with the DMol3 package.59 The optimization was achieved with the Perdew–Burke–Ernzerhof (PBE)60 exchange–correlation functional under the DNP basis set (nearly equivalent to 6-31G** in Gaussian). The dispersion correction contributed by Grimme was considered during calculations.61 The k-point was set to 8 × 8 × 1 for the self-consistent field (SCF) procedure, and 12 × 12 × 1 for the density of states calculation. The conductor-like screening model (COSMO) with a permittivity of 37.5 was invoked to mimic the acetonitrile solvent environment.62 The global orbital cutoff was 4.5 Å.The primitive cell of graphene was extended to a 6 × 6 × 1 supercell. Avoiding the interaction between neighboring lattices, 25 Å was set as the vacuum layer along the direction perpendicular to the graphene surface. After optimization, two carbon atoms on average were replaced with nitrogen atoms to build the N-doped graphene, including a NG atom and a NP atom. Notably, the topological defect was inevitably generated once NP was introduced onto the graphene surface. Herein, the defect carbon atoms were saturated with hydrogen. The calculations mentioned above were adopted for geometry optimization and electronic structure determination.
The optimized structures were further calculated with Quantum ESPRESSO 6.2 to evaluate the TCNQ adsorption energy. Herein, the GBRV ultrasoft pseudopotentials based on the PBE exchange–correlation functional were invoked. Global kinetic energy cutoffs were set to 35 Ry for the involved elements of H, C and N. Kinetic energy was set to 280 Ry for charge density and potential. Grimme's DFT-D3 was included as the long-range dispersion correction method. The electronic smearing value was 0.002 Ry (0.027 eV). The k-point setting was 8 × 8 × 1, the same as that for the calculations in DMol3.
Reactions
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 77. 15 μL ink was cast on the surface of the GC disk for obtaining the Rotating Disk Electrode (RDE). Linear sweep voltammetry (LSV) tests were performed in 0.1 M KOH solution saturated with oxygen from −1 V to 0.2 V at a scan rate of 5 mV s−1 with different rotation rates (200, 400, 600, 900, 1200, and 1600 rpm).
77. 15 μL ink was cast on the surface of the GC disk for obtaining the Rotating Disk Electrode (RDE). Linear sweep voltammetry (LSV) tests were performed in 0.1 M KOH solution saturated with oxygen from −1 V to 0.2 V at a scan rate of 5 mV s−1 with different rotation rates (200, 400, 600, 900, 1200, and 1600 rpm).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 21676100 and 21703093), the Guangdong Natural Science Foundation (No. 2017A030312005 and 2017A030310600), the Science and Technology Program of Guangzhou City (No. 201707010058), the Youth Innovation Talent Project for the Universities of Guangdong (No. 2016KQNCX095), and the Special Talent Fund of Lingnan Normal University (No. ZL1805). We are thankful for the high performance computing support provided by the Information and Network Engineering and Research Center, South China University of Technology.Notes and references
- I. E. L. Stephens, A. S. Bondarenko, U. Grønbjerg, J. Rossmeisl and I. Chorkendorff, Energy Environ. Sci., 2012, 5, 6744 RSC.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed.
- S. Chen, J. Bi, Y. Zhao, L. Yang, C. Zhang, Y. Ma, Q. Wu, X. Wang and Z. Hu, Adv. Mater., 2012, 24, 5593–5597 CrossRef CAS PubMed.
- L. Zhang and Z. Xia, J. Phys. Chem. C, 2011, 115, 11170–11176 CrossRef CAS.
- D. Guo, R. Shibuya, C. Akiba, S. Saji, T. Kondo and J. Nakamura, Science, 2016, 351, 361–365 CrossRef CAS PubMed.
- X. Cui, S. Yang, X. Yan, J. Leng, S. Shuang, P. M. Ajayan and Z. Zhang, Adv. Funct. Mater., 2016, 26, 5708–5717 CrossRef CAS.
- W. J. Jiang, L. Gu, L. Li, Y. Zhang, X. Zhang, L. J. Zhang, J. Q. Wang, J. S. Hu, Z. Wei and L. J. Wan, J. Am. Chem. Soc., 2016, 138, 3570–3578 CrossRef CAS PubMed.
- N. Wu, Y. Lei, Q. Wang, B. Wang, C. Han and Y. Wang, Nano Res., 2017, 10, 2332–2343 CrossRef CAS.
- M. Kuang, Q. Wang, P. Han and G. Zheng, Adv. Energy Mater., 2017, 7, 1700193 CrossRef.
- J. Deng, D. Deng and X. Bao, Adv. Mater., 2017, 29, 1606967 CrossRef PubMed.
- L. Dai, Y. Xue, L. Qu, H. J. Choi and J. B. Baek, Chem. Rev., 2015, 115, 4823–4892 CrossRef CAS PubMed.
- D. Geng, Y. Chen, Y. Chen, Y. Li, R. Li, X. Sun, S. Ye and S. Knights, Energy Environ. Sci., 2011, 4, 760 RSC.
- J. Chen, X. Wang, X. Cui, G. Yang and W. Zheng, Chem. Commun., 2014, 50, 557–559 RSC.
- C. V. Rao, C. R. Cabrera and Y. Ishikawa, J. Phys. Chem. Lett., 2010, 1, 2622–2627 CrossRef CAS.
- S. Yasuda, L. Yu, J. Kim and K. Murakoshi, Chem. Commun., 2013, 49, 9627–9629 RSC.
- L. Lai, J. R. Potts, D. Zhan, L. Wang, C. K. Poh, C. Tang, H. Gong, Z. Shen, J. Lin and R. S. Ruoff, Energy Environ. Sci., 2012, 5, 7936 RSC.
- S. Pylypenko, A. Borisevich, K. L. More, A. R. Corpuz, T. Holme, A. A. Dameron, T. S. Olson, H. N. Dinh, T. Gennett and R. O'Hayre, Energy Environ. Sci., 2013, 6, 2957 RSC.
- Y. Zheng, Y. Jiao, J. Chen, J. Liu, J. Liang, A. Du, W. Zhang, Z. Zhu, S. C. Smith, M. Jaroniec, G. Q. Lu and S. Z. Qiao, J. Am. Chem. Soc., 2011, 133, 20116–20119 CrossRef CAS PubMed.
- J. Liu, P. Song and W. Xu, Carbon, 2017, 115, 763–772 CrossRef CAS.
- H. Kim, K. Lee, S. I. Woo and Y. Jung, Phys. Chem. Chem. Phys., 2011, 13, 17505–17510 RSC.
- U. N. Maiti, W. J. Lee, J. M. Lee, Y. Oh, J. Y. Kim, J. E. Kim, J. Shim, T. H. Han and S. O. Kim, Adv. Mater., 2014, 26, 40–66 CrossRef CAS PubMed.
- T. Schiros, D. Nordlund, L. Palova, D. Prezzi, L. Zhao, K. S. Kim, U. Wurstbauer, C. Gutierrez, D. Delongchamp, C. Jaye, D. Fischer, H. Ogasawara, L. G. Pettersson, D. R. Reichman, P. Kim, M. S. Hybertsen and A. N. Pasupathy, Nano Lett., 2012, 12, 4025–4031 CrossRef CAS PubMed.
- L. Qin, L. Wang, X. Yang, R. Ding, Z. Zheng, X. Chen and B. Lv, J. Catal., 2018, 359, 242–250 CrossRef CAS.
- V. Perazzolo, R. Brandiele, C. Durante, M. Zerbetto, V. Causin, G. A. Rizzi, I. Cerri, G. Granozzi and A. Gennaro, ACS Catal., 2018, 8, 1122–1137 CrossRef CAS.
- X. Dong, S. Chao, F. Wan, Q. Guan, G. Wang and W. Li, J. Catal., 2018, 359, 161–170 CrossRef CAS.
- M. Borghei, N. Laocharoen, E. Kibena-Põldsepp, L.-S. Johansson, J. Campbell, E. Kauppinen, K. Tammeveski and O. J. Rojas, Appl. Catal., B, 2017, 204, 394–402 CrossRef CAS.
- H. B. Yang, J. Miao, S.-F. Hung, J. Chen, H. B. Tao, X. Wang, L. Zhang, R. Chen, J. Gao, H. M. Chen, L. Dai and B. Liu, Sci. Adv., 2016, 2, e1501122 CrossRef PubMed.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, J. Am. Chem. Soc., 2014, 136, 4394–4403 CrossRef CAS PubMed.
- Y. Li, G. Zhong, H. Yu, H. Wang and F. Peng, Phys. Chem. Chem. Phys., 2015, 17, 21950–21959 RSC.
- X. Ning, H. Yu, F. Peng and H. Wang, J. Catal., 2015, 325, 136–144 CrossRef CAS.
- X. Ning, Y. Li, B. Dong, H. Wang, H. Yu, F. Peng and Y. Yang, J. Catal., 2017, 348, 100–109 CrossRef CAS.
- H. Y. Mao, Y. H. Lu, J. D. Lin, S. Zhong, A. T. S. Wee and W. Chen, Prog. Surf. Sci., 2013, 88, 132–159 CrossRef CAS.
- E. C. M. Chen and W. E. Wentworth, J. Chem. Phys., 1975, 63, 3183–3191 CrossRef CAS.
- W. Chen, Y. Sun, J. Guan, Q. Wang, X. Huang and G. Yu, RSC Adv., 2015, 5, 53003–53011 RSC.
- M. R. Suchanski and R. P. Van Duyne, J. Am. Chem. Soc., 1976, 98, 250–252 CrossRef CAS.
- F. Wang, W. Ueda and J. Xu, Angew. Chem., Int. Ed., 2012, 51, 3883–3887 CrossRef CAS PubMed.
- Y. Cao, H. Yu, J. Tan, F. Peng, H. Wang, J. Li, W. Zheng and N.-B. Wong, Carbon, 2013, 57, 433–442 CrossRef CAS.
- Y. T. Lee, N. S. Kim, S. Y. Bae, J. Park, S.-C. Yu, H. Ryu and H. J. Lee, J. Phys. Chem. B, 2003, 107, 12958–12963 CrossRef CAS.
- G.-L. Tian, Q. Zhang, B. Zhang, Y.-G. Jin, J.-Q. Huang, D. S. Su and F. Wei, Adv. Funct. Mater., 2014, 24, 5956–5961 CrossRef CAS.
- G. Ning, Z. Fan, G. Wang, J. Gao, W. Qian and F. Wei, Chem. Commun., 2011, 47, 5976–5978 RSC.
- R. Arrigo, M. E. Schuster, Z. Xie, Y. Yi, G. Wowsnick, L. L. Sun, K. E. Hermann, M. Friedrich, P. Kast, M. Hävecker, A. Knop-Gericke and R. Schlögl, ACS Catal., 2015, 5, 2740–2753 CrossRef CAS.
- S. van Dommele, A. Romero-Izquirdo, R. Brydson, K. P. de Jong and J. H. Bitter, Carbon, 2008, 46, 138–148 CrossRef CAS.
- F. Xu, M. Minniti, P. Barone, A. Sindona, A. Bonanno and A. Oliva, Carbon, 2008, 46, 1489–1496 CrossRef CAS.
- L. Ma, P. Hu, C. Kloc, H. Sun, M. E. Michel-Beyerle and G. G. Gurzadyan, Chem. Phys. Lett., 2014, 609, 11–14 CrossRef CAS.
- H. T. Jonkman and J. Kommandeur, Chem. Phys. Lett., 1972, 15, 496–499 CrossRef CAS.
- J. Kim, D. Khim, K.-J. Baeg, W.-T. Park, S.-H. Lee, M. Kang, Y.-Y. Noh and D.-Y. Kim, Adv. Funct. Mater., 2016, 26, 7886–7894 CrossRef CAS.
- A. Shrestha, M. Batmunkh, C. J. Shearer, Y. Yin, G. G. Andersson, J. G. Shapter, S. Qiao and S. Dai, Adv. Energy Mater., 2017, 7, 1602276 CrossRef.
- H. Wang, J. Jia, P. Song, Q. Wang, D. Li, S. Min, C. Qian, L. Wang, Y. F. Li, C. Ma, T. Wu, J. Yuan, M. Antonietti and G. A. Ozin, Angew. Chem., Int. Ed., 2017, 56, 7847–7852 CrossRef CAS PubMed.
- T. Sharifi, G. Hu, X. Jia and T. Wågberg, ACS Nano, 2012, 6, 8904–8912 CrossRef CAS PubMed.
- T. Kondo, S. Casolo, T. Suzuki, T. Shikano, M. Sakurai, Y. Harada, M. Saito, M. Oshima, M. I. Trioni, G. F. Tantardini and J. Nakamura, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035436 CrossRef.
- M. Lefevre, E. Proietti, F. Jaouen and J. P. Dodelet, Science, 2009, 324, 71–74 CrossRef CAS PubMed.
- G. Wu, K. L. More, C. M. Johnston and P. Zelenay, Science, 2011, 332, 443–447 CrossRef CAS PubMed.
- Z. Chen, D. Higgins, H. Tao, R. S. Hsu and Z. Chen, J. Phys. Chem. C, 2009, 113, 21008–21013 CrossRef CAS.
- S. Xu, Y. Kim, D. Higgins, M. Yusuf, T. F. Jaramillo and F. B. Prinz, Electrochim. Acta, 2017, 255, 99–108 CrossRef CAS.
- W. Qian, H. Yu, F. Wei, Q. Zhang and Z. Wang, Carbon, 2002, 40, 2968–2970 CrossRef CAS.
- G. Ning, C. Xu, X. Zhu, R. Zhang, W. Qian, F. Wei, Z. Fan and J. Gao, Carbon, 2013, 56, 38–44 CrossRef CAS.
- R. Lv, H. Wang, H. Yu and F. Peng, Electrochim. Acta, 2017, 228, 203–213 CrossRef.
- N. I. Kovtyukhova, P. J. Ollivier, B. R. Martin, T. E. Mallouk, S. A. Chizhik, E. V. Buzaneva and A. D. Gorchinskiy, Chem. Mater., 1999, 11, 771–778 CrossRef.
- B. Delley, J. Chem. Phys., 2000, 113, 7756–7764 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc04596h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |