Open Access Article
Open Access ArticleSupramolecular cage encapsulation as a versatile tool for the experimental quantification of aromatic stacking interactions†
Carlo
Bravin
 a,
Giulia
Licini
a,
Giulia
Licini
 a,
Christopher A.
Hunter
a,
Christopher A.
Hunter
 b and
Cristiano
Zonta
b and
Cristiano
Zonta
 *a
*a
aDepartment of Chemical Sciences, University of Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: cristiano.zonta@unipd.it
bDepartment of Chemistry, University of Cambridge, Lensfield Road, Cambridge CB2 1EW, UK
First published on 22nd November 2018
Abstract
The widespread presence of aromatic stacking interactions in chemical and biological systems, combined with their relatively small energetic contribution, have led to a plethora of theoretical and experimental studies for their quantification and rationalization. Typically, π–π aromatic interactions are studied as a function of substituents to gather information about the interaction mechanism. While experiments suggest that aromatic interactions are dominated by local electrostatic contacts between π-electron density and CH groups, theoretical work has raised the possibility that direct electrostatic interactions between local dipoles of the substituents may play a role. We describe a supramolecular cage that binds two aromatic carboxylates in a stacked geometry such that the aromatic substituents are remote in space. Chemical Double Mutant Cycles (DMCs) were used to measure fifteen different aromatic stacking interactions as a function of substituent (NMe2, OMe, Me, Cl and NO2). When both aromatic rings have electron-withdrawing nitro substituents, the interaction is attractive (−2.8 kJ mol−1) due to reduced π-electron repulsion. When both aromatic rings have electron-donating di-methylamino substituents, the interaction is repulsive (+2.0 kJ mol−1) due to increased π-electron repulsion. The results show that aromatic stacking interactions are dominated by short range electrostatic contacts rather than substituent dipole interactions.
Introduction
Quantitative knowledge of the relationship between chemical structure and non-covalent interaction energies is fundamental in order to understand or design both structure and function in chemical and biological systems.1–15 Many research groups have focused their attention on the quantification of aromatic interactions using theoretical and experimental methods. Using a typical physical organic chemistry approach, the factors that govern these interactions have been studied by evaluating the influence of ring substitution on interaction energy.16–20 Solution phase experimental measurements indicate that aromatic interactions are dominated by the electrostatics of short range local contacts between π-electron density or CH–π interactions that depend on the geometry of interaction.21–25 Substituents affect the observed interaction energies by changing the π-electron density and the polarity of the peripheral CH groups. In contrast, most theoretical calculations have been carried out in the gas phase, where dispersion and long range electrostatics play a more important role.26–28 These computational studies suggest that electrostatic interactions between dipoles associated with the ring substituents may play a significant role.29–35 In the experimentally studied systems, the substituents are usually in close proximity, so it is difficult to dissect these contributions. Here we describe a new experimental system for quantifying aromatic interactions that allows this distinction to be made, because the substituents are not in direct contact.We have previously used modified tris(pyridylmethyl)amine (TPMA) metal complexes and imine Dynamic Covalent Chemistry (DCC),36–38 to obtain a variety of supramolecular architectures.39–43 The supramolecular cage 1 shown in Scheme 1 demonstrates particularly interesting molecular recognition properties with respect to dicarboxylate guests.44,45 Here we report the interaction of this cage with monocarboxylate guests and show that these complexes provide a versatile experimental platform for the quantitative determination of substituent effects on aromatic stacking interactions. The results show that for a system where there is no direct contact between the substituents on the aromatic rings, aromatic stacking interactions are dominated by local electrostatic contacts between the π-systems rather than substituent dipole interactions.
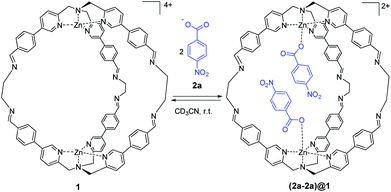 | ||
| Scheme 1 Molecular recognition of 4-nitrobenzoate 2a by cage 1. Counterions are perchlorate for the cage and triethyl ammonium for the guest and they are omitted for clarity. | ||
Results and discussions
As reported in our previous work, supramolecular cage 1 was synthesized taking advantage of DCC. The initial aim of this work was to assess the molecular recognition properties of cage 1 towards aromatic carboxylate guests (Scheme 1).47Sub-stoichiometric addition of 4-nitrobenzoate 2a to cage 1 in acetonitrile lead to the appearance of new signals in the 1H NMR spectrum that were in slow exchange with the signals due to the free cage (Fig. S1 in the ESI†). Integration of the bound cage and guest signals indicate exclusive formation of the cage–guest complex 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2a-2a)@1, and interestingly, no signals due to the 1
2 (2a-2a)@1, and interestingly, no signals due to the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex were detected.48 From the integrals of the free and bound 1H NMR signals, the overall equilibrium constant for formation of the 1
1 complex were detected.48 From the integrals of the free and bound 1H NMR signals, the overall equilibrium constant for formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex (K1K2) was determined (42 ± 4) × 106 M−2. The addition of more than two equivalents of 2a led to a complete conversion to the filled cage (2a-2a)@1 (Fig. S1 in the ESI†). The formation of the 1
2 complex (K1K2) was determined (42 ± 4) × 106 M−2. The addition of more than two equivalents of 2a led to a complete conversion to the filled cage (2a-2a)@1 (Fig. S1 in the ESI†). The formation of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complex (2a-2a)@1 was also confirmed by two-dimensional NMR spectroscopy (ROESY, DOSY) and ESI-MS experiments (Fig. S12–S15, ESI,†).
2 complex (2a-2a)@1 was also confirmed by two-dimensional NMR spectroscopy (ROESY, DOSY) and ESI-MS experiments (Fig. S12–S15, ESI,†).
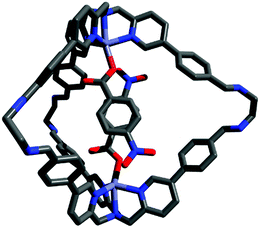
In order to gather structural information on (2a-2a)@1, DFT calculations were carried out. In the most stable conformation, the two guest aromatic rings adopt a face-to-face geometry with the nitro substituents in a pseudo-meta orientation (Fig. 1). The structure of the inclusion complex shown in Fig. 1 appears ideally suited for the determination of the thermodynamic properties of aromatic stacking interactions between the two guests. It is worth noting that in this structure the two nitro substituents are remote in space, so direct interactions between the substituents cannot affect the measured strength of the aromatic interaction. In addition, the two substituents are not parallel, so long range dipole interactions are also minimised relative to local contacts between the π-systems.46
It is possible to dissect out the thermodynamic contribution of the aromatic stacking interaction from all of the other contributions in this system by the chemical Double Mutant Cycle (DMC) approach, which has been used to quantify non-covalent interactions in different systems.49,50 We used n-hexanoate HexA as a reference guest that cannot make aromatic interactions. The approach is illustrated for two different guests with substituents X and Y in Fig. 2 (see Section S3.5). There are a large number of different intermolecular interactions in Complex A which contains the aromatic stacking interaction of interest:
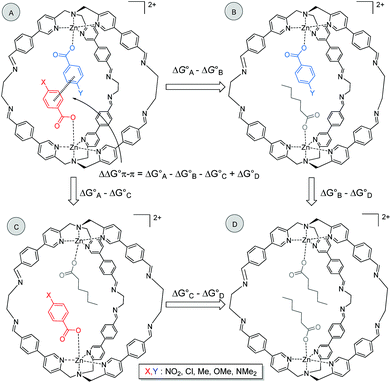 | ||
| Fig. 2 Chemical DMC for measuring the aromatic stacking interaction between two guests. Counterions are perchlorate for the cage and triethyl ammonium for the guest and they are omitted for clarity. | ||
(1) The aromatic stacking interaction between the two guests.
(2) The coordination interaction between the carboxylate group of the guest with substituent X and the zinc ion.
(3) The coordination interaction between the carboxylate group of the guest with substituent Y and the zinc ion.
(4) Interactions of the edges of the aromatic ring with substituent X with the internal walls of the cage.
(5) Interactions of the edges of the aromatic ring with substituent Y with the internal walls of the cage.
(6) Interactions of substituent X with the walls of the cage.
(7) Interactions of substituent Y with the walls of the cage.
(8) Interactions between the carboxylate group of one guest and substituent X on the other guest.
(9) Interactions between the carboxylate group of one guest and substituent Y on the other guest.
Complex A contains all 9 types of interaction listed above. Complex B is missing interactions 4, 6 and 8. Thus the difference between the stabilities of complexes A and B 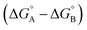 measures the sum of interactions 1, 3, 5, 7 and 9 plus the difference in the strength of zinc–carboxylate coordination bond formed with the aromatic guest with substituent X and the aliphatic guest.
measures the sum of interactions 1, 3, 5, 7 and 9 plus the difference in the strength of zinc–carboxylate coordination bond formed with the aromatic guest with substituent X and the aliphatic guest.
Similarly, Complex C is missing interactions 5, 7 and 9, and Complex D is missing interactions 4, 5, 6, 7, 8 and 9. Thus the difference between the stabilities of complexes C and D 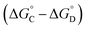 measures the sum of interactions 4, 6 and 8 plus the difference in the strength of zinc–carboxylate coordination bonds formed with the aromatic guest with substituent X and the aliphatic guest. In other words, the only contribution to the difference
measures the sum of interactions 4, 6 and 8 plus the difference in the strength of zinc–carboxylate coordination bonds formed with the aromatic guest with substituent X and the aliphatic guest. In other words, the only contribution to the difference 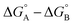 that is not present in the difference
that is not present in the difference 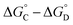 is interaction 1, the aromatic stacking interaction.
is interaction 1, the aromatic stacking interaction.
Thus the DMC in Fig. 2 allows direct determination of the thermodynamic contribution due to the aromatic stacking interaction and removes all of the contributions from the many secondary interactions that are present in this system. Moreover, the DMC analysis is based on the differences in free energies between pairs of complexes, so it is not necessary to measure individual association constants for all 4 complexes shown in Fig. 2. Relative rather than absolute values are all that is required.
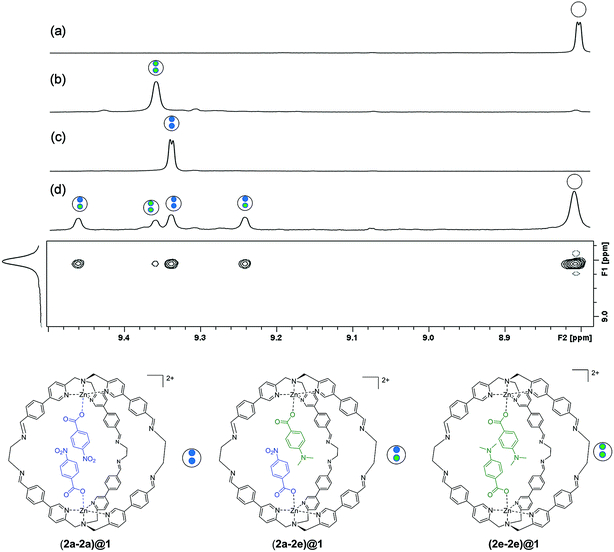
In order for this experiment to work, two guests must be bound in the same cage. We therefore chose 4-chlorobenzoate 2b, 4-methylbenzoate 2c, 4-methoxybenzoate 2d and 4-(dimethylamino)benzoate 2e (Fig. 2), which have similarly sized substituents to 4-nitrobenzoate 2a and should not introduce steric clashes with the cage walls. Fig. 3d illustrates typical results obtained using two different guests that form a mixed cage complex (2a-2e)@1. When 0.1 equivalents of carboxylate 2a and 0.1 equivalents of carboxylate 2e were added to a solution of cage 1 in acetonitrile, four new signals due to the cage pyridine α protons were observed (Fig. 3d). Comparison with the chemical shifts of the homo occupied cages allowed assignment of two of the signals to complexes containing the same guest (9.375 ppm for (2a-2a)@1 and 9.395 ppm for (2e-2e)@1) (Fig. 3b and c). In this case no ROESY cross-peaks between these signals are detected (Section S3.3 in the ESI†). The other two signals were assigned to the complex containing two different guests (2a-2e)@1 thanks to ROESY cross peak correlations (Fig. 3 and ESI† Section S3.3).
Integration of the signals related to the filled cages and the corresponding signal due to the empty cage 1 (8.015 ppm) allowed direct determination of the equilibrium constants for formation of (2a-2a)@1, (2e-2e)@1 and (2a-2e)@1.
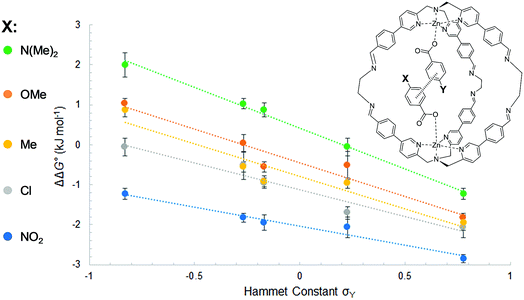
In other words, if two different guests are present in sub-stoichiometric amounts, due to the slow exchange on the 1H NMR timescale it is possible to measure all three equilibrium constants for formation of the hetero- and the two homo-complexes with a single NMR acquisition (Section S3.4 in the ESI†). Using this approach, equilibrium constants were measured for all pairwise combinations of carboxylate guests (2a–2e and HexA). With these values, it was possible to construct fifteen different DMCs to measure the free energy contributions of fifteen different aromatic stacking interactions to the overall stabilities of the complexes (ΔΔG°), (Table S1–S5 and Fig. S5 and S6 in the ESI†) (Table 1).
| Y | X | ||||
|---|---|---|---|---|---|
| NO2 | Cl | Me | OMe | NMe2 | |
| NO2 | −2.8 ± 0.1 | ||||
| Cl | −2.1 ± 0.3 | −1.7 ± 0.1 | |||
| Me | −1.9 ± 0.2 | −1.0 ± 0.1 | −0.9 ± 0.1 | ||
| OMe | −1.8 ± 0.1 | −0.5 ± 0.3 | −0.5 ± 0.1 | 0.0 ± 0.2 | |
| NMe2 | −1.2 ± 0.1 | −0.1 ± 0.2 | +0.8 ± 0.2 | +1.0 ± 0.1 | +2.0 ± 0.3 |
The least favorable interaction occurs when both aromatic rings carry electron-donating dimethylamino groups (+2.0 ± 0.4 kJ mol−1), and the most attractive interaction occurs when both aromatic rings carry electron-withdrawing nitro groups (−2.8 ± 0.1 kJ mol−1). The measured aromatic interaction energies are in line with the previously reported experimental measurements and correlate well with the corresponding Hammett substituent parameters (Fig. 4) and the electrostatic potential of the substituted aromatic rings (Section S3.6).16,17
| ΔΔG° (kJ mol−1) = 0.7 σxσy − 1.5σx − 1.5σy − 0.9 | (1) |
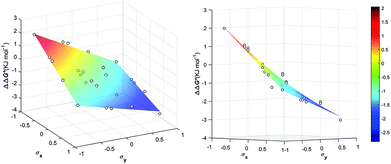 | ||
| Fig. 5 Aromatic stacking energies (kJ mol−1) (z-axis) measured as function of the Hammet constant σY and σY of the encapsulated guests. | ||
Conclusions
In conclusion, both the trends in interaction energy with substituent and the absolute values of the free energies of interaction are very similar to previously reported experimental measurements of aromatic interactions in different systems.16,17 However, the orientation of the substituents in the system reported here (approximately orthogonal) is quite different from the orientation of the aromatic substituents in previous studies (approximately parallel). This observation indicates that aromatic stacking interactions are dominated by short range local electrostatic interactions between the π-faces rather than by substituent dipole interactions.32 In particular, the cage fixes the orientation of the guests in such a way that the polarizing aromatic substituents are not in contact, which means that there are no contributions from direct interactions between the substituents. Moreover the substituents are not parallel, so long range dipole interactions are minimised. The finding that local electrostatic interactions dominate is in line with previous solution phase experimental studies and contradicts ideas based on gas phase theoretical calculations.31,32 The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cage–guest complexes represent a powerful system for the quantification of non-covalent interactions using the DMC approach and provide a versatile platform for controlling assembly and molecular recognition within the supramolecular superstructure.
2 cage–guest complexes represent a powerful system for the quantification of non-covalent interactions using the DMC approach and provide a versatile platform for controlling assembly and molecular recognition within the supramolecular superstructure.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Prof. J. K. Sanders and C. Berton for useful discussions. Financial support from the University of Padova (PRAT-CPDA153122, Progetto Attrezzature Scientifiche finalizzate alla Ricerca) is gratefully acknowledged.Notes and references
- C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525–5534 CrossRef CAS.
- A. E. Meyer, K. R. Castellano and F. Diederich, Angew. Chem., Int. Ed., 2003, 42, 1210–1250 CrossRef PubMed.
- M. L. Salonen, M. Ellermann and F. Diederich, Angew. Chem., Int. Ed., 2011, 50, 4808–4842 CrossRef PubMed.
- S. L. Cockroft and C. A. Hunter, Chem. Commun., 2006, 3806–3808 RSC.
- D. Núñez-Villanueva, G. Iadevaia, A. E. Stross, M. A. Jinks, J. A. Swain and C. A. Hunter, J. Am. Chem. Soc., 2017, 139, 6654–6662 CrossRef PubMed.
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 651–669 RSC.
- M. Yoshizawa, M. Tamura and M. Fujita, Science, 2006, 312, 251–254 CrossRef CAS PubMed.
- C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef CAS PubMed.
- T. K. Ronson, W. Meng and J. R. Nitschke, J. Am. Chem. Soc., 2017, 139, 9698–9707 CrossRef CAS PubMed.
- M. Harder, M. A. Carnero Corrales, N. Trapp, B. Kuhn and F. Diederich, Chem.–Eur. J., 2015, 21, 8455–8463 CrossRef CAS PubMed.
- F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216–5300 CrossRef CAS PubMed.
- B. Bhayana, J. Org. Chem., 2013, 78, 6758–6762 CrossRef CAS PubMed.
- E. Kim, S. Paliwal and C. S. Wilcox, J. Am. Chem. Soc., 1998, 120, 11192–11193 CrossRef CAS.
- L. F. Newcomb and S. H. Gellman, J. Am. Chem. Soc., 1994, 116, 4993–4994 CrossRef CAS.
- M. J. Rashkin and M. L. Waters, J. Am. Chem. Soc., 2002, 124, 1860–1861 CrossRef CAS PubMed.
- S. L. Cockroft, C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Am. Chem. Soc., 2005, 127, 8594–8595 CrossRef CAS PubMed.
- S. L. Cockroft, J. Perkins, C. Zonta, H. Adams, S. E. Spey, C. M. R. Low, J. G. Vinter, K. R. Lawson, C. J. Urch and C. A. Hunter, Org. Biomol. Chem., 2007, 5, 1062–1080 RSC.
- L.-J. Riwar, N. Trapp, B. Kuhn and F. Diederich, Angew. Chem., Int. Ed., 2017, 56, 11252–11257 CrossRef CAS PubMed.
- F. Cozzi, M. Cinquini, R. Annuziata and J. S. Siegel, J. Am. Chem. Soc., 1993, 115, 5330–5331 CrossRef CAS.
- J. Hwang, P. Li, M. D. Smith and K. D. Shimizu, Angew. Chem., Int. Ed., 2016, 55, 8086–8089 CrossRef CAS PubMed.
- G. Santoni, M. Mba, M. Bonchio, W. A. Nugent, C. Zonta and G. Licini, Chem.–Eur. J., 2010, 16, 645–654 CrossRef CAS PubMed.
- F. J. Carver, C. A. Hunter, D. J. Livingstone, J. F. McCabe and E. M. Seward, Chem.–Eur. J., 2002, 8, 2847–2859 CrossRef CAS.
- C. A. Hunter, C. M. R. Low, C. Rotger, J. G. Vinter and C. Zonta, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 4873–4876 CrossRef CAS PubMed.
- H. Adams, C. A. Hunter, K. R. Lawson, J. Perkins, S. E. Spey, C. J. Urch and J. M. Sanderson, Chem.–Eur. J., 2001, 7, 4863–4877 CrossRef CAS.
- C. A. Hunter, C. M. R. Low, C. Rotger, J. G. Vinter and C. Zonta, Chem. Commun., 2003, 3, 834–835 RSC.
- L. Yang, J. B. Brazier, T. A. Hubbard, D. M. Rogers and S. L. Cockroft, Angew. Chem., Int. Ed., 2016, 55, 912–916 CrossRef CAS PubMed.
- L. Yang, C. Adam, G. S. Nichol and S. L. Cockroft, Nat. Chem., 2013, 5, 1006–1010 CrossRef CAS PubMed.
- J. wun Hwang, P. Li and K. D. Shimizu, Org. Biomol. Chem., 2017, 15, 1554–1564 RSC.
- S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855 CrossRef CAS PubMed.
- R. M. Parrish and C. D. Sherrill, J. Am. Chem. Soc., 2014, 136, 17386–17389 CrossRef CAS PubMed.
- S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef CAS PubMed.
- S. E. Wheeler, J. Am. Chem. Soc., 2011, 133, 10262–10274 CrossRef CAS PubMed.
- J. Hwang, P. Li, W. R. Carroll, M. D. Smith, P. J. Pellechia and K. D. Shimizu, J. Am. Chem. Soc., 2014, 136, 14060–14067 CrossRef CAS PubMed.
- J. Hwang, B. E. Dial, P. Li, M. E. Kozik, M. D. Smith and K. D. Shimizu, Chem. Sci., 2015, 6, 4358–4364 RSC.
- J. M. Maier, P. Li, E. C. Vik, C. J. Yehl, S. M. S. Strickland and K. D. Shimizu, J. Am. Chem. Soc., 2017, 139, 6550–6553 CrossRef CAS PubMed.
- P. T. Corbett, J. Leclaire, L. Vial, K. R. West, J.-L. Wietor, J. K. M. Sanders and S. Otto, Chem. Rev., 2006, 106, 3652–3711 CrossRef CAS PubMed.
- S. P. Black, D. M. Wood, F. B. Schwarz, T. K. Ronson, J. J. Holstein, A. R. Stefankiewicz, C. A. Schalley, J. K. M. Sanders and J. R. Nitschke, Chem. Sci., 2016, 7, 2614–2620 RSC.
- A. M. Castilla, T. K. Ronson and J. R. Nitschke, J. Am. Chem. Soc., 2016, 138, 2342–2351 CrossRef CAS PubMed.
- R. Berardozzi, E. Badetti, N. A. Carmo dos Santos, K. Wurst, G. Licini, G. Pescitelli, C. Zonta and L. Di Bari, Chem. Commun., 2016, 52, 8428–8431 RSC.
- E. Badetti, K. Wurst, G. Licini and C. Zonta, Chem.–Eur. J., 2016, 22, 6515–6518 CrossRef CAS PubMed.
- F. A. Scaramuzzo, E. Badetti, G. Licini and C. Zonta, Eur. J. Org. Chem., 2017, 2017, 1438–1442 CrossRef CAS.
- F. A. Scaramuzzo, G. Licini and C. Zonta, Chem.–Eur. J., 2013, 19, 16809–16813 CrossRef CAS PubMed.
- E. Badetti, N. A. C. Dos Santos, F. A. Scaramuzzo, C. Bravin, K. Wurst, G. Licini and C. Zonta, RSC Adv., 2018, 8, 19494–19498 RSC.
- C. Bravin, E. Badetti, F. A. Scaramuzzo, G. Licini and C. Zonta, J. Am. Chem. Soc., 2017, 139, 6456–6460 CrossRef CAS PubMed.
- C. Bravin, C. Badetti, E. Putreddy, R. Pan, F. Rissanen, K. Licini and G. Zonta, Chem.–Eur. J., 2018, 24, 2936–2943 CrossRef CAS PubMed.
- F. J. Carver, C. A. Hunter, F. J. Carver and E. M. Seward, Chem. Commun., 1998, 775–776 RSC.
- Embedded ethylenediamine and the molecular recognition process of cage 1 towards dicarboxylic acid was clarified in ref. 44.
- Cage
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mono-carboxylate 1
mono-carboxylate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex formation was noticed only for the encapsulation of lower affinity mono carboxylate viz.HexA, (ESI† Section S3.2).
1 complex formation was noticed only for the encapsulation of lower affinity mono carboxylate viz.HexA, (ESI† Section S3.2). - S. L. Cockroft and C. A. Hunter, Chem. Soc. Rev., 2007, 36, 172–188 RSC.
- C. A. Hunter, C. M. R. Low, J. G. Vinter and C. Zonta, J. Am. Chem. Soc., 2003, 125, 9936–9937 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details on the competition experiments, DMCs and characterization of all new compounds. See DOI: 10.1039/c8sc04406f |
| This journal is © The Royal Society of Chemistry 2019 |