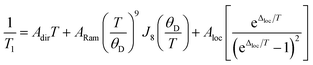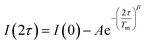Counterion influence on dynamic spin properties in a V(IV) complex

Abstract

Using transition metal ions for spin-based applications, such as electron paramagnetic resonance imaging (EPRI) or quantum computation, requires a clear understanding of how local chemistry influences spin properties. Herein we report a series of four ionic complexes to provide the first systematic study of one aspect of local chemistry on the V(IV) spin – the counterion. To do so, the four complexes (Et₃NH)₂[V(C₆H₄O₂)₃] (1), (n-Bu₃NH)₂[V(C₆H₄O₂)₃] (2), (n-Hex₃NH)₂[V(C₆H₄O₂)₃] (3), and (n-Oct₃NH)₂[V(C₆H₄O₂)₃] (4) were probed by EPR spectroscopy in solid state and solution. Room temperature, solution X-band (ca. 9.8 GHz) continuous-wave electron paramagnetic resonance (CW-EPR) spectroscopy revealed an increasing linewidth with larger cations, likely a counterion-controlled tumbling in solution via ion pairing. In the solid state, variable-temperature (5–180 K) X-band (ca. 9.4 GHz) pulsed EPR studies of 1–4 in o-terphenyl glass demonstrated no effect on spin–lattice relaxation times (T₁), indicating little role for the counterion on this parameter. However, the phase memory time (T_m) of 1 below 100 K is markedly smaller than those of 2–4. This result is counterintuitive, as 2–4 are relatively richer in ¹H nuclear spin, hence, expected to have shorter T_m. Thus, these data suggest an important role for counterion methyl groups on T_m, and moreover provide the first instance of a lengthening T_m with increasing nuclear spin quantity on a molecule.

---

Introduction

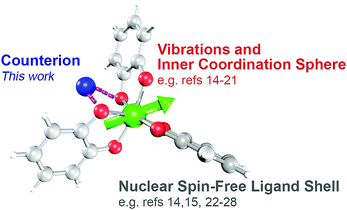
Fundamental investigations of open-shell (d¹–d⁹) transition metal complexes are paving the way to new applications in areas spanning from spintronics to quantum computing.^1–9 One area where these complexes could also find use is electron paramagnetic resonance imaging (EPRI).^10,11 Application of metal ions in EPRI would harness their extraordinary tunability and chemical sensitivity to noninvasively provide physiological information that is invisible to conventional MRI.¹² Toward the foregoing applications, the first proof-of-concept steps entail a deep understanding of the relationship between the properties of a metal-based spin and its chemical surroundings.

Toward EPRI, important spectroscopic quantities are resonance linewidths, spin–lattice relaxation (T₁) and phase memory time (T_m).¹³‡ Understanding how molecular design features affect these properties is an active area of research (Fig. 1).^1,3,6 Among the features of interest are the inner coordination sphere, e.g. geometry,^14–18 vibrations,^19–21 nuclear-spin content,^{14,15,22–28} and electronic spin magnitude.^15,24,25 Such investigations have provided impressive results, potentially enabling molecular information storage near and above liquid N₂ temperatures.^29–31 Among these elegant studies, however, the role of counterion in controlling said properties has yet to be systematically investigated. This knowledge is important: counterions can ion-pair, resulting in close association in solution and in the solid state. These interactions can modulate structure, electronics, and reactivity of metal ions.^32–37 Hence, judicious counterion selection may provide a powerful structural mechanism to control spin properties, or a separate practical property: solubility. Finally, knowledge of counterion effects could enable EPRI to detect biologically relevant ionic and radical species, e.g. K⁺, Ca²⁺, Cu²⁺ or radical cations of amino acids.^11,38,39 Owing to these factors, understanding the role of counterions on spin systems is of prime importance.

Fig. 1 Graphical overview of the significance of this work in tuning the EPR properties of mononuclear transition metal complexes. The complex depicted for the purpose of illustration is the one focused on in this study: [V(C₆H₄O₂)₃]²⁻.

Herein we report the first investigation of the role of counterion on spin properties in a series of mononuclear V(IV) complexes. We synthesized four complexes, (Et₃NH)₂[V(C₆H₄O₂)₃] (1),⁴⁰ (n-Bu₃NH)₂[V(C₆H₄O₂)₃] (2), (n-Hex₃NH)₂[V(C₆H₄O₂)₃] (3), and (n-Oct₃NH)₂[V(C₆H₄O₂)₃] (4), which feature an increasing counterion size from 1–4. These species feature the same open-shell [V(C₆H₄O₂)₃]²⁻ unit, controlling electronic structure and enabling investigation of only the influence of the associated counterion. We use this trend to provide clear-cut demonstrations of important roles that the R₃NH⁺ counterion plays, which are four-fold. First, the larger counterions lead to higher solubilities in a range of polar and nonpolar solvents for this dianionic complex. Second, in relation to EPR properties, we show that the counterion controls the linewidth via the rotational correlation time (τ_corr). In the solid state, we observe that, third, the counterion shows no impact on T₁, but, fourth, does impact T_m, though only at the lowest temperatures. This latter discovery is counter-intuitive, as the largest T_m values are obtained for the counterion that contains the highest number of protons. We attribute this trend to the varying distance of the methyl groups from the V(IV) ion. Hence, we present the first evidence that beyond 5–6 Å, the impact of methyl group rotation on T_m is considerably suppressed relative to shorter distance. Thus, the results herein provide a simple yet important design principle for enhancing a species' solubility while sustaining T_m.

Results and discussion

The synthesis of 1–4 proceeds conveniently, inspired by an initial report of (Et₃NH)₂[V(C₆H₄O₂)₃] (1) by Raymond and co-workers in 1982 (see Scheme 1).⁴⁰ Reaction of one equivalent of vanadyl acetylacetonate, VO(acac)₂ (acac⁻ = acetylacetonate), three equivalents of catechol, and two equivalents of a given trialkylamine in tetrahydrofuran (Scheme 1) yields the desired complexes 2, 3, and 4. Syntheses of 1, 2, and 3 produced dark blue powders and crystals, yet all preparations of 4 produced oils. Oils typically result from the presence of an impurity, yet all analyses indicate high purity (see ESI†). Note that the only crystallographically characterized salt of this cation in the Cambridge Structural Database (CSD),⁴¹ (n-Oct₃NH)₂[{CF₃SO₂NC(O)}₂], has a relatively low melting point of 56 °C.⁴² On this basis, we tentatively conclude that the n-Oct₃NH⁺ counterion induces a freezing point slightly below room temperature (25–30 °C in the glovebox of our lab) for complex 4.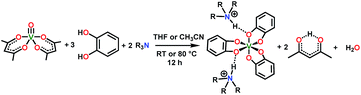

Scheme 1 General synthetic procedure for 1–4. See ESI† for additional details and full characterization data.

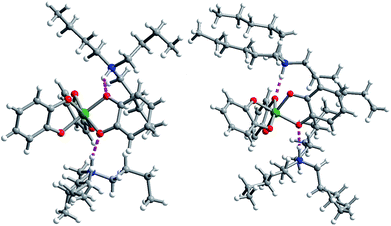
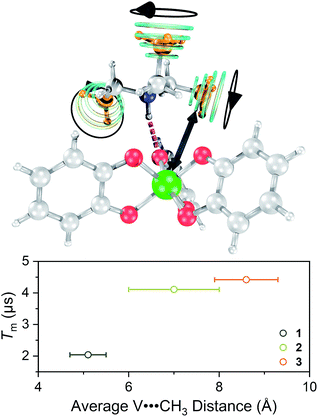
Single crystal X-ray diffraction experiments on crystals of 1 (reported previously),^40,432, and 3 all reveal similar molecular structures of the V[(C₆H₄O₂)₃]²⁻ anion (Fig. 2). In these structures, two trialkylammonium cations are shown to interact with the oxygens of the catecholate ligands through close N–H⋯O contacts. The V⋯C_methyl distances increased across the series, from 4.633(6) to 5.566(6) Å (avg. 5.1(4) Å) in 1, 5.977(4) to 8.828(4) Å (avg. 7(1) Å) in 2, to 8.090(7) to 9.483(8) Å (avg. 8.6(7) Å) in 3.

Fig. 2 Crystal structures of (n-Bu₃NH)₂[V(C₆H₄O₂)₃] (2, left) and (n-Hex₃NH)₂[V(C₆H₄O₂)₃] (3, right) which demonstrate the hydrogen bonds (pink) that hold the ions together. Cocrystallized THF molecules in 2·(THF)₂ are not shown for clarity. Green, red, blue, gray, white spheres represent vanadium, oxygen, nitrogen, carbon, and hydrogen, respectively.

The association observed in the crystal structures appears to have an important impact in solution. Indeed, complexes 1–4 are soluble in a range of solvents, despite the doubly-charged nature of the vanadium species. Common polar solvents such as acetonitrile (CH₃CN), tetrahydrofuran (THF), and dimethylformamide (DMF) dissolve 1–4. However, 1 is significantly less soluble in these solvents than the longer-chain analogues 2–4. The solubility difference is stark in non-polar solvents such as toluene and CS₂, wherein concentrations greater than 100 mM are possible for 2–4, while 1 is nearly insoluble.

Our exploration of the impact of this association on the spin of [V(C₆H₄O₂)₃]²⁻ started with the evaluation of the spin Hamiltonian parameters for 1–4. Here, we leveraged the solubility of these species in o-terphenyl for sample preparation. These samples were then used to collect echo-detected EPR spectra at 5 K. The recorded spectra (Fig. S5†) reveal an eight-line pattern typical for six-coordinate V(IV) ions, wherein the S = 1/2 spin is coupled to the I = 7/2 ⁵¹V nuclear spin.^40,44 Simulation of these spectra were performed using Easyspin⁴⁵ and the following spin Hamiltonian:

Ĥ = gμ_BBŜ − g_Nμ_NBÎ + ÎAŜ + ÎQÎ

Here, g is the rhombic g-tensor, μ_B is the Bohr magneton, B is the external applied magnetic field, Ŝ is the electronic spin, g_N is the nuclear g-tensor, μ_N is the nuclear magneton, Î is the nuclear spin operator, A is the rhombic hyperfine coupling tensor, and Q is the nuclear quadrupole interaction. Rhombic g- and A-parameters (g_x ≠ g_y ≠ g_z, A_x ≠ A_y ≠ A_z) were used for simulation. The parameters for the best simulations are summarized in Tables 1 and S4,† and are in agreement with previously reported analyses.^40,43,44 Spin Hamiltonian parameters are critically sensitive to the electronics of the spin-bearing orbital. Hence, the similarity of the parameters for 1–4 demonstrates negligible effect of the counterion on the electron spin parameters.

Table 1 Spin Hamiltonian parameters of 1–4 in frozen o-terphenyl solution (5 K) and correlation times from solution spectra in CH₃CN, THF, and toluene. See ESI (Table S4) for g- and A-strain parameters for the 5 K spectra

	1	2	3	4
a 1 is insoluble in toluene.
g x	1.942	1.935	1.938	1.942
g y	1.928	1.919	1.922	1.927
g z	1.991	1.982	1.987	1.992
A x (MHz)	310	313	300	313
A y (MHz)	367	363	350	368
A z (MHz)	60	60	52	60
τ corr in CH3CN (ps)	150	187	211	257
τ corr in THF (ps)	151	237	282	348
τ corr in toluene (ps)	—^a	406	438	464

---

With the spin Hamiltonian data in hand, we sought to evaluate the other potential impacts of the counterion on the spin. To do so, we performed room-temperature X-band (ca. 9.8 GHz) continuous-wave electron paramagnetic resonance (CW-EPR) spectroscopy of these complexes in solvents of varying polarity: toluene (dielectric constant, ε = 2.379), THF (ε = 7.52) and CH₃CN (ε = 36.64) (Fig. 3).⁴⁶ The spectra are strikingly similar to one another except in one important feature: linewidth. The peak-to-peak linewidths in the solution spectra for a 10 mM CH₃CN solution, for example, increase from 21.9 to 23.0 to 29.4 to 32.8 G for the lowest field line in 1–4, respectively, increasing with increasing size of the counterion. This trend also is consistent with the THF and toluene solution spectra (Fig. S7 and S8†). The change in linewidth, which trends with the sizes of the cations in 1–4, suggests ion-pair formation.

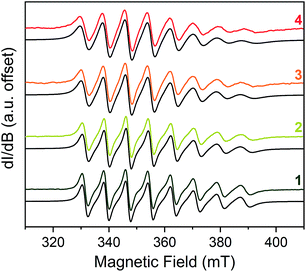Fig. 3 Stacked X-band CW-EPR spectra of 1–4 in CH₃CN (color traces) and simulations (black traces) at ca. 290 K. Note the increase of peak-to-peak linewidths from 1 to 4. See ESI† for additional room-temperature, solution-phase EPR spectra and simulated spin Hamiltonian parameters (Table S6†). Experimental details: 10 mM solutions; 0.63 microwave power; microwave frequency, ca. 9.84 GHz; modulation frequency, 100 kHz; modulation amplitude, 1.0 G; number of scans ranged from 16 to 32 to obtain good signal-to-noise ratios.

Given the consistency in the spin-Hamiltonian parameters between 1–4, the broadening trend should arise from molecular tumbling if ion-pairing persists in solution. Here, such motion is characterized by the rotational correlation time (τ_corr), the time needed for a molecule to rotate one radian (ca. 57.3°). To test this possibility, we simulated the solution spectra with a model that accounted for such motion. We started from the low temperature spin Hamiltonian parameters, modelling the linewidth changes solely via a correlation time. In all solvents, the simulations reveal that the tumbling correlation times increase in the sequence τ_corr(1) < τ_corr(2) < τ_corr(3) < τ_corr(4), which is the order of increasing alkyl chain length on the R₃NH⁺ cation. To explain this behavior, we reason that the hydrogen bonding interaction observed in the solid state is intact in solution. Hence, the increasing size of the counterion from 1–4 induces slower tumbling of the species in solution, consistent with our observed trends (Fig. S9†). Indeed, an analysis of the rotationally effective radii (r) of 1–4 in solution using τ_corr and the Stokes–Einstein equation⁴⁷ reveals that the radii vary between 6.3–6.8 Å for 1, 6.8–8.8 Å for 2, 7.1–9.1 Å for 3, and 7.6–9.2 Å for 4 in these three solvents. We note that for 1–3, these ranges are only slightly larger than the crystallographically determined V⋯CH₃ distances (Table S3†). Taken together, these data corroborate ion-pair existence in solution. Such an argument would also explain the overwhelming solubility of the longer-chain trialkylammonium salts in nonpolar solvents by the formation of neutral adducts. We note that this ion-pairing argument is consistent with the previously cited analysis by Raymond and co-workers.^40,44

Following solution-state investigations, we sought to evaluate the impact of counterion in the solid state. Given the intimate contact between the [V(C₆H₄O₂)₃]²⁻ ion and counterions, we made two hypotheses about the consequences of that association. First, we expected that the counterion binding would suppress motion in the solid state, which would impact both T₁ and T_m. Second, we anticipated that the increasing number of nuclear spin-rich protons from Et₃NH⁺ to n-Oct₃NH⁺ would diminish T_m in trend across 1–4.

To test these hypotheses, we applied variable-temperature pulsed X-band EPR spectroscopic techniques. Measurements were performed on 1 mM frozen solutions of 1–4 in o-terphenyl to minimize spin–spin interactions. We note that o-terphenyl is an under-explored solvent for pulsed studies yet affords three key advantages.⁴⁸ First, it is a frozen glass at room temperature (melting point 58–59 °C; glass transition temperature at ca. −30 °C), enabling access to a wide range of temperature for studies. Second, the compound lacks methyl groups, which can affect T₁ and T_m. Finally, the proton concentration ([¹H] = 46 M) of o-terphenyl is about half of most common organic solvents, which is important since protons impact relaxation times.⁴⁹

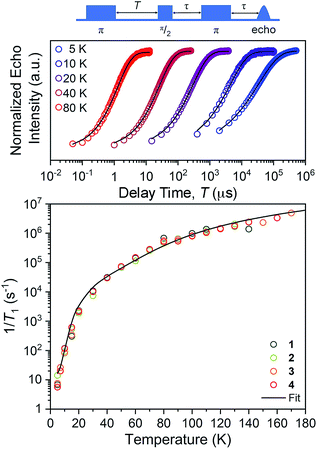
The first relaxation times we explored were the spin–lattice relaxation times. Spin–lattice relaxation is driven via energy exchange between the excited spin system and the surrounding environment. Lattice vibrations are important in this process, hence we anticipated that the counterion would have an important effect here. T₁ measurements were performed at the maximum-amplitude position in the echo detected field-swept spectra at 5 K to obtain good signal intensity for the relaxation profiles. Quantitation of T₁ was performed via inversion recovery measurements at temperatures from 5 to 180 K (Fig. 4 and S10–S12†). At 5 K, T₁ for 1–4 ranged from 71(2) to 178(2) ms and dropped rapidly with increased temperature, finally reaching 0.40(2) to 0.72(2) μs at 140 K.

Fig. 4 (Top) Selected variable temperature inversion recovery curves (color traces) and fits (black trace) for 1. (Bottom) Variable-temperature T₁ and data for 1–4. Data were collected at X-band frequency (ca. 9.4 GHz) on samples of ca. 1 mM concentration in o-terphenyl glass. The black trace is the fit to the direct, Raman, and local mode processes. Error bars are within the width of the data points.

The temperature dependence of T₁ data can reveal what processes govern relaxation, which could yield insight into the role of the counterion. Hence, we modelled the temperature-dependent T₁ data by an equation including direct, Raman, and local mode relaxation processes:¹³

Here, T is temperature, A_dir is the direct process coefficient, A_Ram is the Raman process coefficient, θ_D is the Debye temperature, J₈(x) is the transport integral (see ESI† for full expression), A_loc is the coefficient of the contribution from a local vibration mode, and Δ_loc is the energy of the local mode. Qualitatively, the near exact superimposability of the data for 1–4 suggests that the parameters are extremely similar. Indeed, only one set of parameters is needed to simulate the data for the entire set of complexes (Table S8†). We conclude that the hydrogen bonding and counterions have negligible effect on T₁. A significant amount of recent work suggests that vibrations and motion in the environment are an important contributors to spin–lattice relaxation.^50,51 Our results and others'^21,29 confine the region in which such attention is focused to the inner coordination sphere.

Separate from spin–lattice relaxation, we also hypothesized that motion of the counterion might affect the metal spin phase memory time T_m. We envisioned that small motions of the [V(C₆H₄O₂)₃]²⁻ moiety (or counterions) may occur in the lattice. If true, then thermally driven reorientations of the molecules on the timescale of the spin-echo experiment would shift the resonant EPR frequency, shortening T_m.⁵² We hypothesized that these minor reorientations could be suppressed by the association with the more massive cations. To probe this possibility, we sought to test whether T_m varied with 1–4 as a function of the orientation dependence of the resonant fields. To do so, we first computed the change in resonant field per change in orientation relative to the magnetic field, dB/dθ, for 1–4. These computations were done with the spin Hamiltonian parameters obtained from the simulations of the 5 K EDFS spectra. To test whether dB/dθ impacted T_m in a counterion-dependent fashion, we then performed a field-dependent investigation of the two-pulse Hahn echo decays of 1–4 at 80 K (see Fig. 5 and S13–S15†). The decay curves were fit with the following stretched exponential equation to extract T_m:

Here, I(0) is the initial echo intensity, I(2τ) the intensity of echo as a function of 2τ, the time between the first pulse and the echo (Fig. 6), A the pre-exponential factor, T_m the phase memory time, and β is the stretch parameter. By scanning the entire field range, we were able to inspect T_m as a function of molecular alignment, generally observing peaks close to the canonical perpendicular and parallel orientations.

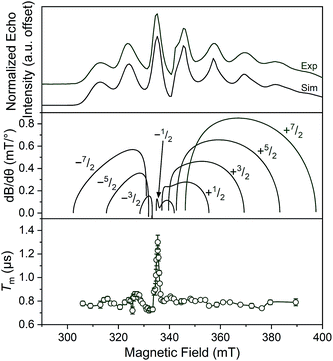Fig. 5 (Top) X-Band (9.460 GHz) echo-detected, field-swept spectra of 1 mM 1 in o-terphenyl solutions at 5 K and simulations. (Middle) Derivative of the resonant field (here, B) with respect to orientation as a function of field for each of the transitions in the EDFS. The dB/dθ values were calculated using microwave frequency = 9.290 GHz (the measurement frequency of the bottom panel) and g- and A-parameters listed in Table 1. (Bottom) Orientation dependence of T_m for 1 at 80 K. See Fig. S13–S15† for plots of T_m for 2–4. Error bars are not shown when smaller than the data symbols for clarity. The green trace is a guide to the eye. For the purposes of clearer comparison across all panels, the 0.17 GHz frequency difference between the EDFS and T_m measurement was accounted for by the application of a + 6 mT shift to the bottom two panels. This value corresponds to the difference in resonant field for g = 2.00 at the two frequencies.

Fig. 6 (Top) Selected variable temperature Hahn echo decay curves (color traces) and fits (black traces) for 1. (Bottom) Variable-temperature T_m data for 1–4. Data were collected at X-band frequency (ca. 9.4 GHz) on samples of ca. 1 mM concentration in o-terphenyl glass. The color traces are guides to the eye. Error bars are within the width of the data points.

We expect to see longer T_ms at instances where dB/dθ is close to zero, and therefore expected the T_m at these points to increase with increasing counterion mass, owing to less motion. Note that although orientation dependence studies on metal ions are found in the literature,^52–55 none exists for the octahedral VO₆ coordination environment. The results demonstrate longer T_ms at the magnetic fields where dB/dθ are ∼0. For example, T_m for 1 reached a maximum of 1.30(6) μs at 329.4 mT wherein the dB/dθ is ca. 0.02, whereas T_ms in high dB/dθ regions are in the range of 0.7–0.8 μs. Beyond this key point, however, we note relatively weak orientation dependence of T_m, which suggests little motion in the solid at 80 K. Furthermore, we observe no trend in this phenomena across the series 1–4.⁵² Thus, we conclude that the counterion is not having a major impact on T_mvia pinning movement in the solid matrix, at least at 80 K.

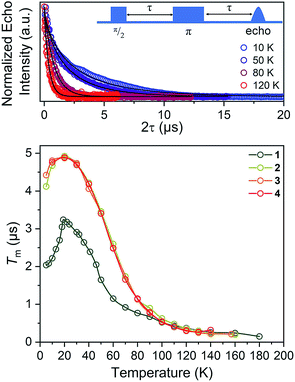
For our final test of counterion effects, we evaluated the impact on the phase memory times as a function of temperature for 1–4. The value of T_m and β govern the shape of the decay curve and reflect the decay mechanism. The magnitudes of T_m for 1–4 in the temperature range of 90–180 K are nearly identical, increasing from an average of 0.26(4) μs at 140 K to an average of 0.78(9) μs at 90 K. Below 90 K, however, the T_m values begin to diverge. With decreasing temperature, T_m increases for all complexes until around 20 K, where T_m reaches a maximum (3.24(6) μs for 1, 4.92(1) μs for 2, 4.87(1) μs for 3, and 4.89(1) μs for 4). Below 20 K, T_m begins to decrease. This decrease is most notable for 1, where T_m drops to 2.04(5) μs at 5 K. However, 2 and 3 also drop, albeit not as strongly (4.922(7) to 4.11(3) μs for 2, 4.87(1) to 4.42(2) μs for 3). For 4, an even smaller drop is seen. It should be noted that the T_ms observed here are in the approximate range of other six-coordinate, V(IV) systems.^14,56 The increase in T_m with decreasing temperature results from an increase of T₁. Indeed, a side-by-side plot of T₁ and T_m (Fig. S20†) demonstrates that is the case. The drop in T_m at the lowest temperatures is indicative of another dynamic process. Following these observations, therefore, there are two remaining questions, first, what is an explanation for the trend in 1–4? Second, what is the origin of the low-temperature downturn in T_m?

Toward an answer to the first of these questions, it is important to note that energy conserving, pair-wise flip flops of nuclear spins are a potent contributor to T_m.^13,57 Hence, the larger values of T_m for 2–4 relative to 1 at lower temperature were unanticipated, as was the observation of the longest T_m values for the two complexes – 3 and 4 – that possess the largest number of protons in their counterions. Indeed, to the best of our knowledge, this is the only report of an increase in T_m following systematic enhancement of nuclear spin-content in a molecule. However, a different environmental factor that can shorten T_m is methyl rotation, wherein the averaging of inequivalent electron-proton couplings produces fast T_m relaxation.^49,58,59 From 1 to 3, the counterion methyl groups move further away from the V(IV) ion, from 5.1(4) Å average for 1 to 8.6(7) Å average for 3 (Fig. 7). These values are estimated from the crystal structure, which may deviate from the distribution of distances when dissolved. Moreover, exact distances for 4 are unavailable due to the absence of a crystal structure. However, the data are nevertheless suggestive of a trend related to methyl group location.

Fig. 7 (Top) Graphical depiction of key parameter that governs T_m–the distance between the vanadium ion (green) and the methyl groups (orange) on the counterion. (Bottom) Observed relationship between T_m and the mean V⋯CH₃ distance for 1–3 at 5 K.

An alternative explanation could be that the nuclear spins of the environmental o-terphenyl units are causing the trend in T_m. In this scenario, the larger counterions more effectively push the o-terphenyl molecules away from the V(IV) ion, limiting their impact. To distinguish between these two possibilities, a closer inspection of the echo decay curves is needed.

Of note in this discussion is the stretch parameter, β,^60,61 obtained from fitting the echo decays of 1–4. Literature reports demonstrate that β values of about 2–2.6 are expected from measurements on open-shell species in solvents without methyl groups.^49,62 In solvents containing methyl groups, in contrast, smaller β values are expected, and the magnitude of β here depends on temperature and the activation energy of methyl rotation.⁶² For 1, β ranged from 0.69(1) to 0.84(1) from 5 to 40 K. For 2–4, β is larger than 1, ranging from 1.28(1) to 1.68(1) in the temperature range of 5 to 40 K. That all of the extracted β values are low is evidence of T_m control by methyl rotation on the counterion. Indeed, if o-terphenyl exclusion were the sole origin of the T_m differences in 1–4, in contrast, then we would expect higher β values than are observed.

On the basis of the foregoing evidence, we also assign the low temperature downturn in 1–4 to the methyl groups, particularly upon inspection of the 5 K T_m trend (Fig. 7). Indeed, at such temperatures, methyl group rotation is not frozen and can proceed via tunnelling.^63–65 Such a possibility is supported by the relative magnitudes of the low-temperature drop in T_m for 1–4, being weaker for the larger R₃NH⁺ ions. Note that other studies appear to feature a weaker downturn in methyl-bearing solvents.^15,66 Here, the methyl group impact might be expected to be greater in 1 and 2 owing to the relative proximity of the counterion.

One final note of significance: the exact dependence of T_m on distance to nearby spins in molecules is ill-explored, only recently evaluated for systems with ¹H nuclei and V(IV) electron spins.^66,67 Those studies indicate that within a distance of about 4.0(4) to 6.6(4) Å, ¹H frequencies are shifted off-resonance owing to hyperfine interactions with the S = 1/2 V(IV) spin, which disables the pair-wise flip flops that shorten T_m. In contrast, outside of this radius (the diffusion barrier²⁸) the ¹H spins are no longer off-resonance, flip–flop motions are enabled, and T_m is shortened. The mechanism for the shortening of T_m by methyl groups appears different and not governed by a diffusion barrier.^49,68 Instead, the closer methyl groups of 1 have a larger impact on T_m. Such observation is consistent with (1) a dipolar interaction and (2) that the CH₃ spins are impacting T_m by a different mechanism than nuclear spin diffusion. The bigger counterions, therefore, must position the methyl groups at sufficient distance that they are less important contributors. This trend has a practical implication: that counterions can employ alkyl chains to enhance solubility without substantially decreasing T_m through the included CH₃ nuclear spins.

Conclusions and outlook

Counterions are an extremely important chemical handle in metal complexes, accompanying any complex that possesses a nonzero charge. The foregoing results provide the first systematic delineation of the control of metal-ion EPR properties through counterion. In particular, we present evidence that counterions can enhance solubility – an important physical property – yet avoid dramatically enhancing relaxation rates. We also demonstrate negligible impact on T₁ in the solid state, an observation at odds with growing assertions of the importance of the secondary coordination sphere on T₁.^50,51 Finally, we show that the counterions control T_m predominantly through the contained methyl groups, when those groups are within roughly 5–6 Å of the metal ion. Thus, the presented information is a key step forward in understanding the role of local chemistry on magnetic complexes. Note that our broader interests lie in understanding how chemistry can control the relaxation times of metal ions at low microwave frequencies. It is this relatively unexplored low-frequency domain that will be explored in future efforts.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank the National Science Foundation (CHE-1836537), Colorado State University, and the University of Denver for supporting this work. C.-Y. L. and J. M. Z. thank Mr Majed Fataftah, Romeo Portillo, Ms. Brooke Livesay, Drs Robert Higgins, Justin Cole, Brian Newell, and Erin Stuckert for fruitful discussion and experimental assistance. A portion of this work was performed at the CSU Central Instrument Facility, which is supported by an NIH-SIG award (1S10OD021814-01) and the CSU-CORES Program.

Notes and references

1. G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546.
2. L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186.
3. J. Lehmann, A. Gaita-Ariño, E. Coronado and D. Loss, J. Mater. Chem., 2009, 19, 1672–1677.
4. E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Chem. Soc. Rev., 2018, 47, 501–513.
5. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
6. M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Chem. Mater., 2017, 29, 1885–1897.
7. R. E. P. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 7992–7994.
8. R. Sessoli, ACS Cent. Sci., 2015, 1, 473–474.
9. J. Olson, Y. Cao, J. Romero, P. Johnson, P.-L. Dallaire-Demers, N. Sawaya, P. Narang, I. Kivlichan, M. R. Wasielewski and A. Aspuru-Guzik, Quantum Information and Computation for Chemistry, 2017.
10. In Vivo EPR (ESR), ed. L. J. Berliner, Springer US, Boston, MA, 2003, Biol. Magn. Reson., vol. 18.
11. J. P. Klare, Biomed. Spectrosc. Imaging, 2012, 1, 101–124.
12. J.-H. H. Ardenkjaer-Larsen, G. S. Boebinger, A. Comment, S. Duckett, A. S. Edison, F. Engelke, C. Griesinger, R. G. Griffin, C. Hilty, H. Maeda, G. Parigi, T. Prisner, E. Ravera, J. van Bentum, S. Vega, A. Webb, C. Luchinat, H. Schwalbe and L. Frydman, Angew. Chem., Int. Ed., 2015, 54, 9162–9185.
13. S. S. Eaton and G. R. Eaton, in Biological Magnetic Resonance, ed. L. J. Berliner, S. S. Eaton and G. R. Eaton, Kluwer academic/Plenum publishers, New York, 2002, Vol. 19, pp. 29–154.
14. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2014, 136, 15841–15844.
15. C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685.
16. M. Atzori, L. Tesi, E. Morra, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 2154–2157.
17. M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244.
18. M. Atzori, A. Chiesa, E. Morra, M. Chiesa, L. Sorace, S. Carretta and R. Sessoli, Chem. Sci., 2018, 9, 6183–6192.
19. L. Escalera-Moreno, N. Suaud, A. Gaita-Ariño and E. Coronado, J. Phys. Chem. Lett., 2017, 8, 1695–1700.
20. L. Tesi, A. Lunghi, M. Atzori, E. Lucaccini, L. Sorace, F. Totti and R. Sessoli, Dalton Trans., 2016, 45, 16635–16643.
21. L. E. Rosaleny, K. Zinovjev, I. Tuñón and A. Gaita-Ariño, arXiv:1808.03234 [cond-mes-hall], 2018.
22. K. Bader, S. H. Schlindwein, D. Gudat and J. van Slageren, Phys. Chem. Chem. Phys., 2017, 19, 2525–2529.
23. J. M. Zadrozny and D. E. Freedman, Inorg. Chem., 2015, 54, 12027–12031.
24. M. S. Fataftah, S. C. Coste, B. Vlaisavljevich, J. M. Zadrozny and D. E. Freedman, Chem. Sci., 2016, 7, 6160–6166.
25. J. M. Zadrozny, M. J. Graham, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Chem. Commun., 2016, 52, 10175–10178.
26. A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201.
27. C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204.
28. W. E. Blumberg, Phys. Rev., 1960, 119, 79–84.
29. C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
30. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Angew. Chem., Int. Ed., 2017, 56, 11445–11449.
31. F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018 DOI:10.1126/science.aav0652.
32. K. Grubel, W. W. Brennessel, B. Q. Mercado and P. L. Holland, J. Am. Chem. Soc., 2014, 136, 16807–16816.
33. G. González-Riopedre, M. R. Bermejo, M. I. Fernández-García, A. M. González-Noya, R. Pedrido, M. J. Rodríguez-Doutón and M. Maneiro, Inorg. Chem., 2015, 54, 2512–2521.
34. S. F. McWilliams, K. R. Rodgers, G. Lukat-Rodgers, B. Q. Mercado, K. Grubel and P. L. Holland, Inorg. Chem., 2016, 55, 2960–2968.
35. A. H. Reath, J. W. Ziller, C. Tsay, A. J. Ryan and J. Y. Yang, Inorg. Chem., 2017, 56, 3713–3718.
36. T. Chantarojsiri, J. W. Ziller and J. Y. Yang, Chem. Sci., 2018, 9, 2567–2574.
37. D. L. J. Broere, B. Q. Mercado, E. Bill, K. M. Lancaster, S. Sproules and P. L. Holland, Inorg. Chem., 2018, 57, 9580–9591.
38. G. Ulrich, P. Turek, R. Ziessel, A. De Cian and J. Fischer, Chem. Commun., 1996, 2461–2462.
39. The Alkali Metal Ions: Their Role for Life, ed. A. Sigel, H. Sigel and R. K. O. Sigel, Springer International Publishing, Cham, Switzerland, 2016, vol. 16.
40. S. R. Cooper, Y. B. Koh and K. N. Raymond, J. Am. Chem. Soc., 1982, 104, 5092–5102.
41. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
42. J. A. P. Sprenger, S. Z. Konieczka, F. A. Brede, C. Kerpen, M. Drisch, K.-D. Franz, N. Ignat'ev, G. J. Reiss, W. Frank and M. Finze, Eur. J. Inorg. Chem., 2015, 5639–5649.
43. C. Milsmann, A. Levina, H. H. Harris, G. J. Foran, P. Turner and P. A. Lay, Inorg. Chem., 2006, 45, 4743–4754.
44. M. Branca, G. Micera, A. Dessi, D. Sanna and K. N. Raymond, Inorg. Chem., 1990, 29, 1586–1589.
45. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
46. CRC Handbook of Chemistry and Physics, ed, J. Rumble, CRC Press, 99th edn, 2018.
47. A. Schweiger and G. Jeschke, Principles of Pulse Electron Paramagnetic Resonance, Oxford University Press, Oxford, 2001.
48. J. Soetbeer, M. Hülsmann, A. Godt, Y. Polyhach and G. Jeschke, Phys. Chem. Chem. Phys., 2018, 20, 1615–1628.
49. A. Zecevic, G. R. Eaton, S. S. Eaton and M. Lindgren, Mol. Phys., 1998, 95, 1255–1263.
50. M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740.
51. M. Atzori, L. Tesi, S. Benci, A. Lunghi, R. Righini, A. Taschin, R. Torre, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2017, 139, 4338–4341.
52. J.-L. Du, K. M. More, S. S. Eaton and G. R. Eaton, Isr. J. Chem., 1992, 32, 351–355.
53. J.-L. Du, G. R. Eaton and S. S. Eaton, J. Magn. Reson., Ser. A, 1995, 117, 67–72.
54. R. Husted, J.-L. Du, G. R. Eaton and S. S. Eaton, Magn. Reson. Chem., 1995, 33, S66–S69.
55. R. Konda, J.-L. Du, S. S. Eaton and G. R. Eaton, Appl. Magn. Reson., 1994, 7, 185–193.
56. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492.
57. S. Takahashi, I. S. Tupitsyn, J. van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79.
58. S. A. Dzuba, A. G. Maryasov, K. M. Salikhov and Y. D. Tsvetkov, J. Magn. Reson., 1984, 58, 95–117.
59. K. Nakagawa, M. B. Candelaria, W. W. Chik, S. S. Eaton and G. R. Eaton, J. Magn. Reson., 1992, 98, 81–91.
60. I. M. Brown, in Time Domain Electron Spin Resonance, ed. L. Kevan and R. N. Schwartzs, John Wiley, New York, 1979, pp. 195–229.
61. K. M. Salikhov and Y. D. Tsvetkov, in Time Domain Electron Spin Resonance, ed. L. Kevan and R. N. Schwartz, John Wiley, New York, 1979, pp. 232–277.
62. M. Lindgren, G. R. Eaton, S. S. Eaton, B.-H. Jonsson, P. Hammarström, M. Svensson and U. Carlsson, J. Chem. Soc., Perkin Trans. 2, 1997, 2549–2554.
63. N. P. Benetis and Y. Dmitriev, J. Phys.: Condens. Matter, 2009, 21, 103201.
64. A. R. Sørnes, N. P. Benetis, R. Erickson, A. S. Mahgoub, L. Eberson and A. Lund, J. Phys. Chem. A, 1997, 101, 8987–8994.
65. J. H. Freed, J. Chem. Phys., 1965, 43, 1710–1720.
66. M. J. Graham, C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 3196–3201.
67. M. J. Graham, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, Inorg. Chem., 2017, 56, 8106–8113.
68. G. R. Eaton and S. S. Eaton, J. Magn. Reson., 1999, 136, 63–68.

---

Footnotes

† Electronic supplementary information (ESI) available: Methods, additional characterization and discussion. CCDC 1862638–1862639. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc04122a

‡ Within the molecular qubit literature, this parameter is frequently also labelled T₂. While there are differences between these two parameters, for the purposes of this manuscript, we are simply referring to the relaxation time obtained from a two-pulse Hahn-echo experiment. See ref. 13 for more detail.

---