Open Access Article
Open Access ArticleStructural control of polyelectrolyte/microemulsion droplet complexes (PEMECs) with different polyacrylates†
Miriam
Simon
 *a,
Patrick
Krause
a,
Leonardo
Chiappisi
*a,
Patrick
Krause
a,
Leonardo
Chiappisi
 ab,
Laurence
Noirez
ab,
Laurence
Noirez
 c and
Michael
Gradzielski
c and
Michael
Gradzielski
 *a
*a
aStranski-Laboratorium für Physikalische und Theoretische Chemie, Institut für Chemie, Technische Universität Berlin, D-10623 Berlin, Germany. E-mail: miriam.simon@tu-berlin.de; michael.gradzielski@tu-berlin.de
bInstitut Laue-Langevin, 38042 Grenoble, France
cLaboratoire Léon Brillouin (CEA-CNRS), Uni. Paris-Saclay, CEA-Saclay, 91191 Gif-sur-Yvette, France
First published on 23rd October 2018
Abstract
The ionic assembly of oppositely charged polyelectrolyte–surfactant complexes (PESCs) is often done with the aim of constructing more functional colloids, for instance as advanced delivery systems. However, PESCs are often not easily loaded with a solubilisate due to intrinsic restrictions of such complexes. This question was addressed from a different starting point: by employing microemulsion droplets as heavily loaded surfactant systems and thereby avoiding potential solubilisation limitations from the beginning. We investigated mixtures of cationic oil-in-water (O/W) microemulsion droplets and oppositely charged sodium polyacrylate (NaPA) and determined structure and phase behaviour as a function of the mixing ratio for different droplet sizes and different Mw (NaPA). Around an equimolar charge ratio an extended precipitate region is present, which becomes wider for larger droplets and with increasing Mw of the NaPA. Static and dynamic light scattering (SLS and DLS) and small-angle neutron scattering (SANS) show the formation of one-dimensional arrangements of microemulsion droplets for polyelectrolyte excess, which become more elongated with increasing Mw (NaPA) and less so with increasing NaPA excess. What is interesting is a marked sensitivity to ionic strength, where already a modest increase to ∼20 mM leads to a dissolution of the complexes. This work shows that polyelectrolyte/microemulsion complexes (PEMECs) are structurally very versatile hybrid systems, combining the high solubilisate loading of microemulsions with the larger-scale structuring induced by the polymer, thereby markedly extending the concept of conventional PESCs. This type of system has not been described before and is highly promising for future applications where high payloads are to be formulated.
Introduction
Microemulsions are thermodynamically stable liquid systems of water, oil and an amphiphile which are single-phase and optically isotropic1 with structural properties that can be explained by the bending elasticity of their amphiphilic monolayers.2,3 Frequent structural types are oil-in-water (O/W) droplets which naturally allow having a rather high content of hydrophobic material dispersed in aqueous solution, which otherwise could not be dissolved. From a fundamental point of view, O/W microemulsion droplets are interesting as they have a well-defined spherical structure and possess a low polydispersity when prepared close to the emulsification boundary.4 From a more practical point of view, microemulsions are an excellent medium for solubilizing active agents, as often needed for formulations in cosmetics, pharmacy, etc.5–8 However, in order to make them more versatile for such applications one may have to add additives like polymers to microemulsions which allow modulating their properties.In a similar direction, polyelectrolyte/surfactant complexes (PESCs) have been studied comprehensively in the past few years. Because of their large structural variety,9–11 that arises from the local structuring by the surfactant and the larger scale structuring by the polymer, they are considered to be very attractive for the purposes of solubilisation and drug delivery.12,13 They have for instance been explored for the case of cationic hydrogels and sodium dodecyl sulfate (SDS), where controlled release of a hydrophobic drug was achieved and the loading capacity depended markedly on the charge density of the polymer.14 Work regarding the solubilisation in PESCs was done for the case of SDS/TX-100 micelles complexed with poly(dimethyldiallylammonium chloride) (PDADMAC). This system showed an unchanged solubilisation power in the complexes compared to the initially present micelles.15 Other studies regarding the solubilisation of hydrophobic compounds within PESCs were concerned with the contaminant oil trichloroethylene (TCE). They confirmed such a solubilisation behaviour of PESCs and their use allowed for enhanced separation by using colloid-enhanced ultrafiltration processes.16 Apart from that, PESCs of oppositely charged surfactant micelles and double hydrophilic polyelectrolytes have been investigated with respect to their ability to solubilize drug molecules, as for instance done for the case of the cationic copolymer poly(ethylene oxide)-g-polyethyleneimine (PEO-g-PEI) and sodium oleate.17 Central for a successful application here is a high drug loading as was seen for doxorubicin (DOX) in PESCs obtained from combining poly(ethylene glycol)-block-poly(4-vinylbenzylphosphonate) (PEG-b-PVBP) with cationic surfactants.18 In general it is important to optimise the ability to solubilise hydrophobic compounds, but typically the solubilisation capacity for drugs or dye molecules in PESCs is rather limited since only certain surfactants show high solubilisation capacities.19
Accordingly an interesting alternative is to use microemulsion droplets, which are structurally well understood and already contain a large amount of solubilised hydrophobic compounds,20 and to complex them with oppositely charged polyelectrolytes, thereby forming polyelectrolyte/microemulsion complexes (PEMECs). This approach avoids the need for optimising the solubilisation properties as it is intrinsically controlled by the microemulsions. It is interesting to note that such mixtures so far have only been investigated very scarcely. In contrast, for instance the modification of microemulsion viscosity by polymeric additives has been studied in some detail and can be enhanced largely by adding hydrophobically modified telechelic water-soluble polymers, where the effect depends largely on the length of the hydrophobic modification and the amount of the added polymer.21–26 Similarly complexes between neutral amphiphilic polymers and water-in-oil (W/O) microemulsions have been studied27 and they can also be transformed into a transient network by ABA copolymers where the A blocks are hydrophilic.28 The effect of polyelectrolytes on the phase behaviour and structure of W/O microemulsions was also studied, but mostly with the aim of forming nanoparticles in these systems.29,30 Note et al. investigated the phase diagram of a negatively charged SDS/pentanol based W/O microemulsion with the cationic polyelectrolyte PEI31 and found that more than 30 wt% PEI can be incorporated within the aqueous phase. The incorporation of PEI leads to a substantial shift of the microemulsion regime within the phase diagram, leading to the formation of bicontinuous and even O/W structures. In one of the few investigations on cationic surfactant–polyanion complexes, it was found that the solubilisation capacity of the micelles increases in the presence of the polymer, due to the additional ionic strength.32 If charged droplets bind to polymers through electrostatic interactions, bridging and/or compactions of the droplets would be expected as well as a decoration of the polyelectrolyte chains with microemulsion droplets.33 In general, the same structural richness is expected here, as seen for PESCs, while guaranteeing a high hydrophobic loading of the surfactant aggregates.
However, nearly no research has been carried out on mixtures of charged microemulsion droplets with oppositely charged polyelectrolytes, where the complexation would be driven by electrostatic interactions and concomitant counterion release and the idea of gaining structural control of the microemulsion system on a larger length scale via polyelectrolyte addition has not been exploited yet.
In order to fill this scientific gap, we investigated oil-in-water (O/W) microemulsion droplets based on tetradecyldimethylamine oxide (TMDAO), which is known to form such microemulsions with different alkanes.34 The droplet size can be increased in a systematic fashion by addition of a cosurfactant, as has been demonstrated in detail in the case of 1-hexanol.35 In addition, these microemulsion droplets can become variably charged without modifying their structure by substituting small amounts of TDMAO with the equivalent cationic surfactant tetradecyltrimethylammonium bromide (TTAB).36–38 Accordingly, these microemulsions are highly suited for a systematic investigation as they are at the same time a well-defined and monodisperse model colloid and attractive for potential applications. It might be noted that we stayed in the range of having small amounts of ionic surfactant as the microemulsion itself is in principle a nonionic one and we just introduced some charges to allow for ionic assembly. As a simple oppositely charged polyelectrolyte we chose the sodium salt of the flexible polyacrylic acid (PAA), sodium polyacrylate (NaPA).
In the present experiments we varied the mixing ratio of microemulsion and NaPA, the radius of the droplets and the molecular weight of the NaPA, with the aim to deduce systematic correlations between these parameters, the phase behaviour and the formed structures. We also studied the effect of the total concentration on the formed structures, as well as a variation of ionic strengths in order to modify the electrostatic interactions in these systems. For the structural characterisation, we employed static and dynamic light scattering, measurements of the ζ-potential, and small-angle neutron scattering (SANS). With the systematic variation of all relevant system parameters, we were able to gain a comprehensive insight into the structural arrangements at the mesoscopic scale as a function of these parameters (since access to the structure and dynamics of self-assembled systems is the key for their understanding39). The combination of these experimental methods shows that the formed polyelectrolyte/microemulsion complexes (PEMECs) are rich in their morphology and controlled by their composition and the details of the polyelectrolyte and microemulsion droplet employed.
Results and discussion
Sample preparation
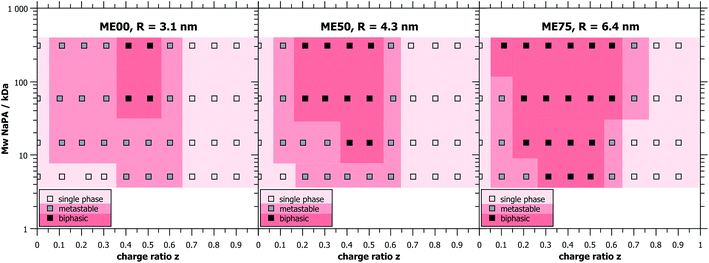
Unless stated otherwise, the oil-in-water (O/W) microemulsion droplets were prepared from a 100 mM stock solution of surfactant where always 5 mol% of zwitterionic TDMAO was substituted by cationic TTAB to obtain weakly charged droplets while keeping the total surfactant concentration constant. Different droplet sizes were achieved by adding different amounts of the cosurfactant hexanol (0, 50 and 75 mM)35 and saturating the mixture with decane (30, 80 and 200 mM, respectively), which resulted in droplet radii of 3.1, 4.3, and 6.4 nm (named ME00, ME50 and ME75, respectively).Different amounts of sodium polyacrylate (NaPA) were added to the microemulsion in order to vary the charge ratio z = [−]/[+] + [−] of the polyelectrolyte/microemulsion complexes (PEMECs) (it might be noted that here we refer to nominal charges, i.e. ionised or ionisable groups (–NMe3 and –COOH), and not actual charges, which for the NaPA and TDMAO depends on the pH and chemical surrounding). The pH was checked after preparation but not further modified in order not to add additional ions to the sample. All samples had pH-values between 7 and 8, where the polyacrylate is about 90% ionised (see Fig. S1†) and TDMAO is only little protonated.
Most samples were prepared from microemulsion and polyacrylate stock solutions, which were then mixed in the desired ratios. However, the same results (complex size and shape) were obtained by mixing all ‘dry’ compounds (TDMAO, TTAB, hexanol, decane, and NaPA) first and adding water afterwards (see Fig. S2† for SANS curves of such an example), so we can safely assume that the observed structures are in thermodynamic equilibrium as they don't depend on the sample history.
Phase behaviour
The determination of the macroscopic phase behaviour is very important since systems of oppositely charged colloids and polyelectrolytes have a tendency to phase separate at the vicinity of charge neutralisation.9,10 This situation is complicated by the fact that this phase separation often occurs very slowly and careful investigation over a period of many days or weeks may be required in order to determine the equilibrium phase diagram.Mixtures of cationic O/W TDMAO/TTAB/decane microemulsion droplets with negatively charged polyacrylate (NaPA) were studied at a fixed surfactant concentration of 100 mM (5 mM cationic TTAB + 95 mM uncharged TDMAO) and different amounts of NaPA to obtain different mixing ratios. In order to gain a comprehensive overview over the phase behaviour, samples were prepared with different microemulsion droplet sizes and different chain lengths of the NaPA. A wide range of precipitation is observed around equimolar charge mixing (z ∼ 0.5) and only for the microemulsion or polyelectrolyte excess single phases are found. It is interesting to note that the biphasic region of the phase diagram has a very asymmetric shape, i.e. a polyelectrolyte excess provides much higher colloidal stability to the systems.
Samples close to the charge equilibrium (z = 0.5) phase separate directly after mixing while samples away from z = 0.5, especially at microemulsion excess, appear turbid at first and need hours or even days for macroscopic phase separation, see Fig. 1. Samples that show phase separation in less than an hour after mixing were labelled biphasic. Metastable samples are samples which need from one hour up to one week to phase separate. Directly after mixing, the metastable samples appeared clear, but then changed colour to bluish and eventually white, before phase separating into a clear liquid and a solid, white precipitate. All samples that still consist of one single phase after one week were considered as thermodynamically stable single phase systems, as they did not evolve during the course of several months (examples of such samples can be seen in Fig. S3†).
It was observed that larger droplets and increasing Mw of the NaPA both lead to a larger biphasic region in the phase diagram. This increase is mostly visible at small z-values (microemulsion excess), where the phase boundary is strongly affected, inducing a much more pronounced precipitation with increasing Mw of NaPA and microemulsion droplet size. In contrast, the behaviour of the phase boundary for large z (polyelectrolyte excess) is basically independent of the Mw of the NaPA (Fig. 1). Immediate phase separation was observed to take place much more likely for the case of large droplets, which indicates a substantially lower kinetic stability of their complexes. It occurs already for the shortest NaPA (for which the small 3.1 nm droplets show rather slow precipitation and the metastability allowed investigating the structures over the whole z-range by light and neutron scattering experiments). This means that the phase behaviour depends strongly on the precise composition of the PEMEC systems.
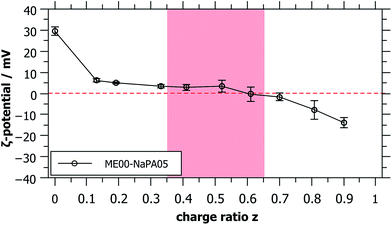
For long time stable single phase regions for smaller or larger z, the samples show different optical appearances ranging from clear to bluish (when being closer to the precipitation area), which indicates the formation of differently sized complexes as a function of z (see Fig. S3†). The formation of mixed aggregates was confirmed by the values of the ζ-potential that reverses sign upon the addition of the NaPA (Fig. 2). What is also interesting to note here is that the ζ-potential is reduced very abruptly upon the addition of NaPA.
Structural characterisation of stable polyelectrolyte/microemulsion complexes (PEMECs)
The study of the phase diagrams has enabled the identification of single-phase regions of the NaPA/ME mixtures, which are either stable or at least long-time metastable. We were now interested to determine how the colloidal structure of these PEMECs depends on their molecular composition.The optical appearance of the samples and the ζ-potential values suggest that differently sized mixed aggregates are formed, which was confirmed by static and dynamic light scattering (SLS and DLS). Since light scattering (both static and dynamic) does not allow deducing mesoscopic structural information, small-angle neutron scattering (SANS) was used to access a refined mesoscopic structural picture. In all these experiments, we systematically varied the mixing ratio of NaPA to ME charges, the molecular weight Mw of the NaPA and the size of the droplets, thereby gaining an insight into how the structure of the PEMECs can be controlled by their composition.
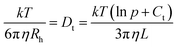 with p = L/d and Ct = 0.312 + 0.565/p − 0.100/p2.40 For example a measured diffusion coefficient of 34.2 μm2 s−1 (ME00–NaPA05, z = 0.7) equals an Rh of 7 nm and corresponds to a rod of 3 nm radius (one ME droplet) and 27 nm length (4.3 densely arranged droplets).
with p = L/d and Ct = 0.312 + 0.565/p − 0.100/p2.40 For example a measured diffusion coefficient of 34.2 μm2 s−1 (ME00–NaPA05, z = 0.7) equals an Rh of 7 nm and corresponds to a rod of 3 nm radius (one ME droplet) and 27 nm length (4.3 densely arranged droplets).
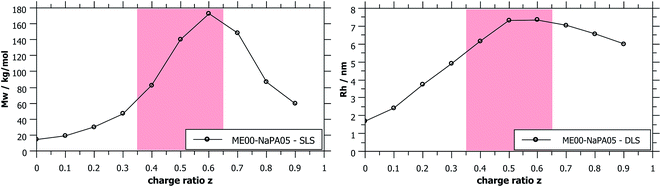 | ||
| Fig. 3 Apparent Mw and Rh obtained from static and dynamic light scattering show the presence of differently sized aggregates of ME and PE depending on the charge ratio z. Metastable samples (shaded in red) were measured while still being homogeneous, typically being 3–5 days old. Measured values for longer NaPAs are given in Fig. S4.† | ||
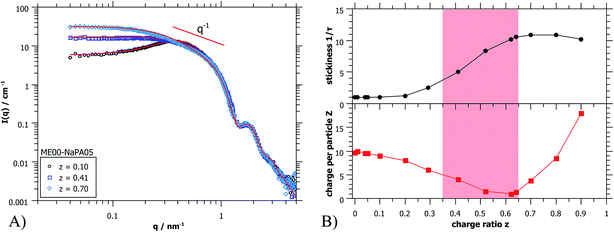
To complete the structural information gained from light scattering, additional SANS data were obtained. In Fig. 4A some selected SANS spectra for the same sample series are shown. The whole series is displayed in Fig. S5.† A very important finding is that the scattering curves for different charge ratios do not change at high q (q > 0.8 nm−1), thereby indicating that in this size range (d < 8 nm), that characterizes the microemulsion droplets, the structure remains unchanged. It might be noted that this finding is valid in general for all systems investigated here, so the size, shape and polydispersity of the initially present microemulsion droplets are not affected by the addition of an oppositely charged polyelectrolyte. This is very important as it means that the microemulsion droplets remain structurally intact and would for instance be available as carriers in delivery systems.
The main difference in scattering intensity is seen at low q (q < 0.3 nm−1), where the structure factor describes the interactions between the particles. This indicates that at small amounts of NaPA the charge of the ME droplets is screened and one observes a continuous increase of intensity with increasing content of NaPA (z = 0.0 − 0.5). Once all ME charges are screened, the PE starts to introduce attractive interactions, which increases the intensity even further. For high NaPA excess (z > 0.6) the intensity starts to decrease somewhat with increasing z, indicating a collapse of the structures, probably due to the large excess of negative charge and the resulting strong electrostatic repulsion between aggregates contained.
For quantitative analysis of the SANS curves the intensity I(q) was approximated as:
| I(q) = 1NV2ΔSLD2P(q)S(q) | (1) |
This model works very well for small droplets and short PE chains. But only attractive and repulsive forces are not enough to describe the more elongated complexes as they are formed by higher Mw polyacrylates (see the ‘Variation of the NaPA Chain Length’).
SLS measurements of samples with differently sized droplets but mixed with the same NaPA at the same charge ratio naturally show a much higher intensity for bigger droplets, i.e. higher Mw complexes are formed, reaching values of 106 g mol−1 (it might also be noted that the hydrodynamic radius, measured with DLS, increases by a factor of 2.5, reaching values of 25 nm, see Fig. 6).
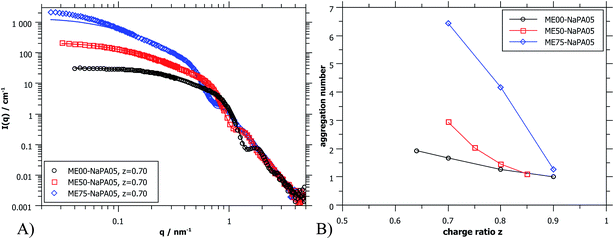 | ||
| Fig. 5 (A) SANS scattering curves (ME00 and ME50 from PAXY at LLB and ME75 from D11 at ILL) of complexes formed with differently sized microemulsion droplets and NaPA05. Solid lines were calculated for a cylindrical arrangement of the droplets.45 (B) Aggregation number Nagg of ME droplets contained in the aggregates as deduced from extrapolated I(0) values of SANS curves (for details see the ESI†). | ||
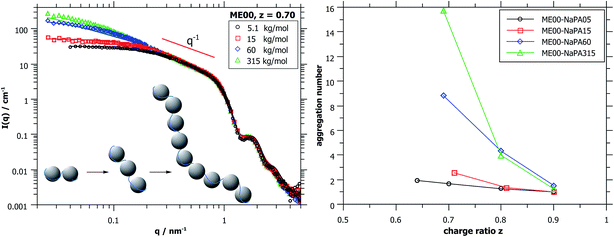
Again, further insight can be obtained from SANS measurements carried out at different mixing ratios z with all droplet sizes; the curves are shown in Fig. S6.† All series show the same general behaviour regardless of the droplet size, but the intensity extrapolated to q = 0, I(0) (or equivalently the Mw of the complexes) increases strongly with increasing droplet size (see Fig. 5A, S7 and S8†). The number of microemulsion droplets contained in one complex was obtained from the scattering at zero angle, I(0) (obtained by extrapolation with Guinier approximation), compared to the forward scattering of a single non-interacting microemulsion droplet. This analysis is described in detail in the ESI† and results are shown in Fig. 5B. Here it was assumed that the contribution of the polyelectrolyte to the scattering intensity can be neglected in comparison to the scattering of the microemulsion droplets. This approach is only meaningful for polyelectrolyte excess as for microemulsion excess one just sees a modification of the interaction potential from which no aggregation number can be deduced. At polyelectrolyte excess, the highest aggregation numbers are found close to the phase boundary. Only 2 of the small droplets seem to be effectively linked in one aggregate but this number increases to 3 and even 6 of the medium and large droplets. The corresponding number of NaPA chains per complex can be calculated as follows:
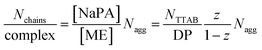 | (2) |
| Name | c/mM (TDMAO/TTAB) | c/mM (hexanol) | c/mM (decane) | R/nm (SANS) | [+]/droplet |
|---|---|---|---|---|---|
| ME00 | 95/5 | 0 | 30 | 3.1 | 12.1 |
| ME50 | 95/5 | 50 | 80 | 4.3 | 23.2 |
| ME75 | 95/5 | 75 | 200 | 6.4 | 51.5 |
| ME | NaPA | z | N droplets/complex | N chains/complex | Comment |
|---|---|---|---|---|---|
| ME00 | 5.1 | 0.7 | 1.7 | 1 | Stiff rod |
| 15 | 0.7 | 2.6 | 0.5 | Stiff rod | |
| 60 | 0.7 | 8.8 | 0.4 | Rod starts to bend | |
| 315 | 0.7 | 15.7 | 0.2 | Exact number of droplets not detectable | |
| ME50 | 5.1 | 0.7 | 2.9 | 3 | Stiff rod |
| 15 | 0.7 | 3.5 | 1.2 | Rod starts to bend | |
| 60 | 0.7 | 12.6 | 1 | Exact number of droplets not detectable | |
| 315 | 0.7 | 22.9 | 0.5 | Exact number of droplets not detectable | |
| ME75 | 5.1 | 0.7 | 6.4 | 14 | Rod starts to bend |
At first glance the results look counterintuitive, as for the small droplets this corresponds to a situation where only one NaPA is involved in the complex. This number then increases to ∼14 NaPA chains in one complex for the largest droplets (ME75). This increase can be explained by the higher number of charges per droplet, which increases with increasing droplet size, and allows for a much more effective electrostatic polyelectrolyte/droplet interaction. At higher mixing ratios (z = 0.9), the NaPA excess is high enough to stabilize each droplet separately, regardless of the size, so the value of Nagg drops to 1. In general, this is a relatively low number of aggregated microemulsion droplets compared to the typical aggregation number observed in PESCs, but it must also be noted that Nagg increases largely with increasing Mw of the NaPA (see the ‘Variation of the NaPA Chain Length’).
The most elongated complexes are present close to the phase boundary. SANS curves at z = 0.7 (Fig. 5A and further curves are shown in S6†) were described by a model of spheres arranged in a cylindrical domain as described in (ref. 45) (for further details also see the ESI†). This model describes more correctly the low q-range of the curves as the sticky hard sphere model since it accounts more correctly for the local shape of the aggregates. Here the elongation becomes clearly more pronounced with increasing size of the microemulsion droplets.
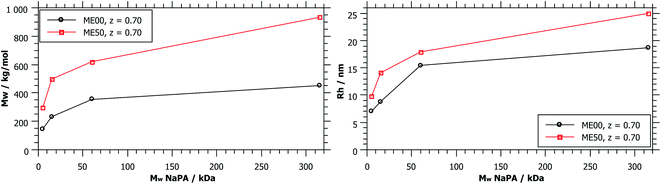
As shown in Fig. 1, complexes formed with longer NaPA chains have a larger two-phase region. For the stable samples in the range of NaPA excess SLS shows a significant increase of the molecular weight of the formed aggregates with increasing Mw of the NaPA (Fig. 6). Simultaneously the hydrodynamic radius determined by DLS substantially increases, for instance for the ME00 system rising from about 7 to almost 20 nm when increasing the Mw of the NaPA from 5.1 to 315 kg mol−1. The growth of PEMECs is confirmed by I(0) from SANS (Fig. S7 and S8†). It is also shown that this is a generic observation, which is valid for all droplet sizes.
The static light scattering at I(0) shows the formation of complexes of higher Mw but does not give further information regarding their structure. If a rod with a diameter of the droplet size was assumed, a measured diffusion coefficient of 15.6 μm2 s−1 (ME00–NaPA60, z = 0.7) would equal a length of 95 nm (15 densely arranged droplets). More information about the exact shape of the formed aggregates can be obtained from SANS measurements. A direct comparison of the SANS curves at a given mixing ratio z (z = 0.7) and for identically sized microemulsion droplets (Fig. 7A) shows that with increasing Mw of the NaPA the SANS intensity at low q increases and shows a more pronounced linear part, which follows a q−1 law, thereby indicating the formation of increasingly more elongated complexes. The elongation of these complexes close to the phase boundary becomes more pronounced when a longer NaPA chain is employed.
One possible explanation for forming elongated complexes would be the transformation of many droplets into a cylinder with a diameter of one droplet. However, as mentioned before, the form factor minimum does not change, so the size and shape of the microemulsion droplets remain the same. Another way to form elongated complexes is by linking several droplets with polyelectrolyte chains in a cylindrical geometry. A comparison of the two models is given in Fig. S9,† showing the significantly better agreement of the second model with the measured data. Accordingly, this model was used to describe the SANS data and to quantify the elongation. The structural parameters for single microemulsion droplets were fixed to be those of the pure microemulsion sample. Additional parameters for the linear arrangement of the droplets are the number N of droplets per aggregate, the mean distance D between droplets in one aggregate and the polydispersity of this distance.
It has to be mentioned here that this model describes the measured data for short chains but the agreement becomes poorer with longer polyacrylate chains. This can be explained by the flexible nature of the polyacrylate backbone. In the model the droplets arrange to form a straight, stiff rod, which gives a slope of q−1 in the SANS data. In practice, however, longer aggregates composed of many droplets will tend to be less straight, which finally would lead to a slope of q−2 for Gaussian coils. The longest polyacrylate chain employed in this work has an Mw of 315 kDa with a stretched chain length of about 850 nm. This polyelectrolyte does not form straight rod-like complexes over the whole length scale but bends over its persistence length, and therefore the SANS data show a slope of q−1.5.
The curves shown in Fig. 7A were described with cylindrical arrangements of 1.5, 3, 11 and 17 droplets per aggregate for Mws of the NaPA of 5.1, 15, 60 and 315 kDa, respectively.45 The model-results for the longest NaPA (315 kDa) are not reliable anymore but here a number of 16 droplets per aggregate can be obtained from the I(0) value of the scattering data. More results obtained from the fits, also for larger droplets, are given in Table S3,† while the aggregation numbers obtained from the forward scattering I(0) are given in Fig. 7B and Table 2.
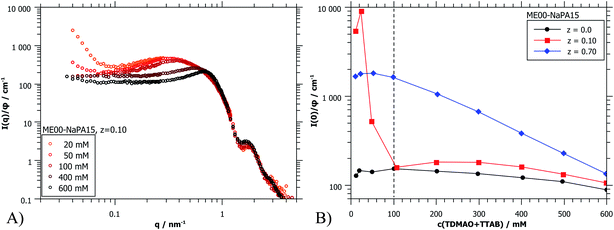
The forward scattering intensities were obtained by Guinier approximation. The results are shown in Fig. 8B and it can be seen that this increase is much more marked on the side of microemulsion excess. Here one may argue that one observes a transition from a space-filling polyelectrolyte/microemulsion network at higher concentration to increasingly isolated clusters due to diluting below the effective overlap concentration. For z = 0.7 a gradual increase of I(0) is observed. Because of the much higher starting concentration of NaPA no concentrations below the effective overlap concentration are reached. But below 100 mM no further changes of the scattering curves are seen upon still diluting further (Fig. 8B and S10†). Apparently here the system is diluted enough that individual complexes are visible.
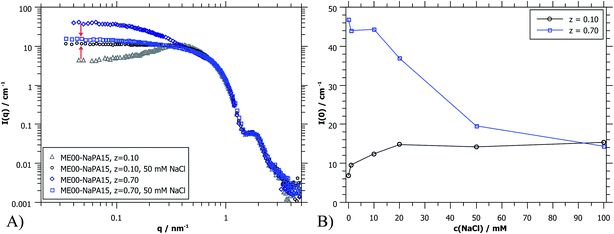
Fig. 9B shows I(0) as a function of ionic strength which modifies the interactions between the droplets. For the case of z = 0.1 (microemulsion excess) the added salt apparently screens the charges of the microemulsion droplets already effectively for less than 20 mM NaCl. This is the expected behaviour for such systems as here the spacing between the droplets becomes much larger than the Debye screening length δ (for 20 mM ionic strength: δ = 2.3 nm).36 However, the behaviour of polyelectrolyte excess is surprising since a concentration of 50 mM seems to be sufficient to dissolve the PEMECs that are held together by electrostatic interactions. This is in striking contrast to observations for polyelectrolyte/surfactant complexes (PESCs) or interpolyelectrolyte complexes (IPECs), where typically an ionic strength of 500–700 mM is required in order to dissolve them.46–48 Apparently the PEMECs studied here possess a very high degree of responsiveness to ionic strength.
Discussion
These experimental observations can be interpreted in terms of molecular build-up of the studied PEMECs. The main parameters to be considered are:- The length of the polyelectrolyte and its charge density.
- The size of the microemulsion droplets (controlled by the amount of 1-hexanol contained) and the number of charges (TTAB content) on them.
- Their mixing ratio as defined by z = [−]/([−] + [+]).
- The ionic strength of the solution.
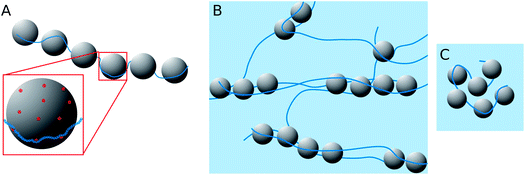
When looking at the present PEMECs it is clear that especially the overlap concentration of the different NaPAs employed varies largely and therefore also their ability to build a space-filling polyelectrolyte network. On the other hand the microemulsion droplets have a rather low number of charges, with about one charge per 12 nm2, while the charge density along the NaPA backbone is rather high, with one charged unit per 0.25 nm (this situation is depicted in Fig. 10A). This makes their interaction delicate explaining why the larger droplets have a higher tendency for precipitating as here simply the number of charges per droplet is higher and therefore it allows more easily compensating for the high charge density of the NaPA (this even more so as they are curved less, thereby making it easier for the NaPA to bend around the microemulsion droplets).
Complexes with longer NaPAs (60 and 315 kg mol−1) prepared at polyelectrolyte excess (z > 0.5) are already above the overlap concentration of the polyelectrolyte (calculated for a stretched chain). So, a network of polyelectrolyte chains is formed in the solution if no microemulsion droplets are present. Adding the oppositely charged microemulsion droplets deforms the network so that the droplets are arranged in one-dimensional complexes, which are held together by several NaPA chains (see Fig. 10B). Effective charge compensation by just one single NaPA chain is entropically unlikely. The extension of this cylindrical structure becomes larger with increasing Mw of the NaPA, as one may expect for longer chains. Therefore the length of one complex increases with increasing length of the NaPA chain, but only to a limited extent as the negative charge density of the complexes rapidly increases due to the fact that the charge density of the NaPA is much higher than that of the microemulsion droplets. This effect is influenced by the size of the droplets as with increasing size the local amount of positive charges increases and therefore the possibility of building larger aggregates becomes electrostatically enhanced. This then explains the experimentally observed elongation of the complexes with increasing droplet size.
The behaviour is also interesting as a function of concentration. By dilution one will reach a critical concentration below the overlap concentration and therefore a network is no longer formed. For the case of polyelectrolyte excess, in the simplest case this then leads to a situation where a single NaPA chain will form a cluster which then contains the number of microemulsion droplets ([ME]/[PA]) according to the stoichiometric composition (see Fig. 10C), which is given as:
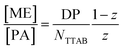 | (3) |
Finally, the rather pronounced sensitivity of the complexes to the addition of salt can be discussed in the context of the driving force of complexation. For the case of counterion release by electrostatic binding of negative polyelectrolyte charges to the positive charges of the microemulsion droplets the driving force can be estimated by ΔGcom = NkT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(V2/V1). V2 is the volume available per counterion after complexation and V1 before complexation. However, the value of V1 for the droplets should be much larger than for an ionic surfactant micelle due to the much lower charge density on the droplet surface, in our case this charge density is only 5% (the droplets contain only 5 mol% of ionic surfactant). Accordingly, the volume (V1) available per ion should be about 20 times more than for a pure micelle (the volume per ion will be given by the surface area times a layer thickness, which should be about the same for both cases and be less than the Bjerrum length). V2 is the volume in solution per free ion, which is inversely proportional to the total ion concentration in solution. Therefore in order that ΔGcom becomes zero (and the driving force for complexation vanishes) if V1 is by a factor of 20 larger one may estimate that a correspondingly lower salt concentration is already effective in dissolving the complexes. This was observed experimentally in this work, as 20–50 mM of salt were enough to dissolve the PEMECs while for typical PESCs 500–700 mM of salt are needed.46–48
ln(V2/V1). V2 is the volume available per counterion after complexation and V1 before complexation. However, the value of V1 for the droplets should be much larger than for an ionic surfactant micelle due to the much lower charge density on the droplet surface, in our case this charge density is only 5% (the droplets contain only 5 mol% of ionic surfactant). Accordingly, the volume (V1) available per ion should be about 20 times more than for a pure micelle (the volume per ion will be given by the surface area times a layer thickness, which should be about the same for both cases and be less than the Bjerrum length). V2 is the volume in solution per free ion, which is inversely proportional to the total ion concentration in solution. Therefore in order that ΔGcom becomes zero (and the driving force for complexation vanishes) if V1 is by a factor of 20 larger one may estimate that a correspondingly lower salt concentration is already effective in dissolving the complexes. This was observed experimentally in this work, as 20–50 mM of salt were enough to dissolve the PEMECs while for typical PESCs 500–700 mM of salt are needed.46–48
Conclusions
In this work, for the first time, the complex formation between oppositely charged oil-in-water (O/W) microemulsion droplets and polyelectrolytes was systematically studied. The charge on the droplets was kept relatively low by only having 5% of the surfactant head groups charged. This allows forming hybrid systems (polyelectrolyte/microemulsion complexes: PEMECs) with highly loaded surfactant carriers in a simple way. To obtain a broad overview of the behaviour of this system, the charge ratio z between the microemulsion and polyelectrolyte (sodium polyacrylate, NaPA), the size of the microemulsion droplets, the NaPA chain length and the overall concentration were varied.Phase diagrams showed that the region of stable complexes becomes smaller with increasing Mw of the NaPA and with increasing size of the microemulsion droplets, as the larger droplets can interact more effectively with the polyelectrolyte. Depending on the charge ratio z between the microemulsion and polyelectrolyte, differently sized and shaped complexes are formed as examined in detail with SANS measurements. In the microemulsion excess region and at high enough concentration the added NaPA simply interconnects microemulsion droplets and reduces their repulsive interactions. The binding to the droplets can be seen in the decreasing number of charges per droplet that was obtained from the structure factor and when diluting the sample below a critical concentration. As z increases further, the complexes quickly become unstable. The closer the charge ratio is to the charge equilibrium, the more easily the samples precipitate as there is less excess charge for stabilisation.
In the polyelectrolyte excess region the complexes are negatively charged on the outside and therefore electrostatically stabilised. The biggest complexes were found close to the phase boundary and they become smaller with increasing polyelectrolyte excess (larger z). In this region structural changes of the complexes were found. Close to the phase boundary, the complexes have a cylindrical shape and are more elongated with longer polyelectrolyte chains. At very high z-values, the NaPA excess is high enough to stabilize each droplet separately. The dependence of the complexes on z was similar for all tested droplet sizes and NaPA chain lengths. The effect was more pronounced for larger droplets, which lead to bigger complexes, as well as for longer NaPA chains. With longer NaPA chains it is possible to link more droplets, so more elongated aggregates are formed.
Upon dilution, one forms complexes of single PE chains decorated with a stoichiometric number of ME droplets, which means that the aggregation number of the effectively observed complexes increases upon dilution. What is also interesting is the high sensitivity of the complexes to salt addition. This can be explained by the rather low charge density of the ME droplets and the correspondingly reduced entropy gain by counterion release in the complexation process.
In summary it can be stated that the examined complexes of O/W microemulsion droplets with oppositely charged polyelectrolytes (PEMECs) are structurally very versatile hybrid systems, responsive to concentration and ionic strength. Many different properties in architecture and size are accessible by systematically tuning the composition. For instance the complex size increases by having longer NaPA chains and bigger ME droplets. Using a microemulsion instead of micelles makes PEMECs markedly superior to conventional PESCs as loaded colloidal carrier systems. This allows combining the high loading capacity of a microemulsion with mesoscopic structuring via polyelectrolyte complexation, thereby having the functionality of both components within a self-assembled hybrid system. Such systems are highly promising for future fundamental investigations and applications in which a high payload is to be formulated within a complex colloidal system, thereby advancing the field of colloid science into the area of controlling microemulsion properties by ionic assembly.
Experimental section
Materials
The surfactants used in the experiments were tetradecyldimethylamine oxide (TDMAO, received as a gift from Stepan company, USA, as a 25% TDMAO solution in water named Ammonyx M. The solution was freeze dried before use) and tetradecyldimethylammonium bromide (TTAB, 99%, Sigma Aldrich, used without further purification). 1-Hexanol (>98%, MERCK-Schuchardt OHG) was used as a cosurfactant and decane (>98%, Fluka Chemika) as oil to form the microemulsions.The employed polyelectrolyte is the sodium salt of polyacrylic acid (PAA), i.e., sodium polyacrylate (NaPA) which was either purchased directly or prepared by adding a stoichiometric amount of NaOH to the PAA. The molecular weights used in this work were: 5.1 kg mol−1 (DP = average degree of polymerization [−]/polymer = 54; sodium salt, used as obtained from Sigma Aldrich), 15 kg mol−1 (DP = 160; sodium salt solution from Sigma Aldrich, freeze dried before use), 60 kg mol−1 (DP = 638; sodium salt, used as obtained from Fluka Chemika) and 240 kg mol−1 (PAA; solution from Acros Organics, prepared by adding a stoichiometric amount of NaOH to the solution and freeze dried before use, which results in an average molecular weight of 315 kg mol−1 for NaPA, DP = 3330). These molecular weights correspond to the lengths of the stretched polyelectrolyte of 14, 40, 160, and 850 nm respectively. The corresponding overlap concentrations for these polymers (assuming fully stretched chains) are 32, 3.9, 0.25, and 0.007 mM (in monomer units).
All samples were prepared in Milli-Q water or D2O (>99.5% D, Eurisotop) for the SANS experiments.
Methods
Static (SLS) and dynamic (DLS) light scattering measurements were performed simultaneously on an ALV/CGS-3 instrument, with a He–Ne laser with a wavelength of λ = 632.8 nm. Pseudo-cross-correlation functions were recorded using an ALV 5000/E multiple-τ correlator at scattering angles θ ranging from 40 to 130° set with an ALV-SP 125 goniometer. The SLS curves were recorded in the same range of the magnitude of the scattering vector (q), with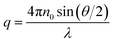 | (4) |
Small angle neutron scattering (SANS) experiments were carried out on the PAXY instrument of the Laboratoire Léon Brillouin (LLB) in Saclay. Measurements were performed in three configurations with sample-to-detector distances of 1.2, 2, and 6 m, collimation lengths of 2, 2, and 6 m and wavelengths of 4, 10, and 10 Å, respectively, to cover a q range from 0.031 to 5.05 nm−1.
Some additional SANS measurements were performed on the V4 instrument at the Helmholtz Zentrum Berlin (HZB).49 The samples were measured at wavelengths of 4.5, 4.5 and 10 Å with sample to detector distances of 1.35, 6.75 and 15.75 m and collimation length of 2, 8 and 16 m respectively.
Further measurements were performed on the D11 instrument at the Institut Laue-Langevin (ILL) in Grenoble.50,51 The samples were measured at a wavelength of 6 Å with sample to detector distances of 1.5, 8 and 34 m and collimation lengths of 8, 8 and 34 m, respectively.
Data reduction for PAXY and V4 data was done using BerSANS software.52 For the D11 data, LAMP software was used.53 The raw intensity data were corrected for the scattering of the background (solvent and sample containers) and weighted by the transmission of the sample. Additionally, the (electronic) background noise was subtracted using a cadmium sample, which absorbs all incoming neutrons. The normalization and absolute scaling were done by using a 1 mm reference sample of distilled water, as an isotropic scatterer. Finally, the 2D data were radially averaged in 1D scattered intensity.
The wavelength smearing of the PAXY and V4 data described by the corresponding resolution parameters was incorporated into the analysis using SASfit software.54 The wavelength spread (FWHM) was 10% and the detector pixels were 5 × 5 mm for both instruments. For D11 measurements the wavelength smearing was included in the x-error. More details are given in the ESI.†
SANS fits were performed in absolute units and it was assumed that all of the surfactant, cosurfactant, and oil are contained in the aggregates. Due to the low concentration and its rather homogeneous distribution in the sample, the polyelectrolyte was not considered explicitly for modelling of the data. More information on the models used to describe the SANS data is given in the ESI.†
ζ-Potential measurements were performed using a Litesizer 500 (Anton Paar) at 25 °C and a wavelength of λ = 658 nm and with a laser power of 40 mW.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Laboratoire Léon Brillouin (LLB), the Helmholz-Zentrum Berlin (HZB) and the Institut Laue-Langevin (ILL) for allocated beamtimes. We also thank Sylvain Prévost for his support during the SANS beamtime at LLB and Uwe Keiderling for his support during the beamtime at HZB. M. Simon thanks the TU Berlin for funding her PhD project.Notes and references
- I. Danielsson and B. Lindman, Colloids Surf., 1981, 3, 391–392 CrossRef CAS.
- P. G. De Gennes and C. Taupin, J. Phys. Chem., 1982, 86, 2294–2304 CrossRef CAS.
- M. Gradzielski, D. Langevin and B. Farago, Phys. Rev. E, 1996, 53, 3900–3919 CrossRef CAS.
- S. H. Chen, Annu. Rev. Phys. Chem., 1986, 37, 351–399 CrossRef CAS.
- P. P. Constantinides, Pharm. Res., 1995, 12, 1561–1571 CrossRef CAS.
- J. Lu, P. J. Liyanage, S. Solairaj, S. Adkins, G. P. Arachchilage, D. H. Kim, C. Britton, U. Weerasooriya and G. A. Pope, J. Pet. Sci. Eng., 2014, 120, 94–101 CrossRef CAS.
- J. Henle, P. Simon, A. Frenzel, S. Scholz and S. Kaskel, Chem. Mater., 2007, 19, 366–373 CrossRef CAS.
- P. Boonme, J. Cosmet. Dermatol., 2007, 6, 223–228 CrossRef PubMed.
- L. Chiappisi, I. Hoffmann and M. Gradzielski, Soft Matter, 2013, 9, 3896–3909 RSC.
- D. Langevin, Adv. Colloid Interface Sci., 2009, 147–148, 170–177 CrossRef CAS PubMed.
- M. Rinaudo, N. R. Kil'deeva and V. G. Babak, Russ. J. Gen. Chem., 2008, 78, 2239–2246 CrossRef CAS.
- L. Chiappisi, M. Simon and M. Gradzielski, ACS Appl. Mater. Interfaces, 2015, 7, 6139–6145 CrossRef CAS PubMed.
- K. Petrak, J. Bioact. Compat. Polym., 1986, 1, 202–219 CrossRef CAS.
- W. Wang and S. A. Sande, Langmuir, 2013, 29, 6697–6705 CrossRef CAS PubMed.
- E. A. Sudbeck, P. L. Dubin, M. E. Curran and J. Skelton, J. Colloid Interface Sci., 1991, 142, 512–517 CrossRef CAS.
- H. Uchiyama, S. D. Christian, E. E. Tucker and J. F. Scamehorn, AIChE J., 1994, 40, 1969–1975 CrossRef CAS.
- T. K. Bronich, A. Nehls, A. Eisenberg and A. V. Kabanov, Colloids Surf., B, 1999, 16, 243–251 CrossRef CAS.
- M. Kamimura, J. O. Kim, A. V. Kabanov, T. K. Bronich and Y. Nagasaki, J. Controlled Release, 2012, 160, 486–494 CrossRef CAS PubMed.
- H. Katumitu, S. Satoshi, S. Shin-ichiro, S. Iwao and J. C. T. Kwak, Bull. Chem. Soc. Jpn., 1995, 68, 2179–2185 CrossRef.
- M. Gradzielski, S. Prévost and T. Zemb, Adv. Colloid Interface Sci., 2017, 247, 374–396 CrossRef PubMed.
- M. Gradzielski, A. Rauscher and H. Hoffmann, J. Phys. IV, 1993, 3, C1-65–C1-79 CrossRef.
- M. Odenwald, H.-F. Eicke and W. Meier, Macromolecules, 1995, 28, 5069–5074 CrossRef CAS.
- E. Michel, M. Filiali, R. Aznar, G. Porte and J. Appell, Langmuir, 2000, 16, 8702–8711 CrossRef CAS.
- P. Malo de Molina, C. Herfurth, A. Laschewsky and M. Gradzielski, Langmuir, 2012, 28, 15994–16006 CrossRef CAS PubMed.
- M. Schwab and B. Stühn, J. Chem. Phys., 2000, 112, 6461–6471 CrossRef CAS.
- P. Malo de Molina, M. S. Appavou and M. Gradzielski, Soft Matter, 2014, 10, 5072–5084 RSC.
- A. Holmberg, P. Hansson, L. Piculell and P. Linse, J. Phys. Chem. B, 1999, 103, 10807–10815 CrossRef CAS.
- C. Quellet, H. F. Eicke, G. Xu and Y. Hauger, Macromolecules, 1990, 23, 3347–3352 CrossRef CAS.
- J. Koetz, J. Bahnemann, G. Lucas, B. Tiersch and S. Kosmella, Colloids Surf., A, 2004, 250, 423–430 CrossRef CAS.
- J. Baier, J. Koetz, S. Kosmella, B. Tiersch and H. Rehage, J. Phys. Chem. B, 2007, 111, 8612–8618 CrossRef CAS PubMed.
- C. Note, J. Koetz and S. Kosmella, J. Colloid Interface Sci., 2006, 302, 662–668 CrossRef CAS PubMed.
- H. Zhang, L. Deng, P. Sun, F. Que and J. Weiss, J. Colloid Interface Sci., 2016, 461, 88–95 CrossRef CAS PubMed.
- E. Buhler, J. Appell and G. Porte, J. Phys. Chem. B, 2006, 110, 6415–6422 CrossRef CAS PubMed.
- G. Oetter and H. Hoffmann, Colloids Surf., 1989, 38, 225–250 CrossRef CAS.
- M. Gradzielski, H. Hoffmann and D. Langevin, J. Phys. Chem., 1995, 99, 12612–12623 CrossRef CAS.
- M. Gradzielski and H. Hoffmann, Adv. Colloid Interface Sci., 1992, 42, 149–173 CrossRef CAS.
- M. Gradzielski and H. Hoffmann, J. Phys. Chem., 1994, 98, 2613–2623 CrossRef CAS.
- B. Farago and M. Gradzielski, J. Chem. Phys., 2001, 114, 10105–10122 CrossRef CAS.
- M. Gradzielski, Curr. Opin. Colloid Interface Sci., 2004, 9, 256–263 CrossRef CAS.
- A. Ortega and J. García de la Torre, J. Chem. Phys., 2003, 119, 9914–9919 CrossRef CAS.
- J. S. Pedersen, D. Posselt and K. Mortensen, J. Appl. Crystallogr., 1990, 23, 321–333 CrossRef.
- R. J. Baxter, J. Chem. Phys., 1968, 49, 2770–2774 CrossRef CAS.
- M. J. Grimson, J. Chem. Soc., Faraday Trans. 2, 1983, 79, 817–832 RSC.
- L. Baba-Ahmed, M. Benmouna and M. J. Grimson, Phys. Chem. Liq., 1987, 16, 235–238 CrossRef CAS.
- L. Chiappisi, S. Prévost and M. Gradzielski, J. Appl. Crystallogr., 2014, 47, 827–834 CrossRef CAS.
- M. Skepo and P. Linse, Phys. Rev. E, 2002, 66, 051807 CrossRef PubMed.
- M. Burkhardt, M. Ruppel, S. Tea, M. Drechsler, R. Schweins, D. V. Pergushov, M. Gradzielski, A. B. Zezin and A. H. E. Müller, Langmuir, 2008, 24, 1769–1777 CrossRef CAS PubMed.
- K. Pojjak, E. Bertalanits and R. Meszaros, Langmuir, 2011, 27, 9139–9147 CrossRef CAS PubMed.
- U. Keiderling and A. Wiedenmann, Phys. B, 1995, 213&214, 895–897 Search PubMed.
- K. Lieutenant, P. Lindner and R. Gahler, J. Appl. Crystallogr., 2007, 40, 1056–1063 CrossRef CAS.
- L. Chiappisi, M. Gradzielski, I. Hoffmann, R. Schweins, M. Simon and H. Yalcinkaya, Interconnecting charged microemulsion droplets via oppositely charged polyelectrolyte – effect of polyelectrolyte structure, Institut Laue-Langevin (ILL), 2016, DOI:10.5291/ILL-DATA.9-12-421.
- U. Keiderling, Appl. Phys. A, 2002, 74, 1455–1457 CrossRef.
- D. Richard, M. Ferrand and G. J. Kearley, J. Neutron Res., 1996, 4, 33–39 CrossRef.
- I. Breßler, J. Kohlbrecher and A. Thünemann, J. Appl. Crystallogr., 2015, 48, 1587–1598 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc04013c |
| This journal is © The Royal Society of Chemistry 2019 |