Crystallographic characterization of Lu₂C_2n (2n = 76–90): cluster selection by cage size

Abstract

The successful isolation and unambiguous crystallographic assignment of a series of lutetium-containing endohedral metallofullerenes (EMFs), Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90), reveal an unrecognized decisive effect of the cage size on the configuration of the encapsulated clusters. The molecular structures of these compounds are unambiguously assigned as Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈. Specifically, when the cage is relatively small, Lu₂@C_2n (2n = 76–86) are all dimetallofullerenes (di-EMFs) and a Lu–Lu single bond could be formed between the two lutetium ions inside the cages. However, when the cage expands further, the valence electrons forming the possible Lu–Lu bond donate to a readily inserted C₂-unit, resulting in the formation of carbide EMFs, Lu₂C₂@C_2n (2n = 86, 88). Consistently, our theoretical results reveal that all these EMFs are thermodynamically favorable isomers. Thus the comprehensive characterization of the series of Lu₂C_76–90 isomers and the overall agreement between the experimental and theoretical results reveal for the first time that the exact configuration of the internal metallic cluster is determined by the cage size, taking a solid step towards the controlled synthesis of novel hybrid molecules which may have potential applications as building blocks of single molecule devices.

---

Introduction

Putting metal atoms or metallic clusters into fullerenes has generated a new class of novel hybrid molecules, defined as endohedral metallofullerenes (EMFs), possessing novel structures and fascinating properties which are different from those of empty fullerenes.^1–4 During the last three decades, EMFs containing different metallic clusters, including metal nitride (M₃N),^5,6 metal carbide (M₂C₂/M₃C₂/M₄C₂),^7–9 metal sulfide (M₂S),^10,11 metal oxide (M₂O/M₄O₂/M₄O₃)^12–14 and metal cyanide (M₃CN/MCN)^15–17 clusters, have been structurally characterized in addition to the conventional EMFs containing only metal atoms (M/M₂/M₃).^18–20

EMFs exhibit a variety of electronic and physicochemical properties which markedly depend on the nature of the encapsulated species.^21,22 One of the most brilliant features of EMFs is the charge transfer from the internal metallic species to the surrounding cage which is revealed to play an important role in determining the stability of the formed molecules.^2,3,23 For example, the C_2v(9)-C₈₂ cage is the most stable one after accepting three electrons, and the corresponding M@C_2v(9)-C₈₂ isomers have the highest production yield among all reported mono-EMFs for a variety of lanthanide elements regardless of the metal type.^24,25 As for cluster EMFs, theoretical and experimental results have suggested that the hexa-anionic I_h(7)-C₈₀ cage is the most suitable candidate for encapsulating an M₃N (M = Sc, Y, Gd, Lu, etc.) cluster.^26,27

In addition to the electronic interactions, the geometry of the cluster, especially the cluster size, also has a significant effect on the cage structure and symmetry. For instance, Dunsch and co-workers proposed theoretically that the small Sc₃N cluster presents a planar geometry inside the D_3h(5)-C₇₈ cage, whereas the larger M₃N (M = Y, Lu, Dy, Tm) clusters prefer the C₂(22 010)-C₇₈ cage that violates the isolated pentagon rule (IPR) to keep their planarity.²⁸ And a subsequent experimental report confirmed that the large Gd₃N unit prefers to adopt the planar geometry in the C₂(22 010)-C₇₈ cage.²⁹ Another example demonstrated that M₃N clusters containing metals with a relatively small radius (e.g. Sc, Y and Gd) are preferentially encapsulated inside a C₈₀ cage. In comparison, larger metals like La and Nd prefer to template C₈₈ or C₉₆.^30,31 Accordingly, it seems that the size, shape, and charge of the encapsulated cluster play important roles in the selection of the complementary carbon cages. However, there is still a lack of experimental evidence to confirm whether the cage size has any influence on the cluster configuration or not. For example, Dunsch et al. proposed that the number of Sc atoms in the internal Gd_xSc_3−xN clusters decreases along with the cage expansion (C₇₈ to C₈₈), as demonstrated by absorption and vibrational spectroscopy, electrochemical studies and density functional theory (DFT) computations.³² Popov et al. reported a systematic computational study on the analysis of the distortions in three classes of EMFs with nitride, sulfide, and carbide clusters, indicating that the preferable shapes of the internal clusters can be altered by the cage size.³³ Moreover, an interesting report from Dorn and co-workers theoretically revealed that the fullerene cage may compress the internal Y₂C₂ cluster to adopt different shapes, from butterfly-like configurations in small cages to nearly linear structures in large cages.³⁴ Nonetheless, there are no crystallographic results showing that the composition of the metallic species is controllable by the cage size.

We herein confirm for the first time that the exact form of the internal metallic cluster is determined by the cage size based on the concrete single-crystal X-ray crystallographic results of ten lutetium-containing endohedrals, namely, Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈. It is revealed that the Lu–Lu distance increases along with the cage expansion as a direct result of the preferential coordination of the Lu atoms with the cage carbon atoms. Accordingly, the small cages can only accommodate a Lu₂ cluster because of the limited inner space, accompanied by the possible formation of a Lu–Lu bond. However, when the cage expands further, a C₂-unit is inserted between the two Lu atoms, which takes over partially the charges from the metals and coordinates with them, making the whole system more stable. The systematic characterization of Lu₂C_76–90 isomers and the overall agreement between experimental and theoretical studies present concrete evidence for the decisive effect of the cage size on the composition of the encapsulated clusters of EMFs.

Results and discussion

Lu-EMFs were synthesized by a direct-current arc discharge method and pure isomers of Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90) were obtained by multistage HPLC separation (see ESI, Fig. S1–S4 for details†). The analytical HPLC chromatograms (Fig. S5†) and the laser-desorption/ionization time-of-flight (LDI-TOF) mass spectra (Fig. S6†) of Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers confirm their high purity. Fig. S7 and Table S1† show the visible-near-infrared (Vis-NIR) absorption spectra and the detailed characteristic bands of Lu₂C_76–90 isomers dissolved in carbon disulfide (CS₂), respectively. The absorption spectra of Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆, Lu₂@C₁(26)-C₈₈ and Lu₂C₂@C_s(32)-C₈₈ are quite different from those of the corresponding EMFs possessing C₈₄, C₈₆ and C₈₈ cages reported before,^15,35–43 indicating their different structures.

Finally, the molecular structures of Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers were unambiguously determined by single-crystal X-ray diffraction (XRD) crystallography to be Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈, respectively, taking advantage of the high-quality of the co-crystals of Lu₂C_2n/Ni^II(OEP) (OEP = 2,3,7,8,12,13,17,18-octaethylporphyrin dianion). Although Lu₂@T_d(2)-C₇₆ was first isolated and confirmed to have a T_d-symmetric cage according to ¹³C NMR spectroscopic studies in combination with scanning tunneling microscopy results,⁴⁴ and D_3h(5)-C₇₈, C_2v(5)-C₈₀, C_2v(9)-C₈₆ and D₂(35)-C₈₈ cages were obtained and crystallographically characterized for EMFs possessing the same cage symmetry, such as Sc₂O@D_3h(5)-C₇₈,⁴⁵ Sc₂O@C_2v(5)-C₈₀,¹² Sc₂C₂@C_2v(9)-C₈₆ (ref. 36) and Sm₂@D₂(35)-C₈₈,⁴⁰ it is noteworthy that the cages of C_2v(7)-C₈₄, C_s(8)-C₈₆, C_s(15)-C₈₆, C₁(26)-C₈₈ and C_s(32)-C₈₈ have never been experimentally reported before in spite of the fact that Sc₂O@C_2v(7)-C₈₄ was theoretically predicted without further experimental evidence.⁴⁶

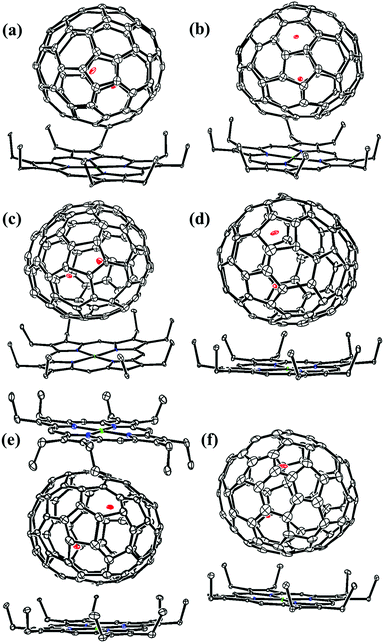
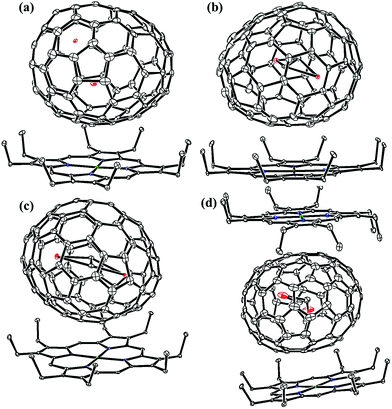
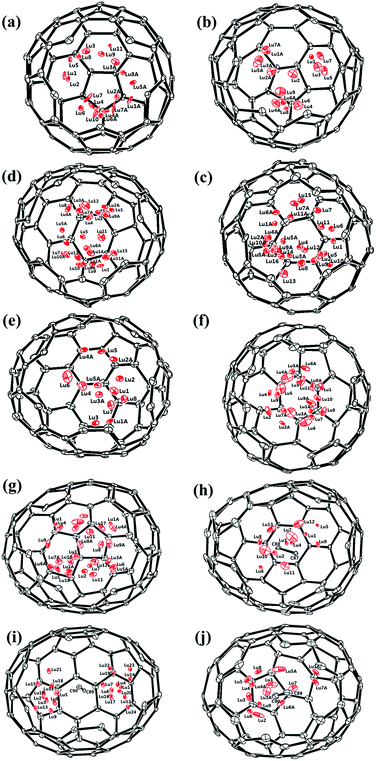
Fig. 1 and 2 portray the molecular structures of Lu₂@C_2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers co-crystallized with the Ni^II(OEP) molecules. For Lu₂@C_s(8)-C₈₆ and Lu₂C₂@D₂(35)-C₈₈, each fullerene cage is surrounded by two Ni^II(OEP) molecules in a sandwich-like arrangement, and the ethyl groups of one of the Ni^II(OEP) molecules are arranged in such a way that they can embrace the fullerene cage from both sides whereas the other endohedrals adopt the normal one-EMF-one-Ni(OEP) fashion. The shortest Ni-cage distances in all the systems fall in the range of 2.631 Å–3.050 Å, suggesting substantial π–π interactions between the fullerene cage and the Ni^II(OEP) molecule(s).^47–49 Inside these cages, the Lu atoms show severe disorder in all EMFs (Fig. 3, Tables S2 and S3, ESI†), indicating a motional behavior of the two Lu ions which may account for the strong Lu-cage interactions by fulfilling the coordination requirements of the Lu ions as much as possible. In detail, 19, 16 and 27 Lu positions are found for the two Lu atoms inside the Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈ and Lu₂@C_2v(5)-C₈₀ cages, respectively, whereas 26, 13 and 20 Lu sites are positioned for the two Lu atoms in the respective Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆ cage. In Lu₂@C₁(26)-C₈₈, 27 Lu sites are positioned for the two Lu atoms. Moreover, 13, 24 and 16 Lu sites are found for the two Lu atoms in Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈, respectively.

Fig. 1 ORTEP drawings of (a) Lu₂@T_d(2)-C₇₆·Ni^II(OEP), (b) Lu₂@D_3h(5)-C₇₈·Ni^II(OEP), (c) Lu₂@C_2v(5)-C₈₀·Ni^II(OEP), (d) Lu₂@C_2v(7)-C₈₄·Ni^II(OEP), (e) Lu₂@C_s(8)-C₈₆·1.5Ni^II(OEP) and (f) Lu₂@C_s(15)-C₈₆·Ni^II(OEP). Thermal contours are drawn at the 10% probability level. Only one fullerene cage and the predominant metal sites are shown, whereas minor metal sites, solvent molecules and H atoms are omitted for clarity.

Fig. 2 ORTEP drawings of (a) Lu₂@C₁(26)-C₈₈·Ni^II(OEP), (b) Lu₂C₂@C_2v(9)-C₈₆·Ni^II(OEP), (c) Lu₂C₂@C_s(32)-C₈₈·Ni^II(OEP) and (d) Lu₂C₂@D₂(35)-C₈₈·Ni^II(OEP). Thermal contours are drawn at the 10% probability level. Only one fullerene cage and the predominant metal sites are shown, whereas minor metal sites, solvent molecules and H atoms are omitted for clarity.

Fig. 3 Perspective drawings showing the disordered lutetium sites. (a) 19 in Lu₂@T_d(2)-C₇₆, (b) 16 in Lu₂@D_3h(5)-C₇₈, (c) 27 in Lu₂@C_2v(5)-C₈₀, (d) 26 in Lu₂@C_2v(7)-C₈₄, (e) 13 in Lu₂@C_s(8)-C₈₆, (f) 20 in Lu₂@C_s(15)-C₈₆, (g) 27 in Lu₂@C₁(26)-C₈₈, (h) 13 in Lu₂C₂@C_2v(9)-C₈₆, (i) 24 in Lu₂C₂@C_s(32)-C₈₈ and (j) 16 in Lu₂C₂@D₂(35)-C₈₈.

Furthermore, the representative structural data of Lu₂@C_76–90 isomers, such as the cage length/width ratio (L/W ratio), major Lu–Lu distance, Lu–Lu distance range and Lu-cage distance, are summarized in Table 1. The Lu–Lu distances between any two opposite Lu sites with comparable occupancy values are in the range of 3.31–3.53 Å, 3.27–3.67 Å, 3.22–3.73 Å, 3.33–3.84 Å, 3.49–3.73 Å, 3.34–3.84 Å and 3.57–3.62 Å for Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆ and Lu₂@C₁(26)-C₈₈, respectively. In contrast, for Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈, which possess relatively large cages, the respective Lu–Lu distances are much longer and fall in 3.94–4.43 Å, 4.45–4.66 Å and 4.14–4.41 Å, respectively. Therefore, in these cages, a C₂-unit is inserted between the two Lu atoms, which fulfills the coordination requirement of the Lu ions by taking over partially the charges from the metal ions. The shortest Lu-cage distances are consistently 2.108 Å, 2.263 Å, 2.065 Å, 2.106 Å, 2.086 Å, 2.103 Å, 2.291 Å, 2.269 Å, 2.319 Å and 2.166 Å for Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈, respectively, which are all shorter than the calculated values for Lu₂@T_d-C₇₆ (2.37–2.42 Å),^50,51 suggesting strong Lu-cage interactions.

Table 1 Cage size, length/width (L/W) ratio, major Lu-Lu distance, calculated Lu-Lu distance, Lu-Lu distance range and the shortest Lu-cage distance of Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_s(6)-C₈₂,³⁹ Lu₂@C_3v(8)-C₈₂,³⁹ Lu₂@D_2d(23)-C₈₄,³⁹ Lu₂@C_2v(7)-C₈₄, Lu₂@C_2v(9)-C₈₆,³⁹ Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C_86, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈

Compound	Cage length (Å)	Cage width (Å)	L/W ratio	Major Lu–Lu distance (Å)^a	Calculated Lu–Lu distance (Å)	Lu–Lu distance range (Å)^b	Shortest Lu-cage distance^c
a Lu–Lu distance between the major Lu sites. b Lu–Lu distance between any two opposite Lu sites with comparable occupancy. c The shortest Lu-cage distance between the major Lu sites and the cage carbon atoms.
Lu2@Td(2)-C76	7.126	7.110	1.00	3.50	3.44	3.14–3.50	2.054
Lu2@D3h(5)-C78	8.338	7.548	1.10	3.27	3.41	3.27–3.67	2.263
Lu2@C2v(5)-C80	8.245	7.896	1.04	3.60	3.72	3.22–3.73	2.065
Lu2@C3v(8)-C82	8.400	8.315	1.01	3.21	3.47	3.21–3.57	2.299
Lu2@Cs(6)-C82	8.413	7.739	1.08	3.59	3.60	3.35–3.67	2.243
Lu2@D2d(23)-C84	8.212	7.934	1.04	3.75	4.00	3.24–3.75	2.135
Lu2@C2v(7)-C84	8.502	8.199	1.04	3.56	3.46	3.33–3.84	2.106
Lu2@C2v(9)-C86	8.991	7.553	1.09	3.43	3.70	3.43–3.72	2.293
Lu2@Cs(8)-C86	8.455	7.296	1.16	3.49	3.53	3.49–3.73	2.086
Lu2@Cs(15)-C86	8.611	7.454	1.16	3.34	3.67	3.34–3.84	2.103
Lu2@C1(26)-C88	9.018	7.501	1.20	3.57	3.65	3.57–3.62	2.291
Lu2C2@C2v(9)-C86	8.986	7.502	1.18	4.41	4.37	3.94–4.43	2.269
Lu2C2@Cs(32)-C88	8.883	7.124	1.25	4.66	4.64	4.45–4.66	2.319
Lu2C2@D2(35)-C88	9.104	7.184	1.27	4.41	4.64	4.14–4.41	2.166

---

It is interesting to find that the small cages (C_76–86) prefer to accommodate a Lu₂ dimer to form di-EMFs whereas carbide cluster metallofullerenes (CCMFs) are formed for Lu₂C₈₈ or Lu₂C₉₀, which possess relatively large cages. We speculate that this phenomenon is caused by the different cage structure parameters, particularly the cage length and width. As clearly shown in Table 1, the cage length and L/W ratio increase in accordance with cage expansion, resulting in a substantial increase of the Lu–Lu distance. In particular, C₈₆-based lutetium-containing EMFs have two different compositions: C_s(8)-C₈₆ (L/W ratio = 1.16) and C_s(15)-C₈₆ (L/W ratio = 1.16) possess relatively round cages and they choose to encapsulate a Lu₂ dimer instead of a Lu₂C₂ cluster because of the limited inner space, whereas the elongated C_2v(9)-C₈₆ (L/W ratio = 1.20) causes the increased Lu–Lu distance because of strong Lu-cage interactions and easy C₂ insertion, resulting in the formation of the CCMF Lu₂C₂@C_2v(9)-C₈₆. As a matter of fact, the cages smaller than C₈₆ can only accommodate a Lu₂ dimer and the larger ones always prefer the Lu₂C₂ composition to make the resultant EMFs more stable.^49,52

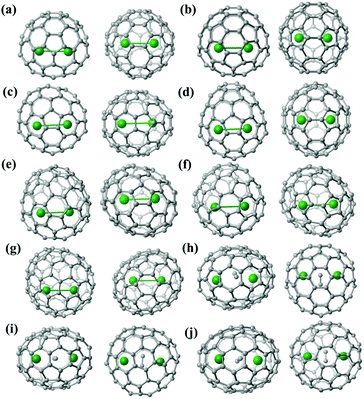
Fig. S8† shows the location of the major Lu₂/Lu₂C₂ cluster relative to the cage orientation in the ten EMFs under study. In Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C₁(26)-C₈₈ and Lu₂C₂@C_s(32)-C₈₈, one major Lu site is situated over a [5,6]-bond, whereas the other one is close to a hexagonal ring. In the other five endohedrals, each prominent Lu position is located over a [5,6]-bond. Moreover, the configurations of the Lu₂C₂ clusters inside the carbon cages are all shaped like a butterfly with two tightly bonded carbon atoms in the respective cage centers. The Lu–C–C–Lu dihedral angles are 132.13°, 145.46° and 142.83° in the C_2v(9)-C₈₆, C_s(32)-C₈₈ and D₂(35)-C₈₈ cages, respectively. Furthermore, the C–C bond lengths of the C₂ unit in Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈ are 1.11 Å, 1.20 Å and 1.00 Å, respectively, which represent typical C–C triple bonds (Fig. S8†).

The redox behaviors of the EMFs under study are characterized by cyclic voltammetry (CV) except for Lu₂@D_3h(5)-C₇₈ and Lu₂@C_2v(5)-C₈₀ due to their extremely low yields (Fig. S9 and S10†). In general, these compounds display one or two oxidation steps together with four reduction steps within the solvent window. It is noteworthy that the electrochemical gaps of Lu₂C_2n (2n = 76, 82, 84, 86, 88, 90) isomers are relatively large (1.19 eV–1.39 eV), indicating their high stability. Moreover, it appears that the CCMFs show better reversibility of the redox processes than the di-EMFs. For instance, several irreversible processes, either reduction or oxidation, are found for Lu₂@T_d(2)-C₇₆, Lu₂@C_2v(7)-C_84, Lu₂@C_s(8)-C₈₆ and Lu₂@C₁(26)-C₈₈, but all of the two oxidation and the four reduction processes are reversible for Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈. Table S6† lists the electrochemical potentials of the EMFs under study. In particular, the first and the second reduction potentials are mutually very close, as are the third and the fourth, but the gap between the third and the second is generally large. These results strongly corroborate their closed-shell electronic configuration with nondegenerate low-lying LUMO and accessible LUMO+1 orbitals. Consequently, such electrochemical behaviors can be regarded as characteristic properties of Lu₂C_2n-type EMFs.⁵³ Accordingly, there are no EPR signals for all the EMFs reported here because of their closed-shell electronic configuration.

The unobserved decisive effect of the cage size on the configuration of the encapsulated clusters stimulates our interest to find a reasonable explanation. DFT calculations at the M06-2X/6-31G*∼SDD level were thus conducted to rationalize the formation of these Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers. Fig. 4 depicts their optimized geometries, which agree well with their respective X-ray structures. The lutetium element has a [Xe]4f¹⁴6s²5d¹ electronic configuration and may keep its 6s electrons due to the relativistic contraction and large stabilization of the 6s atomic orbital. For Lu₂@C_76–88 isomers, the calculated Lu–Lu distances range from 3.41 Å to 3.72 Å, and are all comparable to those observed from our crystallographic data (Tables 1 and S7†). Actually, our results are perfectly consistent with the theoretical predictions reported by Popov and co-workers, who proposed that lutetium atoms are more inclined to adopt the +2 state, and accordingly, Lu–Lu bonding could be favorable in lutetium-containing EMFs.^54,55 In comparison, the calculated Lu–Lu distances in Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈ are as long as 4.37 Å, 4.64 Å and 4.64 Å, respectively, indicating the insertion of a C₂-unit.

Fig. 4 Optimized structures of (a) Lu₂@T_d(2)-C₇₆, (b) Lu₂@D_3h(5)-C₇₈, (c) Lu₂@C_2v(5)-C₈₀, (d) Lu₂@C_2v(7)-C₈₄, (e) Lu₂@C_s(8)-C₈₆, (f) Lu₂@C_s(15)-C_86, (g) Lu₂@C₁(26)-C₈₈, (h) Lu₂C₂@C_2v(9)-C₈₆, (i) Lu₂C₂@C_s(32)-C₈₈ and (j) Lu₂C₂@D₂(35)-C₈₈ (top and side views).

Natural bond orbital (NBO) analysis demonstrates that the two Lu atoms in Lu₂@C_76–88 may form a Lu–Lu single bond with an electron occupancy of 1.97–1.98 e, which is supported by the calculated Wiberg bond orders (WBOs) ranging from 0.94 to 0.98 (Table S7†). Moreover, consistent with the low-lying (6s)σ_g² molecular orbital of the free Lu₂ dimer, the possible Lu–Lu bonds have an spd-hybrid character with the Lu-6s orbitals contributing the most to the metal bonding MOs, and each Lu atom donates one 5d electron and one 6s electron to the cage with the 4f electrons remaining intact. However, for Lu₂C₂@C_86–88, the Lu–Lu single bond could not be formed in the corresponding cage because the valence electrons are partially donated to the C₂-unit, as indicated by the calculated small WBO values ranging from 0.15 to 0.17 (Table S7†), resulting in the formation of the Lu₂C₂ units.

Furthermore, we optimized the structures of different Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers in either the Lu₂@C_2n or Lu₂C₂@C_2n–2 form based on a series of low-energy C_74–90⁴⁻ cages to differentiate their relative stability. Fig. S11–S17† and Table 2 show the optimized structures of the low-energy Lu₂C_76–90 isomers and relative energies as well as HOMO–LUMO gap energies. As clearly shown in Table 2, both Lu₂@T_d(2)-C₇₆ and Lu₂@D_3h(5)-C₇₈ are the lowest-energy ones among all the considered isomers. Moreover, Lu₂@I_h(7)-C₈₀ is 6.6 kcal mol⁻¹ lower in energy than Lu₂@C_2v(5)-C₈₀ when it has a triplet ground state. Therefore, it is highly possible that Lu₂@I_h(7)-C₈₀ is generated together with Lu₂@C_2v(5)-C₈₀ during the arc-discharge process, but it may form insoluble products in the raw soot due to its radical character and thus is absent in the usual solvent extract (Table 2).^56–58 As for Lu₂C₈₂, a previous report has revealed that Lu₂@C_s(6)-C₈₂ and Lu₂@C_3v(8)-C₈₂ are both lower in energy than any of the Lu₂C₂@C₈₀ isomers (Table 2).³⁹ Accordingly, for a composition of Lu₂C_76–82, Lu₂@C_2n is always more stable than the corresponding carbide form Lu₂C₂@C_2n–2, indicating that the formation of di-EMFs is energetically favorable within this cage size range.

Table 2 Optimized structures of low-lying Lu₂C_76–90 isomers with relative energies (kcal mol⁻¹) and HOMO–LUMO gap energies (eV, in parentheses). The isomers labeled in bold are experimentally observed

Compounds	Relative energies of the selected low-lying isomers
Lu2C76	Lu2@Td(2)-C76, 0.0 (2.95)	Lu2C2@C2(13333)-C74, 9.9 (2.98)	Lu2C2@C1(13334)-C74, 17.3 (3.08)	Lu2@C2v(19138)-C76, 19.5 (1.75)	Lu2C2@C1(13384)-C74, 22.7 (3.03)
Lu2C78	Lu2@D3d(5)-C78, 0.0 (2.41)	Lu2@C2v(3)-C78, 5.2 (2.96)	Lu2@Cs(24099)-C78, 12.7 (2.74)	Lu2@C1(22595)-C78, 13.1 (2.89)	Lu2C2@Td(2)-C76, 16.4 (2.81)
Lu2C80	Lu2@Ih(7)-C80, 0.0 (3.31/2.03)	Lu2@C2v(5)-C80, 6.6 (2.88)	Lu2@D5h(6)-C80, 8.0 (2.26)	Lu2@C1(31 891)-C80, 26.4 (2.51)	Lu2C2@D3d(5)-C78, 30.0 (2.60)
Lu2C82	Lu2@C3v(8)-C82,^39 0.0 (3.39)	Lu2@Cs(6)-C82,^39 0.5 (3.03)	Lu2C2@C2v(5)-C80, 19.7 (2.94)	Lu2C2@D5h(6)-C80, 22.7 (2.37)	Lu2C2@Ih(7)-C80, 31.5 (2.16)
Lu2C84	Lu2@D2d(23)-C84,^39 0.0 (2.99)	Lu2C2@C3v(8)-C82, 6.2 (3.42)	Lu2@C2v(7)-C84, 6.4 (3.19)	Lu2C2@Cs(6)-C82, 6.6 (3.08)	Lu2C2@C2v(9)-C82, 8.7 (2.62)
Lu2C86	Lu2@C2v(9)-C86,^39 0.0 (3.10)	Lu2C2@D2d(23)-C84, 8.9 (3.02)	Lu2@Cs(8)-C86, 9.9 (3.37)	Lu2C2@C1(51383)-C84, 13.2 (3.04)	Lu2@Cs(15)-C86, 15.6 (2.77)
Lu2C88	Lu2C2@C2v(9)-C86, 0.0 (3.02)	Lu2@C1(26)-C88, 2.9 (3.06)	Lu2C2@C1(13)-C86, 13.5 (2.91)	Lu2@C1(30)-C88, 14.4 (2.64)	Lu2C2@Cs(15)-C86, 14.4 (2.62)
Lu2C90	Lu2C2@D2(35)-C88, 0.0 (2.86)	Lu2C2@Cs(32)-C88, 1.5 (2.85)	Lu2@D5h(41)-C90, 5.6 (2.73)	Lu2@C1(43)-C90, 6.5 (2.60)	Lu2@C1(21)-C90, 8.5 (3.00)

---

However, Lu₂C_84–86, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, and Lu₂@C_s(15)-C₈₆ and their respective Lu₂C₂@C_2n–2 isomers are mixed in energy, with the recently reported Lu₂@D_2d(23)-C₈₄ and Lu₂@C_2v(9)-C₈₆ being the most stable ones (Table 2).³⁹ These results imply that the formation of CCMFs is gradually favored with increasing cage size. Indeed, as shown in Fig. S16 and S17,† Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@D₂(35)-C₈₈ and Lu₂C₂@C_s(32)-C₈₈ are the lowest-energy Lu₂C₈₈ and Lu₂C₉₀ isomers, respectively. Therefore, as the cage size increases to C₈₈ and C₉₀, the CCMFs are energetically more stable than the corresponding di-EMFs.

Overall, our experimental and theoretical results have unambiguously confirmed that the exact composition of the internal cluster is changed from Lu₂ to Lu₂C₂ along with the cage expansion, which is a synergetic result of C2 insertion and the strong Lu-cage coordination of the Lu ions with the cage carbon atoms. It appears that the C₈₆ cage is a threshold for Lu₂C_2n-type EMFs transforming from di-EMFs to CCMFs. If the transformation is a common phenomenon in other systems, it is expected that larger metals such as erbium, gallium and lanthanum may prefer a larger cage for the transformation from M₂ to M₂C₂ (M = Er, Gd, La). Indeed, Balch. et al. have separated two Gd₂C₉₄ isomers, one of which is structurally confirmed to be a CCMF, namely Gd₂C₂@D₃(85)-C₉₂, while the other is theoretically proposed to be a conventional endohedral, Gd₂@C₂(121)-C₉₄.⁵⁹ A more recent study reported the isolation and crystallographic elucidation of an Er-based CCMF, i.e. Er₂C₂@D₃(85)-C₉₂, confirming again that larger cages tend to accommodate the carbide cluster.⁶⁰ Moreover, for the even larger La³⁺ ions, although the structures of some di-EMFs, namely La₂@D₂(10611)-C₇₂,⁶¹ La₂@C_s(17490)-C₇₆,⁶² La₂@D_3h(5)-C₇₈,⁶³ La₂@I_h(7)-C₈₀,⁶⁴ and La₂@D₅(450)-C₁₀₀ ⁶⁵ have been confirmed by single crystal XRD crystallography, the La³⁺ ions are also more inclined to form carbide structures with some giant cages such as C_90–104, which are rationalized by considering the synergistic effect of inserting a C₂-unit on the stabilization of CCMFs both electronically and geometrically.^47–49

Conclusions

In summary, a series of lutetium-containing EMFs, namely Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_2v(9)-C₈₆, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈, have been isolated and structurally determined. Based on our experimental and theoretical results, a clear correlation between the cage size and the configuration of the internal metallic cluster is revealed. Moreover, we also propose that the C₈₆ cage is the threshold for Lu₂C_2n-type EMFs transforming from di-EMFs to CCMFs. Specifically, the relatively small cages, i.e. C_76–86, choose to encapsulate a Lu₂ cluster with the possible formation of a Lu–Lu bond because of the limited inner space. However, further cage expansion elongates the Lu–Lu distance due to the strong Lu-cage interactions and the insertion of a C₂-unit, resulting in the formation of CCMFs, Lu₂C₂@C_2n (2n = 86, 88). Accordingly, we confirm for the first time that the preferential formation of the Lu₂@C_2n/Lu₂C₂@C_2n–2 composition is determined by the cage size, presenting a practical strategy for the templated synthesis of EMFs possessing desired internal clusters, which may facilitate the application of EMFs as building blocks for molecular devices/machines.

Experimental

Synthesis and isolation of Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90)

Soot containing Lu-EMFs was synthesized by a direct-current arc discharge method and was extracted using carbon disulfide (CS₂). After the removal of CS₂, the residue was dissolved in toluene and the solution was subjected to a multi-stage high-performance liquid chromatography (HPLC) separation. The experimental details are given in the ESI.†

General characterization

High-performance liquid chromatography (HPLC) was conducted on an LC-9130 NEXT machine (Japan Analytical Industry Co., Ltd.) with toluene as the mobile phase. Matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectrometry was performed on a BIFLEX III spectrometer (Bruker Daltonics Inc., Germany). Vis-NIR spectra were obtained on a PE Lambda 750S spectrophotometer in CS₂. Cyclic voltammograms (CV) were measured in 1,2-dichlorobenzene with 0.05 M n-Bu₄NPF₆ as the supporting electrolyte at a Pt working electrode with a CHI660E workstation.

Single crystal XRD measurements of Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90)

The crystallographic data are shown in Tables S4 and S5.† Crystalline blocks of Lu₂C_2n (2n = 76, 78, 80, 84, 86, 88, 90) isomers were obtained by layering a benzene solution of Ni^II(OEP) over a CS₂ solution of the corresponding metallofullerenes at room temperature. Over a 20-day period, the two solutions diffused together, and black crystals formed. Single-crystal XRD measurement of Lu₂@C_s(8)-C₈₆, Lu₂@C_s(15)-C₈₆ and Lu₂C₂@C_2v(9)-C₈₆ was performed at 173 K on a Bruker D8 QUEST machine equipped with a CMOS camera (Bruker AXS Inc., Germany). Crystallographic characterization of Lu₂@T_d(2)-C₇₆, Lu₂@D_3h(5)-C₇₈, Lu₂@C_2v(5)-C₈₀, Lu₂@C_2v(7)-C₈₄, Lu₂@C₁(26)-C₈₈, Lu₂C₂@C_s(32)-C₈₈ and Lu₂C₂@D₂(35)-C₈₈ was performed at 100 K at BL17B station of the Shanghai Synchrotron Radiation Facility. The multi-scan method was used for absorption corrections. The structures were solved by the direct method and were refined with SHELXL-2014/7.⁶⁶ CCDC-1582214 (Lu₂@T_d(2)-C₇₆), CCDC-1582215 (Lu₂@D_3h(5)-C₇₈), CCDC-1582216 (Lu₂@C_2v(5)-C₈₀), CCDC-1582217 (Lu₂@C_2v(7)-C₈₄), CCDC-1582218 (Lu₂@C_s(8)-C₈₆), CCDC-1582219 (Lu₂@C_s(15)-C₈₆), CCDC-1836827 (Lu₂@C₁(26)-C₈₈), CCDC-1836828 (Lu₂C₂@C_2v(9)-C₈₆), CCDC-1836829 (Lu₂C₂@C_s(32)-C₈₈) and CCDC-1836830 (Lu₂C₂@D₂(35)-C₈₈) contain the supplementary crystallographic data for this paper.†

Computational details

Density functional theory calculations were carried out by using the M06-2X⁶⁷ functional in conjunction with the 6-31G* basis set for C^68,69 and SDD basis set and corresponding effective core potential for Lu⁷⁰ (denoted as 6-31G*∼SDD), as implemented in the Gaussian 09 software package.⁷¹

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The financial support from the NSFC (No. 51472095, 51672093, 51602112, 51602097 and 21103224) is gratefully acknowledged. We thank the staff from BL17B beamline of the National Facility for Protein Science Shanghai (NFPS) at the Shanghai Synchrotron Radiation Facility for assistance during data collection. Also, we are grateful to the Analytical and Testing Center in Huazhong University of Science and Technology for all related measurements.

Notes and references

1. L. Bao, P. Peng and X. Lu, Acc. Chem. Res., 2018, 51, 810–815.
2. A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989–6113.
3. X. Lu, L. Feng, T. Akasaka and S. Nagase, Chem. Soc. Rev., 2012, 41, 7723–7760.
4. X. Lu, T. Akasaka and S. Nagase, Acc. Chem. Res., 2013, 46, 1627–1635.
5. T. Cai, L. Xu, M. R. Anderson, Z. Ge, T. Zuo, X. Wang, M. M. Olmstead, A. L. Balch, H. W. Gibson and H. C. Dorn, J. Am. Chem. Soc., 2006, 128, 8581–8589.
6. S. Stevenson, H. M. Lee, M. M. Olmstead, C. Kozikowski, P. Stevenson and A. L. Balch, Chem.–Eur. J., 2002, 8, 4528–4535.
7. H. Kurihara, X. Lu, Y. Iiduka, N. Mizorogi, Z. Slanina, T. Tsuchiya, T. Akasaka and S. Nagase, J. Am. Chem. Soc., 2011, 133, 2382–2385.
8. H. Fang, H. Cong, M. Suzuki, L. Bao, B. Yu, Y. Xie, N. Mizorogi, M. M. Olmstead, A. L. Balch, S. Nagase, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2014, 136, 10534–10540.
9. T.-S. Wang, N. Chen, J.-F. Xiang, B. Li, J.-Y. Wu, W. Xu, L. Jiang, K. Tan, C.-Y. Shu, X. Lu and C.-R. Wang, J. Am. Chem. Soc., 2009, 131, 16646–16647.
10. L. Dunsch, S. Yang, L. Zhang, A. Svitova, S. Oswald and A. A. Popov, J. Am. Chem. Soc., 2010, 132, 5413–5421.
11. N. Chen, M. N. Chaur, C. Moore, J. R. Pinzón, R. Valencia, A. Rodríguez-Fortea, J. M. Poblet and L. Echegoyen, Chem. Commun., 2010, 46, 4818–4820.
12. Q. Tang, L. Abella, Y. Hao, X. Li, Y. Wan, A. Rodríguez-Fortea, J. M. Poblet, L. Feng and N. Chen, Inorg. Chem., 2015, 54, 9845–9852.
13. S. Stevenson, M. A. Mackey, M. A. Stuart, J. P. Phillips, M. L. Easterling, C. J. Chancellor, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 11844–11845.
14. B. Q. Mercado, M. M. Olmstead, C. M. Beavers, M. L. Easterling, S. Stevenson, M. A. Mackey, C. E. Coumbe, J. D. Phillips, J. Paige Phillips, J. M. Poblet and A. L. Balch, Chem. Commun., 2010, 46, 279–281.
15. F. Jin, S. Wang, N. B. Tamm, S. Yang and S. I. Troyanov, Angew. Chem., Int. Ed., 2017, 129, 12152–12156.
16. T.-S. Wang, L. Feng, J.-Y. Wu, W. Xu, J.-F. Xiang, K. Tan, Y.-H. Ma, J.-P. Zheng, L. Jiang, X. Lu, C.-Y. Shu and C.-R. Wang, J. Am. Chem. Soc., 2010, 132, 16362–16364.
17. F. Liu, C.-L. Gao, Q. Deng, X. Zhu, A. Kostanyan, R. Westerström, S. Wang, Y.-Z. Tan, J. Tao, S.-Y. Xie, A. A. Popov, T. Greber and S. Yang, J. Am. Chem. Soc., 2016, 138, 14764–14771.
18. X. Zhang, Y. Wang, R. Morales-Martínez, J. Zhong, C. de Graaf, A. Rodríguez-Fortea, J. M. Poblet, L. Echegoyen, L. Feng and N. Chen, J. Am. Chem. Soc., 2018, 140, 3907–3915.
19. Y. Wang, R. Morales-Martínez, X. Zhang, W. Yang, Y. Wang, A. Rodriguez-Fortea, J. M. Poblet, L. Feng, S. Wang and N. Chen, J. Am. Chem. Soc., 2017, 139, 5110–5116.
20. W. Cai, R. Morales-Martínez, X. Zhang, D. Najera, E. L. Romero, A. Metta-Magaña, A. Rodríguez-Fortea, S. Fortier, N. Chen, J. M. Poblet and L. Echegoyen, Chem. Sci., 2017, 8, 5282–5290.
21. A. Rodríguez-Fortea, A. L. Balch and J. M. Poblet, Chem. Soc. Rev., 2011, 40, 3551–3563.
22. T. Wang and C. Wang, Acc. Chem. Res., 2014, 47, 450–458.
23. S. Yang, T. Wei and F. Jin, Chem. Soc. Rev., 2017, 46, 5005–5058.
24. K. Kobayashi and S. Nagase, Chem. Phys. Lett., 1998, 282, 325–329.
25. L. Bao, C. Pan, Z. Slanina, F. Uhlik, T. Akasaka and X. Lu, Angew. Chem., Int. Ed., 2016, 55, 9234–9238.
26. S. Yang, S. I. Troyanov, A. A. Popov, M. Krause and L. Dunsch, J. Am. Chem. Soc., 2006, 128, 16733–16739.
27. M. Krause and L. Dunsch, ChemPhysChem, 2004, 5, 1445–1449.
28. A. A. Popov, M. Krause, S. Yang, J. Wong and L. Dunsch, J. Phys. Chem. B, 2007, 111, 3363–3369.
29. C. M. Beavers, M. N. Chaur, M. M. Olmstead, L. Echegoyen and A. L. Balch, J. Am. Chem. Soc., 2009, 131, 11519–11524.
30. F. Melin, M. N. Chaur, S. Engmann, B. Elliott, A. Kumbhar, A. J. Athans and L. Echegoyen, Angew. Chem., Int. Ed., 2007, 46, 9032–9035.
31. M. N. Chaur, F. Melin, J. Ashby, B. Elliott, A. Kumbhar, A. M. Rao and L. Echegoyen, Chem.–Eur. J., 2008, 14, 8213–8219.
32. A. L. Svitova, A. A. Popov and L. Dunsch, Inorg. Chem., 2013, 52, 3368–3380.
33. Q. Deng and A. A. Popov, J. Am. Chem. Soc., 2014, 136, 4257–4264.
34. J. Zhang, T. Fuhrer, W. Fu, J. Ge, D. W. Bearden, J. Dallas, J. Duchamp, K. Walker, H. Champion, H. Azurmendi, K. Harich and H. C. Dorn, J. Am. Chem. Soc., 2012, 134, 8487–8493.
35. H. Kurihara, X. Lu, Y. Iiduka, H. Nikawa, M. Hachiya, N. Mizorogi, Z. Slanina, T. Tsuchiya, S. Nagase and T. Akasaka, Inorg. Chem., 2012, 51, 746–750.
36. C.-H. Chen, K. B. Ghiassi, M. R. Cerón, M. A. Guerrero-Ayala, L. Echegoyen, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2015, 137, 10116–10119.
37. C.-H. Chen, L. Abella, M. R. Cerón, M. A. Guerrero-Ayala, A. Rodríguez-Fortea, M. M. Olmstead, X. B. Powers, A. L. Balch, J. M. Poblet and L. Echegoyen, J. Am. Chem. Soc., 2016, 138, 13030–13037.
38. J. Zhang, F. L. Bowles, D. W. Bearden, W. K. Ray, T. Fuhrer, Y. Ye, C. Dixon, K. Harich, R. F. Helm, M. M. Olmstead, A. L. Balch and H. C. Dorn, Nat. Chem., 2013, 5, 880–885.
39. W. Shen, L. Bao, Y. Wu, C. Pan, S. Zhao, H. Fang, Y. Xie, P. Jin, P. Peng, F.-F. Li and X. Lu, J. Am. Chem. Soc., 2017, 139, 9979–9984.
40. H. Yang, H. Jin, B. Hong, Z. Liu, C. M. Beavers, H. Zhen, Z. Wang, B. Q. Mercado, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2011, 133, 16911–16919.
41. C. M. Beavers, T. Zuo, J. C. Duchamp, K. Harich, H. C. Dorn, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2006, 128, 11352–11353.
42. H. Yang, M. Yu, H. Jin, Z. Liu, M. Yao, B. Liu, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2012, 134, 5331–5338.
43. T. Zuo, C. M. Beavers, J. C. Duchamp, A. Campbell, H. C. Dorn, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2007, 129, 2035–2043.
44. H. Umemoto, K. Ohashi, T. Inoue, N. Fukui, T. Sugai and H. Shinohara, Chem. Commun., 2010, 46, 5653–5655.
45. Y. Hao, Q. Tang, X. Li, M. Zhang, Y. Wan, L. Feng, N. Chen, Z. Slanina, L. Adamowicz and F. Uhlík, Inorg. Chem., 2016, 55, 11354–11361.
46. Y.-J. Guo, X. Zhao, P. Zhao and T. Yang, J. Phys. Chem. A, 2015, 119, 10428–10439.
47. W. Cai, L. Bao, S. Zhao, Y. Xie, T. Akasaka and X. Lu, J. Am. Chem. Soc., 2015, 137, 10292–10296.
48. W. Cai, F.-F. Li, L. Bao, Y. Xie and X. Lu, J. Am. Chem. Soc., 2016, 138, 6670–6675.
49. S. Zhao, P. Zhao, W. Cai, L. Bao, M. Chen, Y. Xie, X. Zhao and X. Lu, J. Am. Chem. Soc., 2017, 139, 4724–4728.
50. T. Yang, X. Zhao and E. Osawa, Chem.–Eur. J., 2011, 17, 10230–10234.
51. J. Hao, F. Li, H. Li, X. Chen, Y. Zhang, Z. Chen and C. Hao, RSC Adv., 2015, 5, 34383–34389.
52. B. Christen, H. Christen and S. Xin, J. Am. Chem. Soc., 2017, 139, 3919.
53. X. Lu, Z. Slanina, T. Akasaka, T. Tsuchiya, N. Mizorogi and S. Nagase, J. Am. Chem. Soc., 2010, 132, 5896–5905.
54. A. A. Popov, S. M. Avdoshenko, A. M. Pendás and L. Dunsch, Chem. Commun., 2012, 48, 8031.
55. N. A. Samoylova, S. M. Avdoshenko, D. S. Krylov, H. R. Thompson, A. C. Kirkhorn, M. Rosenkranz, S. Schiemenz, F. Ziegs, A. U. B. Wolter, S. Yang, S. Stevenson and A. A. Popov, Nanoscale, 2017, 23, 7977–7990.
56. A. Velloth, Y. Imamura, T. Kodama and M. Hada, J. Phys. Chem. C, 2017, 121, 18169–18177.
57. Z. Wang, R. Kitaura and H. Shinohara, J. Phys. Chem. C, 2014, 118, 13953–13958.
58. Y. Maeda, T. Tsuchiya, T. Kikuchi, H. Nikawa, T. Yang, X. Zhao, Z. Slanina, M. Suzuki, M. Yamada, Y. Lian, S. Nagase, X. Lu and T. Akasaka, Carbon, 2016, 98, 67–73.
59. H. Yang, C. Lu, Z. Liu, H. Jin, Y. Che, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2008, 130, 17296–17300.
60. A. L. Balch, M. M. Olmstead, X. Powers, C. M. Davison, S. Stevenson and K. R. Tepper, Chem.–Eur. J., 2018, 24, 13479–13484.
61. M. Yamada, Y. Muto, H. Kurihara, Z. Slanina, M. Suzuki, Y. Maeda, Y. Rubin, M. M. Olmstead, A. L. Balch, S. Nagase, X. Lu and T. Akasaka, Angew. Chem., Int. Ed., 2015, 54, 2232–2235.
62. M. Suzuki, N. Mizorogi, T. Yang, F. Uhlik, Z. Slanina, X. Zhao, M. Yamada, Y. Maeda, T. Hasegawa, S. Nagase, X. Lu and T. Akasaka, Chem.–Eur. J., 2013, 19, 17125–17130.
63. B. Cao, H. Nikawa, T. Nakahodo, T. Tsuchiya, Y. Maeda, T. Akasaka, H. Sawa, Z. Slanina, N. Mizorogi and S. Nagase, J. Am. Chem. Soc., 2008, 130, 983–989.
64. L. Bao, M. Chen, C. Pan, T. Yamaguchi, T. Kato, M. M. Olmstead, A. L. Balch, T. Akasaka and X. Lu, Angew. Chem., Int. Ed., 2016, 55, 4242–4246.
65. C. M. Beavers, H. Jin, H. Yang, Z. Wang, X. Wang, H. Ge, Z. Liu, B. Q. Mercado, M. M. Olmstead and A. L. Balch, J. Am. Chem. Soc., 2011, 133, 15338–15341.
66. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
67. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
68. G. A. Petersson and M. A. Al-Laham, J. Chem. Phys., 1991, 94, 6081–6090.
69. G. A. Petersson, A. Bennett, T. G. Tensfeldt, M. A. Al-Laham, W. A. Shirley and J. Mantzaris, J. Chem. Phys., 1988, 89, 2193–2218.
70. X. Cao and M. Dolg, J. Mol. Struct.: THEOCHEM, 2002, 581, 139–147.
71. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09, Gaussian, Inc., Wallingford, CT, USA, 2009.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1582214–1582219; 1836827–1836830. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc03886d

---