Open Access Article
Open Access ArticleDetermination of the electronic structure of a dinuclear dysprosium single molecule magnet without symmetry idealization†
Mauro
Perfetti‡§
 a,
Maren
Gysler‡
a,
Yvonne
Rechkemmer-Patalen
a,
Peng
Zhang
a,
Maren
Gysler‡
a,
Yvonne
Rechkemmer-Patalen
a,
Peng
Zhang
 a,
Hatice
Taştan
a,
Florian
Fischer
a,
Julia
Netz
a,
Wolfgang
Frey
b,
Lucas W.
Zimmermann
c,
Thomas
Schleid
c,
Michael
Hakl
d,
Milan
Orlita
de,
Liviu
Ungur
a,
Hatice
Taştan
a,
Florian
Fischer
a,
Julia
Netz
a,
Wolfgang
Frey
b,
Lucas W.
Zimmermann
c,
Thomas
Schleid
c,
Michael
Hakl
d,
Milan
Orlita
de,
Liviu
Ungur
 f,
Liviu
Chibotaru
f,
Theis
Brock-Nannestad
g,
Stergios
Piligkos
f,
Liviu
Chibotaru
f,
Theis
Brock-Nannestad
g,
Stergios
Piligkos
 g and
Joris
van Slageren
g and
Joris
van Slageren
 *a
*a
aInstitut für Physikalische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany. E-mail: slageren@ipc.uni-stuttgart.de
bInstitut für Organische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany
cInstitut für Anorganische Chemie, Universität Stuttgart, Pfaffenwaldring 55, D-70569 Stuttgart, Germany
dLaboratoire National des Champs Magnétiques Intenses (LNCMI-EMFL), CNRS, UGA, 38042 Grenoble, France
eInstitute of Physics, Charles University, Ke Karlovu 5, 12116 Praja 2, Czech Republic
fTheory of Nanomaterials Group, Katholieke Universiteit Leuven, Celestijnenlaan 220F, 3001 Leuven, Belgium
gDepartment of Chemistry, University of Copenhagen, Universitetsparken 5, 2100, Denmark
First published on 12th December 2018
Abstract
We present the in-depth determination of the magnetic properties and electronic structure of the luminescent and volatile dysprosium-based single molecule magnet [Dy2(bpm)(fod)6] (Hfod = 6,6,7,7,8,8,8-heptafluoro-2,2-dimethyl-3,5-octanedione, bpm = 2,2′-bipyrimidine). Ab initio calculations were used to obtain a global picture of the electronic structure and to predict possible single molecule magnet behaviour, confirmed by experiments. The orientation of the susceptibility tensor was determined by means of cantilever torque magnetometry. An experimental determination of the electronic structure of the lanthanide ion was obtained combining Luminescence, Far Infrared and Magnetic Circular Dichroism spectroscopies. Fitting these energies to the full single ion plus crystal field Hamiltonian allowed determination of the eigenstates and crystal field parameters of a lanthanide complex without symmetry idealization. We then discuss the impact of a stepwise symmetry idealization on the modelling of the experimental data. This result is particularly important in view of the misleading outcomes that are often obtained when the symmetry of lanthanide complexes is idealized.
Introduction
The magnetic properties of complexes containing lanthanides have been intensely investigated for the past fifteen years.1–6 The main reason for this is that many such complexes display slow relaxation of the magnetic moment. As a consequence, they have been named single-molecule magnets (SMMs). Large effective energy barriers towards relaxation of the magnetization that are now approaching 2000 K have been obtained.7–10 This research is in part driven by the idea that such complexes may one day be used for magnetic data storage at the molecular level. For this purpose, the magnetization must be bistable, which is experimentally demonstrated by magnetic hysteresis with appreciable coercivity and remnant magnetization. The highest temperature at which this is observed at conventional field-sweep rates of around 1 T per minute is often called the blocking temperature, and values up to 80 K have been recently reported.8,10 Most lanthanide-based SMMs contain heavy lanthanides such as terbium, dysprosium and erbium, which have large magnetic moments. Especially the Dy3+ ion (ground state total angular momentum J = 15/2) has been much employed. These successes are due to careful engineering of the crystal field, which is instrumental in determining the magnetization dynamics. The splitting of the microstates of the J = 15/2 manifold of Dy3+ into 8 Kramers doublets (KD) is caused by interaction with the electron density of the ligands around the metal ion and can thus be tailored by judicious choice of the coordination sphere. The oblate electronic density of the |±15/2〉 states of dysprosium11 can be stabilized by using axial ligands.12 Such an axial crystal field not only generates a large ground state magnetic moment, but also suppresses transitions between states with opposite orientations of the magnetic moment.13 A perfectly axial crystal field would have D∞h symmetry, which is not compatible with the translational symmetry of a crystal. However, pseudo-axial crystal fields have been obtained for bis-amides,14 bis-methane diides15 and many pentagonal bipyramidal coordination complexes.9,16,17 On the other hand, lower-symmetry complexes with favourable magnetic properties have also been reported, such as various bis-cyclopentadienyl-dysprosium compounds.7,8,10,18,19 Moreover, the majority of lanthanide based SMM reported up to date is characterized by very asymmetric coordination environments.2,20,21 To characterize the electronic structure of such molecules, two approaches have been employed: firstly, ab initio methods have been used to calculate the electronic structure. Alternatively, in experimental studies, the symmetry of the complex has been idealized in order to reduce the number of experimental parameters to be determined. On one side, theoretical predictions need an experimental proof of their correctness. On the other side, symmetry idealization must be used carefully because it can easily lead to wrong results, especially in lanthanide complexes.22–24Even in most polynuclear complexes, the magnetic properties are largely determined by the individual rare earth ions and their immediate surroundings.25 Weak, essentially dipolar interactions between lanthanide ions can cause (undesirable) relaxation enhancement.26 However, in the presence of an inversion center, interactions can lead to exchange-bias-like effects suppressing under-barrier tunneling.27 A different situation arises, when strong magnetic interactions are present, which typically involves lanthanide-radical species. The prime example is the N23− bridged terbium dimer with a hysteresis blocking temperature of 14 K.28 Less exotic species have featured polypyridyl-like bridging ligands that can be reduced to a radical form.29–34 The latter are especially attractive, because the magnetic properties may be switched (electro)chemically by reducing and oxidizing the bridging ligand.31,34
Although the magnetic properties of lanthanide complexes are intimately linked to the electronic structure, spectroscopic investigations of the electronic structure are still rather few.35–41 Magnetic interactions between the ground Kramers doublets in dinuclear lanthanide complexes have been studied in detail by EPR.26,42
Diketonate complexes with polypyridine-related ligands are a widely studied class of complexes due to their great relevance in many fields of science. Their magnetic properties have been the subject of many investigations since the discovery of slow relaxation of the magnetic moment in mononuclear [Ln(acac)3(H2O)2] (Hacac = acetyl acetone).4,43,44 Trinuclear45 and binuclear complexes with pyrazine,46 bipyrimidine,29,47,48 tetrapyridyl pyrazine30 and bispyridyl tetrazine31 have also been widely investigated. The electronic structure of diketonate ligands is very efficient in sensitizing the luminescence of lanthanide ions.49,50 Moreover, many diketonate-metal complexes have been reported to be highly volatile51 and suitable for surface deposition.52 Fluorination of the diketonate ligand quenches non-radiative decay processes, leading to high luminescence quantum yields.53
In this paper, we unravel the magnetic properties and the electronic structure of a dinuclear complex [Dy(fod)3(μ-bpm)Dy(fod)3] (Hfod = 6,6,7,7,8,8,8-heptafluoro-2,2-dimethyl-3,5-octanedione, bpm = 2,2′-bipyrimidine), hereafter abbreviated as Dy2. Ab initio calculations were performed to predict the magnetic and electronic structure of this complex. Single crystal torque magnetometry provided the orientation of the magnetic axes of the ground doublet, in excellent agreement with ab initio predictions. A combination of Luminescence, Far Infrared and Magnetic Circular Dichroism spectroscopies was used to carefully determine 38 energy levels belonging to 9 crystal field multiplets, thus allowing the first analysis of the crystal field of a lanthanide dimer without symmetry idealization.
Results and discussion
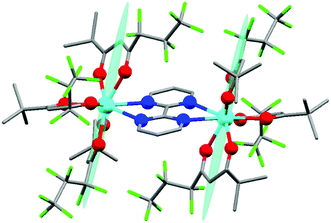
The synthesis of Dy2 is a facile one-step reaction of two equivalents of commercially available [Dy(fod)3] and one equivalent of bpm54 (more details about synthesis and chemical characterization are reported in ESI,† including Table S1, Fig. S1†). In Fig. 1 we report the molecular structure of Dy2. Each metal ion is 8-coordinated by 6 oxygen atoms of the fod ligands and 2 nitrogen atoms of the bpm ligand. The Dy–N bonds (2.585 and 2.602 Å) are slightly longer than the Dy–O bonds (2.315, 2.282, 2.300, 2.299, 2.315 and 2.320 Å). The Dy–Dy distance is 6.770 Å. The angle between the bpm plane and the Dy–Dy axis is 2°. Even though the lack of symmetry around the metals is already evident from Fig. 1, we calculated the best-fit polyhedron around the metal using the SHAPE program55 fixing the number of vertices to 8. The result (Table S2†) indicates that the effective symmetry around the metal is C1; and no symmetry approximation can be applied. For this reason, a characterization based on the spectroscopic and/or thermodynamic investigation of the 8 doublets belonging to the ground Russell Saunders multiplet alone is not sufficient to fully describe the CF acting on the dysprosium ion. Therefore, to study this system we used a combination of theoretical calculations and experimental techniques.Ab initio calculations can provide a detailed picture of the electronic and magnetic structure of lanthanide complexes.56 Therefore, we carried out such calculations on Dy2 within the well-known CASSCF/RASSI/single_aniso framework. The g tensor of the ground Kramers doublet of Dy2 was calculated to be extremely axial (gx = gy = 0.01, gz = 19.55, to be compared with a perfectly axial g tensor gx = gy = 0, gz = 20), due to the essentially pure (96%) |±15/2〉 character (see Table S3† for the orientation and magnitude of the g tensors of all the doublets). Interestingly, the easy axis was predicted to be almost orthogonal to the Dy–Dy direction. The first excited doublet (80% |±13/2〉), separated by 150 cm−1 from the ground state, was also calculated to be axial (gx = 0.26, gy = 0.39, gz = 16.09) and almost collinear with the ground state (8° tilting), thus disfavoring quantum tunnelling of the magnetization. The calculated CF levels of the ground multiplet are reported as red lines in the inset of Fig. 2. The calculated CF parameters are reported in Table S4.† Given the absence of symmetry, an indication of the influence of the parameters of a given order can be obtained calculating the CF strength factors32 (Sk, where k = 2, 4, 6 is the order of the parameters), as reported in Table S5.† The calculations predict a total CF strength Stot = 292 cm−1, dominated by the parameters of fourth order (S4 > S2 > S6). In Table S6† the composition of the CF levels belonging to the ground multiplet is presented.
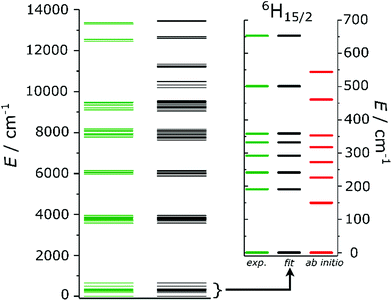 | ||
| Fig. 2 Experimental (green) and fitted (black) energy level splitting. The inset is a zoom on the ground 6H15/2 term, where also the ab initio (red) energies are reported. | ||
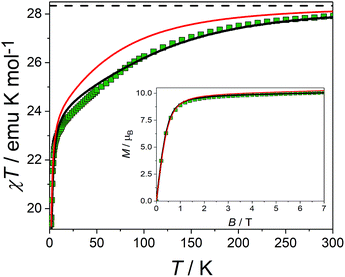
The picture that emerges from ab initio calculations is an extremely axial system, likely to exhibit single molecule magnet behaviour. We thus measured the static and dynamic magnetic properties of this complex and compare them with the outcome of the calculations. In Fig. 3 we report the experimental χT vs. T curve. The χT value at room temperature (27.8 emu K mol−1) is slightly lower than two times the Curie constant of a free Dy3+ ion (28.3 emu K mol−1). The decrease of the χT product on lowering the temperature is mainly attributed to the CF splitting and possibly to the presence of magnetic interactions. The simulated χT product, reported as a red curve in Fig. 3, was obtained using the ab initio-calculated CF parameters and adding an isotropic intramolecular antiferromagnetic (AFM) coupling constant j = 4.2(1) × 10−3 cm−1 (following the +j·Ĵ1·Ĵ2 convention). The AFM interaction is readily explained by the almost perpendicular orientation of the easy axes and the Dy1⋯Dy2 axis.57 In order to estimate the relative magnitudes of the exchange and the dipolar couplings, we calculated the dipolar contribution within the point dipole approximation using the orientation and magnitude of the calculated ground g tensor obtaining jdip = 2.3 × 10−3 cm−1. The calculated value is approximately half of the fitted coupling constant, indicating that the exchange and dipolar contributions in this system have comparable magnitudes. Previous studies in literature reported both similar57 and different58,59 ratios between the dipolar and the exchange contributions. The disagreement between experiments and ab initio simulation at intermediate temperatures (30 < T < 200 K) is attributed to the imperfectly calculated energies and compositions of the CF states. To clarify this discrepancy, we carried out a detailed spectroscopic characterization (see below). In the inset of Fig. 3 we also report the measured and simulated field dependence of the magnetization at low temperature. The excellent agreement with the simulation (red line), provides further evidence of the strong axiality of the ground state. The expected magnetic bistability is experimentally supported by the presence of magnetic hysteresis at temperatures below 2 K (blue line in Fig. 4). Interestingly, the curve shows a double butterfly shape, closing both at zero field and at ±500 Oe. The latter is exactly at the position where simulations according to parameters taken from the ab initio calculations predict a field-induced level crossing. Similar relaxation enhancement at level crossings have been observed in a Dy3 complex.60 In contrast, in a dilute sample of [(Y![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Dy = 19
Dy = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1)2(fod)6(μ-bpm)] (Dy@Y2), the hysteresis loop only closes at zero field (red line in Fig. 4). This corroborates that indeed there is a significant interaction between the two dysprosium ions.
1)2(fod)6(μ-bpm)] (Dy@Y2), the hysteresis loop only closes at zero field (red line in Fig. 4). This corroborates that indeed there is a significant interaction between the two dysprosium ions.
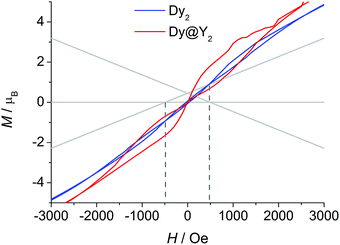 | ||
| Fig. 4 Hysteresis curves recorded on powder samples of Dy2 and Dy@Y2 at 1.8 K with field sweep rates of 100 Oe s−1. The lines are the ab initio calculated energy levels. | ||
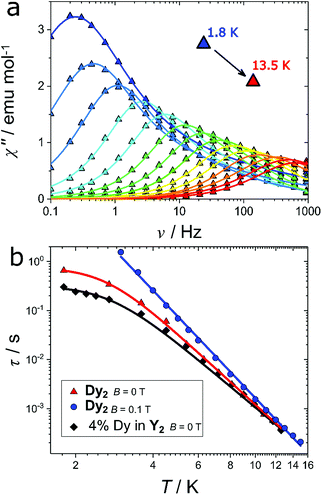
The axiality suggests the possible occurrence of slow relaxation of the magnetization. We thus carried out a study of the magnetization dynamics, where we detected slow relaxation of the magnetic moment both with and without an external applied magnetic field (Fig. S2†). The field scan at the lowest temperature (T = 1.8 K) reveals a double peak in the imaginary component at low fields (H < 500 Oe). This indicates the presence of two active relaxation pathways, as already observed in other mono61 and polynuclear59,62–67 Dy-based complexes. However, in the present case this cannot be attributed to two distinct coordination environments for the Dy(III) ions because the two dysprosium ions are crystallographically related by an inversion centre. A possible explanation is instead the presence of (relatively small) intermolecular interactions that may open an alternative relaxation channel compared to the single ion relaxation, as already observed for other lanthanide complexes.68 When the magnetic field is raised, the relaxation time rapidly increases towards frequencies outside of the experimental window. We thus focused our attention on the temperature scan in zero field and in an optimum field of 0.1 T. The zero-field temperature scan is shown in Fig. 5a (real component reported in Fig. S3†). The out of phase susceptibility (χ′′) vs. frequency (ν) curves were fitted as reported in ESI (Fig. S4† and explanation thereafter) to extract the relaxation times (τ), the width of the distribution (α) and the difference between isothermal and adiabatic susceptibility (χT − χS). The extracted χT − χS values are in good agreement with the χdc values (Fig. S5†), testifying that the observed relaxation processes involve the entire magnetic ensemble. The extracted relaxation times for the slow process are reported in Fig. 5b (red triangles). The almost constant value of τ at low temperatures (T < 3 K) reflects the proximity to the quantum tunneling regime, while at higher temperatures the linear trend of log(τ) vs. log(T) suggests a Raman process as the preferential relaxation channel. Importantly, the experimental data could not be fitted using an Orbach process fixing the energy barrier for the reversal of the magnetization to the calculated energy of the first excited state (151 cm−1) as illustrated in Fig. S6.† The relaxation time was instead well reproduced using the following equation:
| τ−1 = τTI−1 + CTn | (1) |
| Sample | Field (T) | τ TI | C | n |
|---|---|---|---|---|
| Dy2 | 0 | 0.761(7) | 1.32(3) × 10−2 | 4.79(2) |
| 0.1 | — | 1.85(2) × 10−3 | 5.52(5) | |
| 4% Dy in Y2 | 0 | 0.32(1) | 3.8(4) × 10−2 | 4.38(6) |
| 0.1 | — | 1.57(2) × 10−3 | 5.54(5) |
To shed further light on the relaxation mechanisms, we performed a dilution experiment using an approximate ratio 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 between Dy(fod)3 and Y(fod)3 as starting material. The χT product of the resulting compound (hereafter called Dy@Y2) is reported in Fig. S7† and reveals a magnetic dilution of 4% (close to the expected 5%). The field scan of the ac magnetic susceptibility reveals a similar trend compared to the Dy2 derivative (Fig. S8†), however the considerably narrower character of the imaginary component reveals a single relaxation process. Indeed, the ac magnetic susceptibility recorded in zero field (Fig. S9†) could be fitted using only one relaxation process in the whole temperature regime. This reinforces the hypothesis that the second relaxation process observed in Dy2 is produced by intermolecular interactions. The obtained relaxation times, reported in Fig. 5b (black diamonds), were fitted using eqn (1) and the results are reported in Table 1.
19 between Dy(fod)3 and Y(fod)3 as starting material. The χT product of the resulting compound (hereafter called Dy@Y2) is reported in Fig. S7† and reveals a magnetic dilution of 4% (close to the expected 5%). The field scan of the ac magnetic susceptibility reveals a similar trend compared to the Dy2 derivative (Fig. S8†), however the considerably narrower character of the imaginary component reveals a single relaxation process. Indeed, the ac magnetic susceptibility recorded in zero field (Fig. S9†) could be fitted using only one relaxation process in the whole temperature regime. This reinforces the hypothesis that the second relaxation process observed in Dy2 is produced by intermolecular interactions. The obtained relaxation times, reported in Fig. 5b (black diamonds), were fitted using eqn (1) and the results are reported in Table 1.
Although at T > 5 K the two curves are almost superimposable (testified by the similar Raman exponent and pre-factor), the temperature independent relaxation time decreases by a factor 2.4 in the diluted sample, pointing out that the quantum tunneling is enhanced by intermolecular interactions.
Another efficient way to remove the tunneling of the magnetization is the application of an external magnetic field. Indeed, the imaginary component of the magnetic susceptibility, reported in Fig. S10† for Dy2 and in Fig. S11† for 4% Dy in Y2, can be reproduced considering a single Raman relaxation process in the whole investigated temperature range. The extracted relaxation times for the pure and diluted compounds are virtually superimposable (blue circles in Fig. 4b for Dy2, and Fig. S11† for 4 Dy in Y2). In Table 1 we report the fit parameters.
Given the discrepancy between experimental and calculated susceptibility at intermediate temperatures, we performed a completely experimental determination of the electronic structure of Dy2. Although appealing, the experimental determination of the CF of a molecular lanthanide complex without idealized symmetry has never been performed due to the practical challenge in measuring a sufficient number of energy levels to meaningfully fit all the required CF parameters. We tried to overcome this obstacle combining two spectroscopic techniques, namely Luminescence and Magnetic Circular Dichroism, that provide access to CF excitations in a broad energy range.
Luminescence has been demonstrated to be a powerful tool to study magnetic properties of molecules, and several works have established a strong correlation between luminescence and magnetic properties.69–73 We performed luminescence measurements at T = 5 K irradiating at λ = 341 nm (ca. 29![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1), exciting electronic transitions of the ligands. The triplet excited states of the ligands (E(T1(fod)) = 22
300 cm−1), exciting electronic transitions of the ligands. The triplet excited states of the ligands (E(T1(fod)) = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 and E(T1(bpm)) = 27
500 cm−1 and E(T1(bpm)) = 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1) are close to the excited 4F9/2 state (ca. 21
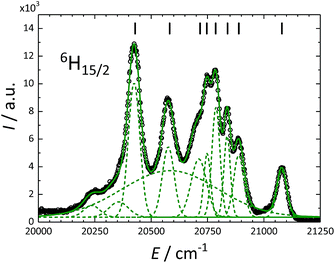
200 cm−1) are close to the excited 4F9/2 state (ca. 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1) of Dy3+, allowing for efficient energy transfer. These measurements allowed to resolve the CF splitting of the ground 6H15/2 state (Fig. 6) and of the 6H13/2 excited multiplet (Fig. S13†). The spectrum reported in Fig. 6 could be satisfactorily reproduced using eleven Gaussian functions, while in principle only 8 components must be detected for a 6H15/2 ground state. We attribute the additional, broader features to vibronic excitations.73 Note that only the crystal field fitting of all experimental energies allowed for unambiguous assignment of the luminescence bands.
000 cm−1) of Dy3+, allowing for efficient energy transfer. These measurements allowed to resolve the CF splitting of the ground 6H15/2 state (Fig. 6) and of the 6H13/2 excited multiplet (Fig. S13†). The spectrum reported in Fig. 6 could be satisfactorily reproduced using eleven Gaussian functions, while in principle only 8 components must be detected for a 6H15/2 ground state. We attribute the additional, broader features to vibronic excitations.73 Note that only the crystal field fitting of all experimental energies allowed for unambiguous assignment of the luminescence bands.
A comparison with the energies calculated ab initio (the green and the red lines in the inset of Fig. 2) reveals that the experimentally derived splitting is larger than that obtained from ab initio calculations. The ratio of experimental and ab initio energies appears to be almost constant for all the KDs. Indeed, a scaling of the calculated energies by a factor 1.2, as reported in Fig. S14,† greatly improves the agreement with the experiments. The applicability of a scaling factor for CASSCF/RASSI-derived energies to match experiments was already reported24,26,42 and recently attributed to the necessity to include the presence of an extended crystal lattice using, e.g., point charges.42
Molecular vibrations are crucial to determine the dynamics of the magnetization,8,74–76 and their presence can be detected using field-dependent FIR spectroscopy. Indeed, the FIR spectra reported in Fig. S15† exhibit several field-dependent weak features (2–3% of the intensity at zero field) between 150 cm−1 and 250 cm−1. The two downward pointing peaks at ca. 184 and 205 cm−1 are attributed to the zero-field crystal field transitions.42,77 Because of the weakness of the signal and the ensuing uncertainty in the exact peak position we did not include the FIR peak energies in the fitting procedure (see below). However, the final fit does yield energy levels in this region.
The number of experimental energies extracted from luminescence data (15 in total) was not sufficient to fully parametrize the CF potential acting on the Dy3+ ion. We thus performed Magnetic Circular Dichroism (MCD) spectroscopy in the Vis-NIR range (5000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1, Fig. S16†) to observe transitions between the ground state and 7 excited multiplets (6H11/2, 6H9/2, 6F11/2, 6H7/2, 6F9/2, 6F5/2, 6F3/2, see Fig. S17†). All the experimentally extracted energies are reported in Fig. 2 as green lines and numerically in Table S7.†
000 cm−1, Fig. S16†) to observe transitions between the ground state and 7 excited multiplets (6H11/2, 6H9/2, 6F11/2, 6H7/2, 6F9/2, 6F5/2, 6F3/2, see Fig. S17†). All the experimentally extracted energies are reported in Fig. 2 as green lines and numerically in Table S7.†
The luminescence and the MCD results together provided a set of 38 experimental energy levels that was used to perform the fit of the CF parameters. We used the full |S,L,J,mJ 〉 basis of the states that for an 4f9 ion gives rise to 2002 states. The single ion Hamiltonian used to describe the system is the sum of a free ion term and a CF term.78 The free ion term can be written as:
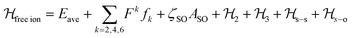 | (2) |
The CF term of the Hamiltonian in Wybourne notation is:
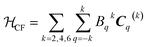 | (3) |
In eqn (3) the number of the Bqk parameters related to the Cqk spherical tensor operators is dependent on the single site symmetry. For the studied compounds, no symmetry restrictions could be applied, and the total number of parameters was therefore 27. The coupling term of the Hamiltonian was neglected at this stage in view of the small coupling strength predicted by the ab initio calculations. The results of the fit are reported in Tables S8 and S9† (last two columns). Due to the large number of experimental parameters, a good initial guess is needed: we thus used the CF parameters obtained from ab initio calculations.
Fig. 2 depicts the experimental (green) and fitted (black) energy levels up to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. An excellent overall agreement is observed. The inset of Fig. 2 is a zoom of the ground 6H15/2 term of Dy3+, in which the average deviation from the experimental values is well-below the experimental error (≪1 cm−1). The outcome of the fitting confirms that the ground KD is highly axial (84% |±15/2〉), as correctly predicted by ab initio calculations (compare Tables S6 and S10†), even though it has a minor (10%) |±13/2〉 component. The first excited state is instead highly mixed. HFEPR measurements performed at three different temperatures (T = 5, 10 and 20 K) revealed that the ground KD is EPR-silent, confirming its highly axial nature. The FIR spectra simulated starting from the set of CF parameters obtained ab initio and by fit are reported in Fig. S18,† together with the experimental results. In the spectra obtained from the ab initio output only the transition between the ground and the first excited doublet is strongly allowed, due to the substantial purity of the states. The simulated transition occurs at lower energy than expected, due to the underestimation of the first excited state. The simulation obtained from the fit of the experiments correctly reproduces both the relative intensity of the peaks and the position of the first peak (at ca. 190 cm−1), while a 15% discrepancy can be seen in the position of the second excitation.
000 cm−1. An excellent overall agreement is observed. The inset of Fig. 2 is a zoom of the ground 6H15/2 term of Dy3+, in which the average deviation from the experimental values is well-below the experimental error (≪1 cm−1). The outcome of the fitting confirms that the ground KD is highly axial (84% |±15/2〉), as correctly predicted by ab initio calculations (compare Tables S6 and S10†), even though it has a minor (10%) |±13/2〉 component. The first excited state is instead highly mixed. HFEPR measurements performed at three different temperatures (T = 5, 10 and 20 K) revealed that the ground KD is EPR-silent, confirming its highly axial nature. The FIR spectra simulated starting from the set of CF parameters obtained ab initio and by fit are reported in Fig. S18,† together with the experimental results. In the spectra obtained from the ab initio output only the transition between the ground and the first excited doublet is strongly allowed, due to the substantial purity of the states. The simulated transition occurs at lower energy than expected, due to the underestimation of the first excited state. The simulation obtained from the fit of the experiments correctly reproduces both the relative intensity of the peaks and the position of the first peak (at ca. 190 cm−1), while a 15% discrepancy can be seen in the position of the second excitation.
The CF strength, reported in Table S11,† is dominated by the fourth order terms (S4 = 537 cm−1), in agreement with the ab initio prediction. Whilst the second order strength (S2 = 286 cm−1) also compares well with ab initio calculations, the sixth order (S6 = 382 cm−1) is almost doubled in the fit. This leads to the overall CF strength obtained from the fit (St = 402 cm−1) being higher than the one predicted by calculations (St = 292 cm−1).
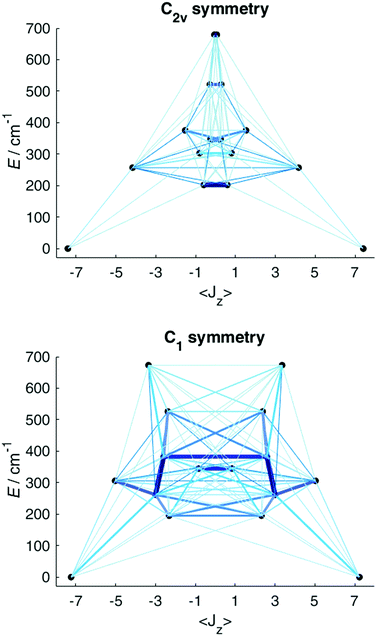
Having obtained a satisfactory fit of all CF parameters, made possible by the large number of experimental energies, the question remains, if adequate fits could have been obtained with using fewer CF parameters. We therefore repeated the fit of the CF parameters using (physically unrealistic) higher symmetries (Fig. 7) compatible with the presence of eight donor atoms in the first coordination sphere (see Table S2†). Clearly, going to higher symmetries leads to more CF parameters being zero by symmetry (Table S9†), thus fewer fit parameters. Fig. 7 demonstrates that for all symmetries higher than C2v satisfactory fits cannot be obtained, and thus that at least 15 CF parameters are required to accurately reproduce the energies. The assumption of C2v symmetry suffices to reproduce the energy spectrum and quantities primarily determined by it, such as the magnetic susceptibility (Fig. S19†). However, the composition of the eigenstates derived from the fits in C1 and C2v symmetries is substantially different (Tables S11 and S12†). Thus, whilst in C2v symmetry, the ground KD is calculated to be essentially fully axial, it is much less so in C1 symmetry. The precise composition of the KDs is of great importance, because it determines the pathway of the relaxation of the magnetization, since all relaxation processes (direct, quantum tunnelling, Raman, Orbach) feature matrix elements of the CF eigenstates. Indeed, both the composition and the main relaxation channels in both symmetries are clearly different (Fig. 8). We thus conclude that models using fewer parameters than those allowed by symmetry lead to erroneous results in this case.
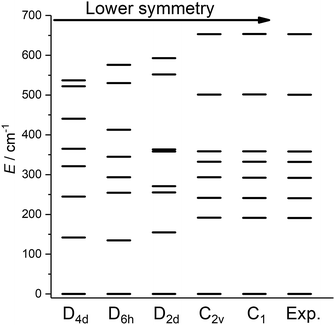 | ||
| Fig. 7 Best fit energy level diagrams on the basis of CF Hamiltonians containing only those terms belonging to the indicated symmetries. | ||
We employed cantilever torque magnetometry (CTM) to have an independent validation of the theoretically determined orientation of the easy axis of the Dy3+ ion. Since the studied complex crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) triclinic space group, the experimental determination of the magnitude and orientation of magnetic anisotropy can be performed unambiguously by means of CTM.79 A sketch of the single crystal orientation is reported in Fig. S20.† The torque curves recorded at two different temperatures (T = 2 and 5 K) are reported in Fig. 9, while all the other measurements are reported in Fig. S21.† They appear very similar in shape and magnitude: they both exhibit two 90° spaced zero-torque points in the 0–180° angular range, in agreement with the crystallographically imposed collinearity of the susceptibility tensors. The zero-torque angles correspond to the projection of the easy axis in the plane of rotation being parallel (easy zero) or perpendicular (hard zero) to the applied field. To avoid overparametrization, the fit was performed fixing the CF parameters to the ones extracted from the fit of the experimental energy levels. In this way, the only parameters free to vary were the three Euler angles that define the orientation of the molecular anisotropy tensor reference frame with respect to the crystallographic one79 (see Table S13† for numerical results). The agreement between experiment and fit is remarkably good, confirming again the goodness of the CF parameters. The orientation of the magnetic susceptibility tensor that we obtained is pictorially reported as a cyan ellipsoid superimposed on the Dy atoms in Fig. 1. The longest axis of the ellipsoid corresponds to the most favoured direction, taken as the molecular z axis in Table S13.† The experimental and calculated z (easy) molecular axes are coincident (angle between the two axes ca. 2°, below the experimental error for the visual alignment of the crystal), while the x and y axes (hard and intermediate, respectively) are shifted by ca. 30° between experiment and theory (compare Table S13†). This discrepancy is expected in highly axial systems, where the identification of small deviations in the anisotropy of the hard plane are often problematic from both the experimental and the theoretical point of view.
triclinic space group, the experimental determination of the magnitude and orientation of magnetic anisotropy can be performed unambiguously by means of CTM.79 A sketch of the single crystal orientation is reported in Fig. S20.† The torque curves recorded at two different temperatures (T = 2 and 5 K) are reported in Fig. 9, while all the other measurements are reported in Fig. S21.† They appear very similar in shape and magnitude: they both exhibit two 90° spaced zero-torque points in the 0–180° angular range, in agreement with the crystallographically imposed collinearity of the susceptibility tensors. The zero-torque angles correspond to the projection of the easy axis in the plane of rotation being parallel (easy zero) or perpendicular (hard zero) to the applied field. To avoid overparametrization, the fit was performed fixing the CF parameters to the ones extracted from the fit of the experimental energy levels. In this way, the only parameters free to vary were the three Euler angles that define the orientation of the molecular anisotropy tensor reference frame with respect to the crystallographic one79 (see Table S13† for numerical results). The agreement between experiment and fit is remarkably good, confirming again the goodness of the CF parameters. The orientation of the magnetic susceptibility tensor that we obtained is pictorially reported as a cyan ellipsoid superimposed on the Dy atoms in Fig. 1. The longest axis of the ellipsoid corresponds to the most favoured direction, taken as the molecular z axis in Table S13.† The experimental and calculated z (easy) molecular axes are coincident (angle between the two axes ca. 2°, below the experimental error for the visual alignment of the crystal), while the x and y axes (hard and intermediate, respectively) are shifted by ca. 30° between experiment and theory (compare Table S13†). This discrepancy is expected in highly axial systems, where the identification of small deviations in the anisotropy of the hard plane are often problematic from both the experimental and the theoretical point of view.
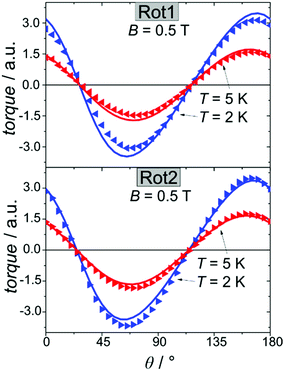 | ||
| Fig. 9 Rotation 1 (top) and rotation 2 (bottom) performed on a single crystal of Dy2 using CTM (see ESI† for details). Symbols refer to the experimental points while lines are the best fits. | ||
Fixing the Dy3+ CF parameters to the values extracted from the fit, we simulated the static magnetic properties. The χT curve was obtained an isotropic intramolecular AFM coupling constant j = 4.2(1) × 10−3 cm−1 (black line in Fig. 3), the same value obtained starting from the ab initio CF parameters. The dipolar part of the coupling obtained using the experimentally determined orientation of the easy axis and the g tensor extracted from the fit is substantially coincident with the one calculated using the ab initio results, confirming the approximate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between dipolar and exchange contribution to the coupling. The inclusion of the coupling constant allows simulating the energetic structure of the Dy2 dimer that shows a level crossing at 503 Oe, in close proximity to the first closing point of the double butterfly hysteresis (500 Oe, compare Fig. 4). This crossing is obviously absent if the coupling is not included, in agreement to the single butterfly shape observed for the diluted sample.
1 ratio between dipolar and exchange contribution to the coupling. The inclusion of the coupling constant allows simulating the energetic structure of the Dy2 dimer that shows a level crossing at 503 Oe, in close proximity to the first closing point of the double butterfly hysteresis (500 Oe, compare Fig. 4). This crossing is obviously absent if the coupling is not included, in agreement to the single butterfly shape observed for the diluted sample.
Conclusions
In this paper we analysed the electronic and magnetic properties of a multifunctional dysprosium dimer. The orientation of the magnetic reference frame calculated ab initio was experimentally verified by single crystal measurements obtaining excellent agreement. The pronounced axiality, suggested by calculations, gives rise to slow relaxation of the magnetization both in zero and in applied dc field. The spin–lattice relaxation time could be improved by magnetic dilution, suggesting a major role of the interactions. The electronic structure of the complex was obtained spectroscopically, thus allowing the experimental derivation of a complete description of the Crystal Field without any symmetry idealization. This is an important result because the most performant single molecule magnets up to date exhibit C1 symmetry.7,8,10Experimental
Synthesis
The compound was synthesized as previously reported in literature.54 Moreover, large air- and moisture-stable single crystals can be easily obtained from the mother solution. Elemental analysis of Dy2: found (calc. for Dy2C68H66F42N4O12)/%: C 36.23 (36.38), H 2.95 (3.08), N 2.49 (2.58). Further chemical characterization is reported in ESI.† In contrast to literature reports, pure heterodinuclear complexes could not be obtained.Spectroscopic measurements
Luminescence powder spectra were acquired on a Horiba FluoroLog3 luminescence spectrometer equipped with an Oxford Instruments helium flow optical cryostat. Magnetic Circular Dichroism (MCD) spectra were recorded on mulls of the solid compounds in transparent vacuum grease on an Aviv 42 CD spectrometer equipped with an Oxford Instruments Spectromag 10 T optical cryomagnet and photomultiplier and InGaAs detectors. HFEPR powder spectra were recorded on a home-built spectrometer. The radiation source (0–20 GHz signal generator, Anritsu) was combined with an amplifier–multiplier chain (VDI) to obtain the desired frequencies. It features a quasi-optical bridge (Thomas Keating) and induction mode detection. The detector is a QCM magnetically tuned InSb hot electron bolometer. The magnet is an Oxford cryomagnet (15/17 T) equipped with a variable temperature inset (1.5–300 K).80Magnetic measurements
Ac and dc magnetometry measurements were performed using a Quantum Design MPMS-XL7 SQUID magnetometer. The sample was measured as a pressed pellet wrapped into Teflon. A single crystal was attached to a square acetate foil with silicon vacuum grease and its faces were indexed using a SCD Oxford Xcalibur3 X-ray diffractometer. The used instrument was a home made two-legged CuBe cantilever separated by 0.1 mm from a gold plate. The cantilever was inserted into an Oxford Instruments MAGLAB2000 platform with automated rotation in a vertical magnet. The capacitance was detected with an Andeen-Hagerling 2500A Ultra Precision Capacitance Bridge.Analysis and fitting
Magnetic data were corrected for diamagnetic contributions using Pascal's constants.81 EPR and magnetic simulations and fits were performed using the easy spin tool82 in MATLAB. The crystal field analysis was performed using the f-shell program.83 Torque fits were performed using a home-made FORTRAN 90 program.Ab initio calculations were carried out on the full molecule by means of the CASSCF/RASSI-SO/SINGLE_ANISO routine using the MOLCAS 7.8 software package.84 One of the two Dy3+ ions was replaced with a diamagnetic Lu3+ ion. Basis sets were taken from the MOLCAS ANO-RCC library (Dy.ANO-RCC…8s7p5d4f2g1h). Complete active space self-consistent field (CASSCF) calculations include 9 electrons in the 7 4f orbitals. Spin–orbit mixing within the restricted active space state interaction (RASSI-SO) procedure included all sextet (6H, 6F, and 6P), 128 quartet (4I, 4F, 4M, 4G, 4K, 4L, 4D, 4H, 4P, 4G, 4F and 4I) and 130 doublet terms (2L, 2K, 2P, 2N, 2F, 2M, 2H, 2D, 2G and 2O). The magnetic exchange interaction strength was calculated using the POLY_ANISO routine in combination with experimental magnetic data.
Author contributions
J. v. S. designed and supervised the research; M. P. recorded CTM, SQUID and MCD (the last together with Y. R.) data, performed the data analysis, the fit of the experimental data and all the simulations; M. G., J. N., L. U. and L. C. performed the ab initio calculations; P. Z., H. T., F. F. synthesized the complex and performed the chemical analysis; W. F. solved the structure; T. S. and L. Z. performed the X-ray powder measurements; M. H. and M. O. performed the FIR measurements; M. G., T. B.-N. and S. P. performed the Luminescence measurements. M. P. and J. v. S. wrote the paper with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Deutsche Forschungsgemeinschaft (SPP1601, SL104/5-1, INST 41/863-1, INST 41/864-1, INST 41/887-1), the Alexander von Humboldt-Foundation (PZ) and COST CM1006 Eufen (MG) for funding. We thank Prof. Roberta Sessoli (Florence) for access to the torque magnetometry setup and Prof. Martin Dressel (Stuttgart) for access to the SQUID magnetometer. Prof. Stoll and Prof. Rauhut (Stuttgart) are kindly acknowledged for scientific discussion on the ab initio calculations.Notes and references
- N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Chem. Rev., 2013, 113, 5110–5148 CrossRef CAS PubMed.
- P. Zhang, Y.-N. Guo and J. Tang, Coord. Chem. Rev., 2013, 257, 1728–1763 CrossRef CAS.
- S.-D. Jiang, B.-W. Wang and S. Gao, in Molecular Nanomagnets and Related Phenomena, ed. S. Gao, Springer Berlin Heidelberg, Berlin, Heidelberg, 2015, pp. 111–141 Search PubMed.
- Lanthanides and Actinides in Molecular Magnetism, ed. R. Layfield and M. Murugesu, Wiley-VCH, Weinheim, 2015 Search PubMed.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- R. Layfield, F.-S. Guo, B. Day, Y.-C. Chen, M.-L. Tong and A. Mansikamäkki, Angew. Chem., Int. Ed., 2017, 56, 11445–11449 CrossRef PubMed.
- C. A. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439 CrossRef CAS PubMed.
- Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074 CrossRef CAS PubMed.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Science, 2018, eaav0652 CrossRef PubMed.
- J. Sievers, Z. Phys. B Condens. Matter, 1982, 45, 289–296 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- L. Ungur and L. F. Chibotaru, Phys. Chem. Chem. Phys., 2011, 13, 20086–20090 RSC.
- N. F. Chilton, Inorg. Chem., 2015, 54, 2097–2099 CrossRef CAS PubMed.
- M. Gregson, N. F. Chilton, A.-M. Ariciu, F. Tuna, I. F. Crowe, W. Lewis, A. J. Blake, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and S. T. Liddle, Chem. Sci., 2016, 7, 155–165 RSC.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, J. Am. Chem. Soc., 2016, 138, 2829–2837 CrossRef CAS PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, Chem. Sci., 2016, 7, 5181–5191 RSC.
- T. Pugh, N. F. Chilton and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 11082–11085 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny and J. R. Long, Chem.–Eur. J., 2014, 20, 9524–9529 CrossRef CAS PubMed.
- R. Sessoli and A. K. Powell, Coord. Chem. Rev., 2009, 253, 2328–2341 CrossRef CAS.
- F. Pointillart, O. Cador, B. Le Guennic and L. Ouahab, Coord. Chem. Rev., 2017, 346, 150–175 CrossRef CAS.
- G. Cucinotta, M. Perfetti, J. Luzon, M. Etienne, P. E. Car, A. Caneschi, G. Calvez, K. Bernot and R. Sessoli, Angew. Chem., Int. Ed., 2012, 51, 1606–1610 CrossRef CAS PubMed.
- M. E. Boulon, G. Cucinotta, J. Luzon, C. Degl'Innocenti, M. Perfetti, K. Bernot, G. Calvez, A. Caneschi and R. Sessoli, Angew. Chem., 2013, 125, 368–372 CrossRef.
- R. Marx, F. Moro, M. Dörfel, L. Ungur, M. Waters, S.-D. Jiang, M. Orlita, J. Taylor, W. Frey and L. Chibotaru, Chem. Sci., 2014, 5, 3287–3293 RSC.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. L. McInnes, L. F. Chibotaru and R. E. P. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS PubMed.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- Y. N. Guo, G. F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. K. Tang, H. J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549 CrossRef CAS PubMed.
- S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701–4711 RSC.
- B. S. Dolinar, S. Gomez-Coca, D. I. Alexandropoulos and K. R. Dunbar, Chem. Commun., 2017, 53, 2283–2286 RSC.
- B. M. Flanagan, P. V. Bernhardt, E. R. Krausz, S. R. Lüthi and M. J. Riley, Inorg. Chem., 2002, 41, 5024–5033 CrossRef CAS PubMed.
- B. M. Flanagan, P. V. Bernhardt, E. R. Krausz, S. R. Lüthi and M. J. Riley, Inorg. Chem., 2001, 40, 5401–5407 CrossRef CAS PubMed.
- P. Zhang, M. Perfetti, M. Kern, P. P. Hallmen, L. Ungur, S. Lenz, M. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Chem. Sci., 2018, 9, 1221–1230 RSC.
- M. Vonci, M. J. Giansiracusa, W. Van den Heuvel, R. W. Gable, B. Moubaraki, K. S. Murray, D. Yu, R. A. Mole, A. Soncini and C. Boskovic, Inorg. Chem., 2017, 56, 378–394 CrossRef CAS PubMed.
- M. Gysler, F. El Hallak, L. Ungur, R. Marx, M. Hakl, P. Neugebauer, Y. Rechkemmer, Y. Lan, I. Sheikin, M. Orlita, C. E. Anson, A. K. Powell, R. Sessoli, L. F. Chibotaru and J. van Slageren, Chem. Sci., 2016, 7, 4347–4354 RSC.
- M. Karbowiak, C. Rudowicz, T. Nakamura, R. Murakami and T. Ishida, Chem. Phys. Lett., 2016, 662, 163–168 CrossRef CAS.
- Y. Rechkemmer, J. E. Fischer, R. Marx, M. Dörfel, P. Neugebauer, S. Horvath, M. Gysler, T. Brock-Nannestad, W. Frey, M. F. Reid and J. van Slageren, J. Am. Chem. Soc., 2015, 137, 13114–13120 CrossRef CAS PubMed.
- K. S. Pedersen, J. Dreiser, H. Weihe, R. Sibille, H. V. Johannesen, M. A. Sørensen, B. E. Nielsen, M. Sigrist, H. Mutka, S. Rols, J. Bendix and S. Piligkos, Inorg. Chem., 2015, 54, 7600–7606 CrossRef CAS PubMed.
- M. Perfetti, M. A. Sørensen, U. B. Hansen, H. Bamberger, S. Lenz, P. P. Hallmen, T. Fennell, G. G. Simeoni, A. Arauzo, J. Bartolomé, E. Bartolomé, K. Lefmann, H. Weihe, J. van Slageren and J. Bendix, Adv. Funct. Mater., 2018, 32(28), 1801846 CrossRef.
- M. A. Sørensen, U. B. Hansen, M. Perfetti, K. S. Pedersen, E. Bartolomé, G. G. Simeoni, H. Mutka, S. Rols, M. Jeong, I. Zivkovic, M. Retuerto, A. Arauzo, J. Bartolomé, S. Piligkos, H. Weihe, L. H. Doerrer, J. van Slageren, H. M. Rønnow, K. Lefmann and J. Bendix, Nat. Commun., 2018, 9, 1292 CrossRef PubMed.
- M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren and N. F. Chilton, J. Am. Chem. Soc., 2018, 140, 2504–2513 CrossRef CAS PubMed.
- S. D. Jiang, B. W. Wang, G. Su, Z. M. Wang and S. Gao, Angew. Chem., Int. Ed., 2010, 49, 7448–7451 CrossRef CAS PubMed.
- W. Chu, Q. Sun, X. Yao, P. Yan, G. An and G. Li, RSC Adv., 2015, 5, 94802–94808 RSC.
- I. F. Díaz-Ortega, J. M. Herrera, T. Gupta, G. Rajaraman, H. Nojiri and E. Colacio, Inorg. Chem., 2017, 56, 5594–5610 CrossRef PubMed.
- Y. Ma, G.-F. Xu, X. Yang, L.-C. Li, J. Tang, S.-P. Yan, P. Cheng and D.-Z. Liao, Chem. Commun., 2010, 46, 8264–8266 RSC.
- W.-B. Sun, B. Yan, L.-H. Jia, B.-W. Wang, Q. Yang, X. Cheng, H.-F. Li, P. Chen, Z.-M. Wang and S. Gao, Dalton Trans., 2016, 45, 8790–8794 RSC.
- W. Yu, F. Schramm, E. Moreno Pineda, Y. Lan, O. Fuhr, J. Chen, H. Isshiki, W. Wernsdorfer, W. Wulfhekel and M. Ruben, Beilstein J. Nanotechnol., 2016, 7, 126–137 CrossRef CAS PubMed.
- K. Binnemans, Chem. Rev., 2009, 109, 4283–4374 CrossRef CAS PubMed.
- K. S. Pedersen, M. A. Sørensen and J. Bendix, Coord. Chem. Rev., 2015, 299, 1–21 CrossRef CAS.
- R. E. Sievers and J. E. Sadlowski, Science, 1978, 201, 217–223 CrossRef CAS.
- L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7(3), 2074–2083 RSC.
- M. Bhaumik and C. Telk, J. Opt. Soc. Am., 1964, 54, 1211–1214 CrossRef.
- M. Irfanullah and K. Iftikhar, Inorg. Chem. Commun., 2010, 13, 694–698 CrossRef CAS.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfield, Angew. Chem., Int. Ed., 2012, 51, 6976–6980 CrossRef CAS PubMed.
- X. Yi, K. Bernot, O. Cador, J. Luzon, G. Calvez, C. Daiguebonne and O. Guillou, Dalton Trans., 2013, 42, 6728–6731 RSC.
- Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951 CrossRef CAS.
- J. K. Tang, I. Hewitt, N. T. Madhu, G. Chastanet, W. Wernsdorfer, C. E. Anson, C. Benelli, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2006, 45, 1729–1733 CrossRef CAS PubMed.
- P. E. Car, M. Perfetti, M. Mannini, A. Favre, A. Caneschi and R. Sessoli, Chem. Commun., 2011, 47, 3751–3753 RSC.
- I. J. Hewitt, Y. H. Lan, C. E. Anson, J. Luzon, R. Sessoli and A. K. Powell, Chem. Commun., 2009, 6765–6767 RSC.
- Y. N. Guo, G. F. Xu, P. Gamez, L. Zhao, S. Y. Lin, R. P. Deng, J. K. Tang and H. J. Zhang, J. Am. Chem. Soc., 2010, 132, 8538–8539 CrossRef CAS PubMed.
- P. H. Lin, T. J. Burchell, L. Ungur, L. F. Chibotaru, W. Wernsdorfer and M. Murugesu, Angew. Chem., Int. Ed., 2009, 48, 9489–9492 CrossRef CAS PubMed.
- I. J. Hewitt, J. Tang, N. Madhu, C. E. Anson, Y. Lan, J. Luzon, M. Etienne, R. Sessoli and A. K. Powell, Angew. Chem., Int. Ed., 2010, 49, 6352–6356 CrossRef CAS PubMed.
- R. J. Blagg, L. Ungur, F. Tuna, J. Speak, P. Comar, D. Collison, W. Wernsdorfer, E. J. McInnes, L. F. Chibotaru and R. E. Winpenny, Nat. Chem., 2013, 5, 673–678 CrossRef CAS.
- Y. Horii, K. Katoh, G. Cosquer, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2016, 55, 11782–11790 CrossRef CAS PubMed.
- J.-K. Ou-Yang, N. Saleh, G. F. Garcia, L. Norel, F. Pointillart, T. Guizouarn, O. Cador, F. Totti, L. Ouahab and J. Crassous, Chem. Commun., 2016, 52, 14474–14477 RSC.
- F. Pointillart, B. Le Guennic, O. Cador, O. Maury and L. n. Ouahab, Acc. Chem. Res., 2015, 48, 2834–2842 CrossRef CAS PubMed.
- M. Ren, S.-S. Bao, R. A. Ferreira, L.-M. Zheng and L. D. Carlos, Chem. Commun., 2014, 50, 7621–7624 RSC.
- F. Pointillart, B. Le Guennic, S. Golhen, O. Cador, O. Maury and L. Ouahab, Chem. Commun., 2013, 49, 615–617 RSC.
- J. Long, R. Vallat, R. A. S. Ferreira, L. D. Carlos, F. A. Almeida Paz, Y. Guari and J. Larionova, Chem. Commun., 2012, 48, 9974–9976 RSC.
- M. Perfetti, F. Pointillart, O. Cador, L. Sorace and L. Ouahab, Molecular Magnetic Materials, Concepts and Applications, 2016, pp. 345–368 Search PubMed.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620 CrossRef PubMed.
- A. Lunghi, F. Totti, S. Sanvito and R. Sessoli, Chem. Sci., 2017, 8, 6051–6059 RSC.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275 RSC.
- Y. Rechkemmer, F. D. Breitgoff, M. Van Der Meer, M. Atanasov, M. Hakl, M. Orlita, P. Neugebauer, F. Neese, B. Sarkar and J. Van Slageren, Nat. Commun., 2016, 7, 10467–10475 CrossRef CAS PubMed.
- C. Görller-Walrand and K. Binnemans, Handb. Phys. Chem. Rare Earths, 1996, 23, 121–283 Search PubMed.
- M. Perfetti, Coord. Chem. Rev., 2017, 348, 171–186 CrossRef CAS.
- P. Neugebauer, D. Bloos, R. Marx, P. Lutz, M. Kern, D. Aguilà, J. Vaverka, O. Laguta, C. Dietrich and R. Clérac, Phys. Chem. Chem. Phys., 2018, 20, 15528–15534 RSC.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- M. Reid, F-shell program, University of Canterbury, New Zealand, 1984 Search PubMed.
- F. Aquilante, L. De Vico, N. Ferré, G. Ghigo, P. å. Malmqvist, P. Neogrády, T. B. Pedersen, M. Pitoňák, M. Reiher and B. O. Roos, J. Comput. Chem., 2010, 31, 224–247 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis and characterization, shape calculations. Ab initio composition and g-tensors. Magnetic, spectroscopic and thermodynamic characterization. Crystal field splitting and composition. CCDC 1829110. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc03170c |
| ‡ Current address: Department of Chemistry, University of Copenhagen, Universitetsparken 5, 2100, Denmark. |
| § These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |