Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Engineering Kitaev exchange in stacked iridate layers: impact of inter-layer species on in-plane magnetism
Ravi
Yadav
 *a,
Mohamed S.
Eldeeb
a,
Rajyavardhan
Ray
ab,
Saicharan
Aswartham
a,
Mihai I.
Sturza
a,
Satoshi
Nishimoto
ac,
Jeroen
van den Brink
*a,
Mohamed S.
Eldeeb
a,
Rajyavardhan
Ray
ab,
Saicharan
Aswartham
a,
Mihai I.
Sturza
a,
Satoshi
Nishimoto
ac,
Jeroen
van den Brink
 ac and
Liviu
Hozoi
a
ac and
Liviu
Hozoi
a
aLeibniz Institute for Solid State and Materials Research, IFW Dresden, Helmholtzstr. 20, 01069 Dresden, Germany. E-mail: r.yadav@ifw-dresden.de
bDresden Center for Computational Materials Science (DCMS), TU Dresden, 01062 Dresden, Germany
cDepartment of Physics, Technical University Dresden, Helmholtzstr. 10, 01069 Dresden, Germany
First published on 3rd December 2018
Abstract
Novel functionalities may be achieved in oxide electronics by appropriate stacking of planar oxide layers of different metallic species, MOp and M′Oq. The simplest mechanism allowing the tailoring of the electronic states and physical properties of such heterostructures is of electrostatic nature—charge imbalance between the M and M′ cations. Here we clarify the effect of interlayer electrostatics on the anisotropic Kitaev exchange in H3LiIr2O6, a recently proposed realization of the Kitaev spin liquid. By quantum chemical calculations, we show that the precise position of H+ cations between magnetically active [LiIr2O6]3− honeycomb-like layers has a strong impact on the magnitude of Kitaev interactions. In particular, it is found that stacking with straight interlayer O–H–O links is detrimental to in-plane Kitaev exchange since coordination by a single H-ion of the O ligand implies an axial Coulomb potential at the O site and unfavorable polarization of the O 2p orbitals mediating the Ir–Ir interactions. Our results therefore provide valuable guidelines for the rational design of Kitaev quantum magnets, indicating unprecedented Kitaev interactions of ≈40 meV if the linear interlayer linkage is removed.
Introduction
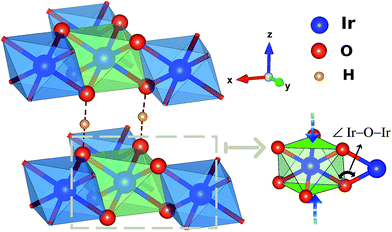
The prospect of realizing spin-liquid (SL) ground states in layered honeycomb materials with strong spin–orbit interactions1,2 has triggered intense research activity in relation to these lattice systems. Quantum SLs are of particular interest in connection with properties such as protection of quantum information and the emergence of Majorana fermions. On a honeycomb lattice (Fig. 1), the essential ingredient for the formation of a quantum SL state is the so-called Kitaev coupling (K) between nearest-neighbor (NN) magnetic sites, a bond-dependent Ising-like exchange1,2 that must be large enough as compared to the more conventional NN Heisenberg J. It reaches quite robust values for d5 electron configurations in iridium honeycomb oxides such as Na2IrO3 (ref. 3 and 4) but also in the ruthenium halide RuCl3.5,6 In the latter, a SL phase is realized by applying an external magnetic field.7,8 | ||
| Fig. 1 Honeycomb-like layer in H3LiIr2O6. A Li ion is present at the center of each hexagonal ring of edge-sharing IrO6 octahedra. | ||
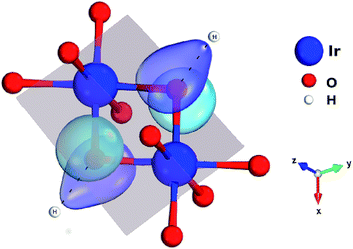
One peculiar prediction on the computational side is an enhancement of the Kitaev coupling K at large Ir–O–Ir bond angles.9 The Ir–O–Ir bond angles are 90° for cubic edge-sharing octahedra, but in most honeycomb compounds they reach larger values due to trigonal compression of the oxygen cages (see Fig. 2). The largest Ir–O–Ir bond angles so far have been reported for H3LiIr2O6, nearly 100°.10 Interestingly, Kitagawa et al. inferred a SL ground state for this material.11 We examined in this context the Kitaev interactions of H3LiIr2O6 but for ideal stacking of the honeycomb layers found rather modest K values as compared to, e.g., Na2IrO3 (ref. 3 and 4) and earlier predictions for 100° Ir–O–Ir angles.9 In an attempt to reconcile these apparently contradicting sets of computational results for large Ir–O–Ir bond angles, we addressed in detail the effect of having a single adjacent H site for each O ion and only ‘vertical’ O–H–O paths for the simplest stacking pattern.10 We establish that the axial potential created through this kind of O–H coordination polarizes and bends towards the O–H link the O 2p orbitals bridging between Ir t2g components orthogonal to the Ir2O2 plaquette (see Fig. 3). Such polarization effects are absent in Li2IrO3 and Na2IrO3, for coordination with several inter-layer cations of the O sites, but for ideal stacking in H3LiIr2O6 (ref. 10) they disrupt Ir–O–Ir electron hopping and consequently reduce the Kitaev exchange.
Numerical tests in which the two H ions next to an Ir2O2 plaquette are simply removed yield an impressively large ferromagnetic (FM) |K| value of 40 meV. Given the experimental indications for a SL ground state in H3LiIr2O6,11 these computational findings provide additional support for the existence of stacking faults10 and H-ion disorder in this system, since larger K's should in principle make the quantum SL more likely. Moreover, our results provide valuable guidelines for the rational design of Kitaev quantum magnets, indicating that electrostatic effects involving inter-layer species are very important and that the largest K values come with a more isotropic distribution of inter-layer cations around a given ligand.
Quantum chemistry exchange couplings
Each IrO6 octahedron shares edges with three NN IrO6 octahedra such that the Ir sites frame a two-dimensional (2D) honeycomb lattice in H3LiIr2O6. Similar to its parent compound α-Li2IrO3, a Li ion is present at the center of each Ir6 hexagon; an essential structural difference is the replacement of Li species between adjacent honeycomb layers by H ions. The octahedral ligand coordination of the Ir sites gives rise to a large gap between the t2g and eg 5d levels. The leading ground-state configuration is therefore 2T2g (t52g), with all five valence electrons in the t2g orbitals. This corresponds to an L = 1 orbital angular momentum12 and via strong spin–orbit coupling yields a magnetically active jeff = 1/2 ground-state doublet and lower-lying, occupied jeff = 3/2 states.2,12 The remarkable feature displayed by NN t52g ions with strong spin–orbit interactions and edge-sharing connectivity of the encircling ligand cages is a large Ising-like interaction K![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) γi
γi![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) γj between spin components perpendicular to a given M2L2 plaquette (L stands for a ligand, see Fig. 2 and 3 for more details). On a honeycomb network of ML6 octahedra this Ising-like coupling is bond dependent, i.e., the index γ(γ ∈ {x,y,z}) is different for each of the three M–M links emerging out of a given metal site M. Following Kitaev's conceptualization and initial analysis,1 strong interactions of this type were suggested to be realized in Ir oxide compounds such as Na2IrO3 and Li2IrO3.2 To derive the strength of K in the related material H3LiIr2O6, and also of additional symmetric anisotropic terms and of the isotropic Heisenberg component, we rely on ab initio many-body computational schemes from quantum chemistry. The NN superexchange is analyzed on clusters of two edge-sharing IrO6 octahedra, embedded in an effective field that models the remaining part of the crystalline lattice.
γj between spin components perpendicular to a given M2L2 plaquette (L stands for a ligand, see Fig. 2 and 3 for more details). On a honeycomb network of ML6 octahedra this Ising-like coupling is bond dependent, i.e., the index γ(γ ∈ {x,y,z}) is different for each of the three M–M links emerging out of a given metal site M. Following Kitaev's conceptualization and initial analysis,1 strong interactions of this type were suggested to be realized in Ir oxide compounds such as Na2IrO3 and Li2IrO3.2 To derive the strength of K in the related material H3LiIr2O6, and also of additional symmetric anisotropic terms and of the isotropic Heisenberg component, we rely on ab initio many-body computational schemes from quantum chemistry. The NN superexchange is analyzed on clusters of two edge-sharing IrO6 octahedra, embedded in an effective field that models the remaining part of the crystalline lattice.
Pairs of adjacent IrO6 octahedra of two slightly different types were reported on the basis of X-ray diffraction data,10 with Ir–O–Ir bond angles of either 99.0 or 99.8 degrees. Since the difference between these two values is rather small, we consider in our calculations a slightly idealized crystal structure with ‘averaged’ Ir–O–Ir bond angles of 99.4° and Ir–Ir bond lengths of 3.08 Å. For two NN octahedra, the C2h point-group symmetry allows two extra, symmetric off-diagonal exchange terms in addition to the isotropic Heisenberg and anisotropic Kitaev components.4 The effective spin Hamiltonian for a pair of pseudospins at NN Ir sites i and j can then be written as
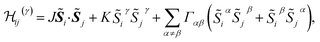 | (1) |
Multiconfigurational wavefunctions were obtained to this end by complete-active-space self-consistent-field (CASSCF) calculations,14 using an active space consisting of six t2g orbitals at the two NN Ir sites (see the Methods section for additional details). Post-CASSCF, we also performed multireference configuration-interaction (MRCI) computations14 accounting for single and double excitations out of the Ir 5d t2g and bridging-ligand 2p orbitals. The reference CASSCF wavefunctions were variationally optimized for the lowest nine singlets and nine triplets, which subsequently entered the spin–orbit treatment to yield 36 spin–orbit states. The lowest four of these states define the actual magnetic problem of two interacting pseudospin-1/2 sites, as pointed out by Jackeli and Khaliullin,2 and were mapped onto the effective spin Hamiltonian (1), in order to derive the NN effective exchange couplings. The other 32 levels lie at significantly higher energy, ≧0.5 eV, and are associated with j ≈ 3/2 to j ≈ 1/2 excitations,2,12 as shown by joint resonant inelastic X-ray scattering (RIXS) and quantum chemistry investigations.15,16 This large gap between the two sets of spin–orbit states, Ir j ≈ 1/2 and j ≈ 3/2, ensures that decoupling these two sectors in the mapping procedure is a safe approximation.2 Such a strategy is also widely applied in the context of f electron superexchange.17 All calculations were performed using the MOLPRO quantum chemistry package.18 Using the same methodology, MRCI exchange couplings in good agreement with experimental data were reported earlier for square-lattice iridates,13,19 the pyrochlore Sm2Ir2O7,20 and the perovskite CaIrO3.21,22
Results and discussion
The M–L–M angle is one of the key factors in tuning the magnitude of the Kitaev and Heisenberg components: as pointed out in ref. 9 and 23, larger angles lead to larger anisotropic interactions in honeycomb t52g oxides. Since in comparison to the related iridates Na2IrO3 and α-Li2IrO3, the Ir–O–Ir angles are on the larger side in H3LiIr2O6 (99–100°),10,11 one would expect Kitaev couplings of larger magnitude in this system. For the other iridates, FM values in the range of 15–20 meV were found by MRCI;4,9 however, for angles close to 100° and ideal stacking of successive honeycomb layers, we here compute a FM K value of only 10.9 meV (see Table 1). This suggests some subtle differences between interactions in H3LiIr2O6 and in, e.g., Na2IrO3, the identification of which constitutes a main purpose of this paper. The actual splittings among the lowest four ‘magnetic’ levels along with the other effective coupling constants are also listed in Table 1, as obtained by both CASSCF and MRCI calculations.| Magnetic splittings | CASSCF + SOC | MRCI + SOC |
|---|---|---|
| Ψ 2 = (↑↑ + ↓↓)/√2 | 0.0 | 0.0 |
| Ψ 3 = (↑↑ − ↓↓)/√2 | 0.3 | 1.1 |
| Ψ S = (↑↓ − ↓↑)/√2 | 3.3 | 4.0 |
| Ψ 1 = (↑↓ + ↓↑)/√2 | 4.9 | 7.1 |
| Effective couplings | K | J | Γ xy | Γ yz = −Γzx |
|---|---|---|---|---|
| CASSCF + SOC | −6.8 | −2.5 | −0.4 | −1.5 |
| MRCI + SOC | −10.9 | 1.8 | −0.6 | −2.0 |
We note that results similar to those provided in Table 1 are obtained by spin–orbit MRCI24 when considering the presence of two, structurally different Ir–Ir links (referred to as B1 and B2) of the type proposed in ref. 10 and 11, with somewhat different bond angles and bond lengths between the B1 and B2 blocks of NN IrO6 octahedra. Estimates for J, K and the off-diagonal couplings were also derived in very recent studies on the basis of density-functional computations.25,26K, for example, becomes significantly stronger in the latter investigations, by a few meV in ref. 25 and by a factor of nearly 2 in ref. 26.
Interlayer electrostatics, impact on Kitaev exchange
From a structural point of view, two groups of compounds can be identified within the family of 5d5 honeycomb iridates: Na2IrO3 and α-Li2IrO3, where each cation in-between the honeycomb-like sheets has six adjacent oxygen sites, and Cu2IrO3 (ref. 27) and H3LiIr2O6,10,11 displaying O–M′–O contacts with just two oxygen NNs for each inter-layer cation M′ if stacking faults are absent.10 For the latter type of interlayer connectivity, coordination by a single M′ cation of each O ligand implies an out-of-plane field and polarization of the O 2p valence electronic cloud along the O–M′–O axis. We quantified the effect of such anisotropic out-of-plane fields in an additional set of calculations, where the two hydrogen ions next to the two O sites shared by Ir NNs (see Fig. 2) were simply taken away.We find that removal of two H's next to the bridging ligands results in a nearly four-fold increase of the Kitaev exchange between in-plane NN ![[S with combining tilde]](https://www.rsc.org/images/entities/i_char_0053_0303.gif) = 1/2 sites: from ≈ −11 meV (see Table 1), it now reaches −40 meV in the spin–orbit MRCI calculations. The proximity of the positive H ions is associated with two different effects on the in-plane spin–spin interactions: (i) the ‘bare’ effect of the H-ion Coulomb potential on on-site orbital energies and intersite hopping matrix elements and (ii) O 2p orbital polarization effects that can additionally affect the Ir–O–Ir orbital overlaps and therefore, once again, the intersite hoppings. To determine which is the dominant mechanism, we performed extra computations at the CASSCF level. NN CASSCF magnetic couplings obtained for a cluster where each of the H ions next to a bridging ligand is removed and the associated ionic charge is redistributed within the embedding are listed on the first line in Table 2. This K value, −27.4 meV, corresponds to the CASSCF states used as a reference in the configuration interaction calculations leading to the MRCI result K = −40 meV. In a second step, we modeled those two H ions as simple point charges (PCs) but did not allow relaxation of the cluster orbitals. In other words, multiconfigurational computations were performed without orbital reoptimization, which are also referred to as frozen-orbital, CASFO calculations. The exchange interactions are somewhat suppressed due to the presence of the nearby positive charge (see the second line in Table 2). However, allowing the orbitals to fully relax, i.e., to react to the axial potential generated by the adjacent unit PCs, results in a much more drastic reduction of the NN magnetic couplings (see the third row in Table 2). This step by step analysis makes it clear that orbital polarization in response to the electrostatic potential induced by the inter-layer H cations is the primary cause of the lower NN interaction constants listed in Table 1.
= 1/2 sites: from ≈ −11 meV (see Table 1), it now reaches −40 meV in the spin–orbit MRCI calculations. The proximity of the positive H ions is associated with two different effects on the in-plane spin–spin interactions: (i) the ‘bare’ effect of the H-ion Coulomb potential on on-site orbital energies and intersite hopping matrix elements and (ii) O 2p orbital polarization effects that can additionally affect the Ir–O–Ir orbital overlaps and therefore, once again, the intersite hoppings. To determine which is the dominant mechanism, we performed extra computations at the CASSCF level. NN CASSCF magnetic couplings obtained for a cluster where each of the H ions next to a bridging ligand is removed and the associated ionic charge is redistributed within the embedding are listed on the first line in Table 2. This K value, −27.4 meV, corresponds to the CASSCF states used as a reference in the configuration interaction calculations leading to the MRCI result K = −40 meV. In a second step, we modeled those two H ions as simple point charges (PCs) but did not allow relaxation of the cluster orbitals. In other words, multiconfigurational computations were performed without orbital reoptimization, which are also referred to as frozen-orbital, CASFO calculations. The exchange interactions are somewhat suppressed due to the presence of the nearby positive charge (see the second line in Table 2). However, allowing the orbitals to fully relax, i.e., to react to the axial potential generated by the adjacent unit PCs, results in a much more drastic reduction of the NN magnetic couplings (see the third row in Table 2). This step by step analysis makes it clear that orbital polarization in response to the electrostatic potential induced by the inter-layer H cations is the primary cause of the lower NN interaction constants listed in Table 1.
A large amount of stacking faults was evidenced in H3LiIr2O6,10 most probably related to the rare situation in which H is bridging two adjacent O sheets. Having the hydroxyl bond in mind, it has been pointed out that an alternative way of writing the chemical formula of this compound is LiIr2O3(OH)3.10 An idealized picture arising from this formula is then that of alternating [LiIr2O6]3− and [LiIr2(OH)6]3+ honeycomb-like layers (or slabs), the latter with all bridging O's replaced by hydroxyl groups, as in the related material Li2Pt(OH)6.28 The weak bonding between layers and the inherent stacking disorder is even better highlighted in such a representation, the frail hydrogen bonds O–H⋯O being more apparent. In this context,10,28 our results strongly suggest the existence of both ‘ideally stacked’11 (i.e., weak, see Table 1) and ‘fault-present’10 (i.e., strong, see Table 2) exchange couplings in this system, which then makes the modelling of the extended magnetic lattice more complicated.
While the role of inter-layer ionic species is analyzed here for H3LiIr2O6, ongoing work29 yields similar results for the copper iridate Cu2IrO3,27 displaying similar O–M′–O interlayer contacts. These data nicely complement earlier findings concerning the sensitivity of various effective magnetic couplings to the position and charge of secondary/tertiary cations in oxide compounds.13,30 Quantities addressed in the earlier investigations were on-site parameters such as g factors13 and zero-field splittings.30 Here it is explicitly shown that also the intersite magnetic couplings can be adjusted by using electrostatic effects involving ionic species beyond the crystalline region (i.e., ‘beyond’ the bridging ligands) that is commonly assumed to be of relevance.
Angle dependence, the Kitaev limit
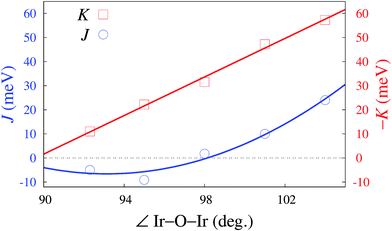
Looking at tuning structural parameters having to do with the honeycomb-like [LiIr2O6]3− slab, we further determined the evolution of both K and J with gradually modifying the Ir–O–Ir bond angles. We focused on atomic configurations where the two H cations next to the bridging ligands are removed since such arrangements are found to yield very large K's and are additionally likely to occur in the actual material. To maintain overall neutrality, the formal ionic charge associated with the two H's was again redistributed within the embedding; the Ir–Ir distance was fixed at 3.08 Å while a variable Ir–O–Ir bond angle was achieved through gradual trigonal distortion of the IrO6 octahedra (see Fig. 2). The resulting K's and J's are shown in Fig. 4. The remarkable feature is that for bond angles close to 98°, J → 0. That is, a purely anisotropic effective magnetic model can be realized according to our calculations for ≈98°, with FM Kitaev coupling constants as large as 31 meV. This critical angle defining on the computational side the Kitaev ‘limit’ is actually not so far from the bond angles reported for H3LiIr2O6 (ref. 11)—according to the quantum chemistry results, only small structural modifications would be required for reaching the regime of vanishing J. Interestingly, it turns out that not only the M–L–M angle constitutes here a tuning knob but also the interatomic distances; especially in the vicinity of the critical value θc, J can be reduced towards zero by also varying the bond lengths, via tensile strain for instance.31Exchange between honeycomb planes
A recent theoretical model32 attempting to explain the experimentally observed magnetic properties of H3LiIr2O6 (ref. 11) assumes interlayer isotropic couplings as large as 10 meV. To verify this assumption we carried out an additional set of calculations, on a cluster having as the active region two IrO6 octahedra that belong to adjacent honeycomb layers and are connected through double O–H–O paths as proposed in ref. 11 (see Fig. 2). A rather similar kind of connectivity is in fact also encountered in the 5d5 triangular-lattice system Ba3IrTi2O9;33 it is often referred to as double-edge connectivity in the case of Ba3IrTi2O9, since there is no cation in-between O sites of NN octahedra in that material.Estimates for double O–O bridges in Ba3IrTi2O9 yield interaction strengths in the range of a few meV, for both Heisenberg and Kitaev exchange.33 For O–H–O links in H3LiIr2O6, we compute by spin–orbit MRCI effective Heisenberg and Kitaev couplings in the region of 1 meV. This suggests that an interaction strength of ≈10 meV as assumed in ref. 32 for the interlayer Heisenberg exchange is rather excessive.
Conclusions
In summary, linear interlayer linkage with oxygen and inter-layer cation sites aligned in three-center bonds perpendicular to the magnetic planes reduces orbital overlap along Ir–O–Ir paths within the honeycomb-like LiIr2O6 layers and the Kitaev couplings, through polarization and bending towards the vertical O–H–O axis of the Kitaev-active O 2p orbital. Here we demonstrate this for stacked [LiIr2O6]3− honeycomb sheets with O–H–O linear linkage but similar effects should govern the magnetism of related compounds such as Cu2IrO3.27 For the latter, the interlayer O–Cu–O linear bonds are also referred to as dumbbell bonds. Interestingly, for the lighter inter-layer cation, a large amount of stacking faults has been experimentally determined.10 Our computational findings indicate that randomness in stacking of the honeycomb layers and H-ion vacancies would remove the axial cationic potential at least for part of the O ligands, which yields an unparalleled Kitaev interaction strength of −40 meV for Ir–O–Ir angles of ≈100°, larger by factors of 2–3 as compared to the honeycomb Kitaev–Heisenberg material Na2IrO3 (ref. 4) and 6 in comparison to RuCl3.5 Our results therefore provide valuable insights into the magnetism of the SL candidate H3LiIr2O6 (ref. 11) and additionally simple rules for achieving the Kitaev SL ground state in other honeycomb iridates: large Ir–O–Ir bond angles in the region of 98°, since J → 0 in that range, and coordination of the honeycomb-plane ligands by more than one inter-layer cation. Both features, the nature and the position of ionic species next to the honeycomb sheets and the size of the Ir–O–Ir bond angles, can be in principle more effectively tailored in stacked heterostructures. First steps are being made in this direction34,35 and it becomes apparent that this research area holds much potential for engineering magnetic couplings in Kitaev–Heisenberg systems.Methods
The magnetic exchange couplings between NN Ir sites were derived by calculations on embedded clusters having two edge-sharing octahedra (Ir2O10 units) as the central region. To properly describe multiorbital physics within the Ir t2g sector, we rely on a CASSCF scheme14 as the starting point. In this frame, the most obvious choice for the active multiconfigurational space is that based on having six t2g orbitals (three t2g orbitals per Ir site) and ten electrons (two holes in the Ir t2g channel). Since all possible electron configurations are here accounted for, we naturally describe in this way superexchange processes involving virtual excited states of t42g–t62g type. Additional intersite excitations, both M–M (t2g–eg) and L–M, enter our correlation treatment in the subsequent MRCI calculations.36,37 Spin–orbit couplings were computed according to the methodology described in ref. 38. To model the finite charge distribution in the immediate neighborhood, the adjacent four octahedra were also explicitly included in the calculations. Energy-consistent relativistic pseudopotentials along with quadruple-zeta basis functions39 were used for the Ir ions of the central unit. All-electron basis sets of quintuple-zeta quality40 were employed for the bridging O ligands while all-electron basis sets of triple-zeta quality40 were used for the other O anions within the two-octahedron central region. Ir4+ sites belonging to octahedra adjacent to the reference unit were described as closed-shell Pt4+ t62g species, using relativistic pseudopotentials and valence triple-zeta basis functions.39 Ligands of these adjacent octahedra that are not shared with the central reference unit were modeled with minimal all-electron atomic-natural-orbital basis sets.41 For the Li NNs we employed total-ion effective potentials with a single s valence basis function42 while two s and one p valence basis functions were used for the H NNs.43To extract the effective magnetic couplings, the lowest four spin–orbit states associated with the t52g–t52g manifold in the quantum chemical treatment were mapped onto the eigenstates of the effective spin Hamiltonian (1). To evaluate all symmetry-allowed coupling constants in (1), we additionally considered the Zeeman coupling term 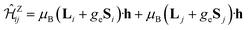 For the latter, all required matrix elements are available in the MOLPRO output data, i.e., the expectation values of the orbital angular momentum (Li, Lj) and spin (Si, Sj) operators (see also ref. 5 and 13 for additional details, in particular, the matrix elements listed in Tables 5 and 6 in ref. 5). The one to one correspondence between Hamiltonian matrix elements obtained at the ab initio and effective-model levels allows us to evaluate all coupling constants involved in (1).5,13,20
For the latter, all required matrix elements are available in the MOLPRO output data, i.e., the expectation values of the orbital angular momentum (Li, Lj) and spin (Si, Sj) operators (see also ref. 5 and 13 for additional details, in particular, the matrix elements listed in Tables 5 and 6 in ref. 5). The one to one correspondence between Hamiltonian matrix elements obtained at the ab initio and effective-model levels allows us to evaluate all coupling constants involved in (1).5,13,20
Additional quantum chemistry computations were performed to investigate the strength of magnetic exchange between Ir sites belonging to adjacent honeycomb layers, connected via double O–H–O pathways. For this set of calculations, an Ir2O12H2 unit was used as the central region. The six NN IrO6 octahedra directly coordinating the two reference octahedra (three NN octahedra around each ‘central’ octahedron) plus eight H NNs lying close to the central fragment were also included in the calculations, for better representation of the immediate neighborhood. The two Ir ions in the central unit were represented by energy-consistent relativistic pseudopotentials along with triple-zeta basis functions.39 All-electron basis sets of quintuple-zeta quality40 were employed for the four O ligands on the O–H–O contacts while all-electron basis sets of triple-zeta quality40 were used for the remaining O ions within the central region; triple-zeta basis sets40 were applied for the two bridging H's. Ir4+ sites belonging to octahedra adjacent to the central region were described as closed-shell Pt4+ t62g species, using relativistic pseudopotentials and valence double-zeta basis functions.39 Ligands of these adjacent octahedra that are not shared with the central reference unit were modeled with minimal all-electron atomic-natural-orbital basis sets.41 For the Li NNs we employed total-ion effective potentials with a single s valence basis function42 while double-zeta basis functions were utilized for the remaining H ions.40 PC embeddings were used in all calculations, as in earlier quantum chemistry investigations of honeycomb iridates.4,9,15
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Calculations were performed at the High Performance Computing Center (ZIH) of the Technical University Dresden (TUD). We thank U. Nitzsche for technical assistance. We acknowledge financial support from the German Science Foundation (Deutsche Forschungsgemeinschaft, DFG—SFB-1143 and STU 695/1-1) and thank V. M. Katukuri, M. B. Valldor, K. Koepernik, M. Richter, and S. L. Drechsler for instructive discussions. R. R. acknowledges financial support from the European Union (ERDF) and the Free State of Saxony via the ESF project 100231947 (Young Investigators Group “Computer Simulations for Materials Design” – CoSiMa).Notes and references
- A. Kitaev, Ann. Phys., 2006, 321, 2–111 CAS.
- G. Jackeli and G. Khaliullin, Phys. Rev. Lett., 2009, 102, 017205 CrossRef CAS PubMed.
- Y. Yamaji, Y. Nomura, M. Kurita, R. Arita and M. Imada, Phys. Rev. Lett., 2014, 113, 107201 CrossRef PubMed.
- V. M. Katukuri, S. Nishimoto, V. Yushankhai, A. Stoyanova, H. Kandpal, S. Choi, R. Coldea, I. Rousochatzakis, L. Hozoi and J. van den Brink, New J. Phys., 2014, 16, 013056 CrossRef.
- R. Yadav, N. A. Bogdanov, V. M. Katukuri, S. Nishimoto, J. van den Brink and L. Hozoi, Sci. Rep., 2016, 6, 37925 CrossRef CAS PubMed.
- S. M. Winter, Y. Li, H. O. Jeschke and R. Valentí, Phys. Rev. B, 2016, 93, 214431 CrossRef.
- S.-H. Baek, S.-H. Do, K.-Y. Choi, Y. S. Kwon, A. U. B. Wolter, S. Nishimoto, J. van den Brink and B. Büchner, Phys. Rev. Lett., 2017, 119, 037201 CrossRef PubMed.
- Z. Wang, S. Reschke, D. Hüvonen, S.-H. Do, K.-Y. Choi, M. Gensch, U. Nagel, T. Rõõm and A. Loidl, Phys. Rev. Lett., 2017, 119, 227202 CrossRef PubMed.
- S. Nishimoto, V. M. Katukuri, V. Yushankhai, H. Stoll, U. K. Rößler, L. Hozoi, I. Rousochatzakis and J. van den Brink, Nat. Commun., 2016, 7, 10273 CrossRef CAS PubMed.
- S. Bette, T. Takayama, K. Kitagawa, R. Takano, H. Takagi and E. Dinnebier, Dalton Trans., 2017, 46, 15216 RSC.
- K. Kitagawa, T. Takayama, Y. Matsumoto, A. Kato, R. Takano, Y. Kishimoto, S. Bette, R. Dinnebier, G. Jackeli and H. Takagi, Nature, 2018, 554, 341–345 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon Press, 1970 Search PubMed.
- N. A. Bogdanov, V. M. Katukuri, J. Romhányi, V. Yushankhai, V. Kataev, B. Büchner, J. van den Brink and L. Hozoi, Nat. Commun., 2015, 6, 7306 CrossRef CAS PubMed.
- T. Helgaker, P. Jorgensen and J. Olsen, Molecular Electronic-Structure Theory, Wiley, Chichester, 2000 Search PubMed.
- H. Gretarsson, J. P. Clancy, X. Liu, J. P. Hill, E. Bozin, Y. Singh, S. Manni, P. Gegenwart, J. Kim, A. H. Said, D. Casa, T. Gog, M. H. Upton, H.-S. Kim, J. Yu, V. M. Katukuri, L. Hozoi, J. van den Brink and Y.-J. Kim, Phys. Rev. Lett., 2013, 110, 076402 CrossRef CAS PubMed.
- L. Hozoi, H. Gretarsson, J. P. Clancy, B.-G. Jeon, B. Lee, K. H. Kim, V. Yushankhai, P. Fulde, D. Casa, T. Gog, J. Kim, A. H. Said, M. H. Upton, Y. J. Kim and J. van den Brink, Phys. Rev. B, 2014, 89, 115111 CrossRef.
- V. Nekvasil and I. Veltruský, J. Magn. Magn. Mater., 1990, 86, 315–325 CrossRef CAS.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 242 CAS.
- V. M. Katukuri, V. Yushankhai, L. Siurakshina, J. van den Brink, L. Hozoi and I. Rousochatzakis, Phys. Rev. X, 2014, 4, 021051 Search PubMed.
- R. Yadav, M. Pereiro, N. A. Bogdanov, S. Nishimoto, A. Bergman, O. Eriksson, J. van den Brink and L. Hozoi, Phys. Rev. Mater., 2018, 2, 074408 CrossRef.
- N. A. Bogdanov, V. M. Katukuri, H. Stoll, J. van den Brink and L. Hozoi, Phys. Rev. B, 2012, 85, 235147 CrossRef.
- M. M. Sala, K. Ohgushi, A. Al-Zein, Y. Hirata, G. Monaco and M. Krisch, Phys. Rev. Lett., 2014, 112, 176402 CrossRef PubMed.
- V. M. Katukuri, S. Nishimoto, I. Rousochatzakis, H. Stoll, J. van den Brink and L. Hozoi, Sci. Rep., 2015, 5, 14718 CrossRef CAS PubMed.
- R. Yadav, R. Ray, M. S. Eldeeb, S. Nishimoto, L. Hozoi and J. van den Brink, Phys. Rev. Lett., 2018, 121, 197203 CrossRef PubMed.
- Y. Li, S. M. Winter and R. Valentí, arXiv:1807.02124, 2018.
- S. Wang, L. Zhang and F. Wang, arXiv:1807.03092, 2018.
- M. Abramchuk, C. Ozsoy-Keskinbora, J. W. Krizan, K. R. Metz, D. C. Bell and F. Tafti, J. Am. Chem. Soc., 2017, 139, 15371–15376 CrossRef CAS PubMed.
- D. E. Bugaris, M. D. Smith and H.-C. zur Loye, Inorg. Chem., 2013, 52, 3836–3844 CrossRef CAS PubMed.
- M. S. Eldeeb, R. Yadav, R. Ray, J. van den Brink and L. Hozoi, unpublished.
- N. A. Bogdanov, R. Maurice, I. Rousochatzakis, J. van den Brink and L. Hozoi, Phys. Rev. Lett., 2013, 110, 127206 CrossRef PubMed.
- R. Yadav, S. Rachel, L. Hozoi, J. van den Brink and G. Jackeli, Phys. Rev. B, 2018, 98, 121107 CrossRef.
- K. Slagle, W. Choi, L. E. Chern and Y. B. Kim, Phys. Rev. B, 2018, 97, 115159 CrossRef.
- A. Catuneanu, J. G. Rau, H.-S. Kim and H.-Y. Kee, Phys. Rev. B, 2015, 92, 165108 CrossRef.
- M. Jenderka, R. Schmidt-Grund, M. Grundmann and M. Lorenz, J. Appl. Phys., 2015, 117, 025304 CrossRef.
- M. Jenderka, J. Barzola-Quiquia, Z. Zhang, H. Frenzel, M. Grundmann and M. Lorenz, Phys. Rev. B, 2013, 88, 045111 CrossRef.
- H.-J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- P. J. Knowles and H.-J. Werner, Theor. Chim. Acta, 1992, 84, 1432–2234 CrossRef.
- A. Berning, M. Schweizer, H.-J. Werner, P. J. Knowles and P. Palmieri, Mol. Phys., 2000, 98, 1823 CrossRef CAS.
- D. Figgen, K. A. Peterson, M. Dolg and H. Stoll, J. Chem. Phys., 2009, 130, 164108 CrossRef PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- K. Pierloot, B. Dumez, P.-O. Widmark and B. O. Roos, Theor. Chim. Acta, 1995, 90, 87 CrossRef CAS.
- P. Fuentealba, H. Preuss, H. Stoll and L. v. Szentpály, Chem. Phys. Lett., 1982, 89, 418–422 CrossRef CAS.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |