Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reduction of CO2 by a masked two-coordinate cobalt(I) complex and characterization of a proposed oxodicobalt(II) intermediate†‡
Lisa
Roy§
 ag,
Malik H.
Al-Afyouni§
b,
Daniel E.
DeRosha§
c,
Bhaskar
Mondal
ag,
Malik H.
Al-Afyouni§
b,
Daniel E.
DeRosha§
c,
Bhaskar
Mondal
 a,
Ida M.
DiMucci
d,
Kyle M.
Lancaster
a,
Ida M.
DiMucci
d,
Kyle M.
Lancaster
 d,
Jason
Shearer
d,
Jason
Shearer
 e,
Eckhard
Bill
a,
William W.
Brennessel
e,
Eckhard
Bill
a,
William W.
Brennessel
 b,
Frank
Neese
f,
Shengfa
Ye
b,
Frank
Neese
f,
Shengfa
Ye
 *f and
Patrick L.
Holland
*f and
Patrick L.
Holland
 *c
*c
aMax Planck Institute for Chemical Energy Conversion, Stiftstraße 34-36, Mülheim an der Ruhr, D-45470, Germany
bDepartment of Chemistry, University of Rochester, Rochester, New York 14618, USA
cDepartment of Chemistry, Yale University, New Haven, Connecticut 06520, USA. E-mail: patrick.holland@yale.edu
dDepartment of Chemistry and Chemical Biology, Baker Laboratory, Cornell University, Ithaca, New York 14853, USA
eDepartment of Chemistry, Trinity University, San Antonio, Texas 78212, USA
fMax Planck Institute for Coal Research, Kaiser-Wilhelm-Platz 1, Mülheim an der Ruhr, D-45470, Germany. E-mail: shengfa.ye@kofo.mpg.de
gCSIR Central Mechanical Engineering Research Institute, Durgapur 713209, India
First published on 9th November 2018
Abstract
Fixation and chemical reduction of CO2 are important for utilization of this abundant resource, and understanding the detailed mechanism of C–O cleavage is needed for rational development of CO2 reduction methods. Here, we describe a detailed analysis of the mechanism of the reaction of a masked two-coordinate cobalt(I) complex, LtBuCo (where LtBu = 2,2,6,6-tetramethyl-3,5-bis[(2,6-diisopropylphenyl)imino]hept-4-yl), with CO2, which yields two products of C–O cleavage, the cobalt(I) monocarbonyl complex LtBuCo(CO) and the dicobalt(II) carbonate complex (LtBuCo)2(μ-CO3). Kinetic studies and computations show that the κN,η6-arene isomer of LtBuCo rearranges to the κ2N,N′ binding mode prior to binding of CO2, which contrasts with the mechanism of binding of other substrates to LtBuCo. Density functional theory (DFT) studies show that the only low-energy pathways for cleavage of CO2 proceed through bimetallic mechanisms, and DFT and highly correlated domain-based local pair natural orbital coupled cluster (DLPNO-CCSD(T)) calculations reveal the cooperative effects of the two metal centers during facile C–O bond rupture. A plausible intermediate in the reaction of CO2 with LtBuCo is the oxodicobalt(II) complex LtBuCoOCoLtBu, which has been independently synthesized through the reaction of LtBuCo with N2O. The rapid reaction of LtBuCoOCoLtBu with CO2 to form the carbonate product indicates that the oxo species is kinetically competent to be an intermediate during CO2 cleavage by LtBuCo. LtBuCoOCoLtBu is a novel example of a thoroughly characterized molecular cobalt–oxo complex where the cobalt ions are clearly in the +2 oxidation state. Its nucleophilic reactivity is a consequence of high charge localization on the μ-oxo ligand between two antiferromagnetically coupled high-spin cobalt(II) centers, as characterized by DFT and multireference complete active space self-consistent field (CASSCF) calculations.
Introduction
Terminal oxo complexes of transition metals are often invoked as intermediates in hydrocarbon activation,1–3 oxygen atom transfer4,5 and water oxidation.6,7 Dinuclear oxo-bridged systems have garnered less attention, even though they have numerous important roles in reactive metallocofactors,8,9 materials,10 catalysts,11 and physiological processes.12 Like other first row transition metals, cobalt has received growing interest for catalysis due to its versatility and low cost.13 In particular, cobalt species containing doubly bridged oxo- or hydroxo-bridged cobalt subunits14 are in focus in the context of water oxidation.15,16 However, dinuclear Co–O–Co compounds with a single oxo bridge, the simplest bridging cobalt oxo species, are rare and only two examples have been reported. Stauber et al. presented a formally dianionic dicobalt(III) oxo species, for which XAS and computational results indicated an unusual electronic structure comprising two cobalt(II) ions, a bridging oxyl radical and an additional “hole” on the supporting ligand.17 The earlier example of a dicobalt oxo species by Zhang et al. does not include sufficient spectroscopic details to establish the oxidation states of the metals.18 Thus, understanding the chemical behavior of dicobalt(II) oxo complexes remains elusive.Here, we describe a new oxodicobalt(II) complex that arises in the context of CO2 reduction. Carbon dioxide is a persistent environmental pollutant and a C1 feedstock for chemical industries, which has inspired a large amount of research on transition metal catalysts for CO2 reduction.19–21 The practical motivations for CO2 transformation are accompanied by fundamental interest in the detailed mechanisms and charge localization in reduced CO2 intermediates.19,22 Here, we focus on cobalt complexes, which are under active study because they are adept at catalytic reductions of CO2 to CO.13,23–31
In the work described here, we use the reduced, unsaturated cobalt site in LtBuCo (1), a “masked” two-coordinate complex supported by the β-diketiminate ligand 2,2,6-6-tetramethyl-3,5-bis[(2,6-diisopropylphenyl)imino]hept-4-yl (LtBu).32 Its reaction with CO2 cleaves a C–O bond in CO2, and we use a combination of experimental kinetics, density functional theory (DFT), and highly correlated domain-based local pair natural orbital coupled cluster theory with single, double, and perturbative triple excitations (DLPNO-CCSD(T)) to show cooperation of two Co ions for facilitating a bimetallic reaction pathway for CO2 reduction. We demonstrate that a likely intermediate is the Co2+–O2−–Co2+ complex LtBuCoOCoLtBu, which can be independently synthesized using N2O. We investigate the electronic structure and reactivity of this new oxodicobalt(II) complex in detail, including multi-reference complete active space self-consistent field (CASSCF) calculations.
Results and discussion
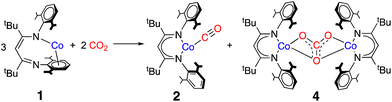
Activation of CO2 by LtBuCo
The cobalt(I) source LtBuCo (1) was synthesized and characterized earlier,32 and features a supporting β-diketiminate ligand that is bound in an unusual k1,η6 binding mode as shown at the left of Scheme 1. The reactivity of 1 includes the binding of Lewis bases like THF, CO, N2, pyridine and PPh3, and the cleavage of C–F bonds in fluoroarenes.32,33 We also reported the activation of O2 at 1.34 Each of these reactions causes ligand rearrangement to the more typical κ2-binding mode of the β-diketiminate ligand in the three-coordinate or four-coordinate products. This led to a description of 1 as a “masked” low-valent two-coordinate Co complex. However, in these studies, a two-coordinate isomer of 1 with κ2-binding of diketiminate was never formed; kinetic studies of the reaction of 1 with pyridine showed a first-order dependence on pyridine coordination which, when combined with supporting DFT investigations, indicated that the incoming ligand coordinates prior to “slipping” of the arene.32 Computational studies on the reaction with CO indicated a similar associative pathway, in which ligand binding precedes diketiminate rearrangement.35 The high reactivity of 1 toward small molecules, in conjunction with our interest in understanding the role of low-valent cobalt complexes in CO2 reduction, prompted us to investigate its reaction with CO2. We were limited to aliphatic hydrocarbon solvents, due to the reaction of 1 with arenes and ethers.32The addition of 10 molar equivalents of CO2 gas to LtBuCo in cyclohexane-d12 causes a slow color change from brown to red-orange over several hours at 10 °C. 1H NMR spectroscopy shows the appearance of new paramagnetically shifted peaks (Fig. S3‡). Comparison of the resultant spectra to those of independently synthesized compounds shows that the products are a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of previously reported LtBuCo(CO) (2)35 and the new carbonate-bridged compound LtBuCo(μ-OCO2)CoLtBu (4) (Scheme 1). Comparison to an internal integration standard indicates that 2 and 4 are each formed in >86% spectroscopic yield. These two products can be separated and isolated as pure solids in 66% and 40% yields, respectively, with the lower isolated yields attributed to losses during crystallization.
1 mixture of previously reported LtBuCo(CO) (2)35 and the new carbonate-bridged compound LtBuCo(μ-OCO2)CoLtBu (4) (Scheme 1). Comparison to an internal integration standard indicates that 2 and 4 are each formed in >86% spectroscopic yield. These two products can be separated and isolated as pure solids in 66% and 40% yields, respectively, with the lower isolated yields attributed to losses during crystallization.
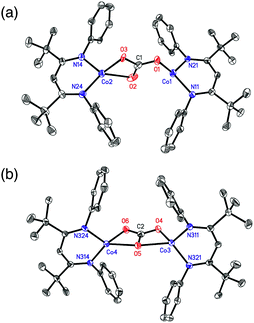
Characterization of the dicobalt(II) carbonate product
X-ray quality crystals of 4 were grown from toluene, and analysis of the diffraction data revealed two independent sites in the asymmetric unit with different carbonate binding modes to the Co centers: (site a) μ-η1:η2 and (site b) μ-η2:η2 (Fig. 1). Site a also had disorders in the core, with two conformations of μ-η1:η2 carbonate in a 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 ratio that differ by which Co atom is η1 and which is η2. The major component in site a is discussed here for simplicity. Two binding modes of a bridging carbonate were also observed in the crystal structure of an analogous Fe complex.36 Most M–O distances are shorter in the Co compound, which is attributable to its smaller ionic radius. However, the Co(1)–O(1) bond in the η1:η2 molecule (1.921(4) Å) (see Table 1) is longer than the analogous Fe–O bond (1.881(1) Å),36 suggesting that π-bonding in the η1–Fe–O interaction is greater than that for the Co–O interaction. Complex 4 has averaged D2h symmetry in solution, as ascertained by the presence of seven signals in the 1H NMR spectrum, suggesting that the carbonate interconverts rapidly between the η1:η2 and η2:η2 binding modes in solution.
23 ratio that differ by which Co atom is η1 and which is η2. The major component in site a is discussed here for simplicity. Two binding modes of a bridging carbonate were also observed in the crystal structure of an analogous Fe complex.36 Most M–O distances are shorter in the Co compound, which is attributable to its smaller ionic radius. However, the Co(1)–O(1) bond in the η1:η2 molecule (1.921(4) Å) (see Table 1) is longer than the analogous Fe–O bond (1.881(1) Å),36 suggesting that π-bonding in the η1–Fe–O interaction is greater than that for the Co–O interaction. Complex 4 has averaged D2h symmetry in solution, as ascertained by the presence of seven signals in the 1H NMR spectrum, suggesting that the carbonate interconverts rapidly between the η1:η2 and η2:η2 binding modes in solution.
| η1:η2 | η2:η2 | ||
|---|---|---|---|
| Expt. | Calc. | ||
| a The optimized geometry with S = 3. The BP86/B1 (B1 = TZVP basis set on Co, O, N and carbonate C, and def2-SVP on the rest of the atoms) level of theory was used to model the η2:η2 conformer. See the ESI for computational details. | |||
| Co(1)–O(1)/Co(3)–O(4) | 1.921(4) | 1.970(3) | 2.01 |
| Co(1)–O(2)/Co(3)–O(5) | 2.720(8) | 2.218(3) | 2.23 |
| Co(2)–O(2)/Co(4)–O(5) | 2.138(5) | 2.211(3) | 2.25 |
| Co(2)–O(3)/Co(4)–O(6) | 1.985(3) | 1.979(2) | 2.00 |
| C(1)–O(1)/C(2)–O(4) | 1.276(8) | 1.321(4) | 1.28 |
| C(1)–O(2)/C(2)–O(5) | 1.290(7) | 1.266(4) | 1.32 |
| C(1)–O(3)/C(2)–O(6) | 1.294(7) | 1.263(4) | 1.28 |
| O(1)–C(1)–O(2)/O(4)–C(2)–O(5) | 121.8(6) | 117.4(3) | 117.60 |
| O(2)–C(1)–O(3)/O(5)–C(2)–O(6) | 116.1(6) | 117.4(3) | 117.61 |
| O(3)–C(1)–O(1)/O(4)–C(2)–O(6) | 122.1(6) | 125.1(3) | 124.79 |
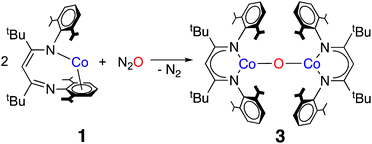
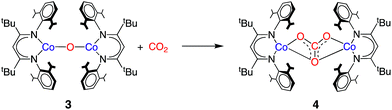
Experimental characterization of a cobalt(II) oxo complex
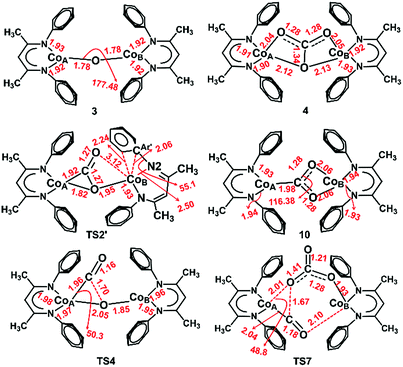
The formation of a carbonate bridge in 4 implicates an unobserved oxocobalt species as an intermediate (see the following sections for calculations). In fact, in an earlier study on CO2 reduction by LtBuFeNNFeLtBu, Sadique et al. proposed that the formation of a carbonate bridge proceeds through an oxodiiron(II) intermediate.37 Despite a number of attempts made using 1H NMR and UV-vis spectroscopy at temperatures between −80 °C and 25 °C, we observed no intermediates during the formation of 4 from LtBuCo and CO2. Therefore, we chose to experimentally test the accessibility of an oxodicobalt(II) species by synthesizing it through a different route. We added 1 equiv. of N2O to a solution of 1 in hexane at room temperature for 4 h, and after workup, red-orange 3 was isolated in 51% yield (Scheme 2). The solid-state structure (Fig. 2 and Table 2) shows 3 to be a dinuclear cobalt complex bridged by a single oxygen atom. The Co–O distance of 1.704(4) Å is much shorter than that in the only other fully characterized oxo-bridged dicobalt complex, which is four coordinated at each cobalt atom and has a Co–O bond distance of 1.995(11) Å.17 The Co–O bond in 3 is shorter than the distance of 1.784(3) Å found in ([Me2NN]Co)2(μ-O)2 ([Me2NN] = 2,4-bis[(2,6-dimethylphenyl)imino]pent-3-yl), a bis(μ-oxo)dicobalt(III) complex reported by Dai et al.38 The Co–O–Co in 3 is slightly bent at 166.9(3)°. The Co–N bond distances are also shorter (<1.96 Å) than those in four-coordinate diketiminatocobalt(II) complexes32 and agree well with those observed for other three-coordinate cobalt(II) complexes.39 The C–C and C–N bond distances within the β-diketiminate of 3 are within the error of the analogous distances in the known three-coordinate cobalt(II) compound LtBuCoCl,40 suggesting that there is no change in the oxidation state of the supporting ligand (see ESI Section O‡). The redox innocence importantly implies a physical oxidation state of +2 for both metal centers.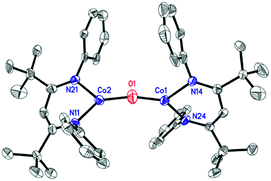 | ||
| Fig. 2 X-ray crystal structure of 3. Thermal ellipsoids are shown at 50% probability. H atoms and isopropyl groups are omitted for clarity. | ||
| Expt. | Calc. | |
|---|---|---|
| a The optimized geometry of the S = 0 ground state (from antiferromagnetic coupling of cobalt site spins) using the BP86/B1 (B1 = TZVP basis set on Co, O, and N; def2-SVP on the rest of the atoms) level of theory. See the ESI for computational details. | ||
| Co1–O1 | 1.704(4) | 1.72 |
| Co1–N24 | 1.913(4) | 1.89 |
| Co1–N14 | 1.950(4) | 1.91 |
| Co2–O1 | 1.699(4) | 1.72 |
| Co2–N11 | 1.919(4) | 1.89 |
| Co2–N21 | 1.949(4) | 1.91 |
| Co1–O1–Co2 | 166.9(3) | 165.5 |
| O1–Co1–N24 | 136.7(2) | 134.5 |
| O1–Co1–N14 | 124.2(2) | 123.8 |
| N24–Co1–N14 | 98.7(2) | 101.7 |
| O1–Co2–N11 | 135.2(2) | 135.5 |
| O1–Co2–N21 | 125.3(2) | 122.9 |
| N11–Co2–N21 | 99.4(2) | 101.6 |
| N24–N14–N21–N11 | 85.8 | 82.3 |
In order to further test the metal oxidation state, we collected cobalt K-edge X-ray absorption spectroscopy (XAS) data for 3 and several previously reported compounds: three-coordinate cobalt(II) complex LtBuCoCl,39 four-coordinate oxygen-coordinated cobalt(II) complex LtBuCo(μ-OH)2CoLtBu, and four-coordinate oxygen-coordinated cobalt(III) complex LtBuCo(μ-O)2CoLtBu.34 The pre-edge and edge features overlapped in all of the compounds, including the previously reported cobalt(II) and cobalt(III) analogues (Fig. S10‡), indicating that XAS does not unambiguously distinguish the oxidation level. This ambiguity is unfortunate, but fairly common.41 Comparison of cobalt(II) and cobalt(III) species using X-ray photoelectron spectroscopy gave similarly ambiguous results.
The presence of an oxo in 3 is particularly notable, given the paucity of cobalt(II) oxo complexes.17,18 CoIII2(μ-O)2 complexes have also been described.34,38 Another relevant comparison is to the diiron(II) complex [LtBuFe]2O,42 which has the same supporting ligand and connectivity as 3. The M–O bond length is shorter for cobalt (Co–O = 1.704(4) Å) than iron (Fe–O = 1.7503(4) Å), as expected from the smaller ionic radius of cobalt(II) versus iron(II). The method of preparing 3 is also interesting, because N2O is often kinetically inert, particularly in reactions with late transition metal complexes.43–45 This serves as another demonstration of the high reactivity of the masked two-coordinate complex LtBuCo toward cleaving strong bonds.32,34
Electronic structure of the Co–O–Co core and its connection to reactivity
Previous studies have highlighted the correlation between reactivity and the electronic structure.46–49 We first carried out broken symmetry density functional theory (DFT) calculations on 3 using the BP86 functional. Geometry optimization with BP86 and a mixed basis set combination, B1 (triple-ζ quality TZVP50 basis set on Co, O, N, and selected C atoms, and a double ζ quality split-valence basis set, def2-SVP,51 on the rest of the atoms, in a polarizable continuum solvent model, CPCM,52 using ε = 2.3 for benzene, and D3BJ empirical dispersion), gave a core geometry that is in good agreement with the X-ray crystal structure, including the slight Co–O–Co bending, as shown in Table 2. Using this geometry, single-point calculations with pure BP86, meta-GGA M06L, and hybrid B3LYP density functionals all predicted a local high-spin d7 configuration for each cobalt center. The two cobalt(II) centers are antiferromagnetically coupled, which is achieved through three pathways as indicated by three spin-coupled pairs with overlaps in the range of 0.2 to 0.5. The metal–ligand interactions are largely ionic, because doubly occupied metal d-centered orbitals and the spin coupled orbital pairs have >90% Co d-parentage. A similar electronic structure is observed for the hypothetical high spin ferromagnetically coupled species. These analyses indicated the electronic structure of 3 to be a dicobalt(II) oxo irrespective of the density functional employed (see ESI Section U‡).The unusual electronic structure of another dicobalt oxo species17 encouraged us to examine the electronic structure of intermediate 3 more carefully. Therefore, we pursued CASSCF calculations (on the DFT-optimized geometry) using an active space that distributes 20 electrons into 13 orbitals (CASSCF(20,13)), the ten cobalt 3d-based orbitals and the three 2p orbitals of the oxo ligand. For the present purpose of analyzing metal–ligand bonding, it is not necessary to employ an enlarged active space including double d and/or p shells of the metal center and the oxo ligand. As shown in Fig. 3, the singlet wavefunction has strong multireference character, with several competing configuration state functions having a weight in the range of 0.2–6.2% (Table S5‡). Inspection of the natural orbitals obtained from the CASSCF(20,13) calculations shows that complex 3 is best described as having two high spin cobalt(II) centers bridged by an oxo ligand, CoII–O2−–CoII. Notably, the electronic structure of 3 differs from that proposed for the previously reported Co–O–Co complex, which contains two cobalt(II) ions, an oxyl ligand, and a “hole” in the supporting ligand.17 Note that due to the substantial multireference character, one cannot apply the CCSD approach to the singlet state. The septet CASSCF(20,13) solution is essentially single reference in nature, because the leading configuration accounts for 88% of the wavefunction. We further enlarged the active space to include diketiminate π and π* orbitals (CASSCF(24,17)), which accounts for the possibility of ligand-based radicals, as discussed above for another dicobalt oxo complex found in the literature.17 However, the larger CASSCF(24,17) active space predicts an identical bonding picture to CASSCF(20,13) (for details, see ESI, Section P‡). Therefore, we discuss only the CASSCF(20,13) solution.
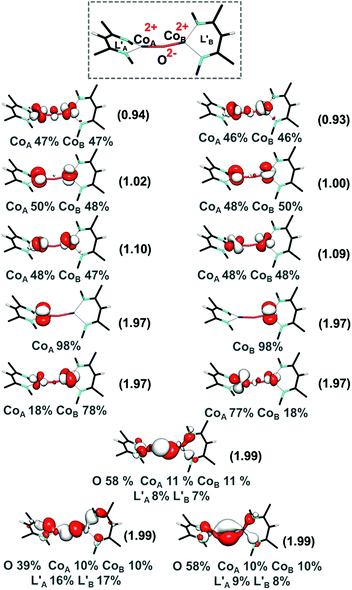 | ||
| Fig. 3 CASSCF(20,13) natural orbitals along with occupation numbers in parentheses for the S = 0 state of intermediate 3. Atomic contributions to each orbital are also shown. | ||
In line with the DFT results, the Co–O interaction computed by CASSCF for 3 is very polar, with only ∼20% cobalt 3d character in the oxygen-based orbitals and predominant cobalt d-parentage (>90%) in the metal-based orbitals. This is quite different from high-valent mononuclear metal–oxo species like ferryls, which feature more covalent metal–ligand interactions.53–56 For example, in [Fe(O)(TMC)(NCCH3)]2+ (TMC = tetramethylcyclam), there is 56% Fe(d) and 32% O(p) character in the Fe–O σ-bond and 54% Fe(d) and 36% O(p) in the Fe–O π-bond.53 The different bonding picture in 3 can be attributed to the lower oxidation state of cobalt and the competitive bonding of the two metal centers with the oxo ligand. Furthermore, the calculated high electron density on the oxygen atom, as found from the population analysis (Mulliken gross atomic charges on O = −0.6195 a.u. and on Co centers = 0.6036 and 0.5989 a.u. at the BP86/def2-TZVPP level of theory; see ESI, Section U‡), is consistent with facile nucleophilic attack on CO2. The bonding picture in 3 contrasts with high-valent metal–oxo intermediates, in which covalent metal–oxo interactions govern the electrophilic reactivity.46,57,58
Kinetic studies on the CO2 reduction pathway
Initial insight into the mechanism of CO2 reduction by LtBuCo was gained through kinetic studies using 1H NMR spectroscopy. After injection of a solution of excess CO2 into a solution of 1 in C6D12 at 10 °C, the reaction was monitored by NMR spectroscopy (see ESI Section C for details‡). The concentrations of 1, 2 and 4 fit to exponential decays over more than six half-lives. The first-order rate constant of 3.7 ± 0.5 × 10−4 s−1 was independent of the flooding concentration of CO2, indicating that the rate law has the form rate = k[1]. The zero-order dependence of the rate on [CO2] indicates that the rate-limiting step occurs prior to CO2 binding and prevents the use of kinetic measurements to elucidate steps after CO2 binding. Hence, we use computations to evaluate these steps below.We considered that 3 could be formed as an intermediate that could react with CO2 rapidly to give 4; if its consumption were more rapid than its formation, it might not be observed during the reaction. With pure samples of 3 in hand, we tested this hypothesis. Treating a solution of 3 in C6D12 with 1.5 equivalents of CO2 for 2 min at 10 °C resulted in a high conversion (75%) of 3 to 4 (Scheme 3 and Fig. S5‡). The much more rapid reaction of CO2 with 3 compared to 1, furnishing the same product, indicates that the reaction of the oxo species with CO2 is kinetically competent to be a step in the formation of 2 and 4 from 1 and CO2.
Computational investigations on the mechanism of CO2 reduction
To gain additional insight into the reaction mechanism, we pursued computations using a model in which the bulky β-diketiminate ligand (LtBu) was slightly truncated to L′ (2,4-bis[(2,6-diisopropylphenyl)imino]pent-3-yl, Chart 1, right) where tBu substituents are replaced by methyl groups. The overlay of the crystal structure of 1 and the optimized geometry with the truncated ligand (Fig. S11 and Table S2‡) shows that truncation leads to negligible differences in key metrical parameters. As above, the BP86(CPCM,D3BJ)/B1 level of theory was employed to optimize geometries and compute frequencies. We chose the local coupled-cluster approach with the DLPNO-CCSD(T) method to verify the reliability of crucial stationary points obtained with the meta-GGA M06L and hybrid B3LYP methods. We note that the CCSD(T) approach cannot be applied to complexes involving two antiferromagnetically coupled metal centers, such as the open-shell singlet state of complex 3. Therefore, we performed the DLPNO-CCSD(T) calculations on the spin-aligned state of the bimetallic complexes. Although the CASSCF approach accounts for static correlation of electrons correctly (i.e. near-degeneracy effects), to produce reliable energies, it has to be followed by CASPT2 or NEVPT2 corrections to capture the dynamic correlation for instantaneous electron motions. Because of the exorbitant computational cost, this combined approach was not used to evaluate the energies of all intermediates and transition states. Instead, we employed open-shell DLPNO-CCSD(T), a straightforward approach, to construct reliable potential energy surfaces. For more details about the computational methods and basis sets used, see ESI, Section A.‡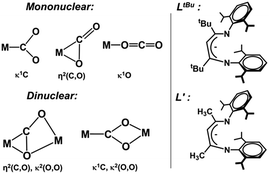 | ||
| Chart 1 (Left) Different binding modes of CO2 to mononuclear and dinuclear metal sites. (Right) Actual and truncated ligand frameworks. | ||
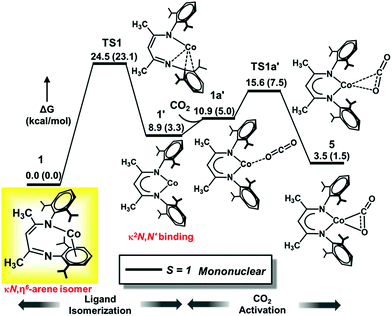
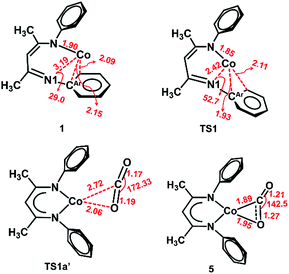
Compound 1 was previously termed a “masked two-coordinate” complex, and two-coordinate isomer 1′ with κ2N,N′ bonding (Fig. 4) is never observed experimentally. Our high-level computations with DLPNO-CCSD(T)/def2-TZVPP and M06L/def2-TZVPP show that two-coordinate isomer 1′ with a κ2N,N′ bonding mode lies at a higher energy than 1 (8.9 kcal mol−1 at DLPNO-CCSD(T)/def2-TZVPP and 3.3 kcal mol−1 at M06L/def2-TZVPP), consistent with the experimental results.
Furthermore, diketiminate isomerization without assistance is experimentally known to have a barrier of >15 kcal mol−1 because no isomerization between binding modes was observed in variable-temperature 1H NMR studies of LtBuCo.32 Consistent with these experiments, our DLPNO-CCSD(T)/def2-TZVPP calculations predict a barrier of ΔG‡ = 24.5 kcal mol−1 for TS1 (Fig. 4), which agrees well with the experimental rate that gives ΔG‡ = 21.0 kcal mol−1 using the Eyring equation (see Section C in the ESI‡). The M06L functional with the def2-TZVPP basis set also delivers a similar value of 23.1 kcal mol−1, whereas B3LYP-D3BJ considerably underestimates the barrier with ΔG‡ = 13.6 kcal mol−1 (Table 3). It is notable that the B3LYP-D3BJ/def2-TZVPP calculations also erroneously predicted triplet κ2N,N′ isomer 1′ to be much lower in energy than κN,η6-arene isomer 1 by 10 kcal mol−1, in disagreement with the experimental data. Hence, for this specific case, the B3LYP-D3BJ method does not give results consistent with those of the experiment. Please note that our earlier calculations on CO2 hydrogenation59,60 demonstrate that even with the D3BJ corrections, the B3LYP functional sometimes cannot appropriately describe non-covalent interactions (in the present case, the metal aryl π-bonding), whereas M06L is designed to account for such weak interactions (see Section H in the ESI‡).61 Hence, in the following sections we discuss the more reliable M06L energies and verify them on-the-fly by the DLPNO-CCSD(T) method and summarize the results obtained with other functionals in the ESI (Sections K and L‡).
To summarize, the N1/CAr movement of the metal center (1 → 1′) represents the rate-limiting transition state of the reaction with CO2 (TS1, Fig. 4), with a calculated barrier of about 24 kcal mol−1. The magnitude of this barrier is in good agreement with the experimentally determined barrier of 21.0 kcal mol−1 that is calculated from the first-order rate constant in the kinetic studies presented above (see ESI part C‡), and the identification of the rate-determining transition state prior to CO2 binding is also consistent with the independence of the rate on [CO2].
The closed-shell singlet κN,η6-arene isomer of L′Co (1) lies 10 kcal mol−1 higher in energy than the triplet congener at the DLPNO-CCSD(T)/def2-TZVPP level of theory (ΔG ∼ 12 kcal mol−1 predicted with M06L/def2-TZVPP). Again, the M06L functional provides similar results to the DLPNO-CCSD(T) method and our calculations show that ligand isomerization on the closed shell singlet surface has a significantly high barrier (ΔG‡ = 49.6 kcal mol−1 using DLPNO-CCSD(T)/def2-TZVPP; ΔG‡ = 46.7 kcal mol−1 using M06L/def2-TZVPP). Therefore, the singlet surface is excluded from further consideration.
The slippage of the β-diketiminate ligand furnishes an open site for CO2 binding. In contrast to the high endergonicity found for the direct CO2 coordination to 1, κ1O-bound CO2-adduct 1a′ is only 2 kcal mol−1 higher in energy than 1′. The κ1-O binding mode in 1a′ has been observed in the uranium complex ((AdArO)3tacn)U(CO2) where the CO2 ligand accepts an electron from the uranium center to produce a UIV–OCO− complex.62 As depicted in Fig. 4, conversion of 1a′ to a more stable η2-CO2 isomer (5) can easily occur by traversing a moderate barrier of 15 kcal mol−1. The two C–O bonds in 5 lengthen relative to those in 1a′, and the CO2 moiety becomes bent with an O–C–O angle of 142.5° (Fig. 5), indicating a substantial shift of electron density from Co to the CO2 π* orbital.59 Intermediate 5 is related to PPMePNi(η2-CO2) (PPMeP = PMe[2-PiPr2-C6H4]2) and (dtbpe)Ni(η2-CO2) (dtpbe = 1,2-bis(di-tert-butylphosphino)ethane), which also feature η2(C,O) coordination.63,64 Earlier computational investigations have suggested that CO2 coordination to metal β-diketiminate fragments (M = Cr, Ni) favors the η2(C,O) binding mode, similar to intermediate 5.65
Due to the abundance of CO2 in solution, an additional CO2 molecule can be envisioned to add to intermediate 5 to produce a metal-bound carboxylate dimer. However, our repeated attempts to locate an intermediate resulting from association of a second CO2 molecule to 5 failed (see ESI, Section S‡). The lack of a mononuclear associative pathway emphasizes the need for bi-functional activation to engender sufficient nucleophilicity to bound CO2.48 The rather low nucleophilicity of the bound CO2 in 5 is not conducive to electron transfer to another incoming CO2. Moreover, the lack of a neighboring Lewis acid, which might help in bending of the incoming CO2 prior to activation, also inhibits facile association of a second CO2 molecule to the mononuclear adduct 5, and hence a mononuclear associative pathway is not possible (see ESI, Section S‡).
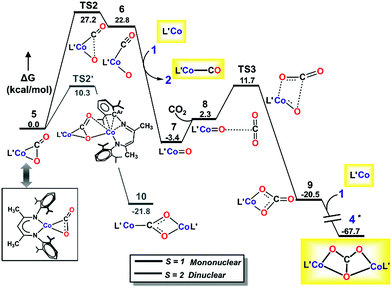
As depicted in Fig. 6, our DLPNO-CCSD(T) calculations predict that the conversion of 5 to L′Co(CO)(O) (6, see ESI Section M for geometry‡) involves a high free-energy barrier in the mononuclear dissociative pathway (TS2, Table 3). Similar barriers were obtained using DLPNO-CCSD(T) (26.7 kcal mol−1), M06L (27.2 kcal mol−1) and B3LYP (30.4 kcal mol−1) calculations, and the latter value is in reasonable agreement with that (35.1 kcal mol−1) calculated in earlier work on a truncated cobalt(I) complex with no substituents on the β-diketiminate (1,3-bis-imino-prop-2-yl).66 Once formed, complex 6 easily transfers CO to 1′, leading to the mononuclear carbonyl complex (2) and a terminal oxo-cobalt species (7, Fig. 6). Complex 7 may initiate nucleophilic attack of the metal-coordinated oxo on incoming CO2 to form a mono-cobalt carbonate species (9) via a four-membered transition state (TS3, ΔG‡ = 9.4 kcal mol−1, Fig. 6). One may envision formation of the bridging oxo 3 from 6 or 7 in the presence of 1. The transformations were computed to have favorable driving forces; however, in the mononuclear dissociative pathway, the generation of 6 entails a high barrier for the C–O bond cleavage. Hence, these two pathways were not considered further (for details, see Section S in the ESI‡). Additionally, in the mononuclear pathway, the high barrier found for the C–O bond cleavage would lead to a buildup of 5, in contrast to the observed reaction course in which no intermediates are evident. This inconsistency with experimental evidence thus indicates that the mononuclear pathway is not feasible. We therefore explored the feasibility of the dinuclear dissociative and associative pathways, which are discussed in the following section.
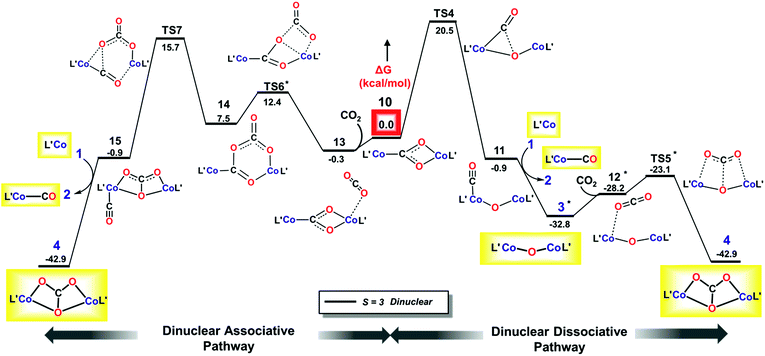
In the dissociative pathway, C–O bond cleavage in 10 passes through TS4 (see the geometry in Fig. 8) to afford an intermediate, L′Co(CO)–O–CoL′ (11), where two cobalt(II) metal centers are bridged by an oxo group, and a terminal carbonyl ligand is bound to one cobalt(II) center. The transformation is thermoneutral (ΔG = −0.9 kcal mol−1 relative to 10) and involves a moderate barrier of 20.3 kcal mol−1 at the coupled-cluster level of theory (DLPNO-CCSD(T)/def2-TZVPP, Table 3) on the S = 3 surface while M06L/def2-TZVPP also predicts a similar result (ΔG‡ = 20.5 kcal mol−1). Furthermore, M06L calculations using the broken symmetry formalism69,70 also furnish a similar barrier (21.9 kcal mol−1) on the singlet surface (Fig. S17‡). We note that attempts to independently synthesize 11 by addition of 1 eq or 1 atm CO to the oxo 3 instead furnished the previously reported complex LtBuCo(CO)2 (see ESI Section D‡).35
As depicted in Section L in the ESI,‡ further conversion of complex 11 to final product 4 has similar reaction energies and barriers for the different spin coupling situations. Therefore, we focus on the septet surface only (computed using M06L(CPCM)/def2-TZVPP) and summarize the results of the singlet state in Section L in the ESI.‡ CO transfer from 11 to 1 to form the three-coordinate L′Co(CO) product (2) and an oxodicobalt(II) species (3) is computed to be highly thermodynamically favored with a reaction free energy of ca. −32 kcal mol−1. The addition of CO2 to the oxo ligand in 3 can easily occur with a low barrier of 5.8 kcal mol−1, in agreement with the observation (see above) that LtBuCoOCoLtBu reacts rapidly with CO2 at room temperature to yield 4.
For the associative mechanism, our calculations show that nucleophilic addition of CO2 to the electron-rich oxygen atom of the bridging carboxylate dianion in 10 can form a C(O)–O–C(O)–O2− bridge between the two cobalt(II) centers in 14via a four-membered transition state (TS6) that lies 13.5 kcal mol−1 above 10. This is followed by rupture of a C–O bond in the original CO2 through TS7 (Fig. 8), which has ΔG‡ = 15.7 kcal mol−1 with M06L/def2-TZVPP and 19.4 kcal mol−1 with DLPNO-CCSD(T)/def2-TZVPP, leading to intermediate 15. This stepwise insertion/rearrangement process is thermoneutral (ΔG = −0.9 kcal mol−1) for the septet state. 15 is a dicobalt(II) carbonate complex with a CO ligand coordinated to one metal center, which is readily transferred to 1 to afford the final products. Comparison of the barriers required for C–O bond breaking as computed for the three pathways shows that the reaction of CO2 with LtBuCo is not likely to follow the mononuclear dissociative pathway, while either of the dinuclear pathways is possible because the computed barriers for TS4 and TS7 are similar, especially those calculated by the more accurate DLPNO-CCSD(T) approach. In contrast to the mononuclear intermediate 5, which does not undergo an associative mechanism, intermediate 10 contains two cobalt(II) centers bridged by a CO22− anion (discussed below on the basis of frontier orbitals) and facilitates further CO2 addition.
For both dinuclear pathways, free energy barriers calculated with B3LYP and M06L functionals employing the def-TZVPP basis set and conducted using the CPCM solvation model were in good agreement with the DLPNO-CCSD(T) benchmark for important transformations, like C–O bond-cleavage viaTS2. A similar situation is also observed for TS4 and TS7 (Table 3). Hence, apart from the ligand isomerization step (TS1), our theoretical results are analogous to those computed by the coupled-cluster approach and are evidently not functional dependent.
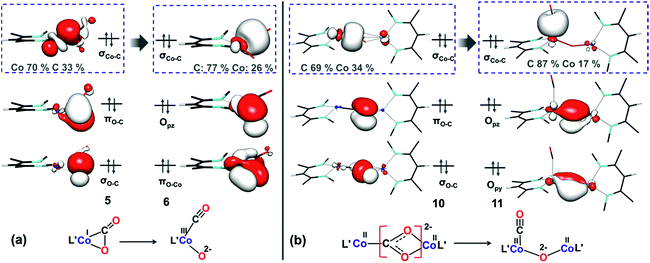 | ||
| Fig. 9 Important orbitals during C–O cleavage mediated by the (a) mononuclear dissociative pathway and (b) dinuclear dissociative pathway at the M06L/def2-TZVPP level of theory. | ||
In the dicobalt intermediate 10, the CO2 moiety is reduced by nearly two electrons, with each metal center donating one electron (Fig. 9b), and the Co–C σ-bonding orbital is predominantly carbon based. The greater electron transfer from the metal to CO2 in 10 relative to 5 reflects the greater ease of oxidizing each metal by only one electron. Furthermore, the dinuclear dissociative pathway entails lower reorganization energy during C–O bond cleavage, because the oxidation states of the metal centers do not change. As shown in ESI, Section Q,‡ the conversion of 14 to 15viaTS7 in the dinuclear associative pathway involves similar electronic structure changes. The target C–O σ-bond cleavage in TS7 results in conversion of the bonding orbital to the oxygen p orbital (Fig. S19‡). Concurrently the same oxygen starts interacting with one cobalt(II) center to form a new Co–O bond. This cooperation between the two metals facilitates C–O bond cleavage and makes the bimetallic pathways dominant.
Literature perspectives
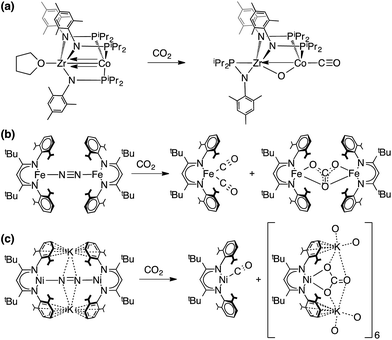
The reaction of CO2 with LtBuCo to give 2 and 4 represents the net reductive cleavage of two molecules of CO2 to CO and CO32−. Chemical fixation and transformation of CO2 has been reported in many earlier studies of dinuclear macrocyclic complexes where CO2 is reduced to form carbonate and CO.72–75 One of the earliest studies by Sorrell et al. included crystallographic characterization of a carbonate-bridged dinuclear copper complex from the reaction of CO2 with a peroxo-dicopper(II) intermediate.72 Homogeneous electrocatalytic CO2 reduction to form CO was originally reported in a well-characterized cobalt system by Eisenberg76 and developed in the research of DuBois77,78 and Kubiak,79 and many further advances in cobalt-based CO2 reduction to CO have been described by Fujita and others.20,23–25,30 This continues to be an active area of research by many groups, and therefore mechanistic insights are important.13,26–29,31Stoichiometric reduction of CO2 to CO using well-defined late 3d metal systems is also relevant. Peters reported that a Fe tris(phosphino)borate complex reacts with CO2 to give binuclear μ-O:μ-CO and C–C coupled μ-oxalato complexes, wherein the relative yields of the two products can be controlled by the choice of solvent.80,81 CO2 reduction to CO using a pyridinediimine stabilized iron(II) precatalyst has also been reported.82 Sadighi et al. identified a unique CO2/CO bridged dinuclear (NHC)Ni complex.83 A particularly cogent precedent is the heterobimetallic cobalt complex Co(iPr2PNMes)3Zr(THF), which cleaves CO2 to CO and oxo (Scheme 4a).24,84
The reaction described here between CO2 and the cobalt(I) source LtBuCo can be compared to the published reactions of CO2 with the iron(I) source LtBuFeNNFeLtBu (Scheme 4b),37 the nickel(I) source LtBuNiNNNiLtBu and the nickel(0) source K2[LtBuNiNNNiLtBu] (Scheme 4c).85 The carbonate products from the Fe and Co reactions are very similar, but the CO products are different. While the iron dinitrogen complex gave the dicarbonyl complex LtBuFe(CO)2,37 the cobalt analogue gave instead the monocarbonyl complex LtBuCo(CO). This difference can be attributed to the extent of backbonding. LtBuFe(CO)2 displays lower CO stretching frequencies (νCO = 1994, 1915 cm−1) as compared to LtBuCo(CO)2 (νCO = 2014, 1949 cm−1), and thus backbonding is weaker in LtBuCo(CO)2 than in the analogous Fe complex. Consistent with weaker bonding in the cobalt dicarbonyl versus the iron dicarbonyl, reaction of LtBuCo(CO)2 with LtBuCo afforded the monocarbonyl complex, whereas LtBuFe(CO) is unknown. Thus, we surmise that the difference in the product distribution between iron and cobalt arises from the relative M–C bond energy of the second CO. In the nickel case, Horn et al. reported two related reactions.85 First, the reaction of the dinickel(I) complex LtBuNiNNNiLtBu with CO2 resulted in reductive coupling to form an oxalate complex (Ni2+C2O4Ni2+), which was not observed in the analogous cobalt system. We speculate that the smaller nickel(I) center cannot access a LtBuNiONiLtBu intermediate and thus is diverted to C–C coupling. On the other hand, reaction of the nickel(0) complex K2[LtBuNiNNNiLtBu] with CO2 gave a nickel(I)–CO complex and a nickel(II) complex of CO32−, which is more similar to the results described here.
It is also worthwhile to compare our results to the electrochemical reduction of CO2 to CO catalyzed by [Ni(cyclam)]+, which we have previously examined computationally.86 These studies showed that formation of an η1-CO2 adduct [Ni(η1-CO2)(cyclam)]+ causes partial electron transfer from the metal center to CO2, similar to complex 5 in the present work. The second electron reduction of CO2 in the [Ni(cyclam)]+ case requires proton donors, where Lewis acid stabilization of [NiII(C(O)OH)(cyclam)]+ enables facile C–O bond cleavage to generate [Ni(CO)(cyclam)]2+ and H2O. Lewis acid stabilization facilitating CO2 cleavage has also been shown clearly in iridium and iron systems by Bernskoetter and Hazari.87,88 Here, the second cobalt stabilizes the growing negative charge on the bound CO2 like a Lewis acid; additionally, the second cobalt in the system described here provides a second electron that is crucial for CO2 reduction.
Conclusions
The masked two-coordinate cobalt(I) complex LtBuCo cleaves the C–O bond in CO2 to form a mononuclear carbonyl complex and a dinuclear carbonate complex. Both DFT and the highly correlated wavefunction-based DLPNO-CCSD(T) calculations show two feasible bimetallic pathways, and the dissociative one is supported by the independent isolation of a kinetically competent dicobalt(II) oxo complex. The electronic structure of this unusual oxo complex was analyzed using the multi-reference CASSCF approach, which showed that the oxo compound is best described as a dicobalt(II) complex, in contrast with an earlier literature compound with redox-active oxyl radical character. The negatively charged oxygen in the new dicobalt(II) oxo compound has nucleophilicity that leads to its rapid reactivity toward carbon dioxide. Overall, the cooperative interactions of the two cobalt centers facilitate charge buildup on CO2, leading to facile activation of this strong bond.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research was supported by the U.S. Department of Energy (DE-FG02-09ER16089), the U.S. National Science Foundation (CHE-1465017, CHE-1454455 and CHE-1565766), the Max Planck Society and the Department of Science and Technology of India (DST/INSPIRE/04/2017/000446). This work is based upon research conducted at the Cornell High Energy Synchrotron Source (CHESS) which is supported by the U.S. National Science Foundation under award DMR-1332208.References
- W. Nam, Y. M. Lee and S. Fukuzumi, Acc. Chem. Res., 2014, 47, 1146–1154 CrossRef CAS PubMed.
- W. N. Oloo and L. Que Jr, Acc. Chem. Res., 2015, 48, 2612–2621 CrossRef CAS PubMed.
- J. Kaizer, E. J. Klinker, N. Y. Oh, J.-U. Rohde, W. J. Song, A. Stubna, J. Kim, E. Münck, W. Nam and L. Que Jr, J. Am. Chem. Soc., 2004, 126, 472–473 CrossRef CAS PubMed.
- S. Hong, H. So, H. Yoon, K. B. Cho, Y. M. Lee, S. Fukuzumi and W. Nam, Dalton Trans., 2013, 42, 7842–7845 RSC.
- H. M. Neu, T. Yang, R. A. Baglia, T. H. Yosca, M. T. Green, M. G. Quesne, S. P. de Visser and D. P. Goldberg, J. Am. Chem. Soc., 2014, 136, 13845–13852 CrossRef CAS PubMed.
- D. Das, S. Pattanayak, K. K. Singh, B. Garai and S. Sen Gupta, Chem. Commun., 2016, 52, 11787–11790 RSC.
- A. I. Nguyen, M. S. Ziegler, P. Ona-Burgos, M. Sturzbecher-Hohne, W. Kim, D. E. Bellone and T. D. Tilley, J. Am. Chem. Soc., 2015, 137, 12865–12872 CrossRef CAS PubMed.
- J. B. Vincent, G. L. Olivier-Lilley and B. A. Averill, Chem. Rev., 1990, 90, 1447–1467 CrossRef CAS.
- M.-H. Baik, M. Newcomb, R. A. Friesner and S. J. Lippard, Chem. Rev., 2003, 103, 2385–2420 CrossRef CAS PubMed.
- W.-M. Bu, L. Ye, G.-Y. Yang, J.-S. Gao, Y.-G. Fan, M.-C. Shao and J.-Q. Xu, Inorg. Chem. Commun., 2001, 4, 1–4 CrossRef CAS.
- B. L. Yonke, J. P. Reeds, P. Y. Zavalij and L. R. Sita, Angew. Chem., Int. Ed., 2011, 50, 12342–12346 CrossRef CAS PubMed.
- W. L. Ying, J. Emerson, M. J. Clarke and D. R. Sanadi, Biochemistry, 1991, 30, 4949–4952 CrossRef CAS PubMed.
- Z. Guo, S. Cheng, C. Cometto, E. Anxolabéhère-Mallart, S.-M. Ng, C.-C. Ko, G. Liu, L. Chen, M. Robert and T.-C. Lau, J. Am. Chem. Soc., 2016, 138, 9413–9416 CrossRef CAS PubMed.
- M. W. Kanan, J. Yano, Y. Surendranath, M. Dincă, V. K. Yachandra and D. G. Nocera, J. Am. Chem. Soc., 2010, 132, 13692–13701 CrossRef CAS PubMed.
- M. W. Kanan, Y. Surendranath and D. G. Nocera, Chem. Soc. Rev., 2009, 38, 109–114 RSC.
- V. Artero, M. Chavarot-Kerlidou and M. Fontecave, Angew. Chem., Int. Ed., 2011, 50, 7238–7266 CrossRef CAS PubMed.
- J. M. Stauber, E. D. Bloch, K. D. Vogiatzis, S. L. Zheng, R. G. Hadt, D. Hayes, L. X. Chen, L. Gagliardi, D. G. Nocera and C. C. Cummins, J. Am. Chem. Soc., 2015, 137, 15354–15357 CrossRef CAS PubMed.
- R.-L. Zhang, J.-S. Zhao, X.-L. Xi, P. Yang and Q.-Z. Shi, Chin. J. Chem., 2008, 26, 1225–1232 CrossRef CAS.
- A. M. Appel, J. E. Bercaw, A. B. Bocarsly, H. Dobbek, D. L. DuBois, M. Dupuis, J. G. Ferry, E. Fujita, R. Hille, P. J. A. Kenis, C. A. Kerfeld, R. H. Morris, C. H. F. Peden, A. R. Portis, S. W. Ragsdale, T. B. Rauchfuss, J. N. H. Reek, L. C. Seefeldt, R. K. Thauer and G. L. Waldrop, Chem. Rev., 2013, 113, 6621–6658 CrossRef CAS PubMed.
- W.-H. Wang, Y. Himeda, J. T. Muckerman, G. F. Manbeck and E. Fujita, Chem. Rev., 2015, 115, 12936–12973 CrossRef CAS PubMed.
- R. Francke, B. Schille and M. Roemelt, Chem. Rev., 2018, 118, 4631–4701 CrossRef CAS PubMed.
- E. Fujita, L. R. Furenlid and M. W. Renner, J. Am. Chem. Soc., 1997, 119, 4549–4550 CrossRef CAS.
- T. Ogata, S. Yanagida, B. S. Brunschwig and E. Fujita, J. Am. Chem. Soc., 1995, 117, 6708–6716 CrossRef CAS.
- S. A. Yao, R. E. Ruther, L. H. Zhang, R. A. Franking, R. J. Hamers and J. F. Berry, J. Am. Chem. Soc., 2012, 134, 15632–15635 CrossRef CAS PubMed.
- D. W. Shaffer, S. I. Johnson, A. L. Rheingold, J. W. Ziller, W. A. Goddard, R. J. Nielsen and J. Y. Yang, Inorg. Chem., 2014, 53, 13031–13041 CrossRef CAS PubMed.
- N. Morlanés, K. Takanabe and V. Rodionov, ACS Catal., 2016, 6, 3092–3095 CrossRef.
- X. M. Hu, M. H. Ronne, S. U. Pedersen, T. Skrydstrup and K. Daasbjerg, Angew. Chem., Int. Ed., 2017, 56, 6468–6472 CrossRef CAS PubMed.
- T. Ouyang, H.-H. Huang, J.-W. Wang, D.-C. Zhong and T.-B. Lu, Angew. Chem., Int. Ed., 2017, 129, 756–761 CrossRef.
- H. Takeda, C. Cometto, O. Ishitani and M. Robert, ACS Catal., 2017, 7, 70–88 CrossRef CAS.
- T. Shimoda, T. Morishima, K. Kodama, T. Hirose, D. E. Polyansky, G. F. Manbeck, J. T. Muckerman and E. Fujita, Inorg. Chem., 2018, 57, 5486–5498 CrossRef CAS PubMed.
- A. Chapovetsky, M. Welborn, J. M. Luna, R. Haiges, T. F. Miller and S. C. Marinescu, ACS Cent. Sci., 2018, 4, 397–404 CrossRef CAS PubMed.
- T. R. Dugan, X. Sun, E. V. Rybak-Akimova, O. Olatunji-Ojo, T. R. Cundari and P. L. Holland, J. Am. Chem. Soc., 2011, 133, 12418–12421 CrossRef CAS PubMed.
- T. R. Dugan, J. M. Goldberg, W. W. Brennessel and P. L. Holland, Organometallics, 2012, 31, 1349–1360 CrossRef CAS.
- D. E. DeRosha, B. Q. Mercado, G. Lukat-Rodgers, K. R. Rodgers and P. L. Holland, Angew. Chem., Int. Ed., 2017, 56, 3211–3215 CrossRef CAS PubMed.
- M. H. Al-Afyouni, E. Suturina, S. Pathak, M. Atanasov, E. Bill, D. E. DeRosha, W. W. Brennessel, F. Neese and P. L. Holland, J. Am. Chem. Soc., 2015, 137, 10689–10699 CrossRef CAS PubMed.
- A. R. Sadique, W. W. Brennessel and P. L. Holland, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2009, 65, M174–M176 CrossRef CAS PubMed.
- A. R. Sadique, W. W. Brennessel and P. L. Holland, Inorg. Chem., 2008, 47, 784–786 CrossRef CAS PubMed.
- X. L. Dai, P. Kapoor and T. H. Warren, J. Am. Chem. Soc., 2004, 126, 4798–4799 CrossRef CAS PubMed.
- P. L. Holland, T. R. Cundari, L. L. Perez, N. A. Eckert and R. J. Lachicotte, J. Am. Chem. Soc., 2002, 124, 14416–14424 CrossRef CAS PubMed.
- K. Ding, P. L. Holland, D. Adhikari and D. J. Mindiola, Inorg. Synth., 2010, 35, 43–45 CAS.
- A. R. Corcos, O. Villanueva, R. C. Walroth, S. K. Sharma, J. Bacsa, K. M. Lancaster, C. E. MacBeth and J. F. Berry, J. Am. Chem. Soc., 2016, 138, 1796–1799 CrossRef CAS PubMed.
- N. A. Eckert, S. Stoian, J. M. Smith, E. L. Bominaar, E. Münck and P. L. Holland, J. Am. Chem. Soc., 2005, 127, 9344–9345 CrossRef CAS PubMed.
- J. T. Groves and J. S. Roman, J. Am. Chem. Soc., 1995, 117, 5594–5595 CrossRef CAS.
- W. B. Tolman, Angew. Chem., Int. Ed., 2010, 49, 1018–1024 CrossRef CAS PubMed.
- I. Bar-Nahum, A. K. Gupta, S. M. Huber, M. Z. Ertem, C. J. Cramer and W. B. Tolman, J. Am. Chem. Soc., 2009, 131, 2812–2814 CrossRef CAS PubMed.
- C. Kupper, B. Mondal, J. Serrano-Plana, I. Klawitter, F. Neese, M. Costas, S. Ye and F. Meyer, J. Am. Chem. Soc., 2017, 139, 8939–8949 CrossRef CAS PubMed.
- P. L. Holland, Acc. Chem. Res., 2008, 41, 905–914 CrossRef CAS PubMed.
- P. L. Holland, Acc. Chem. Res., 2015, 48, 1696–1702 CrossRef CAS PubMed.
- S. Shaik, H. Hirao and D. Kumar, Acc. Chem. Res., 2007, 40, 532–542 CrossRef CAS PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- A. Decker, J.-U. Rohde, L. Que Jr and E. I. Solomon, J. Am. Chem. Soc., 2004, 126, 5378–5379 CrossRef CAS PubMed.
- A. Decker, M. D. Clay and E. I. Solomon, J. Inorg. Biochem., 2006, 100, 697–706 CrossRef CAS PubMed.
- B. Mondal, L. Roy, F. Neese and S. Ye, Isr. J. Chem., 2016, 56, 763–772 CrossRef CAS.
- S. Ye, C.-Y. Geng, S. Shaik and F. Neese, Phys. Chem. Chem. Phys., 2013, 15, 8017–8030 RSC.
- S. Ye and F. Neese, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1228 CrossRef CAS PubMed.
- S. Ye and F. Neese, Curr. Opin. Chem. Biol., 2009, 13, 89–98 CrossRef CAS PubMed.
- B. Mondal, F. Neese and S. Ye, Inorg. Chem., 2015, 54, 7192–7198 CrossRef CAS PubMed.
- B. Mondal, F. Neese and S. Ye, Inorg. Chem., 2016, 55, 5438–5444 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- L. Castro, O. P. Lam, S. C. Bart, K. Meyer and L. Maron, Organometallics, 2010, 29, 5504–5510 CrossRef CAS.
- Y. E. Kim, J. Kim and Y. Lee, Chem. Commun., 2014, 50, 11458–11461 RSC.
- J. S. Anderson, V. M. Iluc and G. L. Hillhouse, Inorg. Chem., 2010, 49, 10203–10207 CrossRef CAS PubMed.
- C. Liu, L. Munjanja, T. R. Cundari and A. K. Wilson, J. Phys. Chem. A, 2010, 114, 6207–6216 CrossRef CAS PubMed.
- C. Liu, T. R. Cundari and A. K. Wilson, Inorg. Chem., 2011, 50, 8782–8789 CrossRef CAS PubMed.
- A. Ariafard, N. J. Brookes, R. Stranger, P. D. Boyd and B. F. Yates, Inorg. Chem., 2010, 49, 7773–7782 CrossRef CAS PubMed.
- J. Agarwal, E. Fujita, H. F. Schaefer III and J. T. Muckerman, J. Am. Chem. Soc., 2012, 134, 5180–5186 CrossRef CAS PubMed.
- B. Kirchner, F. Wennmohs, S. Ye and F. Neese, Curr. Opin. Chem. Biol., 2007, 11, 134–141 CrossRef CAS PubMed.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS.
- Q. Jiang and T. R. Cundari, Comput. Theor. Chem., 2017, 1105, 97–103 CrossRef CAS.
- T. N. Sorrell, W. E. Allen and P. S. White, Inorg. Chem., 1995, 34, 952–960 CrossRef CAS.
- R. J. Haines, R. E. Wittrig and C. P. Kubiak, Inorg. Chem., 1994, 33, 4723–4728 CrossRef CAS.
- J.-M. Chen, W. Wei, X.-L. Feng and T.-B. Lu, Chem.–Asian J., 2007, 2, 710–719 CrossRef PubMed.
- J. Notni, S. Schenk, H. Görls, H. Breitzke and E. Anders, Inorg. Chem., 2008, 47, 1382–1390 CrossRef CAS PubMed.
- B. Fisher and R. Eisenberg, J. Am. Chem. Soc., 1980, 102, 7361–7363 CrossRef CAS.
- J. W. Raebiger, J. W. Turner, B. C. Noll, C. J. Curtis, A. Miedaner, B. Cox and D. L. DuBois, Organometallics, 2006, 25, 3345–3351 CrossRef CAS.
- M. Rakowski Dubois and D. L. Dubois, Acc. Chem. Res., 2009, 42, 1974–1982 CrossRef CAS PubMed.
- E. E. Benson, C. P. Kubiak, A. J. Sathrum and J. M. Smieja, Chem. Soc. Rev., 2009, 38, 89–99 RSC.
- C. C. Lu, C. T. Saouma, M. W. Day and J. C. Peters, J. Am. Chem. Soc., 2007, 129, 4–5 CrossRef CAS PubMed.
- C. T. Saouma, C. C. Lu, M. W. Day and J. C. Peters, Chem. Sci., 2013, 4, 4042–4051 RSC.
- Z. Thammavongsy, T. Seda, L. N. Zakharov, W. Kaminsky and J. D. Gilbertson, Inorg. Chem., 2012, 51, 9168–9170 CrossRef CAS PubMed.
- C. H. Lee, D. S. Laitar, P. Mueller and J. P. Sadighi, J. Am. Chem. Soc., 2007, 129, 13802–13803 CrossRef CAS PubMed.
- J. P. Krogman, B. M. Foxman and C. M. Thomas, J. Am. Chem. Soc., 2011, 133, 14582–14585 CrossRef CAS PubMed.
- B. Horn, C. Limberg, C. Herwig and B. Braun, Chem. Commun., 2013, 49, 10923–10925 RSC.
- J. Song, E. L. Klein, F. Neese and S. Ye, Inorg. Chem., 2014, 53, 7500–7507 CrossRef CAS PubMed.
- T. J. Schmeier, G. E. Dobereiner, R. H. Crabtree and N. Hazari, J. Am. Chem. Soc., 2011, 133, 9274–9277 CrossRef CAS PubMed.
- W. H. Bernskoetter and N. Hazari, Acc. Chem. Res., 2017, 50, 1049–1058 CrossRef CAS PubMed.
Footnotes |
| † This paper is dedicated to the memory of Elena Rybak-Akimova (1961–2018), a valued collaborator and excellent scientist. |
| ‡ Electronic supplementary information (ESI) available: Experimental, spectroscopic, computational, and crystallographic details. CCDC 1829516–1829517. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc02599a |
| § These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |