Investigation of pre-service chemistry teachers’ understanding of radioactive decay: a laboratory modelling activity

Abstract

The first purpose of this study was to introduce a laboratory modelling activity focusing on teaching the concepts of radioactive elements/atoms, radioactive decay, and half-life. The second was to investigate pre-service chemistry teachers’ understanding of these concepts. Fifteen pre-service chemistry teachers who had enrolled in a Physical Chemistry Laboratory course participated in the study. The participants simulated the radioactive decay process of an imaginary radioactive element called Cornium during the laboratory modelling activity. In this way, pre-service chemistry teachers were able to visualize and model what is meant by radioactive decay and half-life. Data sources included responses given to open-response conceptual questions, participants’ drawings about radioactive decay and half-life, semi-structured interviews, activity worksheets, and observation notes. Qualitative analysis of data revealed that the pre-service chemistry teachers had misconceptions about the definition of radioactive elements/atoms, radioactive decay, and the half-life process before the activity. The role of the modelling activity in exposing and eliminating these misconceptions was discussed.

---

Introduction

Chemistry can be studied at three related levels: (1) macroscopic or laboratory (observable changes in matter); (2) sub-micro or molecular (imperceptible changes in structure and processes at the imaginary level); and (3) abstract or symbolic. In this final level, changes are represented in two ways: qualitatively (e.g., using language, diagrams, and symbolism) and quantitatively (e.g., using equations and graphs) (Tasker and Dalton, 2006). The research on how to teach chemistry conceptually suggests that the macroscopic, microscopic, and symbolic nature of chemistry should be taught together. However, in some of the topics in chemistry, these levels may be unlikely to coexist. One of these topics is radioactivity. Because the macroscopic laboratory experiments and demonstrations related to the radioactive decay process and nuclear reactions are not as easy and safe as the macroscopic processes for some chemical reactions, teachers have concerns about how to teach radioactivity, radioactive decay, and half-life. For this reason, modelling and simulation activities can be quite useful for teaching these concepts; they provide a connection between the particulate nature of matter and macroscopic processes. The present study introduces a laboratory modelling activity designed for high school chemistry courses. The activity involves a simulation that teachers can easily use without a dedicated software program. The study also examines the pre-service chemistry teacher participants’ understanding of radioactive elements/atoms, radioactive decay, and half-life.

Radioactivity as a topic of the chemistry curriculum

Radioactivity has historically been a neglected topic in the chemistry curriculum. In 1989, Atwood and Sheline emphasized that very few high school or university chemistry teachers include nuclear chemistry as a part of their courses. They suggested several explanations as to why this topic is left out, including teachers’ weak knowledge base, teachers’ belief that it is not important for students, and the fact that it is frequently the last chapter in the textbooks. Liguori and Adamsen (2013) similarly argued that “nuclear and radiochemistry have never had a special place in the high school curricula” (p. 878). They related this negligence to a lack of training in this subject for some teachers, or a lack of nuclear-related equipment in the school. In a recent study, Ünak (2017) examined and evaluated the present status of nuclear chemistry education in different universities. After an overview of undergraduate chemistry programs at different universities across the world, he found that “nuclear chemistry education doesn’t have a permanent status in chemistry curricula… this verifies the existence of serious educational problems in nuclear chemistry across the world” (p. 61). However, radioactivity is an important issue and should not be neglected. First, it plays a role in developing ideas about the structure of matter. Atwood and Sheline (1989) note several reasons to include nuclear chemistry at an early stage in teachers’ courses, including its role as a baseline for future research; Rutherford's explanation of alpha-particle scattering from metal foils as an atom containing a massive, positively charged core preceded Bohr's clarification of the hydrogen atom spectrum. They also note that in most textbooks, the chapter on atomic structure has only enough nuclear information throughout to clarify the discussion. For example, “isotope,” as a concept, emerged from studies on the chemistry of the natural decay series of Thorium (Th), which were conducted by Frederick Soddy in the early 1900s (L’Annunziata, 2007). But, in textbooks, the concept of the isotope is usually introduced in the unit “The Structure of Matter,” without the radioactivity context. That context is crucial for curricula, textbooks, and course materials to provide more conceptual content to students. Second, radioactivity and its applications to political, economic, and social aspects of human life are repeatedly mentioned in the media, e.g., the consequences of Chernobyl and the recent nuclear accident in Japan. Millar (1994) suggests that from a perspective of “democratic utility,” many people would give high priority to understanding the phenomenon of radioactivity because of links to such issues as nuclear power and the risks of exposure to ionizing radiation.

Other researchers argue that radioactivity's coverage in the media is in fact one of the sources of misconceptions about the topic (e.g., Millar et al., 1990; Çelik Yalçın and Kılıç, 2005; Colclough et al., 2011; Mork, 2011). For example, statements in various media reports such as “a cloud of radiation” and “it contains radiation” (Millar et al., 1990, p. 338), may have encouraged one of the most common misconceptions: the equivalency of radiation and radioactive matter. There are many other prevalent misunderstandings: that an object exposed to radiation becomes radioactive (Prather and Harrington, 2001); that once a material is radioactive it is radioactive forever (Nakiboğlu and Tekin, 2006); that radioactive substances will never vanish (Suzuki, 2012); and that radio isotopes that have a long half-life are more dangerous (Suzuki, 2012).

Some of these misconceptions can be traced to a lack of clarification in mainstream discussions of these topics. Many students and adults do not understand the difference between ionizing and non-ionizing radiation (Rego and Peralta, 2006). For example, X-rays and nuclear radiations are not differentiated (Boyes and Stanisstreet, 1994). Nuclear radiation is thought of as machine-made (not natural) and hence is linked with technological advancements such as lasers (Boyes and Stanisstreet, 1994; Cooper et al., 2003). Another source of the misconceptions is the lack of knowledge about the particle nature of matter and its role in radioactive decay. Prather (2005) claims that one must have a fundamental understanding of how the atom (or atomic nucleus) behaves during the decay process to properly account for radioactive phenomena. In addition, Suzuki (2012) argues that because there are various formula for calculating the activity, decay constant, and radioactive decay law in the textbooks, students usually memorize these equations without understanding that radioactive decay is a random process. In 1944 Erwin Schrödinger explained the nature of radioactive decay as follows: “…But if you are given a single radioactive atom, its probable lifetime is much less certain than that of a healthy sparrow. Indeed, nothing more can be said about it than this: as long as it lives (and that may be for thousands of years) the chance of its blowing up within the next second, whether large or small, remains the same” (p. 78). In brief, the radioactive decay equation can be derived, as an exercise in calculus and probability, as a consequence of two physical principles: a radioactive nucleus has no memory, and decay times for any two nuclei of the same isotope are governed by the same probability distribution (Huestis, 2002). It is difficult for students to understand this characteristic of radioactive decay through formulated equations (Suzuki, 2012).

There is one way to experimentally investigate certain characteristics of radioactivity such as half-life—you can measure the activity of a radioactive material in each of a series of time intervals, plot the data as a function of the accumulated time on semi-log paper, and then measure the slope of the graph. The materials required to do this experiment are as follows: a Geiger counter, a stopwatch, and a radioactive material such as metastable Barium-137 with a 2.55 minute half-life. However, most schools lack this equipment, and the use of radioactive material in the classroom is not always practical or advisable (Hughes and Zalts, 2000). In addition, this experiment alone may be inadequate to demonstrate the random nature of decay to students. Therefore, to teach the radioactive decay and half-life process—taking into account the particulate nature of matter—and eliminate the existing misconceptions, the imaginary sub-micro or molecular level should be brought to the forefront. The present study was designed to introduce a laboratory activity that models the radioactive decay process through a molecular-level simulation exercise. It also examines pre-service chemistry teachers’ understanding of radioactive elements/atoms, radioactive decay, and half-life before and after the modelling activity.

Research on radioactivity in science education

The numbers of studies in science education related to radioactivity are also insufficient. It is noteworthy that most of the existing studies were conducted to determine the views and misconceptions of students and pre-service teachers about radioactivity (e.g., Millar, 1994; Millar and Gill, 1996; Prather and Harrington, 2001; Çelik Yalçın and Kılıç, 2005; Nakiboğlu and Tekin, 2006; Rego and Peralta, 2006; Colclough et al., 2011; Plotz, 2017). In addition, many of these studies discussed radioactivity together with the concept of radiation. The studies that provide and evaluate teaching exercises in this area have been designed with a quantitative method (e.g., Crosier et al., 2000; Tezcan and Erçoklu, 2010; Claiborne and Miller, 2012). Additionally, most studies address the subject of radioactivity at a macroscopic level, e.g., distinctions between the concepts of radioactive material/radiation, irradiation/contamination, and radiation/ionizing radiation (e.g., Millar et al., 1990; Suzuki, 2012; Neumann and Hopf, 2012; Taşoğlu et al., 2015). Studies on a microscopic level—such as why a radioactive sample decays, what happens when it decays, and the predictability of decay and half-life—are lacking. In this respect, there is a gap in the field of teaching radioactivity.

Prather (2005) emphasized in his study that to correct student misconceptions about irradiation and contamination, it is critical to investigate students’ understanding of the role the atom plays in the radioactive decay process (p. 346). There are some tools to help students better understand radioactive decay and half-life—wet-lab experiments (Mak, 1999; Liguori and Adamsen, 2013; Pilakouta et al., 2016), model-based teaching activities (Schultz, 1997; Hoeling et al., 1999; Hughes and Zalts, 2000; Klein and Kagan, 2010; Bakaç et al., 2011; Claiborne and Miller, 2012), computer-based exercises (Crosier et al., 2000; Jesse, 2003; Mork, 2011; Jona and Vondracek, 2013; Sauter et al., 2013), and calculation exercises (Huestis, 2002; Ball, 2004). The exponential law of decay for radioactive atoms is usually taught with simulation exercises such as dice throwing or coin flips (e.g., Schultz, 1997; Jesse, 2003; Klein and Kagan, 2010; Bakaç et al., 2011). The simulation exercise used in this study is similar to dice throwing or coin toss simulations in terms of its analogical nature. The difference that sets it apart is its use in concurrence with the modelling activity described below.

Designing the laboratory modelling activity

Models and modelling—the production and revision of models using the dynamic and non-linear processes involved in the development of scientific knowledge (Justi and Gilbert, 2002)—have a critical role in science education. Models can serve different purposes, such as visualizing abstract constructs (Francoeur, 1997); providing a foundation when predicting and scientifically explaining a phenomenon (Gilbert et al., 1998); and simplifying and describing complicated phenomena (Rouse and Morris, 1986). However Kenyon et al. (2011) have argued that many models used in classrooms do not support learners in attempting to explain or predict phenomena. They find that the traditional use of models, such as making a model of a volcano using baking soda and vinegar at the elementary level, is useful only to demonstrate physical appearance, not to investigate volcanic activity and attempt to explain why a volcano erupts or predict when one might erupt next (p. 7). To address this issue, Kenyon et al. (2011) proposed a modelling practice consisting of four stages: construct, use, evaluate and revise (p. 4). They argued that this modelling practice supported learners distinguishing scientific modelling practices from the traditional use of models in classrooms. Drawing from these ideas, in this study, this four-step modelling practice was used to investigate radioactive decay and half-life, and to try to explain the random nature of radioactive decaying and the predictability of half-life. To simulate the radioactive decay process, a laboratory simulation exercise (Chiappetta and Koballa, 2002) was used in the third stage—evaluate the model.

The terms “laboratory modelling” and “laboratory simulation” are used in this study to distinguish from computer-based modelling activities and computer-based simulations. The number of studies examining the effect of computer-based simulations on students’ conceptual understanding has started to increase with the development of technology (Stern et al., 2008; Rutten et al., 2012), putting computers at the forefront in simulation research. In the chemistry classroom, computer-based learning environments attempt to make explicit the information embedded in traditional molecular representations, as well as provide a visual representation of molecular interactions for students to observe. However, a molecular simulation exercise does not have to be computer-based. In this study, one example of a laboratory molecular-level simulation exercise is illustrated.

Methodology

Research questions

The study was guided by the following research questions:

(1) What are pre-service chemistry teachers’ understandings of radioactive elements/atoms, radioactive decay, and half-life?

(2) How does the use of a laboratory simulation exercise influence pre-service chemistry teachers’ understanding of radioactive elements/atoms, radioactive decay, and half-life?

Participants

Data were collected from a convenience sample of 15 pre-service chemistry teachers (9 females and 6 males) attending a Physical Chemistry Laboratory course in the fall of 2018. The laboratory course is a one-semester course; there is no prerequisite for this course in the teacher education program. All participants had previously taken two semesters of physical chemistry courses. However, they stated that the topic of radioactivity had not yet been taught in their teacher training program.

Implementation of laboratory modelling activity

The modelling activity began with a pre-laboratory discussion to review some basic concepts related to radioactive decay. Participants were asked questions, e.g., what happens when a radioactive element decays? Why are some atoms unstable? Then, participants were grouped by twos or threes and the stages of the modelling practice (Kenyon et al., 2011) were implemented as follows.

Construct a model. In this stage, the groups were asked to make drawings on the first activity sheet about what happens when radioactive elements decay. The researcher asked them to brainstorm a list of components that they would want to include in their models of the radioactive decay process. They were also asked to write a brief explanation of their model. While the groups were constructing their models, the researcher asked them questions, e.g., What does this figure in your drawing represent? Each group presented their models to the whole class. During the presentations, the participants used the following concepts: radioactive decay, half-life, unstable atom, nuclear reactions, decay rate, radiation, and alpha, beta, and gamma radiation. The researcher did not interfere to correct any misconceptions that were determined in this stage.

Use a model. The pre-service chemistry teachers were asked to use their models to make a prediction about when a radioactive element called Cornium (²¹⁰₈₃Cm), an imaginary element assigned to corn kernels, would decay and what its half-life would be. They were also asked to write a brief explanation and illustrate how their models predicted decay time and half-life of the Cornium element on a second activity sheet. While the groups were using their models, the researcher asked them about the strengths and weaknesses of their models. The groups had an opportunity to think about the predictability of the decay time and half-life of a radioactive element. Thus, they considered again the following concepts: radioactive decay, half-life, unstable atoms, nuclear reactions, decay rate, radiation, and alpha, beta, and gamma radiation. Many participants stated that they were missing something in terms of relevant information.

Evaluate a model: In this stage, the laboratory simulation exercise (Chiappetta and Koballa, 2002) was implemented as an example of an authentic model of the radioactive decay process to evaluate the participants own models. In this exercise, each group was given one box (square, cardboard, with covers), which had a mark such as X on one of the inside walls. The researcher placed 100 kernels of corn into each box. It was noted that each kernel of corn has a pointed end. The groups were then asked the following question to discuss: What are the chances of a particulate kernel pointing to the side marked X? Then, all groups followed the following procedure:

• Shake the box with cover six times.

• Remove the kernels that are pointing to the side with the X. Determine how to label any kernels pointing at the X side's corners.

• Draw a data table to record the numbers of kernels taken out and the number left.

• Repeat this exercise for ten trials.

• Graph the results on the semi-log paper. How do you label the axes of the graph?

After all groups drew their graphs, it was discussed with the whole class that the laboratory exercise is also a model that simulates the radioactive decay process. Materials and events in the simulation exercise were compared with their representations (see Table 1). Scientific definitions of the following concepts—half-life, unstable atom, nuclear reaction, radioactive decay, decay rate, radiation, alpha, beta, and gamma decay—were addressed by the researcher. In addition, the “binding energy” and “band of stability” concepts, which had not been mentioned during participant brainstorming, were explained to clarify the theories about radioactive decay. It was emphasized that radioactive decay has a random nature. Any misconceptions determined in the early stages were debated among the whole class. Finally, the strengths and weaknesses of the simulation exercise (given in Table 2) were clarified.

Table 1 Comparison of materials and events with their representations in the simulation exercise

Materials and events	Entities and events they represent
Corn kernels	Unstable atoms of Cornium element
Each trial	Radioactive decay
The chance of each kernel's pointed end pointing to the side marked	The random nature of radioactive decay
The number of trials that it takes to use up half the kernels	Half-life

---

Table 2 Strengths and weaknesses of simulation exercise

Strengths	Weaknesses
It reflects the particulate nature of matter.	There is not an indication of the type of radiation (e.g., alpha or beta radiation).
It represents radiations.	There is no representation of energy.
It represents the random nature of decay very well. The decay chance of each kernel is the same.	Decayed corn kernels are taken out of the box.
The half-life can be predicted. (You can predict it by graphing results; number of kernels remaining in the box versus trials.)

---

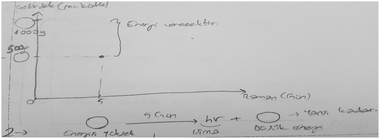
It has been argued that although it has some weaknesses, this simulation activity is an effective model because it demonstrates the random nature of radioactive decay and predicts half-life. Before the groups graphed their results, they were asked what kind of line they expect. Then, they compared their expectations with their graphs. It was discussed that there was variation in the graphs; however, instead of an error, it may be due to the fact that the smaller the sample, the greater the variation. It was emphasized that the curve would be very smooth in an experiment measuring the radioactivity of a real radioactive material. Finally, groups were asked to find the half-life of the Cornium element, guided with the following question: how many trials did it take to use up half of the kernels that were left?

Revise a model. In this stage, the groups tried to revise their models by comparing the simulation exercise with their original models.

Data collection and analysis

In this study, a laboratory modelling activity focusing on teaching radioactive elements/atoms, radioactive decay, and half-life is introduced. The researcher/author investigated how the activity influenced the participants’ understanding of these concepts. For this purpose, a qualitative study was conducted. Data sources included responses given to open-response conceptual questions and regarding participant drawings about radioactive decay and the half-life process, in addition to semi-structured interviews, activity worksheets, and observation notes. The open-response conceptual questions are given below:

• Have you learned about radioactivity before? If so, in which class did you learn?

• What are radioactive elements and atoms?

• How can you tell if a substance is radioactive?

• What happens when a radioactive element decays? Please draw it and explain.

• Does a radioactive element/atom change when it decays? Please explain.

• Why do some elements/atoms decay?

• When does a radioactive substance/atom decay?

• What is “half-life”?

Open-response conceptual questions and activity worksheets were prepared by the researcher with the aim of probing pre-service chemistry teachers' understanding of radioactive decay process. The pre-service teachers responded to the questions in writing before and after implementing the activity. Their drawings about the radioactive decay process and explanations about them were obtained from the first activity worksheet and the second open-response conceptual question. Semi-structured interviews were conducted before and after implementing the activity with the aim of eliminating the unclear responses and gaining rich data for an in-depth analysis.

The data were analyzed and evaluated by the modelling constant comparative method (CCM) (Strauss and Corbin, 1998). The CCM was chosen to analyze the data to increase internal and external validity, because comparisons increase the internal validity of the findings. As Boeije (2002) states, “one criterion for qualitative research is that the researcher tries to describe and conceptualize the variety that exists within the subject under study. Variation or range exists by the grace of comparison and looking for commonalities and differences in behavior, reasons, attitudes, perspectives and so on. Finally, constant comparison is connected with external validity” (p. 393). The comparisons were made as follows: (1) comparison within single open-response conceptual questions; (2) comparison among respective open-response conceptual questions; (3) comparison between drawings and interviews; (4) comparison between open-response conceptual questions of different participants; and (5) comparison between drawings of different participants. During the comparisons, the participants’ understanding of the definition of radioactive elements/atoms fell into four emergent categories: scientific, not unscientific but insufficient, unscientific, and do not know. Understandings about radioactive decay and the half-life process obtained from the participants' drawings were coded under four categories as well:

(a) decaying and halving was understood as the same process;

(b) an object of radioactive decay was compared to the disappearing mass of a whole;

(c) the type of radiation emitted was not clear; and

(d) there was no indication or explanation of the probabilistic nature of decay and/or the predictability of the half-life.

Finally, understanding about radioactive decay process and half-life obtained from answers to open-ended questions were coded under the four categories; (a) changing after radioactive decay, (b) reason of radioactive decay, (c) nature of radioactive decay, (d) definition of half-life.

The reliability of the coding process was tested by an independent coder, who was an expert in the field of radioactivity. Reliability checks between researcher and a single outside expert have precedent in the field. Before the coding process, the coders discussed the category definitions and then compared their coding both qualitatively (20% of the coding) and quantitatively (calculating percentage agreement). The percentage agreement score was 95%.

Ethical precautions

Ethical approval for the study is gained from Institutional Review Board for this study. All participants were volunteers, pre-service teachers enrolled in a Physical Chemistry Laboratory course. The participants’ names have been replaced by pseudonyms in the study to protect identity of them.

Results and discussion

Participants’ understanding about radioactive atoms, radioactive decay, and half-life processes (and how these understandings change) are presented in sub-headings below.

Understandings about definitions of radioactive elements/atoms

The pre-service chemistry teachers’ understanding of the definition of radioactive elements/atoms was obtained primarily from open-ended conceptual questions. These understandings were analyzed before and after the activity; those data are given in Table 3.

Table 3 Pre-service chemistry teachers' (PCTs’) understanding of the definition of radioactive element/atom

	Before the activity	No. of PCTs	After the activity	No. of PCTs
Scientific	Material which contains unstable atoms which will spontaneously “decay” to form other types of atoms by emitting radiation in the form of particles and gamma rays.	1	Atoms that are unstable, meaning they have an imbalance of neutrons and protons, and will spontaneously “decay” to form other types of atoms by emitting radiation in the form of particles and gamma rays.	6
	Atoms that are unstable, meaning they have an imbalance of neutrons and protons.	1	Atom with a nucleus that falls outside the band of stability.	5
Not unscientific but insufficient	A radiant substance.	4	Atoms with n/p > 1	3
	A luminescent substance	1
	Atoms whose nuclei change.	1	Atoms with an atomic number greater than 83	1
	High energy substances.	1
Unscientific	A radioactive substance that vanishes over time and is transformed into energy.	1		0
	A toxic substance.	2
	A substance that reacts under high temperature and pressure.	1
	A substance that occurs as a result of nuclear reaction.	1
Do not know		1		0

---

Before the activity, participants’ definitions of radioactive atoms were mostly not unscientific but insufficient. Only one pre-service teacher thought that radioactive atoms emit both rays and particles. One of the misconceptions was that “radioactive substances vanish over time and are transformed into energy.” Based on this misunderstanding, it may be concluded that the participant confused the concepts of radioactivity and radioactive material. Radioactivity is a characteristic feature of a radioactive substance and is exhausted over time. Radioactive substances are not vanished but transformed into a stable substance at the end of the decaying process. After the activity, participants had no misconceptions about the definitions of radioactive elements/atoms. It was observed that the pre-service teachers mentioned the particulate nature of matter more in the definitions. However, a few pre-service teachers still had insufficient understandings.

Understanding about radioactive decay and half-life processes

The pre-service chemistry teachers’ understanding of the radioactive decay and half-life processes was obtained by analyzing all data collection tools. One of these tools was the participants’ individual and group drawings modelling the radioactive decay process. Examples of these drawings before the simulation exercise are given in Table 4.

Table 4 PCTs’ drawings modeling radioactive decay process before the simulation exercise

1. Individual drawing:	Explanation: “The structure changes when decayed, but I don't know how it changes.”
2. Group drawing:	Explanation: no explanation
3. Group drawing:	Explanation: “When the high-energy nucleus, which is initially 1000 g, is decayed, its mass is reduced by half (500 g) with lower energy. The energy of h·ν is released.”

---

Only one participant could illustrate that the numbers of atoms in the radioactive substance decrease, noting the particulate nature of matter, but she could not illustrate in her drawing how they decrease or what happens to the decayed atoms (see Table 4, first individual drawing). One of the pre-service teachers illustrated the decay process by writing a reaction equation. It was observed that nine of the fifteen participants could not create a drawing that models radioactive decay and half-life processes. Before the simulation exercise, the understandings from the individual drawings and group drawings obtained from the activity were coded as follows:

Decaying and halving was understood as the same process. In both the second and third groups’ drawings, the majority of participants equate the decaying process with halving (see Table 4). They were asked to model a radioactive decaying process but drew a halving process instead. The researcher asked directly, is a single decay sufficient for reaching the half-life? The pre-service chemistry teachers answered “Yes, it is,” “Yes it is possible,” etc.

An object of radioactive decay was compared to the disappearing mass of a whole. The participants did not refer to the particulate nature of matter in their drawings. Questions about what exactly decays and what happens to the decaying object were asked to each group. In general, they stated that the “mass of radioactive material is decayed.” Some groups stated that “the mass is transformed into energy,” but they did not know how; others explained that “the mass is not conserved.” No group members mentioned the transformations in the nucleus during decay. In Table 4, in the second group's drawing, a solid radioactive substance with a labeled mass of 6m changes to a substance with the mass of 3m after one half-life. The other 3m mass was not shown. These findings are consistent with Prather's study. Prather (2005) investigated students’ beliefs about the role of atoms in radioactive decay and half-life. He found that students believe that half of a radioactive object disappears after a half-life.

The type of radiation emitted was not clear. Only one group illustrated the radiation accompanying decay as “h·ν” (see Table 4, third group drawing). But they did not explain what this radiation is. In the answers given to open-ended questions, one pre-service chemistry teacher was knowledgeable about the types of radiation; this information was not illustrated in group drawings.

There was no indication or explanation about the probabilistic nature of decay and/or the predictability of the half-life. In the “use a model” stage of the modelling activity, the participant groups could not use their drawings to predict decay time and half-life. They clearly stated that they were not aware whether decay times and half-life could be predicted. Only one group stated that the half-life was dependent on the order of reaction and asked about the order of radioactive decay process. With this question, it was discussed whether or not radioactive half-life is dependent on the initial amount of radioactive material. In this discussion, several pre-service chemistry teachers’ misconceptions about half-life emerged. For example, one said that “as the radioactive material decreases, the half-life is prolonged” and “half-life changes continuously.” In order to eliminate these misconceptions, the groups were asked to record the data obtained from the simulation exercise to the Excel program. Then, they were asked to determine reaction order for decay of the Cornium element using a graph. The participants had already learned the graphical method with the experiment of “Reaction rate and concentration of reactant” in the laboratory. When creating the graph in Excel, students and researcher discussed the importance of entering the number of corn kernels instead of the concentration, and the number of trials instead of time. The pre-service teachers determined the order for the decay of the Cornium element according to the explanations given below:

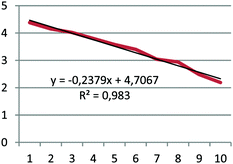
(1) For the first-order process, a plot of the natural logarithm of the number of kernels remaining in the box versus number of trials is a straight line with a slope of −k;

(2) For the second-order process, a plot of the inverse of the number of kernels remaining in the box versus number of trials is a straight line with a slope of k.

Each group except one determined that the decay was a first-order process. The group that came to a different conclusion may have counted corn kernels incorrectly during the exercise; they noted that there might be a mistake in their data. Because the pre-service chemistry teachers already understood that the half-lives of the first-order reactions did not depend on the initial concentration, they also realized that the half-life in radioactive decay was not dependent on the initial concentration. They found the value of the rate constant, k, from the slope of the curve they obtained in the graph, and then determined the half-life of the Cornium element as 3 or 3.5 trials. The data, graph, and half-life value submitted by one group are given in Table 5 as an example.

Table 5 The data, graph and half-life value of a group

The data			Graph	Half-life value
No. of trial	No. of kernels	ln(no. of lernels)
1	80	4.38		t 1/2 = ln 2/k = 0.693/0.2373 ≅ 3
2	64	4.15
3	56	1.02
4	45	3.8
5	36	3.58
6	30	3.4
7	21	3.04
8	19	2.94
9	12	2.48
10	9	2.19

---

Participants’ understandings about radioactive decay and half-life processes, as obtained from answers to open-ended conceptual questions, are given in Table 6. Those findings indicate generally that before the activity most of the participants had “no idea” (indicating declining to submit a theory or guess) about changes after radioactive decay, reasons for radioactive decay, nature of radioactive decay, or the definition of “half-life.” After the activity, participants offered responses for each category. Most of the misconceptions, before the activity, fell under the category of the nature of radioactive decay. Nine participants responded “no idea” about the nature of decay; some of the remaining participants thought decay was continuous and endless.

Table 6 PCTs’ understanding about radioactive decay and half-life processes

	Before the activity	No. of PCTs	After the activity	No. of PCTs
Changes after radioactive decay	A new substance is formed which is low in mass	1	A new substance is formed which is low in mass	2
	Chemical change	2	The numbers of protons and neutrons change	2
	Numbers of neutron change	2	Numbers of neutron change	2
	Reactivity of decayed material increases	1	Stable nuclei are formed	5
	New substances are formed	1	The identity of the atom changes	1
	No change	2	New substances are formed	1
	No idea	6
Reasons for radioactive decay	External effect	1	Reaching stable n/p ratio	12
	Instability	3	Having low binding energy	3
	Characteristic feature of substance	1
	Not conservation of entropy	1
	Daylight exposure	1
	Electron exchange	1
	Not conservation of temperature and pressure	1
	No idea	6
Nature of radioactive decay	Continuous and endless	2	Probabilistic nature	5
	Need to give energy	1	It continues until stable atoms are formed	2
	Neutron bombardment	1	The decay time is unclear for a radioactive nucleus	1
	When instability is maximum	2	It can happen at any moment	4
	No idea	9	Random nature	3
Definition of half-life	Time for the mass of the radioactive substance to halve	6	This is the time for the number of undecayed radioactive nuclei/atoms to be halved	11
	It is half the time it takes for a radioactive substance to decay	2	Time for a radioactive substance mass of 2m to become mass of m	4
	It's time the radioactive material started to decay	2
	No idea	5

---

Suzuki (2012) mentioned in his study that many students think that a radioactive substance will never vanish because of their misinterpretation about half-life. That is, students believe that radioactive substances reduce to a half, then a quarter, then an eighth of their original levels at each half-life, never quite reaching zero. Based on the half-life definitions and drawings given by the participants in the current study, who think that decay is continuous and endless, it was observed that they explained half-life similarly to those in Suzuki's research. Some participants thought that there would be an external effect (e.g., energy or neutron bombardment) with radioactive decay. After the activity, all participants used expressions emphasizing the probabilistic nature of decay, such as “probabilistic nature,” “the decay time is unclear” and “random nature.” Before the activity, the pre-service chemistry teachers offered unscientific explanations of the reasons for radioactive decay such as “daylight exposure,” “electron exchange,” and a lack of “conservation of temperature and pressure.” Nakiboğlu and Tekin (2006) also found similar misconceptions in their study about radioactive decay rate—for example, “the radioactive decay rate depends on the physical conditions” (p. 1715).

After the activity, all participants were able to give causal explanations in accordance with the nuclear stability theory about the reasons for radioactive decay.

It was observed that some participants were not able to accurately define “half-life” before the activity. This may be due to a lack of knowledge about what exactly is “halving.” Some participants thought that half-life refers to the “time it takes for a radioactive substance to decay.” Some answers, such as “it's [the] time [when] the radioactive material started to decay” supported the idea that decaying and halving are being confused for one another—a misconception which emerged from the drawings as well.

One of the most significant findings, obtained from both the drawings and the open-ended conceptual questions about half-life, is the fact that the number of radioactive nuclei/atoms that remain after decay was initially ignored by all participants. “Half-life” should be defined as the time taken for the number of undecayed radioactive nuclei/atoms to decrease by half the initial amount. Conversely, the pre-service chemistry teachers drew the radioactive material as a whole; when this material halved, the mass of the whole also divided into two in their illustrations. After the activity, most of the participants were able to accurately define half-life in the open-ended conceptual questions. However, their modelling of the radioactive decay and half-life processes did not look as expected (see Table 7). The particulate nature of matter was rarely illustrated in the drawings. However, the explanations for the drawings illustrated a slightly stronger development of the participants’ understanding (see third individual drawing and its explanation, Table 7). As seen in the first and second drawing, the groups were able to illustrate the emitting radiation better than they could before the activity. Furthermore, after the activity, they determined that there should be a different drawing for each type of radioactive decay.

Table 7 PCTs’ drawings modeling radioactive decay process and half-life after the simulation exercise

1. Group drawing: from the stage of revise a model	Explanation: no explanation
2. Group drawing: from the stage of revise a model	Explanation: atoms that are unstable will spontaneously “decay” to form other types of atoms by emitting radiation in the form of particles and rays.
3. Individual drawing:	Explanation: this drawing illustrates half-life. Initially 5000 g mass radioactive material undergoes many decays by emitting particle and ray. When the numbers of undecayed nuclei are halved, the mass is halved.

---

Conclusions and implementations

The simulation exercise described in the present study identifies three essential elements of a real radioactive decay process and half-life experiment. These are (1) that the number of atoms that decay in an interval of time is proportional to the number of radioactive atoms present, (2) that the process is random, and (3) that the process is exponential. The findings of this study indicate that the use of a simulation exercise that includes these elements can help students progress in their understanding of the probabilistic nature of decay and the predictability of half-life for large numbers of radioactive atoms. Another important finding of the study is that pre-service chemistry teachers rarely illustrated the particulate nature of matter to model the radioactive decay process and half-life, either before or after the activity. Although the corn kernels represented the radioactive atoms in the simulation exercise, the participants did not refer to the particulate nature of matter to create their group drawings (in the “revise a model” stage) or to create the individual drawings after the activity. In the drawings, decay was illustrated in terms of the whole mass of a substance; it was understood that during decay this mass disappears. However, some pre-service teachers were able to refer to the particulate nature of matter in their explanations of their drawings and answers to open-ended questions.

One explanation for relating decay to mass is the deficiencies in the definitions of half-life in the textbooks. One textbook describes it as “the length of time required for half of a ‘radioactive sample’ to disintegrate.” Another explanation is the phrasing of some questions and solutions in the textbooks. For example: If the half-life of 2 grams of a “radioactive substance” is 3 hours, how many grams was this substance 15 hours ago? The solution of this question is given below.

64 g ← 32 g ← 16 g ← 8 g ← 4 g ← 2 g

Fifteen hours ago, the radioactive material was 64 grams. Material that is referred to as “radioactive” could be a substance, a sample, or unstable atoms. Radioactive substances involve both stable and unstable atoms. Therefore, it may be more accurate to use the terms “radioactive atom” or “radioactive isotope” instead of “radioactive substance” and “radioactive sample” in the definition of half-life and in the question given above. In addition, the solution path of the question given above encourages learners to illustrate decay in terms of the whole mass of a substance.

Although we had explicitly discussed the weaknesses of the laboratory simulation exercise during the activity (see Table 2), these weaknesses may have also contributed to the issues some participants had no drawing the radioactive decay and half-life processes as expected. Removing decayed corn kernels from the box may have been misleading; in reality, decayed atoms transform into another atom—they do not go anywhere. The removal of corn kernels may have encouraged the pre-service chemistry teachers to draw the mass of the radioactive substance disappearing (see Table 7, third individual drawing).

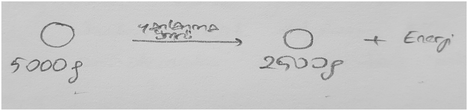
After the activity, the participants were expected to create drawings that correctly illustrated the half-life process (see Fig. 1). In this drawing, the gray-colored particles represent the decayed radioactive atoms; white particles represent undecayed atoms. After each half-life, the number of undecayed atoms is reduced by half. The total mass does not change.

Fig. 1 The expected drawings from the PCTs which illustrated the half-life process.

One implication of this study is a recommended change to the simulation in future implementations. In order to represent how total mass does not change, the kernels removed from the box should be replaced by an equal number of colored kernels. This will also indicate that decayed atoms are transformed into other atoms.

In the four-stage modelling activity, pre-service chemistry teachers had the opportunity to think and discuss the phenomenon studied in each of the stages. During the use of their model, they realized that they had no knowledge of when a radioactive substance would decay or how to predict its half-life. For this reason, the simulation exercise focused on teaching the probabilistic nature of radioactive decay, and as a result finding the half-life became more meaningful for them. Teachers or researchers using this four-stage modelling activity should be aware of students’ misconceptions and lack of knowledge, and follow their learning process through the stages of the modelling activity. Therefore, the results of the current study indicate that a laboratory simulation is more effective when used in conjunction with a modelling activity.

Conflicts of interest

There are no conflicts to declare.

References

1. Atwood C. H. and Sheline R. K., (1989), Nuclear chemistry: include it in your curriculum, J. Chem. Educ., 66(5), 389.
2. Bakaç M., Taşoğlu A. K. and Uyumaz G., (2011), Modelling radioactive decay, Procedia – Soc. Behav. Sci., 15, 2196–2200.
3. Ball D. W., (2004), How radioactive is your banana? J. Chem. Educ., 81(10), 1440.
4. Boeije H., (2002), A Purposeful Approach to the Constant Comparative Method in the Analysis of Interviews, Qual. Quant., 36, 391–409.
5. Boyes E. and Stanisstreet M., (1994), Children's ideas about radioactivity and radiation: sources, mode of travel, uses and dangers, Res. Sci. Technol. Educ., 12 145–60.
6. Çelik Yalçın A. and Kılıç Z., (2005), Misconceptions of Students and the Effects of the course Books on Such Misunderstandings Sample Topic: Radioactivity, Gazi Eğitim Fakültesi Dergisi, 25(3), 125–141.
7. Chiappetta E. L. and Koballa T. R., (2002), Science instruction in the middle and secondary schools, New Jersey: Merrill Prentice Hall.
8. Claiborne L. L. and Miller C. F., (2012), Teaching radioactive decay and radiometric dating: an analog activity based on fluid dynamics, J. Geosci. Educ., 60, 114–122.
9. Colclough N. D., Lock R. and Soares A., (2011), Pre-service teachers’ subject knowledge of and attitudes about radioactivity and ionising radiation, Int. J. Sci. Educ., 33(3), 423–446.
10. Cooper S., Yeo S. and Zadnik M., (2003), Australian students’ view on nuclear issues: does reaching alter prior beliefs? Phys. Educ., 38, 123–129.
11. Crosier J. K., Cobb S. V. and Wilson J. R., (2000), Experimental Comparison of Virtual Reality with Traditional Teaching Methods for Teaching Radioactivity, Educ. Inform. Technol., 5, 329.
12. Gilbert J. K., Boulter C. and Rutherford M., (1998), Models in explanations, Part 1: Horses for courses?. Int. J. Sci. Educ., 20(1), 83–97.
13. Hoeling B., Reed D. and Siegel P. B., (1999), Going bananas in the radiation laboratory, Am. J. Phys., 67(5), 440–442.
14. Huestis S. P., (2002), Understanding the origin and meaning of the radioactive decay equation, J. Geosci. Educ., 50, 524–527.
15. Hughes E. A. and Zalts A., (2000), Radioactivity in the Classroom, J. Chem. Educ., 77, 613–614.
16. Jona K. and Vondracek M., (2013), A remote radioactivity experiment, Phys. Teach., 51(1), 25–27.
17. Jesse K. E., (2003), Computer simulation of radioactive decay, Phys. Teach., 41(9), 542–543.
18. Justi R. and Gilbert J. K., (2002), Modelling, teachers’ views on the nature of modelling, and implications for the education of modellers, Int. J. Sci. Educ., 24(4), 369–387.
19. Kenyon L., Davis E. A. and Hug B., (2011), Design approaches to support pre-service teachers in scientific modelling, J. Sci. Teach. Educ., 22(1), 1–21.
20. Klein L., and Kagan D., (2010), “Radio-Active” Learning: Visual Representation of Radioactive Decay Using Dice, Phys. Teach., 48(1), 45–45.
21. L’Annunziata M. F., (2007), Radioactivity: Introduction and History, Amsterdam: Elsevier Science.
22. Liguori L. and Adamsen T. C. H., (2013), Learning Nuclear Chemistry through Practice: A High School Student Project Using PET in a Clinical Setting, J. Chem. Educ., 90(7), 877–882.
23. Mak S., (1999), Radioactivity experiments for project investigation, Phys. Teach., 37, 536.
24. Millar R., (1994), School students’ understanding of key ideas about radioactivity and ionizing radiation Pub, Understand. Sci., 3(1) 53–70.
25. Millar R. and Gill J. S., (1996) School students' understanding of processes involving radioactive substances and ionizing radiation, Phys. Educ., 31, 27.
26. Millar R., Klaassen C. W. and Eijkelhof H. M., (1990), Teaching about radioactivity and ionising radiation: an alternative approach, Phys. Educ., 25, 338–342.
27. Mork S. M., (2011), An interactive learning environment designed to increase the possibilities for learning and communicating about radioactivity, Interact. Learn. Environ., 19(2), 163–177.
28. Nakiboğlu C. and Tekin B. B., (2006), Identifying students’ misconceptions about nuclear chemistry: a study of Turkish high school students, J. Chem. Educ., 83, 1712–1718.
29. Neumann S. and Hopf M., (2012), Students' conceptions about ‘radiation’: Results from an explorative interview study of 9th grade students, J. Sci. Educ. Tech., 21(6), 826–834.
30. Pilakouta M., Savidou A. and Vasileiadou S., (2016), A laboratory activity for teaching natural radioactivity, Eur. J. Phys., 38(1), 015801.
31. Plotz T., (2017), Students’ conceptions of radiation and what to do about them. Phys. Educ., 52.
32. Prather E., (2005), Students’ beliefs about the role of atoms in radioactive decay and half-life, J. Geosci. Educ., 53(4), 345–354.
33. Prather E. E. and Harrington R. R., (2001), Student understanding of ionizing radiation and radioactivity, J. Coll. Sci. Teach., 31 89–93.
34. Rego F. and Peralta L., (2006), Portuguese students’ knowledge of radiation physics, Phys. Educ., 41(3), 259–262.
35. Rouse W. B. and Morris N. M., (1986), On looking into the black box: prospects and limits in the search for mental models, Psychol. Bull., 100(3), 349–363.
36. Rutten N., Van Joolingen W. R. and Van Der Veen J. T., (2012), The learning effects of computer simulations in science education, Comput. Educ., 58(1), 136–153.
37. Sauter M., Uttal D. H., Rapp D. N., Downing M. and Jona K., (2013), Getting real: the authenticity of remote labs and simulations for science learning, Distance Educ., 34(1), 37–47.
38. Schrödinger E., (1944), What Is Life? The physical aspect of the living cell and mind, Cambridge: Cambridge University Press.
39. Schultz E., (1997), Dice-Shaking as an Analogy for Radioactive Decay and First-Order Kinetics, J. Chem. Educ., 74 (5), 505–507.
40. Stern L., Barnea N. and Shauli S., (2008), The effect of a computerized simulation on middle school students’ understanding of the kinetic molecular theory, J. Sci. Educ. Technol., 17(4), 305–315.
41. Strauss A. and Corbin J., (1998), Basics of qualitative research: techniques and procedures for developing grounded theory, London: Sage.
42. Suzuki T., (2012), The misconceptions on radiation and radioactivity, Lat. Am. J. Phys. Educ.6(1), 75–77.
43. Tasker R. and Dalton R., (2006), Research into practice: visualisation of the molecular World using animations, Chem. Educ. Res. Prac., 7(2), 141–159.
44. Taşoğlu A. K., Ateş Ö. and Bakaç M., (2015), Prospective physics teachers' awareness of radiation and radioactivity, Eur. J. Phys. Educ.6(1), 1–14.
45. Tezcan H., and Erçoklu H. F., (2010), The comparison of the traditional and constructivist methods as regards to success of students in radioactivity teaching and the elimination of their misconceptions, J. Turk. Educ. Sci., 8(1), 201–225.
46. Ünak T., (2017), What Is Exactly the Scope of Nuclear Chemistry and Its Educational Position between Other Chemistry Branches? Adv. Chem. Eng. Sci., 7, 60–75.

---