Profiling the combinations of multiple representations used in large-class teaching: pathways to inclusive practices
João Elias Vidueira
Ferreira
 a and
Gwendolyn Angela
Lawrie
a and
Gwendolyn Angela
Lawrie
 *b
*b
aFederal Institute of Education, Science and Technology of Pará (IFPA), Pará State, Brazil
bSchool of Chemistry and Molecular Biosciences, The University of Queensland, St Lucia, Queensland, Australia. E-mail: g.lawrie@uq.edu.au
First published on 16th September 2019
Abstract
Teachers select multiple representations and adopt multiple visualization approaches in supporting their students to make meaning of chemical phenomena. Representational competence underpins students’ construction of their mental models of concepts thus it is important that teachers consider this while developing instructional resources. In tertiary chemistry, teachers typically use PowerPoint slides to guide lectures. This instructional resource is transferred between different teachers each semester and, while the sequence of topics are likely to be discussed and agreed upon, the content of the slides can evolve organically in this shared resource over time. The aim of this study was to analyse a teacher-generated resource in the form of a consensus set of course slides to characterise the combination and diversity in representations that students had encountered. This study was set in a unique context since the semester's lecture slides represented a distillation of consensus representations used by multiple chemistry lecturers for at least a decade. The representations included: those created by the lecturers; textbook images (from several texts); photographs and images sourced from the internet. Individual representations in each PowerPoint slide were coded in terms of the level of representation, mode and potential function in supporting deeper understanding of chemistry concepts. Three representational organizing frameworks (functional taxonomy of multiple representations, modes of representation and the chemistry triplet levels of thinking) were integrated to categorise the representations. This qualitative data was subjected to hierarchical cluster analysis and several relationships between the categories and topics taught were identified. Additional qualitative data in the form of student reflections on the perceived utility of specific representations were collected at the end of the semester. The findings from this study inform the design and choice of instructional resources for general chemistry particularly in combining representations to support deeper learning of concepts. A broader goal and application of the findings of this study is to identify opportunities for translation of representations into alternative modalities to widen access and participation in learning chemistry for all students. An example of a strategy for translating representations into tactile modes for teaching the topic of phase change is shared.
Introduction
As students transition between multiple classrooms and learning spaces, they encounter countless different representations of science concepts across their learning journey. Their teachers will select, sequence and share the representations in primary or secondary science classrooms (largely guided by textbooks). In contrast, students who continue on to tertiary studies will be expected to demonstrate greater autonomy and engage independently with multiple forms of representation from multiple sources as learners.Evidence suggests that teachers believe that they should adopt several visualization approaches to support meaning making by students, this practice can be explained through variation theory (Bussey et al., 2013; Patron et al., 2017). Visualization approaches include ways that teachers present phenomena in visual modes to their students, such as: active drawing on black/whiteboards, static images, physical objects, experiments, video clips and animations. A teacher's choice of external representations is likely to be informed by their own experiences and mental models of concepts – their pedagogies will also draw on their beliefs as they respond to their learners’ needs and existing conceptions. This construct can be described as a teacher's topic specific pedagogical knowledge, TSPK, and is interwoven with their teaching context (Gess-Newsome, 2015; Lawrie et al., 2019).
The importance of the choice of representations is emphasised by published research into learning with representations and through visualization. These researchers identify with many different disciplinary fields including cognitive science, educational psychology, learning sciences, pre-service teacher preparation, science education and chemistry education. Therefore, multiple perspectives and theories exist. Ainsworth and Newton (2014) captured this diversity through a review of over four hundred journal articles that explored visual representations in science published between 2010–2012. They found significant overlap in the goals of researchers and teaching practitioners in terms of the use of a diverse range of multiple representations. These authors also identified a gap in the literature regarding the teacher's role in mediating the ways that representations are used to support student learning.
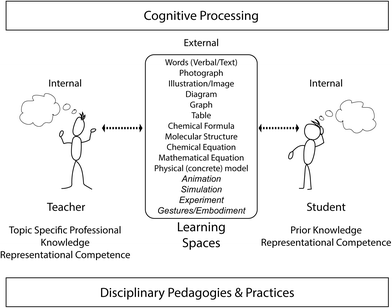
In classroom practice, external representations are artifacts that are placed in a public domain by the teacher to symbolize a concept or idea. These artifacts are typically presented to students with the aim of engaging them in the construction of their own internal depictive representations, often referred to as mental models (Hinton and Nakhleh, 1999; Schnotz et al., 2002; Gilbert, 2005; Gilbert, 2016). Once an internal mental model has been re-represented in the public domain, either by a teacher or a student, it becomes an expressed model in the form of an external representation (Fig. 1). As part of their design or collation of instructional resources, teachers will often combine multiple external representations involving a range of modalities that they believe will best support student learning (Waldrip and Prain, 2006; Wu and Puntambekar, 2012; Patron et al., 2017).
An individual learner must develop representational competence to be successful in learning science, and this involves recognizing, constructing, interpreting, transforming, and connecting external representations (Kozma and Russell 1997; Ainsworth, 1999; Kozma et al., 2000; Wu et al., 2001; diSessa, 2004; Ainsworth, 2006; Carolan et al., 2008; Stieff et al., 2011; Rau 2017).
Learning is made possible through noticing or discerning something in a representation and reasoning about it in a meaningful way, this involves paying attention to, reflecting on, and constructing connections (Eriksson et al., 2014; Airey and Linder, 2017; Rau, 2017). Representational competence is further developed as learners become fluent in the modes of disciplinary discourse which involve the representations, tools and activities or practices of a discipline, known as a ‘critical constellation’ of modes (Airey and Linder, 2009). Teachers are able to scaffold learners in disciplinary discourse through modelling their own thinking while making disciplinary norms and practices explicit. Their explanations and modelling of chemistry thinking are an important form of verbal and gestural representation. Eventually, as learners gain knowledge, skills and independence, teacher scaffolding of representational competence can be faded out. This process of enculturation of learners into disciplinary ways of knowing through facilitation of their learning as part of a discipline community is underpinned by sociocultural learning theories (Kozma et al., 2000; Kozma, 2003).
In the disciplinary domain of chemistry, the process of learning is highly dependent on how teachers choose and combine external representations of concepts that cannot be ‘seen’ (Prain and Waldrip, 2006; Carolan et al., 2008; Wu and Puntambekar, 2012; Taber, 2013; Patron et al., 2017). A well-established paradigm (informed by cognitive science research) exists in chemistry that can support teachers’ pedagogies and practices. Alex Johnstone's triplet relationship identifies three levels of thinking that experienced chemists translate between with ease (Johnstone, 1982; Johnstone, 1991; Johnstone, 1993; Johnstone, 2000; Johnstone, 2010; Gilbert and Treagust, 2009; Talanquer, 2011; Taber 2013). These levels include: that which is ‘seen’ around us in material forms or as physical and chemical changes (macroscopic); that which cannot be ‘seen’ in the particulate domain involving individual entities such electrons, atoms, molecules and ions (submicroscopic); and the array of symbolic and iconic abstractions (symbolic) that represent each entity at both the macro and the submicroscopic levels. The fundamental principle behind the triplet relationship is that chemists adopt an array of representations across each level of thinking to express their mental models and practices – their individual representational competence will lie at some point on a continuum between novice and expert in the discipline. There is evidence that when teachers make the levels of thinking in chemistry explicit, and discuss features of representations, students can improve their understanding (Hilton and Nichols, 2011).
Learners’ prior knowledge has a substantial influence on their visual attention to representations. Those with higher levels of prior chemistry knowledge notice conceptually relevant features in representations whereas those with lower prior knowledge only notice surface features (Cook, 2006; Cook et al. 2007; Corradi et al., 2014). This aligns with research that demonstrates that expert chemists cluster external representations according to their deeper understanding of concepts – in contrast, novice chemists only examine the surface or material features of individual representations. Evidence to support this claim arises from the context of the practices of expert and professional chemists (Kozma and Russell, 1997; Kozma et al., 2000; Kozma, 2003) and also in the ways that students learn chemistry (Kozma, 2003; Cook, 2006; Cook et al. 2007; Stains and Talanquer, 2007).
Theoretical framework
The development of pedagogies and practices that address individual students’ ability to cognitively process and connect representations are core to chemistry education. When exploring teachers’ selection and combination of representations to develop teaching and learning resources (learning objects), several relevant theories should inform practice.A single concept can be re-represented and shared in a wide range of modalities but representations are most commonly found in visual, symbolic and verbal modes (Ainsworth, 1999; Lemke, 2004; Gilbert, 2005; Airey and Linder, 2009; Prain and Waldrip, 2006; Tang et al., 2014). Strategic instructional design to support students in their construction of their mental models involves shared visualization through carefully integrated representations in a shared learning space (Fig. 1). This term ‘visualization’ is therefore attributed to either the entity that is the shared external representation of the internal image held by an individual, noun, or the process of interaction with the internal mental model, verb (Gilbert et al., 2008).
Representations presented in different modes can engage learners in multisensory experiences (Prain and Waldrip, 2006) particularly through the use of multimedia, for example videos or animations, which can involve both visual and verbal representations in parallel. Cognitive processing of representations by an individual as they develop their mental models involves the integration of separate text and visual cognitive channels (Schnotz et al., 2002; Mayer, 2005).
Effective learning through engagement with multiple representations requires that learners recognize how information is encoded within each representation and how this relates to their prior understanding (Ainsworth, 1999; Ainsworth 2006). Recommendations for pedagogical practice involve the adoption of a semiotic approach and strategies that provide optimal access to supporting students’ discernment of relevant aspects of representations through variation (Airey and Linder, 2017). Different representations may be coordinated to explicate an underlying concept or abstraction across modes or within the same mode of representation. The choice in form and function of representations for activities and tasks that support learning in practice can be informed by the designs, functions and tasks (DeFT) framework (Ainsworth, 2006; Ainsworth, 2008). Representational competence is developed while learning with, and through, representations (Gilbert, 2005; Gilbert, 2008; Rau, 2017). As learners develop their competencies, they are likely to encounter increasingly more sophisticated representations and may be required to coordinate multi-representational and dynamic displays (Wu et al., 2001; Stieff et al., 2011).
It is therefore possible to combine too many representations in parallel resulting in cognitive overload of working memory (Sweller, 1994; Ainsworth, 2008). The coordinated placement of information using multiple media is known to provide an affordance and includes the spatial contiguity effect where the careful location in proximity of visuals and words to scaffold explanations has a positive influence on learning (Mayer and Sims, 1994; Mayer, 2003). As teachers become more engaged in blended learning environments, strategic scaffolding is required to guide their students in learning with representations online (Quintana et al., 2005).
The theories that have been briefly considered above combine to provide evidence that multiple external representations can facilitate student learning but require careful integration. There are several mechanisms for learning that depend on features, modes and the information encoded in individual representations. It is also evident that the way in which representations are combined and displayed can have a negative impact on cognitive processing. In this study, we explore how teachers have combined multiple representations to produce a single learning object. The methodology has been formulated, informed by theory, to characterise the multiple representations adopted in terms of modes, discipline-based encoded formalisms and features, and their potential to function in the support of learning.
Rationale for study
Several studies have focussed on evaluating representations and how they have been used in textbooks since this resource is often considered as guiding a curriculum for teachers. Analyses have considered how representations are related to the written text and their perceived function (Gkitzia et al., 2011; Kumi et al., 2013; Nyachwaya and Wood, 2014; Nyachwaya and Gillaspie, 2016; Upahi and Ramnarain, 2018). A rubric has been developed to categorise Johnstone's levels of representation in chemistry textbook images (Gkitzia et al., 2011) and this has been adopted in subsequent studies of chemistry textbook representations (Nyachwaya and Wood, 2014; Upahi and Ramnarain, 2018). While this is a useful approach for characterising any representations that students are potentially exposed to that originate in chemistry textbooks, it does not capture the wider range of representations that a teacher may adopt in practice. Recent interest in how students interact with multiple representations has resulted in a framework that enabled analysis of students’ own construction of representations (Tang et al., 2014). Nitz et al., (2014) developed an instrument to enable analysis of external representations used in a secondary level classroom, insights were gained from the students’ perspectives.Very few studies have explored the selection or combination of representations adopted by tertiary teachers to support learning in their ‘classrooms’. The traditional lecture format remains dominant in tertiary STEM learning environments, despite a shift towards more active-learning pedagogies (Stains et al., 2018). Currently, no single tool or framework exists to inform evaluation of the diversity in content representations that are collated by tertiary teachers in their teaching resources, across a large suite of concepts. The absence of a formal curriculum at the tertiary level also complicates the situation since no expectations exist in terms of the scope or depth of content that will be scaffolded by the teaching resources. Textbooks are usually recommended reading but not necessarily central to teaching resources.
In this study, we have piloted an evaluation methodology that may guide the characterisation of multiple representations in tertiary chemistry teaching contexts. Our approach integrated three separate, and highly regarded, representational frameworks as a strategy to capture and characterise the combination of multiple external representations in the lecture resource that has been used during a general chemistry course. These three frameworks are:
1. Alex Johnstone's triplet relationship, which was adopted to reveal and discriminate any potential patterns by topic in the use of representations in chemistry. The three representational levels (macroscopic, submicroscopic (submicro), symbolic) were applied to categorise the representations. It is acknowledged that this is a very simplified application of these levels and that ambiguities often exist in the assignment of levels (Talanquer, 2011; Taber, 2013).
2. John Gilbert's framework that recognises the different modes of representations that can be used to support visualization of concepts was also applied. These modes included: concrete (sometimes referred to as material or physical), verbal, symbolic, visual, and gestural representations (Gilbert et al. 1998; Gilbert, 2005). This study aimed to discriminate representations in terms of their format in the lecture slides hence not all modes were included (elaborated further in methods).
3. Shaaron Ainsworth's functional taxonomy of multiple representations (a core element of the DeFT framework, Ainsworth, 2006) was applied to consider how combinations of multiple representations on a single slide could potentially function to support learning. A functional analysis of representations is important in considering their educational purpose (Ainsworth, 2018). Representations were considered in terms of whether they had potential to work with each other to present information that was different (complement), whether they linked a familiar concept to something unfamiliar supporting interpretation (constrain) or whether, in combination, they enabled learners to extend, relate or abstract their existing knowledge (construct) without reorganizing that knowledge.
In this study, the teaching resource that has been analysed is a set of PowerPoint slides that have been used to support teaching of specific concepts in a general chemistry course. This core set of slides has been adopted as a resource for teaching for at least ten years and has been used by multiple tertiary teachers (faculty). A large number of teachers contributed to the collation and annual revision of these slides, many of whom no longer teach the course for various reasons. This means that the teachers’ rationale for their selection and combination of representations in the instructional design of this resource is not accessible. This is acknowledged as a limitation of the current study. However, as an affordance, the contribution by so many teachers towards the preparation of this lecture resource presents a unique opportunity. The combination of representations in each slide can be considered to be a consensus position that resonates with individual tertiary teachers’ TSPK (Schultz et al., 2018). The intended pedagogical function or origin of many of the representations is not known in terms of their inclusion in the slides in this study. Assuming that the teachers were not aware of Ainsworth's framework to inform instructional design, our aim was to consider whether any combination of multiple representations in a single slide may have ‘accidentally’ functioned to scaffold students’ deeper construction of their understanding.
The slide set for an entire course of study was chosen rather than focusing on a single lecture or specific topic to enable the capture of the full range of representations that students had encountered across a whole semester. Hierarchical statistical analysis has been applied to identify patterns and categorical connectivity between representations also aiming to identify any critical combinations of multiple external representations that may exist. This study represents an example of research-based evaluation of practice to inform instructional design. The questions that guided the analysis of data were:
• What are the predominant characteristics of representations chosen by instructors for inclusion in a general chemistry teaching resource?
• What topics tend to be illustrated using multiple representations that have been combined in a way that could support deeper learning?
• What forms of representation do students recall having encountered during their lectures (post-instruction)?
The findings of this study aim to inform translation of teaching resources and practices with the goal of ensuring access and participation in learning by all students particularly in blended learning environments in future courses. A strategic objective was to identify potential combinations of representations for translation into different modalities, such as tactile forms. An example of an approach to support learning by students with disabilities, such as visual impairment, informed by findings is shared in Appendix 5.
Methods
Context for the study
The context for this study is a first-year general chemistry course at a large, research-intensive tertiary institution in Australia. Very large cohorts of students (>1100) typically enroll in this course annually. It is assumed that students have completed high school chemistry or equivalent prior to completing this course since this is the prerequisite preparation. Due to teaching space restrictions, the cohort is typically divided into three sections, each section is taught by a separate teacher (lecturer). Over the past decade, the learning activities within these lectures have shifted from didactic approaches to more active learning approaches. Despite this shift, the content and activities are still presented using PowerPoint slides, every teacher uses the common core set of slides to present the concepts that will be tested through quiz and examination assessment. These core slides represent an instructional resource that has evolved across a decade of iterations of general chemistry courses and has been edited by at least 20 tertiary teachers. The slides contain a collection of representations that have been sourced from multiple textbooks, derived from internet sources and created by the teachers themselves (diagrams, drawings and photos).Coding of individual representations
The coding of individual representations through application of a deductive framework (including Johnstone's representational levels) is a recognised strategy for analysing textbook representations (Gkitzia et al., 2011; Kumi et al., 2013). In this current study, the representations collated in the PowerPoint slides have been analysed by deductive coding applying three separate frameworks, detailed in Table 1:| Framework | Category | Code | Examples of representations in this category |
|---|---|---|---|
| Johnstone (2000) | Symbolic | S | Electrons, electron configuration, chemical formulas, reaction equations, dipoles, arrows, graphs |
| Submicro | SM | Orbitals, atoms, ions, molecules, structures, particulate arrangements | |
| Macroscopic | M | Substances, experiments, real world objects | |
| Gilbert (2005) | Symbolic | S | Electrons, electron configuration, chemical formulas, reaction equations, dipoles, arrows |
| Static visual | SV | Pictures, diagrams, tables, graphs, | |
| Verbal | V | This was assigned only to written text in this study. | |
| Gestural | G | This was not assigned as part of this study. | |
| Ainsworth (2006) | Complement | 1 | When an individual representation contains information that complements another in terms of concepts or the process of thinking. |
| Constrain | 2 | When an individual representation that is familiar is combined with another is unfamiliar in representing the same concept or it clarifies an ambiguity. | |
| Construct | 3 | When multiple representations are combined with the intention of constructing deeper understanding through either abstraction, extension or. |
(i) Johnstone's (2000) levels of thinking in chemistry (macroscopic, submicroscopic and symbolic);
(ii) Gilbert's (2005) modes of external representations in science (excluding concrete and gestural representations which are not explicitly captured in the slides); and
(iii) Ainsworth's (2006) functional taxonomy of multiple representations (complement, constrain and construct).
Application of Ainsworth's taxonomy (Table 1) as a coding framework required assignment of the potential functionality of individual representations (Ainsworth, 1999; Ainsworth, 2006). The top level of the taxonomy was used to assign codes for the purpose of hierarchical cluster analysis and subsequent statistical analysis. This coding involved consideration of each individual representation by the researchers in terms of how its features or information could potentially enable its function. When the information in an individual representation complemented the information in a second representation on the same slide, both were assigned as complementary. Representations that combined to potentially clarify a concept and avoid mis-interpretation were assigned as serving to function as constraining thinking.
Slides in which multiple representations combined to potentially support the construction of deeper understanding by students were considered carefully to identify the potential affordance of the combination. The potential to function through construction of understanding by ‘Abstraction’ was attributed to combinations of Multiple external representations (MERs) that could enable the creation of mental models that would support application of new procedures. This coding was guided by Ainsworth's advice (1999, p. 141) for encouraging abstraction ‘It is hoped that by providing learners with a rich source of domain representations they will translate or construct references across these representations’. ‘Extension’ was attributed when knowledge could be applied by students to directly translate between a known and an unknown representation. ‘Relational’ was assigned when two representations were interlinked and required the same knowledge to enable interpretation. The latter was coded where representations in slides appeared to have been intentionally combined to support students’ skills in translating between them.
Two steps were applied to check the reliability of the coding scheme, initially three lectures were coded by the two researchers independently then compared (both researchers have doctorates in chemistry and are tertiary teachers). Discrepancies were discussed to decide on the final coding framework (Table 1). The slides were subsequently 100% coded by one researcher (JEFV) and 25% coded by the second researcher (GL) to achieve a consensus of greater than 90%.
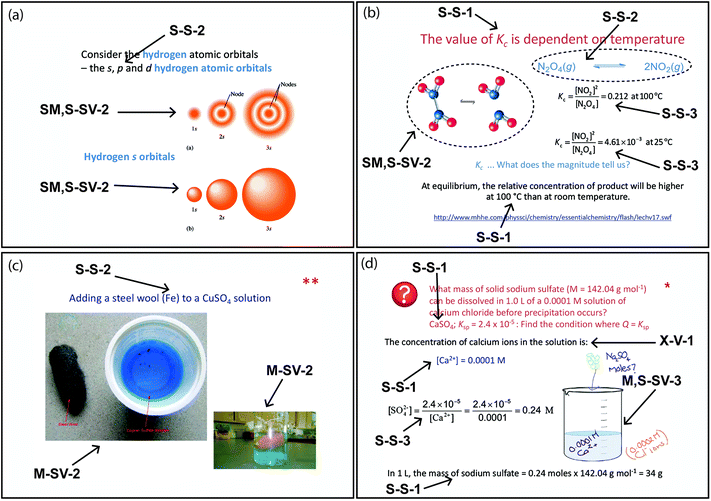
For ease of cross-referencing, a combination label was generated and assigned to each representation. This label contained the codes displayed in the sequence ‘Johnstone’–‘Gilbert’–‘Ainsworth’. For example, in Fig. 2 the submicro representation of a molecular orbital (bottom right) is assigned ‘Submicro’-‘Static visual’-‘constrain’ labelled as ‘SM-SV-2’.
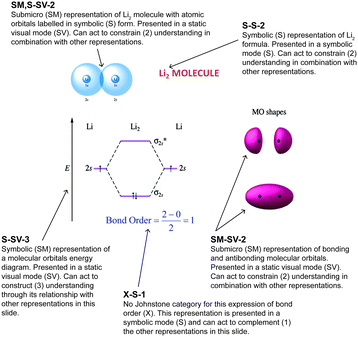 | ||
| Fig. 2 Example of the application of the coding scheme to the representations on a single PowerPoint slide. S = symbolic, SM = submicro, SV = static visual, X = no category. | ||
In chemistry, symbols and icons are frequently used to represent particles (including electrons, atoms, ions, etc.). A single static visual representation which comprised multiple symbols within its composition was assigned the codes of symbolic (Johnstone) and static visual (Gilbert) resulting in the label S-SV-. In the example shown in Fig. 2, the symbols for electrons that were used in the static visual representation of the molecular orbital diagram or in the picture of the molecule involving the atomic orbitals, were not coded separately according to Gilbert's modes of representation. When a representation did not fit any of the representational level categories in the Johnstone framework, it was assigned as ‘X’.
The category designated as ‘symbolic’ appeared in two separate frameworks. It was assigned to chemical symbols, chemical equations, stoichiometry, mathematical equations and graphs in Johnstone's levels of chemistry thinking (Johnstone, 2000) and the symbolic mode of representation (Gilbert, 2005) which included: chemical symbols and formulae, chemical equations, and mathematical expressions and equations. Significant overlap in coding for ‘S’ was observed across these two frameworks – the main distinction is that graphs were designated as symbolic in Johnstone's levels of thinking whereas they were categorized as static visual in Gilbert's modes of representation. We acknowledge the ambiguity in assigning Johnstone's levels separately as either symbolic or submicro in representations of molecular structures that included both a Lewis structure and geometry in terms of bonds (Talanquer, 2011). There were several representations for which it was difficult to assign a single code and these were each discussed by researchers, where appropriate two codes were assigned as was the case of the submicro representation of the Li2 molecule in Fig. 2.
It was not mandatory for teachers to refer to any single or combination of representations contained within the slides in their practice. However, it has been assumed for the purpose of this study that students will encounter the representations on the slides regardless of whether they were explicitly referred to as part of teacher explanations. A complication that emerged during the assignment of macroscopic representations arose in the case of slides that included a hyperlink to a YouTube video or a web-based simulation of a concept. This constituted an additional visualization approach that teachers could choose to use while teaching. It was also possible that the teacher did not use the hyperlinked representations therefore the external content was not explicitly included in the coding analysis. In fact, the hyperlink was almost always flagged by a screenshot image of a macroscopic or sub-micro representation of the activity in the slide. Therefore the representation that was used to flag the hyperlink was coded in the analysis to capture its potential contribution in supporting learning.
Application of Ainsworth's functional taxonomy of representations required the researchers to decide which representations may already be familiar to students. It was assumed that the majority of students possessed prior experience of high school chemistry concepts (a prerequisite to enrollment in the general chemistry course). Representations that are commonly used in high school text books and related resources were assumed to be familiar to students. Examples include the use of half-arrows as the symbol for electrons, ball and stick or space-filling structures used to represent simple molecules, the ‘syntax’ of chemical equations and simple equilibrium constant expressions.
An example of this assumption is in the combination of the static visual representation of ‘familiar’ atomic orbital shapes (Fig. 2, top left) with the unfamiliar static visual representation of molecular orbital shapes. These representations combined in this slide have been coded as constrain since they depict the difference in volumes and shapes of the orbitals. The molecular orbital energy diagram (Fig. 2, bottom left) was considered to be unfamiliar to students and has been coded as functioning to ‘construct’ deeper understanding through its relation to the static visual submicro diagram of the atomic and molecular orbital representations. It may be inferred that the inclusion of the energy diagram enables students to build their understanding through comparing and contrasting the representations combined on this single slide. The researchers assigned ‘construct by relation’ because the inclusion of energy diagram encourages translation between different representations. The bond order equation in Fig. 2 is coded as complementary (X-S-1) because it re-presented information that had been introduced on the previous slide.
Additional categories were introduced during the coding to provide more granularity of information in terms of the range of formats of representations that had been used, these included: photos, illustrations, diagrams, graphs, tables, molecular formulas, molecular structures, mathematical equations and chemical equations.
At the commencement of data analysis, lecture recordings had also been considered as a potential source of data. It was hoped that gestures as a representational mode, according to the Gilbert framework, might be included. It was quickly discovered that the individual lecturers used substantially different gestures to emphasize representations and support explanations (mouse, laser pointer, annotating slides on a visualizer, verbal emphasis and embodiment). The coding became too complex very quickly, based on these additional sources of data, because the three teachers in parallel streams adopted different individual approaches in their teaching. This diversity in how teachers engage with a common instructional resource would form the basis of a separate interesting study.
Statistical analysis
Statistical data analysis was applied to explore the patterns and relationships in the categorical data. Bar graphs enabled the direct comparison of the number of counts for each category of representation. Spearman correlation coefficients measured the strength of the associations between the eighteen individual categorical variables used to code the representations. Boxplots (Microsoft Excel) were used in exploratory data analysis to display minimum, first quartile, median, third quartile and maximum values, informing both location and spread of data in terms of categories (Tukey, 1977). Outliers were identified and the symmetry and skewness were evaluated so this display of data provided additional insights into the distribution of categories of representations by lecture topic.Hierarchical cluster analysis
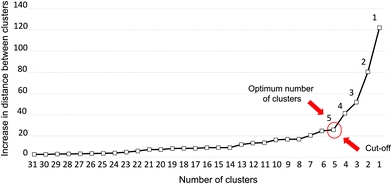
Hierarchical cluster analysis (HCA) was employed to uncover possible relationships in the data according to properties assigned to representations through coding (SPSS). HCA has been used previously in chemistry education research to explore categorical relationships (Linenberger and Holmes, 2014; Raker and Holmes, 2014). A data matrix was constructed where each line comprised an individual lecture topic and the columns were the 18 categories of representations (according to framework category and representation type). Data in this matrix were standardized so that they had equal metrics and, consequently, equal weight. Each variable was changed to a z-score: mean of 0 and standard deviation of 1. The display of the results for the HCA was achieved through a dendrogram (also known as a tree diagram). The dendrogram is a graphical representation that facilitates the recognition of groups and reveals any similarities/differences measured in terms of the distance between clusters. The approach chosen to generate the dendrogram employed the squared Euclidean distance and Ward's linkage method (Ward, 1963). This methodology uses the agglomerative clustering criterion based on the minimization of the squared Euclidean distances of the lecture topics from the centre of gravity of the cluster to which they have been assigned. Ward's method employs the within-cluster (squared) distances and the between-cluster (squared) distances (Rencher, 2003). Applying this strategy, each sample is first defined as its own cluster, then other samples are grouped together to form new clusters until they are all part of a single cluster. The dendrogram illustrates the stages of the linkage where the length of the branches (distance) linking two clusters is related to their similarity. Long branches indicate low similarity while shorter branches indicate higher similarity. The appropriate number of clusters was determined through a scree plot of distances versus the number of clusters (state of agglomeration) and confirmed by plotting the increase in distances versus the number of clusters (Yim and Ramdeen, 2015). The scree plot is shown in Appendix 1 Fig. 8.Student perceptions of lecture representations they encountered
Additional qualitative data were collected in this study to gain insights into which representations students valued during the semester. It was decided that a survey would collect a broader sample of student perceptions compared to individual interviews or focus groups. All students enrolled in a single course (n = 1207) were invited to participate in the online questionnaire. Institutional ethical approval was gained and students were required to opt in to the study through informed consent. Two items were included in the questionnaire to collect students’ perceptions regarding representations they had encountered in lectures. These items were:• ‘Please take a moment to either think back or look over your lecture notes then give us an example of a specific visual representation that you found most helpful in constructing your understanding of a concept.’ Students were guided to enter a response for each of the three modules that the lecture sequence had been divided into (taught by separate academics).
• ‘Which type of representations do you find most difficult to interpret or understand when you are learning chemistry, please give an example from the slides in [course code] this semester? Explain why.’
Written entries were filtered to remove any incomplete responses (empty fields) then analysed to assign the category of representation. Several entries did not refer to specific forms of representations but the cited topic was included as part of the analysis.
The student responses to items were coded according to Johnstone's levels of thinking and Gilbert's modes of delivery (Table 1) arranged by each module in the course. The students had not been asked to nominate combinations of representations hence the Ainsworth framework was not applied in coding this data.
Results
A total of 3367 separate representations were coded across 932 PowerPoint slides that had been used as the resource to support the teaching of general chemistry concepts in lectures across a single semester. This resource comprised the collation of multiple representations by multiple tertiary chemistry teachers over a time period of at least a decade, the sequence of topics was determined by the teaching teams and not guided by a textbook. It was assumed that the intentional combination of these representations had served to support teacher explanations and student problem-solving activities in class. Since the composition of the teaching team had changed several times during the past decade, it was difficult to confirm any intentions or attribute any content creation to a specific individual teacher. The teachers’ verbal discourse in explanations or gestures during lectures while interacting with the slides have not been included in the analysis in this study. The focus of this study is on the representations that students had engaged with visually.Dominant forms of representations encountered by students
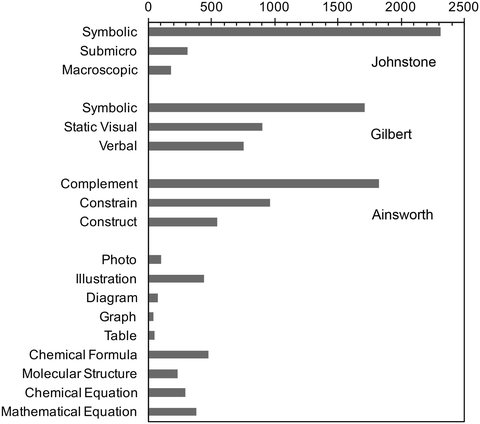
The number of counts in each category, organized by each separate coding framework, are presented in Fig. 3. It is evident that symbolic representations were the most predominant category adopted by the tertiary chemistry teachers (including symbols, formulas, chemical and mathematical equations and disciplinary formalisms such as arrow representations and electron notation). A focus on accurate usage of symbols in terms of what they represented was evident within the slides along with the disciplinary formalisms in terms of understanding the ‘grammar’ involved in applying these symbolic representations (Taber, 2009).The analysis of the content in the slides indicated that the teachers had frequently begun a topic by introducing the symbolism that they assumed students had encountered in high school chemistry. This served to reinforce and extend students’ representational fluency (for example 1s, 2s and 3s in Fig. 4a).
This practice aligns with the recommendation that students should be able to connect their prior understanding and reinforce past knowledge through familiar representations as a foundation to enable them to engage with new representations (Ainsworth, 1999). Many examples where multiple symbolic representations (S) were combined to support construction of understanding by extension were evident within the slides, for example in the topic of Lewis structures.
Relatively few representations were categorized as the macroscopic (M) and submicro (SM) levels of thinking in comparison to the symbolic domain (Fig. 3). The submicro representations included particles and molecule structures (Fig. 4a and b). Macroscopic representations were mostly divided into photos or images of experiments, substances and real world contexts (full details in Appendix 2 Table 4). Several slides contained the hyperlinks to external multimedia resources including videos of submicro and macroscopic processes (typically experiments) embedded in slides. Hyperlinks to dynamic simulations for molecular shape and gas properties that reinforce visualization at the submicro level were evident in the lecture slides. While these links existed, we can only imply that the teachers used these dynamic, multimodal representations interactively during class. Actual use of these representations in practice was not confirmed as part of this study.
Several in-class demonstrations (demos) were used in the third module of the course to reinforce the macroscopic level of thinking in chemistry in the learning environment. These demo links were coded as photos or static visual representations (Fig. 4c). The photo of the demo in the slides served to prompt the lecturer to transition to the experiment, we did not observe classroom practice to confirm whether the demo was actually performed.
The distribution of the codes within each category of representation has been presented as a boxplot revealing additional insights (Fig. 5). Symbolic representations coded according to both Johnstone's levels and Gilbert's static visual mode showed a large variation in values, evident on comparison of the box heights and length of whiskers. This large variability is also observed in the boxplots for the category of the complement function according to Ainsworth's taxonomy. In contrast, a low variation between the boxplots was observed in the categories of photo, graph and table reflecting the relatively low number of these coded on slides. The centre of the distribution (median) values in the boxplots were different for most categories with the exceptions of macroscopic and submicro categories and static visual and verbal modes.
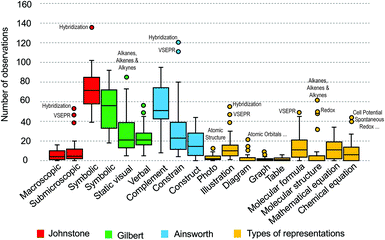 | ||
| Fig. 5 Boxplot displays of the distribution of representations by lecture topic in each category. The furthest separated outliers have been labelled by lecture topic. | ||
Asymmetric distributions were observed in most boxplots with the larger area of the box tending to be above the median value.
For example, the top of the box for the submicro category lies at around 12 observations per slide, this indicates that 75% of the lessons contained fewer than 12 submicro representations. This frequency is relatively small if we take into consideration that the single lecture for the topic Hybridization depicts 54 submicro representations (the maximum number observed across all lectures). Similarly, this analysis reveals that 75% of the lectures contained fewer than five instances of representations of molecular structures.
Symbolic representations and representations used in a complementary role were observed to have a tendency to exhibit the highest number of representations per lecture, indicating that each of these were popular categories (Fig. 3).
A Kruskal–Wallis analysis (Kruskal and Wallis, 1952) provided strong evidence of significant difference (p < 0.001) between the mean ranks of at least one pair of the three categories associated to Johnstone's levels of thinking (Table 1). This difference (p < 0.001) was also observed for the three categories associated to Gilbert's modes of representation through the Kruskal–Wallis analysis. Further, this test indicated a significant difference (p < 0.001) between the mean ranks of at least one pair of groups for the three codes attributed to Ainsworth's taxonomy (Table 1). Consequently, Mann–Whitney U tests (Appendix 3 Table 5) were conducted for post hoc pairwise comparisons among the groups applying a Bonferroni correction to control for type I error (Gordon et al., 2007). Each category of representation comprised 32 lectures. The results for Johnstone's categories revealed that symbolic representation (mean rank = 48.50) tended to display larger values than macroscopic representation (mean rank = 16.50). A statistically significant difference was found (U = 0, Z = −6.88, p < 0.001, large effect size: r = −0.86). A similar result was found when comparing symbolic (mean rank = 48.28) and submicro (mean rank = 16.72) categories. The former tended to show the larger values (U = 7, Z = −6.79, p < 0.001, large effect size: r = −0.85). However, no difference was found between macroscopic and submicro (U = 458, Z = −0.73, p = 0.467). In considering categories assigned to Gilbert's modes, symbolic representations (mean rank = 42.70) were more abundant than static visual (mean rank = 22.30) representations, a statistically significant difference (U = 185.5, Z = −4.39, p < 0.001, large effect size: r = −0.55). The symbolic category (mean rank = 45.44) also had larger values than the verbal category (mean rank = 19.56) that were significant (U = 98, Z = −5.56, p < 0.001, large effect size: r = −0.70). No difference was found between static visual (mean rank = 33.08) and verbal (mean rank = 31.92) (U = 493.5, Z = −0.25, p = 0.804) representations in terms of the categories in Gilbert's framework. In relation to Ainsworth's codes, a statistically significant difference was identified between the complement (mean rank = 43) and constrain function categories (mean rank = 22) (U = 176, Z = −4.51, p < 0.001, large effect size: r = −0.56) and also between complement (mean rank = 46.97) and construct functions (mean rank = 18.03) (U = 49, Z = −6.22, p < 0.001, large effect size: r = −0.78). No statistically significant difference was found between the constrain (mean rank = 37.75) and construct (mean rank = 27.25) function categories (U = 344, Z = −2.26, p = 0.024). In summary, symbolic representations are the most abundant of the coding categories for both Johnstone's and Gilbert's frameworks (Table 1). In relation to Ainsworth's taxonomy, representations that appeared to function in a complementary role were most often adopted by teachers in the resource that was analysed in this study.
Most boxplots displayed outliers situated at values above the boxes for each category and each outlier is associated with an individual lecture topic (several outliers are labelled by topic in Fig. 5). The symbolic representation boxplot (Johnstone framework) contains a single outlier, the Hybridization lecture, in which 136 symbolic representations were used. The teachers had employed an exceedingly high number of symbols, combined with submicro representations, to teach the formalisms related to concept of combining atomic orbitals to form new hybrid orbitals. The valence shell electron pair repulsion (VSEPR) and Hybridization lectures are also outliers due to the high numbers of combinations of representations that were considered to be constraining interpretation (Ainsworth taxonomy).
The boxplot for submicro representations revealed three outlier lectures attributed to a very high number of submicro representations of orbitals, atoms and molecules. The topics of these three outlier lectures were Hybridization (n = 54), VSEPR (n = 46), and Kinetic theory, ideal gases and intermolecular forces (n = 38). The lecture for Alkanes, Alkenes and Alkynes is an outlier in the boxplot for the mode of static visual with 85 individual representations (61 molecular structures, 16 illustrations depicting molecules and 8 photos showing common objects made of these three main groups of aliphatic hydrocarbons). The majority of these representations indicated a teaching intention to demonstrate the spatial arrangement of atoms and chemical bonds employing structural formulas and line structures.
An interesting observation was that the lecture topic of Atomic Structure contained the highest number of photo representations (n = 12). It is evident as the outlier in the boxplot for this category (Fig. 5) and is surprising since this topic could be regarded as mostly likely to involve symbolic and submicro entities which cannot be visualized through a photo. Four of these photos were images of different materials so revealed an intention by the teachers to relate the presence of atoms to the constitution of matter as a macroscopic phenomenon. The other eight photos portrayed famous scientists, all Nobel Laureates, including Bohr, Curie, Einstein and Planck from different sources. The teachers’ intention was clearly to highlight the importance of the historical context of human endeavour.
Multiple representations that have potential to combine in ways to support deeper learning
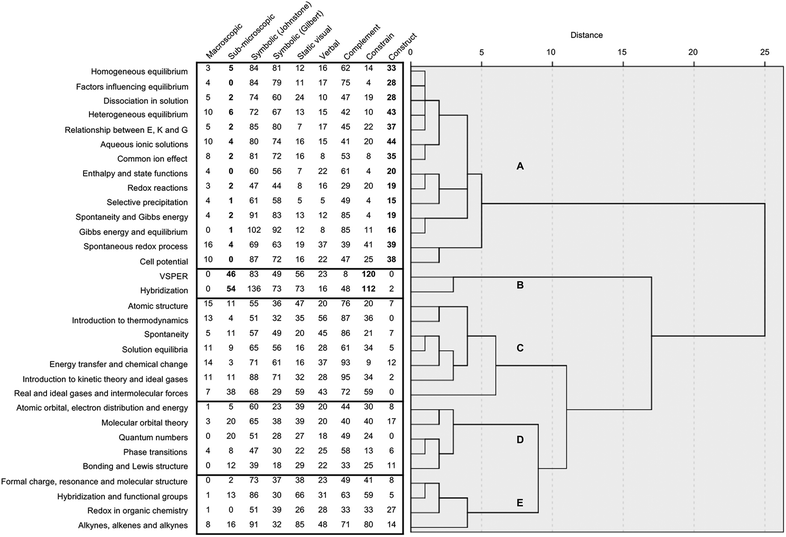
The categories of representation that were applied during coding became the variables that informed the HCA. The topics that appear within the same cluster share many characteristics, so the similarity between them is higher than with topics that formed different clusters. The similarity among lecture topics in a group is measured by a scale indicating the distance between them (a short distance means high similarity).
Table 2 shows the mean ranked values for the categories of representations within the five different clusters. This table gives an overview regarding the distribution of values for these categories in each cluster. A Kruskal–Wallis test yielded significant p values (p < 0.05) for all the categories of representation except those of photos, graphs and tables. Results from this Kruskal–Wallis test suggest that, for the categories with statistically significant p values, clusters are meaningfully different. That, is one or more of the clusters had different ranked sum distributions compared to other clusters. Consequently, at least one cluster group differed from the other cluster groups. Statistical tests for post hoc pairwise comparisons to identify which cluster was significantly different were not feasible because several clusters possess a small sample size (Cluster B contains only 2 lecture topics and Cluster E only 4 lecture topics). Since further statistical analysis for Clusters B-E was considered not feasible, due to the low number of lecture topics in each, the differences noted between these clusters will be described using the values presented in Fig. 6 and Table 2.
| Representation | Cluster | Kruskal–Wallis H testa (d.f. = 4) | ||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | ||
| a Chi-square. b Significant difference (p < 0.05). | ||||||
| Macroscopic | 18.07 | 3.50 | 26.43 | 8.20 | 10.50 | 17.9b |
| Submicro | 9.46 | 31.50 | 21.14 | 23.90 | 16.25 | 18.0b |
| Symbolic (Johnstone) | 19.61 | 27.00 | 12.93 | 6.10 | 19.63 | 11.7b |
| Symbolic (Gilbert) | 23.96 | 20.25 | 13.50 | 4.50 | 8.75 | 20.8b |
| Static visual | 8.14 | 29.50 | 20.14 | 21.80 | 26.25 | 22.0b |
| Verbal | 9.46 | 14.75 | 25.93 | 16.60 | 25.38 | 18.7b |
| Complement | 14.82 | 7.00 | 27.36 | 10.30 | 15.88 | 14.1b |
| Constrain | 9.86 | 31.50 | 18.79 | 17.90 | 26.50 | 17.3b |
| Construct | 25.00 | 4.00 | 7.71 | 11.40 | 14.75 | 22.87b |
| Photo | 18.50 | 4.00 | 21.43 | 12.70 | 11.88 | 8.1 |
| Illustration | 8.79 | 31.50 | 23.43 | 20.80 | 18.50 | 19.7b |
| Diagram | 12.21 | 25.25 | 18.29 | 25.60 | 12.63 | 13.0b |
| Graph | 16.75 | 8.00 | 20.79 | 20.00 | 8.00 | 8.1 |
| Table | 19.54 | 20.75 | 10.36 | 17.80 | 12.88 | 6.0 |
| Molecular formula | 20.61 | 28.25 | 11.79 | 8.20 | 14.88 | 11.7b |
| Molecular structure | 11.29 | 25.75 | 17.57 | 14.70 | 30.50 | 18.8b |
| Mathematical equation | 20.71 | 3.50 | 20.00 | 9.80 | 10.50 | 11.9b |
| Chemical equation | 24.64 | 6.00 | 13.29 | 7.40 | 10.25 | 21.2b |
On this basis, some differences between the clusters are clearly apparent. In Fig. 6, all 14 lecture topics in Cluster A contained representations that appear to have the potential to function as supporting construction of understanding (values range between 15 to 44 counts for each lecture topic). In Cluster B, the topic of VSPER contains no representations coded as ‘construct’, and Hybridization contains only two. In the remaining three clusters (C, D and E), fewer than 15 counts of representations coded as ‘construct’ were observed in any lecture topic, except for Molecular orbital theory in Cluster D (17 counts) and Redox in organic chemistry in Cluster E (27 counts).
Cluster B grouped only two lecture topics and these contained the highest number of representations that had been coded as functioning to ‘constrain’ interpretation. The lecture topics of VSEPR (120 counts) and Hybridization (112 counts) exceeded any other lecture topic in other clusters (the highest was 80 counts for the topic Alkanes, Alkenes & Alkynes). Cluster C lecture topics exhibited the highest range of values (between 61–95 counts) in terms of representations that were coded as the complement function in comparison to other clusters (A, ranging between 29–85 counts; B, 8 & 48 counts; D, 33–58 counts; and E, 33–71 counts).
In summary, Cluster A is identified as the grouping of lecture topics being most abundant in representations that were coded as potentially functioning to construct understanding; Cluster B as abundant in representations that were coded as functioning to potentially constrain understanding and Cluster C as characterized by an abundance of complementary representations compared to other clusters. Clusters D and E presented a moderate range of values for all of the categories of complement, constrain and construct.
The statistical analysis enabled identification of the specific topics where instances of slides existed in which multiple representations were coded as combining to have potential to support students’ construction of deeper understanding. Cluster A contained the highest numbers of representations that were coded as having potential to combine to support students in constructing deeper understanding, according to Ainsworth's taxonomy (Ainsworth, 2006). This cluster also had the greatest separation by relation to the other clusters, the apparent origin of this difference is revealed when the dendrogram is expanded to show the distribution of additional representation categories in terms of type (Fig. 7).
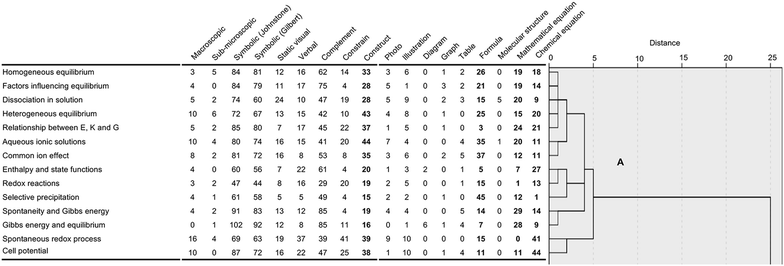 | ||
| Fig. 7 Cluster A expanded from the dendrogram shown in Fig. 6 to include the distribution of the forms of representation. Values in bold emphasise the forms of representation that had the highest overall use in comparison to other clusters. | ||
Cluster A comprised fourteen topics that focussed on spontaneous processes including solubility and redox reactions. Relatively few submicro representations were used to support teaching of concepts in lectures in Cluster A. In contrast, equations and mathematical equations were dominant. The Spearman's correlation analysis (Appendix 3 Table 5) reinforced the strong association between the use of macroscopic representations and their potential to support construction of deeper understanding (rho = 0.83, p < 0.0003), an example of a combination of representations is shown in Fig. 4d. The strength of the correlation is based on the rule of thumb proposed by Hinkle et al. (2003).
Cluster B contained only two lecture topics, VSPER and Hybridization, which can be considered as outlier topics given that they form a very small cluster (Hair et al., 2010). Hybridization contains 54 submicro representations whereas VSPER contained 46 and these lectures contain the highest usage of submicro representations. In Cluster B, the majority of representations depicted orbitals, electrons, atoms, molecules and ions. It is interesting to note that it was found that VSPER and Hybridization lectures included large numbers of representations coded as potentially constraining understanding of concepts according to Ainsworth's taxonomy.
Cluster C comprised seven lecture topics and is characterized by a stronger tendency to use representations in a complementary manner, notably verbal text. The topics Introduction to thermodynamics, Spontaneity, Energy transfer and chemical change and Introduction to kinetic theory and ideal gases employed more than 85 representations that were coded as a complementary function in each lecture. This is the highest number observed for individual lectures across all the clusters. Macroscopic representations were also prevalent in Cluster C in the form of photos and illustrations. This cluster also contained the lecture topic Atomic Structure that included photos of scientists.
The two remaining clusters, D (five lecture topics) and E (four lecture topics), were more difficult to clearly discriminate in terms of a definitive aggregation relationship from the HCA. The group of lecture topics in cluster D appeared to be generally connected to bonding concepts (excluding Phase Transition). The lectures relating to Quantum Numbers and Molecular Orbital Theory contained the equal fourth highest number of representations at the submicro level of thinking. Cluster E could be identified as being focussed on introductory organic chemistry ideas and contained the highest number of molecular structures displayed mainly through static visual representations overall. 2-Dimensional arrangements of atoms in a molecule were identified as the predominant format.
Students’ perceptions of representations they had encountered during lectures
Since a goal of this study was to inform future instructional design, the perspectives of students who had recently encountered the representations in the lecture slides were sought. The participating students shared useful reflections on the representations that they had either found useful or difficult to engage with (it is not known whether these students had attended lectures in person or viewed lecture recordings).The students’ responses to two open response survey items were coded according to both Johnstone's and Gilbert's frameworks, this data is summarised in Table 3. Ainsworth's framework was not applied because the students had not been asked to nominate multiple representations. The low response rate of 147 students (12% course enrolment) was most likely attributed to the timing of data collection as post-semester.
| Module lecture (L) clusters | Level (count) | Representation mode | Highly cited topics linked to a representation mode (count) |
|---|---|---|---|
| Module 1 | S (43) | Diagram (34) | |
| Cluster B: 2L | Drawing (3) | Lewis structures & molecular orbitals | |
| Cluster C: 2L | Graph (2) | Orbital penetration & shielding | |
| Cluster D: 3L | Table (1) | ||
| Cluster E: 3L | |||
| SM (86) | 3D diagram (21) | Molecule shapes & hybrid orbitals | |
| Diagram (16) | |||
| Drawing (6) | |||
| Models (30) | Structures | ||
| Photo (1) | Molecular structure | ||
| Simulation (2) | |||
| Table (2) | VSEPR Tables | ||
| S & SM (2) | Diagram (1) | Molecular orbitals | |
| Drawing (1) | Molecules & electron configurations | ||
| Module 2 | M (12) | Demo (1) | |
| Cluster A: 5L | Diagrams (5) | System & surroundings | |
| Cluster C: 5L | Drawing (1) | ||
| Cluster D: 1L | Video (3) | ||
| S (62) | Diagrams (29) | Phase diagrams (19) & energy transfer | |
| Equations (3) | |||
| Graph (25) | Q/K relationship (7) | ||
| SM (7) | Animations (1) | Gas molecules | |
| Diagrams (2) | Molecule polarity | ||
| Drawing (1) | Hydrogen bonds | ||
| Simulation (5) | PhET simulations | ||
| S & SM (3) | Simulation (3) | Gas laws (PhET) | |
| Module 3 | M (31) | Demo (17) | |
| Cluster A: 9L | Diagrams (2) | ||
| Cluster C: 1L | Drawing (1) | ||
| Cluster E: 1L | Photo (1) | Galvanic cell | |
| Video (6) | |||
| M & S (52) | Demo (1) | ||
| Diagrams (23) | Galvanic cell (52) | ||
| Drawing (10) | |||
| S (21) | Diagrams (4) | Phase diagrams | |
| Equation (3) | |||
| graph (12) | Q/K relationship (6) | ||
| Table (1) | ICE table | ||
| SM (3) | Diagrams (1) | ||
| Simulation (1) | |||
| Video (1) | |||
| S & SM (1) | Diagrams (1) | Organic redox | |
| S & SM & M (1) | Drawing (1) | Galvanic cell: movement of charges and ions | |
Module 1 included lectures that addressed topics identified across several of the clusters identified in the HCA. The category of representation that appeared to be most highly favoured was coded as the submicro level of thinking (Table 3). These SM representations related to learning about structure and bonding (topics cited included Lewis structures, VSEPR, molecular orbitals and hybrid orbitals). Students also gave strong feedback that the use of physical molecular models and drawing structures or diagrams had been useful in class. These modes of representation were not captured as part of the analysis of lecture slides but have emerged as important from the students’ perspective.
For module 2, which contained lecture topics that had a strong focus on thermodynamic concepts from Cluster A, students indicated that symbolic representations in the form of graphs and diagrams were most useful. In particular they highlighted phase diagrams (n = 19 students) as a useful representation. Another specific representation that 14 students cited as useful were the bar graphs (used in lectures in both modules 2 and 3) that displayed a quantitative comparison of Q vs. K ratios to support the prediction of the direction a reaction would proceed to achieve equilibrium.
The majority of lecture topics within Module 3 were grouped in Cluster A in hierarchical structure analysis. Students placed exceptionally strong value on macroscopic representations, either in the form of demos (n = 18) or images and drawings created by the lecturer. Representations of galvanic cells (n = 56) were the most highly cited, including 14 references to hand drawn representations by the lecturer. This macro level of representation of a specific concept had clearly supported learning from the perspective of students. Analysis of these topics (Spontaneous redox processes and Cell potential) in Fig. 7 confirms the high numbers of representations in the categories of Macro, Construct and Chemical Equations used.
When students were asked to share which particular representations they perceived had been difficult to learn with, or understand, a wide variety of representations were nominated students (n = 122). Despite this, the role of lecturer explanations emerged as a strong theme during analysis of responses. Regardless of the topic or specific representation, 28% of students indicated that a lecturer explanation was required to support their understanding or their ability to interpret the representations, four examples of student references are provided below:
Diagrams which are somewhat ambiguous, such as that outlining the electron shell filling order, (with 1s, 2s, 2p etc. with diagonal backwards downwards facing arrows on it) I found this difficult to understand without the explanation, however when it was explained, this was clear.
Equations – often the central focus of slides, there was no context, comprehension or explanation of its components, necessity, requirements, conditions or anything relevant. Almost every equation was like this. Unless the lecturer explained each term, there was no way of gaining that sort of information.
Hybridisation diagrams, specifically involving two different atoms. They were not explained in sufficient detail in my opinion and I had to frequently look at 3rd party sources to get an adequate understanding.
Thermodynamics because there were a lot of new terms introduced (i.e.; entropy, Gibbs free energy) and the explanation was not really explicit enough for me to understand although I watched the lecture recordings over and over again to truly understand in the end, I referred to other YouTube videos.
Student feedback complemented the categorical analysis of the representations in lecture slides to inform instructional design. It was evident that representation of concepts through verbal explanations (discourse) and teacher modelling is critical for supporting students’ learning through representations, particularly when they are encountering them for the first time. Many students stated that they had found it difficult to interpret individual representations or make links between several representations suggesting that they had perhaps experienced a degree of cognitive overload at points during the semester.
Discussion
The enormous number of individual representations that students had encountered within slides during a 13-week semester emphasizes the need for teachers to consider scaffolding the development of students’ representational competencies. The associated cognitive demand of processing so many representations introduces a risk of overloading working memory. This may potentially impact on a student's learning if they do not understand any individual representation, known as a fragmentation impediment (Taber, 2001). Indeed, when asked for their perceptions, students self-reported that they had found either interpreting individual representations or translating between combinations of representations difficult (in some cases both).The degree of teacher scaffolding impacts on the learners’ representational competences and success is dependent on students’ prior learning and their learning goals (Ainsworth, 2006). A teacher's selection of, and approaches to, combining multiple representations should be further explored in terms of pedagogical functions (Ainsworth and Newton, 2014; Ainsworth, 2018). The instructional resource that formed the basis of this study is an object of learning in which multiple teachers have combined representations therefore it provides an example of how variation theory applies in practice (Bussey et al., 2013). The selection and combination of representations in each slide served to support the common intentions for student learning shared by multiple teachers in their lectures. These representations originated from multiple sources and it is probable that their creators had different intentions or purposes in mind for them. It is therefore possible that students may experience unintended influences during learning from the inherent design of individual representations.
In this study, symbolic representations were found to be the most prevalent form adopted by the tertiary teachers. These are ubiquitous to the discipline of chemistry and as Taber notes ‘Symbolic representations become second nature to the teacher, being highly integrated with conceptual understanding and subject knowledge’ (2009, p. 75). From a pedagogic perspective in chemistry, the symbolic domain cannot often be separated discretely from the macroscopic and submicro conceptual levels of thinking since these levels are also represented and communicated by symbols (Taber, 2013).
Two decades ago, Gabel (1999) called for teachers to move away from relying substantially on the symbolic level (the most abstract level) and to incorporate more macroscopic and submicro representations – the findings of this study indicate that teachers are still substantially reliant on symbolic forms of representation.
Very limited use of macroscopic representations was observed in slides across the whole course. This is particularly concerning since students are known to find it difficult to link submicro levels of thinking to macroscopic levels of representation (Hinton and Nakhleh, 1999). Indeed, in this study, the students indicated that they had particularly valued macroscopic representations in the form of experimental demonstrations, images and when teachers drew galvanic cell diagrams. While the student feedback in this study is not claimed to be generalizable due to the low response rate, it is clear that future instructional design needs to address this deficiency.
We acknowledge that as part of this study Johnstone's triplet levels of thinking (symbolic, submicro and macroscopic) have been considered to be separate categories in the evaluation framework. It is recommended that they be considered in parallel during instructional design since the ability to fluently recognise relationships between representations and translate between these different levels of thinking is considered to be a characteristic of expert thinking in the domain of chemistry (Johnstone, 2010). Johnstone warned that teachers may be able to ‘flit’ around the triplet, however, for learners this process was likely to be cognitively demanding.
Most teachers do not consult the chemistry education research literature routinely to inform their pedagogies and practices. Instead they rely more on their own experiences and reflections on student learning (Childs, 2009; Herrington and Daubenmire, 2016). New strategies for sharing research findings that inform classroom practice and representational pedagogies at all levels of chemistry education need to be identified as a priority. This might be achieved through professional organisations, peer networks and social media (Ainsworth and Newton, 2014).
Chemical equations were most prevalent in Cluster A compared to other clusters with many equations being coded as supporting construction of understanding when combined with other forms of representation. A correlation was observed between the categories of chemical equation and verbal representations in cluster A (Appendix 3 Table 5). This relationship requires further investigation in regard to the nature of verbal representations which included instructions, descriptions and questions.
Students indicated that they had found teacher explanations to be very important in supporting their ability to understand the use of equations and their interpretation, or translation, between the representations in the topics in this cluster. Talanquer (2011) reinforces Johnstone's (1982, 1991) claim that thermodynamics tends to operate only on the descriptive macroscopic and representational symbolic explanatory levels due to abstract concepts such as internal energy and entropy. Gibbs energy was a concept identified as a particularly difficult concept to understand by many students in this study hence further attention is required in considering the pedagogical function of the different representations in thermodynamics topics.
A large number of static visual and submicro representations were categorised as potentially being used to constrain and support the development of mental models of entities that are too small to be ‘seen’ throughout the lectures. These were particularly evident in Cluster B which grouped only two lecture topics: VSEPR and Hybridisation. Students indicated that their learning had been supported for these topics when their lecturers used additional representations in the form of physical (concrete) models and drawings to support explanations. Physical models and hand-drawn representations were not captured as part of the analysis of lecture slides in this study but these modes are well known to be an important part of the array of representations that teachers use in practice for teaching bonding concepts (Patron et al., 2017). Their use in lectures represents evidence of inherent TSPK applied by the tertiary teachers and can be explored further.
Conclusions & limitations of this study
The application of three frameworks (including the chemistry levels of thinking, typological and taxonomic structures) to analyse multiple representations in lecture slides presents a new strategy in the evaluation of an instructional resource. The resource in this study was curated for a specific teaching context by multiple teachers who drew on multiple sources therefore contrasts with prior studies that have focussed on analysis of textbooks that are used across multiple contexts. Several patterns and relationships in the way representations had been combined were identified that can inform future instructional design of resources for specific topics.The findings from analysis of the lecture resource in this study has raised awareness of the scale and complexity of the quantity and forms of representations that students are required to navigate within a short period of time (typically 13 weeks). The combination of multiple representations in developing students’ representational competencies can introduce cognitive overload for students with low prior experience or competence. Therefore, the findings of this study have triggered a review of the lecture resources by the current teaching team with the aim of improving ways in which representations are combined. Single representations that had been used gratuitously and appeared to be redundant have been removed to reduce cognitive load. Greater attention has been paid to how representations will be combined to support student development of representational competence particularly in terms of submicro and macroscopic levels of thinking. Future resources used in the teaching context of this study will be designed informed by the Design, Function and Tasks (DeFT) framework (Ainsworth, 2006) in parallel with Johnstone's levels of thinking. Topics that have initially been targeted include thermodynamics concepts.
It is important to acknowledge that student engagement and learning with representations should be evaluated in parallel with measuring the efficacy of the instructional design. This additional lens was not within the scope of the current study since the focus was on categorising the large number of representations within the single learning object. Insights that were gained from student perception data have reinforced the diversity of ways in which students had perceived the utility of the different modes of representation and range of difficulties encountered. Assessment of learning will depend on whether it is measuring how learners understand the relationship and ability to translate between representations or their understanding of each representation in isolation (Ainsworth, 1999). This assessment will require careful design.
Several limitations in this study are acknowledged. The representations were characterized in the absence of any explicit detail of their intended pedagogical function or purpose by the teachers that had selected them. It was not possible to identify the original creator of the content on each slide due to the changing annual composition of the teaching team over at least a decade.
The use of lecture slides as the unit of analysis is a limitation of this study. The representations on the slides are used in a lecture environment where learners engage with these representations supported by their lecturers who use additional modalities of representation including explanations (verbal); real-time drawing (gestural) and embodiment through hand and arm motion (gestural). These additional representations are dependent on an individual teacher and an interesting future study would be to compare the additional representations introduced by multiple teachers using a subset of slides in their practice to guide students in understanding representations.
In applying Ainsworth's taxonomy to categorise how representations can be combined to potentially support deeper learning, an assumption was made regarding students’ familiarity with certain representations. They were assumed to have completed high school chemistry, or equivalent, as a prerequisite to enrollment in the course. While this assumption was only applied to representations that are very common in high school resources, students might not have encountered them.
This study was originally initiated to inform instructional design and encourage more inclusive practices. One example of a design strategy that emerged has been shared in the Appendix 5 to inspire teachers in possible ways of combining representations to support students’ learning in the topic of phase diagrams (identified as a topic in which diagrams had been found useful by several students in this study).
Conflicts of interest
There are no conflicts of interest to declare.Appendix 1
The identification of the correct number of clusters in a cluster solution is a combination of the statistical separation observed (e.g. in the dendrogram) and a theoretical judgment of the practical differences among the cluster set. In this work, a scree plot (the increase in the distance between clusters versus number of clusters formed) was used to decide the number of clusters to be analyzed in the dendrogram (Fig. 8). The number of clusters was identified by the first large increase in distance (elbow) and the optimum number of clusters is five (the number related to the beginning of the first large increase). Five clusters would suffice for the final partition, providing evidence that this solution was indeed appropriate. Moreover, we can see five distinct clusters in the dendrogram (Fig. 9A–E).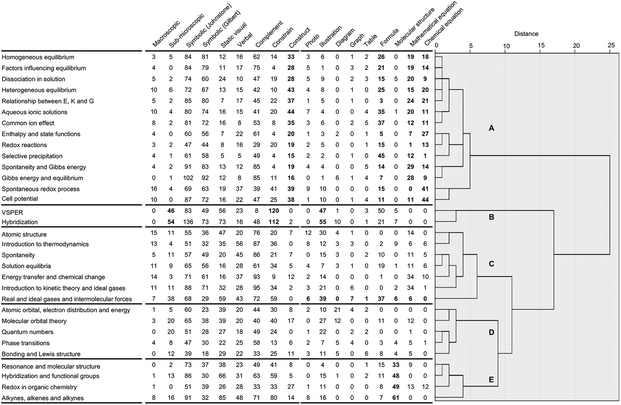 | ||
| Fig. 9 Dendrogram displaying five hierarchical clusters (A–E) based on relationships between the assigned properties of representations. | ||
Appendix 2
| Module | Lesson | Description of the photo | Module | Lesson | Description of the photo |
|---|---|---|---|---|---|
| M1 | L2 | Metallic bar | L201 | Ice | |
| Ice | Liquid water | ||||
| Volumetric balloon × 2 | L21 | Stones | |||
| Scientist × 8 | Syringe with NO2/N2O4 solution | ||||
| L3 | Scientist | Tractor in a plantation | |||
| L4 | Scientist × 2 | L22 | Cars in a big city | ||
| L5 | Scientist | Experiment involving Le Chatelier's Principle × 3 | |||
| Ball-and-stick models × 2 | Scientist | ||||
| L10 | Plastic cup | L23 | Sublimation | ||
| Grains | Experiment supercritical fluids | ||||
| Bank note | M3 | L26 | (NH4)2Cr2O7 decomposition | ||
| Pills | Magnetite attracting clips | ||||
| Beehive | Saturated NaCl solution | ||||
| Chair | Landscape of Queenstown Tasmania | ||||
| Compact disk | L27 | Liquid solution inside a beaker | |||
| Man on a Kayak | Scale formation in boilers × 2 | ||||
| M2 | L14 | Child with balloons | Diet Coke and Mentos | ||
| Perfume | L28 | Conductivity in acidic solution × 2 | |||
| Scientist | Vegetable (anthocyanine) | ||||
| L15 | Dry ice | Flower (anthocyanine) | |||
| Iceberg × 2 | Cups with different acidic solutions | ||||
| Volumetric balloon with Cl2 | L29 | Beaker with aqueous solution of NaCl × 2 | |||
| Petri dish with Br2 liquid | The Dead Sea × 2 | ||||
| Solid iodine | Bottle of Sports Drink | ||||
| L16 | Cold frost, beaker and digital thermometer | Pool hardness raiser × 2 | |||
| Sugar solution in test tube | L30 | Test tube with saturated NaCl solution | |||
| Yellow saturated solution in test tube | Mollusc (calcite) | ||||
| Beaker and bottle of ethanol | Pteropod (aragonite) | ||||
| Beaker with ethanol | L31 | Beaker with saturated aqueous solution of PbI2 | |||
| Reaction in test tube | Selective precipitation in test tubes | ||||
| Calorimeter and volumetric balloon | L32 | Iron wool and CuSO4 solution × 2 | |||
| Chemists solving stoichiometry | L33 | Adding zinc rod into a CuSO4 solution × 3 | |||
| L17 | Metallic tank | Adding copper rod into a CuSO4 solution × 7 | |||
| Animation | L34 | Lemon battery | |||
| L18 | Mountain | L35 | The glowing pickle | ||
| L20 | Fire in a forest | L36 | Silver mirror | ||
| Scientist |
Appendix 3
| Macroscopic | Submicroscopic | Symbolicc | Symbolicd | Static visual | Verbal | Complement | Constrain | Construct | Photo | Illustration | Diagram | Graph | Table | Molecular formula | Molecular structure | Mathematical equation | Chemical equation | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a Bold values for r > 0.7 and p < 0.0003. b Bonferroni correction to the alpha value (p = 0.05/171 = 0.0003) according to Gordon et al. (2007). c Symbolic according to Johnstone (1993). d Symbolic according to Gilbert (2005). | ||||||||||||||||||
| Macroscopic | 1 | |||||||||||||||||
| Submicroscopic | 0.31 | 1 | ||||||||||||||||
| Symbolicc | −0.12 | −0.15 | 1 | |||||||||||||||
| Symbolicd | −0.20 | 0.10 | 0.92 | 1 | ||||||||||||||
| Static visual | 0.62 | 0.38 | 0.17 | 0.08 | 1 | |||||||||||||
| Verbal | 0.30 | −0.09 | −0.12 | −0.14 | 0.01 | 1 | ||||||||||||
| Complement | −0.57 | −0.44 | 0.59 | 0.58 | −0.22 | −0.31 | 1 | |||||||||||
| Constrain | 0.45 | 0.34 | 0.03 | −0.04 | 0.44 | 0.45 | −0.69 | 1 | ||||||||||
| Construct | 0.83 | 0.53 | 0.02 | 0.06 | 0.55 | 0.44 | −0.54 | 0.57 | 1 | |||||||||
| Photo | 0.49 | 0.52 | −0.22 | −0.07 | 0.58 | 0.06 | −0.28 | 0.07 | 0.45 | 1 | ||||||||
| Illustration | 0.65 | 0.47 | −0.12 | −0.25 | 0.67 | 0.32 | −0.54 | 0.66 | 0.62 | 0.28 | 1 | |||||||
| Diagram | −0.45 | −0.43 | 0.09 | 0.09 | −0.29 | −0.04 | 0.44 | −0.27 | −0.42 | −0.57 | −0.49 | 1 | ||||||
| Graph | −0.04 | −0.22 | 0.30 | 0.19 | 0.09 | −0.32 | 0.33 | −0.22 | −0.03 | −0.02 | 0.01 | −0.17 | 1 | |||||
| Table | −0.10 | −0.18 | 0.58 | 0.47 | 0.45 | −0.34 | 0.49 | −0.15 | −0.08 | 0.01 | −0.08 | 0.10 | 0.13 | 1 | ||||
| Molecular formula | 0.15 | 0.38 | −0.31 | −0.16 | 0.15 | −0.47 | −0.12 | −0.24 | 0.13 | 0.50 | 0.02 | −0.50 | 0.25 | 0.03 | 1 | |||
| Molecular structure | 0.27 | 0.22 | −0.11 | −0.12 | 0.52 | −0.24 | −0.27 | 0.23 | 0.25 | 0.48 | 0.15 | −0.17 | 0.06 | 0.25 | 0.19 | 1 | ||
| Mathematical equation | −0.27 | 0.09 | 0.72 | 0.77 | 0.02 | −0.46 | 0.50 | −0.20 | −0.13 | −0.01 | −0.37 | 0.09 | 0.23 | 0.41 | −0.16 | 0.30 | 1 | |
| Chemical equation | 0.41 | 0.03 | 0.04 | −0.02 | 0.06 | 0.89 | −0.21 | 0.37 | 0.51 | −0.06 | 0.47 | −0.06 | −0.29 | −0.28 | −0.48 | −0.41 | −0.39 | 1 |
Appendix 4
Table 6.| Mean ranked values | Mean ranked values | U | Z | p | r | ||
|---|---|---|---|---|---|---|---|
| a Bonferroni correction to the alpha value (p = 0.05/3 = 0.017) according to Gordon et al. (2007). b Effect size (large r = 0.5, medium r = 0.3 and small r = 0.1) according to Cohen (1988). | |||||||
| Johnstone | |||||||
| Macroscopic | 30.81 | Submicroscopic | 34.19 | 458 | −0.73 | 0.467 | −0.09 |
| Macroscopic | 16.50 | Symbolic | 48.50 | 0 | −6.88 | <0.001 | −0.86 |
| Submicroscopic | 16.72 | Symbolic | 48.28 | 7 | −6.79 | <0.001 | −0.85 |
| Gilbert | |||||||
| Symbolic | 42.70 | Static visual | 22.30 | 185.5 | −4.39 | <0.001 | −0.55 |
| Symbolic | 45.44 | Verbal | 19.56 | 98 | −5.56 | <0.001 | −0.70 |
| Static visual | 33.08 | Verbal | 31.92 | 493.5 | −0.25 | 0.804 | −0.03 |
| Ainsworth | |||||||
| Complement | 43.00 | Constrain | 22.00 | 176 | −4.51 | <0.001 | −0.56 |
| Complement | 46.97 | Construct | 18.03 | 49 | −6.22 | <0.001 | −0.78 |
| Constrain | 37.75 | Construct | 27.25 | 344 | −2.26 | 0.024 | −0.28 |
Appendix 5 Example of instructional strategy to increase the multimodality of representations and widen access to learning
The question might be asked – why bother categorizing all the representations used in every lecture in a single chemistry course instead of focussing on specific topics? Widening participation in learning in chemistry can be achieved through inclusive learning and teaching practices and this presents an important challenge for teachers across all teaching contexts. The outcomes from this study are currently informing the pedagogical function of representations in course redesign, particularly those that can be targeted for re-representation in multiple modalities to support deeper learning. Given the importance of external representations in learning chemistry, researchers have recommended that teachers think ahead to adopt strategies that are inclusive of any visually impaired students in a chemistry class (Jones and Broadwell, 2008). A wide range of strategies exist to translate representations into more accessible formats such as translating two dimensional images into three dimensional modes.Published research into inclusive practices for teaching and learning in a classroom that includes blind and visually impaired students is sparse with a bias towards supporting laboratory learning. Two commonly adopted strategies include the expansion of verbal descriptions supported by assistive technologies (Harshman et al., 2013) and the introduction of strategically designed tactile representations (Boyd-Kimball, 2012; Harshman et al., 2013). Diagrams and molecular structures can lend themselves to being supported by verbal explanations but this process becomes onerous as the complexity of a molecular structure increases (Miecznikowski et al., 2015). 3D tactile resources provide strong support for the visualization of submicro representations by students (Smothers and Goldston, 2010).
One of the authors of this study (Vidueira Ferreira) currently teaches blind and visually impaired students in his institution hence possesses expertise in identifying surface features that are required in designing tactile representations that can support the development of mental models for these students. To explore the feasibility of creating tactile resources that could supplement 2D representations, the topic of phase changes was selected to develop a combination of multimodal representations. Phase change diagrams were cited by students in this study as particularly useful representations in learning. Very few submicro representations were observed in the existing lecture resources used to support teaching of this topic.
A tactile representation of a phase diagram of water was created using swell paper (Fig. 10a), combined with braille description key for each boundary and labels (Fig. 10b). Swell paper (also known as Piaf paper) enables a representation where key features are raised on the paper surface introducing tactility and spatial information (Supalo and Kennedy, 2014). The intention is to combine this symbolic representation of the phase diagram with the submicro level representation of physical magnetic water molecules (Fig. 10c) also linked to macroscopic observations of the different phases of water in real life (not shown).
Acknowledgements
The funding provided by the Federal Institute of Education, Science and Technology of Pará (IFPA) to support João Elias Vidueira Ferreira's postdoctoral research at The University of Queensland is gratefully acknowledged. The investment of professional knowledge, by multiple chemistry teaching academics, into the preparation of the teaching resource that formed the basis of this study is fully acknowledged.References
- Ainsworth S., (1999), The functions of multiple representations, Comput. Educ., 33, 131–152.
- Ainsworth S., (2006), DeFT: A conceptual framework for considering learning with multiple representations, Learn. Instr., 16, 183–198.
- Ainsworth S., (2008), The educational value of multiple-representations when learning complex scientific concepts, in Gilbert J. K., Reiner M. and Nakhleh M. (ed.), Visualization: Theory and practice in science education, New York, NY: Springer, pp. 191–208.
- Ainsworth S., (2018), Multiple representations and multimedia learning, in Fischer F., Hmelo-Silver C. E., Goldman S. R. and Reimann P. (ed.), International handbook of the learning sciences, New York: Routledge, pp. 96–105.
- Ainsworth S., and Newton L., (2014), Teaching and researching visual representations: shared vision or divided worlds? in Eilam B. and Gilbert J. K. (ed.), Science teachers’ use of visual representations, Dordrecht, The Netherlands: Springer International Publishing, pp. 29–49.
- Airey J., and Linder C., (2009), A disciplinary discourse perspective on university science learning: achieving fluency in a critical constellation of modes, J. Res. Sci. Teach.46(1), 27–49.
- Airey J., and Linder C., (2017), Social semiotics in university physics education, in Treagust D. F., Duit R. and Fischer H. E. (ed.), Multiple representations in physics education. Dordrecht, The Netherlands: Springer International Publishing, pp. 95–122.
- Boyd-Kimball D., (2012), Adaptive instructional aids for teaching a blind student in a nonmajors college chemistry course, J. Chem. Educ.89, 1395–1399.
- Bussey T. J., Orgill M., and Crippen K. J., (2013), Variation Theory: a theory of learning and useful theoretical framework for chemical education research, Chem. Educ. Res. Pract., 14, 9–22.
- Carolan J., Prain V., and Waldrip B., (2008), Using representations for teaching and learning in science, Teach. Sci., 54(1), 18–23.
- Childs P. E., (2009), Improving chemical education: turning research into effective practice, Chem. Educ. Res. Pract., 10, 180–203.
- Cohen J., (1988), Statistical power analysis for the behavioural sciences, 2nd edn, Hillsdale, NJ: Lawrence Erlbaum Associates.
- Cook M. P., (2006), Visual representations in science education: the influence of prior knowledge and cognitive load theory on instructional design principles, Sci. Educ., 90, 1073–1091.
- Cook M., Wiebe E. N, and Carter G., (2007), The Influence of Prior Knowledge on Viewing and Interpreting Graphics With Macroscopic and Molecular Representations, Sci. Educ., 92, 848–867.
- Corradi D. M. J, Elen J., Schraepen B., and Clarebout G., (2014). Understanding Possibilities and Limitations of Abstract Chemical Representations for Achieving Conceptual Understanding, Int. J. Sci. Educ., 36(5), 715–734, DOI:10.1080/09500693.2013.824630.
- diSessa A., (2004), Metarepresentation: native competence and targets for instruction, Cognit. Instr., 22, 293–331, DOI:10.1207/s1532690xci2203_2.
- Eriksson U., Linder C., Airey J., and Redfors A., (2014), Who needs 3D when the universe is flat? Sci. Educ., 98(3), 412–442.
- Gabel D. L., (1999). Improving teaching and learning through chemistry education research: a look to the future, J. Chem. Educ., 76(4), 548–554.
- Gess-Newsome J., (2015), A model of teacher professional knowledge and skill including PCK: results of the thinking from the PCK Summit, in Berry A., Friedrichsen P. and Loughran J. (ed.), Re-examining Pedagogical Content Knowledge in Science Education, New York, NY: Routledge, pp. 28–42.
- Gilbert J. K., (2005), Visualization: a metacognitive skill in science and science education, in Gilbert J. K. (ed.), Visualization in science education. Dordrecht, Netherlands: Springer, pp. 9–27.
- Gilbert J. K., (2008), Visualization: An emergent field of practice and enquiry in science education, in Gilbert J. K., Reiner M. and Nakhleh M. (ed.), Visualization: Theory and practice in science education, New York, NY: Springer, pp. 3–24.
- Gilbert J. K., (2016), The Contribution of Visualisation to Modelling-Based Teaching, in Gilbert J. K. and Justi R., Modelling-based Teaching in Science Education, Models and Modeling in Science Education, pp. 121–148, DOI:10.1007/978-3-319-29039-3_7.
- Gilbert J. K., and Treagust D. F., (2009), Towards a coherent model for macro, submicro and symbolic representations in chemical education, in Gilbert J. K. and Treagust, D. (ed.), Models and modeling in science education: Multiple representations in chemical education, New York, NY: Springer, pp. 333–350.
- Gilbert J. K., Boulter C., Rutherford M., (1998), Models in explanations, Part 1: Horses for courses? Int. J. Sci. Educ., 20(1), 83–97.
- Gilbert J. K., Reiner R., and Nakhleh M., (2008), in Gilbert J. K., Reiner M. and Nakhleh M. (ed.), Visualization: Theory and practice in science education. New York, NY: Springer, pp 3–24.
- Gkitzia V., Salta K., and Tzougraki C., (2011), Development and application of suitable criteria for the evaluation of chemical representations in school textbooks, Chem. Educ. Res. Pract., 12, 5–14.
- Gordon A., Glazko G., Qiu X., and Yakovlev A., (2007), Control of the mean number of false discoveries, Bonferroni and stability of multiple testing, Ann. Appl. Stat., 1(1), 179–190, DOI:10.1214/07-AOAS102.
- Hair Jr. J. F., Black W. C., Babin B. J. and Anderson R. E., (2010), Multivariate data analysis, Upper Saddle River, NJ: Pearson Prentice Hall.
- Harshman J., Lowery Bretz S., and Yezierski E., (2013), Seeing Chemistry through the Eyes of the Blind: A Case Study Examining Multiple Gas Law Representations, J. Chem. Educ., 90(6), 710–716, DOI:10.1021/ed3005903.
- Herrington D., and Daubenmire P. L., (2016), No teacher is an island: bridging the gap between teachers’ professional practice and research findings, J. Chem. Educ., 93(8), 1371–1376.
- Hilton A., and Nichols K., (2011), Representational classroom practices that contribute to students’ conceptual and representational understanding of chemical bonding, Int. J. Sci. Educ., 33(11), 2215–2246.
- Hinkle D. E., Wiersma W. and Jurs S. G., (2003), Applied statistics for the behavioural sciences. Boston: Houghton Mifflin.
- Hinton M. E., and Nakhleh M. B., (1999), Students' microscopic, macroscopic, and symbolic representations of chemical reactions, Chem. Educ., 4(4), 1–29.
- Johnstone A. H., (1982), Macro- and micro-chemistry, Sch. Sci. Rev., 64(227), 377–379.
- Johnstone A. H., (1991), Why is science difficult to learn? Things are seldom what they seem, J. Comput. Assisted Learn., 7, 75–83.
- Johnstone A. H., (1993), The development of chemistry teaching: a changing response to changing demand, J. Chem. Educ., 70(9), 701–705.
- Johnstone A. H., (2000), Teaching of chemistry – logical or psychological? Chem. Educ. Res. Pract. Eur., 1, 9–15.
- Johnstone A. H., (2010), You can’t get there to here, J. Chem. Educ., 81(1), 22–29.
- Jones M. G. and Broadwell B., (2008) Visualization Without Vision: Students with Visual Impairment, in Gilbert J. K., Reiner M. and Nakhleh M. (ed.), Visualization: Theory and practice in science education, New York, NY: Springer, pp. 283–294.
- Kozma R., (2003), The material features of multiple representations and their cognitive and social affordances for science understanding, Learn. Instr., 13, 205–226.
- Kozma R., and Russell J., (1997), Multimedia and understanding: expert and novice responses to different representations of chemical phenomena, J. Res. Sci. Teach., 43(9), 949–968.
- Kozma R., Chin E., Russell J., and Marx N., (2000), The roles of representations and tools in the chemistry laboratory and their implications for chemistry learning, J. Learn. Sci., 9(2), 105–143.
- Kruskal W. H. and Wallis W. A., (1952), Use of ranks in one-criterion variance analysis, J. Am. Stat. Assoc., 47(260), 583–621, DOI:10.1080/01621459.1952.10483441.
- Kumi B. C., Olimpo J. T., Bartlett F., and Dixon B. L., (2013), Evaluating the effectiveness of organic chemistry textbooks in promoting representational fluency and understanding of 2D-3D diagrammatic relationships, Chem. Educ. Res. Pract., 14, 177–187.
- Lawrie G. A., Schultz M., Bailey C. H., and Dargaville B. L., (2019), Personal journeys of teachers: an investigation of the development of teacher professional knowledge and skill by expert tertiary chemistry teachers, Chem. Educ. Res. Pract., 20(1), 132–145, 10.1039/c8rp00187a.
- Lemke J. L., (2004), The literacies of science, in Saul E. W. (ed) Crossing borders in literacy and science instruction: Perspectives on theory and practice, Newark, DE: International Reading Association/National Science Teachers Association, pp. 33–47.
- Linenberger K. J. and Holmes T. A., (2014), Results of a national survey of biochemistry instructors to determine the prevalence and types of representations used in during instruction and assessment, J. Chem. Educ., 91, 800–806, DOI:10.1021/ed400201v.
- Mayer R. (2003), The promise of multimedia learning: using the same instructional design methods across different media, Learn. Instr., 13, 125–139.
- Mayer R. E., (2005), The Cambridge handbook of multimedia learning, New York: Cambridge University Press, pp. 31–48.
- Mayer R. and Sims V., (1994), For Whom Is a Picture Worth a Thousand Words? Extensions of a Dual-Coding Theory of Multimedia Learning, J. Educ. Psychol., 86(3), 389–401.
- Miecznikowski J., Guberman-Pfeffer M., Butrick E., Colangelo J., and Donaruma C., (2015), Adapting Advanced Inorganic Chemistry Lecture and Laboratory Instruction for a Legally Blind Student, J. Chem. Educ., 92, 1344–1352.
- Nitz S., Prechtl H. and Nerdl C., (2014), Survey of classroom use of representations: development, field test and multilevel analysis, Learn. Environ. Res., 17, 401–422, DOI:10.1007/s10984-014-9166-x.
- Nyachwaya J. M. and Gillaspie M., (2016), Features of representations in general chemistry textbooks: a peek through the lens of the cognitive load theory, Chem. Educ. Res. Pract., 17, 58–71.
- Nyachwaya J. M., and Wood N. B., (2014), Evaluation of chemical representations in physical chemistry textbooks, Chem. Educ. Res. Pract., 15, 720–728.
- Patron E., Wikman S., Edfors I., Johansson-Cederblad B. and Linder C., (2017), Teachers’ reasoning: classroom visual representational practices in the context of introductory chemical bonding, Sci. Educ., 101, 887–906, DOI:10.1002/sce.21298.
- Prain V. and Waldrip B., (2006), An Exploratory Study of Teachers’ and Students’ Use of Multi-modal Representations of Concepts in Primary Science, Int. J. Sci. Educ., 28(15), 1843–1866, DOI:10.1080/09500690600718294.
- Quintana C., Zhang M., and Krajcik J. (2005), A framework for supporting metacognitive aspects of online inquiry through software-based scaffolding, Educ. Psychol., 40(4), 235–224.
- Raker J. R. and Holmes T. A., (2014), Investigating Faculty Familiarity with Assessment Terminology by Applying Cluster Analysis To Interpret Survey Data. J. Chem. Educ., 91, 1145–1191.
- Rau M. A., (2017), Conditions for the effectiveness of multiple visual representations in enhancing STEM learning, Educ. Psychol. Rev., 29, 727–761.
- Rencher A. C., (2003), Methods of multivariate analysis. New York, USA: John Wiley & Sons.
- Schnotz W., Bannert W., and Seufert T., (2002), Towards an integrative view of text and picture comprehension: Visualization effects on the construction of mental models, in Graesser A., Otero J. and Leon J. A. (ed.), The psychology of science text comprehension, Hillsdale, NJ: Erlbaum, pp. 385–416.
- Schultz M., Lawrie G. A., Bailey C. H., and Dargaville B. L., (2018), Characterisation of teacher professional knowledge and skill through content representations from tertiary chemistry educators, Chem. Educ. Res. Pract., 19, 508–519, 10.1039/c8rp00187a.
- Smothers S. S. and Goldston M. J., (2010), Atoms, elements, molecules, and matter: An Investigation into the congenitally blind adolescents’ conceptual frameworks on the nature of matter, Sci. Educ., 94(3), 448–477, DOI:10.1002/sce.20369.
- Stains M., and Talanquer V., (2007), Classification of chemical substances using particulate representations of matter: An analysis of student thinking, Int. J. Sci. Educ., 29(5), 643–661.
- Stains M., Harshman J., Barker M. K., Chasteen S. V., Cole R., DeChenne-Peters S. V., Eagan Jr., M. K., Esson J. M., Knight J. K., Laski F. A., Levis-Fitzgerald M., Lee C. J., Lo S. M., McDonnell L. M., McKay T. A., Michelotti N., Musgrove A., Palmer M. S., Plank K. M., Rodela T. M., Sanders E. R., Schimpf N. G., Schulte P. M., Smith M. K., Stetzer M., Van Valkenburgh B., Vinson E., Weir L. K., Wendel P. J., Wheeler L. B. and Young A. M., (2018), Anatomy of STEM teaching in North American universities, Science, 359(6383), 1468–1470, DOI:10.1126/science.aap8892.
- Stieff M., Hegarty M., and Deslongchamps G., (2011), Identifying representational competence with multi-representational displays, Cognition Instr., 29(1), 123–145, DOI:10.1080/07370008.2010.507318.
- Supalo C. A. and Kennedy S. H., (2014), Using Commercially Available Techniques To Make Organic Chemistry Representations Tactile and More Accessible to Students with Blindness or Low Vision, J. Chem. Educ., 91, 1745–1747, DOI:10.1021/ed4005936.
- Sweller J., (1994), Cognitive Load Theory, Learning Difficulty and Instructional Design, Learn. Instr., 4(4), 295–312.
- Taber K. S., (2001), The mismatch between assumed prior knowledge and the learner's conceptions: a typology of learning impediments, Educ. Stud., 27(2), 159–171.
- Taber K. S., (2009), Learning at the symbolic level, in Gilbert J. K., Treagust D. (ed.), Multiple Representations in Chemical Education, Models and Modeling in Science Education: Multiple representations in chemical education, New York, NY: Springer, pp. 75–105, DOI:10.1007/978-1-4020-8872-8-5.
- Taber K. S., (2013), Revisiting the chemistry triplet: drawing upon the nature of chemical knowledge and the psychology of learning to inform chemistry education, Chem. Educ. Res. Pract., 14, 156–168.
- Talanquer V., (2011), Macro, submicro, and symbolic: the many faces of the chemistry “triplet”, Int. J. Sci. Educ., 33(2), 179–195.
- Tang K.-S., Delgado C., and Moje E. B., (2014), An Integrative Framework for the Analysis of Multiple and Multimodal Representations for Meaning-Making in Science Education, Sci. Educ., 98(20), 305–326.
- Tukey J. W., (1977), Exploratory data analysis, Reading, MA: Addison-Wesley.
- Upahi J. E. and Ramnarain U., (2018), Representations of chemical phenomena in secondary school chemistry textbooks, Chem. Educ. Res. Pract, 20(1), 146–159, 10.1039/c8rp00191j.
- Ward J. H., (1963), Hierarchical grouping to optimize an objective function, J. Am. Stat. Assoc., 58(301), 236–244, DOI:10.1080/01621459.1963.10500845.
- Wu H.-K. and Puntambekar S., (2012), Pedagogical Affordances of Multiple External Representations in Scientific Processes, J. Sci. Technol. Educ.21(6), 754–767, DOI:10.1007/s10956-011-9363-7.
- Wu H.-K., Krajcik J. S. and Soloway E., (2001), Promoting Understanding of Chemical Representations: Students' Use of a Visualization Tool in the Classroom, J. Res. Sci. Teach., 38(7), 821–842.
- Yim O. and Ramdeen K. T., (2015), Hierarchical Cluster Analysis: Comparison of Three Linkage Measures and Application to Psychological Data, Quant. Methods Psychol., 11(1), 8–21.
| This journal is © The Royal Society of Chemistry 2019 |