Directional coupling in spatially distributed nanoreactors

Abstract

Silica based hollow nanospheres filled with a reactant solution act as nanoreactors. A close packed ensemble of the nanoshells comprise a porous medium through which a chemical front can propagate. The front velocity decreases as the chemical signal, in the shape of a reaction-diffusion front, is transmitted from one sphere to the other due to the high curvature at the contact points. Experiments reveal that front propagation occurs through the cavity of the nanoshells because surface activity of filled nanoparticles itself cannot support chemical front across the medium.

---

Fireflies flash in a synchronized manner during summer nights, a flock of birds often arrange themselves in a V-shaped formation while they migrate to hotter regions in autumn. These self-organized temporal or spatial patterns are the result of collective behavior which is brought about by mutual communication among the individual entities. Unidirectional coupling, such as the signal transmission existing between neurons in the brain, can also support complex dynamics. Systematic investigation of simpler chemical and biochemical systems provides valuable information in understanding the result of coupling between the autonomous components. An array of electrochemical oscillators can be manipulated by external forcing of smaller oscillating units yielding appropriate entrainment of oscillating phases, which can lead to the desired synchrony.¹ Various behaviors with emergent phenomena, like temporal synchronized oscillations^2,3 or even spatial chimera states,⁴ are found when interaction between cation-exchange resins are investigated in the Belousov–Zhabothinsky (BZ) reaction.

The communication between individual entities can be classified by their origin (physical or chemical), strength (weak or strong) or direction (unidirectional or mutual). If the coupling strength is weak, only local communication is available for the individual units. Abou-Hassan, Rossi and co-workers have demonstrated that short range interactions between phospholipid vesicles⁵ or microdroplets⁶ filled with BZ reaction can give rise to front propagation. The appearance of microfluidic devices has also led to the observation of novel types of dynamic behavior by embedding the homogeneous chemistry inside droplets of micrometer size. Gorecki and his team⁷ have utilized these “microreactors” to generate frequency transformators where various types of resonances are observed even in small droplet networks, while Epstein's group⁸ have found phase and anti-phase oscillations by finely tuning the chemical conditions. Different spatiotemporal patterns, like Turing structures,⁹ segmented waves, etc., even in 3D^10,11 are exhibited when the BZ reaction is placed in water-in-oil microemulsions.

Holló and Lagzi have recently shown that unidirectional coupling can be achieved between two oscillatory systems separated by a silicon membrane¹² where the diffusion of carbon dioxide from one unit to the other is the driving force controlling the system dynamics. Unidirectional inhibitory communication between four almost identical BZ oscillators in continuously stirred tank reactors has yielded new stable modes besides the in-phase and anti-phase, and the existence of bistability has been observed both experimentally and theoretically.¹³

Hollow inorganic nanospheres (HINS) are popular materials in a wide variety of fields like analytical, bio- and electrochemistry.^14,15 Silica nanoshells are useful ultrasound contrast agents because of their enhanced stability.¹⁶ HINS can also be arranged in two-dimensional arrays to be applied as efficient photodetectors.¹⁷ A unique opportunity suggested by Geng et al.¹⁸ is the nanocoating of living cells which can provide protecting conditions for the cells to survive. Due to the properties of nanomaterials, the cells may also have new functions in the nanoshells. Gao and co-workers¹⁹ have selectively functionalized HINS by building carboxylic groups into the outer shell and amino groups into the inner one. With this spatial separation of the acidic and basic properties, the catalytic activities can be greatly enhanced as illustrated in a one-pot cascade reaction of deacetylation followed by the Henry reaction. Amino-functionalized counterparts are the bases of promising composite catalysts.^20,21 Furthermore they exhibit strong hydrogen ion-binding capabilities which can be utilized to fine tune the characteristics of chemical waves.²²

The objective of the present work is to investigate a system arising from the unidirectional coupling of hollow inorganic nanoshells filled with the reactants of a simple autocatalytic reaction. The chlorite–tetrathionate (CT) reaction—autocatalytic with respect to hydrogen ions²³—has been selected as our model system, since it can exhibit self-sustained propagating reaction fronts in slight chlorite excess.²⁴ It is one of the most widely used reaction-diffusion systems as not only it can support diffusion-driven instability^25–27 but also it can result in complex chemo-hydrodynamic patterns when other transport processes are present.^28–30

The silica nanospheres are synthesized as described previously.^22,31 Sphere-shaped polystyrene templates are first prepared with radical polymerization from styrene monomers using polyvinylpyrrolidone as stabilizer³²—similarly to the work of Sandberg and co-workers³³—except that oxygen is eliminated by bubbling nitrogen gas through the dispersion, which is homogenized by sonication following the addition of the initiator potassium persulfate.³¹ Silica coating is achieved by mixing cetyltrimethylammonium bromide and ammonia with tetraethyl orthosilicate as given in ref. 31. Finally the templates are removed by calcination leading to the formation of hollow silica nanospheres. The morphology of the nanoparticles is confirmed by TEM measurements and the size distribution is determined based on more than 200 measurements for each type (see Fig. 1). The templates have an average diameter of 654 ± 35 nm, while the silica coated nanospheres 693 ± 45 nm yielding a 50 ± 8 nm thickness for the HINS.

Fig. 1 Characterization of the nanospheres. TEM image of the template (a), the silica coated template (c), and the HINS (e). The size distribution of the corresponding nanoparticles (b and d), the thickness of the HINS (f).

The required solutions are prepared using reagent grade chemicals in Millipore water. All the experiments are carried out at room temperature (25 ± 1 °C). The following stock solutions are prepared: 0.05 M K₂S₄O₆, 0.2 M NaClO₂, 0.04 M NaOH, 0.208 M sodium dodecyl sulphate (SDS), and 5.7 mM bromophenol blue (BPB).

After the synthesis of the nanoparticles, 15 mg of nanospheres (hollow or templated) are placed in the mixture of 2.275 ml water, 1 ml of NaOH, and 0.1 ml SDS. Following a 3 min sonication and a 10 min stirring, 0.25 ml of K₂S₄O₆, 0.125 ml of BPB and finally 0.25 ml of NaClO₂—corresponding to the conditions yielding chemical fronts^24,25,34,35—are added to the suspension which is then stirred for an additional 2–3 minutes to achieve uniform soaking of the nanoparticles. The suspension is then filtered using a membrane filter and the filtrate is dried and stored at room temperature before use.

To prepare the gel reaction matrix, first 0.09 g of agarose is measured into a solution of 4.55 ml water, 2.00 ml NaOH and 0.20 ml SDS. The covered mixture is sonicated for 3 min then heated and stirred for 13 min at 50 °C. The solution is cooled at room temperature for 2 min and 0.50 ml K₂S₄O₆, 0.25 ml of BPB added and the solution is stirred for 2 min. Finally 0.50 ml of NaClO₂ is added to the reactant mixture which is poured into a circular Petri dish of 4 cm in diameter. The solution (with the same concentrations as for the nanospheres) is allowed to gel at room temperature for 30 min. We cut out a desired slab along the diagonal, hence creating two separate gel layers with preset gap width (1–6 mm) between them ensuring that there is no connection between the two parts. Two capillary tubes with outer diameter of 1 mm are placed between the two slices as spacers as shown in Fig. 2(a). A connecting bridge is created by placing the reactant loaded hollow or templated silica nanoshells into the gap bounded by the capillaries. Circular waves ∼7–8 mm far from the connecting bridge are generated in one side with a drop of sulphuric acid of 0.04 M solution (approx. 1 mm in diameter initially). The experimental system is covered to prevent evaporation.

Fig. 2 Experimental setup (a). Snapshots 100 min (b), 390 min (c), and 395 min (d) after the front initiation. The dark blue areas correspond to reactants and the bright yellow areas to products, while the white areas represent the empty spaces separating the two gel pieces. The wave propagates from left to right. Field of view: 9.60 mm × 7.16 mm.

We have performed our experiments in a Petri dish and the reaction system is monitored from above by a charged coupled device, while the system is illuminated from below using a light source (see Fig. 2(a)). The images have then been recorded onto a personal computer at time delay of 1 minute and later analyzed using in-house codes. First the colored images are converted into gray scale images where 0 corresponds to the dark (blue in our scenario), while 255 to the bright (yellow) colors. The front position—defined as the location of the inflection point of gray scale intensity, i.e., front profile—was determined along a line of propagation.

The silica based nanospheres are hollow and can encapsulate reaction solution within themselves and thereby can be employed as nanoreactors. Upon contact with the hydrogel, the cluster of the tiny reactors are wetted and act as a porous reaction matrix. Fig. 2(b)–(d) shows two gel slices 3.08 mm apart which are joined by capillaries forming physical pillars to keep together the bridging particles. The empty space between the capillaries are filled with nanoshells which now serves as a bridge between the two gel pieces. The addition of a tiny sulfuric acid drop initiates the autocatalytic reaction resulting in a color change because the reactant mixture is dark blue and the product light yellow. This sharp color change separating the reactant from the products, called a chemical front, propagates through the gel with constant speed due to the coupling between reaction and diffusion.^22,25 In Fig. 2 the front travels from left to right, hence it enters the bridge from the left. The front propagates through the bridge and reaches the other end generating a new curved front upon exiting. The time lapse images reveal that the front slows down significantly when it travels through the nanoshells.

The front profiles spanning through the two gel and nanospheres are depicted in Fig. 3. For clarity, the dashed lines mark the space filled with nanoparticles between the gels. As the front passes a region, the grey scale intensity increases significantly. The large spacing between the gray scale profiles indicates that the wave speed is high in the gel on the left, whereas the spacing greatly diminishes in the middle branch implying slow propagation. The exiting curved reaction front on the right reestablishes similar spacing, i.e., the front regains similar speed as the one in the left gel. From this observation we can affirm that the velocity of the wave decreases dramatically as it encounters the nanoparticles. The nanoparticles which are closely packed to form the bridge restrict the movement of the wave from one particle to the other resulting in a significant slow down of the wave.

Fig. 3 Profiles of wave propagation. The dashed lines indicate the border of the gel system. The left and right panel corresponds to the wave propagation in the gel and the middle branch to wave propagation through the bridge of nanospheres. The time difference between each line is 1 min (t = 0–5 min), 50 min (t = 5–490 min) and 1 min (t = 490–495 min).

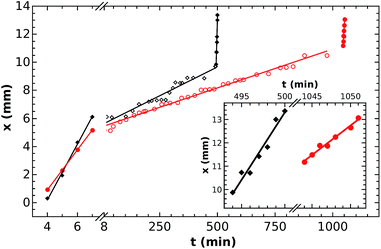
For characterization of the wave propagation we have determined the front position as a function of time (see Fig. 4). The experiments are chosen such that the length of the bridge differs significantly. Since the position varies linearly with time in each segment, the velocity of front propagation is constant as it is equal to the slope, in both the gels and the center bridge. The speed of the entering wave is constant within the experimental errors (1.42 ± 0.01 and 1.26 ± 0.09 mm min⁻¹) in good agreement to previous experiments in gels.²² When the wave travels inside, the velocity is determined to be in the μm min⁻¹ range (5.5 ± 0.1 and 8.2 ± 0.4 μm min⁻¹). The slopes of the first and the third segments are similar, which confirms that the velocity of the wave in the gel at the entrance of the nanobridge and leaving it remains similar as the reaction matrix is the same. There is a slight decrease, enlarged in the inset of Fig. 5, in the exact velocity values beyond the exit from 0.58 ± 0.01 mm min⁻¹ to 0.25 ± 0.01 mm min⁻¹ for the 3.08 mm bridge because of the unavoidable drying of the hydrogel and the slow change in the chemical composition in the time span of the experiment.

Fig. 4 Front position as a function of time for bridges of different length. The black diamonds and red circles correspond to cases with bridge length of 3.07 mm and 5.23 mm, respectively. The filled symbols depict the propagation in gel, the hollow ones that inside the bridge. The inset shows the wave propagation upon exiting the nanoparticle bridges.

Fig. 5 Transmission time as a function of bridge length. The straight black line represents the linear fitting.

The HINS filled with fresh reactant solution act as nanoreactors with an inner volume of ∼110 aL that contains ∼10⁶ number of reactant molecules considering the concentrations. At this particle density, concentration fluctuations due to stochastic events do not yet become significant, hence bulk chemical kinetics can be considered valid. The velocity of an autocatalytic wave (v) depends on the rate of reaction, the diffusion of species and geometric constrains according to³⁶

v = v₀ + DK (1)

where v₀ is the velocity of the planar wave which scales with ^37,38 with k being an apparent first-order rate constant and D the diffusion coefficient of the autocatalytic species (hydrogen ion in this case). For a concave wave emanating from a point source the curvature (K) is negative, e.g. for a spherical front with radius r it is K = −2/r, resulting in a decrease in propagation velocity. The significant slowing down inside the bridge arises because the HINS nanoreactors are spatially coupled via confined contact points, through which the chemical front must pass through as it travels across the cluster. The high curvature (with K ≪ 0) at these locations is responsible for the critical slowing down as the wave enters a nanosphere filled with the fresh reactants. This is corroborated with experiments where templated inorganic nanospheres are used instead of the hollow ones. Under such conditions there are no reactant solution within the nanospheres, no front propagation is observed through the bridge revealing that wave activity inside the nanospheres is necessary for self-sustained propagation; reactant solutions wetting the outer surface of the templated nanospheres alone cannot support reaction-diffusion fronts.

Since the front velocity remains constant within the experimental errors as the wave propagates through the pack of hollow nanospheres, a transmission time can be determined that should vary with the bridge length. Fig. 4 illustrates that the time required for the wave to travel through the bridge increases as the length, and hence the number of nanoparticles, increases. For sufficiently long bridges (L > 2 mm), the transmission time is a linear function of the length according to

τ/h = 3.84 ± 0.12 (L/mm) − 4.96 ± 0.34 (2)

However, when the bridge length exceeds 4.4 mm, the transmission time deviates from the linear relationship due to the slow drying of the inert agarose matrix and the deterioration of reactants in the hydrogel.

In conclusion, we have demonstrated that close-packed hollow nanosphere containing a chemically active reactant medium inside can act as an assembly of nanoreactors with unidirectional coupling between them via autocatalytic front propagation. On the macroscale the ensemble can sustain a pure reaction-diffusion front with constant velocity suggesting that a simple device based on the transmission of a chemical signal may be designed to amplify the change in hydrogen ion concentration through the use of hollow inorganic nanospheres.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the financial support of the National Research, Development and Innovation Office (K112531), GINOP-2.3.2-15-2016-00013 projects and the University of Szeged Open Access Fund (4359).

References

1. A. Zlotnik, R. Nagao, I. Z. Kiss and J.-S. Li, Nat. Commun., 2016, 7, 10788.
2. A. F. Taylor, M. R. Tinsley, F. Wang, Z. Huang and K. Showalter, Science, 2009, 323, 614–617.
3. M. R. Tinsley, S. Nkomo and K. Showalter, Nat. Phys., 2012, 8, 662–665.
4. J. F. Totz, J. Rode, M. R. Tinsley, K. Showalter and H. Engel, Nat. Phys., 2018, 14, 282–285.
5. R. Tomasi, J.-M. Noël, A. Zenati, S. Ristori, F. Rossi, V. Cabuil, F. Kanoufi and A. Abou-Hassan, Chem. Sci., 2014, 5, 1854–1859.
6. K. Torbensen, S. Ristori, F. Rossi and A. Abou-Hassan, J. Phys. Chem. C, 2017, 121, 13256–13264.
7. J. Guzowski, K. Gizynski, J. Gorecki and P. Garstecki, Lab Chip, 2016, 16, 764–772.
8. M. Toiya, V. K. Vanag and I. R. Epstein, Angew. Chem., Int. Ed., 2008, 47, 7753–7755.
9. V. K. Vanag and I. R. Epstein, Phys. Rev. Lett., 2001, 87, 228301.
10. T. Bánsági Jr, V. K. Vanag and I. R. Epstein, Science, 2011, 331, 1309–1312.
11. I. R. Epstein, Chem. Commun., 2014, 50, 10758–10767.
12. G. Holló and I. Lagzi, J. Phys. Chem. A, 2019, 123, 1498–1504.
13. P. S. Smelov, I. S. Proskurkin and V. K. Vanag, Phys. Chem. Chem. Phys., 2019, 21, 3033–3043.
14. N. A. Dhas and K. S. Suslick, J. Am. Chem. Soc., 2005, 127, 2368–2369.
15. Y. Liu, J. Goebl and Y. Yin, Chem. Soc. Rev., 2013, 42, 2610–2653.
16. A. Liberman, J. Wang, N. Lu, R. D. Viveros, C. A. Allen, R. F. Mattrey, S. L. Blair, W. C. Trogler, M. J. Kim and A. C. Kummel, Adv. Funct. Mater., 2015, 25, 4049–4057.
17. X. Chen, H. Yang, G. Liu, F. Gao, M. Dai, Y. Hu, H. Chen, W. Cao, P. Hu and W. Hu, Adv. Funct. Mater., 2018, 28, 1705153.
18. W. Geng, L. Wang, N. Jiang, J. Cao, Y.-X. Xiao, H. Wei, A. K. Yetisen, X.-Y. Yang and B.-L. Su, Nanoscale, 2018, 10, 3112–3129.
19. J. Gao, X. Zhang, Y. Lu, S. Liu and J. Liu, Chem.–Eur. J., 2015, 21, 7403–7407.
20. X. Du and J. He, Nanoscale, 2012, 4, 852–859.
21. C.-Y. Lin, W.-P. Li, S.-P. Huang, C.-S. Yeh and C.-M. Yang, J. Mater. Chem. B, 2017, 5, 7598–7607.
22. E. Lantos, N. P. Das, D. S. Berkesi, D. Dobó, A. Kukovecz, D. Horváth and A. Tóth, Phys. Chem. Chem. Phys., 2018, 20, 13365–13369.
23. A. K. Horváth, I. Nagypál, G. Peintler and I. R. Epstein, J. Am. Chem. Soc., 2004, 126, 6246–6247.
24. L. Szirovicza, I. Nagypál and E. Boga, J. Am. Chem. Soc., 1989, 111, 2842–2845.
25. A. Tóth, I. Lagzi and D. Horváth, J. Phys. Chem., 1996, 100, 14837–14839.
26. A. Tóth, B. Veisz and D. Horváth, J. Phys. Chem. A, 1998, 102, 5157–5159.
27. M. Fuentes, M. N. Kuperman and P. De Kepper, J. Phys. Chem. A, 2001, 105, 6769–6774.
28. D. Horváth, T. Bánsági Jr and A. Tóth, J. Chem. Phys., 2002, 117, 4399–4401.
29. J. Yang, A. D'Onofrio, S. Kalliadasis and A. De Wit, J. Chem. Phys., 2002, 117, 9395–9407.
30. D. Horváth, S. Tóth and A. Tóth, Phys. Rev. Lett., 2006, 97, 194501.
31. D. G. Dobó, D. Berkesi and A. Kukovecz, J. Mol. Struct., 2017, 1140, 83–88.
32. K. M. Koczkur, S. Mourdikoudis, L. Polavarapu and S. E. Skrabalak, Dalton Trans., 2015, 44, 17883–17905.
33. L. I. C. Sandberg, T. Gao, B. P. Jelle and A. Gustavsen, Adv. Mater. Sci. Eng., 2013, 2013, 6.
34. A. Tóth, D. Horváth and A. Siska, J. Chem. Soc., Faraday Trans., 1997, 93, 73–76.
35. A. K. Horváth, J. Phys. Chem. A, 2005, 109, 5124–5128.
36. I. R. Epstein and J. A. Pojman, An Introduction to Nonlinear Dynamics: Oscillations, Waves, Patterns, and Chaos, Oxford University Press, Oxford, 1998.
37. R. Luther, Z. Elektrochem., 1906, 12, 596–600.
38. R. Luther, translated by R. Arnold, K. Showalter and J. J. Tyson, J. Chem. Educ., 1987, 64, 740–742.

---