Enhanced sodium ion conductivity in Na₃VS₄ by P-doping

Abstract

All-solid-state sodium-ion batteries are promising candidates for renewable energy storage applications, owing to their high safety, high energy density, and the abundant resources of sodium. The critical factor for an all-solid-state battery is having a sodium solid electrolyte that has high Na ion conductivity at room temperature and outstanding thermal stability, low flammability, and long battery lifespan. Herein, a new Na ion solid-state electrolyte, Na₃VS₄, is prepared by a solid state reaction. It shows conductivity of ∼1.16 × 10⁻⁸ to 1.46 × 10⁻⁶ S cm⁻¹ from 25 to 100 °C. The sodium ion conductivity was enhanced to ∼1.49 × 10⁻⁷ to 1.20 × 10⁻⁵ S cm⁻¹ through P substitution for V in the composition Na₃P_0.1V_0.9S₄. Such sodium ion conduction enhancement could be attributed to P substitution for V leading to a wider Na migration path and the generation of sodium vacancies.

---

Introduction

There is growing demand for high performance rechargeable batteries used in large-scale energy storage, including electric vehicles and backup storage at individual houses and large-scale solar and wind farms.¹ To date, rechargeable battery technology is dominated by lithium ion batteries, but the geographically constrained Li resources will ultimately push up prices, in turn limiting their application potential in large-scale energy storage. Moreover, from a battery producer viewpoint, principal importance is always given to material abundance and low cost when designing an electrode, i.e., sodium, which is an abundant element in nature while lithium is not. As one classic ion battery, the sodium ion battery has risen to prominence as a key supplement for large-scale energy storage systems.² However, severe safety issues also exist in sodium ion batteries using organic liquid electrolytes, because of extremely high reactivity of volatile sodium metal and flammable organic liquid electrolytes.^3–6 Among various methods for improving the safety of electrolytes, the inorganic solid electrolytes have been proposed for development of thermally stable electrolytes.⁷ Compared with traditional organic electrolytes, solid state electrolytes have excellent thermal stability,⁸ low flammability, and potentially better battery life due to the increased electrochemical stability.^9,10 Based on these advantages, solid-state electrolytes are considered to the most promising components for next generation secondary batteries.

Sulfur-based Na-ion solid electrolytes offer promising room temperature conductivities. The tetragonal phase of Na₃PS₄ had been known as a sodium conductor for more than 20 years.¹¹ Na₃PS₄ has gained renewed attention since Hayashi et al. synthesized a room temperature stable glass–ceramic phase, which showed a Na ionic conductivity of 2 × 10⁻⁴ S cm⁻¹ and subsequently increased to 4.6 × 10⁻⁴ S cm⁻¹ by using high purity raw materials.^12–15 The conductivity of (1 − x)c–Na₃PS_4−xNa₄SiS₄ pseudo-binary system could achieve as high as 7.4 × 10⁻⁴ S cm⁻¹ at x around 0.0629.^16,17 The Cl-doped tetragonal Na₃PS₄ (ref. 18) (t-Na_2.9375PS_3.9375Cl_0.0625) solid electrolyte displayed a Na ion conductivity exceeded 1 × 10⁻³ S cm⁻¹ at room-temperature. Moreover, the cell parameters had played an important role for Na ion transport, such as Na₃PSe₄ (ref. 19) and Na₃SbS₄,²⁰ which owned larger cell parameters than Na₃PS₄, their ionic conductivity increased to 1.16 × 10⁻³ S cm⁻¹ and 3 × 10⁻³ S cm⁻¹, respectively. Recently, Luo and Wang reported a Na-ion solid-state electrolyte of Na₃P_0.62As_0.38S₄,²¹ which had a high ionic conductivity of 1.46 × 10⁻³ S cm⁻¹. Richards et al. reported a family of Na₁₀MP₂S₁₂ (M = Sn, Ge, and Si) with a high ionic conductivity of 4 × 10⁻⁴ S cm⁻¹ for Na₁₀SnP₂S₁₂, and also predicted a super high ionic conductivity of 10.28 × 10⁻³ S cm⁻¹ for Na₁₀SiP₂S₁₂ based on first-principles simulations.^22,23 Nonetheless, the sodium superionic conductors are still rate and their room-temperature ionic conductivities can't satisfy the actual needs. Looking for new solid-state sodium ion conductor is highly anticipated for all-solid-state rechargeable sodium ion batteries.

Na₃VS₄ crystals were reported more than twenty years ago,²⁴ which adopted a tetragonal structure closely related to the Na₃PS₄.¹¹ However, there is no attention on its sodium ionic conductivity so far. In this study, Na₃VS₄ was synthesized by solid state method, which owns sodium ionic conductivity of ∼1.16 × 10⁻⁸ to 1.46 × 10⁻⁶ S cm⁻¹ from 25 °C to 100 °C. In order to improve its sodium ionic conductivity, P-doped Na₃VS₄ (i.e. Na₃P_xV_1−xS₄, 0 ≤ x ≤ 0.2) was prepared, which resulted in higher Na-ion conductivity of ∼1.49× 10⁻⁷ to 1.20 × 10⁻⁵ S cm⁻¹ from 25 °C to 100 °C on composition x = 0.1.

Experimental section

Synthesis

Na₃P_xV_1−xS₄ (0 ≤ x ≤ 0.2) electrolytes were prepared by solid-state reaction in vacuum. The stoichiometric amounts of Na₂S (Aladdin, >95%), P₂S₅ (Aladdin, 99%), and V (Aladdin, 99.99%) were well-mixed and ground with an agate mortar and pestle for one hour. Then, the mixture powder was vacuum-sealed in a quartz tube and heated at 500 °C for 6 h with a heating or cooling rate of 2 °C min⁻¹. All the processes were carried out in a high purity argon-filled glove box with H₂O and O₂ below 0.1 ppm.

Materials characterization

The X-ray diffraction (XRD) data of as-synthesized samples were collected using a PANalytical X'pert Powder X-ray diffractometer equipped with a Cu Kα radiation operating at an accelerating voltage of 40 kV and current of 40 mA. For Rietveld refinement, the data was acquired in the 2θ range of 10–80° with 0.2028° min⁻¹. For all the XRD measurements, to avoid any undesirable influence of air exposure, the as-obtained powders were sealed in an air-tight container with Kapton tape in an argon-filled glove box. The Rietveld refinements of the XRD data were carried out using Topas-Academic software.²⁵ Raman scattering measurements were performed using DXR Raman Microscope with a 532 nm excitation source. In order to avoid any undesirable influence of air exposure, the as-obtained powders were sealed in an air-tight quartz box.

Electrochemical tests

The alternate current (AC) impedance spectroscopy measurements were performed by using a Solartron SI1260 impedance/gain-phase analyzer over a temperature range from 25 to 100 °C and a frequency range from 10⁶ to 10⁻¹ Hz. The pellets (φ 6 mm) for AC impedance spectroscopy measurements were pressed from powders at 1000 MPa. The density of the pressed pellet was about 2.14 g cm⁻³, and achieved a theoretical density of 90%. Platinum foil was placed on both sides of the pellets as electrodes and current collectors. Platinum wire were attached to both sides as current collectors in a cell. The electrochemical stability of as-obtained sample with metallic sodium was determined via linear sweep voltammograms (LSV) of the Na/Na₃VS₄/Pt and Na/Na₃P_0.1V_0.9S₄/Pt cells at a scan rate of 0.2 mV s⁻¹ from 1 to 6 V at room temperature. To determine electronic conductivity, potentiostatic direct current (DC) polarization measurements were performed on Pt/Na₃VS₄/Pt and Pt/Na₃P_0.1V_0.9S₄/Pt cells by using a Solartron SI1287 electrochemical interface at 25 °C.

Results and discussion

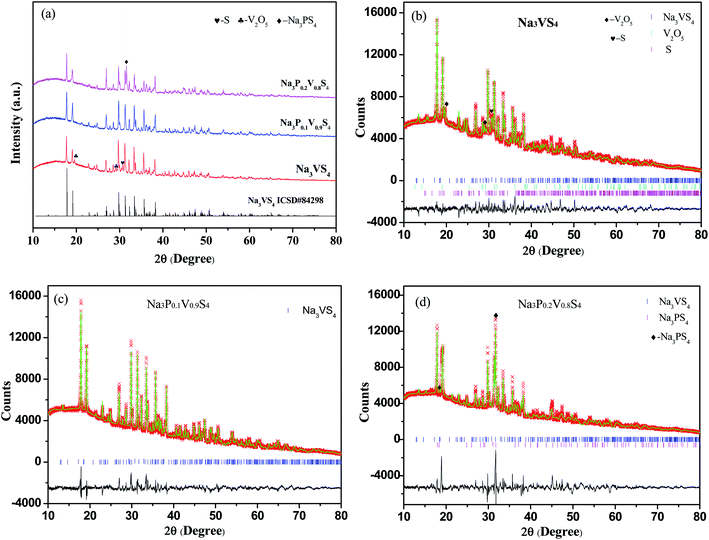
The crystalline phase of as-synthesized samples by solid-state reaction were characterized by XRD. The XRD patterns were shown in Fig. 1, the halo patterns from 10° to 30° reflected from the polyimide film. As shown in Fig. 1a, the major diffraction peaks of Na₃VS₄ could index in tetragonal system with the space group P4̄21c (space group no. 114)²⁴ beside some impurities, such as V₂O₅, S. The XRD data of Na₃VS₄ was also analyzed with Rietveld refinement (Fig. 1b). The fitting was satisfactory with rather low factors of R_wp ∼ 4.98% and R_p ∼ 3.61%. The cell parameters are a = b = 13.5246(1) Å and c = 7.9500(7) Å, with a unit volume of 1454.1(1) ų. According the Rietveld refinement results, the content of V₂O₅ and S was 2.62 wt% and 6.78 wt%, respectively. Detailed structural informations, including the atomic parameters determined from Rietveld refinement, were listed in Table 1. After P-doping, the Na₃P_0.1V_0.9S₄ sample could get a single phase (Fig. 1a), however, it exists a second phase of Na₃PS₄ in Na₃P_0.2V_0.8S₄ (Fig. 1a and d). This indicate that the solid-solution in Na₃V_1−xP_xS₄ was rather small. The Rietveld refinement of Na₃P_0.1V_0.9S₄ with tetragonal Na₃VS₄ structure model was shown in Fig. 1c. The refined profiles fitted well the observed data, which converged to R_wp ∼ 5.03% and R_p ∼ 3.68%. The refined structural data and refinement parameters were listed in Table 2. The ratio of V/P is 0.88(5)/0.12(5) from the result of Rietveld refinement, which is agreed with the normal composition. The unit cell parameters obtained from the Rietveld refinement are a = b = 13.5051(7) Å, c = 7.9468(4) Å, V = 1449.4(1) ų, which is a little less than those of Na₃VS₄. The compared cell parameters were given in Table 3. Due to the ionic radius of P⁵⁺ (0.29 Å)¹¹ is smaller than that of V⁵⁺ (0.46 Å),²⁵ P doping reduces the unit cell parameters.

Fig. 1 (a) XRD patterns of Na₃P_xV_1−xS₄, (0 ≤ x ≤ 0.2) samples. (b) Rietveld refinement plots of XRD for tetragonal Na₃VS₄, the reliability factors are R_wp = 4.98% and R_p = 3.61%. (c) Rietveld refinement plots of XRD for tetragonal Na₃P_0.1V_0.9S₄, the reliability factors are R_wp = 5.03% and R_p = 3.68%. (d) Rietveld refinement plots of XRD for tetragonal Na₃P_0.2V_0.8S₄, the reliability factors are R_wp = 7.79% and R_p = 5.18%.

Table 1 The final refined structural parameters of Na₃VS₄.^a

Atom	Site	x	y	z	Occupancy	Biso (Å^2)
a Space group: P4̄21c, a = b = 13.5246(1) Å, c = 7.9500(7) Å, V = 1454.1(2) Å^3.
Na1	4d	0	0.5	0.5314(26)	1	0.9(5)
Na2	4c	0.5	0.5	0.7260(29)	1	0.9(5)
Na3	8e	0.7528(13)	0.5468(10)	0.8531(16)	1	0.9(5)
Na4	8e	0.7544(13)	0.8004(9)	0.9030(20)	1	0.9(5)
V1	8e	0.0100(5)	0.7409(5)	0.7849(9)	1	2.6(2)
S1	8e	0.6806(7)	0.5051(9)	0.5262(12)	1	1.2(3)
S2	8e	0.8660(7)	0.6853(7)	0.6699(13)	1	1.2(3)
S3	8e	0.6069(7)	0.9049(8)	0.7042(15)	1	1.2(3)
S4	8e	0.5805(8)	0.6409(9)	0.8972(13)	1	1.2(3)

---

Table 2 The final refined structural parameters of Na₃P_0.1V_0.9S₄^a

Atom	Site	x	y	z	Occupancy	Biso (Å^2)
a Space group: P4̄21c, a = b = 13.5051(5) Å, c = 7.9467(4) Å, V = 1449.5(1) Å^3.
Na1	4d	0	0.5	0.5606(19)	1	1.7(2)
Na2	4c	0.5	0.5	0.7189(19)	0.92(3)	1.7(2)
Na3	8e	0.7580(9)	0.5477(7)	0.8339(13)	1	1.7(2)
Na4	8e	0.7577(9)	0.7970(7)	0.9361(15)	1	1.7(2)
V1/P1	8e	0.0101(3)	0.7347(3)	0.7811(5)	0.88(5)/0.12(5)	0.2(2)
S1	8e	0.6860(5)	0.5140(5)	0.5226(9)	1	0.8(1)
S2	8e	0.8748(5)	0.6877(5)	0.6752(10)	1	0.8(1)
S3	8e	0.6129(5)	0.8929(5)	0.6967(12)	1	0.8(1)
S4	8e	0.5744(6)	0.6609(6)	0.8843(8)	1	0.8(1)

---

Table 3 The cell parameters of Na₃VS₄ and Na₃P_0.1V_0.9S₄

Composition	a/b (Å)	c (Å)	V (Å^3)
Na3VS4	13.5246(1)	7.9500(7)	1454.1(2)
Na3P0.1V0.9S4	13.5051(5)	7.9467(4)	1449.5(1)

---

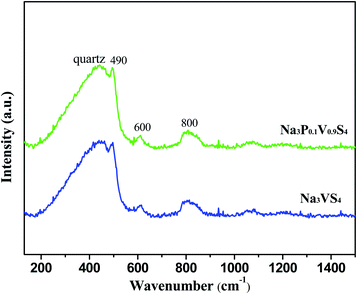
Fig. 2 shows the Raman spectrum of Na₃VS₄ and Na₃P_0.1V_0.9S₄ at room temperature. The broad peak located at 450 cm⁻¹ derived from the quartz box, and the peaks situated at about 490, 600 and 800 cm⁻¹ could assign to the V–S or V/P–S vibrations of the isolated of VS₄³⁻ or V/PS₄³⁻ group, verifying the successful formation of VS₄³⁻ or V/PS₄³⁻ group.^12,20

Fig. 2 Raman spectrum of Na₃VS₄ and Na₃P_0.1V_0.9S₄.

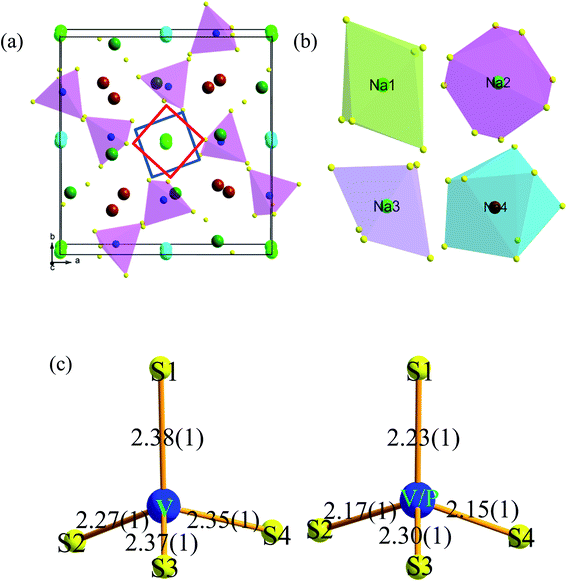
The crystal structure of tetragonal Na₃VS₄ viewed along c axes is given in Fig. 3a. The crystallographic structure unit cell can be simply described as consisting of isolated VS₄³⁻ tetrahedral groups separated by sodium cations. In unit cell, the Na1, Na2, Na3, Na4 atoms sit on 4d, 4c, 8e, 8e Wyckoff sites, V atoms locate at 8e sites and S atoms situate in 8e Wyckoff sites. The V–S distance are 2.38(1) Å (V–S1), 2.28 Å(1) (V–S2), 2.37(1) Å (V–S3), 2.36(1) Å (V–S4) and the S–V–S angles are 104.3° (S4–V–S1), 115.4° (S2–V–S1), 102.3° (S3–V–S2), 111.3° (S3–V–S4), 114.5° (S3–V–S1), 108.8° (S2–V–S4). In the crystal structure, Na atoms site on 4d (Na1), 4c (Na2), 8e (Na3), 8e (Na4) Wyckoff sites with different coordination environments (Fig. 3b), which are six-coordination for Na1, eight-coordination for Na2, six-coordination for Na3 and seven-coordination for Na4, respectively. Especially, Na2 atom connects to eight sulfur atoms and from an anion framework, all of these Na2 ion diffusion channels are constructed along mutually perpendicular paths (inset in the Fig. 3a). This anion framework is body-centered cubic framework, which benefits Na ion diffusion. This phenomenon similar to Gerbrand Ceder and co-workers proposed design principles for superionic conductors, they suggested that the body-centered cubic frameworks allow the migration of ions with a lower activation barrier than in other close-packed frameworks, thus resulting in fast ion diffusion.²⁶ Moreover, because of the ionic radius of P⁵⁺ less than the V⁵⁺, the bond length of V/P–S is shorter than that of V–S (Fig. 3c). Also, as comparing in Table 4, the average bond length of Na2–S in Na₃V_0.9P_0.1S₄ (3.60(6) Å) was larger than that of Na₃VS₄ (3.51(7) Å), indicating that sulfur anion channels in Na₃P_0.1V_0.9S₄ were larger than the sulfur anion channels in Na₃VS₄. The larger channel reduced the force between sodium and sulfur, which is beneficial for Na ion diffusion.

Fig. 3 (a) The crystal structure of Na₃VS₄ viewed along c, Na1 (turquoise), Na2 (bright green), Na3 (green), Na4 (brown), V (blue), S (yellow). (b) Na1 (turquoise), Na2 (bright green), Na3 (green), Na4 (brown) coordination environments. (c) Atomic and bond lengths of VS₄ and V/PS₄ polyhedron.

Table 4 The bond length of Na2–S in Na₃VS₄ and Na₃V_0.9P_0.1S₄

Na3VS4	Length (Å)	Na3V0.9P0.1S4	Length (Å)
Na2–S1(×2)	3.15(1)	Na2–S1(×2)	3.25(1)
Na2–S1(×2)	2.91(1)	Na2–S1(×2)	2.98(1)
Na2–S4(×2)	2.58(1)	Na2–S4(×2)	2.69(1)
Na2–S4(×2)	5.41(1)	Na2–S4(×2)	5.48(1)
〈L〉	3.51(6)	〈L〉	3.60(7)

---

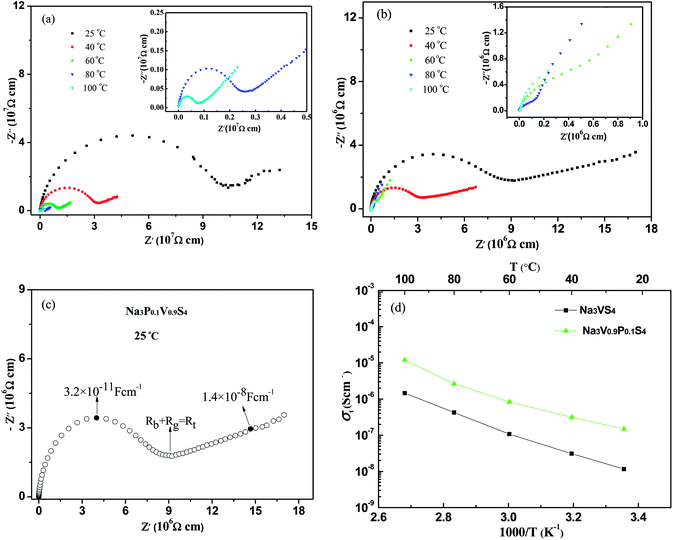
The conductivity of pressed pellets of Na₃VS₄ and Na₃V_0.9P_0.1S₄ were evaluated by AC impedance spectroscopy, which were conducted in the frequency range from 10⁶ Hz to 0.1 Hz at 25–100 °C. The Nyquist plots of the impedance spectra of Na₃VS₄ and Na₃P_0.1V_0.9S₄ were shown in Fig. 4a and b, respectively. The impedance spectra both of Na₃VS₄ and Na₃P_0.1V_0.9S₄ contained a semicircle in the high-frequency region, which became smaller with increasing temperature. In the low frequency region, the semicircle segments follow a Warburg-type impedance,^27–29 which is associated with capacitive behavior and similar to the blocking electrodes.³⁰ The linear spike in the low-frequency region indicates Na₃VS₄ and Na₃P_0.1V_0.9S₄ were typical ionic conductor.

Fig. 4 (a) Nyquist impedance plot of Na₃VS₄ from 25 to 100 °C. (b) Nyquist impedance plot of Na₃P_0.1V_0.9S₄ from 25 to 100 °C. (c) Typical complex impedance plots of Na₃P_0.1V_0.9S₄ at 25 °C, R_b, R_g and R_t denote bulk, grain boundary and total resistivities, respectively. (d) Arrhenius conductivity plots of Na₃VS₄ and Na₃P_0.1V_0.9S₄ from 25 to 100 °C.

The Nyquist plot of Na₃P_0.1V_0.9S₄ at 25 °C (Fig. 4c) comprised bulk, grain boundary and electrode polarization. The high-frequency semicircle is characterized by a capacitance about 3 × 10⁻¹¹ F cm⁻¹ and could be attributed to ion transport in the crystalline and crystalline grains.³¹ The electrode response was a Warburg-type spike characteristic of ion conductor. The total ionic conductivity (σ_t) could be calculated according to the formula:³¹

σ = R/(L·S) (1)

where R is the total resistance, which could be gained from the Nyquist plot, L is height of pellet, S is the contact area. Arrhenius plots of the total ionic conductivity σ for Na₃VS₄ and Na₃P_0.1V_0.9S₄ were depicted in Fig. 3d.

The linear dependence of log σ_t versus (1/T) follows the Arrhenius law and indicates phase stability over the given temperature range. As show in the Table 5, the total ionic conductivity of Na₃VS₄ located in the range from 1.16 × 10⁻⁸ S cm⁻¹ at 25 °C to 1.46 × 10⁻⁶ S cm⁻¹ at 100 °C. However, the total ionic conductivity of Na₃P_0.1V_0.9S₄ placed 1.49 × 10⁻⁷ S cm⁻¹ at 25 °C to 1.20 × 10⁻⁵ S cm⁻¹ at 100 °C, which almost one order of magnitude higher than those of Na₃VS₄. The activation energy E_a for the sodium-ion conductor is determined from the slope of the linear Arrhenius plot using below equation:³²

σ_t = A exp(−E_a/k_BT) (2)

where σ_t is the total ionic conductivity, A is the pre-exponential parameter, T is absolute temperature, E_a is the activation energy, and k_B is the Boltzmann constant. The calculated activation energy of Na₃VS₄ is 0.65 eV, while it is 0.54 eV for Na₃P_0.1V_0.9S₄. The lower activation energy of Na₃P_0.1V_0.9S₄ than that of Na₃VS₄ indicated that the diffusion rate of sodium ions in Na₃P_0.1V_0.9S₄ is higher than those of Na₃VS₄ leading to higher conductivity.

Table 5 Total ionic conductivity of Na₃VS₄ and Na₃P_0.1V_0.9S₄

Composition	25 °C (S cm^−1)	40 °C (S cm^−1)	60 °C (S cm^−1)	80 °C (S cm^−1)	100 °C (S cm^−1)
Na3VS4	1.16 × 10^−8	3.11 × 10^−8	1.07 × 10^−7	4.23 × 10^−7	1.46 × 10^−6
Na3P0.1V0.9S4	1.49 × 10^−7	3.14 × 10^−7	8.30 × 10^−7	2.63 × 10^−6	1.20 × 10^−5

---

Compared with Na₃VS₄, the P-doping Na₃P_0.1V_0.9S₄ showed higher Na ionic conductivity. Through P substitution for V on Na₃P_0.1V_0.9S₄ composition, it could decrease the size of V/PS₄³⁻ tetrahedra and enlarge some sulfur anion channels. From the Rietveld refinement of Na₃P_0.1V_0.9S₄ data, the occupancy of Na2 sites contains 92% Na plus 8% vacancies rather than full occupancy of Na. Recently, theoretical investigations on both Na₃PS₄ (ref. 14) and Na₃PSe₄ (ref. 19) revealed that a defect-driven diffusion mechanism (either Na ion interstitial or Na ion vacancy) accounts for the high ionic conductivity. Actually, Na ion deficiency is the reality during synthesis as it is a very reactive metal. Therefore, an ultrafast ion diffusion is expected if the conductor meets the prerequisites of sodium vacancy defects. In this work, these are about 8% of sodium vacancies in the Na2 position, therefore, these sodium vacancies are conducive to the diffusion of sodium ions. Benefit from these favorable features, P doping Na₃V_0.9P_0.1S₄ gets higher Na ion conductivity.

The total conductivity generally includes ionic conductors, minor electrons and/or holes (σ_(e+h)). Na₃VS₄ and Na₃P_0.1V_0.9S₄ total conductivity can be expressed by σ_t = σ_Na⁺ + σ_(e+h). The transference number for sodium ions is accordingly derived by t_Na⁺ = σ_Na⁺/σ_t.²⁰ To evaluate the exactly contribution of the electronic contribution to the total conductivity in the Na₃VS₄ and Na₃P_0.1V_0.9S₄ electrolytes, potentiostatic (0.5 V was used in the present work) DC measurements were carried out on Pt/Na₃VS₄/Pt and Pt/Na₃P_0.1V_0.9S₄/Pt cells at 25 °C. The electronic conductivity curves were displayed in Fig. 5a and b. When the measurement was performed, as there are no external sources for Na⁺ ions, the electrodes are therefore blocking for Na⁺ ions, and the conductivity at steady stage under a DC voltage could be ascribed to the electronic conduction. According to the chronoamperometric curves, the electronic resistance can calculate from the formula R = U/I at steady stage, and then according to eqn (1) get the electronic conduction. The calculated values of σ_(e+h) are about 8.60 × 10⁻⁹ and 1.76 × 10⁻⁸ S cm⁻¹ for Na₃VS₄ and Na₃P_0.1V_0.9S₄, respectively. Therefore, the calculated transport number of sodium ions (t_Na⁺) are about 0.3 for Na₃VS₄ and 0.9 for Na₃P_0.1V_0.9S₄ according to t _Na⁺ = σ_Na⁺/σ_t, indicating that P-doing could greatly improve the transport number of sodium ions leading to higher total conductivity.

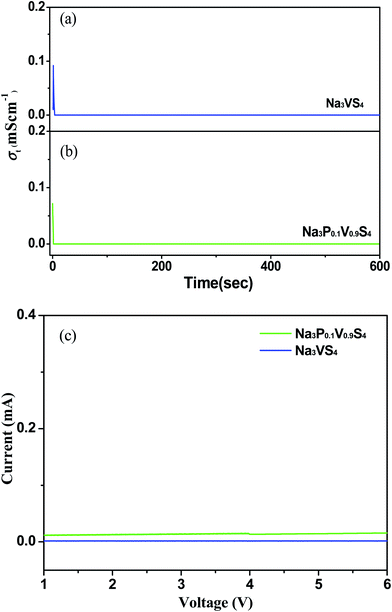Fig. 5 Electronic conductivity curves for Na₃VS₄ (a) and Na₃P_0.1V_0.9S₄ (b), (c) LSV curves of Na₃VS₄ and Na₃P_0.1V_0.9S₄.

The electrochemical stability of Na₃VS₄ and Na₃P_0.1V_0.9S₄ with metallic sodium was estimated by using linear sweep voltammograms (LSV) on the Na/Na₃VS₄/Pt and Na/Na₃P_0.1V_0.9S₄/Pt cells,³³ as shown in Fig. 5c. Both of LSV curves do not appear apparent redox peak, indicating Na₃VS₄ and Na₃P_0.1V_0.9S₄ solid-state electrolytes exhibit a high electrochemical stability window up to 6 V.

Conclusion

In summary, a new Na-ion solid-state electrolyte Na₃VS₄ with the space group P4̄21c was synthesized and investigated. Na1, Na2, Na3 and Na4 atoms locate at the 4d, 4c, 8e and 8e Wyckoff sites in the structure, respectively. Na2 atom sites bound to eight sulfur atoms and from a body-centered cubic anion framework, which is beneficial for Na ion diffusion. The total ionic conductivity of the parent composition Na₃VS₄ is ∼1.16 × 10⁻⁸ to 1.46 × 10⁻⁶ S cm⁻¹ from 25 to 100 °C. After substituting for V with P, the P-doping composition Na₃P_0.1V_0.9S₄, got the conductivity of 1.49 × 10⁻⁷ to 1.20 × 10⁻⁵ S cm⁻¹ from 25 to 100 °C, which was higher than that of parent Na₃VS₄. The improvement of ion conductivity could ascribe to small P substitution for the large V giving rise to broaden the Na migration path and create of sodium vacancies. Also, both of Na₃VS₄ and Na₃P_0.1V_0.9S₄ solid-state electrolytes exhibit a high electrochemical stability window up to 6 V. This work will enrich the field of view sulfate-based sodium ion conductors and paves a new way to design new solid-state conductors for the next generation of solid-state Na ion batteries.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the financial support of the National Natural Science Foundation of China (No. 21622101) and Guangxi Natural Science Foundation (No. 2017GXNSFBA198149).

References

1. D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29.
2. H. Kim, Z. Ding, M. H. Lee, K. Lim and G. Yoon, Adv. Energy Mater., 2016, 6, 1600943.
3. X. B. Cheng, R. Zhang, C. Z. Zhao, F. Wei, J. G. Zhang and Q. Zhang, Adv. Sci., 2016, 3, 1500213.
4. H. Cheng, J. Liang and Z. Tao, Adv. Mater., 2011, 23, 1695–1715.
5. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
6. D. Bruce, K. Haresh and J. M. Tarascon, Science, 2011, 334, 928–935.
7. J. J. Kim, K. Yoon, I. Park and K. Kang, Small Methods, 2017, 1, 1700219.
8. J. Zhang, H. Wen, L. Yue, J. Chai, J. Ma and P. Hu, Small, 2017, 13, 1–10.
9. K. Noriaki, H. Kenji, Y. Yuichiro, H. Masaaki, K. Ryoji and Y. Masao, Nat. Mater., 2011, 10, 682–686.
10. Y. Kato, S. Hori, T. Saito, K. Suzuki, M. Hirayama and A. Mitsui, Nat. Energy, 2016, 1, 16030.
11. M. Jansen and U. Henseler, J. Solid State Chem., 1992, 99, 110–119.
12. A. Hayashi, K. Noi, A. Sakuda and M. Tatsumisago, Nat. Commun., 2011, 3, 856.
13. A. Hayashi, K. Noi, N. Tanibata, N. Motohiro and M. Tatsumisago, J. Power Sources, 2011, 258, 420–423.
14. N. J. J. D. Klerk and M. Wagemaker, Chem. Mater., 2016, 28, 3122–3130.
15. K. Noi, A. Hayashi and M. Tatsumisago, J. Power Sources, 2014, 269, 260–265.
16. N. Tanibata, K. Noi, A. Hayashi, N. Kitamura, Y. Idemoto and M. Tatsumisago, ChemElectroChem, 2014, 1, 1130–1132.
17. N. Tanibata, K. Noi, A. Hayashi and M. Tatsumisago, RSC Adv., 2014, 4, 17120.
18. I. H. Chu, C. S. Kompella, N. Han, Z. Zhu, S. Hy and Z. Deng, Sci. Rep., 2016, 6, 33733.
19. L. Zhang, K. Yang, J. Mi, L. Lu, L. Zhao and L. Wang, Adv. Energy Mater., 2015, 5, 1501294.
20. L. Zhang, D. Zhang, K. Yang, X. Yan, L. Wang and J. Mi, Adv. Sci., 2016, 3, 1600089.
21. Z. Yu, S. Sl, S. Jh, D. Wang, X. Luo and Q. Huang, Adv. Mater., 2017, 29, 1605561.
22. M. Duchardt, U. Ruschewitz, S. Dehnen and B. Roling, Angew. Chem., Int. Ed., 2018, 57, 1351.
23. W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim and S. P. Ong, Nat. Commun., 2016, 7, 11009.
24. K. O. Klepp and G. Gabl, Eur. J. Solid State Inorg. Chem., 1997, 34, 1143–1154.
25. A. A. C. Coelho Software, Brisbane, Australia, 2005.
26. Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026.
27. P. Bron, S. Johansson, K. Zick, J. Schmedt auf der Günne, S. Dehnen and B. Roling, J. Am. Chem. Soc., 2013, 135, 15694–15697.
28. M. Tatsumisago, M. Nagao and A. Hayashi, J. Asian Ceram. Soc., 2013, 1, 17–25.
29. M. Duchardt, U. Ruschewitz, S. Dehnen and B. Roling, Angew. Chem., Int. Ed., 2017, 57, 1351–1355.
30. X. Feng, P. H. Chien, Z. Zhu, I. H. Chu, P. Wang, M. Immediato-Scuotto, H. Arabzadeh, S. P. Ong and Y. Y. Hu, Adv. Funct. Mater., 2019, 29, 1807951.
31. T. S. Irvine, C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138.
32. G. Sahu, L. Zhan, J. Li, Z. Liu and C. Liang, Energy Environ. Sci., 2014, 7, 1053–1058.
33. G. K. Kim, Y. J. Lim, H. Kim, Z. Liu and G. B. Cho, Energy Environ. Sci., 2015, 8, 3589–3596.

---