Open Access Article
Open Access ArticleTransport of polymer-modified nanoparticles in nanochannels coated with polymers
Lujuan Li,
Qianqian Cao *,
Hao Liu,
Zhiqing Gu,
Ying Yu,
Fengli Huang and
Chuncheng Zuo
*,
Hao Liu,
Zhiqing Gu,
Ying Yu,
Fengli Huang and
Chuncheng Zuo
College of Mechanical and Electrical Engineering, Jiaxing University, Jiaxing 314001, P. R. China. E-mail: qqcao@zjxu.edu.cn
First published on 28th November 2019
Abstract
Using molecular dynamics simulations based on explicit-solvent model, we study migration of polymer-modified nanoparticles through nanochannels coated with polymers. The polymers densely grafted on the spherical nanoparticle and the channel surface form spherical polymer brush (SPB) and planar polymer brush (PPB), respectively. The migration of the neutral polymer-modified nanoparticle is driven by electroosmotic flow (EOF). The effects of the electric field strength and the SPB–PPB interaction on polymer conformations and transport dynamics of the SPB are explored. The migration velocity of the SPB reduces as the interaction between the SPB and the PPB increases. For strong SPB–PPB interaction, the directional migration of the SPB can be triggered only after the electric field strength exceeds a critical value. The high EOF velocity forces the center of mass of the spherical nanoparticle to keep near the central region of the channel due to high shear rate close to the brush–fluid interface. Unlike electrophoresis of charged polymer-grafted spherical particles, the SPB adopts a more extended conformation in the plane perpendicular to the EOF direction.
1 Introduction
Electrokinetic phenomena widely occur in nanofluidic and microfluidic systems.1–3 In particular, the interfacial properties have significant effects on electrokinetic transport of fluid through nanochannels. Polymer brushes are frequently used to modify the properties of the channel surfaces. For the charged surfaces, through minimizing the interactions between the analyte and the grafting surface the polymer brushes can suppress electroosmotic flow (EOF) and prevent analyte from adsorbing on the surface. As a result, polymer-coating capillary electrophoresis is employed as a common separation method for biomacromolecules (DNA and protein) to improve separation performance.4–7Electric double layer (EDL) forms near a charged surface when the surface is immersed in electrolyte solution. The EDL consists of the stern and diffuse layers. When an electric field is applied along the channel direction, directional migration of counterions within the EDL triggers the EOF. If the charged surface of the channel is coated by a polymer layer, the ionic distribution in the EDL can be influenced. The effect significantly depends on the properties of the polymer layer, especially the layer thickness. The EOF can be strongly inhibited if the layer thickness largely exceeds the EDL thickness. This is because the immobility of grafted polymer chains exerts resistance force to the fluid. For sparse polymer coating, there exists linear relationship between the EOF mobility and the grafting density under weak electric field and strong electrostatic screening.8 However, unlike the bare surface without polymer coating, the coupling of the conformational dynamics of grafted polymer chains and the fluid dynamics makes resulting ionic distribution and fluid transport more complicated. This becomes obvious when the thickness of the polymer layer is comparable to the EDL thickness. Therefore, modulation of the EOF via coating polymers on the channel surface is related to many factors. Though much attention was paid,9–13 some electrohydrodynamics problems which occur in such systems remain to be settled.
The polymer coating can affect the EOF characteristics and also modify interactions between the surfaces of channels and analytes. In capillary electrophoresis, adsorption of analytes on the surface of capillary reduces efficiency and reproducibility of separation. For biomolecule separation, a polymer coating on the charged wall is required to minimize analyte–wall interactions and suppress the EOF. In the work, we study transport of polymer-coated nanoparticle through the channel modified by polymers driven by the EOF. The nanoparticles grafted with polymers can be classified as soft colloids. When polymers are densely coated on the surface of a spherical particle, the coated polymer layer is also called spherical polymer brush (SPB). The SPB can modify the physicochemical properties of the particle surfaces, which is of broad applications, such as colloid stabilization14,15 and drug delivery.16,17 The conformational behavior of the SPB has been widely discussed by theoretical and computer simulation methods.18–24 Recently, electrophoresis of spherical colloids grafted with charged polymers (such as polyelectrolytes and polyampholytes) was also studied by means of molecular dynamics (MD) simulations considering long-ranged hydrodynamic interactions based on lattice-Boltzmann method.25,26 Nonzero electrophoresis mobility was observed for net-neutral particles. For grafted polyampholytes, we found that the mobility of the net-neutral particles remarkably depends on the structures of the polymer layer.26
MD simulations provide insight into electrohydrodynamics for systems with polymer-modified surfaces. So far, most computational studies focus on the EOF through polymer-coated channels.27–36 However, how nanoparticles migrate through channels modified by polymers are not studied thoroughly. Our previous work has addressed transport mechanisms of nanoparticles in polymer-coated nanochannels.37 The conformational behavior of the brush and the interactions between the brush and nanoparticles influence translocation of nanoparticles. When the nanoparticles are coated by polymers, the interactions between polymer chains grafted on the channel surface and ones grafted on the nanoparticle may affect the conformations of the polymer layer and the transport of the nanoparticle. In the study, the grafting density investigated is higher than the critical grafting density. The polymer layer on the surface of the spherical particle corresponds to a SPB, and the polymers grafted on the channel surface form planar polymer brush (PPB). In addition, we employ explicit solvent model to simulate the system. Though implicit solvent model is computationally efficient, it may be problematic for the complex system investigated here. We will analyze the effects of the interactions between the SPB and the PPB, and the electric field strength on the brush conformations and the transport dynamics of the SPB. The remainder of the paper in structured as follows: we give an introduction to the model system and the simulation method in the next section. The Results and discussion are presented in Section 3. We finish with the Conclusion in Section 4.
2 Model and simulation method
The nanochannel consisting of two apposing solid walls grafted with neutral polymers which form the PPB is modeled based on coarse-grained MD method. Each wall contains two layers of solid atoms arranged to form a (1 1 1) plane of FCC crystal. The polymer chains each containing Nm = 15 monomers are uniformly arranged in a square lattice with the spacing d = ρg−1/2. The grafting density ρg denotes the number of grafted polymer chains per unit area. We set the grafting density to ρg = 0.125σ−2. The spherical nanoparticle with a radius Rc = 4σ is coated by the SPB. The surface of the nanoparticle consists of 201 neutral beads which distribute on the core surface uniformly. Nc = 30 polymer chains each containing Ncm = 15 monomers are linked to grafting points which are chosen from the surface beads on the nanoparticle. The number density of the fluid is taken as ρf = 0.81σ−3. There are 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 661 solvent particles added in the model system. The salt concentration is c0 = 0.025σ−3, and the charge density of the channel wall is ρwc = 0.4σ−2. The salt ions are modeled as beads that are the same as solvent particles, but carry monovalent charges. All wall particles are frozen. The counterions for the charged walls are added to neutralize the system. The dimensions of simulation box along x and z directions are Lx = Ly = 41.3σ and Lz = 27σ (not including the walls).
661 solvent particles added in the model system. The salt concentration is c0 = 0.025σ−3, and the charge density of the channel wall is ρwc = 0.4σ−2. The salt ions are modeled as beads that are the same as solvent particles, but carry monovalent charges. All wall particles are frozen. The counterions for the charged walls are added to neutralize the system. The dimensions of simulation box along x and z directions are Lx = Ly = 41.3σ and Lz = 27σ (not including the walls).
The short-range interaction between any two particles separated by a distance r is described by a shifted LJ potential with interaction strength ε and diameter σ:
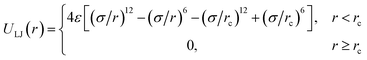 | (1) |
The purely repulsive interactions with the cut-off radius rc = 21/6σ and the interaction strength ε = 1.0εLJ are used except for pairs formed from monomers of the SPB and monomers of the PPB. εLJ is the unit of the energy. The cut-off radius of interactions between the SPB and the PPB is set to rc = 2.5σ. Their interaction strength ε = εsw is tuned in a range of 0.1εLJ to 1.0εLJ. Neighboring monomers of the polymer chains are connected by finitely extensible nonlinear elastic (FENE) potential with the maximum bond length lmax = 1.5σ and the spring constant kb = 30εLJ/σ2:
| Ub(l) = −(kblmax2/2)ln(1 − l2/lmax2) | (2) |
The Coulomb potential is used to model the electrostatic interaction between two charged particles of valencies Zi and Zj:
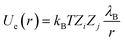 | (3) |
All MD simulations in a NVT ensemble are performed by LAMMPS supporting high parallelization performance.40 The target temperature of the system keeps at T = 1.2εLJ/kB during the simulation by coupling the system to a dissipative particle dynamics (DPD) thermostat:41
FDij = −γwD(rij)(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij·vij) ij·vij)![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij ij
| (4) |
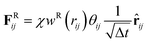 | (5) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ij = (ri − rj)/rij, and vij = vi − vj. Two constants γ and χ are used to characterize the strength of the dissipative force FD and that of the random force FR. They are coupled each other based on the fluctuation–dissipation theorem χ2 = 2γkBT. We set γ to 1.5εLJτ/σ2 with τ as the time unit. Δt is the time step size. θij is a symmetric Gaussian random variable with zero mean and unit variance. The weight functions wD(rij) and wR(rij) are expressed as:
ij = (ri − rj)/rij, and vij = vi − vj. Two constants γ and χ are used to characterize the strength of the dissipative force FD and that of the random force FR. They are coupled each other based on the fluctuation–dissipation theorem χ2 = 2γkBT. We set γ to 1.5εLJτ/σ2 with τ as the time unit. Δt is the time step size. θij is a symmetric Gaussian random variable with zero mean and unit variance. The weight functions wD(rij) and wR(rij) are expressed as:
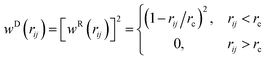 | (6) |
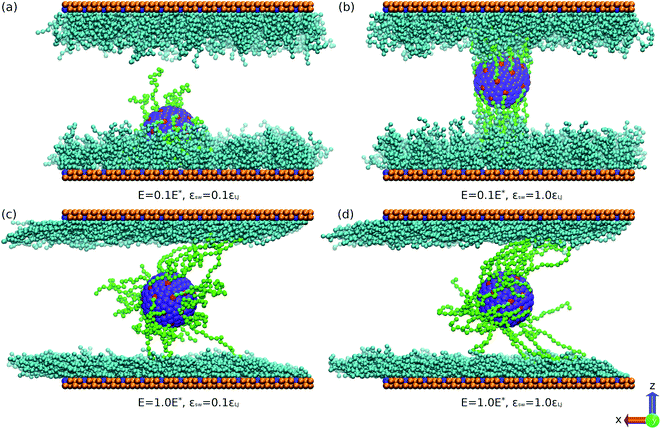
In nonequilibrium flow simulations, the DPD thermostat can naturally avoid a profile bias and correctly reproduce hydrodynamic correlations. The velocity-Verlet algorithm with the time step 0.005 is used to calculate the trajectory of the particles. We run 5 × 105 time steps for equilibration. Then, the electric field is applied and a simulation for 1 × 106 time steps is carried out. Finally, we further run 2 × 106 time steps for gathering sufficient statistics. The electric field is applied along the x direction. The unit of electric field strength E is taken as E* = εLJσ−1/(4πε0σεLJ)1/2. If the basic units are set to σ = 0.3 nm, T = 300 K and m = 3 × 10−26 kg (mass unit), we obtain E* = 1.07 V nm−1.42 The corresponding range of electric field is E = 0.107 V nm−1 to 1.28 V nm−1. To depict our model, the simulation snapshots are provided in Fig. 1.
3 Results and discussion
First, we present the density profiles of several components at strong and weak electric field in Fig. 2. Only half the channel along the z direction is shown due to symmetry of the density profiles. The interaction parameter εsw between the SPB and the PPB has negligible effect on the particle distribution. The oscillation of the monomer density near the surface (z < 3σ) is caused by ordered arrangement of wall particles. At the strong electric field E = 1.0E* (Fig. 2a), the monomer density shifts towards the channel surface, corresponding to more compact polymer layer compared to the weak electric field E = 0.1E* (Fig. 2b). This also leads to the migration of ions away from the surface, in particular for the anions which are counterions of the charged surface. The density of anions is approximately equal to that of cations in the central region of the channel. The difference of distribution between anions and cations mainly occurs close to the channel surface at E = 0.1E*. However, at E = 1.0E* there is evident density difference of ions in the brush–fluid interface. This indicates that at the weak electric field the EOF generated in the PPB is weakened by the friction between polymer chains and fluid, but at the strong electric field the friction is decreased effectively because of the shift of the EDL towards the brush–fluid interface. Further, the EOF induced by the electric field changes the monomer density. The EOF velocity and the influence of the electric field on the EOF will be discussed below.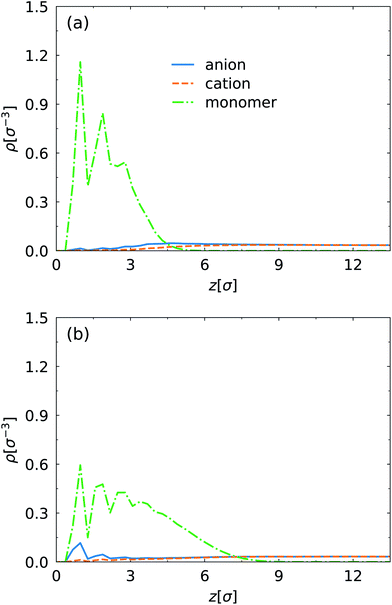 | ||
| Fig. 2 Density profiles of monomers of grafted polymers on the channel surfaces, cations and anions along the z direction at (a) E = 1.0E* and (b) 0.1E* for εsw = 0.1εLJ. | ||
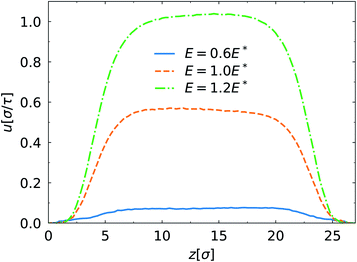
Fig. 3 shows the EOF velocity for different electric field strength. Analogous to the density profiles above, the SPB–PPB interaction influences weakly the EOF through the channel. The EOF is inhibited strongly close to the wall by the polymer layer. The plug-like flow profiles are observed not taking into account the suppressed flow region. Compared to the case of E = 0.6E*, further enhancement of the electric field results in significant increase of the EOF velocity. When the electric field is weak, E < 0.6E*, its effect on the EDL is negligible and the EDL is in the inner of the polymer brush. Therefore, the EOF velocity is obviously low due to strong friction from the polymers mentioned above. If the electric field becomes sufficiently high, the EDL moves towards the brush–fluid interface leading to reduced friction. From the monomer and ion density profiles (Fig. 2), we note that the change of the electric field also affects the conformation of the PPB accompanied by the ion distribution. Moreover, the structure of the EDL depends on the ion distribution. The coupling of the EOF dynamics and the polymer conformations is ubiquitous in the polymer-coated channels with charged surfaces.27,32
Further, we analyse the relationship between the migration velocity us of the SPB and the SPB–PPB interaction strength εsw. Because the monomers of the SPB are neutral, the driving force of the SPB migration originates from the EOF. The attractive interaction between the SPB and the PPB tends to reduce the SPB velocity. As shown in Fig. 4, us decreases as the SPB–PPB interaction enhances. For weak SPB–PPB interaction, such as εsw < 0.6εLJ, there is little effect of the SPB–PPB interaction on the SPB velocity. It becomes obvious at strong SPB–PPB interaction. Additionally, at strong SPB–PPB interaction and weak electric field, all chains of the SPB strongly bind to some chains grafted on the channel surfaces, such as the case of E = 0.1E* and εsw = 1.0εLJ (Fig. 1b). There are about half the chains from the SPB bound to some chains grafted on the top surface, and other chains interact with some chains grafted on the bottom surface. We found that the weak electric field, E < 0.6E*, can not drive migration of the SPB via the EOF. When the drag force from the EOF overcomes the binding force at strong electric field (Fig. 1d), the strong binding between the SPB and the PPB is destroyed.
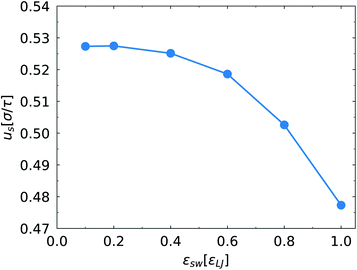 | ||
| Fig. 4 Migration velocity us of the SPB along the channel direction as a function of εsw at E = 1.0E*. | ||
The electric field exerts force on the counterions in the EDL and has direct influence of the EOF velocity. As shown in Fig. 5, enhancing the electric field causes the increase of the EOF velocity. However, due to the overlapping of the brush region and the EDL, the electric field also changes the conformations of the grafted polymers on the channel surface via the EOF, which conversely affects the structure of the EDL. This leads to nonlinear relationship between the EOF velocity and the electric field strength. At E < 0.4E*, the brush possesses stronger inhibition on the EOF. Owing to the relatively weak EOF, the conformation of the PPB and the distribution of the ions near the channel surface are marginally impacted.
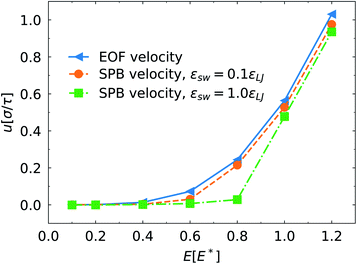 | ||
| Fig. 5 Migration velocity us of the SPB and the average EOF velocity far away for the polymer layer along the channel direction as a function of the electric field strength. | ||
We also compared the EOF velocity and the SPB migration velocity under different electric fields. It was found that at εsw = 0.1εLJ, the effect of the electric field on the SPB velocity is consistent with the EOF velocity except for slightly small velocity difference. At εsw = 1.0εLJ, the drag force from the polymer chains grated on the channel surface results in lower migration velocity of the SPB. In addition, we note that evident migration of the SPB is triggered until the electric field exceeds a critical value (about 0.8E*) where a significant velocity difference between the SPB and the bulk fluid is identified. At stronger electric field, the drag force overwhelms the SPB–PPB interaction. Moreover, only end segments of some chains on the SPB contact with the PPB (Fig. 1d). These factors lead to remarkable increase of the SPB velocity.
Fig. 6 shows evolution of center of mass (COM) of the spherical nanoparticle along the z direction as a function of simulation time. In all simulations, the nanoparticle is initially placed in the center of the channel. At E = 0.1E*, the SPB moves towards one surface of the channel for εsw = 0.1εLJ. As shown in Fig. 1a, the SPB is trapped within the bottom polymer layer. For strong SPB–PPB interaction, the COM of the nanoparticle is closer to the center of the channel. Nevertheless, in a long simulation the SPB can be trapped in one polymer layer grated on the top or bottom surface due to non-balanced force stemming from Brownian motion of the chains. The present simulations indicate that weak binding of polymer chains between the SPB and the PPB accelerates offset of the SPB. When the strong electric field is applied, the oscillation of the COM is intensified regardless of the SPB–PPB interaction strength. It is clear that the shear rate of the EOF is approximately zero close to the center of the channel, and thus the chains are not stretched. When the chains move towards the wall, the extension becomes strong owing to high shear rate. The chains tend to be highly extended where the local shear rate is higher, but there is less probability to find a chain in that region. Such feature was also observed for shear-induced migration of DNA in microchannels.43 Therefore, the steady position of the SPB keeps close to the center of the channel. In addition, at E = 1.0E* the oscillation of the COM is somewhat stronger for εsw = 1.0εLJ compared to εsw = 0.1εLJ.
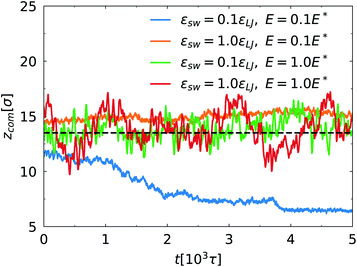 | ||
| Fig. 6 Time evolution of center of mass of the nanoparticle along the z direction for different E and εsw. The dashed line denotes the center of the channel. | ||
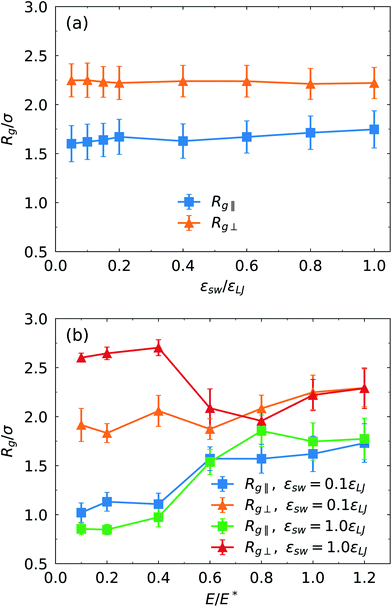
Finally, we study the effects of the SPB–PPB interaction and the electric field on the radius of gyration (ROG) of the chains on the SPB. Due to nonuniform flow field, the radius of gyration also shows anisotropy. Here, we calculate the perpendicular Rg⊥ and parallel Rg∥ components of the ROG according to following formulas:
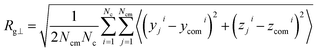 | (7) |
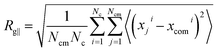 | (8) |
4 Conclusions
In summary, we applied molecular dynamics simulations to investigate transport dynamics of polymer-modified nanoparticles through nanochannels coated with polymers. The driving force originates from the EOF generated by migration of counterions in the EDL. Due to the overlapping of the EDL and the PPB grafted on the channel surface, the EOF is significantly suppressed in particular at weak electric field. The enhancement of the electric field leads to the decrease of the PPB thickness, corresponding to increased monomer density. Moreover, the thinning of the brush increases the effective width of the channel and induces the shift of counterion distribution towards the brush–fluid interface. This reduces the resistance of migration of counterions accompanied by strong EOF. Therefore, the increase of the monomer density or the thinning of the brush under strong electric field results in higher migration velocity of the SPB.The coupling between the conformation of the PPB and the EOF dynamics leads to nonlinear dependence of the EOF velocity on the electric field. Further, the EOF influences binding of the polymer chains of the SPB to the PPB and migration behavior of the SPB. At a fixed electric field strength, the increase of the SPB–PPB interaction inhibits migration of the SPB. Moreover, the relationship between the migration velocity and the SPB–PPB interaction shows non-linearity. Due to attractive interaction between the SPB and the PPB, the movement of the SPB is slower compared to the fluid far away from the PPB. At weak electric field, strong SPB–PPB binding can completely limit migration of the SPB. It was found that for strong SPB–PPB interaction a critical electric field is identified to move the SPB. The results also reveal that the SPB tends to migrate close to the central region of the channel at strong electric field owing to high flow shear rate near the brush–fluid interface. The calculation on perpendicular and parallel components of the radius of gyration indicates that the chains grafted on the nanoparticle are extended more strongly along the perpendicular direction of the electric field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by Zhejiang Provincial Natural Science Foundation of China (Grant No. LY19A020006) and the project (D) of Qianjiang talent plan. Z. G., Y. Y. and C. Z. also acknowledge financial support from Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ19E020003) and National Natural Science Foundation of China (Grant No. 11802102 and 51775242), respectively.References
- W. Sparreboom, A. van den Berg and J. C. Eijkel, Principles and applications of nanofluidic transport, Nat. Nanotechnol., 2009, 4, 713–720 CrossRef CAS PubMed.
- C. Zhao and C. Yang, Advances in electrokinetics and their applications in micro/nano fluidics, Microfluid. Nanofluid., 2012, 13, 179–203 CrossRef.
- H.-C. Chang, G. Yossifon and E. A. Demekhin, Nanoscale electrokinetics and microvortices: How microhydrodynamics affects nanofluidic ion flux, Annu. Rev. Fluid. Mech., 2012, 44, 401–426 CrossRef.
- E. A. S. Doherty, K. D. Berglund, B. A. Buchholz, I. V. Kourkine, T. M. Przybycien, R. D. Tilton and A. E. Barron, Critical factors for high-performance physically adsorbed (dynamic) polymeric wall coatings for capillary electrophoresis of DNA, Electrophoresis, 2002, 23, 2766–2776 CrossRef CAS PubMed.
- M. N. Albarghouthi, T. M. Stein and A. E. Barron, Poly-N-hydroxyethylacrylamide as a novel, adsorbed coating for protein separation by capillary electrophoresis, Electrophoresis, 2003, 24, 1166–1175 CrossRef CAS PubMed.
- H. Bi, S. Meng, Y. Li, K. Guo, Y. Chen, J. Kong, P. Yang, W. Zhong and B. Liu, Deposition of PEG onto PMMA microchannel surface to minimize nonspecific adsorption, Lab Chip, 2006, 6, 769–775 RSC.
- R. Haselberg, L. van der Sneppen, F. Ariese, W. Ubachs, C. Gooijer, G. J. de Jong and G. W. Somsen, Effectiveness of Charged Noncovalent Polymer Coatings against Protein Adsorption to Silica Surfaces Studied by Evanescent-Wave Cavity Ring-Down Spectroscopy and Capillary Electrophoresis, Anal. Chem., 2009, 81, 10172–10178 CrossRef CAS PubMed.
- J. L. Harden, D. Long and A. Ajdari, Influence of end-grafted polyelectrolytes on electro-osmosis along charged surfaces, Langmuir, 2001, 17, 705–715 CrossRef CAS.
- J. Znaleziona, J. Petr, R. Knob, V. Maier and J. Ševčík, Dynamic coating agents in CE, Chromatographia, 2008, 67, 5–12 CrossRef.
- J. Bernal, I. Rodríguez-Meizoso, C. Elvira, E. Ibáñez and A. Cifuentes, Fast and easy coating for capillary electrophoresis based on a physically adsorbed cationic copolymer, J. Chromatogr., 2008, 1204, 104–109 CrossRef CAS PubMed.
- G. Paumier, J. Sudor, A.-M. Gue, F. Vinet, M. Li, Y. J. Chabal, A. Estève and M. Djafari-Rouhani, Nanoscale actuation of electrokinetic flows on thermoreversible surfaces, Electrophoresis, 2008, 29, 1245–1252 CrossRef CAS PubMed.
- K. E. Allan, C. E. Lenehan, D. A. Khodakov, H. J. Kobus and A. V. Ellis, High-performance capillary electrophoretic separation of double-stranded oligonucleotides using a poly-(ethylpyrrolidine methacrylate-co-methyl methacrylate)-coated capillary, Electrophoresis, 2012, 33, 1205–1214 CrossRef CAS PubMed.
- L. Hajba and A. Guttman, Recent advances in column coatings for capillary electrophoresis of proteins, Trends Anal. Chem., 2017, 90, 38–44 CrossRef CAS.
- Y. Mei, Y. Lu, F. Polzer, M. Ballauff and M. Drechsler, Catalytic activity of palladium nanoparticles encapsulated in spherical polyelectrolyte brushes and core-shell microgels, Chem. Mater., 2007, 19, 1062–1069 CrossRef CAS.
- C. Schneider, A. Jusufi, R. Farina, F. Li, P. Pincus, M. Tirrell and M. Ballauff, Microsurface potential measurements: Repulsive forces between polyelectrolyte brushes in the presence of multivalent counterions, Langmuir, 2008, 24, 10612–10615 CrossRef CAS PubMed.
- K. Y. Win and S.-S. Feng, Effects of particle size and surface coating on cellular uptake of polymeric nanoparticles for oral delivery of anticancer drugs, Biomaterials, 2005, 26, 2713–2722 CrossRef CAS PubMed.
- S. A. Kulkarni and S.-S. Feng, Effects of particle size and surface modification on cellular uptake and biodistribution of polymeric nanoparticles for drug delivery, Pharm. Res., 2013, 30, 2512–2522 CrossRef CAS PubMed.
- P. Pincus, Colloid stabilization with grafted polyelectrolytes, Macromolecules, 1991, 24, 2912–2919 CrossRef CAS.
- A. Jusufi, C. Likos and M. Ballauff, Counterion distributions and effective interactions of spherical polyelectrolyte brushes, Colloid Polym. Sci., 2004, 282, 910–917 CrossRef CAS.
- Y. Mei, K. Lauterbach, M. Hoffmann, O. V. Borisov, M. Ballauff and A. Jusufi, Collapse of Spherical Polyelectrolyte Brushes in the Presence of Multivalent Counterions, Phys. Rev. Lett., 2006, 97, 158301 CrossRef PubMed.
- F. Lo Verso, S. A. Egorov, A. Milchev and K. Binder, Spherical polymer brushes under good solvent conditions: Molecular dynamics results compared to density functional theory, J. Chem. Phys., 2010, 133, 184901 CrossRef PubMed.
- Q. Cao, C. Zuo and L. Li, Electrostatic binding of oppositely charged surfactants to spherical polyelectrolyte brushes, Phys. Chem. Chem. Phys., 2011, 13, 9706–9715 RSC.
- Q. Cao and M. Bachmann, Polyelectrolyte adsorption on an oppositely charged spherical polyelectrolyte brush, Soft Matter, 2013, 9, 5087–5098 RSC.
- L. Li, Q. Cao and C. Zuo, Effect of Counterion Valence on Conformational Behavior of Spherical Polyelectrolyte Brushes Confined between Two Parallel Walls, Polymers, 2018, 10, 363 CrossRef PubMed.
- S. Raafatnia, O. A. Hickey and C. Holm, Electrophoresis of a spherical polyelectrolyte-grafted colloid in monovalent salt solutions: Comparison of molecular dynamics simulations with theory and numerical calculations, Macromolecules, 2015, 48, 775–787 CrossRef CAS.
- Q. Cao, L. Li and C. Zuo, Electrohydrodynamics of spherical polyampholyte-grafted nanoparticles: Multiscale simulations by coupling of molecular dynamics and lattice-boltzmann method, J. Polym. Sci., Part B: Polym. Phys., 2017, 55, 1435–1448 CrossRef CAS.
- F. Tessier and G. W. Slater, Modulation of Electroosmotic Flow Strength with End-Grafted Polymer Chains, Macromolecules, 2006, 39, 1250–1260 CrossRef CAS.
- O. A. Hickey, J. L. Harden and G. W. Slater, Molecular Dynamics Simulations of Optimal Dynamic Uncharged Polymer Coatings for Quenching Electro-osmotic Flow, Phys. Rev. Lett., 2009, 102, 108304 CrossRef PubMed.
- O. A. Hickey, C. Holm, J. L. Harden and G. W. Slater, Influence of Charged Polymer Coatings on Electro-Osmotic Flow: Molecular Dynamics Simulations, Macromolecules, 2011, 44, 9455–9463 CrossRef CAS.
- R. Qiao, Control of Electroosmotic Flow by Polymer Coating: Effects of the Electrical Double Layer, Langmuir, 2006, 22, 7096–7100 CrossRef CAS PubMed.
- M. Monteferrante, S. Melchionna, U. Marconi, M. Cretich, M. Chiari and L. Sola, Electroosmotic flow in polymer-coated slits: a joint experimental/simulation study, Microfluid. Nanofluid., 2015, 18, 475–482 CrossRef CAS.
- Q. Cao, C. Zuo, L. Li, Y. Ma and N. Li, Electroosmotic flow in a nanofluidic channel coated with neutral polymers, Microfluid. Nanofluid., 2010, 9, 1051–1062 CrossRef.
- Q. Cao, C. Zuo, L. Li, Y. Yang and N. Li, Controlling electroosmotic flow by polymer coating: a dissipative particle dynamics study, Microfluid. Nanofluid., 2011, 10, 977–990 CrossRef.
- Q. Cao, C. Zuo, L. Li and Y. Zhang, Modulation of electroosmotic flow by electric field-responsive polyelectrolyte brushes: a molecular dynamics study, Microfluid. Nanofluid., 2012, 12, 649–655 CrossRef.
- Q. Cao and H. You, Electroosmotic Flow in Mixed Polymer Brush-Grafted Nanochannels, Polymers, 2016, 8, 438 CrossRef PubMed.
- Q. Cao, Anisotropic electrokinetic transport in channels modified with patterned polymer brushes, Soft Matter, 2019, 15, 4132–4145 RSC.
- Q. Cao, C. Zuo, L. Li, Y. Li and Y. Yang, Translocation of nanoparticles through a polymer brush-modified nanochannel, Biomicrofluidics, 2012, 6, 034101 CrossRef PubMed.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, Adam Hilger, Bristol, 1988 Search PubMed.
- I. C. Yeh and M. L. Berkowitz, Ewald summation for systems with slab geometry, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comp. Physiol., 1995, 117, 1–19 CrossRef CAS.
- T. Soddemann, B. Dunweg and K. Kremer, Dissipative particle dynamics: A useful thermostat for equilibrium and nonequilibrium molecular dynamics simulations, Phys. Rev. E, 2003, 68, 046702 CrossRef PubMed.
- Q. Cao, X. Tian and H. You, Electrohydrodynamics in nanochannels coated by mixed polymer brushes: effects of electric field strength and solvent quality, Modell. Simul. Mater. Sci. Eng., 2018, 26, 035003 CrossRef.
- R. M. Jendrejack, D. C. Schwartz, J. J. De Pablo and M. D. Graham, Shear-induced migration in flowing polymer solutions: Simulation of long-chain DNA in microchannels, J. Chem. Phys., 2004, 120, 2513–2529 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |