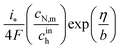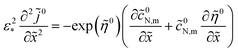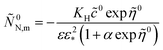DOI:
10.1039/C9RA07794D
(Paper)
RSC Adv., 2019,
9, 38797-38806
Nafion film transport properties in a low-Pt PEM fuel cell: impedance spectroscopy study
Received
25th September 2019
, Accepted 7th November 2019
First published on 27th November 2019
Abstract
Unexpected over-linear transport loss in low-Pt PEM fuel cells has been a subject of numerous studies and discussions in literature. Most of the authors agree that these losses are due to oxygen transport in the Nafion film covering Pt/C agglomerates in the cathode catalyst layer (CCL). We develop a model for PEM fuel cell impedance, which takes into account oxygen transport through the film. The model is fitted to experimental impedance spectra of a low-Pt PEM fuel cell. Fitting gives the film thickness in the range of 10 to 13 nm, and the film transport resistivity decreasing from 1.2 s cm−1 to 0.2 s cm−1 as the cell current density increases from 50 to 800 mA cm−2. Fitting returns low value of the through-plane oxygen diffusivity in the CCL, indicating that the low-Pt electrode is partially flooded.
1 Introduction
High cost of platinum stimulates worldwide interest in lowering Pt loading in polymer electrolyte membrane fuel cell (PEMFC) electrodes. Sluggish kinetics of the oxygen reduction reaction makes PEMFC cathode a largest “consumer” of the precious metal. Due to linear dependence of the cell current density on Pt active surface, one would expect linear decay of cell performance with lowering of Pt loading. However, experiments1,2 have shown unexpected over-linear decrease of the cell current in low-Pt cells. The reason for this effect has been widely discussing in literature. Grezler et al.1 attributed poor low-Pt cell performance to oxygen transport through the Nafion film covering Pt/C agglomerates. However, the measured oxygen transport resistance gave unrealistically high Nafion film thickness of about 35 nm. Owejan et al.3 studied a series of cathodes varying Pt loading while keeping the cathode thickness constant using dilution of Pt/C particles with bare carbon particles. However, the results of their study did not explain the effect of poor low-Pt cathode performance. Weber and Kusoglu4 provided qualitative arguments in favor of increased resistance due to oxygen transport through the Nafion film in low-Pt cells. Choo et al.5 showed that the oxygen transport resistance in a low-Pt cathode can partly be reduced by increasing water partial pressure which indirectly implies that the origin of performance loss is related to oxygen transport in Nafion. Kudo et al.6 measured oxygen transport resistance in a thin Nafion film and demonstrated that the dominant part of the transport resistivity is due to Pt/ionomer interface. More discussions of the problem and references can be found in recent reviews.7,8
An alternative explanation of poor performance of low-Pt cathodes has been suggested by Muzaffar et al.9 They processed numerous experimental polarization curves and showed that the thin, low-Pt electrodes are prone to flooding. Essentially, the effect is due to much lower surface of liquid water in a thin electrode, which strongly reduces its water evaporation ability.10
In this work, we report a single-pore transient model for the CCL performance, which includes oxygen transport through the Nafion film. A static version of the model has been analyzed in ref. 11. In the limit of fast proton and through-plane oxygen transport in the CCL, analytical solution for the CCL performance has been derived. The solution reveals the limiting current density due to oxygen transport through the Nafion film; moreover, this limiting current appears to be proportional to the CCL thickness.11 This result may explain a strong effect of the Nafion film on performance of low-Pt electrodes, as these electrodes are three to four times thinner, than the standard systems.
Below, the transient model is used for construction of numerical impedance model of a cell. Fitting of model impedance to experimental spectra of the low-Pt cell shows that the Nafion film thickness varies in the range of 10 to 13 nm, while the Nafion film transport resistance decreases with the cell current. To the best of our knowledge, this result is a first measurement of Nafion film thickness and transport parameter in an operating low-Pt PEM fuel cell. At low currents, the though-plane oxygen diffusion coefficient in the electrode appears to be close to the oxygen diffusivity in liquid water, indicating that the low-Pt cathode is partially flooded. It is worth noting that with minor modifications, the model below can be used for processing the spectra of electrochemical power sources utilizing thin electrolyte films over active materials (e.g., in supercapacitors,12 or Li-ion batteries13).
2 Experimental
Spatial electrochemical impedance spectroscopy (EIS) recording and measurements of localized current density and voltage have been performed using a segmented cell system and a test station developed at Hawaii Natural Energy Institute. The segmented cell setup consists of the cell hardware, the custom designed current transducer system, the data acquisition device and a single cell test station. Details of the segmented cell system can be found in our previous publications.14,15
The segmented cell hardware design is based on 100 cm2 cell and consists of non-segmented and segmented flow field plates. Both flow field plates have the same ten parallel channel serpentine design and arranged in co-flow configuration. The segmented plate consists of 10 segments with an area of 7.6 cm2 each arranged in two parallel rows from inlet (segment 1) to outlet (segment 10). Each segment has its own current collector and gas diffusion layer (GDL). The segmentation was applied to the cathode.
In this work, Gore catalyst coated membranes (CCM) with the active area of 100 cm2 were used. Catalyst loading was 0.1 mgPt cm−2 for anode and cathode with the catalyst layer thickness of 3–4 μm. The thickness of reinforced membrane varied in the range of 16–18 μm. Sigracet 25BC was used as GDLs for both electrodes. 25BC consists of carbon paper and microporous layer (MPL) with total thickness of 220–235 μm and porosity of 80%. Segmented GDLs were used on the cathode side, whereas a single and uniform GDL was applied at the anode. Teflon gaskets (125 μm) were employed for both electrodes to ensure required compression ratio.
The cell was operated with H2/air gas configuration at a temperature of 80 °C. The anode/cathode conditions were 2/4 stoichiometry, 100%/50% relative humidity and 150/150 kPa backpressure. The EIS curves were recorded under galvanostatic control of the overall cell over the frequency range from 0.05 Hz to 10 kHz with 11 steps per decade. The amplitude of sinusoidal current perturbation signal was chosen to provide a cell voltage response of 10 mV or lower. EIS were recorded simultaneously from 10 segments and from the whole cell. In this work, we have processed only the whole cell spectra using, however, measured values of the local current density in impedance calculations.
3 Model
3.1 Transient performance equations
SEM pictures show that pores in real cathode catalyst layers (CCLs) are formed by numerous agglomerates of Pt/C particles, surrounded by a thin Nafion film.16 An idealized straight single pore penetrating through the whole CCL depth is shown schematically in Fig. 1a. We will model this system by cylindrical pore of the radius Rp with the thin Nafion film separating the void pore volume from the cylindrical Pt wall of the radius Rm (Fig. 1b).
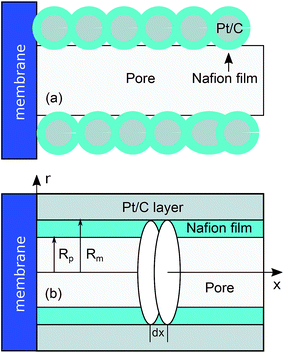 |
| | Fig. 1 (a) Schematic of a single pore in the CCL, (b) the system for modeling. | |
The model below is a transient extension of the static model for polarization curve of the system in Fig. 1b. Due to strong electrochemical coupling of potential, current and oxygen concentration in a fuel cell, we first need a time-dependent oxygen mass transport equation in the pore volume. Consider cylindrical element of the pore/Nafion film volume of the radius Rm and the thickness dx (Fig. 1b). The oxygen diffusive flux along the pore is Dp∂c/∂x, where Dp is the effective oxygen diffusion coefficient, and c is the local oxygen concentration in the pore. The balance of fluxes in the pore element leads to
| |
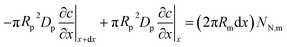 | (1) |
where
| |
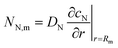 | (2) |
is the radial oxygen flux at the metal/Nafion interface consumed in the ORR,
cN is the dissolved oxygen concentration in the Nafion film and
DN is the effective oxygen diffusivity in the film.
Dividing both sides of eqn (1) by πRp2dx, we come to
| |
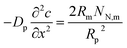 | (3) |
The transient version of
eqn (3) reads
| |
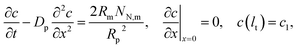 | (4) |
where
c1 is the oxygen concentration at the CCL/GDL interface, and
lt is the CCL thickness (the pore length).
Oxygen transport through the Nafion film along the radial direction is described by
| |
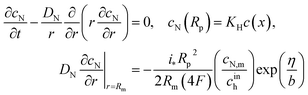 | (5) |
Here,
KH is the dimensionless Henry constant (mol mol
−1) for oxygen solubility in Nafion,
cN,m ≡
cN(
Rm),
cinh is the reference (inlet) oxygen concentration,
b is the ORR Tafel slope, and
i* is the ORR exchange current density. The first boundary condition in
eqn (5) is obvious, while the second means that the oxygen flux at the Nafion/Pt interface equals the flux consumed in the ORR at the Pt surface. This flux is given by the product of the Tafel ORR rate
by the characteristic length
Rp2/(2
Rm). This boundary condition provides correct transition to the limiting case of vanishing Nafion film. Indeed, setting
KH = 1,
Rp =
RM, we may omit
eqn (5), set
cN =
c and substitute the flux on the right side of the second boundary condition in
eqn (5) instead of
NN,m into
eqn (4). This gives
| |
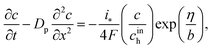 | (6) |
which is a standard macrohomogeneous model (MHM) equation for oxygen transport in the CCL.
The system of eqn (4) and (5) is completed by proton current conservation equation in the Nafion film:
| |
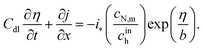 | (7) |
where
Cdl is the double layer capacitance. Using the Ohm's law
| |
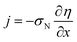 | (8) |
to eliminate
j from
eqn (7), we get
| |
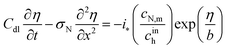 | (9) |
where
σN is the Nafion film proton conductivity.
To simplify calculations we introduce dimensionless variables
| |
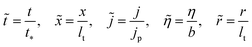 | (10) |
where
| |
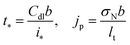 | (11) |
are the characteristic time of double layer charging and current density for proton transport, respectively. With this,
eqn (4),
(5) and
(9) transform to
| |
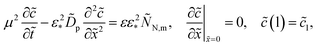 | (12) |
| |
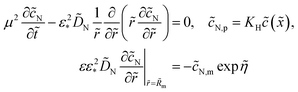 | (13) |
| |
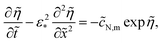 | (14) |
where
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) N,p
N,p ≡
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) N
N(
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) p
p). In
eqn (12), the dimensionless flux
ÑN,m is given by
| |
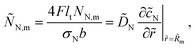 | (15) |
the oxygen diffusion coefficients are normalized according to
| |
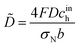 | (16) |
and
ε,
μ and
ε* are the dimensionless parameters
| |
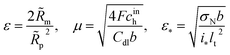 | (17) |
3.2 Static equations
For further references, we need a system of static equations for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0,
0, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 and
0 and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0. Here, the superscript 0 marks the static variables. The procedure of the static equations derivation is described in ref. 11; for completeness, this procedure is reproduced in Appendix. The resulting system of equations for
0. Here, the superscript 0 marks the static variables. The procedure of the static equations derivation is described in ref. 11; for completeness, this procedure is reproduced in Appendix. The resulting system of equations for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0 and
0 and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0 is
0 is| |
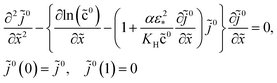 | (18) |
| |
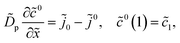 | (19) |
where α > 0 is a constant parameter:| |
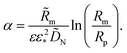 | (20) |
With ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and
) and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) at hand, the static overpotential
) at hand, the static overpotential ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) is obtained from
) is obtained from| |
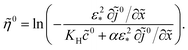 | (21) |
3.3 Equations for the perturbation amplitudes
Now we can excite the system with small-amplitude harmonic perturbations of the form| |
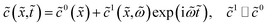 | (22) |
and similar for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) N and
N and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) . Here, the superscript 1 denotes perturbation amplitudes,
. Here, the superscript 1 denotes perturbation amplitudes, ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) = ωt*, and ω is the angular frequency of the AC signal. Substituting these Fourier-transforms into eqn (12)–(14), subtracting the respective static equations, expanding exponent in eqn (14) over small
= ωt*, and ω is the angular frequency of the AC signal. Substituting these Fourier-transforms into eqn (12)–(14), subtracting the respective static equations, expanding exponent in eqn (14) over small ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 1 and neglecting the term with perturbation product, we get a system of linear equations for the perturbation amplitudes in the ω-space:
1 and neglecting the term with perturbation product, we get a system of linear equations for the perturbation amplitudes in the ω-space:| |
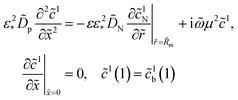 | (23) |
| |
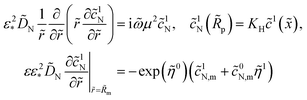 | (24) |
| |
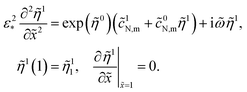 | (25) |
The right boundary condition in eqn (23) describes continuity of the oxygen concentration perturbation at the CCL/GDL interface. Here, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1b is the perturbation amplitude of the oxygen concentration in the GDL, which is determined from the solution of oxygen transport in the GDL (see below).
1b is the perturbation amplitude of the oxygen concentration in the GDL, which is determined from the solution of oxygen transport in the GDL (see below).
Taking into account the second boundary condition to eqn (24), eqn (23) transforms to
| |
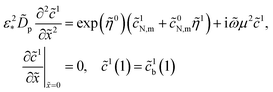 | (26) |
The system (24)–(26) can be simplified. Solving eqn (24) and setting ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) m in the solution we get
m in the solution we get ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1N,m, which appears in eqn (25) and (26):
1N,m, which appears in eqn (25) and (26):
| |
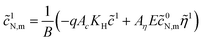 | (27) |
where
| |
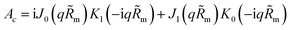 | (28) |
| |
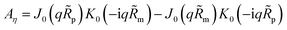 | (29) |
| |
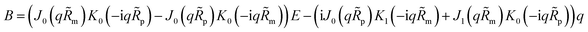 | (30) |
and
| |
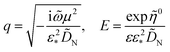 | (31) |
Here,
J0,
J1 are the Bessel functions of the first kind, and
K0,
K1 are the modified Bessel functions of the second kind. Therefore, the problem for perturbation amplitudes is reduced to the system of two
eqn (25) and
(26), with the coefficient functions given by
eqn (49),
(21) and
(27).
3.4 Cathode side impedance
To solve the system (25) and (26) we need the amplitude of oxygen concentration perturbation at the CCL/GDL interface, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1b(1), which appears in the boundary condition to eqn (26). This amplitude is given by17
1b(1), which appears in the boundary condition to eqn (26). This amplitude is given by17| |
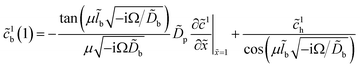 | (32) |
where Ω is the reduced frequency| |
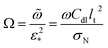 | (33) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) b is the dimensionless oxygen diffusion coefficient in the GDL of a thickness lb:
b is the dimensionless oxygen diffusion coefficient in the GDL of a thickness lb:| |
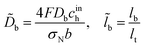 | (34) |
and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h is the amplitude of the oxygen concentration perturbation in channel. The latter value is obtained from the Fourier-transformed oxygen transport equation in the channel (ref. 18, chapter 6)
1h is the amplitude of the oxygen concentration perturbation in channel. The latter value is obtained from the Fourier-transformed oxygen transport equation in the channel (ref. 18, chapter 6)| |
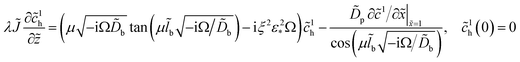 | (35) |
Here, ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = z/L is the dimensionless distance along the channel,
= z/L is the dimensionless distance along the channel, ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) = Jlt/(σNb) is the dimensionless mean current density in the cell,
= Jlt/(σNb) is the dimensionless mean current density in the cell,| |
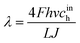 | (36) |
is the oxygen (air) flow stoichiometry, v is the flow velocity in the channel, h is the cathode channel depth, L is the channel length, and ξ is the dimensionless parameter| |
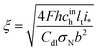 | (37) |
3.5 Impedance calculations and numerical details
The whole problem is, thus, reduced to the core system (25), (26) with the Robin-type right boundary condition for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1, which follows from eqn (32):
1, which follows from eqn (32):| |
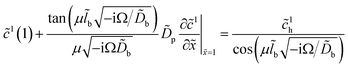 | (38) |
The coefficient functions in eqn (25) and (26) are given by eqn (49), (21) and (27). Eqn (38) contains ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h(
1h(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ), which is determined from eqn (35). Note that iterations are required, as eqn (35) contains the derivative ∂
), which is determined from eqn (35). Note that iterations are required, as eqn (35) contains the derivative ∂![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1/∂
1/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ; for detailed discussion of this model see (ref. 18, chapter 6). Finally, the system impedance is calculated according to
; for detailed discussion of this model see (ref. 18, chapter 6). Finally, the system impedance is calculated according to| |
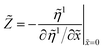 | (39) |
The complex eqn (25), (26) and (35) have been transformed to equivalent system of real equations for the real and imaginary parts of ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 1,
1, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1 and
1 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h. The problem has been solved numerically in Python environment using the boundary-value and Cauchy problem solvers from the Python library SciPy. Following the quasi-2D approach,19 the cell has been separated into N virtual segments; solution to eqn (35) provided the channel value
1h. The problem has been solved numerically in Python environment using the boundary-value and Cauchy problem solvers from the Python library SciPy. Following the quasi-2D approach,19 the cell has been separated into N virtual segments; solution to eqn (35) provided the channel value ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h(
1h(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ) for each segment. The local impedance of the nth segment
) for each segment. The local impedance of the nth segment ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) seg,n has been calculated according to eqn (39); the total cell impedance
seg,n has been calculated according to eqn (39); the total cell impedance ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) cell has been obtained from
cell has been obtained from
| |
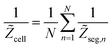 | (40) |
where
N = 10. An important element of cell impedance is “external” capacitance
Cext.
20 Due to impurities, water in the CCL is a weak electrolyte, and
Cext represents seemingly the carbon/water DL capacitance as a separate element connected in parallel to the cell impedance
Zcell,
eqn (40). Incorporation of
Cext greatly improves the quality of spectra fitting in the high-frequency region, and it leads to realistic values of the catalyst layer proton conductivity.
20 The total cell impedance
Ztot has thus been calculated from equation
| |
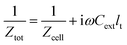 | (41) |
The model impedance has been fitted to the experimental impedance of the whole cell using the least_squares routine and the trf method from the SciPy.21 The merit function to be minimized is
| |
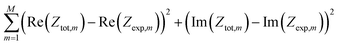 | (42) |
where
Zexp is the measured impedance, and index
m enumerates experimental frequency points. The
trf algorithm implements a constrained method of minimization; description of this method states that “The method … efficiently explore the whole space of variables.”
21 An alternative Levenberg–Marquardt (LM) algorithm works faster; however, being not constrained, in some cases LM returns physically unrealistic parameters.
Eight cell parameters have been declared as the fitting ones: b, Cdl, σN, Dp, Db, DN, lN and Cext. Fitting has been performed assuming that in all the segments these parameters are the same, i.e., possible variation of parameters along the channel coordinate has been neglected.
4 Results and discussion
Fig. 2 shows the model Nafion film impedance ZN calculated for the cell current density of 50 mA cm−2 and the parameters indicated in figure caption and in Table 1. The film impedance has been separated as following: first, the complete cell impedance with the parameters from Table 1 has been calculated. Second, the impedance with KH = 1 and infinite oxygen diffusion coefficient in the Nafion film has been calculated. Subtracting the second impedance from the first one gives the “pure” Nafion film impedance (Fig. 2).
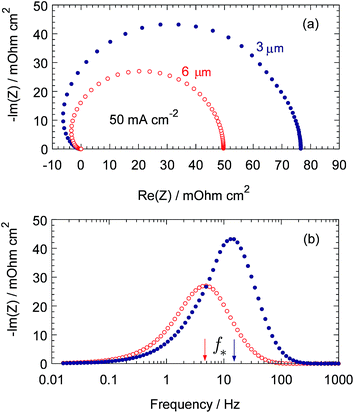 |
| | Fig. 2 (a) Model Nyquist spectrum of the Nafion film impedance, (b) Frequency dependence of the imaginary part of impedance. Parameters for calculations: b = 0.025 V, Cdl = 25 F cm−3, σN = 3 × 10−3 S cm−1, Dp = 5 × 10−6 cm2 s−1, DN = 1 × 10−6 cm2 s−1, Db = 0.18 cm2 s−1. Points: the CCL thickness lt = 3 μm, open circles: lt = 6 μm. | |
Table 1 Cell geometrical and operating parameters. A/C stands for anode/cathode
| Catalyst loading A/C, mg cm−2 |
0.1/0.1 |
| CCL thickness (pore length) lt, cm |
3 × 10−4 (3 μm) |
| Nafion film thickness lN, cm (assumed) |
10−6 (10 nm) |
| GDL thickness lb, cm |
230 × 10−4 (230 μm) |
| Open pore radius Rp, cm (assumed) |
10−5 (100 nm) |
| Channel depth h, cm |
0.15 |
| Channel length L, cm |
57 |
| ORR exchange current density i*, A cm−3 (assumed) |
10−3 |
| Henry's constant for oxygen solubility in water at 80 °C, mol mol−1 |
6.76 × 10−3 |
| Flow stoichiometry A/C |
2/4 |
| Relative humidity A/C |
100%/50% |
| Cathode absolute pressure, kPa |
150 |
| Cell temperature, K |
273 + 80 |
As can be seen, for the CCL thickness of 3 μm, the characteristic (summit) frequency f* of ZN (corresponding to the peak of −Im(ZN)) is about 12 Hz (Fig. 2b), which is a rather surprising result. Indeed, Nafion film may be thought of as a finite-length transport layer connected to the Pt surface. Warburg solution gives for the characteristic angular frequency of this layer ω* = 2.54DN/lN2. With the parameters from Table 1 and Fig. 2 caption we get ω* ≃ 2.54 × 106 s−1, or f* ≃ 600 kHz. This value is nearly two orders of magnitude higher than the maximal frequency usually used in impedance spectroscopy of fuel cells.
In fact, the pore and Nafion film form a unified, two-layer transport system for oxygen molecules. The characteristic frequency of O2 transport in this system is determined by the slowest part of the pathway, which is transport in the void pore. Calculation of ZN with twice larger CCL thickness (6 μm) confirms this conclusion: f* becomes four times lower (≃4 to 5 Hz, Fig. 2b). Both values of f* in Fig. 2b agree well with the Warburg finite-length transport frequency f* = 2.54Dp/(2πlt2) calculated with the pore transport parameters.
This result raises the question on possibility of separation of the oxygen transport impedances in the pore volume and in the Nafion film. Fortunately, though the characteristic frequencies of these processes are the same, their spectral dependencies are different. Fig. 3 shows the frequency dependencies of oxygen transport impedance in the Nafion film (dots) and in the pore volume (open squares). As can be seen, the right “wing” of the pore-transport spectrum decays faster, than the right wing of the Nafion film transport spectrum (Fig. 3). This allows the model to distinguish the two processes.
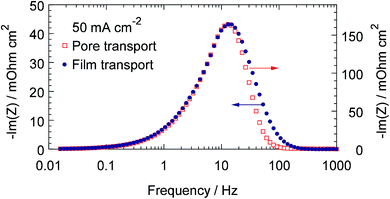 |
| | Fig. 3 Frequency dependencies of the imaginary part of impedance of the oxygen transport in the Nafion film (points) and in the pore volume (open squares). Parameters for calculations are the same as in Fig. 2. | |
Nyquist plots and Im(Z)–frequency dependencies of the fitted model and experimental spectra for the cell currents of 25 and 400 mA cm−2 are shown in Fig. 4 and 5. Though the quality of fitting is not perfect, it is quite acceptable in the range of frequencies above 3 Hz, which is of largest interest in this work. Lower quality of fitting the spectrum for 400 mA cm−2 below 3 Hz (Fig. 5b) is most likely due to non-uniformity of the cell transport parameters along the channel. The small semicircle in the LF region in Fig. 4b represents the impedance due to oxygen transport in the cathode channel.22
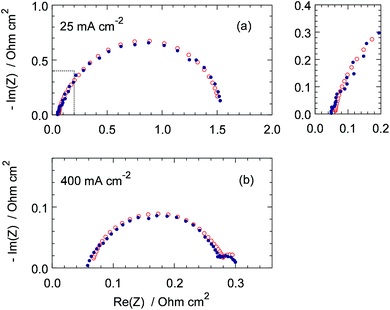 |
| | Fig. 4 Experimental (points) and fitted model (open circles) Nyquist plots of the cell impedance for the indicated current densities. The model and experimental points are shown for the same frequencies. | |
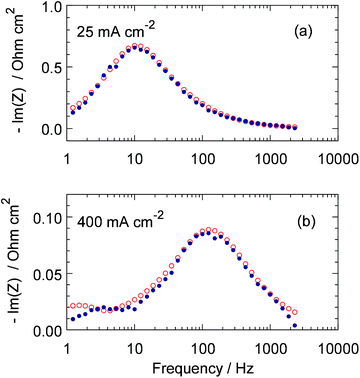 |
| | Fig. 5 Experimental (points) and fitted model (open circles) frequency dependencies of Im(Z) for the same spectra as in Fig. 4. | |
Note that the spectra in Fig. 4 do not exhibit 45° straight line in the high-frequency region (Fig. 4a, right panel). Typical modern PEMFCs exhibit high slope of Nyquist impedance spectra in the HF region; this slope greatly exceeds following from theory 45° (ref. 23). There have been a lot of discussions in literature on the origin of this effect. Recently, we have suggested that the large slope is due to “external” capacitance Cext connected in parallel to our model impedance (see also discussion above).20
The parameters resulted from fitting are shown in Fig. 6. Of largest interest is the oxygen diffusion coefficients in the Nafion film DN (Fig. 6a) and the Nafion film thickness (Fig. 6b). As can be seen, DN varies in the range 1 × 10−6 cm2 s−1 to ≃6 × 10−6 cm2 s−1 (Fig. 6a). The lowest value of DN agrees well with the oxygen diffusivity in the bulk Nafion 117, which is 0.96 × 10−6 cm2 s−1 (ref. 24). The reason for DN variation with the cell current is not clear yet; perhaps, this variation is due to change of the film surface properties.6 On the other hand, the oxygen transport model above is essentially a two-scale model, with the large-scale through-plane oxygen transport modeled as a transport in a straight pore, and the small-scale transport to the Pt/C surface perpendicular to the pore. In Fig. 1, the small-scale transport path is represented by the Nafion film; however, part of this path could include transport through the primary nanopores. The transport properties of these pores could vary with the cell current, which may contribute to the variation of effective DN with current density.
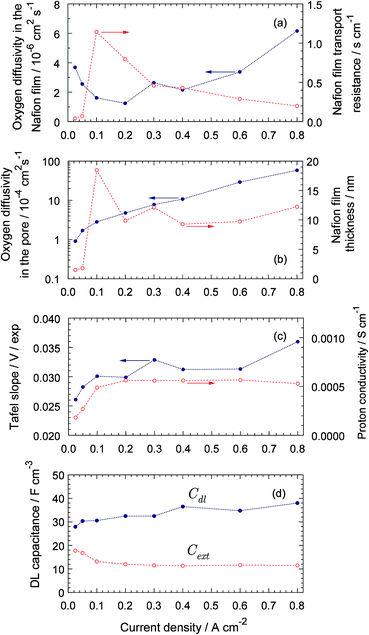 |
| | Fig. 6 Cell parameters resulted from spectra fitting vs. cell current density. (a) Oxygen diffusivity in the Nafion film and the film transport resistivity. (b) Oxygen diffusivity in the pore volume and the Nafion film thickness, (c) ORR Tafel slope per exponential basis and Nafion film proton conductivity, (d) Double layer capacitance Cdl and “external” capacitance Cext. | |
Excluding the low-current points, the Nafion film thickness varies in the range of 10 to 13 nm without any distinct correlation with the current density (Fig. 6b); this thickness agrees well with the literature data.25,26 The points for 25, 50 and 100 mA cm−2 on this plot could be not accurate, as at small currents, the contribution of oxygen transport in Nafion film to Ztot is small and the model may not be able to capture it. The transport resistivity of the film RN = lN/DN decays from 0.8 s cm−1 at 200 mA cm−2 down to 0.2 s cm−1 at 800 mA cm−2 (Fig. 6a).
The ORR Tafel slope exhibits variation in the range of 26 to 35 mV per exponential basis, around the average value of ≃ 30 mV (Fig. 6c), which translates to typical for Pt/C systems value of 70 mV per decade.27 The Pt/Nafion double layer capacitance grows from 30 to 40 F cm−3 (Fig. 6d). This growth seemingly is due to cleaning of Pt surface from oxides at lower cell potentials.28
The CCL proton conductivity is nearly constant at 6 × 10−4 S cm−1 (Fig. 6c). The oxygen diffusion coefficient in the pore volume increases by two orders of magnitude, from 10−4 to ≃ 10−2 cm2 s−1 (Fig. 6b). The origin of this growth yet is unknown; possible explanation would be formation of a pressure gradient pushing liquid water out of the CCL. The low-current value of Dp suggests that the low-Pt CCL is partially flooded. Indeed, the oxygen diffusion coefficient in pure water at 80 °C is 0.53 × 10−4 cm2 s−1 (ref. 29) and the low-current part of the curve in Fig. 6d is close to this value.
Table 2 shows the contributions of various transport processes to the total differential resistivity of the cell at the current density of 200 mA cm−2. As can be seen, already at quite moderate current density, among all the oxygen transport processes on the cathode side, Nafion film gives the largest contribution to the voltage loss.
Table 2 Oxygen transport resistivities in the low-Pt PEMFC resulted from fitting the spectrum for 200 mA cm−2
| Oxygen transport |
Differential resistivity, mΩ cm2 |
| In the Nafion film |
48.7 |
| In the GDL |
21.9 |
| In the channel |
11.9 |
| In the void pore |
7.07 |
5 Conclusions
We report a model for PEM fuel cell impedance taking into account oxygen transport through the Nafion film covering Pt/C agglomerates. The cathode catalyst layer is modeled by a cylindrical straight pore penetrating through the CCL thickness. The pore is separated from a coaxial Pt/C cylinder by the thin Nafion film. The impedance model is based on the oxygen diffusion equations along the void pore and through the Nafion film, coupled by the Tafel equation for the ORR rate at the film/metal interface. In the limit of zero Nafion film thickness the model reduces to the standard macrohomogeneous model for the CCL performance. The numerical impedance model is fitted to experimental impedance spectra of a low-Pt PEM fuel cell with the cathode Pt loading of 0.1 mgPt cm−2. Fitting gives the oxygen diffusion coefficient in the film increasing from 1.5 × 10−6 to 6 × 10−6 cm2 s−1 as the cell current increases from 200 to 800 mA cm−2. The low-current value of 1.5 × 10−6 cm2 s−1 by the order of magnitude agrees well with the oxygen diffusivity in the bulk Nafion 117. The Nafion film thickness varies in the range of 10 to 13 nm showing no correlation with the cell current. Overall, the oxygen transport resistivity of the film decreases from ≃ 1 to 0.2 s cm−1 with the growth of the cell current density. Last but not least, fitting returns low value of the through-plane oxygen diffusivity in the CCL, which indicates that the low-Pt electrode is partly flooded.
Appendix
Derivation of static equations
Th system of equations for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0,
0, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N and
0N and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 is obtained from eqn (12)–(14) by chalking out the time derivatives:
0 is obtained from eqn (12)–(14) by chalking out the time derivatives:| |
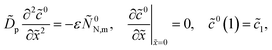 | (43) |
| |
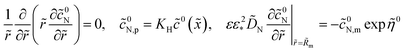 | (44) |
| |
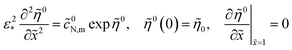 | (45) |
where the superscript 0 marks the steady-state variables.
Unfortunately, the total static overpotential ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 appearing in eqn (45) is unknown; calculation of this parameters requires iterations. The impedance measurements are usually done at constant current density in the cell
0 appearing in eqn (45) is unknown; calculation of this parameters requires iterations. The impedance measurements are usually done at constant current density in the cell ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0, and to avoid iterations, the static electric problem has to be reformulated in terms of the proton current density
0, and to avoid iterations, the static electric problem has to be reformulated in terms of the proton current density ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ). Consider first the static version of eqn (7); in the dimensionless variables this equation reads
). Consider first the static version of eqn (7); in the dimensionless variables this equation reads
| |
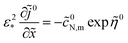 | (46) |
Here,
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N,m
0N,m depends parametrically of
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif)
(see below).
To derive equation for ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0 equivalent to eqn (45), we differentiate eqn (46) over
0 equivalent to eqn (45), we differentiate eqn (46) over ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , which gives
, which gives
Substituting here exp
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0
0 from
eqn (46) and using the Ohm's law
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0
0 = −∂
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0
0/∂
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif)
, after simple algebra we come to
| |
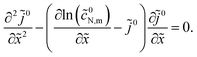 | (47) |
To find
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N,m
0N,m we solve
eqn (44):
| |
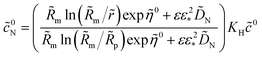 | (48) |
Setting
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif)
=
![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) m
m in this solution, we obtain
| |
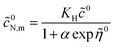 | (49) |
where
α is given by
eqn (20). With this,
eqn (46) takes the form
| |
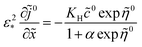 | (50) |
Solving
eqn (50) for exp
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0
0 we find
| |
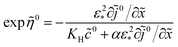 | (51) |
Calculating ∂![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(
ln(![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N,m)/∂
0N,m)/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) with eqn (49), we get
with eqn (49), we get
| |
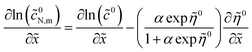 | (52) |
Taking into account the Ohm's law ∂
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0
0/∂
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif)
= −
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0
0 and
eqn (51), we get
| |
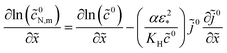 | (53) |
Using
eqn (53) in
eqn (47) we finally get a problem for
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0
0,
eqn (18). A great advantage of the problem
(18) is that the boundary conditions are known and iterations are not required.
To find equation for the static oxygen concentration in the pore volume ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0, we note that eqn (48) allows us to calculate the flux Ñ0N,m, which appears in eqn (43). Calculating derivative ∂
0, we note that eqn (48) allows us to calculate the flux Ñ0N,m, which appears in eqn (43). Calculating derivative ∂![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N/∂
0N/∂![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) , multiplying the result by
, multiplying the result by ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) N and setting
N and setting ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) m, we get
m, we get
Using here
eqn (51), we come to
| |
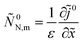 | (54) |
With this,
eqn (43) transforms to
| |
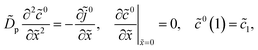 | (55) |
Integrating this equation once, we come to
eqn (19), which is a standard MHM equation for oxygen transport in the CCL.
30
Thus, the static problem is reduced to the system of eqn (18) and (19). With ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and
) and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), the static overpotential
), the static overpotential ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 is obtained from eqn (51), which leads to eqn (21). If necessary, the radial shape of dissolved oxygen concentration
0 is obtained from eqn (51), which leads to eqn (21). If necessary, the radial shape of dissolved oxygen concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N can be calculated from eqn (48).
0N can be calculated from eqn (48).
Conflicts of interest
There are no conflicts to declare.
Nomenclature
 | Marks dimensionless variables |
| b | ORR Tafel slope, V |
| Cdl | Double layer volumetric capacitance, F cm−3 |
| Cext | “External” capacitance (see text), F cm−3 |
| c | Oxygen molar concentration in the pore, mol cm−3 |
| cb | Oxygen molar concentration in the GDL, mol cm−3 |
| ch | Oxygen molar concentration in the channel, mol cm−3 |
| cN | Oxygen molar concentration in the Nafion film, mol cm−3 |
| cinh | Reference (inlet) oxygen concentration, mol cm−3 |
| Dp | Oxygen diffusion coefficient in the pore, cm2 s−1 |
| DN | Oxygen diffusion coefficient in the Nafion film, cm2 s−1 |
| F | Faraday constant, C mol−1 |
| i* | ORR volumetric exchange current density, A cm−3 |
| i | Imaginary unit |
| j | Local proton current density along the pore, A cm−2 |
| j0 | Cell current density, A cm−2 |
| KH | Henry's constant for oxygen solubility in water, mol mol−1 |
| lt | Pore length (CCL thickness), cm |
| lN | Nafion film thickness, cm |
| NN | Oxygen flux in the Nafion film, mol cm−2 s−1 |
| Rm | Radius of a Pt/C tube, cm |
| Rp | Pore radius, cm |
| r | Radial coordinate, cm |
| v | Flow velocity in the cathode channel, cm s−1 |
| x | Coordinate along the pore, cm |
| z | Coordinate along the channel, cm |
Subscripts
| 0 | Membrane/CCL interface |
| 1 | CCL/GDL interface |
| t | Catalyst layer |
Superscripts
| 0 | Steady-state value |
| 1 | Small-amplitude perturbation |
Greek
| α | Dimensionless parameter, eqn (20) |
| ε* | Dimensionless Newman's reaction penetration depth, eqn (17) |
| ε | Dimensionless parameter, eqn (17) |
| η | ORR overpotential, positive by convention, V |
| λ | Air flow stoichiometry, eqn (36) |
| ξ | Dimensionless parameter, eqn (37) |
| σN | Nafion film proton conductivity, S cm−1 |
| Ω | Dimensionless reduced angular frequency of the AC signal, eqn (33) |
| ω | Angular frequency of the AC signal, s−1 |
Acknowledgements
T. Reshetenko gratefully acknowledges funding from US Office of Naval Research (N00014-18-1-2127) and US Army Research Office (W911NF-15-1-0188). The authors are thankful to Günter Randolf and Jack Huizingh for valuable help with the system operation, and to the Hawaiian Electric Company for ongoing support of the Hawaii Sustainable Energy Research Facility.
Notes and references
- T. Grezler, D. Gaulk and P. Sinha, J. Electrochem. Soc., 2012, 159, F831–F840 CrossRef.
- A. Kongkanand and M. F. Mathias, J. Phys. Chem. Lett., 2016, 7, 1127–1137 CrossRef CAS PubMed.
- J. P. Owejan, J. E. Owejan and W. Gu, J. Electrochem. Soc., 2013, 160, F824–F833 CrossRef CAS.
- A. Z. Weber and A. Kusoglu, J. Mater. Chem. A, 2014, 2, 17207–17211 RSC.
- M.-J. Choo, K.-H. Oh, J.-K. Park and H.-T. Kim, ChemElectroChem, 2015, 2, 382–388 CrossRef CAS.
- K. Kudo, R. Jinnouchi and Y. Morimoto, Electrochim. Acta, 2016, 209, 682–690 CrossRef CAS.
- A. Kongkanand, W. Gu and M. Mathias, Fuel Cells and Hydrogen production, Springer, New–York, 2018, pp. 323–342 Search PubMed.
- A. Kusoglu, Fuel Cells and Hydrogen production, Springer, New York, 2018, pp. 417–438 Search PubMed.
- T. Muzaffar, T. Kadyk and M. Eikerling, Sustainable Energy Fuels, 2018, 2, 1189–1196 RSC.
- M. Eikerling, J. Electrochem. Soc., 2006, 153, E58–E70 CrossRef CAS.
- A. Kulikovsky, Electrochem. Commun., 2019, 103, 61–65 CrossRef CAS.
- W. Wei, W. Ye, J. Wang, C. Huang, J.-B. Xiong, H. Qiao, S. Cui, W. Chen, L. Mi and P. Yan, ACS Appl. Mater. Interfaces, 2019, 11, 32269–32281 CrossRef CAS PubMed.
- M. D. Murbach and D. T. Schwartz, J. Electrochem. Soc., 2018, 165, A297–A304 CrossRef CAS.
- T. V. Reshetenko, G. Bender, K. Bethune and R. Rocheleau, Electrochim. Acta, 2011, 56, 8700–8710 CrossRef CAS.
- T. Reshetenko and A. Kulikovsky, J. Electrochem. Soc., 2017, 164, F1633–F1640 CrossRef CAS.
- P. Dobson, C. Lei, T. Navessin and M. Secanell, J. Electrochem. Soc., 2012, 159, B514–B523 CrossRef CAS.
- T. Reshetenko and A. Kulikovsky, J. Electrochem. Soc., 2016, 163, F1100–F1106 CrossRef CAS.
- A. Kulikovsky, Analytical Models for PEM Fuel Cell Impedance, Self-publishing, Eisma, 2018, http://www.amazon.com/Andrei-Kulikovsky/e/B00KBW7KVY Search PubMed.
- T. Reshetenko and A. Kulikovsky, J. Electrochem. Soc., 2018, 165, F291–F296 CrossRef CAS.
- T. Reshetenko and A. Kulikovsky, J. Electrochem. Soc., 2019 DOI:10.1149/2.1201915.jes.
- scipy.optimize.least_squares, 2018, https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.least_squares.html Search PubMed.
- A. Kulikovsky and O. Shamardina, J. Electrochem. Soc., 2015, 162, F1068–F1077 CrossRef CAS.
- A. A. Kulikovsky and M. Eikerling, J. Electroanal. Chem., 2013, 691, 13–17 CrossRef CAS.
- V. A. Sethuraman, S. Khan, J. S. Jur, A. T. Haug and J. Weidner, Electrochim. Acta, 2009, 54, 6850–6860 CrossRef CAS.
- S. Holdcroft, Chem. Mater., 2014, 26, 383–393 CrossRef.
- M. Lopez-Haro, L. Guétaz, T. Printemps, A. Morin, S. Escribano, P.-H. Jouneau, P. Bayle-Guillemaud, F. Chandezon and G. Gebel, Nat. Commun., 2014, 5, 5229 CrossRef CAS PubMed.
- Y. Liu, C. Ji, W. Gu, J. Jorne and H. A. Gasteiger, J. Electrochem. Soc., 2011, 158, B614–B621 CrossRef CAS.
- Y. Liu, M. Mathias and J. Zhang, Electrochem. Solid-State Lett., 2010, 13, B1–B3 CrossRef CAS.
- P. Han and D. M. Bartels, J. Chem. Phys., 1996, 100, 5597–5602 CrossRef CAS.
- M. Eikerling and A. A. Kornyshev, J. Electroanal. Chem., 1998, 453, 89–106 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a and
Andrei Kulikovsky
a and
Andrei Kulikovsky *b
*b
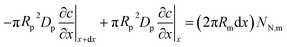
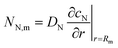
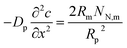
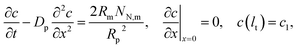
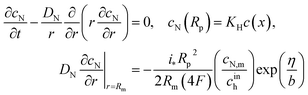
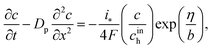
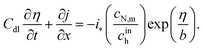
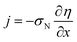
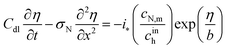
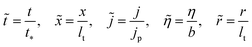
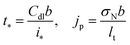
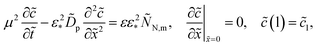
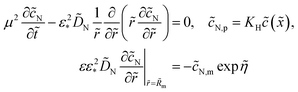
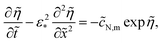
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) N,p ≡
N,p ≡ ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) N(
N(![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) p). In eqn (12), the dimensionless flux ÑN,m is given by
p). In eqn (12), the dimensionless flux ÑN,m is given by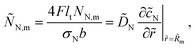
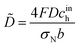
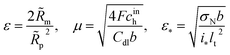
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0,
0, ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 and
0 and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0. Here, the superscript 0 marks the static variables. The procedure of the static equations derivation is described in ref. 11; for completeness, this procedure is reproduced in Appendix. The resulting system of equations for
0. Here, the superscript 0 marks the static variables. The procedure of the static equations derivation is described in ref. 11; for completeness, this procedure is reproduced in Appendix. The resulting system of equations for ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0 and
0 and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0 is
0 is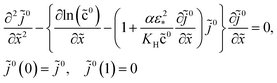
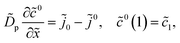
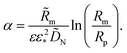
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and
) and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) at hand, the static overpotential
) at hand, the static overpotential ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) is obtained from
) is obtained from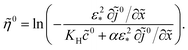
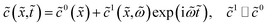
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) N and
N and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) . Here, the superscript 1 denotes perturbation amplitudes,
. Here, the superscript 1 denotes perturbation amplitudes, ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) = ωt*, and ω is the angular frequency of the AC signal. Substituting these Fourier-transforms into eqn (12)–(14), subtracting the respective static equations, expanding exponent in eqn (14) over small
= ωt*, and ω is the angular frequency of the AC signal. Substituting these Fourier-transforms into eqn (12)–(14), subtracting the respective static equations, expanding exponent in eqn (14) over small ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 1 and neglecting the term with perturbation product, we get a system of linear equations for the perturbation amplitudes in the ω-space:
1 and neglecting the term with perturbation product, we get a system of linear equations for the perturbation amplitudes in the ω-space: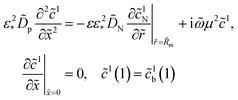
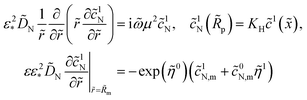
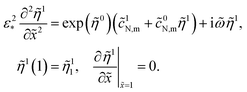
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1b is the perturbation amplitude of the oxygen concentration in the GDL, which is determined from the solution of oxygen transport in the GDL (see below).
1b is the perturbation amplitude of the oxygen concentration in the GDL, which is determined from the solution of oxygen transport in the GDL (see below).
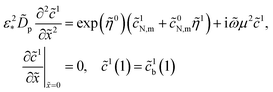
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) m in the solution we get
m in the solution we get ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1N,m, which appears in eqn (25) and (26):
1N,m, which appears in eqn (25) and (26):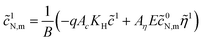
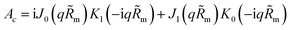
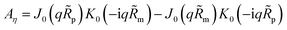
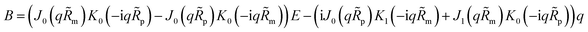
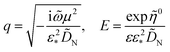
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1b(1), which appears in the boundary condition to eqn (26). This amplitude is given by17
1b(1), which appears in the boundary condition to eqn (26). This amplitude is given by17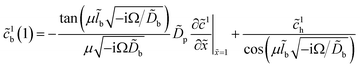
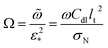
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) b is the dimensionless oxygen diffusion coefficient in the GDL of a thickness lb:
b is the dimensionless oxygen diffusion coefficient in the GDL of a thickness lb: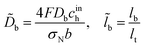
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h is the amplitude of the oxygen concentration perturbation in channel. The latter value is obtained from the Fourier-transformed oxygen transport equation in the channel (ref. 18, chapter 6)
1h is the amplitude of the oxygen concentration perturbation in channel. The latter value is obtained from the Fourier-transformed oxygen transport equation in the channel (ref. 18, chapter 6)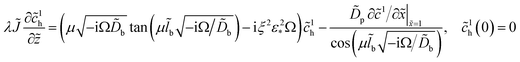
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = z/L is the dimensionless distance along the channel,
= z/L is the dimensionless distance along the channel, ![[J with combining tilde]](https://www.rsc.org/images/entities/i_char_004a_0303.gif) = Jlt/(σNb) is the dimensionless mean current density in the cell,
= Jlt/(σNb) is the dimensionless mean current density in the cell,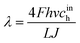
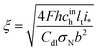
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1, which follows from eqn (32):
1, which follows from eqn (32):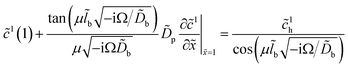
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h(
1h(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ), which is determined from eqn (35). Note that iterations are required, as eqn (35) contains the derivative ∂
), which is determined from eqn (35). Note that iterations are required, as eqn (35) contains the derivative ∂![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1/∂
1/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ; for detailed discussion of this model see (ref. 18, chapter 6). Finally, the system impedance is calculated according to
; for detailed discussion of this model see (ref. 18, chapter 6). Finally, the system impedance is calculated according to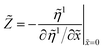
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 1,
1, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1 and
1 and ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h. The problem has been solved numerically in Python environment using the boundary-value and Cauchy problem solvers from the Python library SciPy. Following the quasi-2D approach,19 the cell has been separated into N virtual segments; solution to eqn (35) provided the channel value
1h. The problem has been solved numerically in Python environment using the boundary-value and Cauchy problem solvers from the Python library SciPy. Following the quasi-2D approach,19 the cell has been separated into N virtual segments; solution to eqn (35) provided the channel value ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1h(
1h(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) ) for each segment. The local impedance of the nth segment
) for each segment. The local impedance of the nth segment ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) seg,n has been calculated according to eqn (39); the total cell impedance
seg,n has been calculated according to eqn (39); the total cell impedance ![[Z with combining tilde]](https://www.rsc.org/images/entities/i_char_005a_0303.gif) cell has been obtained from
cell has been obtained from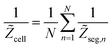
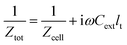
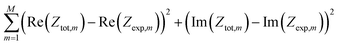


![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0,
0, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N and
0N and ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 is obtained from eqn (12)–(14) by chalking out the time derivatives:
0 is obtained from eqn (12)–(14) by chalking out the time derivatives: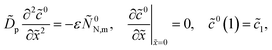
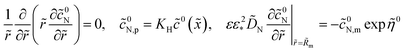
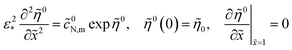
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 appearing in eqn (45) is unknown; calculation of this parameters requires iterations. The impedance measurements are usually done at constant current density in the cell
0 appearing in eqn (45) is unknown; calculation of this parameters requires iterations. The impedance measurements are usually done at constant current density in the cell ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0, and to avoid iterations, the static electric problem has to be reformulated in terms of the proton current density
0, and to avoid iterations, the static electric problem has to be reformulated in terms of the proton current density ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) (
(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ). Consider first the static version of eqn (7); in the dimensionless variables this equation reads
). Consider first the static version of eqn (7); in the dimensionless variables this equation reads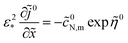
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N,m depends parametrically of
0N,m depends parametrically of ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) (see below).
(see below).
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0 equivalent to eqn (45), we differentiate eqn (46) over
0 equivalent to eqn (45), we differentiate eqn (46) over ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , which gives
, which gives![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 from eqn (46) and using the Ohm's law
0 from eqn (46) and using the Ohm's law ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0 = −∂
0 = −∂![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0/∂
0/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) , after simple algebra we come to
, after simple algebra we come to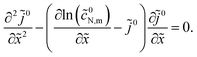
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N,m we solve eqn (44):
0N,m we solve eqn (44):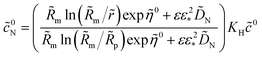
![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) m in this solution, we obtain
m in this solution, we obtain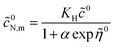
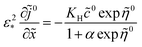
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 we find
0 we find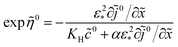
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(
ln(![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N,m)/∂
0N,m)/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) with eqn (49), we get
with eqn (49), we get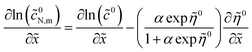
![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0/∂
0/∂![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = −
= −![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0 and eqn (51), we get
0 and eqn (51), we get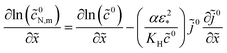
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0, eqn (18). A great advantage of the problem (18) is that the boundary conditions are known and iterations are not required.
0, eqn (18). A great advantage of the problem (18) is that the boundary conditions are known and iterations are not required.
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0, we note that eqn (48) allows us to calculate the flux Ñ0N,m, which appears in eqn (43). Calculating derivative ∂
0, we note that eqn (48) allows us to calculate the flux Ñ0N,m, which appears in eqn (43). Calculating derivative ∂![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N/∂
0N/∂![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) , multiplying the result by
, multiplying the result by ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) N and setting
N and setting ![[r with combining tilde]](https://www.rsc.org/images/entities/i_char_0072_0303.gif) =
= ![[R with combining tilde]](https://www.rsc.org/images/entities/i_char_0052_0303.gif) m, we get
m, we get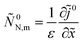
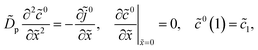
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ) and
) and ![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif) 0(
0(![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) ), the static overpotential
), the static overpotential ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) 0 is obtained from eqn (51), which leads to eqn (21). If necessary, the radial shape of dissolved oxygen concentration
0 is obtained from eqn (51), which leads to eqn (21). If necessary, the radial shape of dissolved oxygen concentration ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 0N can be calculated from eqn (48).
0N can be calculated from eqn (48).