Thermal and structural properties, and molecular dynamics in organic–inorganic hybrid perovskite (C₂H₅NH₃)₂ZnCl₄

Abstract

The thermal and structural properties and molecular dynamics of layered perovskite-type (C₂H₅NH₃)₂ZnCl₄ are investigated by differential scanning calorimetry, thermogravimetric analysis, and magic angle spinning nuclear magnetic resonance spectroscopy. The thermal properties and phase transitions are studied. Additionally, the Bloembergen–Purcell–Pound (BPP) curves for the ¹H spin–lattice relaxation time T_1ρ in the C₂H₅NH₃ cation and for the ¹³C T_1ρ in C₂H₅ are shown to have minima as a function of inverse temperature. This observation implies that these curves represent the rotational motions of ¹H and ¹³C in the C₂H₅NH₃ cation. The activation energies for ¹H and ¹³C in the C₂H₅NH₃ cation are obtained; the molecular motion of ¹H is enhanced at the C-end and N-end of the organic cation, and that at the carbons of the main chain is not as free as that for protons at the C-end and N-end.

---

I. Introduction

Hybrid organic–inorganic compounds allow for the possibility of combining the properties of organic and inorganic materials at the molecular level.^1–4 This class of hybrid materials is very broad and offers a wide set of different structures, properties, and potential applications.^5–12 A new type of layered perovskite multiferroic, (C₂H₅NH₃)₂CuCl₄, as a metal organic compound was found by Kundys et al.⁶ Multiferroics refer to materials that simultaneously have two or more of the following properties: spontaneous ferroelectricity, ferromagnetism, or ferroelasticity.¹³ (C₂H₅NH₃)₂CuCl₄ crystallizes in a layered perovskite structure consisting of nearly isolated layers of corner-sharing ZnCl₆ octahedra, and the interlayer distance is approximately 10 Å, where the layers are separated by two layers of ethylammonium cations (C₂H₅NH₃)⁺.¹⁴ The NH₃ polar heads of the chains are linked to the chlorine ions of the ZnCl₆ octahedra by three hydrogen bonds N–H⋯Cl. The organic chains are joined by weak hydrogen bonds from the NH₃ groups to the Cl ions. One interesting series is the metal–organic hybrids of chemical formula such as (C₂H₅NH₃)₂ZnCl₄ with perovskite-type transition metal salts. A study of the electrical, dielectric, and optical properties of (C₂H₅NH₃)₂ZnCl₄ was reported by Mohamed et al.¹⁵ They found that (C₂H₅NH₃)₂ZnCl₄ is a layered perovskite-type compound that undergoes five phase transitions at 231 K, 234 K, 237 K, 247 K, and 312 K as determined by differential scanning calorimetry (DSC).¹⁵ The intensities of the endotherm peaks at 231 K, 237 K, and 312 K are very weak and perhaps correspond to second-order transformations. Tello¹⁶ reported a ferroelastoelectric phase transition at 243.3 K by optical and X-ray measurements with a group theoretical analysis. The phase transitions in this crystal are mostly connected to changes in the arrangement of the alkylammonium chains. The crystal structure of (C₂H₅NH₃)₂ZnCl₄ at room temperature is orthorhombic. Fig. 1 reveals that its atomic arrangement can be described by an alternation of the organic and inorganic entities in the bc plane. This compound is characterized by two simple hydrogen bonds N–H⋯Cl linking the organic (C₂H₅NH₃)⁺ cation to the (ZnCl₄)²⁻ tetrahedral anions.¹⁷ This compound is crystallized in the orthorhombic system with a space group of Pna2₁ at room temperature, and the lattice parameters are a = 10.043 Å, b = 17.594 Å, c = 7.397 Å, and molecules per unit cell, Z = 4.¹⁸ The Zn atoms in (C₂H₅NH₃)₂ZnCl₄ are tetrahedrally coordinated, while the Cu atoms in (C₂H₅NH₃)₂CuCl₄ are octahedrally coordinated. Although the chemical composition of the Zn and Cu compounds is similar, the coordination of the metal atom is different.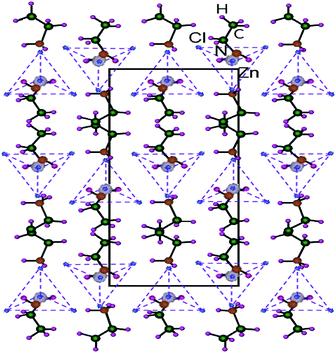

Fig. 1 Orthorhombic structure of a (C₂H₅NH₃)₂ZnCl₄ crystal for bc-plane at room temperature.¹⁸

The structural geometry and molecular dynamics of the organic molecules within the layered hybrid structure are important for determining the influence of temperature on the evolution of structural phase transitions in the perovskite structure. Physical properties in particular depend on the characteristics of the metallic anion and the organic cation. Until now, the physical properties of (C₂H₅NH₃)₂ZnCl₄ have been reported by a few research groups, whereas the thermal properties and molecular dynamics have not been studied.

The goal of this work is to analyze the crystal growth, thermodynamic properties, and structural dynamics of a (C₂H₅NH₃)₂ZnCl₄ single crystal. The analysis is based on DSC, thermogravimetric analysis (TGA), and magic angle spinning nuclear magnetic resonance (MAS NMR). We measured the line widths, chemical shifts, and spin–lattice relaxation times (T_1ρ) in the rotating frame using ¹H MAS NMR, ¹³C cross-polarization (CP)/MAS NMR, and ¹⁴N static NMR as a function of temperature. The molecular dynamics of the (C₂H₅NH₃) cation were investigated near the phase transition temperatures, and we discussed the activation energies for the molecular dynamics of C₂H₅ and NH₃ in the (C₂H₅NH₃)⁺ cation. Furthermore, we have compared the molecular motions of (C₂H₅NH₃)₂ZnCl₄ obtained here and those of the previously reported (C₂H₅NH₃)₂CuCl₄.

II. Experimental methods

Crystals of (C₂H₅NH₃)₂ZnCl₄ were prepared by dissolving stoichiometric amounts of the starting materials, commercial CH₃CH₂NH₂·HCl (ethylamine hydrochloride, Aldrich 98%) and ZnCl₂, in water. Single crystals were grown by a slow evaporation of the aqueous solution at room temperature. The obtained crystals were colorless and hexagonal in shape.

The thermal stability was checked by means of TGA and optical polarizing microscopy. The TGA curve at a heating rate of 10 °C min⁻¹ was measured under N₂ atmosphere, and the mass of the powdered sample used in the TGA experiment was 6.63 mg. The phase transitions were performed by DSC in the temperature range of 300–670 K with 10 °C min⁻¹ heating rates.

The line widths, chemical shifts, and T_1ρ values for (C₂H₅NH₃)₂ZnCl₄ were obtained by ¹H MAS NMR and ¹³C CP/MAS NMR at Larmor frequencies of ω₀/2π = 400.13 and 100.62 MHz, respectively, using a Bruker 400 MHz NMR spectrometer at the Korea Basic Science Institute, Western Seoul Center. Powdered samples were placed within a 4 mm CP/MAS probe, and the MAS rate for ¹H and ¹³C measurements, to minimize spinning sideband overlap, was set to 10 kHz. The ¹H T_1ρ values were determined using a π/2 − t sequence by varying the duration of spin-locking pulses. ¹³C T_1ρ values were measured by varying the duration of the spin-locking pulse applied after the CP preparation period. The width of the π/2 pulse used for measuring T_1ρ for ¹H and ¹³C was 3.7 μs, with the spin-locking field set at 67.56 kHz. The chemical shifts and T_1ρ were measured over a temperature range of 180–430 K.

In addition, the ¹⁴N NMR spectra of the (C₂H₅NH₃)₂ZnCl₄ single crystals in the laboratory frame were measured using a Unity INOVA 600 NMR spectrometer at the same facility. The static magnetic field was 14.1 T and the Larmor frequency was set to ω₀/2π = 43.345 MHz. The ¹⁴N NMR experiments were conducted using a solid-echo (π/2–t–π/2–t) pulse sequence. The width of the π/2 pulse was 4 μs.

III. Experimental results

Fig. 2 shows the simultaneous TGA and DSC curves for the (C₂H₅NH₃)₂ZnCl₄ single crystal. A drastic weight loss onset occurred at 460 K (=T_d), which is attributed to the beginning of the evaporation of C₂H₅NH₂ and HCl due to partial thermal decomposition. The sample lost weight sharply between 500 K and 670 K, with a corresponding weight loss of 48%, which agrees almost exactly with the content of the organic component (45.53%) of C₂H₅NH₃Cl in (C₂H₅NH₃)₂ZnCl₄. DSC studies on the perovskite were undertaken to demonstrate structural transitions below the melting/decomposition point. In the DSC curve, the endotherm peaks at 320 K, 376 K, and 438 K correspond to the phase transitions. The (C₂H₅NH₃)₂ZnCl₄ undergoes phase transitions at 438 K, 376 K, and 320 K, which are denoted as the T_C1, T_C2, and T_C3 with decreasing temperature. As the temperature increases, the crystal is constantly colorless and transparent (300 K, 400 K, 450 K), and then it starts melting near 460 K. The crystal is melted near 475 K, as shown in the inset in Fig. 2.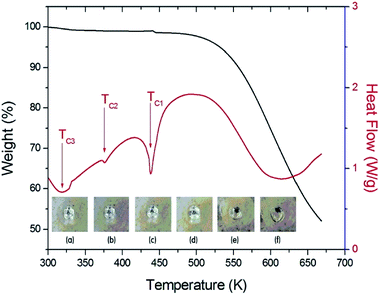

Fig. 2 TGA and DSC curves of (C₂H₅NH₃)₂ZnCl₄ crystal (inset: changes of a (C₂H₅NH₃)₂ZnCl₄ crystal according to the temperature: (a) 300 K, (b) 400 K, (c) 450 K, (d) 460 K, (e) 470 K, and (f) 475 K).

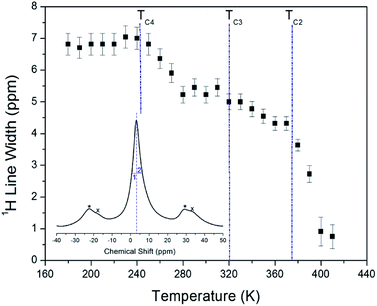
The ¹H NMR spectra at a frequency of 400.13 MHz were obtained by MAS NMR. The ¹H spectrum recorded at 300 K is shown in the inset in Fig. 3. The observed resonance line has an asymmetric shape, as the full-width at half-maximum (FWHM) values on the left side (symbol 1) and right side (symbol 2) are not the same. The asymmetric line shape is attributed to the two overlapping lines for C₂H₅ and NH₃. Additionally, the FWHM line width narrows significantly with increasing temperature, as shown in Fig. 3. Note that there is no abrupt change in the line width near T_C3 and T_C4, whereas near T_C2 it is abruptly decreased. Here, the T_C4 (=247 K) is the previously reported phase transition temperature.¹⁶

Fig. 3 Line widths for ¹H MAS NMR spectrum of (C₂H₅NH₃)₂ZnCl₄ as a function of temperature (inset: ¹H MAS NMR spectrum of (C₂H₅NH₃)₂ZnCl₄ represented spinning sidebands indicated by asterisks and crosses at 300 K).

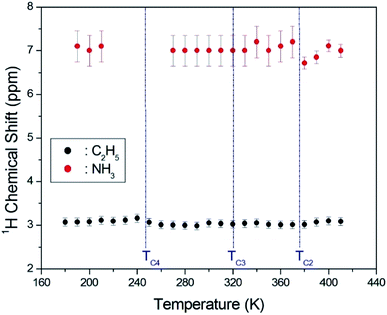
The asymmetric line shape in the inset in Fig. 3 is attributed to the C₂H₅ and NH₃ overlapping lines. Thus, the overlapping peak is very broad. However, the spinning sidebands of the two types are evident in Fig. 3. Therefore, the peaks for C₂H₅ and NH₃ by distance of sidebands can be distinguished. The spinning sidebands for C₂H₅ were marked with asterisks, while those for NH₃ were marked with crosses. The peak of the lower chemical shift was attributed to ¹H in C₂H₅, while that of the higher chemical shift was attributed to ¹H in NH₃. The spectrum at 300 K consisted of two peaks at chemical shifts of δ = 3.05 ppm and δ = 7 ppm, which were assigned to the ¹H in the ethyl group C₂H₅ and the ammonium group NH₃, respectively. The ¹H chemical shifts for methyl and ammonium groups were nearly constant with temperature, as shown in Fig. 4.

Fig. 4 Chemical shifts for ¹H MAS NMR of (C₂H₅NH₃)₂ZnCl₄ as a function of temperature.

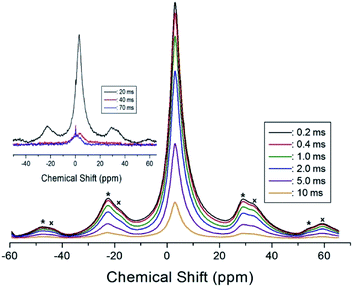
In order to obtain the ¹H relaxation time values, the magnetization recovery curves as a function of delay time were measured at several temperatures for (C₂H₅NH₃)₂ZnCl₄. The magnetization recovery curves for various delay times for ¹H at 300 K are shown in Fig. 5. All traces obtained can be described by the single-exponential function^19,20

P(t)/P₀ = exp(−t/T_1ρ), (1)

where P(t) is the magnetization as a function of the spin-locking pulse duration t, and P₀ is the total nuclear magnetization of the proton at thermal equilibrium. The recovery traces are shown for delay times ranging from 0.2 ms to 70 ms. The T_1ρ values were obtained from the slopes of the delay time vs. intensity. This analysis method was used to obtain the T_1ρ values for the protons, which are plotted as a function of inverse temperature in Fig. 6. From these results, the spin–lattice relaxation time in the rotating frame was obtained, and its temperature dependences are shown in Fig. 6.

Fig. 5 The ¹H recovery traces as a function of the delay time at 300 K.

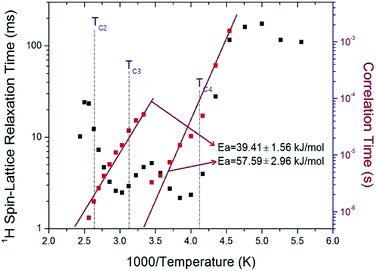Fig. 6 ¹H spin–lattice relaxation times T_1ρ in the rotating frame and correlation time of (C₂H₅NH₃)₂ZnCl₄ as a function of inverse temperature.

The T_1ρ values of protons in the (C₂H₅NH₃)₂ZnCl₄ are almost continuous near T_C3 and T_C4, and these values are on the order of a few milliseconds. The T_1ρ values abruptly decreased with temperature in the region approaching T_C2. The relaxation time for the ¹H nucleus has minimum values of 2.17 ms and 2.48 ms at 260 K and 330 K, respectively. This feature of T_1ρ indicates distinct molecular motions. The T_1ρ values are related to the corresponding values of the rotational correlation time, τ_C, which is a direct measure of the rate of molecular motion. For the spin–lattice relaxation time in the rotating frame, the experimental value of T_1ρ can be expressed in terms of the correlation time τ_C for the molecular motion as suggested by the Bloembergen–Purcell–Pound (BPP) theory:^21,22

T_1ρ⁻¹ = (N/20)(γ_H γ_Cħ/r_H–C³)²{4f(ω₁) + f(ω_H − ω_C) + 3f(ω_C) + 6f(ω_H + ω_C) + 6f(ω_H)}; f(ω₁) = τ_C/(1 + ω₁²τ_C²), f(ω_H − ω_C) = τ_C/[1 + (ω_H − ω_C)²τ_C²], f(ω_C) = τ_C/(1 + ω_C²τ_C²), f(ω_H + ω_C) = τ_C/[1 + (ω_H + ω_C)²τ_C²], f(ω_H) = τ_C/(1 + ω_H²τ_C²). (2)

Here, γ_H and γ_C are the gyromagnetic ratios for the ¹H and ¹³C nuclei, respectively; N is the number of directly bound protons; r_H–C is the H–C internuclear distance; ħ is the reduced Planck constant; ω_H and ω_C are the Larmor frequencies of ¹H and ¹³C, respectively; and ω₁ is the frequency of the spin-locking field of 67.56 kHz. We analyzed our data assuming that T_1ρ would show a minimum when ω₁τ_C = 1, and that the BPP relation between T_1ρ and the characteristic frequency ω₁ could be applied. We sensitively controlled the minima in the T_1ρ temperature variations and the slopes around the minima. From these results, the value of (γ_Hγ_Cħ/r_H–C³)² for the constant in eqn (2) was obtained. We then calculated the temperature dependences of the τ_C values for protons by using the obtained values of (γ_Hγ_Cħ/r_H–C³)². The temperature dependence of τ_C follows a simple Arrhenius equation:²¹

τ_C = τ₀ exp(−E_a/RT), (3)

where τ₀ is a pre-exponential factor, T is the temperature, R is the gas constant, and E_a is the activation energy. Thus, the slope of the linear portion of a semi-log plot should yield E_a. The E_a value for the rotational motion can be obtained from the log τ_C vs. 1000/T curve shown in Fig. 6; we obtained E_a = 39.41 ± 1.56 kJ mol⁻¹ and E_a = 57.59 ± 2.96 kJ mol⁻¹ for high and low temperatures, respectively. Here, T_1ρ and E_a for ¹H are averaged for all hydrogens in the (C₂H₅NH₃) cation. The rotational motion for protons at the end of the organic cation is more activated at the low temperature than at the high temperature.

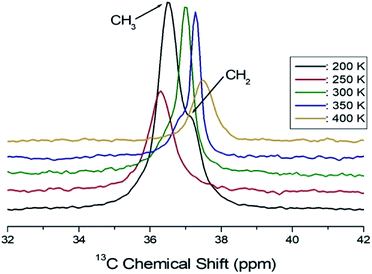
Structural analysis of the ¹³C in C₂H₅ was also performed using ¹³C CP/MAS NMR. The ¹³C MAS NMR spectrum for (C₂H₅NH₃)₂ZnCl₄ is shown in Fig. 7 as a function of temperature. The overlapped two signals in the spectrum for CH₃ and CH₂ in C₂H₅ are shown in Fig. 7. The resonance line has an asymmetric shape, similar to the ¹H line shape. At 200 K, the chemical shifts of δ = 36.51 ppm and δ = 37.12 ppm with respect to tetramethysilane (TMS) are assigned to CH₃ and CH₂, respectively. The chemical shifts above 250 K were only continuous changes, whereas there was an abrupt change near 250 K. The change in the chemical shift is associated with a structural phase transition occurring at this temperature.

Fig. 7 ¹³C CP/MAS NMR spectra of (C₂H₅NH₃)₂ZnCl₄ measured at different several temperatures.

The nuclear magnetization was also measured as a function of delay time in order to obtain the ¹³C T_1ρ values. The signal intensity of the nuclear magnetization recovery curves for ¹³C is described by a single exponential function of eqn (1) at all temperatures. The ¹³C T_1ρ values for C₂H₅ in (C₂H₅NH₃)₂ZnCl₄ are plotted as a function of inverse temperature in Fig. 8. The ¹³C T_1ρ values near the phase-transition temperatures T_C3 and T_C4 are approximately continuous, whereas the T_1ρ near T_C2 is abruptly decreased, similar to the ¹H T_1ρ. The T_1ρ value for carbon at room temperature is 13.65 ms. The T_1ρ curve below T_C2 can be reproduced by BPP theory, and the BPP curve shows a minimum of 6.30 ms at 260 K. The correlation time for the rotational motion of C₂H₅ is obtained, and the activation energy from the log τ_C vs. 1000/T curve shown in Fig. 8; we obtained E_a = 21.13 ± 1.27 kJ mol⁻¹.

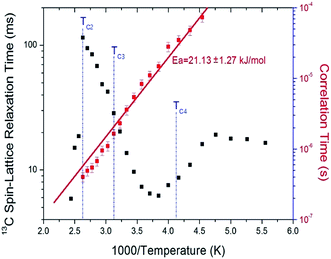Fig. 8 ¹³C spin–lattice relaxation times T_1ρ in the rotating frame and correlation time of (C₂H₅NH₃)₂ZnCl₄ as a function of inverse temperature.

In order to obtain information concerning the phase transition near 247 K (=T_C4), the NMR spectrum of ¹⁴N (I = 1) in the laboratory frame was obtained. Two resonance signals with respect to NH₄Cl were expected from the quadrupole interactions of the ¹⁴N nucleus. The ¹⁴N NMR spectra in (C₂H₅NH₃)₂ZnCl₄ single crystals between 220 K and 290 K are plotted in Fig. 9. The number of resonance lines varies near 243 K; the ¹⁴N signals below 240 K show two resonance lines denoted by symbol 1, whereas those above 240 K show four resonance lines denoted by symbols 1 and 2. These four signals are attributed to the N(1) and N(2) sites in the physically inequivalent NH₃ (1) and NH₃ (2) ions, respectively. The abrupt splitting of the ¹⁴N NMR line is related to the phase transition at 247 K. This splitting of the ¹⁴N resonance signals is nearly constant with temperature. However, the ¹⁴N NMR spectrum above 300 K could not be detected due to a low intensity.

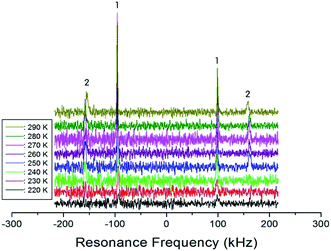Fig. 9 The resonance frequency of ¹⁴N NMR spectra in (C₂H₅NH₃)₂ZnCl₄ single crystal between 220 K and 290 K.

IV. Conclusion

We discussed the molecular motions of cations of Zn-based hybrid materials based on NMR studies. The present work is devoted to the crystal growth, DSC, TGA, and NMR spectroscopy of the (C₂H₅NH₃)₂ZnCl₄ compound. The thermal stability at different temperatures was considered. The cation dynamics in a layered perovskite-type (C₂H₅NH₃)₂ZnCl₄ single crystal were investigated as a function of temperature by ¹H MAS NMR, ¹³C CP/MAS NMR, and ¹⁴N static NMR experiments. There was no jump in T_1ρ across the phase transition at T_C3 and T_C4, while T_1ρ showed a slight jump at T_C2. To obtain detailed information about the cation dynamics of this crystal, the spin–lattice relaxation time T_1ρ in the rotating frame for both ¹H and ¹³C were obtained, revealing that these atoms undergo rotational motions. The BPP curves for the ¹H T_1ρ in C₂H₅NH₃ cation and for the ¹³C T_1ρ in C₂H₅ were shown to have minima as a function of inverse temperature. This implies that these curves represent the rotational motions of ¹H and ¹³C. The activation energy for ¹H in the C₂H₅NH₃ cation is E_a = 39.41 kJ mol⁻¹ above 290 K and 57.59 kJ mol⁻¹ below 290 K, whereas that for ¹³C in the C₂H₅NH₃ cation is 21.13 kJ mol⁻¹. Furthermore, the carbon dynamics of C₂H₅ undergo rotation slower than protons. This implies that molecular motion is enhanced at the carbon-end and nitrogen-end of the organic cation, whereas molecular motion is not free at the main chain carbons of the organic cation.

Moreover, we compared the phase transition temperatures and molecular motions of the previously reported (C₂H₅NH₃)₂CuCl₄ (ref. 23) and those of (C₂H₅NH₃)₂ZnCl₄ studied here. The difference between these compounds is only the inorganic cation. (C₂H₅NH₃)₂ZnCl₄ and (C₂H₅NH₃)₂CuCl₄ are characterized by five (231, 234, 237, 247, and 312 K) and four (236, 330, 357, and 371 K) phase transitions, respectively. Furthermore, the molecular motions affecting the spin–lattice relaxation time T_1ρ in (C₂H₅NH₃)₂ZnCl₄ are very different from those for (C₂H₅NH₃)₂CuCl₄. The activation energies obtained from T_1ρ by the ¹H and ¹³C measurements for the two compounds are summarized in Table 1. The E_a for ¹H in (C₂H₅NH₃)₂ZnCl₄ are the values at high temperatures above 290 K and the low temperatures below 290 K, respectively. In the case of (C₂H₅NH₃)₂CuCl₄, E_a for each C₂H₅ and NH₃ is shown at a temperature range from 180 K to 240 K.²³ The values of E_a obtained from the ¹H measurements of (C₂H₅NH₃)₂ZnCl₄ are larger than those of (C₂H₅NH₃)₂CuCl₄, whereas those obtained from the ¹³C measurments are similar. These results indicate that the activation energies obtained from the ¹H measurements for the H–Cl–Zn bond in (C₂H₅NH₃)₂ZnCl₄ without the paramagnetic ions is larger than that for the H–Cl–Cu bond in (C₂H₅NH₃)₂CuCl₄ including paramagnetic ions. These differences are due to the differences in the electronic structure of the Zn²⁺ and Cu²⁺ ions, particularly, the d electrons, which screen the nuclear charge from the motion of the outer electrons. Zn²⁺ has filled d shell, whereas Cu²⁺ has one s electron outside the closed d shell. It is also likely due to several other factors, such as different coordination of the metal atom, different lattice constants, and hydrogen bonding strength. This suggests that the differences in the chemical properties of metal ions are responsible for the variations in the characteristics of the phase transitions and molecular motions in these crystals. This study can motivate us to find a solution for improving the material features as well as solar cell performance using lead-free perovskites based on Zn or Cu in market-competitive optoelectronic materials for photovoltaics (PV) and light emitting diodes (LED) applications.^3,24,25

Table 1 Activation energies, E_a (kJ mol⁻¹) for ¹H and ¹³C nuclei in (C₂H₅NH₃)₂ZnCl₄ and (C₂H₅NH₃)₂CuCl₄

	(C2H5NH3)2ZnCl4	(C2H5NH3)2CuCl4 (ref. 23)
^1H	39.41 ± 1.56 (for all hydrogen above 290 K)	12.19 ± 1.30 (for C2H5 below 240 K)
^1H	57.59 ± 2.96 (for all hydrogen below 290 K)	8.33 ± 0.50 (for NH3 below 240 K)
^13C	21.13 ± 1.27 (for C2H5)	21.35 ± 0.45 (for CH3)
^13C		19.72 ± 1.76 (for CH2)

---

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Basic Science Research program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education (2018R1D1A1B07041593).

References

1. O. M. Yaghi, G. Li and H. Li, Nature, 1995, 378, 703.
2. D. B. Mitzi, J. Chem. Soc., Dalton Trans., 2001, 48, 1.
3. J. A. Aramburu, P. G. Fernandez, N. R. Mathiesen, J. M. G. Lastra and M. Moreno, J. Phys. Chem. C, 2018, 122, 5071.
4. C. N. R. Rao, A. K. Cheetham and A. Thirumurugan, J. Phys.: Condens. Matter, 2008, 20, 83202.
5. F. Chiarella, A. Zappettini, P. Ferro, T. Besagni, F. Licci, A. Cassinese, M. Barra, R. Vaglio and C. Aruta, Cryst. Res. Technol., 2005, 40, 1028.
6. B. Kundys, A. Lappas, M. Viret, V. Kapustianyk, V. Rudyk, S. Semak, Ch. Simon and I. Bakaimi, Phys. Rev. B, 2010, 81, 224434.
7. P. Zolfaghari, G. A. de Wijs and R. A. de Groot, J. Phys.: Condens. Matter, 2013, 25, 295502.
8. C. B. Mohamed, K. Karoui, F. Jomni, K. Guidara and A. B. Rhaiem, J. Mol. Struct., 2015, 1082, 38.
9. E. Suprayoga, A. A. Nugroho, A. O. Polyakov, T. T. M. Palstra and I. Watanabe, J. Phys.: Conf. Ser., 2014, 551, 12054.
10. R. Yadav, D. Swain, P. P. Kundu, H. S. Nair, C. Narayana and S. Elizabeth, Phys. Chem. Chem. Phys., 2015, 17, 12207.
11. R. Lefi, F. B. Naser and H. Guermazi, J. Alloys Compd., 2017, 696, 1244.
12. F. B. Nasr, R. Lefi and H. Guermazi, J. Mol. Struct., 2018, 1165, 236.
13. H. Schmid, Ferroelectrics, 1994, 162, 317.
14. J. Ding, H. Li, L. Wen, X. Kang, H. Li and J. Zhang, J. Magn. Magn. Mater., 2013, 346, 91.
15. C. B. Mohamed, K. Karoui, M. Tabellout and A. B. Rhaiem, J. Alloys Compd., 2016, 688, 407.
16. M. J. Tello, A. Lopez-Echarri, J. Zubillaga, I. Ruiz-Larrea, F. J. Zuniga, G. Madariaga and A. Gomez-Cuevas, J. Phys.: Condens. Matter, 1994, 6, 6751.
17. C. B. Mohamed, K. Karoui and A. B. Rhaiem, Phase Transitions, 2018, 91, 1162.
18. C. B. Mohamed, K. Karoui, A. Bulou and A. B. Rhaiem, Physica E, 2017, 87, 141.
19. J. L. Koenig, Spectroscopy of Polymers, Elsevier, New York, 1999.
20. A. R. Lim, RSC Adv., 2018, 8, 18656.
21. A. Abragam, The Principles of Nuclear Magnetism, Oxford University press, Oxford, 1961.
22. J. Mcbrierty and K. J. Packer, Nuclear Magnetic Resonance in Solid Polymers, Cambridge University Press, Cambridge, 1993.
23. A. R. Lim and Y. L. Joo, RSC Adv., 2018, 8, 34110.
24. Q. Chen, N. D. Marco, Y. Yang, T.-B. Song, C.-C. Chen, H. Zhao, Z. Hong, H. Zhou and Y. Yang, Nano Today, 2015, 10, 355.
25. A. M. Elseman, A. E. Shalan, S. Sajid, M. M. Rashad, A. M. Hassan and M. Li, ACS Appl. Mater. Interfaces, 2018, 10, 11699.

---