Open Access Article
Open Access ArticleModelling and prediction of the thermophysical properties of aqueous mixtures of choline geranate and geranic acid (CAGE) using SAFT-γ Mie†
Silvia Di Lecce‡
 a,
Georgia Lazaroua,
Siti H. Khalita,
Claire S. Adjiman
a,
Georgia Lazaroua,
Siti H. Khalita,
Claire S. Adjiman a,
George Jackson
a,
George Jackson a,
Amparo Galindo
a,
Amparo Galindo *a and
Lisa McQueenb
*a and
Lisa McQueenb
aDepartment of Chemical Engineering, Centre for Process Systems Engineering, Institute for Molecular Science and Engineering, South Kensington Campus, Imperial College London, London SW7 2AZ, UK. E-mail: a.galindo@imperial.ac.uk
bChemical Development, GSK, 1250 S Collegeville Rd, Collegeville, PA 19426, USA
First published on 21st November 2019
Abstract
Deep-eutectic solvents and room temperature ionic liquids are increasingly recognised as appropriate materials for use as active pharmaceutical ingredients and formulation additives. Aqueous mixtures of choline and geranate (CAGE), in particular, have been shown to offer promising biomedical properties but understanding the thermophysical behaviour of these mixtures remains limited. Here, we develop interaction potentials for use in the SAFT-γ Mie group-contribution approach, to study the thermodynamic properties and phase behaviour of aqueous mixtures of choline geranate and geranic acid. The determination of the interaction parameters between chemical functional groups is carried out in a sequential fashion, characterising each group based on those previously developed. The parameters of the groups relevant to geranic acid are estimated using experimental fluid phase-equilibrium data such as vapour pressure and saturated-liquid density of simple pure components (n-alkenes, branched alkenes and carboxylic acids) and the phase equilibrium data of mixtures (aqueous solutions of branched alkenes and of carboxylic acids). Geranate is represented by further incorporating the anionic carboxylate group, COO−, which is characterised using aqueous solution data of sodium carboxylate salts, assuming full dissociation of the salt in water. Choline is described by incorporating the cationic quaternary ammonium group, N+, using data for choline chloride solutions. The osmotic pressure of aqueous mixtures of CAGE at several concentrations is predicted and compared to experimental data obtained as part of our work to assess the accuracy of the modelling platform. The SAFT-γ Mie approach is shown to be predictive, providing a good description of the measured data for a wide range of mixtures and properties. Furthermore, the new group-interaction parameters needed to represent CAGE extend the set of functional groups of the group-contribution approach, and can be used in a transferable way to predict the properties of systems beyond those studied in the current work.
1 Introduction
Deep-eutectic solvents (DESs) and room temperature ionic liquids (RTILs) are increasingly recognised as advantageous materials for use as carriers of active pharmaceutical ingredients and formulation additives.1–3 DESs exhibit physical properties which are similar to those of conventional ILs such as low volatility over a relatively wide liquid range and non-flammability, and as such can be considered as a new class of ionic liquids.2 In terms of definition, the only difference between RTILs and DESs is the ratio of the components in the mixtures. RTILs are usually defined as organic salts with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cation
1 cation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) anion molar ratio and melting points below 100 °C, while DESs are more generally defined as mixtures of charged and neutral components. A series of studies of DESs/RTILs for a number of anion/cation/solvent combinations have been tested,4–7 and mixtures of choline and generate (CAGE) were shown to offer promising therapeutical properties, including powerful antibacterial activity against a variety of drug-resistant bacteria, fungi and viruses, low toxicity, and enhancement of the transdermal delivery of proteins and antibacterial drugs. The mixture with a 1
anion molar ratio and melting points below 100 °C, while DESs are more generally defined as mixtures of charged and neutral components. A series of studies of DESs/RTILs for a number of anion/cation/solvent combinations have been tested,4–7 and mixtures of choline and generate (CAGE) were shown to offer promising therapeutical properties, including powerful antibacterial activity against a variety of drug-resistant bacteria, fungi and viruses, low toxicity, and enhancement of the transdermal delivery of proteins and antibacterial drugs. The mixture with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 choline
2 choline![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) geranate mol ratio was shown to be especially effective.4,8
geranate mol ratio was shown to be especially effective.4,8
Following these findings, it is of interest to develop a better understanding of CAGE mixtures through the acquisition of new data and the development of molecular models capable of delivering accurate estimates and predictions of the physical properties of CAGE and its aqueous solutions, as these are immediately relevant to further biomedical applications and are needed to facilitate process modelling for the manufacture of medicinal products based on this solvent. Available work relating to the physical properties of CAGE is, however, currently limited. Mitragotri and co-workers have presented molecular-dynamics simulations with all-atom and coarse-grained force fields to study the structural properties of CAGE in the presence of water,9 and its activity on the cell membrane of Gram-negative E. coli in the absence of water.7 A key finding of the experiments and molecular-dynamics simulations studies thus far is that water molecules can induce changes in the structure of CAGE for mole fractions of water higher than ∼0.65. As the amount of water in the solutions increases, the hydrogen bonds between choline and geranate are disrupted and the formation of microstructures between geranic acid molecules is promoted.9
In addition to molecular-dynamics simulations, molecular-based equations of state are useful tools to study and predict the thermodynamic properties of complex fluid mixtures. The perturbed-chain statistical associating fluid theory (PC-SAFT)10 has been shown to describe accurately the solid–liquid equilibria of a number of DESs11–13 and the liquid–liquid equilibria data of several RTILs.14–16 In these studies, short-range association sites were used to mimic hydrogen bonding interactions between species but the anion and cation were not treated as explicitly charged species. In aqueous solutions, the presence of charged species critically affects the thermodynamic properties of the mixtures. Thus, accounting for coulombic interactions is expected to provide a better description of the physical properties and lead to more predictive models of these complex systems.
The SAFT-γ Mie group-contribution approach17,18 is a recently developed version of the SAFT family of equations of state, based on a Mie (generalised Lennard-Jones) potential of variable repulsive and attractive range. In this approach, the group-contribution premise that the properties of a molecule or mixture can be determined by accounting for the appropriate contributions of the chemical moieties (functional groups) in the system of interest is adopted. The parameters describing the functional groups (methylene CH2, methyl CH3, carboxyl COOH, etc.) and their interactions are derived in a sequential manner, with the determination of each new group–group interaction based on that of previous groups. From the characterisation of a relatively small number of groups it is then possible to evaluate the properties of a much larger set of systems, including mixtures. The approach has been shown to be accurate for the prediction of thermodynamic properties, phase equilibria (vapour–liquid, liquid–liquid, and solid–liquid) of complex mixtures,18 as well as for the solubility and octanol–water partition coefficients of organic molecules of interest in pharmaceutical applications.19 Of particular relevance to this discussion is the fact that charged compounds can be accounted for in the methodology.20,21 Furthermore, the SAFT-γ Mie approach has the added advantage of maintaining a direct link between the molecular model and the corresponding macroscopic equilibrium properties, which allows it to be used for the development of force-field parameters for use in molecular simulation,22,23 from which structural, interfacial and transport properties can also be studied.
Given the importance of CAGE, we present here new experimental data for the osmotic pressure of aqueous solutions of CAGE and develop appropriate functional group models for use within the SAFT-γ Mie platform relevant to the molecules in the CAGE mixture. Further, we demonstrate that our group-contribution approach delivers accurate predictions of the osmotic pressure. Details of the experimental and theoretical methodologies are presented in the following section, with results reported in Section 3, and conclusions in Section 4.
2 Methods
2.1 Experimental
1H NMR and 13C1H NMR spectra were obtained on a Bruker Avance 400 spectrometer at 298 K and referenced to the residual solvent signal. DEPT-135 and 2D correlation spectra were used to aid assignments but have not been otherwise documented. (CD3)2SO was bought from Sigma and used as received. Mass spectra were obtained by directly injecting CAGE into a Waters single quadrupole detector at 4.2 kV capillary voltage. The IR spectrum was run on a PerkinElmer Spectrum 100 using an ATR attachment. Elemental analysis was carried out by Stephen Boyer (London Metropolitan University).A sample of CAGE was prepared following the procedure described by Zakrewsky et al.4 Choline bicarbonate (80 wt% solution in water, 2.68 g, 13.72 mmol) was purchased from Sigma and used as received. Geranic acid (85%) was purchased from Sigma and was recrystallised five times from cold HPLC-grade acetone (VWR) before use. A solution of choline bicarbonate (80 wt% in water, 2.68 g, 13.72 mmol) was diluted further with water (4 mL), then added to neat geranic acid (4.62 g, 27.43 mmol). The reaction was stirred until CO2 evolution ceased (3 hours). Water was then removed by azeotrope with toluene under reduced pressure. The resulting colourless viscous oil was dried under high vacuum at 40 °C for 16 hours (yield 6.02 g, 100%).
1H NMR (400.1 MHz, (CD3)2SO): 10.19 (v br s, [2H], OH), 5.57 (d, J = 1.2 Hz, [2H], H2), 5.07 (br t, J = 6.5 Hz, [2H], H6), 3.83–3.88 (m, [2H], H2′), 3.41–3.46 (m, [2H], H1′), 3.13 (s, [9H], H3′), 1.95–2.10 (m, [14H], H4, H5, H9), 1.64 (s, [6H], H8/10), 1.56 (s, [6H], H8/10) ppm.
13C1H NMR (100.6 MHz, (CD3)2SO): 169.92 (C, C1), 148.22 (C, C3), 130.96 (C, C7), 123.74 (CH, C6), 122.36 (CH, C2), 67.22 (CH2, C1′), 55.01 (CH2, C2′), 53.07 (t, J = 3.5 Hz, CH3, C3′), 39.87 (CH2, C4), 25.83 (CH2, C5), 25.43 (CH3, C9), 17.61 (CH3, C8/10), 17.48 (CH3, C8/10) ppm.
IR (ATR): 2968, 2915, 1694, 1646, 1548, 1479, 1437, 1397, 1375, 1317, 1228, 1158, 1088, 1055, 1006, 954, 867, 821, 692 cm−1.
MS (positive ion): m/z 104.2 ([choline]+, 100%), 207.4 ([(choline)2–H]+, 33%), 375.5 ([(choline)2 + geranate]+, <5%), 478.6 ([(choline)3 + geranate–H]+, <5%), 646.7 ([(choline)3 + (geranate)2]+, <5%), 749.8 ([(choline)4 + (geranate)2–H]+, <5%), 917.8 ([(choline)4 + (geranate)3]+, <5%). (Negative ion): m/z 167.2 ([geranate]−, 90%), 335.4 ([H(geranate)2]−, 5%), 438.5 ([CAGE–H]−, 100%), 709.6 ([CAGE + choline + geranate]−, <5%), 980.7 [CAGE + (choline)2 + geranic acid + geranate]−, <5%.
Analysis calc. for C25H45NO5 (439.33): C 68.29; H 10.32; N 3.19. Found: C 68.33; H 10.45; N 3.14.
Copies of the corresponding NMR, IS and MS spectra can be found in the ESI.†
CAGE solutions were prepared with de-ionised, distilled water (Honeywell lot DT295-B-US) from serial dilutions of a solution obtained by mixing CAGE liquid and water. The concentration was adjusted for water content, which was estimated from thermal gravimetric analysis of the CAGE mixture immediately prior to use. Thermal gravimetric data was generated using a TA Instrument TGA Discovery series (2.2489 mg, 10 °C min−1, 22.5 to 350 °C). Aliquots (10 μL) of each solution were analysed in triplicate on the same day as preparation using a Wescor vapour-pressure osmometer VAPRO model 5600 calibrated with 290, 100 and 1000 mmol kg−1 standards (Optimole™). The osmotic pressure, Π = cRT was determined from the measured osmotic concentrations c, with R the gas constant and T the temperature.
2.2 SAFT-γ Mie model and theory
In the SAFT-γ Mie group-contribution approach17,18 molecules are represented as associating hetero-segmented chains consisting of fused spherical segments that interact via Mie potentials of variable range24 with short-range directional interactions incorporated by embedding square-well association sites on any given segment. The total Helmholtz free energy A of a mixture of n components at a given temperature T, volume V, and composition vector N = (N1, N2, …, Nn), where Nj denotes the number of molecules of component j, is obtained as the sum of six contributions arising from a perturbation approach:17,18,20| A = Aideal + Amonomer + Achain + Aassociation + ABorn + Aion. | (1) |
A given chemical functional group k is characterised by a number  of identical spherical segments and a shape factor, Skk (0 ≤ Skk ≤ 1), which represents the contribution made by each group to the overall free energy of the molecule considered. The interaction between two groups k and l is described using the Mie potential:24
of identical spherical segments and a shape factor, Skk (0 ≤ Skk ≤ 1), which represents the contribution made by each group to the overall free energy of the molecule considered. The interaction between two groups k and l is described using the Mie potential:24
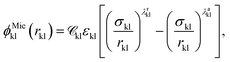 | (2) |
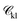 is a function of the Mie potentials exponents:
is a function of the Mie potentials exponents:
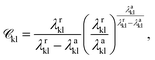 | (3) |
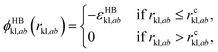 | (4) |
The model parameters characterising the interactions between unlike functional groups k and l can be obtained through combining rules in the first instance. The unlike segment diameter σkl is obtained using a Lorentz-like arithmetic mean of the like diameters,28 i.e.,
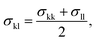 | (5) |
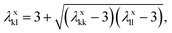 | (6) |
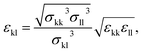 | (7) |
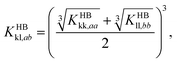 | (8) |
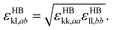 | (9) |
These combining rules provide a useful first estimate of the values of these parameters. In practice, however, the unlike dispersion energy and repulsive exponent, as well as the unlike association energy and bonding volume are typically estimated by comparison to target experimental thermophysical properties of substances belonging to chemical families or mixtures in which the functional group is present.
In the case of charged groups, a value for the Born cavity diameter, σBornkk, also has to be specified. This is taken from previous work, for known groups, or assigned a value following the Rashin and Honig29 recipe (σBornkk = 1.07σkk). In addition, the unlike dispersion energy parameter between charged groups is obtained using20
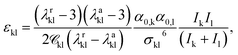 | (10) |
2.3 Thermodynamic properties
Standard thermodynamic relations and phase-equilibrium conditions are applied to calculate a range of equilibrium thermodynamic properties such as the vapour pressure and saturated-liquid density of pure substances and the mean ionic activity coefficients, osmotic coefficients and osmotic pressures of the solutions.The pressure and chemical potential μiV = μi(T, V, N) of a component i are obtained from the Helmholtz free energy at given T, V and N as
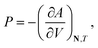 | (11) |
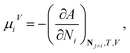 | (12) |
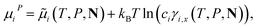 | (13) |
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) i(T, P, N) is the chemical potential of the reference term of component i, kB the Boltzmann constant, and ci the concentration of component i; the subscript x denotes that γi,x is expressed in units commensurate with those of ci. It is often convenient to measure the concentration in terms of the mole fraction xi of the component and to refer to the standard symmetrical activity coefficient expressed in terms of xi. The reference term of the chemical potential
i(T, P, N) is the chemical potential of the reference term of component i, kB the Boltzmann constant, and ci the concentration of component i; the subscript x denotes that γi,x is expressed in units commensurate with those of ci. It is often convenient to measure the concentration in terms of the mole fraction xi of the component and to refer to the standard symmetrical activity coefficient expressed in terms of xi. The reference term of the chemical potential ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) i(T, P, N) is identical to the chemical potential of pure component i at the same thermodynamic conditions, i.e.,
i(T, P, N) is identical to the chemical potential of pure component i at the same thermodynamic conditions, i.e., ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) i = μ0i(T, P).
i = μ0i(T, P).
For ionic species, the chemical potential is expressed using an asymmetric convention in which the activity coefficient γi,* has a value equal to one in the limit of infinite dilution; due to electroneutrality, a pure ion does not exist in an isolated state, so that ionic species cannot be related to a pure one-component system. In practice, this activity coefficient is calculated using the fugacity coefficient at the specified system conditions φi(T, P, N), normalised by the fugacity coefficient at infinite dilution, 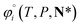 , i.e.,
, i.e.,
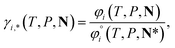 | (14) |
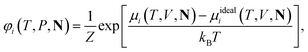 | (15) |
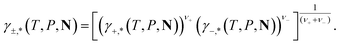 | (16) |
The osmotic coefficient, Φ(T, P, N), of a solution is obtained by calculating the activity coefficient of the solvent j from the following equation:
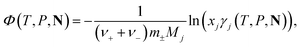 | (17) |
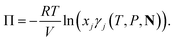 | (18) |
The liquid–liquid and vapour–liquid equilibria are obtained by imposing thermal, mechanical, and chemical equilibrium across the different phases, i.e., the temperature, pressure, and chemical potential of each component in each phase are set to be equal. The vapour pressure is calculated assuming that the charged species are non-volatile. The equality of chemical potential is imposed for each neutral species in all the phases considered (α, β, …, Nphase):
| μjα = μjβ = … = μjNphase. | (19) |
For each pair of charged species, i and i′, the fluid-phase equilibrium is imposed as described in ref. 20 and 30:
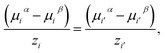 | (20) |
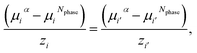 | (21) |
We use the percentage average absolute deviation (% AADR) of a property R,
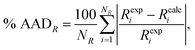 | (22) |
3 Results and discussion
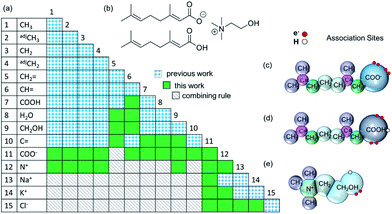
In order to model CAGE with the SAFT-γ Mie approach all of the relevant group-interaction parameters have to be determined. Functional groups are developed in a successive manner, with the characterisation of new group based on that of previously determined values.Each component of the mixture is decomposed into its functional groups, with the assumption that the properties of the solution can be determined as appropriate functions of the chemically distinct functional groups that the compounds comprise and, that the contribution of each functional group to the molecular properties is independent of the molecular structure in which the group appears (see Fig. 1). One should also note that in the case of small molecules such as water, the entire molecule constitutes also a group.
As discussed in the Methods section, each functional group k is characterised by a fused spherical segment or, for larger groups such as CH2OH, by a number 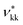 of identical fused segments. The overlap of the different segments is taken into account by using the shape factor Skk, which determines how much each segment contributes to the overall molecular properties. The matrix of functional groups and interactions required to characterise the mixtures of interest are summarised in Fig. 1(a). A number of the group parameters have been characterised in earlier work.18 In the current paper we expand the group-interaction matrix by estimating the interaction parameters needed to model CAGE; these are summarised in Tables 2–4.
of identical fused segments. The overlap of the different segments is taken into account by using the shape factor Skk, which determines how much each segment contributes to the overall molecular properties. The matrix of functional groups and interactions required to characterise the mixtures of interest are summarised in Fig. 1(a). A number of the group parameters have been characterised in earlier work.18 In the current paper we expand the group-interaction matrix by estimating the interaction parameters needed to model CAGE; these are summarised in Tables 2–4.
| Group k | COO− | Cl− | N+ | Na+ | K+ |
| Ik/eV | 3.4700 | 3.6127 | 14.534 | 47.286 | 31.630 |
| α0,k/(10−24 cm3) | 4.2042 | 3.6600 | 1.1000 | 0.1790 | 0.8300 |
| Group k | Skk | σkk/Å | σBornkk/Å | λrkk | λakk | (εkk/kB)/K | NST,k | nH,k | ne1,k | ne2,k | Ref. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CH3 | 1 | 0.57255 | 4.0773 | — | 15.050 | 6.0000 | 256.77 | — | — | — | — | 17 |
| adjCH3 | 1 | 0.57255 | 4.0773 | — | 15.050 | 6.0000 | 256.77 | — | — | — | — | This work |
| CH2 | 1 | 0.22932 | 4.8801 | — | 19.871 | 6.0000 | 473.39 | — | — | — | — | 17 |
| adjCH2 | 1 | 0.22932 | 4.8801 | — | 19.871 | 6.0000 | 473.39 | — | — | — | — | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
1 | 0.44890 | 4.3175 | — | 20.271 | 6.0000 | 300.90 | — | — | — | — | 18 |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
1 | 0.20040 | 4.7488 | — | 15.974 | 6.0000 | 952.54 | — | — | — | — | 18 |
| COOH | 1 | 0.55593 | 4.3331 | — | 8.0000 | 6.0000 | 405.78 | 3 | 1 | 2 | 3 | 18 |
| H2O | 1 | 1.00000 | 3.0063 | — | 17.020 | 6.0000 | 266.68 | 2 | 2 | 2 | — | 68 |
| CH2OH | 2 | 0.58538 | 3.4054 | — | 22.699 | 6.0000 | 407.22 | 2 | 1 | 2 | — | 19 |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
1 | 0.15330 | 4.0330 | — | 8.0000 | 6.0000 | 1500.0 | — | — | — | — | 69 |
| COO− | 1 | 0.55593 | 4.3331 | 4.6364 | 8.0000 | 6.0000 | 21.264 | 1 | — | 4 | — | This work |
| N+ | 1 | 0.15069 | 3.0755 | 3.2908 | 8.8971 | 6.0000 | 62.971 | 1 | 1 | — | — | This work |
| Na+ | 1 | 1.00000 | 2.3200 | 3.3600 | 12.000 | 6.0000 | 31.711 | 0 | 20 | |||
| K+ | 1 | 1.00000 | 3.0400 | 4.3440 | 12.000 | 6.0000 | 90.097 | 0 | 20 | |||
| Cl− | 1 | 1.00000 | 3.3400 | 3.8740 | 12.000 | 6.0000 | 113.77 | 0 | 20 |
| Group k | Group l | (εkk/kB)/K | λrkk | Ref. | Group k | Group l | (εkk/kB)/K | λrkk | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| CH3/adjCH3 | CH3/adjCH3 | 256.77 | 15.05 | 17 | CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Cl− | CR | CR | This work |
| CH3/adjCH3 | CH2/adjCH2 | 350.77 | CR | 17 | COOH | COOH | 405.78 | 8.0000 | 18 |
| CH3/adjCH3 | CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
333.48 | CR | 18 | COOH | H2O | 289.76 | CR | 19 |
| CH3/adjCH3 | CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
252.41 | CR | 18 | COOH | CH2OH | 656.80 | CR | 19 |
| CH3/adjCH3 | COOH | 255.99 | CR | 18 | COOH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
609.87 | CR | This work |
| CH3/adjCH3 | H2O | 358.18 | 100 | 19 | COOH | COO− | 405.78 | 8 | This work |
| CH3/adjCH3 | CH2OH | 333.20 | CR | 19 | COOH | N+ | CR | CR | This work |
| CH3/adjCH3 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
281.40 | CR | 69 | COOH | Na+ | CR | CR | This work |
| CH3 | COO− | 255.99 | CR | This work | COOH | K+ | CR | CR | This work |
| adjCH3 | COO− | 509.37 | CR | This work | COOH | Cl− | CR | CR | This work |
| CH3/adjCH3 | N+ | 462.18 | CR | This work | H2O | H2O | 266.68 | 17.020 | 68 |
| CH3/adjCH3 | Na+ | CR | CR | This work | H2O | CH2OH | 353.37 | CR | 19 |
| CH3/adjCH3 | K+ | CR | CR | This work | H2O | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
310.91 | 8 | This work |
| CH3/adjCH3 | Cl− | CR | CR | This work | H2O | COO− | 171.61 | CR | This work |
| CH2/adjCH2 | CH2/adjCH2 | 473.39 | 19.871 | 17 | H2O | N+ | 1481.3 | 21.217 | This work |
| CH2/adjCH2 | CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
386.80 | CR | 18 | H2O | Na+ | 539.68 | CR | 20 |
| CH2/adjCH2 | CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
459.40 | CR | 18 | H2O | K+ | 376.25 | CR | 20 |
| CH2/adjCH2 | COOH | 413.74 | CR | 18 | H2O | Cl− | 95.406 | CR | 20 |
| CH2/adjCH2 | H2O | 423.63 | 100 | 19 | CH2OH | CH2OH | 407.22 | 22.699 | 19 |
| CH2/adjCH2 | CH2OH | 423.17 | CR | 19 | CH2OH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
799.66 | CR | This work |
| CH2/adjCH2 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
286.58 | CR | 69 | CH2OH | COO− | 656.80 | CR | This work |
| CH2 | COO− | 413.74 | CR | This work | CH2OH | N+ | 440.99 | CR | This work |
| adjCH3 | COO− | 780.24 | CR | This work | CH2OH | Na+ | CR | CR | This work |
| CH2/adjCH2 | N+ | 348.30 | CR | This work | CH2OH | K+ | CR | CR | This work |
| CH2/adjCH2 | Na+ | CR | CR | This work | CH2OH | Cl− | CR | CR | This work |
| CH2/adjCH2 | K+ | CR | CR | This work | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
1500 | 8.0000 | 69 |
| CH2/adjCH2 | Cl− | CR | CR | This work | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
COO− | 609.87 | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
300.90 | 20.271 | 18 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
N+ | CR | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
275.75 | CR | 18 | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Na+ | CR | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
COOH | 387.25 | 94.463 | This work | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
K+ | CR | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
H2O | 375.51 | CR | This work | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Cl− | CR | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
CH2OH | 203.76 | CR | This work | COO− | COO− | 405.78 | 8 | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
CR | CR | This work | COO− | N+ | 24.280 | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
COO− | CR | CR | This work | COO− | Na+ | 9.9125 | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
N+ | CR | CR | This work | COO− | K+ | 23.999 | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Na+ | CR | CR | This work | COO− | Cl− | 21.265 | CR | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
K+ | CR | CR | This work | N+ | N+ | 394.86 | 9.9448 | This work |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Cl− | CR | CR | This work | N+ | Na+ | CR | CR | This work |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
952.54 | 15.974 | 18 | N+ | K+ | CR | CR | This work |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
COOH | 453.13 | CR | This work | N+ | Cl− | 61.989 | CR | This work |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
H2O | 332.21 | 17.309 | This work | Na+ | Na+ | 31.711 | 12 | 20 |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
CH2OH | 414.91 | CR | This work | Na+ | K+ | CR | CR | This work |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
1195.3 | CR | This work | Na+ | Cl− | 27.938 | CR | 20 |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
COO− | 453.13 | CR | This work | K+ | K+ | 90.097 | 12 | This work |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
N+ | CR | CR | This work | K+ | Cl− | 61.010 | CR | 20 |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
Na+ | CR | CR | This work | Cl− | Cl− | 113.77 | 12 | 20 |
CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) |
K+ | CR | CR | This work |
| Group k | Site of group k | Group l | Site a of group l | (εHBab,kl/kB)/K | KHBab,kl/Å3 | Ref. |
|---|---|---|---|---|---|---|
| COOH | H | COOH | H | 6427.9 | 0.80620 | 18 |
| COOH | e1 | H2O | H | 1451.8 | 280.89 | 19 |
| COOH | e2 | H2O | H | 1252.6 | 150.98 | 19 |
| COOH | H | H2O | e1 | 2567.7 | 270.09 | 19 |
| COOH | e1 | CH2OH | H | 1015.5 | 21.827 | 19 |
| COOH | e2 | CH2OH | H | 547.40 | 53.150 | 19 |
| COOH | H | CH2OH | e1 | 524.00 | 14.017 | 19 |
| H2O | e1 | H2O | H | 1985.4 | 101.69 | 68 |
| H2O | e1 | CH2OH | H | 621.68 | 425.00 | 19 |
| H2O | H | CH2OH | e1 | 2153.2 | 147.40 | 19 |
| H2O | H | COO− | e1 | 802.20 | 52.560 | This work |
| H2O | e1 | N+ | H | 2783.7 | 15.536 | This work |
| CH2OH | e1 | CH2OH | H | 2097.9 | 62.310 | 19 |
| CH2OH | H | N+ | e1 | 1247.2 | 286.83 | This work |
As has already been mentioned, the characterisation of the group-interaction parameters is done in a successive manner. We proceed to analyse first the performance of the model in predicting the properties of pure geranic acid, follow with aqueous geranic acid mixtures, aqueous carboxylate salts solutions, and finally choline chloride and aqueous CAGE solutions.
3.1 Geranic acid
The group-interaction parameters required to model geranic acid are estimated using experimental phase-equilibrium data of pure compounds (e.g., n-alkanes, n-alkenes, branched alkenes) and mixtures (e.g., branched alkenes and carboxylic acids), as shown below.Pure-component experimental data32–35 are used to characterise the unlike interactions between the carboxylic group COOH and the alkene groups (either linear CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) , or branched C
, or branched C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ). The experimental vapour–pressure data for pure branched and unsaturated carboxylic acids used to perform the parameter estimations, and to assess the predictive capability of the resulting models, are shown in Fig. 2. Although most of the group-interaction parameters needed to calculate the vapour pressure of the compounds presented in the figure are not optimised for these systems, the model is found to provide a good description of the experimental data.
). The experimental vapour–pressure data for pure branched and unsaturated carboxylic acids used to perform the parameter estimations, and to assess the predictive capability of the resulting models, are shown in Fig. 2. Although most of the group-interaction parameters needed to calculate the vapour pressure of the compounds presented in the figure are not optimised for these systems, the model is found to provide a good description of the experimental data.
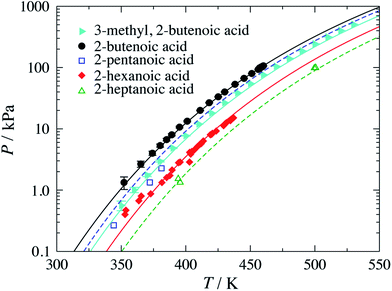 | ||
| Fig. 2 Vapour pressure of branched and unsaturated carboxylic acids. The symbols correspond to the experimental data for 3-methyl-2-butenoic acid,32 2-butenoic acid,33 2-pentenoic acid,34 2-hexenoic acid32 and 2-heptenoic acid.35 The filled symbols indicate experimental data used in the parameter estimation, while the open symbols are the data used to determine the adequacy of the theoretical description. The continuous curves correspond to calculations and predictions using SAFT-γ Mie group-contribution approach. | ||
A summary of the % AAD values for the vapour pressure and saturated-liquid density for the branched alkenes and unsaturated carboxylic acids considered in our current work is presented in Table 5. The reported values for the vapour pressure and saturated-liquid density, % AAD Pvap = 7.96% and % AAD ρsat = 3.94%, are slightly higher than the typical % AAD obtained for alkanes and carboxylic acids.19,36 We note that both the CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) and C
and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) are very small groups with shape factors of 0.20037 and 0.15330, respectively. The small groups thus make a smaller contribution to the thermophysical properties of the solution, and are thus more difficult to characterise. In the case of 2-pentenoic acid we find an especially large deviation of 34.5%; while this may suggest that further effort is required to refine the group-interaction parameters, we also highlight a large error reported in the experimental data source.34
are very small groups with shape factors of 0.20037 and 0.15330, respectively. The small groups thus make a smaller contribution to the thermophysical properties of the solution, and are thus more difficult to characterise. In the case of 2-pentenoic acid we find an especially large deviation of 34.5%; while this may suggest that further effort is required to refine the group-interaction parameters, we also highlight a large error reported in the experimental data source.34
| Compound | T/K | NP | % AAD Pvap | Ref. | T/K | Nρ | % AAD ρsat | Ref. |
|---|---|---|---|---|---|---|---|---|
| 2-Butenoic acid | 352–460 | 23 | 2.67 | 33 | ||||
| 2-Pentenoic acid | 350–450 | 11 | 34.5 | 34 | ||||
| 2-Hexenoic acid | 352–437 | 30 | 11.2 | 32 | ||||
| 3-Methyl-2-butenoic acid | 350–530 | 19 | 20.7 | 32 | 350–530 | 19 | 2.18 | 32 |
| 2-Methyl-1-butene | 274–413 | 30 | 3.63 | 34 | 183–408 | 24 | 4.37 | 34 |
| 2-Methyl-1,3-butadiene | 215–328 | 58 | 1.59 | 34 | 193–433 | 14 | 5.06 | 34 |
| Average | 7.96 | 3.94 |
Once these groups have been characterised, the SAFT-γ Mie approach can be used to predict the vapour pressure of geranic acid. In comparisons with the available experimental data37–39 (see Fig. 3(a)), we find an over-prediction of the vapour pressure of geranic acid, with an % AAD= 67.4%. Although this value is rather large, we note the scarcity of data, the discrepancies between the various experimental sources, and the small values of the pressures, with most data points two orders of magnitude below atmospheric pressure.
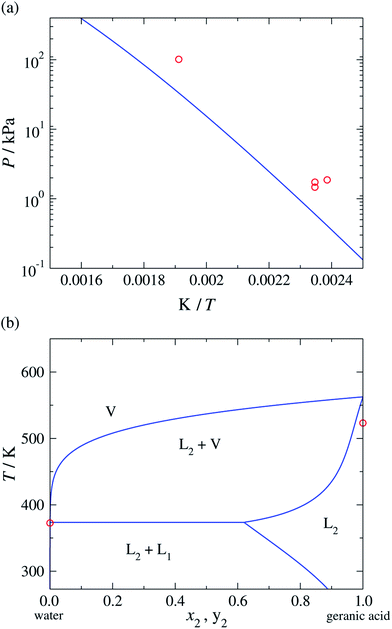 | ||
| Fig. 3 (a) Vapour pressure of geranic acid. (b) Temperature-composition phase diagram of water (1) + geranic acid (2) at a constant pressure of P = 101.325 kPa. The red symbols correspond to the experimental data37–39 and the continuous curves to the predictions obtained with the SAFT-γ Mie group-contribution approach. | ||
Following the decomposition of geranic acid into the appropriate functional groups and the estimation of the relevant group-interaction parameters, we proceed to develop the interaction parameters between the functional groups of geranic acid and water. Experimental vapour–liquid equilibrium (VLE) and liquid–liquid equilibrium (LLE) data of binary mixtures of n-alkenes and water are used to determine the unlike dispersion energy and repulsive-range parameters between H2O and the three unsaturated groups: CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) , CH
, CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) and C
and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) . More specifically, VLE data of propylene + water and 2-methyl-1,3-butadiene + water mixtures and LLE data of 1-butene + water mixtures are used.40 Despite the limited experimental data available for these systems, the SAFT-γ Mie calculations are found to be in relatively good agreement with the experimental data: we find % AADs for all the LLE and VLE data of 5.51% and 5.72%, respectively (see Tables 6 and 7). Once all of the group interactions are characterised, the approach can be used to model a range of thermophysical properties of geranic acid and water mixtures at different thermodynamic states, for broad ranges of compositions, temperatures and pressures. The predicted temperature-composition binary phase diagram of the mixture at a constant pressure P = 101.325 kPa is shown in Fig. 3(b), where regions of vapour–liquid and liquid–liquid equilibria can be seen. As in the case of pure geranic acid, there is a lack of experimental data for the mixture, which makes the analysis of the adequacy of our model in reproducing the experimental data difficult.
. More specifically, VLE data of propylene + water and 2-methyl-1,3-butadiene + water mixtures and LLE data of 1-butene + water mixtures are used.40 Despite the limited experimental data available for these systems, the SAFT-γ Mie calculations are found to be in relatively good agreement with the experimental data: we find % AADs for all the LLE and VLE data of 5.51% and 5.72%, respectively (see Tables 6 and 7). Once all of the group interactions are characterised, the approach can be used to model a range of thermophysical properties of geranic acid and water mixtures at different thermodynamic states, for broad ranges of compositions, temperatures and pressures. The predicted temperature-composition binary phase diagram of the mixture at a constant pressure P = 101.325 kPa is shown in Fig. 3(b), where regions of vapour–liquid and liquid–liquid equilibria can be seen. As in the case of pure geranic acid, there is a lack of experimental data for the mixture, which makes the analysis of the adequacy of our model in reproducing the experimental data difficult.
| Mixture | T/K | NP | % AAD PDew | Ref. |
|---|---|---|---|---|
| Propylene + water | 311–344 | 15 | 7.25 | 70 |
| Mixture | P/kPa | NP | % AAD T | Ref. |
|---|---|---|---|---|
| 2-Methyl-1,3-butadiene + 1-butanol | 101.330 | 6 | 0.28 | 40 |
3.2 Aqueous solutions of carboxylate salts
The modelling of aqueous carboxylate salt solutions requires the development of the anionic carboxylate functional group, COO−, and its interactions with other groups, including H2O. We have characterised these interactions by considering aqueous solutions of sodium carboxylate salts, R–COO−Na+, of various chain lengths (where R is CH3–(CH2)n with 0 ≤ n ≤ 4). We treat the salts as strong electrolytes, fully dissociated in aqueous solutions, neglecting the formation of ion pairs between the carboxylate anions and the alkali metal cations. This is consistent with experimental evidence, where the strength of ion pairing has been reported to be very weak,43 for the shorter alkyl carboxylate anions, namely formate and acetate salts.44–46 We note, however, that the short-chain salts exhibit typical 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolyte behaviour, whereas salts with chains longer than C4 exhibit increasingly atypical behaviour due to the aggregation of the anion in solution,47–50 with critical micellar concentrations reported to decrease as the alkyl chain length is increased.47 It is important to note that in its current formulation the SAFT-γ Mie approach does not account for the formation of micelles.
1 electrolyte behaviour, whereas salts with chains longer than C4 exhibit increasingly atypical behaviour due to the aggregation of the anion in solution,47–50 with critical micellar concentrations reported to decrease as the alkyl chain length is increased.47 It is important to note that in its current formulation the SAFT-γ Mie approach does not account for the formation of micelles.
The group interactions needed to model carboxylate salt solutions are estimated using experimental osmotic coefficient data41,42 of dilute and moderately concentrated salt solutions up to mR-COO−Na+ ≤ 1.0 mol kg−1 for the shorter alkylates (CH3COONa, C2H5COONa and C3H7COONa) and up to mR-COO−Na+ ≤ 0.7 mol kg−1 for larger carboxylate salts (C4H9COONa and C5H11COONa).
The SAFT-γ Mie model parameters for the COO− group are based on those previously determined for the uncharged carboxylic group (COOH), assuming that the overall shape of the COOH functional group does not change appreciably with the loss of a proton: identical values are used for the number of spherical segments 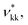 the shape factor Skk, and the segment diameter σkk, as well as for the exponents (λrkk, λakk) of the Mie potential to model COO− as to model COOH. The diameter required for the calculation of the Born term of the COO− group is obtained following the method proposed by Rashin and Honig;29 i.e.,
the shape factor Skk, and the segment diameter σkk, as well as for the exponents (λrkk, λakk) of the Mie potential to model COO− as to model COOH. The diameter required for the calculation of the Born term of the COO− group is obtained following the method proposed by Rashin and Honig;29 i.e., 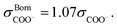 The dispersion energy εkk between ions is calculated using the polarisability α0 and the ionisation potential I (electron affinity) of the COO− functional group by applying eqn (10), as for previous models developed for ionic groups.20 The values used for the polarisability and the electron affinity are reported in Table 1. The unlike dispersion energy for the COO−–Na+ pair is also obtained with eqn (10), using the experimental values of α0 and I shown in Table 1, and the unlike interactions between H2O and Na+ are take from ref. 20. The unlike dispersion energy parameters between COO− and the alkyl groups are given the same values as those between COOH and the alkyl groups. In terms of the interaction of the COO− group with H2O, the unlike diameter is obtained using the standard combining rule presented eqn (5) (in effect resulting in the same value as σCOOH,H2O between the COOH group and H2O). The only interactions which are refined relate to the unlike dispersion and association interactions between COO− and H2O. Four association sites of type e, corresponding to the lone pairs of electrons of the oxygen atoms in the COO− group are considered. This is consistent with the fact that this anion is reported to have a symmetrical structure, with the alkali cations showing no significant tendency to interact preferentially with any one of the oxygens atoms.43 This is in contrast to the association interactions used to represent the COOH group, where the two oxygen atoms are clearly distinguishable, resulting in two distinct peaks in the photoelectron spectrum.51 Self-association between COO− ions is not considered. The SAFT-γ Mie model parameters for COO− are given in Table 2.
The dispersion energy εkk between ions is calculated using the polarisability α0 and the ionisation potential I (electron affinity) of the COO− functional group by applying eqn (10), as for previous models developed for ionic groups.20 The values used for the polarisability and the electron affinity are reported in Table 1. The unlike dispersion energy for the COO−–Na+ pair is also obtained with eqn (10), using the experimental values of α0 and I shown in Table 1, and the unlike interactions between H2O and Na+ are take from ref. 20. The unlike dispersion energy parameters between COO− and the alkyl groups are given the same values as those between COOH and the alkyl groups. In terms of the interaction of the COO− group with H2O, the unlike diameter is obtained using the standard combining rule presented eqn (5) (in effect resulting in the same value as σCOOH,H2O between the COOH group and H2O). The only interactions which are refined relate to the unlike dispersion and association interactions between COO− and H2O. Four association sites of type e, corresponding to the lone pairs of electrons of the oxygen atoms in the COO− group are considered. This is consistent with the fact that this anion is reported to have a symmetrical structure, with the alkali cations showing no significant tendency to interact preferentially with any one of the oxygens atoms.43 This is in contrast to the association interactions used to represent the COOH group, where the two oxygen atoms are clearly distinguishable, resulting in two distinct peaks in the photoelectron spectrum.51 Self-association between COO− ions is not considered. The SAFT-γ Mie model parameters for COO− are given in Table 2.
As with the previous systems, the development of the interaction parameters follows a stepwise procedure. The H2O–COO− unlike interaction parameters (εkl, εHBkl and KHBkl) are optimised using osmotic coefficient data of aqueous solutions of sodium butanoate for concentrations up to mR-COO−Na+ ≤ 1 mol kg−1 and of sodium pentanoate and hexanoate salts for concentrations up to mR-COO−Na+ ≤ 0.7 mol kg−1. Carboxylate salts with shorter alkyl chains than butanoate are not considered in the parameter estimation procedure as the COO− group is expected to have a large polarising effect on the neighbouring alkyl groups in such compounds. We note that similar assumptions were made in the development of the COOH group,36 which was characterised using carboxylic acids with chain lengths larger than C4.
Nevertheless, it is important to be able to model shorter chain-length carboxylates, and we develop tailored models specifically for these compounds. In order to take into account the polarization effect in the shorter-chained carboxylic acids and carboxylate salts, second-order adjacent groups adjCH2 and adjCH3 are introduced to model the acetates and propanoates. The same like- and unlike-interaction parameters are employed for these adjacent functional groups as for the regular CH2 and CH3 alkyl groups, but different adjCH2–COO− and adjCH3–COO− unlike parameters between the adjacent alkyl groups and the carboxylate group are determined; these are estimated from an additional parameter estimation procedure using osmotic coefficient data of aqueous sodium propanoate and sodium acetate solutions at standard conditions for concentrations up to mR-COO−Na+ ≤ 1.0 mol kg−1. Thus, when modelling a carboxylate CH3–(CH2)n–COO−, one uses the adjCH3–COO− and adjCH2–COO− unlike interactions for n = 0, 1, 2 and the CH3–COO− and CH2–COO− interactions for n > 2. All the SAFT-γ Mie group parameters used in our current work are summarised in Tables 2–4.
The performance of the SAFT-γ Mie group-contribution approach for aqueous solutions of sodium carboxylate salts is assessed by predicting the thermodynamic properties of a number of systems at several thermodynamic states not considered in the parameter estimation procedure. The osmotic coefficient, the mean ionic activity coefficient, liquid-phase density and vapour pressure beyond the concentration range included in the parameter estimation are predicted and compared to experimental data in Fig. 4. We note that experimental data for both the density and the vapour pressure are scarce for solutions of carboxylate anions larger than CH3COO−. The activity and osmotic coefficients of dilute solutions exhibit a concentration dependence which is typical of that for strong electrolyte solutions and the magnitude of both is seen to increase with increasing chain length of the salt. The theoretical predictions are seen to be in good overall agreement with the experimental data available in the lower range of concentrations, both in terms of the activity and the osmotic coefficients. The concentration dependence of the activity and osmotic coefficients for the larger chain carboxylate salts (≥C4) exhibit a change in slope from positive to negative, with a maximum at a specific concentration (cf. Fig. 4(b) and (d)), which is related to micelle formation.47–50 The current SAFT-γ approach does not account for these aggregates, and as a result the predictions are seen to deviate from the data at higher concentrations for the butanoate and pentanoate salts.
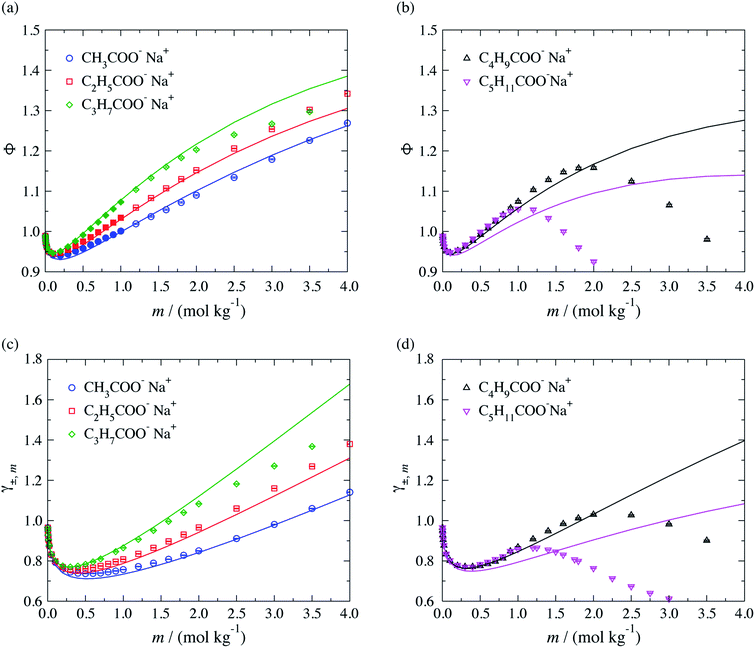 | ||
| Fig. 4 Concentration dependence of (a and b) the osmotic coefficient Φ and (c and d) mean ionic activity coefficient γ±,m for aqueous sodium carboxylate salts of different chain lengths at a temperature of T = 298 K and pressure of P = 101.325 kPa. The continuous curves are obtained using the SAFT-γ Mie group-contribution approach. The filled symbols represent the experimental data41,42 considered for the parameter estimation while the open symbols are used to assess the adequacy of the theoretical prediction. The different symbols correspond to different compounds as specified in the legend. | ||
The isobaric liquid density ρ of aqueous sodium-carboxylate solutions is displayed in Fig. 5 as a function of the concentration for a temperature range of 288.15–318.15 K. The SAFT-γ Mie predictions are seen to be in good overall agreement with the available experimental data, with densities that increase with increasing salt concentration and decrease with increasing temperature. In Fig. 5(b) the model is seen to reproduce the experimental decrease in liquid density with increasing chain length of the carboxylate anions. The model overestimates the available liquid-phase density data52–59 of sodium carboxylate aqueous solutions at low (mR-COO−Na+ < 0.75 mol kg−1) concentration (as a consequence of the overestimation of the density of pure water at the conditions considered), and underestimates the density at high concentrations (mR-COO−Na+ ≥ 0.75 mol kg−1).
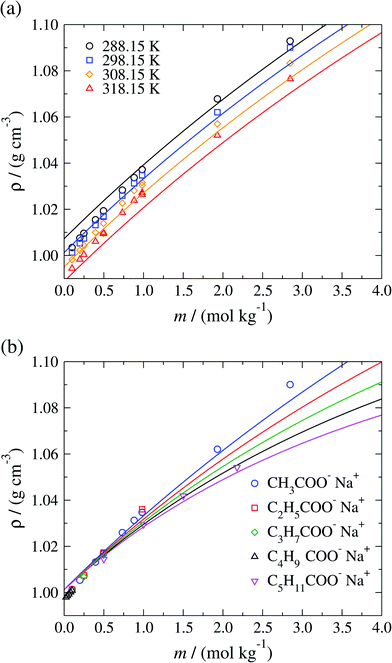 | ||
| Fig. 5 Concentration dependence of the liquid-phase density ρ of (a) aqueous sodium acetate solutions at a pressure of P = 101.325 kPa over the temperature range 288.15–318.15 K, and (b) of different aqueous sodium carboxylate salt solutions at standard conditions, namely P = 101.325 kPa and T = 298.15 K for several carboxylate chain lengths. The continuous curves correspond to predictions using the SAFT-γ Mie group-contribution approach and the symbols to experimental data.52–59 The different symbols correspond to different conditions and compounds as specified in the legends. | ||
The versatility of the SAFT-γ Mie group-contribution approach is further illustrated in Fig. 6, where the concentration dependence of the vapour pressure of aqueous solutions of sodium acetate at 298.15 K and 308.15 K is shown. The SAFT-γ Mie theoretical predictions can be seen to reproduce the experimental results with quantitative accuracy. It is interesting to note that even though the model parameters are estimated from osmotic coefficient data for aqueous solutions of sodium carboxylate at T = 298.15 K and P = 101.325 kPa and only for a low range of concentrations, the other properties can be predicted accurately across a broad range of thermodynamic states.
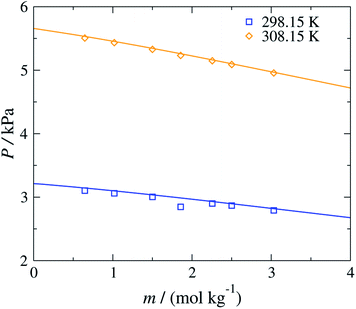 | ||
| Fig. 6 Concentration dependence of the vapour pressure P of aqueous sodium acetate solutions at 298.15 and 308.15 K. The continuous curves are obtained using the SAFT-γ Mie group-contribution approach. The symbols represents the experimental data.60 The different symbols correspond to different conditions as specified in the legend. | ||
Moreover, the models developed here can also be used to study aqueous solutions of potassium carboxylate. We now predict the osmotic and activity coefficients and vapour pressures of potassium acetate aqueous solutions. This test allows us to assess the transferability of the parameters that characterise the COO−–H2O interactions, which are of key importance in representing the target CAGE mixture. As with other ions, the COO−–K+ unlike ion–ion dispersion energy is obtained with eqn (10), using the experimental values of α0 and I given in Table 1, and the unlike interactions between H2O and K+ are taken from ref. 20. The concentration dependence of the osmotic and activity coefficient of several aqueous solutions of potassium acetate at standard conditions are shown in Fig. 7, where the model is seen to provide a good description of the experimental data. A small underestimation of the data for salt concentration higher than mR-COO−Na+ ≥ 2.5 mol kg−1 is noted, which may be related to ion aggregation and ion-pairing, a feature not considered in our current model. A very satisfactory representation of the vapour pressure for these systems over a broad range of temperatures can be seen Fig. 7(c) and (d).
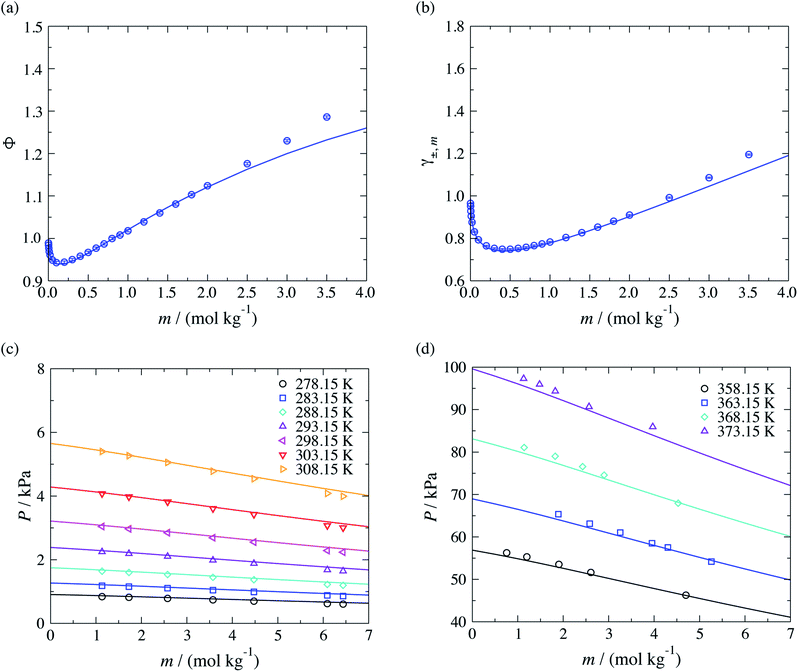 | ||
| Fig. 7 Prediction of thermophysical properties of aqueous solutions of potassium acetate for different thermodynamic states. Concentration dependence of (a) the osmotic coefficient Φ and (b) mean ionic activity coefficient γ±,m at a temperature of T = 298 K and a pressure of P = 101.325 kPa, and concentration dependence (c) of the vapour pressure over the temperature range 278.15–303.15 K and (d) of the vapour pressure over the temperature range 358.15–373.15 K. The continuous curves correspond to the SAFT-γ Mie group-contribution approach. The symbols represent the experimental data for osmotic and activity coefficients,41 and the vapour pressures.61,62 The different symbols corresponds to different conditions as specified in the legend. | ||
We emphasise that this excellent agreement between the thermophysical properties predicted for a wide range of thermodynamic conditions and the experimental data is achieved using a unique set of transferable intermolecular parameters between the carboxylate group COO− and H2O for all the aqueous carboxylate salt solutions considered. The SAFT-γ Mie model developed for these systems is shown to be transferable and robust. The performance of the model will be further assessed for choline chloride and CAGE in the following sections.
3.3 Aqueous solutions of choline choride
We model choline chloride as fully dissociated in water. An N+ group is used in the cation, which is characterised using parameters based on those of the uncharged N group present in triethanolamine.63 The unlike dispersion energy parameters between N+ and the alkyl groups and between N+ and CH2OH are given the same values as those between N and the alkyl groups and between N and CH2OH, respectively.63 The COO−–Cl− unlike dispersion energy is obtained with eqn (10), using the experimental values of α0 and I given in Table 1, and the unlike interactions between H2O and Cl− are taken from ref. 20. The parameters summarised in Tables 2–4 are used to predict the isobaric temperature-composition vapour–liquid equilibria of aqueous solutions of choline chloride.64 The resulting SAFT-γ Mie predictions are shown in Fig. 8 as a function of the salt concentration for various pressures. It is encouraging to see that although a group-contribution approach is used in the development of the model of choline chloride, with all the interactions transferred from group interactions characterised using other compounds and thermodynamic states, or through combining rules, our calculations provide a description of the vapour–liquid equilibria which are in close agreement with the available experimental data.64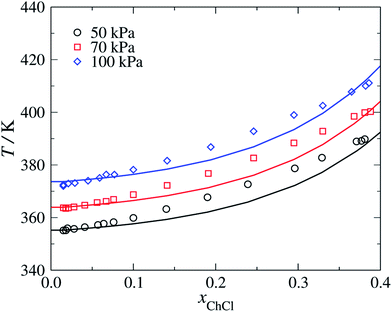 | ||
| Fig. 8 Isobaric vapour–liquid equilibria for aqueous solution of choline chloride (ChCl) at pressures of P = 50, 70 and 100 kPa. The continuous curves correspond to SAFT-γ Mie predictions and the symbols to the experimental data.64 | ||
3.4 Aqueous mixture of choline, geranate and geranic acid (CAGE)
In addition to the groups characterised thus far, the description of the thermodynamic properties of aqueous solutions of CAGE requires the determination of the interactions between the CH2OH group and the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) and CH
and CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) groups; the unlike dispersion energies between these groups are given in Table 2. In the characterisation of these interactions we have used experimental vapour–liquid equilibrium data of 1-propene + 1-propanol and 2-methyl-1,3-butadiene + 1-butanol binary mixtures (see Table 6). Having characterised these group interactions it is possible to carry out predictive calculations of the thermodynamic properties of the CAGE + water mixture of interest with the SAFT-γ Mie group-contribution approach. CAGE is modelled as a 1
groups; the unlike dispersion energies between these groups are given in Table 2. In the characterisation of these interactions we have used experimental vapour–liquid equilibrium data of 1-propene + 1-propanol and 2-methyl-1,3-butadiene + 1-butanol binary mixtures (see Table 6). Having characterised these group interactions it is possible to carry out predictive calculations of the thermodynamic properties of the CAGE + water mixture of interest with the SAFT-γ Mie group-contribution approach. CAGE is modelled as a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio mixture of choline
1 mole ratio mixture of choline![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) geranate
geranate![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) geranic acid, and the calculated density of the mixtures is used to convert from mole fraction to molarity in order for direct comparisons with the experimental data.
geranic acid, and the calculated density of the mixtures is used to convert from mole fraction to molarity in order for direct comparisons with the experimental data.
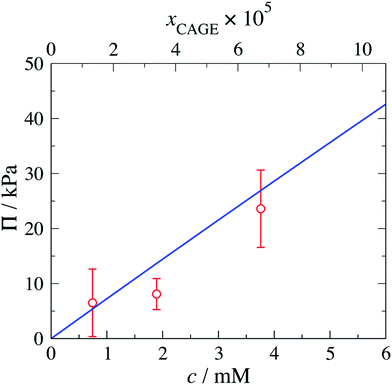
The predicted osmotic pressure for CAGE + water mixtures as a function of concentration is shown in Fig. 9 together with the experimental values obtained in this work. The measured data and corresponding SAFT-γ Mie predictions can also be found in Table 8. We note the relatively larger standard deviation reported for the lowest concentration in Table 8 is caused by one of the three repeated values at this concentration returning a value of zero. The zero reading may have been due to poor sampling or to a cancellation of thermodynamic effects. The osmometer directly compares the dew point depression of the CAGE + water sample with an internal water reference. It is known that CAGE + water mixtures undergo structural re-arrangements. If these re-arrangements were associated with an exothermic change, the energy released may have increased the temperature and thus cancelled the effect of dew-point depression, resulting in an overall reading value of zero. The instrument thermocouple has a resolution of 0.00031 °C.
| xCAGE × 105 | c/(103× mol L−1) | ΠexpCAGE/kPa | ΠSAFTCAGE/kPa | % AAD |
|---|---|---|---|---|
| 1.33 | 0.74278 | 6.50 ± 6.1340 | 5.3867 | 17.118 |
| 3.39 | 1.8907 | 8.10 ± 2.8140 | 13.629 | 67.759 |
| 6.75 | 3.7589 | 23.6 ± 7.0357 | 26.888 | 14.125 |
In terms of the agreement of the SAFT-γ Mie calculations and the experimental data we emphasise that the experimental data presented in this section are not considered in the development of the model for these solutions. The good agreement between the predictions and the measured data highlights the capability and robustness of the models developed here.
4 Conclusions
The SAFT-γ Mie group-contribution approach is used to predict the osmotic pressure of mixture involving choline, geranate, and geranic acid (CAGE) and the adequacy of the approach is assessed by comparison with new experimental measurements obtained as part of this work. A number of new SAFT-γ Mie groups and group interactions, including ionic groups, appropriate to model the system of interest are characterised using a variety of experimental phase-equilibrium and solution data for pure components and mixtures. The model is successively tested by carrying out predictive calculations for representative mixtures, conditions, and properties not used in the parameter development. The SAFT-γ predictions are shown to be in very good overall agreement with the experimental data for the systems tested. In particular we develop a model for aqueous solutions of carboxylate salts, assuming the charged species are fully dissociated in water and neglecting micelle formation. The model developed is found to be predictive and fully transferable to other carboxylate salts solutions at different thermodynamic conditions, up to concentrations where micellisation is expected. A model for choline chloride is also presented, considering the anion and cation as dissociating species in water. We further extend the set of functional groups in the SAFT-γ Mie approach introducing new groups, such as COO− and N+. The resulting model is then used to predict the osmotic pressure of aqueous CAGE solutions, which is found in excellent agreement with experimental measurements. These encouraging results confirm the transferability and robustness of the SAFT-γ group-contribution approach for the prediction of thermodynamic properties of complex mixtures in general and highlights its promise for applications involving deep-eutectic solvent mixtures and ionic liquids in particular.Data statement
Data underlying this article can be accessed on Zenodo at https://zenodo.org/record/3540689#.Xcv6WFf7Q2x, and used under the Creative Commons Attribution license.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from GSK. We are also grateful to Tom Welton and his group for the sample of CAGE used in this work, and especially to David Pugh for his help in the preparation and analysis of the CAGE samples. We thank the Engineering and Physical Sciences Research Council (EPSRC) of the UK for additional funding to the Molecular Systems Engineering Group through Grants EP/E016340/1 and EP/J014958/1. GL is thankful to Pfizer and SHK to Petronas for the award of PhD studentships. CSA acknowledges support from the EPSRC via a Leadership Fellowship (EP/J003840/1). AG acknowledges the funding of a Research Chair by the Royal Academy of Engineering and Lilly (RCSRF1819/7/33).References
- S. N. Pedro, M. G. Freire, C. S. Freire and A. J. Silvestre, Expert Opin. Drug Delivery, 2019, 16, 497–506 CrossRef PubMed.
- E. L. Smith, A. P. Abbott and K. S. Ryder, Chem. Rev., 2014, 114, 11060–11082 CrossRef CAS PubMed.
- I. M. Marrucho, L. C. Branco and L. P. N. Rebelo, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 527–546 CrossRef CAS PubMed.
- M. Zakrewsky, K. S. Lovejoy, T. L. Kern, T. E. Miller, V. Le, A. Nagy, A. M. Goumas, R. S. Iyer, R. E. Del Sesto, A. T. Koppisch, D. T. Fox and S. Mitragotri, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13313–13318 CrossRef CAS PubMed.
- M. Zakrewsky, A. Banerjee, S. Apte, T. L. Kern, M. R. Jones, R. E. D. Sesto, A. T. Koppisch, D. T. Fox and S. Mitragotri, Adv. Healthcare Mater., 2016, 5, 1282–1289 CrossRef CAS PubMed.
- A. Banerjee, K. Ibsen, Y. Iwao, M. Zakrewsky and S. Mitragotri, Adv. Healthcare Mater., 2017, 6, 1601411 CrossRef PubMed.
- K. N. Ibsen, H. Ma, A. Banerjee, E. E. Tanner, S. Nangia and S. Mitragotri, ACS Biomater. Sci. Eng., 2018, 4, 2370–2379 CrossRef CAS.
- E. E. L. Tanner, K. N. Ibsen and S. Mitragotri, J. Controlled Release, 2018, 286, 137–144 CrossRef CAS PubMed.
- E. E. L. Tanner, K. M. Piston, H. Ma, K. N. Ibsen, S. Nangia and S. Mitragotri, ACS Biomater. Sci. Eng., 2019, 5, 3645–3653 CrossRef CAS.
- J. Gross and G. Sadowski, Ind. Eng. Chem. Res., 2001, 40, 1244–1260 CrossRef CAS.
- S. P. Verevkin, A. Y. Sazonova, A. K. Frolkova, D. H. Zaitsau, I. V. Prikhodko and C. Held, Ind. Eng. Chem. Res., 2015, 54, 3498–3504 CrossRef.
- L. F. Zubeir, C. Held, G. Sadowski and M. C. Kroon, J. Phys. Chem. B, 2016, 120, 2300–2310 CrossRef CAS PubMed.
- P. V. Pontes, E. A. Crespo, M. A. Martins, L. P. Silva, C. M. Neves, G. J. Maximo, M. D. Hubinger, E. A. Batista, S. P. Pinho, J. A. Coutinho, G. Sadowski and C. Held, Fluid Phase Equilib., 2017, 448, 69–80 CrossRef CAS.
- X. Ji, C. Held and G. Sadowski, Fluid Phase Equilib., 2012, 335, 64–73 CrossRef CAS.
- A. Nann, C. Held and G. Sadowski, Ind. Eng. Chem. Res., 2013, 52, 18472–18481 CrossRef CAS.
- H. Passos, I. Khan, F. Mutelet, M. B. Oliveira, P. J. Carvalho, L. M. Santos, C. Held, G. Sadowski, M. G. Freire and J. A. Coutinho, Ind. Eng. Chem. Res., 2014, 53, 3737–3748 CrossRef CAS.
- V. Papaioannou, T. Lafitte, C. Avendaño, C. S. Adjiman, G. Jackson, E. A. Müller and A. Galindo, J. Chem. Phys., 2014, 140, 054107 CrossRef PubMed.
- S. Dufal, V. Papaioannou, M. Sadeqzadeh, T. Pogiatzis, A. Chremos, C. S. Adjiman, G. Jackson and A. Galindo, J. Chem. Eng. Data, 2014, 59, 3272–3288 CrossRef CAS.
- P. Hutacharoen, S. Dufal, V. Papaioannou, R. M. Shanker, C. S. Adjiman, G. Jackson and A. Galindo, Ind. Eng. Chem. Res., 2017, 56, 10856–10876 CrossRef CAS.
- D. K. Eriksen, G. Lazarou, A. Galindo, G. Jackson, C. S. Adjiman and A. J. Haslam, Mol. Phys., 2016, 114, 2724–2749 CrossRef CAS.
- G. Lazarou, Development of the SAFT-γ Mie equation of state for predicting the thermodynamic behaviour of strong and weak electrolytes, PhD Thesis, Imperial College London, 2017.
- C. Avendaño, T. Lafitte, A. Galindo, C. S. Adjiman, G. Jackson and E. A. Müller, J. Phys. Chem. B, 2011, 115, 11154–11169 CrossRef PubMed.
- E. A. Müller and G. Jackson, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 405–427 CrossRef PubMed.
- G. Mie, Ann. Phys., 1903, 316, 657–697 CrossRef.
- M. Born, Z. Phys., 1920, 1, 45–48 CrossRef CAS.
- L. Blum, J. Chem. Phys., 1974, 61, 2129–2133 CrossRef CAS.
- L. Blum, Mol. Phys., 1975, 30, 1529–1535 CrossRef CAS.
- J. Rowlinson, Liquids and liquid mixtures: Butterworths monographs in chemistry, Boston, Butterworth, 1982 Search PubMed.
- A. A. Rashin and B. Honig, J. Phys. Chem., 1985, 89, 5588–5593 CrossRef CAS.
- C. Großmann and G. Maurer, Fluid Phase Equilib., 1995, 106, 17–25 CrossRef.
- Process Systems Enterprise, gPROMS ModelBuilder V. 5.0.1, http://www.psenterprise.com/gproms Search PubMed.
- Y. Van-Chin-Syan, Y. A. Raevskii, V. Kochubei and K. Z. Kotovich, Russ. J. Phys. Chem., 1997, 71, 1416–1580 Search PubMed.
- R. D'isouza and A. S. Teja, Chem. Eng. Commun., 1987, 61, 13–22 CrossRef.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg, MD, 2019, 20899 Search PubMed.
- R. Hans, R. Max and L. Walther, Ber. Dtsch. Chem. Ges., 1902, 35, 4265–4272 CrossRef.
- M. Sadeqzadeh, V. Papaioannou, S. Dufal, C. S. Adjiman, G. Jackson and A. Galindo, Fluid Phase Equilib., 2016, 407, 39–57 CrossRef CAS.
- A. Scheunert, Liebigs Ann., 1902, 324, 97–112 CrossRef.
- F. Tiemann and F. W. Semmler, Ber. Dtsch. Chem. Ges., 1893, 26, 2708–2729 CrossRef.
- R. Kuhn, F. Köhler and L. Köhler, Biol. Chem., 1936, 242, 171–197 CrossRef CAS.
- T. Lesteva, E. Khrapkova, V. Gilmutdinova, V. Chernaya and E. Sire, J. Appl. Chem. USSR, 1974, 47, 1813–1816 Search PubMed.
- W. J. Hamer and Y. Wu, J. Phys. Chem. Ref. Data, 1972, 1, 1047–1100 CrossRef CAS.
- O. D. Bonner, J. Solution Chem., 1988, 17, 999–1002 CrossRef CAS.
- E. F. Aziz, N. Ottosson, S. Eisebitt, W. Eberhardt, B. Jagoda-Cwiklik, R. Vácha, P. Jungwirth and B. Winter, J. Phys. Chem. B, 2008, 112, 12567–12570 CrossRef CAS PubMed.
- P. G. Daniele, A. De Robertis, C. De Stefano, S. Sammartano and C. Rigano, J. Chem. Soc., Dalton Trans., 1985, 2353–2361 RSC.
- D. Archer and C. Monk, J. Chem. Soc., 1964, 3117–3122 RSC.
- J. Oscarson, S. Gillespie, J. Christensen, R. Izatt and P. Brown, J. Solution Chem., 1988, 17, 865–885 CrossRef CAS.
- E. R. Smith and R. Robinson, J. Chem. Soc., Faraday Trans., 1942, 38, 70–78 RSC.
- G. Douhéret and A. Viallard, Fluid Phase Equilib., 1982, 8, 233–250 CrossRef.
- P. Ekwall and P. Stenius, Acta Chem. Scand., 1967, 21, 1767–1772 CrossRef CAS.
- F. Eriksson, J. C. Eriksson and P. Stenius, Colloids Surf., 1981, 3, 339–356 CrossRef CAS.
- P. Jungwirth and B. Winter, Annu. Rev. Phys. Chem., 2008, 59, 343–366 CrossRef CAS PubMed.
- T. S. Banipal, K. Singh, P. K. Banipal, A. K. Sood, P. Singh, G. Singh and P. Patyar, J. Chem. Eng. Data, 2008, 53, 2758–2765 CrossRef CAS.
- S. Bochmann, P. M. May and G. Hefter, J. Chem. Eng. Data, 2011, 56, 5081–5087 CrossRef CAS.
- J. Wang, Z. Yan, K. Zhuo and J. Lu, Biophys. Chem., 1999, 80, 179–188 CrossRef CAS PubMed.
- Z.-N. Yan, Q.-T. Cheng, J.-J. Wang and D.-Z. Liu, Acta Phys.-Chim. Sin., 1999, 15, 662–667 CAS.
- T. S. Banipal, K. Singh and P. K. Banipal, J. Solution Chem., 2007, 36, 1635–1667 CrossRef CAS.
- Z. Yan, J. Wang and J. Lu, J. Chem. Eng. Data, 2001, 46, 217–222 CrossRef CAS.
- A. Chmielewska, A. Wypych-Stasiewicz and A. Bald, J. Mol. Liq., 2005, 122, 110–115 CrossRef CAS.
- J. Wang, Z. Yan and J. Lu, J. Chem. Thermodyn., 2004, 36, 281–288 CrossRef CAS.
- R. Beyer and M. Steiger, J. Chem. Thermodyn., 2002, 34, 1057–1071 CrossRef CAS.
- R. Beyer, Characterization of binary and ternary electrolyte systems with anions of organic acids. Measurement of the water activity coefficient and thermodynamic modeling, PhD Thesis, University of Hamburg, 2001.
- Z. Z. Li B and Y. Luo, Chin. J. Chem. Eng., 1986, 1, 102–110 Search PubMed.
- F. Perdomo, S. H. Khalit, C. S. Adjiman, G. Jackson and A. Galindo, 2019, in preparation.
- P. J. Carvalho, I. Khan, A. Morais, J. F. Granjo, N. M. Oliveira, L. M. Santos and J. A. Coutinho, Fluid Phase Equilib., 2013, 354, 156–165 CrossRef CAS.
- N. Pyper, C. Pike and P. Edwards, Mol. Phys., 1992, 76, 353–372 CrossRef CAS.
- Z. Lu and R. E. Continetti, J. Phys. Chem. A, 2004, 108, 9962–9969 CrossRef CAS.
- D. R. Lide, Handbook of Chemistry and Physics: CRC Handbook, CRC Press, London, UK, 86th edn, 2005 Search PubMed.
- S. Dufal, T. Lafitte, A. J. Haslam, A. Galindo, G. N. Clark, C. Vega and G. Jackson, Mol. Phys., 2015, 113, 948–984 CrossRef CAS.
- P. Hutacharoen, Prediction of partition coefficients and solubilities of active pharmaceutical ingredients with the SAFT-γ Mie group-contribution approach, PhD Thesis, Imperial College London, 2017.
- C. Li and J. J. McKetta, J. Chem. Eng. Data, 1963, 8, 271–275 CrossRef CAS.
- Q. Sun, X. Ma, X. Guo and J. Zhang, Fluid Phase Equilib., 2013, 346, 1–7 CrossRef CAS.
- T. W. Leland, J. J. McKetta and K. A. Kobe, Ind. Eng. Chem. Res., 1955, 47, 1265–1271 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07057e |
| ‡ Current address: Department of Chemistry, Molecular Sciences Research Hub, White City Campus, Imperial College London, London W12 0BZ, UK. |
| This journal is © The Royal Society of Chemistry 2019 |