A DFT study for silicene quantum dots embedded in silicane: controllable magnetism and tuneable band gap by hydrogen

Abstract

This paper presents a design for silicene quantum dots (SiQDs) embedded in silicane. The shape and size of an embedded SiQD are managed by hydrogen atoms. A first-principles method was used to evaluate the magnetism as well as the electronic and structural properties of embedded SiQDs of various shapes and sizes. The shape of the embedded SiQD determined its electronic structure as well as the dot size. Moreover, the magnetic properties of SiQDs in silicane were highly shape dependent. The triangular SiQDs were all magnetic, some small parallelogram SiQDs were nonmagnetic, and all others were antiferromagnetic; almost all hexagonal SiQDs were nonmagnetic. An unequal number of bare Si atoms at the A and B sites was identified as a critical factor for establishing magnetism in embedded SiQDs. The tip of a triangular SiQD enhanced the magnetic moment of the dot. The parallelogram SiQD with two tip atoms appeared as a magnetic needle and has potential for use in spintronic applications. SiQDs embedded in silicane can be used in the design of silicon-based nanoelectronic devices and binary logic based on nanoscale magnetism.

---

Introduction

Quantum dots (QDs) have attracted substantial research interest because of their various physical properties, design flexibility, and wide application (e.g., optical devices, biosensing, and quantum computing).^1–7 QDs are well known for their highly tuneable characteristics. Composition and structure determine the physical and chemical properties of QDs, and the physical properties can also be altered as a function of shape, size, and strain.^8–10 The electronic properties of zero-dimensional QDs are molecule-like with respect to their complete confinement.^11,12

In 2004, the discovery of graphene introduced new avenues for developments in materials science.¹³ Two-dimensional (2-D) graphene and beyond are entirely new types of materials and have introduced remarkable prospects for nanomaterials. The growth of single-layer group IV materials is expected to further expand the types of traditional semiconductor materials available. These materials attract substantial interest not only for fundamental research but also for electronic device applications. Because silicon is the primary material used for fabricating electronic devices, single-layer silicene has also been studied extensively.^14–17 It can shorten the application gap of new types of materials and reduce the industry cost. The structure of silicene is similar to that of graphene, with the exception that silicon atoms buckle in a perpendicular rather than planar direction.^16,17 In silicene, silicon atoms exhibit sp³ hybridization, which results in a buckled hexagonal structure; however, silicene also retains linear energy bands in the vicinity of K and K′ points in the first Brillouin zone and high charge carrier mobility, which is similar to graphene. Nevertheless, the buckled structure of silicene provides opportunities for tuning the band gap, such as applying the external field, and enables facile chemical adsorption.^14,17–20 Recently, the first silicene transistor was produced.²¹

Silicene can also be fully hydrogenated on both sides in a similar fashion to graphene. Fully hydrogenated silicene, referred to as silicane, opens a considerable band gap.^22,23 The material changes from a metal to a semiconductor during the hydrogenation process of silicene to silicane. Research has revealed that hydrogen can change the magnetic configuration of some carbon-based materials such as graphite and graphene.^24–26 Some partially hydrogenated graphene is magnetic because of localized and unpaired electrons from unhydrogenated carbon atoms. Carbon atoms with or without a hydrogen in hydrogenated graphene prefer to aggregate and form separated C and CH domains.²⁷ Hydrogenation constitutes a novel method for tuning properties with unprecedented potential for applications.²⁴ Similarly, hydrogenation may alter the magnetic configuration of silicene. Partially hydrogenated silicene also favours the separation of hydrogenated and unhydrogenated regions.²⁸ Separated areas of silicene and silicane can provide new patterns for silicon-based 2-D nano devices, enabling the synthesis of a 2-D silicene quantum dot embedded in silicane.

Silicene quantum dots (SiQDs) are expected to have great potential for use in a wide range of applications, such as biosensing, bioimaging, therapeutics, drug delivery, photovoltaics, and catalysis.^29–33 SiQDs embedded in silicane can be patterned through hydrogenation and are excellent candidates for use in the design of nano devices. This research revealed that the shape of a SiQD not only alters its electronic structure but also its magnetism. The electronic properties of SiQDs change as a function of both size and shape. This paper presents the electronic and magnetic properties of SiQDs embedded in silicane.

Computational details

Method

This investigation was based on the density functional theory³⁴ with generalized gradient approximation.³⁵ The potentials adopted were based on the projector augmented-wave method^36,37 and were in the Perdew–Burke–Ernzerhof functional form both for the silicon and hydrogen ions.³⁸ The wave functions were expanded by plane waves. Moreover, the energy convergence was tested and the cutoff energy of 312.5 eV was used. Spin polarization was included. Spin–orbit coupling was also considered, but its effect was marginal and could be ignored in this system. The Monkhorst–Pack scheme was adopted for k-point sampling. The k-point mesh was tested up to 9 × 9 × 1, and the k-mesh of 3 × 3 × 1 was used. The system was relaxed until the Hellmann–Feynman force was less than 0.01 eV Å⁻¹. The system was simulated using a supercell with a periodic boundary condition in the x–y plane and a vacuum layer in the z-direction. The 8 × 8 and 12 × 12 supercells in the x–y plane were considered, which had as many as 256 and 576 atoms, respectively. A vacuum layer thickness of 20 Å was used to prevent the artificial atomic interaction between adjacent supercells. The VASP code was used in the calculations.

Structures

Both silicene and silicane have a honeycomb lattice. The hexagonal structure contains two different sites, referred to as A and B sites. The atoms situated at the A and B sites are buckled on the opposite sides of the silicene plane. For silicane, the hydrogen atom adsorbed on the Si atoms at the A and B sites are also on the opposite side of the silicene and enhance the buckling of atoms at the A and B sites. The embedded SiQDs presented in Fig. 1 are in the region of Si atoms without hydrogen atoms adsorbed in the silicane. The pink balls denote hydrogen atoms and have been enlarged to clarify the shape of the QDs. These regions can be a triangle, parallelogram, or hexagon. The triangular dot is referred to as the embedded triangular SiQD, and the name of QDs with other shapes adhere to the same rule. The embedded triangular and parallelogram SiQDs all have zigzag (ZZ) edges, and the hexagonal QDs with zigzag and armchair (AC) edges were investigated (Fig. 1a). Two types of SiQDs were considered for the triangular and parallelogram dots. The type-I triangular SiQD had bare Si atoms at three tips, and the type-I parallelogram SiQD had bare Si atoms at two tips, as can be seen in the upper part of Fig. 1b and c. When the three (two) tip atoms in the type-I triangular (parallelogram) SiQDs adsorb hydrogen atoms, they become the type-II SiQDs (as presented in the lower part of Fig. 1b and c). The type-II triangular and parallelogram SiQDs all consist of hexagons, which is similar to the hexagonal SiQDs with zigzag edges. N denotes the number of bare Si atoms without hydrogen atoms inside the SiQD. The side view of an embedded parallelogram SiQD is also drawn in Fig. 1d to have a clear picture for the QD embedded in silicane. The number of Si and H atoms in the system of a SiQD embedded in silicane are 128 (288) and 128–N (288–N), respectively, for 8 × 8 (12 × 12) supercell.

Fig. 1 Structures of SiQDs embedded in silicane: (a) hexagonal SiQDs with zigzag edges (ZZ) and armchair edges (AC), type-I and type-II of (b) the triangular SiQDs, and (c) the parallelogram SiQDs. (d) Side view of the embedded parallelogram SiQD shown in the upper part of (c) along the y-direction. Pink and black balls denoted hydrogen atoms and silicene atoms, respectively.

Results and discussion

Six shapes of embedded SiQDs were investigated, all of which exhibited notable magnetic and electronic properties. The shapes of embedded SiQDs alter not only their electronic properties but also their magnetic properties, and their size affects the band dispersion and energy gap (E_g) as well as the magnetism of the SiQDs embedded in silicane. The magnetism as well as the electronic and structural properties are discussed in the following.

Magnetism

The total energy calculations revealed that all embedded triangular SiQDs are magnetic. The spin charge density (SCD) distributions are depicted in Fig. 2. The Si atoms adsorbed with hydrogen atoms are not spin-polarized and reside outside of the SiQD. The Si atoms without adsorbed hydrogen have opposing spin orientations at the A and B sites. The yellow isosurface denotes the majority spin at the A site, and the blue isosurface is the minority spin at the B site. For the type-I triangular SiQDs (Fig. 2a), the Si atoms at three tips have the largest magnetic moment with the majority spin, and the magnetic moment decreases to its minimum from the tip to the center of the edge. However, the magnetic moment of the edge atoms is still larger than that of the inner atoms, and the reduction of the SCD is more significant for a large triangular SiQD than a small one. The hydrogen atoms nearest to the edge Si atom in the embedded QD also have a low SCD. The Si atoms with minority spin have a much smaller magnetic moment than those with majority spin. The magnetic moment of the Si atoms with minority spin also decreases from the edge to the inner part of the SiQD. For the type-II triangular SiQDs (Fig. 2b), the three tip atoms are saturated by hydrogen atoms and the magnetic moment of the Si atoms is dramatically reduced. The magnetic moment of the edge Si atoms remains larger than that of the inner atoms. In contrast to the Si atoms at the center of the edge in type-I, those at the center of the edge in type-II exhibit a larger magnetic moment, with the value decreasing from the center to the tip.

Fig. 2 Spin charge densities of (a) type-I, and (b) type-II silicene triangular dots embedded in silicane. Spin charge densities of (c) type-I and (d) type-II silicene parallelogram QDs embedded in silicane. (e) Spin charge density of hexagonal QD with armchair edges and forty bare Si atoms. The yellow isosurface denote the majority spin, and the blue one is the minority spin.

The parallelogram SiQDs embedded in silicane also comprise two types (Fig. 2c and d): type-I has two tips and type-II has no tips. The type-I parallelogram SiQDs appear to be antiferromagnetic, except for the SiQD with eight Si atoms, which is nonmagnetic. As indicated in Fig. 2c, the two tip atoms of the parallelogram SiQD also have the largest magnetic moment but with an opposing spin orientation. The magnetic moment of the edge Si atoms decreases from the tip to the corner, and that of Si atoms also decreases from the outer part to the inner part of the SiQD. The SCD orientation of the Si atom at the A site is the opposite of that at the B site. A type-I parallelogram SiQD has the appearance of a magnetic needle. Type-II parallelogram SiQDs are nonmagnetic because the size is not sufficiently large. When the number of bare Si atoms of the type-II parallelogram SiQD reaches 126, the SiQD becomes antiferromagnetic (Fig. 2d). Without two tip atoms, the magnetic moment of the type-II parallelogram SiQDs is much smaller than that of the type-I parallelogram SiQDs. The decrease in the magnetic moment of the type-II parallelogram SiQD from the edge to the inner part is more rapid than it is in the type-I parallelogram SiQD.

The embedded hexagonal SiQDs with zigzag edges in silicane all prefer the nonmagnetic state, whereas the hexagonal SiQD with armchair edges also favours the nonmagnetic state, except for the SiQD with forty bare Si atoms, which is presented in Fig. 2e and exhibits weak magnetism. The SCD of this forty-atom hexagonal SiQD is much lower than that of triangular and parallelogram SiQDs. The SCD is highest at the three corners of the hexagonal SiQD with forty bare Si atoms. The total magnetic moment of the forty-atom hexagonal SiQD is only 1.015 μ_B because the numbers of bare Si atoms at the A site (N_A) and B site (N_B) in the QD are not equal. The difference in the number of Si atoms at the A site and B site (ΔN = N_A − N_B) is equal to two in this forty-atom hexagonal SiQD with armchair edges.

The total magnetic moment (μ_tot) of the triangular SiQDs embedded in silicane increases in accordance with the number of bare Si atoms N in a SiQD (Fig. 3a). The type-I embedded triangular SiQDs have a larger total magnetic moment than the type-II triangular SiQDs, and the value of the magnetic moment of the type-I SiQD is more than twice that of the type-II SiQD. The μ_tot values of the type-I embedded triangular graphene QDs (GQD) are also plotted for comparison (green circles in Fig. 3). The μ_tot of the triangular GQD is nearly the square root of N (Fig. 3a). The total magnetic moment of the triangular SiQD is lower than that of the triangular GQD because the spin polarization of the triangular SiQD is weaker than that of the triangular GQD. In other words, spin polarization is primarily provided by the p_z orbital of the C atom in GQD but is mainly from the p_z orbital and some hybridization of the s, p_x, and p_y orbitals of the Si atom in the SiQD. The rate of increase of the total magnetic moment of the embedded SiQD is less than that of the embedded GQD. The magnetic character of the triangular QD can be treated as unequal to N_A and N_B in the QD. The μ_tot of the triangular SiQD is smaller than that of the triangular GQD for the weaker spin polarization in the SiQD. For triangular GQDs, the total magnetic moment is nearly equal to ΔN. As can be seen in Fig. 3b, the ΔN–μ_tot curve is linear for the triangular GQD, but the ΔN–μ_tot curves indicate a sublinear relation for the triangular SiQD. The ΔN–μ_tot relations of type-I triangular GQD and SiQD for N ≥ 4 are as follows:

μ^GQD_tot = 0.983ΔN + 0.068, (1)

μ^SiQD_tot = −0.0332(ΔN)² + 1.17ΔN − 0.228. (2)

Fig. 3 Total magnetic moment of an embedded SiQD as a function of (a) number of bare Si atoms N, and of (b) the difference of the number of bare Si atoms at A site and at B site (ΔN). The total magnetic moment of type-I embedded graphene triangular QDs is drawn for comparison (green circles).

The ΔN–μ_tot relation of type-II triangular SiQD (N ≥ 13) is

μ_tot = −0.0441(ΔN)² + 0.987ΔN − 0.669. (3)

The inequality of N_A and N_B in the embedded QDs produces the magnetic character of a SiQD, such as the forty-atom hexagonal SiQD with armchair edges and the triangular GQDs and SiQDs. The SiQD with equal N_A and N_B values prefers a nonmagnetic state (hexagonal SiQDs) or antiferromagnetic state (parallelogram SiQDs), and the magnetic character of a SiQD depends on its shape.

Electronic structure

Silicane is a semiconductor with a wide band gap. The band structure density of state (DOS) of a SiQD embedded in silicane is displayed in Fig. 4–6. Some flat bands reside in the wide band gap of silicane or penetrate into the bands of silicane in either nonmagnetic or magnetic QDs. These flat bands are contributed by the bare Si atoms inside the QD, whereas the curved bands belong to the bulk silicane.

Fig. 4 Band structures of (a) type-I and (b) type-II silicene triangular dots embedded in silicane. Density of states (DOS) of (c) type-I and (d) type-II embedded SiQDs. The DOS of silicane is also shown in (c), and the green lines in (c) and (d) are the DOS of silicane. The magenta solid lines and the blue dash lines refer to the majority and the minority spin states, respectively.

Fig. 5 Band structures of (a) type-I and (b) type-II silicene parallelogram dots embedded in silicane. DOS of parallelogram embedded SiQDs are in (c) for type-I and in (d) for type-II. The green lines in (c) and (d) are the DOS of silicane. The solid magenta lines and dashed blue lines are referred to the majority and minority spin, respectively, for both band dispersion and DOS of QDs. The solid blue lines are for the nomagnetic states.

Fig. 6 Band structures of silicene hexagonal dots with (a) zigzag edges and (b) armchair edges embedded in silicane. DOS of hexagonal embedded SiQDs are in (c) for zigzag edges and in (d) for armchair edges. The green lines in (c) and (d) are the DOS of silicane. The solid magenta and dashed blue lines refer the majority and minority spin both for band dispersion and DOS of QDs. The solid blue lines are for the nomagnetic states.

Fig. 4 displays the band structures and DOS of the embedded triangular SiQDs, all of which are magnetic. Some of the flat bands are distributed inside the wide band gap of the silicane, but some are hidden in the bulk bands. The flat bands with majority and minority spins near the bulk band of the silicane prefer to separate in type-I (Fig. 4a) but penetrate each other in type-II (Fig. 4b). In the low energy region (−0.5 to 0.5 eV), the flat valence bands are classified as the majority spin states, oppositely, the flat conduction bands belong to the minority spin states. The number of flat bands increase with N for both spin orientations in the embedded triangular SiQDs, those bands created by the increase in N concentrate in a particular region (e.g., the top of the valence band at approximately 0.25 eV); moreover, the one doubly degenerate band that forms when N = 25 increases to one doubly degenerate band and one nondegenerate band when N = 36. The lowest conduction band (LCB) and highest valence band (HVB) are doubly degenerate for N = 25 and 36 of the type-I triangular SiQD and N = 22 and 33 of the type-II triangular SiQD but are nondegenerate when N = 49 for the type-I SiQD and N = 46 for the type-II SiQD. The E_g is the difference between the LCB (minority spin) and HVB (majority spin). When the size of the embedded triangular SiQD increases, the valence bands and conduction bands move closer together. For the type-II triangular SiQD (Fig. 4b), the band shift is not significant for either spin orientation as N increases. The LCB with minority spin appears to become fixed as the size of the QD increases, and the E_g of the type-II triangular SiQD is smaller than that of the type-I SiQD. The DOSs also reveal that the states located in band gap of silicane are all referred to the SiQDs. Those valence states have distinct spin (majority spin) with the conduction states (minority spin) in the low energy region.

The band structure and DOS of the type-I embedded parallelogram SiQDs presents antiferromagnetic characteristics (Fig. 5a and c); this is also true for the type-II SiQDs when N ≥ 126. The bands with distinct spin states are degenerate. The flat bands are also in the wide band gap of the silicane, and some penetrate into the bands of the silicane. The E_g decreases as the size of the SiQD increases (Fig. 5). Without the two tip atoms, the small type-II parallelogram SiQD is nonmagnetic (Fig. 5b and d); furthermore, the LCB and the HVB are nondegenerate and become closer as N increases from 48 to 70. The E_g decreases as the size of the type-II SiQD increases under nonmagnetic conditions. However, the E_g of the type-II parallelogram SiQD is also smaller than that of the type-I SiQD. When N ≥ 126, the type-II parallelogram SiQD transforms from a nonmagnetic to antiferromagnetic semiconductor.

Fig. 6 displays the band structure and DOS of the embedded hexagonal SiQDs. The embedded hexagonal SiQDs with zigzag edges are all nonmagnetic semiconductors (Fig. 6a and c). Some of the flat bands of the SiQDs are also inside the wide band gap of the silicane and the others in the bulk band of the silicane. The LCB and HVB become closer as the size of the SiQD increases, indicating that the E_g decreases when the size of the hexagonal SiQD increases. The LCB and HVB are nondegenerate for N = 6 but are doubly degenerate for the hexagonal SiQD when N = 24 or 54. Fig. 6b and d displays the band structure and DOS of the hexagonal SiQD with armchair edges embedded in silicane. The hexagonal SiQD with armchair edges at N = 40 is a magnetic semiconductor with an E_g that is smaller than that of the hexagonal SiQD when N = 60, which is a nonmagnetic semiconductor. The SiQD at N = 25 behaves like a metal because one band crosses with the Fermi level (Fig. 6d). The hexagonal SiQDs with armchair edges are nonmagnetic, except for when N = 40. However, their electronic properties are diverse.

The E_g values of the six types of embedded SiQDs in silicane are plotted in Fig. 7. The N–E_g relations of the hexagonal SiQDs are indicated in Fig. 7a. The embedded hexagonal SiQD with zigzag edges has the largest E_g, 1.78 eV (N = 6), which decreases as N increases. The large zigzag-edged hexagonal SiQD (N = 150) still has an E_g of 0.36 eV. The E_g values of the embedded hexagonal SiQDs with armchair edges are diverse and do not correspond to the size of the SiQDs. The E_g values of the embedded triangular and parallelogram SiQDs are provided in Fig. 7b and c, respectively. The E_g values of the type-I embedded triangular and parallelogram SiQDs decrease as N increase. The N–E_g curve of the type-II triangular and parallelogram SiQDs differs from that of the type-I SiQDs. The E_g of the type-II triangular SiQD first increases and then decreases as N increases (Fig. 7b). For the type-II embedded parallelogram SiQD, the E_g decreases from 0.94 eV to 0.042 eV as N increases from 16 to 96, and then the E_g increases with N because the SiQD transitions from a nonmagnetic to antiferromagnetic semiconductor at N = 126. Moreover, the E_g also decreases with the increasing size of the SiQD.

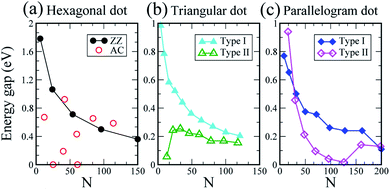Fig. 7 The E_g of the (a) hexagonal, (b) triangular, and (c) parallelogram silicene dot embedded in silicane.

Structural properties

The SiQD embedded in silicane can be constructed by desorbing the hydrogen atoms from silicane because the bare Si atoms prefer to distribute continuously and form separate regions of Si atoms with and without hydrogen. The desorption energy may originate from heating, and the desorption energy per hydrogen atom (E_des) of an embedded SiQD can be calculated as follows:where the total energy of the embedded SiQD, silicane, and hydrogen molecule are denoted by E^SiQD_tot, E^silicane_tot, and respectively.

Fig. 8 presents the E_des of a hydrogen atom of a particular SiQD embedded in silicane. The desorption energy of a single hydrogen atom is approximately 1.33 eV, and the E_des of the smallest triangular SiQD with four bare Si atoms decreases to 0.98 eV per H. The E_des of the triangular SiQD decreases from 0.98 eV per H for the smallest SiQD with four bare Si atoms to 0.65 eV per H for the larger SiQD with N = 121. The E_des of embedded SiQDs of all shapes follows a decay curve as the SiQD increases in size, indicating that after the first hydrogen atom is desorbed, others can be desorbed more easily; thus, an embedded SiQD can be constructed. The decay rate of the E_des of SiQDs is shape-dependent. The discrepancy between the E_des of SiQDs with different shapes is less than 20 meV per H.

Fig. 8 Desorption energy per hydrogen atom of the SiQD for different shapes of silicene quantum dot embedded in silicane.

The lattice stability of the embedded SiQD by external force is drawn Fig. 9. The strain ε is defined as where a and a₀ are the lattice constant of silicane with and without external force. The energy curve of various strains and embedded SiQD with different shapes are presented. The theoretical lattice constant of silicane (3.895 Å) and silicene (3.869 Å) in this work is in accordant with other previous works.^39,40 In our calculation, the SiQD is well separated to simulate a single embedded QD. The theoretical lattice constant of silicane is used, because the QD is embed in silicane. The lattice constant is dominated by silicane. The strain-energy curve of silicane and silicene are also plotted for comparison. The energy curves of the hexagonal SiQD with N = 24, triangular SiQD with N = 36, and parallelogram SiQD with N = 8 are quite close the energy curve of silicane. Silicene is more sensitive to the homogeneous strain than silicane. When the tensile strain is larger than 3%, the system of the embedded SiQD is more sensitive than the silicane, but still less sensitive than silicene.

Fig. 9 The strain-energy curves for the embed SiQD with different shapes. The number of bare Si atoms in hexagonal, triangular, and parallelogram SiQDs are 24, 36 and 8, respectively.

Conclusions

A first-principles calculation was performed on SiQDs embedded in silicane with respect to the magnetism as well as electronic and structural properties of SiQDs of various shapes and sizes. The decay curve of the desorption energy per hydrogen atom demonstrates that SiQD embedded in silicane can be constructed. The shape of a SiQD determines its electronic structure as well as its dot size. The magnetic properties of a SiQD embedded in silicane are highly shape dependent. Triangular SiQDs are all magnetic, whereas some small parallelogram SiQDs are nonmagnetic and all others are antiferromagnetic; moreover, almost all hexagonal SiQDs are nonmagnetic, the exception being armchair-edged hexagonal SiQD with N = 40. The unequal number of bare Si atoms at the A and B sites in a SiQD is a critical factor for establishing magnetism in an embedded SiQD, such as the triangular SiQD or the forty-atom hexagonal SiQD with armchair edges. The tips of a triangular SiQD increase the magnetic moment, and larger triangular SiQDs correspond with a higher magnetic moment because of the increased difference between the number of Si atoms at the A and B sites. When the number of Si atoms at the A and B sites in a SiQD are equal, the SiQD can be either nonmagnetic (hexagonal SiQD with zigzag edges) or antiferromagnetic (large parallelogram SiQD). The parallelogram SiQD with two tip atoms has an appearance similar to that of a magnetic needle and can be applied in nanoscale registrations of digital information. SiQDs embedded in silicane can also be used to design silicon-based microelectronic devices.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work was supported by the Ministry of Science and Technology of Taiwan (ROC) under grant numbers MOST 105-2112-M-182-002-MY3. Author also thank the National Centers for Theoretical Sciences and High-performance Computing of the ROC for the computation support.

References

1. C. X. Guo, H. B. Yang, Z. M. Sheng, Z. S. Lu, Q. L. Song and C. M. Li, Angew. Chem., Int. Ed., 2010, 49, 3014–6727.
2. I. V. Martynenko, A. P. Litvin, F. Purcell-Milton, A. V. Baranov, A. V. Fedorov and Y. K. Gun'ko, J. Mater. Chem. B, 2017, 5, 6701–6727.
3. S. Jin, D. H. Kim, G. H. Jun, S. H. Hong and S. Jeon, ACS Nano, 2013, 7, 1239–1245.
4. P. Yuan, W. Tian, Y. Zeng, Z. Zhang and J. Zhang, Org. Electron., 2014, 15, 3577–3583.
5. T. S. Sreeprasad, A. A. Rodriguez, J. Colston, A. Graham, E. Shishkin, V. Pallem and V. Berry, Nano Lett., 2013, 13, 1757–1763.
6. L. A. Ponomarenko, F. Schedin, M. I. Katsnelson, R. Yang, E. W. Hill, K. S. Novoselov and A. K. Geim, Science, 2008, 320, 356–358.
7. S. Zhu, Y. Song, J. Wang, H. Wan, Y. Zhang, Y. Ning and B. Yang, Nano Today, 2017, 13, 10–14.
8. M. Fujii, H. Sugimoto and S. Kano, Chem. Commun., 2018, 54, 4375–4389.
9. F. Schäffler, D. Tobben, H.-J. Herzog, G. Abstreiter and B. Hollander, Semicond. Sci. Technol., 1992, 7, 260–266.
10. Y. Takahashi, M. Nagase, H. Namatsu, K. Kurihara, K. Iwdate, Y. Nakajima, S. Horiguchi, K. Murase and M. Tabe, Electron. Lett., 1995, 31, 136–137.
11. R. W. Knoss, Quantum dots: Research technology and, applications, Nova Science Publishers Inc., New York, 2009, ch. 1, p. 1.
12. A. Berthelot, I. Favero, G. Cassabois, C. Voisin, C. Delalande, P. Roussignol, R. Ferreira and J. M. Gérard, Nat. Phys., 2006, 2, 759–764.
13. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
14. Y. Du, J. Zhuang, H. Liu, X. Xu, S. Eilers, K. Wu, P. Cheng, J. Zhao, X. Pi, K. W. See, G. Peleckis, X. Wang and S. X. Dou, ACS Nano, 2014, 8, 10019–10025.
15. D. Jose and A. Datta, Acc. Chem. Res., 2014, 47, 593–602.
16. S. Cahangirov, M. Topsakal, E. Aktürk, H. Şahin and S. Ciraci, Phys. Rev. Lett., 2009, 102, 236804.
17. P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. L. Lay, Phys. Rev. Lett., 2012, 108, 155501.
18. T. P. Kaloni, G. Schreckenbach and M. S. Freund, J. Phys. Chem. C, 2014, 118, 23361–23367.
19. T. P. Kaloni, Y. C. Cheng and U. Schwingenschlögl, J. Appl. Phys., 2013, 113, 104305.
20. T. P. Kaloni, M. Modarresi, M. Tahir, M. R. Roknabadi, G. Schreckenbach and M. S. Freund, J. Phys. Chem. C, 2015, 119, 11896–11901.
21. L. Tao, E. Cinquanta, D. Chiappe, C. Grazianetti, M. Fanciulli, M. Dubey, A. Molle and D. Akinwande, Nat. Nanotechnol., 2015, 10, 227–231.
22. R.-W. Zhang, C.-W. Zhang, W.-X. Ji, S.-J. Hu, S.-S. Yan, S.-S. Li, P. Li, P.-J. Wang and Y.-S. Liu, J. Phys. Chem. C, 2014, 118, 25278–25283.
23. V. Zólyomi, J. R. Wallbank and V. I. Fal'ko, 2D Materials, 2014, 1, 011005.
24. H. González-Herrero, J. M. Gómez-Rodríguez, P. Mallet, M. Moaied, J. J. Palacios, C. Salgado, M. M. Ugeda, J.-Y. Veuillen, F. Yndurain and I. Brihuega, Science, 2016, 352, 437–441.
25. B. R. Wu and C. K. Yang, Sci. Rep., 2015, 5, 15310.
26. J. Zhang, J. Fu, F. Shi, Y. Peng, M. Si, L. Cavallo and Z. Cao, Nanoscale, 2018, 10, 14100–14106.
27. B. R. Wu and C. K. Yang, AIP Adv., 2012, 2, 012173.
28. J. Qiu, H. Fu, Y. Xu, Q. Zhou, S. Meng, H. Li, L. Chen and K. Wu, ACS Nano, 2015, 9, 11192–11199.
29. F. A. Zwanenburg, A. S. Dzurak, A. Morello, M. Y. Simmons, L. C. L. Hollenberg, G. Klimeck, S. Rogge, S. N. Coppersmith and M. A. Eriksson, Rev. Mod. Phys., 2013, 85, 961.
30. Y. Wang, R. Hu, G. Lin, I. Roy and K.-T. Yong, ACS Appl. Mater. Interfaces, 2013, 5, 2786–2799.
31. J. Shen, Y. Zhu, X. Yang and C. Li, Chem. Commun., 2012, 48, 3686–3699.
32. J. Ge, M. Lan, B. Zhou, W. Liu, L. Guo, H. Wang, Q. Jia, G. Niu, X. Huang, H. Zhou, X. Meng, P. Wang, C.-S. Lee, W. Zhang and X. A. Han, Nat. Commun., 2014, 5, 4596.
33. D. Iannazzo, A. Pistone, M. Salamò, S. Galvagno, R. Romeo, S. V. Giofré, C. Branca, G. Visalli and A. D. Pietro, Int. J. Pharm., 2017, 518, 185–192.
34. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
35. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687.
36. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
37. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
39. P. Pflugradt, L. Matthes and F. Bechstedt, New J. Phys., 2014, 16, 075004.
40. Q. Peng and S. De, Nanoscale, 2014, 6, 12071–12079.

---