Open Access Article
Open Access ArticleComputational assessments of diastereoselective [4+2] cycloaddition and 1,3-borotopic shift of a dearomatized tertiary boronic ester intermediate: reactivities explained through transition-state distortion energies†
Aqeel A. Hussein *ab,
Faisal A. Almalkic,
Alaa M. Alqahtanic and
Sergey Shityakov
*ab,
Faisal A. Almalkic,
Alaa M. Alqahtanic and
Sergey Shityakov d
d
aFaculty of Dentistry, University of Al-Ameed, Karbala P.O. No: 198, Iraq
bDepartment of Chemistry, University of Southampton, Southampton, Hampshire SO17 1BJ, UK. E-mail: aahh1f19@soton.ac.uk
cDepartment of Pharmaceutical Chemistry, Faculty of Pharmacy, Umm Al-Qura University, Makkah 21955, Saudi Arabia
dDepartment of Anesthesia and Critical Care, University of Würzburg, 97080 Würzburg, Germany
First published on 26th July 2019
Abstract
Interception of a dearomatized tertiary boronic ester, formed through a kinetically and thermodynamically favorable 1,2-metalate rearrangement/anti-SN2′ elimination of an activated ortho-lithiated benzyl amine, in a [4+2] cycloaddition or 1,3-borotopic shift has been investigated by density functional theory (DFT). Although superacitvated “naked” Li+ was found to greatly promote 1,3-borotopic shift, the diastereoselective [4+2] cycloaddition was favored. It was revealed that the factor that controls the diastereoselectivity was the steric bulk provided by the diene, which is in agreement with experimental diastereoselectivity. A comparison of unreactive dienophiles such as maleic anhydride, diethyl maleate, and others with 4-phenyl-3H-1,2,4-triazole-3,5(4H)-dione (PTAD) was found to be in an excellent agreement with the experiments; where their lack of reactivity is attributed to the high deformation energies of the interacting components to achieve the transition state structure which was pronounced with the high energy of LUMO orbitals.
Introduction
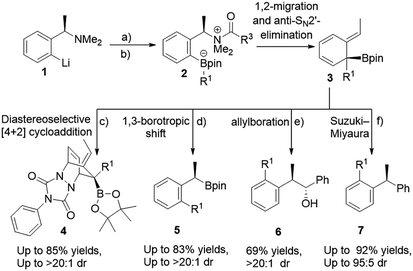
The use of boronic esters in asymmetric synthesis is a highly versatile and robust approach, due to the important stereospecific transformations through stereoinvertive or stereoretentive pathways into many functionalities that lead to complex structures.1 For instance, bortezomib, which is a treatment for relapsed and refractory multiple myeloma, is an α-amino boronic acid that possess potent inhibitors of a serine protease.2 Thus, advancing pertinent novel methods to synthesize enantiopure alkyl boronic esters with structurally complex functionalities is exceedingly favorable.3 Accordingly, an extensive endeavour to access an enantiospecific coupling of secondary and tertiary boronic esters to aromatics through transition-metal catalyzed processes has been made, though it is practically still challenging and not generally applicable.4–6 Quite recently, Aggarwal and co-workers reported a considerable scope of stereospecific transition metal-free sp2–sp3 coupling of chiral secondary and tertiary boronic esters with electron-rich aryl lithium reagents.7 Subsequently, they demonstrated an enantiospecific synthesis of ortho-substituted benzylic boronic esters via a 1,2-metalate rearrangement/anti-SN2′ elimination/1,3-borotropic shift reaction sequence starting from enantioenriched α-substituted benzylamines (Scheme 1).8a The essential part of this sequence is that it progresses through a dearomatized tertiary boronic ester intermediate 3, followed by 1,3-borotropic shift or participating in allylboration, or allylic Suzuki–Miyaura cross-coupling reactions to provide complex enantioenriched products (Scheme 1).8 Importantly, they have stated that the favorable rearomatization is a driving force for these transformations, although an 1,3-brotopic shift is an exceedingly slow process (formation of 5, 6, and 7, Scheme 1). Regarding this, it has been reported that using a Lewis acid promotes an 1,3-shift at a faster rate.9 Aggarwal and co-workers were then intrigued in diverting reactivity of intermediate 3 through the interception in a Diels–Alder cycloaddition reaction (Scheme 1). Very recently, they published a simple one-pot procedure through the interception of the dearomatized intermediate 3 with a dienophile (PTAD) in a diastereoselective [4+2] cycloaddition to generate highly complex three-dimensional boron-containing molecular structures (Scheme 1-c).10 This intermediate has been used in total syntheses11 and different transition metal-catalyzed transformations.12We were then captivated in a number of issues arising from these transformations; (1) realizing the formation of this intermediate in a compelling mechanism, (2) understanding the facial selectivity in the Diels–Alder cycloaddition which should give us a clue to rationalize the origin behind high diastereoselectivity, (3) realizing the reactivity of cycloaddition and 1,3-borotopic in the absence and presence of a Lewis acid, and (3) due to the notably limited reactivity of cyclohexadienes evaluation of the other dienophiles in [4+2] cycloaddition have raised further questions corresponding to the demand of matched/mismatched reactivities between the HOMO and LUMO orbitals. Herein, we interpret a DFT study on the diastereoselective [4+2] cycloaddition of the dearomatized tertiary boronic ester, explaining the formation of such a stable dearomatized intermediate, comparing reactivity of 1,3-borotopic shift with and without a Lewis acid, and highlighting the important role of a bulk group in producing three-dimensional boron-containing molecular structures diastereoselectivily. Furthermore, we will rationalize reactivities of different dienophiles from the point of frontier molecular orbital (FMO) analysis and distortion/interaction energies.
Results and discussion
All our simulations were obtained by means of DFT calculations using the ωB97XD/6-311+G(2d,3pd) level of theory in both the gas phase and tetrahydrofuran (THF) as a representative solvent (SMD solvation model) otherwise mentioned based on gas-phase optimized geometries by ωB97XD/6-31G(d). Generally, we have not seen noticeable discrepancies between calculations in the gas phase and implicit solvent, so all our discussions and comparisons will be based on gas phase otherwise mentioned.Reaction mechanism
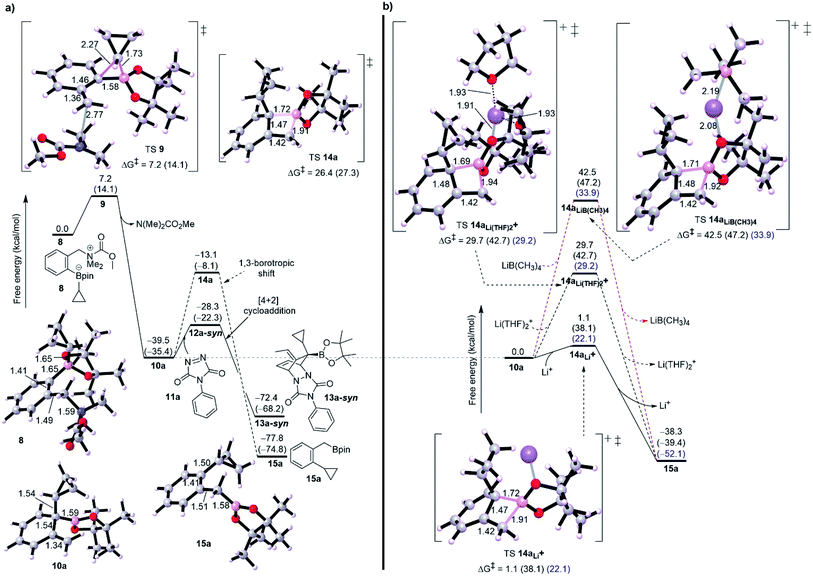
Initially, we started our investigation with the formation of dearomatized tertiary boronic ester 10, from the activated intermediate 8 (Fig. 1-a). Here, we have used acetyl chloride (MeCOCl) as an activated group instead of ClCO2CMe2CCl3 to reduce computational demand. DFT simulations show that formation of 10a by 1,2-migration and anti-SN2′-elimination mechanism needs a barrier of 7.2 kcal mol−1 as a favorable exergonic reaction (−39.5 kcal mol−1), where R1 is cyclopropyl group. This would explain the desirable formation of intermediate 10a according to the experimental observations reported by Aggarwal and co-worker.8a,10 Aggarwal et al. showed that 1,3-shift occurs only when a Lewis acid like NaBPh4 was added to the reaction.8a They performed an in situ salt metathesis with NaBPh4 in noncoordinating chloroform to accordingly give “naked” Li+BPh4− and the latter efficiently catalyzed the reaction to afford the benzylic boronate. In this regard, the “naked” lithium cation with very weakly coordinating anions (BPh4−) has been shown to be a superactivated lithium cation, substantially enhancing a Lewis acidic character and mediating various organic reactions.13 Thus, we were then interested in investigating the 1,3-borotopic shift in the presence and absence of a “naked” Lewis acid.On one hand, and in the absence of Lewis acid (Fig. 2-a), a substantial barrier of 26.4 kcal mol−1 is required to overcome TS 14a to release benzylic boronate product 15a although this shift is a thermodynamically favorable step (−38.3 kcal mol−1).8a,9a The calculated activation of rearomatization (26.4 kcal mol−1, k = 2.8 × 10−7) is in line with the experimental observation that this process is exceedingly slow in the absence of NaBPh4.9 In comparison, the addition of such a good dienophile like PTAD, a reduced barrier [4+2] cycloaddition reaction takes place via TS 12a-syn with barrier of just 11.1 kcal mol−1 as an exergonic step (13a-syn, −32.9 kcal mol−1) (Fig. 2-a). The low barrier for cycloaddition totally outpaces 1,3-shift when a Lewis acid is absent, and a good dienophile is present.
On the other hand, when the superactivated Lewis acid was involved, the barrier of 1,3-shift varies based on the proposed TS (Fig. 2-b). Here, we have proposed three TSs to understand how Lewis acid catalyzes the reaction. When the noncoordinating “naked” Li+ was used, a barrierless shift of 1.1 kcal mol−1 in gas phase was obtained via TS 14aLi+, and this barrier increases to 22.1 kcal mol−1 in CHCl3 and to 38.1 kcal mol−1 in THF. To match the experimental conditions, the difference in barrier between THF and CHCl3 is reasonable and in accord with the fact that using CHCl3 was the choice to promote the 1,3-shift. Coordinating two THF solvents to the “naked” Li+ has effectively increased the barrier to around 29.0 kcal mol−1 in both gas phase and chloroform (see TS 14aLi(THF)2+, Fig. 2-b) whereas 42.7 kcal mol−1 in THF. Furthermore, using a “non-naked” lithium salt, LiB(CH3)4, led to the highest barrier for 1,3-shift (see TS 14aLiB(CH3)4, Fig. 2-b). Finally, these results confirm the reality that the need for a superactivated Lewis acid with a noncoordinating solvent is tremendously necessary to facilitate the 1,3-borotopic shift, however this is still disfavored compared to [4+2] cycloaddition in THF or CHCl3, plausibly consistent with the experimental observations.
Rationalization of diastereoselectivity of the [4+2] cycloaddition
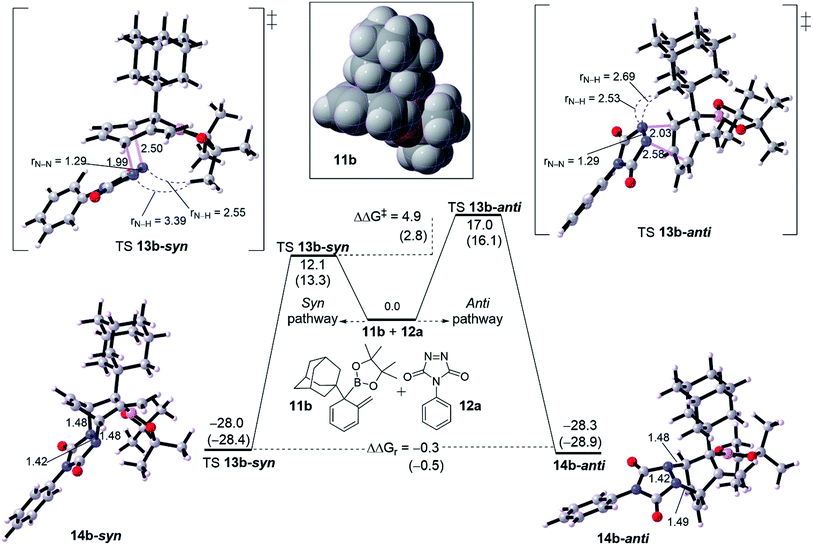
We turned out our eyes into a rationalization of the diastereoselectivity of cycloadduct formation. DFT calculations were performed with two examples of dearomatized intermediate 10. These dienes were chosen based on the size of the α-position (R1 group). Fig. 2 shows a diastereoselective bifurcation of [4+2] cycloaddition for intermediate 10b and dienophile 11a leading to syn and anti-product, where R1 is an and α-branched large group. Interception of the diene 10b with 11a has been found to proceed through an asynchronous concerted TS 12b-syn with a free energy barrier of 12.1 kcal mol−1 as an exergonic reaction (13b-syn, −28.0 kcal mol−1). Here, the N1–C1 bond in TS 12b-syn is 1.99 Å whereas N2–C2 bond is 2.50 Å, resulting in an asynchronousity of 0.51 Å between the two bonds growing along the TS.The anti pathway, 10b → 13b-anti, proceeds with higher barrier of 17.0 kcal mol−1 (ΔΔG‡ = 4.9 kcal mol−1) in a slightly similar exergonic step (ΔΔGr = −0.5 kcal mol−1). This would explain that the syn is the kinetic product whereas the anti is the thermodynamic product. The asynchronousity along TS 12b-anti increases into 0.55 Å. This activation energy difference between the isomeric pathways would reflect the experimental diastereoselectivity (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 d.r.).10 Computational evaluations about the origin behind the high selectivity indicate that, along TS, the bulk steric between the dienophile and quaternary substituted group is responsible for the isomeric preference. Along TS 12b-syn the steric distance between CH3 group in the Bpin of the diene moiety and N–N moiety in the dienophile (PTAD) is 3.39 Å and 2.55 Å for N1–H[CH3]Bpin and N2–H[CH3]Bpin respectively. However, the TS 12b-anti has shorter steric distances of 2.53 Å and 2.69 Å for N1–H[R1] and N2–H[R1] respectively, where R1 is adamantyl group. This means that steric hindered provided by the Bpin moiety is less effective than adamantly group, and consequently leading to highly syn selectivity (>20
1 d.r.).10 Computational evaluations about the origin behind the high selectivity indicate that, along TS, the bulk steric between the dienophile and quaternary substituted group is responsible for the isomeric preference. Along TS 12b-syn the steric distance between CH3 group in the Bpin of the diene moiety and N–N moiety in the dienophile (PTAD) is 3.39 Å and 2.55 Å for N1–H[CH3]Bpin and N2–H[CH3]Bpin respectively. However, the TS 12b-anti has shorter steric distances of 2.53 Å and 2.69 Å for N1–H[R1] and N2–H[R1] respectively, where R1 is adamantyl group. This means that steric hindered provided by the Bpin moiety is less effective than adamantly group, and consequently leading to highly syn selectivity (>20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 d.r.).
1 d.r.).
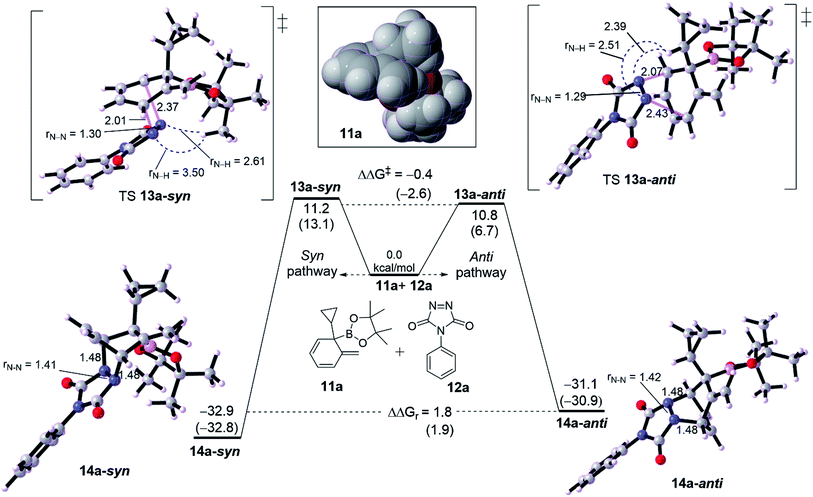
We then probed the computational diastereoselectivity when R1 is small such as cyclopropyl, the dearomatized intermediate 10a, to rationalize the experimental observations (Fig. 3). Experimentally, low diastereoselectivity for cyclohexadiene 10a was obtained (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6 d.r.).10 DFT calculations show that cycloaddition of 10a with 11a on both pathways are energetically similar although the effect of solvent on calculation was somewhat different. The formation of syn product 13a-syn via an asynchronous concerted TS 12a-syn needs 11.2 kcal mol−1 whereas a slightly lower barrier of 10.8 kcal mol−1 (TS 12a-anti, ΔΔG‡ = −0.4 kcal mol−1) was seen for the anti product 13a-anti. Thermodynamically, 13a-anti has a thermodynamic preference of ΔΔGr = 1.8 kcal mol−1. The calculated difference in activation energy between both TSs 12a-syn and 12a-anti reflects the obtained diastereoselectivity (1
1.6 d.r.).10 DFT calculations show that cycloaddition of 10a with 11a on both pathways are energetically similar although the effect of solvent on calculation was somewhat different. The formation of syn product 13a-syn via an asynchronous concerted TS 12a-syn needs 11.2 kcal mol−1 whereas a slightly lower barrier of 10.8 kcal mol−1 (TS 12a-anti, ΔΔG‡ = −0.4 kcal mol−1) was seen for the anti product 13a-anti. Thermodynamically, 13a-anti has a thermodynamic preference of ΔΔGr = 1.8 kcal mol−1. The calculated difference in activation energy between both TSs 12a-syn and 12a-anti reflects the obtained diastereoselectivity (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.6) with the inconsiderable preference for the anti over syn product. The asynchronousity of both TSs is lower than for those with adamantly-substituted TSs (see Fig. 2). Noticeably, the steric distance between the N–N moiety and cyclopropyl along the TS 12a-anti is relatively shorter than in 12b-anti, correspondingly TS 12a-anti has a lower barrier than TS 12b-anti by around 6.2 kcal mol−1. This would reveal that the steric distance between N
1.6) with the inconsiderable preference for the anti over syn product. The asynchronousity of both TSs is lower than for those with adamantly-substituted TSs (see Fig. 2). Noticeably, the steric distance between the N–N moiety and cyclopropyl along the TS 12a-anti is relatively shorter than in 12b-anti, correspondingly TS 12a-anti has a lower barrier than TS 12b-anti by around 6.2 kcal mol−1. This would reveal that the steric distance between N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N moiety of PTAD is not only the case in determining the preferability, but the steric bulk is effective too (see the spacefilling model for the dearomatized intermediates 10a and 10b in Fig. 2 and 3). Although PTAD 11a represents an excellent dienophile to react with cyclohexadiene, scoping other dienophiles is highly favorable (see below).
N moiety of PTAD is not only the case in determining the preferability, but the steric bulk is effective too (see the spacefilling model for the dearomatized intermediates 10a and 10b in Fig. 2 and 3). Although PTAD 11a represents an excellent dienophile to react with cyclohexadiene, scoping other dienophiles is highly favorable (see below).
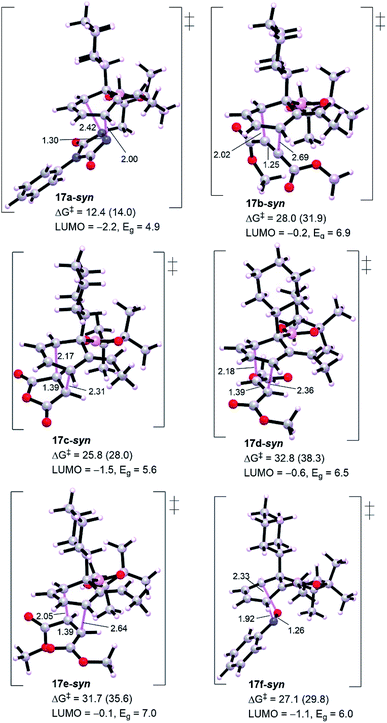
Exploring other dienophiles: we decided to perform a broader computational search for other 2π-components that could react with cyclohexadiene intermediate in a similar fashion and analogy with the cycloaddition processes. Although Aggarwal and co-workers10 chose PTAD 11a to be the dienophile based on the reported studies that addressed the poor reactivity of cyclohexadienes towards cycloaddition reactions,11 other dienophiles (11b–11f) were also tested (Scheme 2). Indeed, all these dienophiles were unreactive towards cycloaddition,10 therefore, we then turned our attention into understanding their lack of reactivity by means of DFT calculations (Fig. 4).
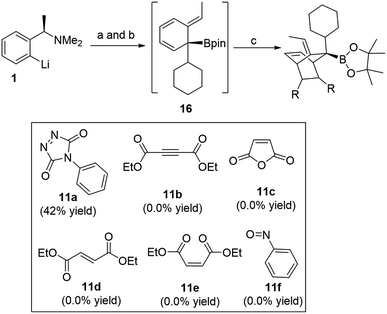 | ||
| Scheme 2 Other dienophiles investigated by Aggarwal and co-workers. (a) CyBpin, THF, −78 °C to rt; (b) ClCO2CMe2CCl3, −78 °C to rt; (c) dienophile, THF, −78 °C to rt or 50 °C. | ||
Generally, from Fig. 3 all the dienophiles except PTAD revealed high energy barriers (25.8–32.8 kcal mol−1) with the lowest calculated one for maleic anhydride 11c (TS 17c-syn, ΔG‡ = 25.8 kcal mol−1) and the highest one for diethyl fumarate (TS 17d-syn, ΔG‡ = 32.8 kcal mol−1), much too high to be observed under the reaction conditions in comparison to triply-reduced barrier for PTAD (TS 17a-syn, ΔG‡ = 12.4 kcal mol−1). Diethyl maleate (11e) and nitrosobenzene (11f) display a comparable barrier to diethyl fumarate (11d) and diethyl acetylenedicarboxylate (11b), respectively. Our DFT simulations show that these barriers are in accord with the energy gaps calculated for the intermediate diene 16 and corresponding dienophiles, the lowest molecular orbital (LUMO) energy of the dienophile the lowest barrier for cycloaddition. Thus, the interception of cyclohexadiene with PTAD will be exceptionally more reactive than other dienophiles. It has been reported that cyclobutenone and cyclopropenone are 1000 to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times more reactive than cyclohexanone, at room temperature, toward cycloaddition process.14,15 The high barriers would primarily explain the unsuccessful cycloadditions, and to assess the origin behind this failure we have performed distortion/interaction analysis to estimate the contributions of interaction and distortion energies of the geometrical deformation to the activation energy that achieve the transition state (Table 1). This approach was described by Houk and co-workers.16 The approach involves separating the TS into its components (diene and dienophile) which is followed by single point energy calculations of the obtained separated reactive components with their respective TS geometries preserved. The difference in energy between the distorted fragments and optimized ground state geometries is the distortion energy (ΔE‡,tdis) of the diene and the dienophile, whereas the interaction energy is the difference between the activation energy and the distortion energy (ΔE‡int = ΔE‡ − ΔE‡dis).
000 times more reactive than cyclohexanone, at room temperature, toward cycloaddition process.14,15 The high barriers would primarily explain the unsuccessful cycloadditions, and to assess the origin behind this failure we have performed distortion/interaction analysis to estimate the contributions of interaction and distortion energies of the geometrical deformation to the activation energy that achieve the transition state (Table 1). This approach was described by Houk and co-workers.16 The approach involves separating the TS into its components (diene and dienophile) which is followed by single point energy calculations of the obtained separated reactive components with their respective TS geometries preserved. The difference in energy between the distorted fragments and optimized ground state geometries is the distortion energy (ΔE‡,tdis) of the diene and the dienophile, whereas the interaction energy is the difference between the activation energy and the distortion energy (ΔE‡int = ΔE‡ − ΔE‡dis).
| TS | ΔE‡ | ΔE‡,tdis | ΔE‡,1dis | ΔE‡,2dis | ΔE‡int |
|---|---|---|---|---|---|
| a ΔE‡,tdis, ΔE‡,1dis and ΔE‡,2dis represents the total, diene, and dienophile distortion energies respectively. | |||||
| 17a-syn | −2.4 (−0.5) | 19.8 (19.5) | 15.7 (16.2) | 4.1 (3.3) | −22.2 (−20.0) |
| 17b-syn | 10.3 (14.2) | 29.2 (30.2) | 13.3 (14.1) | 15.9 (16.1) | −18.9 (−16.0) |
| 17c-syn | 10.0 (12.2) | 30.9 (31.2) | 21.4 (22.0) | 9.5 (9.2) | −20.9 (−19.0) |
| 17d-syn | 12.4 (17.9) | 35.4 (36.6) | 24.1 (24.9) | 11.3 (11.7) | −23.0 (−16.7) |
| 17e-syn | 14.2 (18.1) | 35.6 (34.8) | 17.7 (18.3) | 17.9 (16.5) | −21.4 (−16.7) |
| 17f-syn | 10.7 (13.4) | 20.6 (21.0) | 17.6 (18.1) | 3.0 (2.9) | −9.9 (−7.6) |
Table 1 shows a good understandable correlation between activation energies and reactant distortion energies. Due to the high distortion energies associated with accessing the transition state geometry, the reactivity of these dienophiles is then decreased compared with PTAD. Studies by Houk and co-workers investigated the superior reactivity of PTAD as a dienophile for such systems.17 For all TSs shown in Table 1, except TS 17f-syn that depicts lower interaction energy because of its dienophile nitrosobenzene has a reduced distortion energy of around 3.0 kcal mol−1, the calculated interaction energies are nearly comparable (−18.9 to −23.0 kcal mol−1). This is believed to be consistent with the fact that all these dienophiles and diene have essentially constant interacting frontier molecular orbitals.14
Conclusions
We have exhibited a DFT study, using the ωB97XD/6-311+G(2d,3pd)//6-31G(d) level of theory in both the gas phase and THF/SMD, on the diastereoselective [4+2] cycloaddition of the dearomatized tertiary boronic ester intermediate with a profoundly reactive dienophile PTAD. The reaction mechanism of this intermediate formation was disclosed to follow 1,2-metalate rearrangement/anti-SN2′ elimination from an activated ortho-lithiated benzylamine, displayed as a depressed barrier and thermodynamically exergonic step. Competition between [4+2] cycloaddition and 1,3-borotopic shift was calculated to be in an immense preference for the cycloaddition pathway either in the presence of absence of superactivated “naked” Li+, wherein the absence of a Lewis acid 1,3-borotopic is exceedingly slow consistent with the experimental conditions. Simulations speculate the aspect that is controlling the diastereoselectivity in producing three-dimensional boron-containing molecular structures was divulged to be the steric bulk, adamantyl group provides an α-branched broad steric bulk compared with a compact cyclopropyl. Finally, we have compared the lack of reactivity of other dienophiles (11b–11f) with PTAD (11a), where the unlikely energy barriers (25.8–32.8 kcal mol−1) are attributed to the high distortion energies of the interacting components that form the TS structure and this was conspicuous with the high LUMO energies.Computational details
All mechanical quantum calculations were performed using Gaussian 09.18 The geometries were fully optimized at the hybrid meta-generalized gradient dispersion-corrected approximation ωB97XD,19 with the basis set 6-31G(d).20 All minima intermediates were verified by the absence of negative eigenvalues in the vibrational frequency analysis. Transition state structures were found using the Berny algorithm,21 and verified by vibrational analysis. The transition states were visualized by animating the negative eigenvector coordinate. Single-point energies of the optimized geometries were evaluated using larger basis set 6-311+G(2d,3pd).20 The thermal corrections evaluated from the unscaled vibrational frequencies at the ωB97XD/6-31G(d) level of theory were then added to the ωB97XD/6-311+G(2d,3pd) electronic energies to obtain the free energies. The effect of solvent was included via the solvation model based on density (IEFPCM-SMD) using tetrahydrofuran (THF) or chloroform (CHCl3) as a representative solvent medium.22 In order to determine the minimum energy path (MEP) on the potential energy surface (PES), intrinsic reaction coordinate (IRC) calculations, by defining the phase for the transition vector motion along the path, were performed for the identified transition states using the Hessian-based Predictor–Corrector integrator to confirm the reaction path proceeding in both directions (reactant and product), in which the Hessian was recomputed every 3 predictor steps with a step size along the reaction path of 0.05 bohr.23 All energies reported in this paper are Gibbs free energies at 298.15 K using unscaled frequencies. All activation free energies are quoted relative to infinitely separated reagents. Optimized structures are illustrated using CYLview.24Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the computational resources from the iridis4 supercomputer supported by the University of Southampton. AAH acknowledges the University of Southampton/School of Chemistry for providing the visitor-status research position (2717441/EB00-VISIT). Many thanks to the referees for their valuable comments and suggestions.References
- For review boron chemistry see: (a) D. S. Matteson, J. Org. Chem., 2013, 78, 10009–10023 CrossRef CAS PubMed; (b) D. G. Hall, Boronic Acids, Vol 2: Preparation and Applications in Organic Synthesis, Medicine and Materials, 2nd edn, 2011, pp. 1–701 CrossRef; (c) D. S. Matteson,Stereodirected Synthesis with Organoboranes, Springer, Berlin, 1995 CrossRef; (d) C. Sandford and V. K. Aggarwal, Chem. Commun., 2017, 53, 5481–5494 RSC; (e) D. Leonori and V. K. Aggarwal, Acc. Chem. Res., 2014, 47, 3174–3183 CrossRef CAS PubMed.
- (a) D. S. Matteson, Med. Res. Rev., 2008, 28, 233–246 CrossRef CAS PubMed; (b) R. Smoum, A. Rubinstein, V. M. Dembitsky and M. Srebnik, Chem. Rev., 2012, 112, 4156–4220 CrossRef CAS PubMed.
- B. S. L. Collins, C. M. Wilson, E. L. Myers and V. K. Aggarwal, Angew. Chem., Int. Ed., 2017, 56, 11700–11733 CrossRef CAS PubMed.
- (a) D. Leonori and V. K. Aggarwal, Angew. Chem., Int. Ed., 2015, 54, 1082–1096 CrossRef CAS PubMed; (b) C. Y. Wang, J. Derosa and M. R. Biscoe, Chem. Sci., 2015, 6, 5105–5113 RSC; (c) A. H. Cherney, N. T. Kadunce and S. E. Reisman, Chem. Rev., 2015, 115, 9587–9652 CrossRef CAS PubMed.
- (a) S. M. Zhou, M. Z. Deng, L. J. Xia and M. H. Tang, Angew. Chem., Int. Ed., 1998, 37, 2845–2847 CrossRef CAS; (b) M. Rubina, M. Rubin and V. Gevorgyan, J. Am. Chem. Soc., 2003, 125, 7198–7199 CrossRef CAS PubMed; (c) T. Ohmura, T. Awano and M. Suginome, J. Am. Chem. Soc., 2010, 132, 13191–13193 CrossRef CAS PubMed; (d) T. Awano, T. Ohmura and M. Suginome, J. Am. Chem. Soc., 2011, 133, 20738–20741 CrossRef CAS PubMed; (e) B. W. Glasspoole, M. S. Oderinde, B. D. Moore, A. Antoft-Finch and C. M. Crudden, Synthesis, 2013, 45, 1759–1763 CrossRef CAS; (f) D. Imao, B. W. Glasspoole, V. S. Laberge and C. M. Crudden, J. Am. Chem. Soc., 2009, 131, 5024–5025 CrossRef CAS PubMed; (g) S. C. Matthew, B. W. Glasspoole, P. Eisenberger and C. M. Crudden, J. Am. Chem. Soc., 2014, 136, 5828–5831 CrossRef CAS PubMed.
- For related trifluoroborates see: (a) G.-H. Fang, Z.-J. Yan and M.-Z. Deng, Org. Lett., 2004, 6, 357–360 CrossRef CAS PubMed; (b) D. L. Sandrock, L. Jean-Gérard, C.-y. Chen, S. D. Dreher and G. A. Molander, J. Am. Chem. Soc., 2010, 132, 17108–17110 CrossRef CAS PubMed; (c) J. C. H. Lee, R. McDonald and D. G. Hall, Nat. Chem., 2011, 3, 894 CrossRef CAS PubMed; (d) G. A. Molander and S. R. Wisniewski, J. Am. Chem. Soc., 2012, 134, 16856–16868 CrossRef CAS PubMed; (e) L. Li, S. Zhao, A. Joshi-Pangu, M. Diane and M. R. Biscoe, J. Am. Chem. Soc., 2014, 136, 14027–14030 CrossRef CAS PubMed; (f) Y. Z. Lou, P. Cao, T. Jia, Y. L. Zhang, M. Wang and J. Liao, Angew. Chem., Int. Ed., 2015, 54, 12134–12138 CrossRef CAS PubMed.
- For coupling of chiral secondary and tertiary boronic esters with electron-rich aryl lithium reagents see: (a) A. Bonet, M. Odachowski, D. Leonori, S. Essafi and V. K. Aggarwal, Nat. Chem., 2014, 6, 584 CrossRef CAS PubMed; (b) M. Odachowski, A. Bonet, S. Essafi, P. Conti-Ramsden, J. N. Harvey, D. Leonori and V. K. Aggarwal, J. Am. Chem. Soc., 2016, 138, 9521–9532 CrossRef CAS PubMed.
- (a) S. Aichhorn, R. Bigler, E. L. Myers and V. K. Aggarwal, J. Am. Chem. Soc., 2017, 139, 9519–9522 CrossRef CAS PubMed; (b) B. Rubial, B. S. L. Collins, R. Bigler, S. Aichhorn, A. Noble and V. K. Aggarwal, Angew. Chem., Int. Ed., 2019, 58, 1366–1370 CrossRef CAS PubMed.
- For the use of a Lewis acid in 1,3-borotopic see: (a) F. W. van der Mei, H. Miyamoto, D. L. Silverio and A. H. Hoveyda, Angew. Chem., Int. Ed., 2016, 55, 4701–4706 CrossRef CAS PubMed; (b) Y. Kitazawa, R. Takita, K. Yoshida, A. Muranaka, S. Matsubara and M. Uchiyama, J.of Org. Chem., 2017, 82, 1931–1935 CrossRef CAS PubMed.
- C. Tillin, R. Bigler, R. Calo-Lapido, B. S. L. Collins, A. Noble and V. K. Aggarwal, Synlett, 2019, 30, 449–453 CrossRef CAS.
- S. P. Roche and J. A. Porco, Angew. Chem., Int. Ed., 2011, 50, 4068–4093 CrossRef CAS PubMed.
- For transition metal-catalyzed transformations of the dearomatized boronic ester see: (a) M. Okumura, A. S. Shved and D. Sarlah, J. Am. Chem. Soc., 2017, 139, 17787–17790 CrossRef CAS PubMed; (b) M. Okumura and D. Sarlah, Synlett, 2018, 29, 845–855 CrossRef CAS; (c) L. W. Hernandez, U. Klöckner, J. Pospech, L. Hauss and D. Sarlah, J. Am. Chem. Soc., 2018, 140, 4503–4507 CrossRef CAS PubMed.
- (a) Y. Kitazawa, R. Takita, K. Yoshida, A. Muranaka, S. Matsubara and M. Uchiyama, J. Org. Chem., 2017, 82, 1931–1935 CrossRef CAS PubMed; (b) K. Fujiki, S.-y. Ikeda, H. Kobayashi, A. Mori, A. Nagira, J. Nie, T. Sonoda and Y. Yagupolskii, Chem. Lett., 2000, 29, 62–63 CrossRef.
- R. S. Paton, S. Kim, A. G. Ross, S. J. Danishefsky and K. N. Houk, Angew. Chem., Int. Ed., 2011, 50, 10366–10368 CrossRef CAS PubMed.
- For reactivity of other dienes see: (a) R. Sustmann, M. Böhm and J. Sauer, Ber. Dtsch. Chem. Ges., 1979, 112, 883–889 CrossRef CAS; (b) J. Sauer and R. Sustmann, Angew. Chem., 1980, 92, 773–801 CrossRef CAS; (c) J. Sauer and R. Sustmann, Angew. Chem., Int. Ed. Engl., 1980, 19, 779–807 CrossRef.
- For distortion/interaction model see: (a) K. N. Houk, F. Liu, Y.-F. Yang, & X. Hong The Distortion/Interaction Model for Analysis of Activation Energies of Organic Reactions, Appl. Theor. Org. Chem., 2018, pp. 371–402 Search PubMed; (b) F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS PubMed.
- For reactivity of PTAD towards other systems see: (a) J. S. Chen, K. N. Houk and C. S. Foote, J. Am. Chem. Soc., 1998, 120, 12303–12309 CrossRef CAS; (b) B. J. Levandowski and K. N. Houk, J. Org. Chem., 2015, 80, 3530–3537 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- (a) T. Clark, J. Chandrasekhar, G. W. Spitznagel and P. V. R. Schleyer, J. Comput. Chem., 1983, 4, 294–301 CrossRef CAS; (b) M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS; (c) R. C. Binning and L. A. Curtiss, J. Comput. Chem., 1990, 11, 1206–1216 CrossRef CAS; (d) M. P. McGrath and L. Radom, J. Chem. Phys., 1991, 94, 511–516 CrossRef CAS.
- (a) H. B. Schlegel, J. Comput. Chem., 1982, 3, 214–218 CrossRef CAS; (b) X. Li and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 835–839 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- (a) H. P. Hratchian and H. B. Schlegel, J. Chem. Phys., 2004, 120, 9918–9924 CrossRef CAS PubMed; (b) M. A. Collins, Theor. Chem. Acc., 2002, 108, 313–324 Search PubMed; (c) K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. C. Y. Legault, 1.0b, Universitéde Sherbrooke, Canada, 2009, http://www.cylview.org Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03820e |
| This journal is © The Royal Society of Chemistry 2019 |