Open Access Article
Open Access ArticleStudy on the thermal stress evolution in large scale KDP crystals during the crystal extraction process
Pingping Huang a,
Shenglai Wang*a,
Jianxu Ding
a,
Shenglai Wang*a,
Jianxu Ding b,
Duanliang Wangc,
Bo Wanga,
Hui Liua,
Longyun Xua,
Liyuan Zhanga,
Xianglin Lia and
Yining Liud
b,
Duanliang Wangc,
Bo Wanga,
Hui Liua,
Longyun Xua,
Liyuan Zhanga,
Xianglin Lia and
Yining Liud
aState Key Laboratory of Crystal Materials, Shandong University, Jinan 250100, China. E-mail: slwang67@sdu.edu.cn
bCollege of Materials Science and Engineering, Shandong University of Science and Technology, Qingdao 266590, China
cShandong Provincial Key Laboratory of Laser Polarization and Information Technology, College of Physics and Engineering, Qufu Normal University, Qufu, 273165, China
dCollege of Material Science and Engineering, Shandong University, Jinan 250061, China
First published on 3rd July 2019
Abstract
Transient numerical calculations were carried out to predict the evolution of temperature and thermal stress in traditionally grown large-size KDP crystals during the removal process, considering two methods that are used to accomplish the crystal extraction. The influence of the crystal size and the difference of temperature between the crystal and environment on the stresses inside the KDP crystals were also investigated in detail. Results indicate that, in both processes of isolating crystals, the highest stress transfers from the crystal periphery to the internal part from the early to the later time stage. In the case of extracting the crystal from solution directly after crystallization and exposing to air, the maximum stress at the crystal periphery is larger than that inside the crystal, and the probability of failure from the outside surface of crystals is large. In the case of retaining the solution for a time after crystallization, the maximum stress in the crystal internal region is larger than that of the crystal surface, leading to a large possibility to originate cracks in the inner region. Both increased crystal sizes and increased temperature differences between the crystals and the environment at the end of crystal growth are factors which aggravate crystal cracking. The maximum stress in crystals in the case of retaining the solution is less than that in the case of extracting the solution, which brings about a decreased likelihood of cracking. Thus, retaining solution for a period of time after the growth is completed, such as 96 h, is suggested to be adopted to accomplish successful crystal extraction.
1. Introduction
Due to its excellent electrical and optical properties, such as transparency over a wide region of the optical spectrum, high damage threshold to laser radiation and relatively high nonlinear efficiency, KH2PO4 (KDP) has been the subject of a wide variety of investigations for over half a century. Especially, the reproducible growth to large size endows KDP to have a unique position for use as electro-optic switches and frequency converters in large-aperture laser systems, such as in inertial confinement fusion (ICF) engineering.1–3 However, its applications are usually limited by its inherent shortcomings such as temperature sensitivity, high brittleness, deliquescence and softness, and cracks often occur during the crystal growth and post-processing procedure.4–8The crystals need to be removed from the crystallizer after the completion of crystal growth. Usually, two ways are implemented to accomplish the traditionally grown large-size crystal extraction. One way is to remove the solution from the crystallizer vessel when the KDP crystal reaches the expected size, allowing the crystal to reach to an equilibrium state slowly with the environment.1 Another way is to decrease the temperature of both the growth solution and crystals naturally to room temperature, and then extract the solution and remove the crystals.9 Apparently, KDP crystals undergo a temperature-change after finishing growth using either of these methods. Environment temperature change could cause a temperature gradient in the crystallizer and a non-uniform temperature field would appear in the KDP crystal, ultimately generating thermal stress.
Actually, cracking of large-scale KDP crystals frequently occurs with a number of multifarious features. In the case of extracting the solution after completion of the crystal growth, cracking usually occurs within 12 h and extends to the crystal periphery. In the condition of retaining the solution, instead cracking usually originates from the interface of the cap region and transparent region with or without propagating to the outside surface after 48 h.10 Once cracking occurs, the crack propagation process is too transitory to see owing the high brittleness of KDP crystals.11 Therefore, it is hard to observe the crack initiation point and propagation process. Moreover, the larger the crystal size and the larger the temperature difference between crystals and the environment, the higher the probability of crystal cracking. However, there is still insufficient systematic investigation on this process. Thus, it is necessary to explore factors related to the cracking of KDP crystals, points where cracks start and directions which they propagate along, on the purpose of guidance to produce large-aperture crystals safely.
Studies about stresses introduced by temperature changes have been widely performed on other crystals. Galazka12 analytically studied a time-dependent stress field in LiNbO3 and SrLaAlO4 single crystals immediately after their extraction from melts. It indicated that during rapid extraction from melts the crystals underwent high thermal shock which was sufficient to induce crack formation at the crystal periphery. Ma et al.13 predicated the evolution of temperature and thermal stress in sapphire single crystals during the cooling process by a heat exchange method, and found that the narrow bottom region of the sapphire crystal was subjected to high thermal stress during the cooling process, which could be responsible for the seed cracking of the as-grown crystal. Meanwhile, Wang et al.14 studied the effect of heater power allocation on the thermal stress evolution during the Kyropoulos sapphire cooling process. The results showed that large stresses were usually present in the regions near the ‘throat’ and ‘bottleneck’ of the crystal, and the stress significantly decreased as the power ratio was increased.
For KDP crystals, Zhang et al.15 have measured the tensile and compressive strength along [001] and [100] directions, and pointed out that the tensile strength was one order of magnitude less than the compressive strength. Our previous work16 reported the relationship between temperature non-uniformity in 30–40 mm small KDP crystals and their cracking, during a mimetic extraction process. Results revealed that when temperature differences in a cooling crystal exceeded 4 °C, the maximum stress appeared at the crystal periphery, resulting in a probability of cracking from the outside surface of the crystals. Wang et al.17 reported the thermal stress distribution induced by weak absorption for KDP and 70%-DKDP crystals of small sizes with dimension of 10 × 10 × 5 mm, and found that the thermal stress distribution along z- and x-cut samples was different, which was mainly attributed to the anisotropy of KDP along the x and z directions. However, for KDP crystals of large scale of about 500 mm that are used in ICF engineering, the relationship between thermal stresses induced by temperature non-uniformity and the cracking during the crystal extraction has not been explored.
This paper aims to simulate numerically the temperature and stress distribution in traditionally grown large KDP crystals when removed from the crystallizer, either with or without prior solvent contact after crystallization. Meanwhile, effects of the crystal size and the temperature difference between the crystal and environment on the stresses inside the KDP crystals are also investigated. In addition, it is worth noting that temperature field calculations are based on experimental measured environment temperatures.
2. Experimental
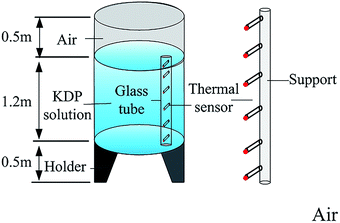
Fig. 1 shows the crystallizer vessel used in the experiment. Both the temperature of air around the crystallizer and solution in the crystallizer were measured to calculate the temperature variation of the crystal surrounding after the growth was completed. The crystallizer unit was of 0.6 m radius and 2.2 m total height. A support with height of 2.2 m, which was 0.2 m away from the crystallizer, was used to place thermal sensors to measure air temperatures over the entire range. In the crystallizer vessel, the solution was in the height range of 0.5–1.7 m. A long glass tube encircling thermal sensors was placed 0.1 m from the inner wall of the crystallizer. Thermal sensors with a measurement accuracy of 0.1 °C can be moved in the vertical direction. Over 10 min was required to achieve a steady temperature at each position.3. Numerical simulation
Thermal analysis
To investigate the thermal field inside KDP crystals after being affected by environment temperature, a quarter of the model was used as the simulation domain because of the four-fold symmetry of the model. The simulation domain of the two different cases are shown in Fig. 2a and b, respectively. The stress calculation was conducted on the KDP crystal, including the seed, the cap region and the transparent region, as seen in Fig. 2c. In order to study the dependence of thermal stresses on crystal sizes, crystals with aperture of 0.3 × 0.3 m, 0.4 × 0.4 m and 0.5 × 0.5 m were considered in the simulation. For the three sizes of crystals, the heights of the cap region were 0.15, 0.2 and 0.25 m, respectively. The seed height was 0.02 m and the total length of crystals were 1 m. In the second treatment case, solution filled the crystallizer with radius of 0.6 m and height of 1.2 m, and the crystallizer vessel thickness was 0.01 m. The points A, B and C on crystals were observation points that were used for tracing the stress evolution. The radial path EF was located at 0.4 m under the top of KDP crystals, which is chosen for analyzing the temperature distribution. In the simulation domain, an unstructured tetrahedral mesh was used in the cap region and other regions were meshed with hexahedral elements. Additionally, 100 × 118 elements were meshed in radial and axial directions, respectively, in the simulation domain shown in Fig. 2b, and it was fine enough to obtain a grid-independent solution.The thermal field simulation in the two cases were dealt with the transient thermal conduction between the KDP crystal and media. The energy conservation equation governing the thermal field is written as:
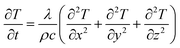 | (1) |
Certain assumptions were proposed to simplify the computation in the second case. The buoyancy convection in the solution was ignored due to the small temperature difference throughout it. Besides, radiation was also not taken into account because of the low difference of temperature between the KDP crystal and the solution.
The heat transfer equation was solved by the finite volume method with ANSYS Fluent software, with a transient simulation. In the first condition, the KDP crystal was considered as exposed to the atmosphere, then the Robin condition was applied to the crystal surface as:
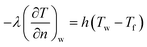 | (2) |
The hr according to radiation could be calculated from the formula:19
 | (3) |
The hf according to natural convection can be obtained by the experimental relation:
| Nu = C(Gr Pr)n | (4) |
 | (5) |
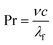 | (6) |
 | (7) |
 | (8) |
In the first case (direct air contact), the external temperature Tf applied to the outer surface of KDP crystals was the measured air temperature as measured in Fig. 3a. The heat transfer coefficient h was calculated by eqn (3)–(8) according to the different crystal sizes and the variation of initial temperatures of crystals.
In the second case (solution contact), the initial temperature of the KDP crystal and solution were 20 °C, the Robin condition was applied to the outer surface of crystallizer, the coefficient of convection heat transfer h was 10 W m−2 K−1, and the environment temperature Tf was the air temperature measured as seen in Fig. 3a. The solution temperature was distributed with a gradient, so that it affected the temperature uniformity of the KDP crystals. For the thermal exchange between KDP crystals and the solution the solution and the crystallizer were dealt with as a coupling interface.
Thermo-elastic stress analysis
In general, temperature variation within an elastic continuum can lead to thermal stresses. Linear thermoelasticity theory is based on the relationship between the linear addition of thermal strains and mechanical strains. The stress–strain relationship for an anisotropic solid body has been described by Lambropoulos:20| σ = C[ε − α(T − Tref)] | (9) |
 | (10) |
In addition, the strain ε in eqn (9) is computed based on the displacement field and can be described by the formula as follows:
 | (11) |
Based on the thermal field of KDP crystals calculated from thermal analysis, the mechanical analysis was carried out using the finite element method in ANSYS Mechanical. Fine solid elements with tetrahedral or hexahedral structure were used to mesh the calculation domain, as shown in Fig. 2c. The structure constraint applied to the KDP crystal also can be seen in Fig. 2c, and the detailed description was as follows: two displacement constraints ux = 0, vy = 0 were applied to the symmetry plane of (100) and (010), respectively, and in the intersection of two symmetry planes, wz = 0 was applied. As reported by Zhang,22 the stress of KDP crystal increases about 1% in the case of considering the gravity in comparison to not doing so, and here the role of gravity on the thermal stress in our simulation was ignored. As the density of the KDP crystal and solution were 2338 and 1200 kg m−3, respectively, as shown in Table 1, the effect from the buoyancy is even less that from the gravity, and so the buoyancy was also not taken into account.
| Material | Cap region | KDP crystal | KDP solution | Growth tank |
|---|---|---|---|---|
| Density (kg m−3) | 2200* | 2338 | 1200 | 1180 |
| Heat conductivity (W m−1 K−1) | 1.09* | 1.21‖c | 0.635 | 0.19 |
| 1.34⊥c | ||||
| Specific heat (J kg−1 K−1) | 816* | 857 | 4174 | 1461 |
| Thermal expansion coefficient (K−1 10−6) | 48.94* | 42.1‖c | — | — |
| 26.4⊥c | ||||
| Young's modulus/GPa | 19.63 | — | — | |
| Poisson's ratio | 0.06 | Represented by eqn (10) | — | — |
The material properties involved in the simulation are summarized in Table 1.
4. Results
Experimental results
Fig. 3 shows the temperatures of air and KDP solution vs. height measured at different times. As seen in Fig. 3a, the air temperature almost maintains a stable value in 120 h after the finishing of crystal growth. However, with the increasing height, the air temperatures goes up gradually, about 2.2 °C temperature difference exists in the 2.2 m height range. It can be observed from Fig. 3b that solution temperatures gradually decrease with increased time. After 24 h, temperatures decrease by 0.4 °C uniformly. At 72 and 120 h, solution temperatures reduce continuously and a temperature gradient also appears because of the effect of air temperature.In order to validate the numerical simulation, we performed a calculation firstly for the second way of taking out crystals (delayed removal from solution). In this computation, we set the initial temperature of the solution to be 20 °C, and the air temperatures shown in Fig. 3a were set as the boundary conditions. Fig. 3c shows the calculated and measured solution temperatures along the vertical direction at three different times. The calculation approach demonstrates a good agreement with the practical measurement.
Simulation results
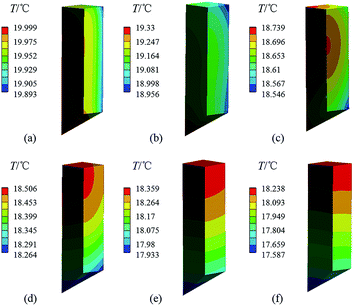
In the following, points A, B and C refer to Fig. 2b.Temperature and stress distribution in KDP crystals with dimension of 0.5 m. We assumed that the growth was completed at 20 °C and air temperatures shown in Fig. 3a was applied as the boundary condition. Fig. 4 and 5 show the temperature and stress distributions, respectively, calculated in a 0.5 m × 0.5 m aperture KDP crystal at different times after the growth was finished, in the case of extracting the solution (exposure to air). Stresses in this calculation are expressed by the maximum principle stress, σ1, since the first strength theory is widely used to determine the fracture of brittle materials.27,28 It can be seen that the temperature uniformity of crystal is gradually changed by the effect of the surrounding temperature. In the early stage, temperatures are high in the main body and low at the top, bottom and crystal periphery. The maximum stress is located near the center of the outside surface edge (marked as point A in Fig. 2b), and denoted by a small square tagged “Max” in Fig. 5a and b. Relatively high stresses occur at the cap region. The stress is very small, even less than zero, in the large center part of the transparent region, as shown in Fig. 5a and b. As time goes on, temperatures becomes high in the top and low at the bottom because the influence derived from the environment temperature is gradually increased. Meanwhile, the highest stress transfers to the interface between the cap region and transparent region (labelled as point B in Fig. 2b), as shown in Fig. 5d–f.
Fig. 6 presents the maximum σ1 evolution in the outside surface (point A) and in the interior (point B) of the 0.5 m size crystal. It is found that stresses at the exterior increase firstly and then decrease rapidly. A peak stress of 1.581 MPa occurs at 3 h after the isolation of the crystal. The maximum σ1 in the interior increases continuously and reaches a peak value of 1.01 MPa at 72 h and is very close to the value obtained from the steady-state calculation. The position where maximum σ1 is located transfers around 15 h. The maximum peak stress at the crystal periphery is obviously larger than that reached in the interior throughout the entire temperature variation process, which leads to a large probability of cracking starting from the crystal outer surface.
 | ||
| Fig. 6 The maximum σ1 evolution at the outside surface (point A) and interior (point B) of the 0.5 m crystal in the case of extracting the solution. | ||
Effect of crystal sizes on stresses in KDP crystal. Fig. 7a–c present the maximum σ1 evolution in the outside surface (point A), the interior (point B) and the top end of the cap region (point C) for 0.5, 0.4 and 0.3 m sized crystals during the entire process, respectively. Results illustrate that stresses at point A increase firstly and then decrease, showing the same variation characteristics. However, compared to the result that shows the peak σ1 of 1.581 MPa at 3 h after the extraction of the solution in the 0.5 m size crystal, the 0.3 m and 0.4 m size crystals show their peak σ1 of 1.372 and 1.513 MPa at 1 and 2 h, respectively. With increase of crystal size, stresses at point A rise. A prominent difference is observed at 24 h when the σ1 in the 0.5 m size crystal is 6.05 times of that in the 0.3 m size crystal. Differing from the stress variation at point A, both stresses of point B and C increase quickly in the early stage and approach a steady value gradually over time. The stresses in point B are higher than that in point C. In addition, stresses in point B and C also show the same dependence on sizes. In the early period, stresses of 0.3 m size crystal go up rapidly and show the biggest values. All three sizes of crystals have the nearly equal stresses at later times.
Effect of crystal temperatures at the end of growth on stresses in KDP crystals. To understand the effect of temperature differences between crystals and the environment at the end of growth on stresses of KDP crystals, we assumed two situations that crystal growth was finished at temperatures of 22 and 24 °C, which were higher than the room temperature. Fig. 8 demonstrates the evolution of maximum σ1 at points A, B and C in a 0.5 m size crystal with three different initial temperatures. As can be found, in the condition of initial temperature at 24 °C, the maximum σ1 at point A and B are 5.068 and 3.205 MPa, respectively, which are 3.20 and 3.16 times of those in the case of an initial temperature of 20 °C. Therefore, the rise of temperature difference between the crystal and environment leads to a substantial stress increase, which causes a much increased potential of cracking both in the outside surface and in the interior of crystals.
Temperature and stress distribution in KDP crystals with dimension of 0.5 m. Fig. 9 and 10 shows the temperature and stress distributions calculated in a 0.5 m KDP crystal at different times after finishing the crystal growth, in the case of retaining the solution. It can be found that, the evolutions of thermal field and stress of the crystal are similar to that in the first case with direct air exposure. In the initial stage, the temperature is high in the internal part and low at the outside, causing the stress to be small in the interior and large at the crystal periphery. The maximum stress appears around the center of the outside surface edge, as seen in Fig. 10a. When temperature change proceeds to later times, the temperature becomes high at the top and low at the bottom of the crystal, and the highest stress transfers its location to the edge of the cap region, with gradually increased values over time.
Fig. 11 presents the evolution of maximum σ1 in the crystal periphery (point A) and in the interior (point B). It is clearly seen that the maximum σ1 transfers the location at 96 h after the end of crystal growth. The maximum σ1 in the outside surface increases firstly and then decreases, reaching the peak value of 0.326 MPa at 72 h, which is less than the σ1 of 1.581 MPa in the case of extracting the solution, and the time that peak value appears is later than the time of 3 h in the first case. Thus, the potential of cracking in the crystal periphery decreases. Meanwhile, in the case of retaining the solution, crystals require approximately 360 h to reach a steady state, which is five times longer than the first case. The maximum σ1 of 0.983 MPa in the crystal interior is almost equal to that of 1.01 MPa in the case of extracting the solution, implying that there is similar probability of cracking from the crystal interior. However, during the entire temperature-change process, the maximum stress in the interior is larger than that at the outer surface, causing a large risk of cracking inside the body of the crystal, which is opposite to the condition of extracting the solution.
 | ||
| Fig. 11 The evolution of maximum σ1 in the outer surface (point A) and in the interior (point B) of a 0.5 m size crystal in the case of retaining solution. | ||
Effect of crystal sizes on stresses in KDP crystals. In the case of retaining the solution, thermal analysis and stress calculation were also conducted on 0.3 and 0.4 m crystals. Fig. 12a displays the evolution of maximum σ1 at the external surface (point A) of various crystals. It can be noted that the peak stresses of point A appear at 96 h for the 0.3 and 0.4 m size crystals, which is later than the time of 72 h in the 0.5 m size crystal. With the enlargement of crystal sizes, stresses increase significantly during the entire temperature-change process. Maximum σ1 in the 0.5 m crystal is nearly three times larger than that of the 0.3 m crystal.
To study factors that affect stress values at the crystal periphery, we plot temperatures vs. radial length in transversal section around the midpoint along the height (marked EF in Fig. 2b, which is located at 0.4 m under the top of the KDP crystals) for the three sizes of crystals in Fig. 12b at the time of 72 h. It is revealed in Fig. 12b that the crystal with dimension of 0.5 m has the lowest temperature and the highest temperature gradient, especially in the region near the outer surface. As regard to the crystal with 0.3 m dimension, it exactly has the opposite characteristics for both temperature and temperature gradient, meaning that the temperature is the highest and the temperature gradient is the lowest. As for the 0.4 m size crystal, the temperature gradient is moderate. In comparison of the relationship of stresses in different sizes of crystals, as shown in Fig. 12a, it is rational to speculate that the radial temperature gradient of crystals is responsible for the stress values at the crystal periphery. The increased crystal sizes therefore result in increased stresses.
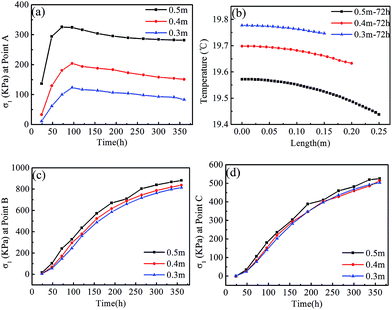 | ||
| Fig. 12 The evolution of maximum σ1 at different positions in the three sizes of crystals and the temperature profile at the time at which peak σ1 is a maximum, in the case of retaining the solution: (a) point A, (b) temperature profile along the path of EF, labelled in Fig. 2b, (c) point B and (d) point C. | ||
Fig. 12c and d present the evolution of maximum σ1 in the crystal interior (point B) and the top end of the cap region (point C). Temperature drops in crystals lead to an increased thermal mismatch stress between the cap region and transparent region, thus stresses at points B and C increase monotonously with increased time. With the rise of crystal sizes, stresses of point B increase gently in comparison to that of point A. The biggest difference between the stresses of point B in a 0.5 m size crystal and a 0.3 m size crystal is 8% among all moments. Stresses on the point C are less than that on point B, and also the size dependence is less.
5. Discussion
Simulation results for the two methods to remove large-scale KDP crystals reveal that, differences exist between them, such as the crack origination position and the cracking moment. In the case of extracting (removing) the solution, heat extraction from the crystal is strong, a large radial temperature gradient occurs inside the crystal in the early stage, and this results in the peak stress appearing at the outside surface within 3 h after the end of crystal growth. As the temperature-change evolves, stresses at the outside surface reduce with the decrease of radial temperature gradient. Nevertheless, the differences of material property between the cap region and the transparent region of crystals makes the interface of these two regions become a location of high stress due to the gradual increase of the axial temperature gradient. During the entire temperature-change process, the maximum stress at the crystal periphery is larger than that at the interface, which induces a big probability of cracking at the outer surface in the early period. This is consistent with the cracks observed from practical observations that usually occurs within the early hours, such as 12 h, and extends to the crystal periphery. When the solution is retained, the radial temperature gradient of crystals become small as a result of the weak heat dissipation from crystals. In this case, the maximum stress is located at the edge of cap region which is larger than the stress at the outside surface. So, cracking is likely to occur inside crystals in the later stage of the temperature-change. When performing the experiment via the second route, cracks are normally observed to originate from the interface of the cap region and the transparent region with or without propagating to the crystal periphery around 48 h or a few days later. These phenomena illustrate that simulated results exactly coincide with the actual observation well.The difference of temperature between the crystal and environment at the end of growth is one of the main factors leading to crystal cracking. Simulation results in the case of extracting the solution indicate that, when the average environment temperature is about 17.3 °C, the maximum stress of the crystal with an initial temperature of 24 °C is three times larger than that of a crystal with an initial temperature of 20 °C. In addition, crystal size enlargement is another factor causing the crystal cracking. Temperature non-uniformity in crystals enhances with the increasing crystal sizes, which means that a larger radial temperature gradient exists in a bigger crystal, so that stresses at the crystal periphery increase also. For instance, in the case of extracting the solution, the maximum stress of a 0.5 m size crystal is raised 15% comparing to that in a 0.3 m size crystal.
In this paper, the maximum of calculated stress of a 0.5 m size KDP crystal during crystal extraction is 1.58 MPa, which is far less than the measured tensile strength of 6.67 MPa.15 That a large-scale crystal cracking occurs with such a minor stress is possibly attributed to the size effect. Generally speaking, failure strength of a brittle material is dominated by small defects in it, and its failure strength deviates greatly due to the deviation of the defect size. The probability of large-sized defects being contained in a sample rises as the size of a sample increases.29 The Weibull weakest-link model leads to a strength dependency on specimen size as:30
 | (12) |
On basis of the eqn (12) and fracture stress of 5.74 MPa16 in a small KDP crystal, the predicted fracture stress in different sizes of KDP crystals are listed in Table 2. The Weibull modulus, m = 5.05, was obtained from the bending strength measurement of KDP crystals.33 It can be seen from Table 2 that, due to the crystal size of 35 × 35 × 56 mm being similar to that of the 30 × 30 × 30 mm specimen used in the tensile strength test, the fracture stress of 5.74 MPa is close to the tensile strength of 6.67 MPa. When the crystal size is enlarged, estimated fracture stresses decrease markedly, which makes the calculated thermal stresses approximate equal to the predicted fracture stresses. When the crystal size reaches 0.4 and 0.5 m, in the case of extracting the solution, the simulated maximum stresses of 1.51 and 1.58 MPa are larger than the estimated fracture stress for the corresponding sizes of crystals. Even in the case of retaining the solution, the maximum stress of 0.98 MPa in a 0.5 m size crystal is close to the predicted fracture stress of 1.13 MPa, indicating that a potential of crystal cracking exists.
| Calc. maximum σ1 (MPa) | |||
|---|---|---|---|
| Crystal sizes (cm) | Estimated fracture strength (MPa) | Extraction case | Retaining case |
| 3.5 × 3.5 × 5.6 | 5.7416 | ||
| 30 × 30 × 100 | 1.39 | 1.37 | 0.93 |
| 40 × 40 × 100 | 1.24 | 1.51 | 0.94 |
| 50 × 50 × 100 | 1.13 | 1.58 | 0.98 |
Of course, cracking in large-size KDP crystals is complicated. The superposition of both structural stress and thermal stress is probably responsible for their failure. On the one hand, impurities are unavoidable in the KDP crystal growth,34 which would result in lattice distortion due to incorporation of impurities into the crystal.35 On the other hand, owing to the difference in segregation coefficient of solute at different temperatures, lattice mismatch is probably induced among multi-layers of the KDP crystal.36 Both the lattice distortion and mismatch would produce structural stress in the crystal. However, structural stress is hard to keep the same for each crystal, a larger sample may have a greater value. So the amount of extra thermal stress needed to trigger cracking is lower. Besides, we also realized that the simulation was just applied for the ideal model, whereas real conditions are more complicated. However, it is worth noting that our predictions are in good coincidence with the actual observations, such as the cracking tine, the crack initiation and crack propagation directions.
A conclusion also can be drawn from our simulation that, retaining the solution after completion of the crystal growth can reduce the maximum stress inside the crystal. Finally, in order to decrease the danger of crystal cracking in a certain size, it is vital to reduce the difference of temperature between the crystal and environment when the growth is completed. Additionally, retaining solution for a period of time (such as 96 h) after the crystal growth is suggested to be adopted to accomplish the crystal extraction.
6. Conclusions
Numerical simulation was conducted to investigate the traditionally grown large-scale KDP crystal cracking during the taking out process, by solving temperature and thermal stress evolution for the two methods implemented to accomplish the crystal extraction. From the results, the following conclusion can be drawn: (1) in the case of extracting (removing) the solution, the maximum stress at the crystal periphery is larger than that inside the crystal, and there is a big probability to produce cracks at the outer surface of crystals in the early stage. In the condition of retaining the solution, the highest stress at the crystal periphery decreases markedly, and the maximum stress is located at the edge of cap region, thus the potential of cracking from the crystal inside body is large a few days later. These results agree well with the actual experimental observations. (2) With an increase of the crystal sizes, the maximum stress inside the crystal increases prominently. Meanwhile, the fracture stress values that trigger the crystal cracking decreases gradually, which means that the larger the sizes of crystals, the larger is the risk of crystal cracking. (3) When temperature differences between the KDP crystal and the surrounding environment exceeds 2.7 °C, large KDP crystals with dimensions around 0.4 m are in severe danger of cracking. (4) In order to reduce the risk of crystal cracking, it is vital to decrease the temperature difference between the crystal and environment at the end of growth. In addition, retaining the solution in the crystallizer for a period of time, such as 96 h, after the completion of crystal growth, is suggested to be helpful to optimize the crystal extraction. Last but not the least, the simulation about the thermal stress evolution in large scale KDP crystals could offer a insight for the research of other crystal cracking phenomena.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by National Natural Science Foundation of China (No. 51321062, 11847079, 51602174) and the Natural Science Foundation of Shandong Province (No. ZR2018BEM008, ZR2016EMQ04).Notes and references
- N. Zaitseva and L. Carman, Prog. Cryst. Growth Charact. Mater., 2001, 43, 1 CrossRef CAS
.
- S. L. Wang, X. Sun and X. Tao, Growth and Characterization of KDP and Its Analogs, Springer Handbook of Crystal Growth, Heidelberg, Berlin, 2010 Search PubMed
.
- W. Li, G. Yu, S. Wang, J. Ding, X. Xu, Q. Gu, D. Wang and P. Huang, RSC Adv., 2017, 7, 17531 RSC
.
- H. Chen, Y. Dai, Z. Zheng, H. Gao and X. Li, Mach. Sci. Technol., 2011, 15, 231 CrossRef CAS
.
- Q. Zhao, Y. Wang, G. Yu, S. Dong and X. Zhang, J. Mater. Process. Technol., 2009, 209, 4169 CrossRef CAS
.
- L. Deng, H. Yang, X. Zeng, B. Wu, P. Liu, X. Wang and J. Duan, Int. J. Mach. Tools Manuf., 2015, 94, 26 CrossRef
.
- P. Huang, S. Wang, D. Wang, H. Liu, G. Liu and L. Xu, CrystEngComm, 2018, 20, 3171 RSC
.
- P. Huang, J. Ding, D. Wang, H. Liu, L. Xu, X. Li, B. Wang, G. Liu and S. Wang, CrystEngComm, 2019, 21, 1329 RSC
.
- D. Wang, T. Li, S. Wang, J. Wang, C. Shen, J. Ding, W. Li, P. Huang and C. Lu, Opt. Mater. Express, 2017, 7, 533 CrossRef CAS
.
- Y. Su, Study on the mechanical properties and cracking phenomenon of KDP crystal, Shandong University, Jinan, 2012, p. 5 Search PubMed
.
- C. H. Guin, M. D. Katrich, A. I. Savinkov and M. P. Shaskolskaya, Krist. Tech., 1980, 15, 479 CrossRef CAS
.
- Z. Galazka, Cryst. Res. Technol., 1999, 34, 635 CrossRef CAS
.
- W. Ma, W. Zhao, M. Wu, G. Ding and L. Liu, J. Cryst. Growth, 2017, 474, 37 CrossRef CAS
.
- S. Wang and H. Fang, Appl. Therm. Eng., 2016, 95, 150 CrossRef
.
- Q. Zhang, D. Liu, S. Wang, N. Zhang, X. Mu and Y. Su, J. Synth. Cryst., 2009, 38, 1313 CAS
.
- P. Huang, D. Wang, W. Li, H. Liu, G. Liu and S. Wang, J. Chin. Ceram. Soc., 2018, 46, 929 Search PubMed
.
- D. Wang, C. Shen, J. Lan, P. Huang, Z. Cui, T. Kang, Y. Niu, S. Wang, J. Wang and R. I. Boughton, J. Alloys Compd., 2019, 790, 212 CrossRef CAS
.
- S. Yang and W. Tao, Heat Transfer, Heigher Education Press, Beijing, 4th edn, 2006 Search PubMed
.
- B. Wang, Numerical simulation study on stress state during KDP growth and cooling process with translational method, Chongqing University, 2015, pp. 34–35 Search PubMed
.
- J. C. Lambropoulos, J. Cryst. Growth, 1987, 84, 349 CrossRef CAS
.
- O. Lubin and C. Gouedard, Proc. SPIE, 1999, 3492, 802 CrossRef CAS
.
- N. Zhang, Q. Y. Zhang, S. L. Wang and Y. Sun, J. Funct. Mater., 2011, 12, 2133–2136 Search PubMed
.
- Q. Zhang, N. Zhang, S. Wang and D. Liu, J. Funct. Biomater., 2009, 40, 1584 CAS
.
- D. N. Nikogosyan, Nonlinear optical crystals: a complete survey, Springer Science & Business Media, 2006 Search PubMed
.
- H. F. Robey and D. Maynes, J. Cryst. Growth, 2001, 16 Search PubMed
.
- M. Mohammadi and J. Davoodi, Mol. Simul., 2018, 44, 1304 CrossRef CAS
.
- N. Miyazaki, J. Cryst. Growth, 2002, 236, 455 CrossRef CAS
.
- X. Jin, S. Wang, L. Dong and B. Xu, Eng. Failure Anal., 2018, 83, 102 CrossRef
.
- N. Miyazaki and N. Koizumi, J. Mater. Sci., 2006, 41, 6313 CrossRef CAS
.
- G. D. Quinn, J. Am. Ceram. Soc., 2003, 86, 508 CrossRef CAS
.
- Y. Torres, R. Bermejo, F. J. Gotor, E. Chicardi and L. Llanes, Mater. Des., 2014, 55, 851 CrossRef CAS
.
- F. Farahani and R. Gholamipour, J. Alloys Compd., 2017, 695, 2740 CrossRef CAS
.
- P. Huang, Study on the cracking of KDP crystal by experimental and simulation method, Shandong University, 2019, p. 99 Search PubMed
.
- S. Zhu, S. Wang, J. Ding, G. Liu, W. Liu, L. Liu, D. Wang, W. Li, Q. Gu and X. Xu, J. Cryst. Growth, 2014, 388, 98 CrossRef CAS
.
- J. Zhang, S. Wang, C. Fang, X. Sun, Q. Gu, Y. Li, B. Wang, B. Liu and X. Mu, Mater. Lett., 2007, 61, 2703 CrossRef CAS
.
- L. Liu, S. Wang, G. Liu, D. Wang, W. Li and J. Ding, J. Synth. Cryst., 2015, 44, 1443 CAS
.
| This journal is © The Royal Society of Chemistry 2019 |