DOI:
10.1039/C9RA02191D
(Paper)
RSC Adv., 2019,
9, 13949-13958
Significance of triple torsional correlations in proteins†
Received
21st March 2019
, Accepted 21st April 2019
First published on 7th May 2019
Abstract
The free energy landscape (FEL) of a given complex molecular system is fundamentally the joint probability density of its many comprising degrees of freedom (DOFs). Computation of a complete FEL at atomistic scale is unfortunately intractable for a typical biomolecular system. The challenge of entropy calculation comes from various correlations among different DOFs. The common strategy to treat such complexity is expansion of the full correlation into various orders of local correlations. In reality, expansion is usually cut off at the second order (i.e. pairwise interactions) for protein torsional correlations without reliable estimation of the resulting error. Here, we estimated the mutual information of different torsion sets and found that triple correlations were significant for both local/distant residue pairs and consecutive backbone torsional segments. As expected, the third order approximations were found to be consistently better than the second order approximations. These findings were true for all analyzed proteins with different folds, were independent of the two different force fields utilized to generate trajectory sets, and were therefore likely to be of general importance for proteins. Additionally, binning strategies are of universal importance for numerical computation of correlations, we here provided a detailed comparison between equal-width and equal-sample binning for different bin numbers and demonstrated the impact of binning strategies on variances and biases of calculated mutual information. Our observation suggested that caution should be taken when quantitative comparison of correlations were intended between different studies with different binning strategies.
1 Introduction
Interesting properties of complex molecular systems are mainly based on interactions and the resulting correlations between/among comprising DOFs. Proteins are certainly not exceptions and correlations of their molecular DOFs have attracted much attention of the scientific community. Historically, intra-molecular correlations of proteins have been studied from two related but distinct perspectives. The first was calculation of free energy landscape (FEL), full understanding of which has been believed to give us complete capacity for understanding concerned molecular systems. The second perspective was to study protein motional correlations so as to facilitate understanding functions.
In calculating FEL, direct effect of molecular interactions were usually accounted for by their energetic contributions while the resulting correlations were calculated as entropic contributions. The second order correction to the quasi-harmonic entropic calculation was systematically investigated,1,2 and the correction was found to be significant for the investigated molecular systems. Mutual information expansion (MIE) was utilized to calculate configurational entropy for small molecules with truncation at the third order.3 King and Tidor developed maximum information spanning tree (MIST) calculation of molecular entropy and carried out detailed comparison with MIE.4 Metadynamics5 strived to identify strongly correlated local clusters from molecular DOFs and subsequently utilized collective variables to simplify characterization of FEL. These studies greatly advanced our understanding of the FEL complexity. However, complete understanding of protein FEL concerned not only minima but also pathways and saddle points. To this regard, methodologies such as transition path sampling6 and string method7 provided useful tools. Nevertheless, to explain behavior of our interested proteins from their full FEL remained a great challenge.
A distinctive, but less ambitious perspective in investigating correlations between/among protein molecular DOFs was to study protein motional correlations so as to help explain functions, especially intramolecular signal/information transmission between/among parts of protein molecules. Intensive studies have been carried out based on analysis of molecular dynamics (MD) simulation trajectories.8–23 Earlier studies were limited to very short time scales (sub-nanoseconds).8–10 More recent studies20,21,24,25 mainly focused on mechanisms of long-range signal transmission, which was essential for functionally important protein allostery. Both linear correlation13,18,22 and mutual information12,14,20 analysis were widely utilized. Beyond correlation analysis of atomic positions and torsions, more complexed forms of correlations at larger spatial scales, such as second order mutual information based residue–residue coupling,14 (Dis)similarity index,25 energy network analysis26 and pKa variation computation27 were also investigated.
Past studies of correlations in proteins mainly focused on pair correlations.12,18,22,28 Systematic evaluations of correlations beyond the second order seem natural and understanding of which is certainly helpful as we proceed to more quantitative and reliable analysis of proteins. However, due to the sampling difficulty, direct and explicit characterization of third and higher order torsional correlations in proteins has not been systematically performed. Here, we estimated the influence of triple (the third order) torsional correlations in both inter-residue coupling and local backbone segments. It was found that for both cases, contributions of triple torsional correlations were significant for all analyzed datasets. We analyzed 19 molecular dynamics (MD) simulation trajectory sets of 9 globular and 10 membrane proteins generated with CHARMM force fields, and 4 MD simulation trajectory sets of soluble proteins generated with AMBER force field. As one would intuitively expect, the third order approximations were found to be better than the second order approximations. We also found that linear combinations of the second and the third order mutual information approximation presented consistently and significantly better approximations to the full inter-residue torsional mutual information than the third order approximations. It was important to note that the full inter-residue torsional mutual information, the second and the third order approximations were all underestimated for the method we utilized. As a matter of fact, all discrete calculation of mutual information suffered from this problem to some extent. Our reported mutual information were based on the correlations probabilities of bins. We used m = 3 to divide torsions and the correlations caused by all significant conformational change were captured. With larger m we would certainly get more correlations when originally within-larger-bin correlations that were neglected being counted. Correlations caused by significant torsional conformational change (e.g. gauch+ to gauch−), which were captured by binning with m = 3, usually dominate torsional correlations to the similar extent. We therefore believed that the qualitative trend will not change with larger m.
2 Methodology
2.1 MD trajectory sets
MD trajectory sets of 9 globular proteins were selected from data sets of our previous study28 (1bta, 1rgh, 2bnh, 2pka, 3f3y, 5pti, 7rsa, BamE, HEWL). The details of these simulations can be found in previous study.28–32 Six α helical membrane protein trajectory sets are: bacterior rhodopsin (pdb code: 1c3w, 400 ns), zeta–zeta transmembrane dimer (2hac, 150 ns), GlpG (2ic8, 150 ns), ABC-transporter BtuCD (2qi9, 120 ns), uracil transporter UraA (3qe7, 140 ns), and transmembrane domain of the M2 protein (pdb code 3bkd, 170 ns). Four β barrel membrane protein trajectory sets are: mouse VDAC1 (3emn, 180 ns), membrane transporter FecA (1kmo, 250 ns), Ompf (pdb code 1hxx, 200 ns) and BamA (4k3b, 800 ns). Membrane protein MD simulations were performed with NAMD software package, version 2.9 using CHARMM36 force fields. The proteins are solvated with TIP3 water and POPC lipid. 100 mM Na+ and Cl− were added to neutralize net charges of our simulation systems. Periodic boundary conditions were used, a switch distance of 10 Å and a cutoff distance of 12 Å were used for non-bonded interactions. Particle Mesh Ewald (PME) were used to calculate the long-range electronic interactions. All systems were minimized and then heated to 310 K. The system was equilibrated in the NPT ensemble for 1 ns. Production runs were performed in the NPT ensemble at 310 K with simulation time step 2 fs. All membrane protein trajectories are recorded with an interval of 2 ps. These 19 trajectory sets are generated with CHARMM36 (addressed as CHARMM below) force fields. Trajectory sets of four proteins are generated with AMBER99SB (-ILDN for BPTI, addressed as AMBER below) force field, they are BPTI (from D. E. Shaw group33), CDK2 (ref. 28) (20 μs), HEWL (800 ns), EH3_sam (3 μs). CDK2, HEWL and HEWL trajectories were generated in a similar protocol with these previous trajectories except utilization of the AMBER force fields and package. Secondary structure identity assignment were described in our previous study.28
2.2 Joint distributions and probability density
To calculate joint distributions for multiple-torsion sets (e.g. single residues, residue pairs or multiple consecutive backbone torsions), we first divided each torsion into m bins, L(i) (i = 1, 2,…,m) is the width of the ith bin. For a n-torsion (t1, t2,…,tn) set, there were mn different states based on such partition of participating torsions. We first constructed joint distributions of a n-torsion set X with mn bins. The order of bins was determined by eqn (2). The probability density f(xi) of each bin were shown below. p(xi) was the probability that data points fell within the ith bin. w(xi) is the volume of the ith bin for a torsion set or the width of the ith bin for a single torsion.| | |
f(xi) = p(xi)/w(xi) (i = 1, 2,…,mn)
| (1) |
| | |
w(xi) = L1(k1)L2(k2)…Ln(kn), (k = 1, 2,…,m; i = k1 × m1−1 + k2 × m2−1 +…+ kn × mn−1)
| (2) |
2.3 Estimation of mutual information
The entropy S of a torsion or multiple-torsion sets could be expressed with eqn (3), f(x) was the probability density function of a torsion or multiple-torsion sets.| |
 | (3) |
To calculate the entropy S, we first divided a torsion (n = 1) or multiple-torsion sets A into mn bins. The probability density within each bin was approximated as being uniform and could be calculated with eqn (4), f(Ai) was the probability density in the ith bin, p(Ai) was the probability that data points fell within the ith bin. w(Ai) is the width (for one torsion) or volume (for multiple-torsion sets) of a bin.
| | |
f(Ai) = p(Ai)/w(Ai) (i = 1, 2,…,mn)
| (4) |
The entropy of A can subsequently be estimated as below:
| |
 | (5) |
Similarly, the joint entropy of two torsions or two multiple-torsion sets A and B can be estimated as below:
| |
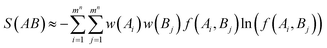 | (6) |
| | |
f(Ai, Bj) = p(Ai, Bj)/(w(Ai)w(Bj))
| (7) |
The mutual information between A and B was calculated as below:
| |
 | (8) |
nA and
nB were number of torsions in torsion set
A and
B.
Sp(
A) was the entropy calculated with bin joint distributions. In
eqn (8) wis were canceled, therefore mutual information (MI) between two torsion sets could be calculated with bin probability
p(
Ai)s (the probability that data points fell within the
ith bin) instead of bin probability density
f(
Ai) =
p(
Ai)/
w(
Ai). The bin widths could be chosen as we wished.
In numerical computations, probability densities had to be approximated with various forms of histograms. Strategies of binning (distribution of bin width and number of bins) apparently would impact the accuracy of concerned approximations. For any given distribution of bin width, increasing number of bins would result in better accuracy if sufficient statistics was available. However, for given number of bins, the effect of bin width distributions was more subtle. To choose for appropriate binning strategies, we tested two extreme bin width distributions, equal-width binning where all bins had the same width and equal-sample binning where all bins had approximately equal number of samples (number of samples might not necessary be even multiples of number of bins), for bin numbers m ranging from 3 to 36. We utilized calculation of backbone torsional pair mutual information for hen egg white lysozyme (HEWL) trajectory set to perform the tests. For each given value of m and bin width distribution we calculated mutual information of each adjacent backbone torsional pair (phi-psi or psi-phi) 20 times, each of which corresponded to a random start point of binning. As accuracy of mutual information calculation depended on number of bins, we calculated the mutual information for each adjacent backbone torsional pair with m = 180 to serve as the reference value (MIref). Upon completing the above mentioned calculations, we computed the coefficient of variation (Cv = σ/μ) for each torsional pair based upon 20 calculated values and subsequently we obtained the mean Cv of all HEWL backbone torsional pairs (see Fig. 1a). σ and μ were standard deviation and mean value of the 20 calculated mutual information for relevant torsional pair respectively. To evaluate the effect of bin numbers, we calculated average mutual information values MImean of all adjacent torsional pairs based on 20 calculations. Subsequently, the relative error were calculated with Re = |(MIref − MImean)/MIref| (see Fig. 1b). The correlation coefficient were calculated with ρMImean,MIref = cov(MImean, MIref)/σMImeanσMIref, where cov was covariance operation and σ was relevant standard deviations (see Fig. 1c). For small m value significantly less variation (Fig. 1a) and smaller bias (Fig. 1b) were observed for equal-sample binning. While for larger m values, the opposite was observed although the turning point of m value for variation and bias was different. More importantly, equal-sample binning consistently exhibited better correlation with the calculated reference mutual information. As expected, all calculated mutual information were smaller than the reference value due to the small bin number. In our (as well as other binning) calculation, the probability density inside each bin was considered to be a constant and the correlations exist within individual bins were missing. Apparently, the extent of missing correlations would be more severe for larger bins (smaller bin numbers).
 |
| | Fig. 1 Comparison of equal-width binning and equal-sample binning. We calculated mutual information of HEWL neighboring backbone torsions with different m value. (a) Coefficient of variation of MI that calculated with bins divided with randomly selected start point. (b) Relative error of estimated MI (calculated with m ranging from 3 to 36). The reference value MIref was calculated with m = 180. (c) Correlation coefficient of estimated MI and reference MIref. | |
To calculate mutual information between two torsion sets A and B, we utilized eqn (8) to estimate the full mutual information of two residues. The involved number of bins increase exponentially with number of torsions in participating residues as mnA+nB. While large bin numbers theoretically produce more accurate mutual informations, the memory and sampling burden would render calculation for large residues with 5 or more torsions extremely difficult. Therefore, based upon the above binning strategy comparison, we chose (m = 3) (starting from π) and the equal-sample binning in this study to characterize the significance of triple torsional correlations. In calculation of inter-residue mutual information, we estimated spurious correlations by random permutation. For Lys–Lys Lys–Arg Arg–Arg residue pairs, even with m = 3, spurious correlations were obtained with mutual information much larger than 0.01. So to residues with large side chains m = 3 was large enough to generate spurious correlations for our data sets. Therefore, we excluded Lys–Lys Lys–Arg and Arg–Arg residue pairs in our comparison and chose m = 3 so as not to be severely influenced by spurious correlations with larger m.
2.4 Inter-residue mutual information calculation
Both backbone (ϕ, ψ) and side chain torsions were included in the torsion set of each residue. Full mutual information between two residues A and B, with nA and nB torsions were calculated based on entropies of torsion sets A, B and AB = A∪B, which were derived from joint distributions of torsion sets in A, B and AB:| | |
MI ≈ Sp(A) + Sp(B) − Sp(AB)
| (9) |
| |
 | (10) |
| |
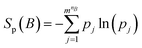 | (11) |
| |
 | (12) |
m is the number of partitions for each torsion, in this study m = 3.
Approximate second order mutual information MI2 between two residues A and B were calculated based on the second order expansion of entropies, which were calculated according to the following equations:
| | |
MI2 ≈ Sp2(A) + Sp2(B) − Sp2(AB)
| (13) |
| |
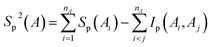 | (14) |
| | |
Ip(Ai, Aj) = Sp(Ai) + Sp(Aj) − Sp(Ai, Aj)
| (15) |
| |
 | (16) |
| |
 | (17) |
In eqn (16) p(Aik) represents probability of the torsion Ai fell in its kth partition. In eqn (17) p(AikAjl) represents the probability of the torsion Ai fell in its kth partition and the torsion Aj fell in its lth partition simultaneously. Sp2(B) and Sp2(AB) were calculated similarly as Sp2(A).
Approximate third order mutual information MI3 between two residues A and B were calculated based on the following third order expansions:
| | |
MI3 ≈ Sp3(A) + Sp3(B) − Sp3(AB)
| (18) |
| |
 | (19) |
| | |
Ip(Ai, Aj) = Sp(Ai) + Sp(Aj) − Sp(Ai, Aj)
| (20) |
| | |
Ip(Ai, Aj, Ak) = Sp(Ai) + Sp(Aj) + Sp(Ak) − Sp(Ai, Aj) − Sp(Ai, Ak) − Sp(Aj, Ak) + Sp(Ai, Aj, Ak)
| (21) |
| |
 | (22) |
In eqn (20) and (21), Sp(Ai) and Sp(Ai, Aj) were calculated as in eqn (16) and (17). p(AiuAjvAkw) in eqn (22) was the probability of the torsion Ai fell in its uth partition, the torsion Aj fell in its vth partition, and the torsion Ak fell in its wth partition simultaneously. Sp3(B) and Sp3(AB) were calculated similarly as Sp3(A).
2.5 Local joint distributions of consecutive backbone torsion segments
As far as a consecutive segment of n protein backbone torsions (ϕ and ψ) were concerned, we were ultimately interested in their joint distributions p(x), x = (x1, x2,…,xn) of the corresponding backbone torsion vector x. The extent of intra-secondary-structure (ISS) backbone torsional correlations in primary sequence might be effectively characterized by the quality of approximate joint distributions constructed from various orders of local conditional probabilities. The first p1(x), second p2(x), third p3(x) and fourth p4(x) ordered approximations were shown below:| |
 | (23) |
| |
 | (24) |
| |
 | (25) |
| |
 | (26) |
In these equations the joint distributions were represented by conditional probabilities. In eqn (24) only the correlations of immediate neighboring torsions were used, other correlations were considered to be transmitted (communicated) by these immediate neighboring correlations. In eqn (25) and (26) only the correlations of two and three immediate neighboring torsions were considered.
By chain rule of conditional probability, we have:
| | |
p(x1, x2) = p(x1)p(x2|x1)
| (27) |
| | |
p(x1, x2, x3) = p(x2, x1)p(x3|x2, x1)
| (28) |
| | |
p(x1, x2, x3, x4) = p(x3, x2, x1)p(x4|x3, x2, x1)
| (29) |
Therefore, eqn (24) (the second order approximation), (25) (the third order approximation) and (26) (the fourth order approximation) may be rewritten as:
| |
 | (30) |
| |
 | (31) |
| |
 | (32) |
and it was immediately seen from
eqn (30)–(32) that calculation of these approximate joint probabilities were only dependent on local joint probabilities of subsets of concerned variables. Building additional higher ordered approximations was straight forward, we limited our analysis to the fourth and lower ordered approximations due to limitation of available statistics.
To gauge the quality of various ordered local approximations, we calculated KL divergence between observed joint distributions of consecutive ISS backbone n torsion sets and corresponding approximations. We had to utilize small bin number due to limitation of available statistics. To reduce both the variation and the bias of small number of bins, we again utilized equal-sample binning with m = 3. As in calculation of entropy (see eqn (8)), integration based on probability density may be approximated by bin probabilities as shown below:
| |
 | (33) |
with
f(
x) and
fl(
x) being the joint probability density and its
lth ordered approximation,
pl being the
lth ordered approximation of joint distribution as calculated in discrete (histogram) forms of
eqn (23)–(26).
pl(
Ai) is the probability that sample fell in the
ith of the
mn bins in a
lth ordered approximate joint distribution
pl.
2.6 Spurious correlations, simulation convergence analysis and data selection in inter-residue mutual information calculation
2.6.1 Removal of spurious correlations by random permutation. In calculation of mutual information between two residues, torsional values of all concerned torsional DOFs for each data point were taken from the same MD snapshot. When DOFs of the two participating residues (in a residue pair) were given torsional values from two independently and randomly selected MD snapshots, then calculated correlation between the two residues should disappear when the number of data points was sufficiently large. Therefore, to remove potential spurious correlations due to limited number of snapshots, we first randomly permuted MD trajectory sets so that torsional values of a pair of residues were taken from two random snapshots. All residue pairs with mutual information larger than 0.01 (MISC > 0.01) in randomly permuted data sets were excluded from analysis.
2.6.2 Data exclusion based on convergence. A residue pair pass the random permutation tests was not necessarily converged in its torsional phase space. To remove residue pairs that contained insufficiently sampled torsions, we divided trajectory sets of each protein into three equally sized subsets, and compared the inter-residue mutual information calculated from the total data set (MItot) and three subsets (MIsubset1, MIsubset2, MIsubset3). If a large difference existed as judged by (MIdiff = (abs(MItot − MIsubset1) + abs(MItot − MIsubset2) + abs(MItot − MIsubset3))/(MItot × 3) > 0.5), we excluded the corresponding residue pair.For inter-residue correlation analysis, to test sampling convergence, we first selected significantly correlated residue pairs with mutual information greater than 0.05 from all possible residue pairs (npair) of each given protein; Secondly, we selected residue pairs with small spurious correlations (MISC < 0.01) from the remaining residue pairs; thirdly, we selected residue pairs that satisfy convergence criteria (MIdiff < 0.5). Number of selected residue pairs for seven trajectory sets were listed in Table 1.
Table 1 Number of residue pairs selected for the seven trajectory sets
| Protein |
npair |
MI > 0.05 |
MISC < 0.01 |
MIdiff < 0.5 |
| 1bta |
3916 |
161 |
120 |
67 |
| 1rgh |
4560 |
328 |
292 |
116 |
| 2bnh |
103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
5449 |
1120 |
563 |
| 5pti |
1653 |
205 |
93 |
44 |
| 7rsa |
7626 |
1610 |
1140 |
465 |
| cdk2 |
44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 253 253 |
6040 |
1636 |
928 |
| HEWL |
8256 |
971 |
830 |
464 |
For joint distribution approximation analysis of consecutive backbone torsional segments, to test sampling convergence, we divided trajectory sets into three equally sized subsets, and calculated the KL divergences of each pair. We obtained three KL values for a backbone torsion and choose the largest value KLsubset as the final result. We removed backbone torsions with KLsubset over 0.2 in joint distribution approximations. For calculating KLsubset we divided backbone torsions into 60 equal width bins.
3 Results
3.1 Inter-residue torsional mutual information in proteins
Inter-residue mutual information (MI) was calculated14 and found to be useful in predicting relevant residues involved in protein allostery. However, the extent of biases (approximations) of the second order mutual information expansion (MIE) was not analyzed. As in that work, the DOFs we chose were backbone and side chain torsions. We analyzed MD trajectory sets of 7 proteins in this part of study. For each residue A, we divided each comprising torsion into three approximately equal-sample partitions and calculated their joint distributions. For a residue pair (A and B), the full mutual information MI between the two residues were calculated according to eqn (9)–(12). We only selected significantly correlated residue pairs (MI > 0.05) and excluded residue pairs with spurious correlations and insufficient sampling (see Spurious correlations in the Methods section).
After obtaining the full mutual information of residue pairs as the reference, we calculated approximate mutual information of the same set of residue pairs using MIE with cutoffs at the second (MI2, eqn (13)–(17)) and the third order (MI3) respectively (eqn (18)–(22)). Details of these calculations were explained in the Methods section.
We plotted distributions of MI2 − MI and MI3 − MI for four representative proteins in Fig. 2. It was evident that distributions of MI3 − MI exhibit much sharper and narrower peak than that of MI2 − MI for the four proteins shown, and similar results were observed for other proteins we analyzed but not shown. Therefore, we concluded that at least for the utilized force fields, triple torsional correlations contributed significantly to inter-residue mutual information. To illustrate relative values for MI, MI2 and MI3, we choose ten residue pairs with the largest absolute value of MI2 − MI and plotted corresponding MI, MI2 and MI3 in Fig. 3. As expected, MI3 were better approximations than MI2 in all cases. Although values of MI, MI2 and MI3 were not unanimously ordered, MI was bounded by MI2 and MI3 for majority cases and this property was potentially useful (see section below) in predicting MI with MI2 and MI3 when calculation of MI is much more difficult than calculation of MI2 and MI3. As demonstrated by Table 1, convergence of full mutual information is rather difficult for significant number of residue pairs, which were excluded from comparison in this study. Due to the exponential increase in need for sampling with increasing higher orders, generating trajectories for the third order expansion calculation would likely to be easier by orders of magnitude.
 |
| | Fig. 2 Distributions of MI2 − MI and MI3 − MI, MI2 is the inter-residue mutual information estimated using the second-order MIE. MI3 is the inter-residue mutual information estimated using the third-order MIE and MI is the full inter-residue mutual information calculated directly from the joint distributions. Residue pairs with MI < 0.05 are excluded in constructing these plots. | |
 |
| | Fig. 3 Mutual information values of the selected ten residue–residue pairs for four different trajectory sets. Ten residue pairs with the largest absolute values of MI2 − MI are selected for each protein. | |
3.2 Linear combinations of the second and the third order approximations of inter-residue mutual information
As shown above, the third order approximations (MI3) were consistently better than the second order approximations (MI2). We expected to obtain better approximations as higher ordered approximations were utilized. However, exponentially increasing needs for both analysis computational power and raw data preventing us from brute force utilization of higher ordered approximations. In a theoretically rigorous expansion, coefficients for each order was given. However, if we somehow represented the fourth and all higher ordered terms with the second and the third order terms, and if such representation could better approximating higher ordered terms than simply ignoring them, optimizing coefficients for the second and the third order terms might be useful. We therefore carried out a linear regression analysis to solve parameters (a1, a2 and b) in the following equation:| | |
MILR = a1 × MI2 + a2 × MI3 + b
| (34) |
and to predict an optimal approximate mutual information (MILR) based on linear combinations of the second and the third order approximations. We performed five fold cross validation with the results shown in Tables 2–4. From Table 2, it was apparent that for all five validation sets (Vset), MSELR was significantly and consistently smaller than MSE3, which was significantly and consistently smaller than MSE2 as expected. Parameters from five training sets were quite consistent (3). As one would intuitively expect, a2 took larger value than a1 since MI3 were better approximations than MI2. It was noted that the computational cost for linear regression analysis was trivial when compared to calculations of joint probabilities and entropies. Therefore, this strategy might be potentially quite effective in improving accuracy of inter-residue torsional correlations. It was important to note that these coefficients were obtained for equal-sample binning strategy with m = 3, caution should be applied in direct utilization of these numbers for analysis with other binning strategy.
Table 2 Mean squared error (when compared with the full mutual information) of the second order approximations (MSE2), the third order approximations (MSE3) and that of their optimized linear combinations (MSELR). Data for all 5 validation sets (Vset) were listed
| Vset |
MSE2 |
MSE3 |
MSELR |
| 1 |
0.00517 |
0.00196 |
0.00019 |
| 2 |
0.00837 |
0.00225 |
0.00024 |
| 3 |
0.00911 |
0.00285 |
0.00021 |
| 4 |
0.01575 |
0.00601 |
0.00031 |
| 5 |
0.00533 |
0.00318 |
0.00023 |
Table 3 Parameters a1, a2 and b from the five training sets
| Train sets |
a1 |
a2 |
b |
| 1 |
0.36391182 |
0.53388144 |
0.010004 |
| 2 |
0.37253283 |
0.52327209 |
0.010256 |
| 3 |
0.36793552 |
0.53070647 |
0.010176 |
| 4 |
0.35997187 |
0.54698256 |
0.009906 |
| 5 |
0.35433510 |
0.53695367 |
0.011474 |
Table 4 Average values of the full mutual information (MI), of the second order approximation (MI2), of the third order approximation (MI3) and that of the their linear combinations (MSELR). Data for all 5 validation sets (Vset) were listed
| Vset |
MI |
MI2 |
MI3 |
MILR |
| 1 |
0.119272 |
0.125381 |
0.115698 |
0.117400 |
| 2 |
0.130858 |
0.154655 |
0.120024 |
0.130675 |
| 3 |
0.118299 |
0.147873 |
0.101547 |
0.118476 |
| 4 |
0.143535 |
0.198191 |
0.117558 |
0.145551 |
| 5 |
0.102747 |
0.106783 |
0.099821 |
0.102911 |
3.3 Various ordered approximations for joint distributions of consecutive ISS backbone torsion segments for different secondary structures
Here we investigated non-overlapping segments of 8 consecutive ISS backbone torsions (n = 8). For each selected segment, we calculated its joint distribution p(x) and its first, second, third and fourth ordered approximations p1(x), p2(x), p3(x) and p4(x) according to eqn (23), (30)–(32). KL divergences (KLj between p(x) and pj(x), j = 1, 2, 3,4) were calculated subsequently according to eqn (33) and their distributions were shown in Fig. 4. One immediately saw that KL1 was consistently large for all secondary structure segments investigated, regardless of their specific types (α helix, β strand or loop), indicating that the first order approximation was not a good option to substitute for the joint probability distribution in all cases. As one would intuitively expect, higher ordered approximations were better than lower ordered approximations for all three types of secondary structure segments investigated, as indicated by significantly smaller KL divergences for higher orders of approximations. Additionally, KL divergences between the full joint distributions and their second, third and fourth ordered approximations (KLi(α) ≈ KLi(β) < KLi(L) (i = 2, 3, 4)) were similar for α helices and β strands, while that of loops are considerably larger. These observations suggest that observed torsional correlations in loops were significantly more long-ranged than that in α helices and β strands. Our selection of fragment length n = 8 was limited by statistics as the available number of fragments with more than 8 consecutive torsions are quite small after some backbone torsions were excluded due to unsatisfactory convergence and sampling (see Methods).
 |
| | Fig. 4 Probability distributions of KL divergence between observed joint distributions and their various ordered approximations (see eqn (1), (8)–(10)) of 8-torsion segments for α helices, β strands and loops (indicated in parenthesis as α, β and L). The number in the second parenthesis is the average KL divergence calculated from the corresponding distribution. This figure is based on analysis of trajectory sets based on CHARMM force-fields as not sufficiently good statistics are available for trajectories generated by AMBER force-fields. | |
4 Discussion
Entropy of a system could be expanded as a series of increasingly higher-ordered information terms:34| |
 | (35) |
with nA being the number of DOFs in a molecular system A. Unfortunately, this equation was not practically useful when calculating the conformational entropy of proteins because the requirement for sampling rapidly became intractable. We utilized the second- and third-order correlation terms to estimate residue entropies in proteins and calculated correlations between residues. While as expected, third order approximations exhibited smaller error than the second order approximations, we found that reorganization of the exact same information (linear combinations of the second and the third order results) significantly improved over the third order approximations with trivial additional computational costs, this idea might be useful for other complex molecular systems as well.
We analyzed trajectory sets generated with two different force fields (CHARMM and AMBER) for a wide variety of protein folds. When the influence of triple correlations is concerned, similar and consistent observed significance suggest their potentially general importance for proteins. It was important to note that significant inter-residue torsional correlations were rare as demonstrated by Table 1. All our inter-residue correlation analysis were targeted to these small subsets of residue pairs. Our speculation that triple torsional correlations were of general importance for inter-residue correlations were only meant for these significantly correlated residue pairs, and such importance was essentially independent of identity of protein molecules, as least in our limited but diversified observations. It was evident that for any pair of residues with negligible correlations, discussion of triple correlations was meaningless. However, for local backbone segment correlation analysis based on joint distribution calculations, all non-overlapping and consecutive local segments with the same secondary structure assignment were included. Therefore, the observed importance of the third and higher ordered local correlations were essentially over the whole primary sequence for all analyzed proteins.
Here in order to calculate joint distributions for multiple torsion sets, we divided each torsion into 3 bins. This would result in underestimation of mutual information for all residue pairs as demonstrated by Fig. 1. However, the requirement for sampling rapidly became intractable for larger bin numbers and most residues would be excluded from such analysis as no full joint distribution could be obtained reliably. Nevertheless, relative importance of the second order and third order contributions were estimated with consistent binning and the results should be qualitatively meaningful. The impact of binning strategy (bin width distribution and bin number selection) was universal for all numerical analysis of correlations. Usually, calculation within each individual investigation was consistent. However, in different studies, binning strategies could be wildly different. We therefore strongly urge readers to be cautious especially when quantitative comparison was intended between/among different computation investigations with different binning strategies.
It was also important to note that inter-residue correlations we calculated were correlations of internal motions between residues. The overall translation and rotation of residues were not accounted for in such calculations. It was undoubtable that there were various extent of correlations for overall translation and rotation of residues, and for clusters of them as well. How internal motions of residues (or clusters of which) collaborated with their overall translation/rotation to accomplish biological functions were yet to be understood. Complex quantities proposed recently such as (Dis)similarity index,25 energy network analysis26 and pKa variation27 effectively provided consideration of both coupling of internal motions and overall translational and rotational motion between various parts of proteins. Nonetheless, mechanistic analysis and understanding remain to be tackled. We had plan to investigate this issue in our future work.
One well accepted approximate expression for the joint probability of a molecular system with multiple DOFs is the Kirkwood superposition35 as shown below:
| |
 | (36) |
with

being the product of probabilities over all subsets of variables of size
i in the variable set
ν. This superposition was expressed as lower order joint distributions for all possible combinations of DOFs in contrast to
eqn (23),
(30)–(32), where only local joint probabilities of neighboring DOFs up to certain order were utilized. In analysis of local backbone segments, our utilization of chain rule of conditional probability assumed that all influence from other molecular DOFs to a given DOF is communicated through its neighboring DOFs. Of course, this is not exactly true as long-range interactions (
e.g. electrostatic interactions) could not be fully accounted for by such treatment. Our approximations showed that with the second-order neighboring correlations, the protein backbone local torsional joint density can be described reasonably well in stable secondary structures (helices and strands). Long range correlations were relatively rare in these structures. These observations suggested that when we study the structure or movement of stable segments (helices and strands) in proteins, it may be an efficient way with acceptable accuracy to consider up to the second-order correlations of neighboring DOFs. This idea might be useful in structural refinement for both protein design and structure prediction. However, when loop structures were concerned, consideration of higher (third and fourth) ordered correlations becomes more important.
5 Conclusions
Binning strategies were of great importance in numerical analysis of correlations. We first provided a detailed comparison of equal-width binning and equal-sample binning for various bin numbers in calculation of torsional mutual information. It was important to note that quantitative comparison of correlation calculations between different studies should be highly cautious when different binning strategies were utilized. Based on such comparison and sampling limitation, we chose equal-sample binning with 3 partitions for each torsion to perform calculations of residue pair mutual information and local joint probabilities of consecutive ISS backbone torsional segments. Based on analysis of extensive MD trajectories for many globular and membrane proteins, we gauged errors of the second- and third-order approximations of inter-residue torsional mutual information. We found as expected that third-order approximations were better than the second-order approximations. Additionally, linear combinations of the second- and third-order approximations significantly improved over third-order approximations with trivial additional computational cost. It was found that third-order torsional correlations were important in proteins for both inter-residue torsional mutual information and local torsional joint distributions of consecutive backbone segments. Through construction of consecutive backbone torsional joint distributions from lower ordered expansions, we found that ISS backbone torsional correlations for loops were significantly more sequentially long-ranged than those of α helices and β strands.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work has been supported by the National Key Research and Development Program of China (2017YFB0702500), by the postdoctoral start up fund from Jilin University (801171020439), by National Natural Science Foundation of China (31270758), and by the Fundamental Research Funds for the Central Universities (451170301615).
Notes and references
- R. Baron, P. H. Hünenberger and J. A. McCammon, J. Chem. Theory Comput., 2009, 5, 3150–3160 CrossRef CAS PubMed.
- A. a. Polyansky, A. Kuzmanic, M. Hlevnjak and B. Zagrovic, J. Chem. Theory Comput., 2012, 8, 3820–3829 CrossRef CAS PubMed.
- B. J. Killian, K. J. Yundenfreund and M. K. Gilson, J. Chem. Phys., 2007, 127, 1534 Search PubMed.
- B. M. King, N. W. Silver and B. Tidor, J. Phys. Chem. B, 2012, 116, 2891–2904 CrossRef CAS PubMed.
- A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601 CrossRef.
- F. a. Escobedo, E. E. Borrero and J. C. Araque, J. Phys.: Condens. Matter, 2009, 21, 333101 CrossRef PubMed.
- L. Maragliano, A. Fischer, E. Vanden-Eijnden and G. Ciccotti, J. Chem. Phys., 2006, 125, 24106 CrossRef PubMed.
- T. Ichiye and M. Karplus, Proteins: Struct., Funct., Bioinf., 1991, 11, 205217 CrossRef PubMed.
- P. H. Hünenberger, A. Mark and W. van Gunsteren, J. Mol. Biol., 1995, 252, 492–503 CrossRef PubMed.
- N. Garnier, D. Genest and M. Genest, Biophys. Chem., 1996, 58, 225–237 CrossRef CAS.
- L. Meinhold and J. C. Smith, Biophys. J., 2005, 88, 2554–2563 CrossRef CAS PubMed.
- O. F. Lange and H. Grubmüller, Proteins: Struct., Funct., Bioinf., 2006, 62, 1053–1061 CrossRef CAS PubMed.
- D. W. Li, D. Meng and R. Brüschweiler, J. Am. Chem. Soc., 2009, 131, 14610–14611 CrossRef CAS PubMed.
- C. L. Mcclendon, G. Friedland, D. L. Mobley, H. Amirkhani and M. P. Jacobson, J. Chem. Theory Comput., 2009, 5, 2486 CrossRef CAS PubMed.
- D. W. Li, S. A. Showalter and R. Brüschweiler, J. Phys. Chem. B, 2010, 114, 16036 CrossRef CAS PubMed.
- R. Brüschweiler, Nat. Chem., 2011, 3, 665 CrossRef PubMed.
- K. H. Dubay, J. P. Bothma and P. L. Geissler, PLoS Computational Biology, 2011, 7, e1002168 CrossRef CAS PubMed.
- R. B. Fenwick, S. Esteban-Martín, B. Richter, D. Lee, K. F. Walter, D. Milovanovic, S. Becker, N. A. Lakomek, C. Griesinger and X. Salvatella, J. Am. Chem. Soc., 2011, 133, 10336–10339 CrossRef CAS PubMed.
- L. Dong and R. Brüschweiler, J. Phys. Chem. Lett., 2012, 3, 1722 CrossRef PubMed.
- A. Pandini, A. Fornili, F. Fraternali and J. Kleinjung, FASEB J., 2012, 102, 225a Search PubMed.
- E. Papaleo, K. Lindorff-Larsen and G. L. De, Phys. Chem. Chem. Phys., 2012, 14, 12515–12525 RSC.
- R. B. Fenwick, L. Orellana, S. Estebanmartín, M. Orozco and X. Salvatella, Nat. Commun., 2014, 5, 4070 CrossRef CAS PubMed.
- A. Fenley, B. J. Killian, V. Hnizdo, A. Fedorowicz, S. S. Dan and M. K. Gilson, J. Phys. Chem. B, 2014, 118, 6447 CrossRef CAS PubMed.
- P. Sfriso, A. Emperador, L. Orellana, A. Hospital, J. L. Gelpí and M. Orozco, J. Chem. Theory Comput., 2012, 8, 4707 CrossRef CAS PubMed.
- M. Tiberti, G. Invernizzi and E. Papaleo, J. Chem. Theory Comput., 2015, 11, 4404 CrossRef CAS PubMed.
- A. A. Ribeiro and V. Ortiz, J. Phys. Chem. B, 2015, 119, 1835–1846 CrossRef CAS PubMed.
- E. J. M. Lang, L. C. Heyes, G. B. Jameson and E. J. Parker, J. Am. Chem. Soc., 2016, 138, 2036–2045 CrossRef CAS PubMed.
- S. Long and P. Tian, Sci. Rep., 2016, 6, 34481 CrossRef CAS PubMed.
- W. Li, W. Meng and P. Tian, Chem. Res. Chin. Univ., 2015, 31, 149–155 CrossRef CAS.
- L. Zhao, W. Li and P. Tian, PLoS One, 2013, 8, e60553 CrossRef CAS PubMed.
- K. Wang, S. Long and P. Tian, PLoS One, 2015, 10, e0129846 CrossRef PubMed.
- L. Zhao, P. Zhang, S. Long, L. Wang and P. Tian, J. Mol. Model., 2015, 21, 190 CrossRef PubMed.
- D. E. Shaw, P. Maragakis, K. Lindorff-Larsen, S. Piana, R. O. Dror, M. P. Eastwood, J. a. Bank, J. M. Jumper, J. K. Salmon, Y. Shan and W. Wriggers, Science, 2010, 330, 341–346 CrossRef CAS PubMed.
- H. Matsuda, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 3096–3102 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02191d |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *c
*c


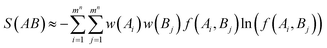


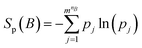

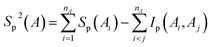












![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740
740![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 253
253


 being the product of probabilities over all subsets of variables of size i in the variable set ν. This superposition was expressed as lower order joint distributions for all possible combinations of DOFs in contrast to eqn (23), (30)–(32), where only local joint probabilities of neighboring DOFs up to certain order were utilized. In analysis of local backbone segments, our utilization of chain rule of conditional probability assumed that all influence from other molecular DOFs to a given DOF is communicated through its neighboring DOFs. Of course, this is not exactly true as long-range interactions (e.g. electrostatic interactions) could not be fully accounted for by such treatment. Our approximations showed that with the second-order neighboring correlations, the protein backbone local torsional joint density can be described reasonably well in stable secondary structures (helices and strands). Long range correlations were relatively rare in these structures. These observations suggested that when we study the structure or movement of stable segments (helices and strands) in proteins, it may be an efficient way with acceptable accuracy to consider up to the second-order correlations of neighboring DOFs. This idea might be useful in structural refinement for both protein design and structure prediction. However, when loop structures were concerned, consideration of higher (third and fourth) ordered correlations becomes more important.
being the product of probabilities over all subsets of variables of size i in the variable set ν. This superposition was expressed as lower order joint distributions for all possible combinations of DOFs in contrast to eqn (23), (30)–(32), where only local joint probabilities of neighboring DOFs up to certain order were utilized. In analysis of local backbone segments, our utilization of chain rule of conditional probability assumed that all influence from other molecular DOFs to a given DOF is communicated through its neighboring DOFs. Of course, this is not exactly true as long-range interactions (e.g. electrostatic interactions) could not be fully accounted for by such treatment. Our approximations showed that with the second-order neighboring correlations, the protein backbone local torsional joint density can be described reasonably well in stable secondary structures (helices and strands). Long range correlations were relatively rare in these structures. These observations suggested that when we study the structure or movement of stable segments (helices and strands) in proteins, it may be an efficient way with acceptable accuracy to consider up to the second-order correlations of neighboring DOFs. This idea might be useful in structural refinement for both protein design and structure prediction. However, when loop structures were concerned, consideration of higher (third and fourth) ordered correlations becomes more important.



