Open Access Article
Open Access ArticleThermodynamic, structural and dynamic properties of ionic liquids [C4mim][CF3COO], [C4mim][Br] in the condensed phase, using molecular simulations†
Joel Sánchez-Badilloa,
Marco Gallo *b,
Ricardo A. Guirado-López
*b,
Ricardo A. Guirado-López c and
Jorge López-Lemusd
c and
Jorge López-Lemusd
aFacultad de Ciencias Químicas, Universidad Autónoma de San Luis Potosí, Zona Universitaria, Av. Manuel Nava No. 6, San Luis Potosí, C.P. 78210, Mexico
bTecnológico Nacional de México/ITCJ, Av. Tecnológico No. 1340, Cd. Juárez, Chihuahua, C.P. 32500, Mexico. E-mail: mgallo@itcj.edu.mx
cInstituto de Física “Manuel Sandoval Vallarta”, Universidad Autónoma de San Luis Potosí, Álvaro Obregón No. 64, San Luis Potosí, C.P. 78000, Mexico
dFacultad de Ciencias, Universidad Autónoma del Estado de México, Toluca, Estado de México C.P. 50000, Mexico
First published on 3rd May 2019
Abstract
In this work a series of thermodynamic, structural, and dynamical properties for the 1-butyl-3-methylimidazolium trifluoroacetate ([C4mim][CF3COO]) and 1-butyl-3-methylimidazolium bromide, ([C4mim][Br]) ionic liquids (ILs) were calculated using Non-polarizable Force Fields (FF), parameterized using a methodology developed previously within the research group, for condensed phase applications. Properties such as the Vapor-Liquid Equilibrium (VLE) curve, critical points (ρc, Tc), Radial, Spatial and Combined Distribution Functions and self-diffusion coefficients were calculated using Equilibrium Molecular Dynamics simulations (EMD); other properties such as shear viscosities and thermal conductivities were calculated using Non-Equilibrium Molecular Dynamics simulations (NEMD). The results obtained in this work indicated that the calculated critical points are comparable with those available in the literature. The calculated structural information for these two ILs indicated that the anions interact mainly with hydrogen atoms from both the imidazolium ring and the methyl chain; the bromide anion displays twice the hydrogen coordination number than the oxygen atoms from the trifluoroacetate anion. Furthermore, Non-Covalent interactions (NCI index), determined by DFT calculations, revealed that some hydrogen bonds in the [C4mim][Br] IL displayed similar strength to those in the [C4mim][CF3COO] IL, in spite of the shorter O−–H distances found in the latter IL. The majority of the calculated transport properties presented reasonable agreement with the experimental available data. Nonetheless, the self-diffusion coefficients determined in this work are under-estimated with respect to experimental values; however, by escalating the electrostatic atomic charges for the anion and cation to ±0.8e, only for this property, a remarkable improvement was obtained. Experimental evidence was recovered for most of the calculated properties and to the best of our knowledge, some new predictions were done mainly in thermodynamic states where data are not available. To validate the FF, developed previously within the research group, dynamic properties were also evaluated for a series of ILs such as [C4mim][PF6], [C4mim][BF4], [C4mim][OMs], and [C4mim][NTf2] ILs.
Introduction
Ionic liquids (ILs) are molten salts composed of only cations and anions in a liquid state at temperatures below 100 °C.1 In the last two decades these substances have attracted great interest because of their physicochemical properties such as low vapor pressure, thermal stability, decomposition at high temperatures, isothermal compressibilities similar to water, large electrochemical windows, wide range of shear viscosities, and suitability for applications as extracting agents, heat transfer fluids, electrolytes for batteries, lubricants, and catalysts.2–6 ILs are considered as a green alternative for the replacement of Volatile Organic Compounds (VOCs) in many industrial processes without the necessity of major changes in the main flow sheet and equipment.7It is known that by combining different cations and anions, it is possible to design ILs with specific properties for well-defined applications.8 Nevertheless, the experimental search for specific ILs can be an expensive and a time consuming task, therefore different economical alternatives need to be employed such as computer simulations. Molecular Dynamics simulations can describe molecular and atomic interactions to predict and evaluate a wide range of physicochemical properties of ILs. This allows the design of new solvents with unique physicochemical properties, and also the possibility of evaluating different properties at extreme conditions of pressure and temperature, conditions difficult to achieve experimentally.9 These simulations will approximate the experimental values of thermodynamic and transport properties only if the used Force Field (FF) describes accurately the energetic interactions between atoms and molecules.10,11 Recent publications have stressed the existence of multiple shortcomings in some of the available classical FF, including inadequate solvent dynamics, errors in the prediction of hydrogen-bonding strength, inadequate mixture phase behavior, and errors in solvent structure and interactions.12–15 Recent contributions have modified the atomic partial charges and Lennard-Jones parameters, in computer simulations by considering the dielectric constant as a target property in order to mimic the miscibility observed experimentally between two different liquids.16,17
In the literature, there is a constant need for reliable and accurate IL FF14,18,19 able to capture, among others, the local electrostatic properties,20 microscopic dynamics,21 and vibrational spectra;22 as indicated by Maginn,18 many FFs already published have not been validated yet against reliable and sensitive properties such as enthalpy of vaporization, and dynamic properties. The lack of an accurate classical FF for predicting thermodynamic, structural, and transport properties for specific substances hinders the design of new ILs solvents for condensed applications. Different research groups13,23–31 have developed classical FFs for different ILs and evaluated their capabilities to predict different properties such as: density, enthalpy of vaporization, surface tension, heat capacity at constant pressure, cohesive energy, structural properties, and in a reduced extent, properties such as: VLE curves, self-diffusion coefficients, dielectric constants, thermal conductivities, viscosities, etc. A comprehensive review regarding the prediction of thermodynamic, structural, and dynamic properties of ILs, using Molecular Dynamics simulations can be found in Batista et al.6 and references therein.
It is also known that ILs decomposed far below their critical temperature,32 nevertheless these hypothetical critical points are important for the development of thermodynamic equations-of-state and for elucidating their thermodynamic behavior.32,33 Critical thermodynamic properties for ILs have been calculated by using both molecular simulations32–34 and theoretical methods.35–37 Experimental, theoretical, and simulated values for both thermodynamic and transport properties for the ILs studied in this work are presented in Tables 1 and 2. Also, in this work, dynamic properties for the [C4mim][PF6], [C4mim][BF4], [C4mim][OMs] and [C4mim][NTf2] ILs were calculated, since these ILs have been studied extensively, particularly, these ILs have been tested as reaction media in condensed phase.28,38–40 The developed FF for these ILs has been published in previous works.24,41
| IL | Critical temperature, Tc [K] | Critical density, ρc [g cm−3] | ||
|---|---|---|---|---|
| sim | es | sim | es | |
| a For the [C4mim][PF6], [C4mim][BF4], and [C4mim][OMs] ILs, the critical properties were calculated in our previous work.24 | ||||
| [C4mim][PF6] | 1228.3 (ref. 24) | 1187 (ref. 43) | 0.268 (ref. 24) | 0.373 (ref. 36) |
| 1105 ± 25 (ref. 42) | 1102 (ref. 43) | 0.227 ± 0.019 (ref. 42) | ||
| 719.4 (ref. 36) | ||||
| [C4mim][BF4] | 1267.7 (ref. 24) | 1240 (ref. 43) | 0.210 (ref. 24) | 0.345 (ref. 36) |
| 1252 ± 4 (ref. 32) | 1158 (ref. 43) | 0.181 ± 0.002 (ref. 32) | ||
| 643.2 (ref. 36) | ||||
| [C4mim][OMs] | 1277.4 (ref. 24) | 1054.8 (ref. 36) | 0.228 (ref. 24) | 0.334 (ref. 36) |
| [C4mim][NTf2] | 1203 ± 4 (ref. 34) | 1077 (ref. 43) | 0.265 ± 0.006 (ref. 34) | 0.424 (ref. 36) |
| 1216 ± 14 (ref. 33) | 1012 (ref. 43) | 0.250 ± 0.003 (ref. 33) | ||
| 1269.9 (ref. 36) | ||||
| [C4mim][CF3COO] | N/A | 1271 (ref. 37) | N/A | 0.356 (ref. 36) |
| 826.8 (ref. 36) | ||||
| [C4mim][Br] | N/A | 834.9 (ref. 36) | N/A | 0.376 (ref. 36) |
| IL | Shear viscosity, η [cP] | Self-diffusion coefficient, Dib [10−7 cm2 s−1] | Thermal conductivity, λ [W m−1 K−1] | ||||
|---|---|---|---|---|---|---|---|
| exp | sim | exp | sim | exp | sim | es | |
| a Cation/anion.b At 298 K.c At 350 K.d At 353 K.e At 360 K.f At 298.15 K.g At 358.15 K.h At 5.74 mol L−1 IL concentration in aqueous solution.i At 358 K. | |||||||
| [C4mim][PF6] | 224.74 (ref. 44) | 264.4 (ref. 13)b | 6.17/5.26 (ref. 44)c | 4.7/3.2 (ref. 29)d | 0.145 (ref. 50) | N/A | 0.147 (ref. 53) |
| 228.81 (ref. 46) | 39 (ref. 29)d | 6.43/5.14 (ref. 45)c | 0.145 (ref. 51) | ||||
| 257.36 (ref. 46) | 31.3 (ref. 49)e | 0.173 (ref. 52) | |||||
| 450 (ref. 47) | 231.3 (ref. 49)e | ||||||
| 25.51 (ref. 44)c | |||||||
| 27.08 (ref. 48)c | |||||||
| 32.33 (ref. 46)c | |||||||
| [C4mim][BF4] | 90.61 (ref. 44) | 97.8 (ref. 13)b | 10.21/10.2 (ref. 44)c | 9.7/8.2 (ref. 29)d | 0.169 (ref. 54) | N/A | 0.167 (ref. 53) |
| 86.8 (ref. 46) | 111.2 (ref. 31)b | 9.69/10.1 (ref. 45)c | 0.186 (ref. 55) | ||||
| 107.32 (ref. 48) | 0.190 (ref. 52) | ||||||
| 219 (ref. 47)f | |||||||
| [C4mim][OMs] | 31.25 (ref. 56)g | N/A | 5.48/4.89 (ref. 56)g | N/A | N/A | N/A | 0.171 (ref. 53) |
| [C4mim][NTf2] | 46.24 (ref. 44) | 537.8 (ref. 59) | 14.06/11.23 (ref. 44)c | 4.91/3.35 (ref. 59)c | 0.126 (ref. 59)f | 0.107 (ref. 59) | 0.123 (ref. 53) |
| 46.5 (ref. 46) | 45 (ref. 11)f | 13.80/11.68 (ref. 45)c | 10.9/7.8 (ref. 29)d | 0.127 (ref. 61) | |||
| 46.44 (ref. 57) | 72.09 (ref. 60)f | ||||||
| 46.79 (ref. 58) | 49.9 (ref. 13)b | ||||||
| 69 (ref. 47)f | |||||||
| [C4mim][CF3COO] | 63.2 (ref. 62) | N/A | 11.18/10.23 (ref. 44)c | 19.8/17.2 (ref. 29)d | N/A | N/A | 0.166 (ref. 53) |
| 70.02 (ref. 44) | 11.1/9.76 (ref. 45)c | ||||||
| [C4mim][Br] | 200 (ref. 63) | 231.1 (ref. 13)b | 2./N/A (ref. 66)c | 22/21.08 (ref. 68)e | N/A | N/A | 0.159 (ref. 53) |
| 230 (ref. 63)b | 19.8/N/A (ref. 67)d | ||||||
| 161.05 (ref. 64)b,h | 9.1/N/A (ref. 68)i | ||||||
| 1486.49 (ref. 65)b | |||||||
Tables 1 and 2 present both the experimental and simulated physicochemical properties available in the literature for the six ILs studied; and to the best of our knowledge, there is scarce reported data for the [C4mim][OMs], [C4mim][CF3COO], and [C4mim][Br] ILs.
The shear viscosity (η) the self-diffusion coefficient (Di) and the thermal conductivity (λ) are called transport properties, and various Molecular Dynamics simulations reported in the literature tend either to underestimate or overestimate the experimental data.6,59 Different types of developed FF in the literature such as all-atom AA, and united-atom UA, for the same IL, provide dissimilar results in the estimation of transports properties, as can be seen in Table 2. Transport properties of some ILs have been calculated by using the Green–Kubo formalism (based on Equilibrium Molecular Dynamics (EMD)), and Non-Equilibrium Molecular Dynamics (NEMD) simulations through both the SLLOD methodology and the Periodic Perturbation method (PPM).6,18,59 Hess69 published an article evaluating different methodologies including Green–Kubo, SLLOD, and the PPM for the calculation of the shear viscosity for water and a Lennard-Jones fluid. In their conclusions, Hess indicated that the PPM is the method of choice, because of its indifference with respect to the electrostatic treatment, and its efficiency compared with equilibrium methods. Several authors69,70 in the literature have indicated that the Green–Kubo formalism requires the pressure tensor, presenting large fluctuations along the simulations, resulting in slow convergence for high viscosity systems such as IL,71 and displaying high statistical uncertainties due to the large simulation times needed to equilibrate the system.72
An alternative technique to compute the shear viscosity is the non-equilibrium Periodic Perturbation Method (PPM). The PPM is a technique that introduces an external force by means of applying an acceleration to the system, producing a periodic velocity profile that is subsequently adjusted with a cosinoidal equation to obtain the shear viscosity.69 By employing this methodology, Sprenger et al.11 calculated the shear viscosity of several ILs using the General AMBER Force Field GAFF.73 These same authors reported a shear viscosity value of 45 cP for the [C4mim][NTf2] IL at 298.15 K, in excellent agreement with experimental results. A specified value of 0.03 nm ps−2 was chosen for the acceleration amplitude in their viscosity calculations, resulting in more accurate values in agreement with experimental data.
Liu et al.59 developed an AA FF using GAFF parameters73 and calculated the shear viscosity for the [C4mim][NTf2] IL by using the Green–Kubo formalism. They obtained a value of 537.80 cP at 300 K, which is an order of magnitude higher than the experimental value. Picálek and Kolafa49 evaluated the capability of both UA FF30 and AA FF26 in determining the shear viscosity for the [C4mim][PF6] IL by using NEMD techniques. They found that the AA FF overestimated from 4–8 times the shear viscosity in comparison with the UA FF for a wide range of temperatures; the UA FF presented good agreement against experimental values. Indeed, several research groups in the literature stressed that both the FF quality and the methodology used to obtain the shear viscosity, play a significant role in the determination of accurate values for this property.11,13,49,59
The self-diffusion coefficients for ILs can be calculated through EMD simulations by using the Velocity Auto Correlation Functions VACF, based on the Green–Kubo formalism, or by using the Mean Square Displacement MSD, along with the Einstein equation.29,59 Ramya et al.74 evaluated the effect of anion size in the structure and dynamics of a series of [C6mim][X] IL (with X equals to Cl, Br, BF4, PF6, OTf, and NTf2) by using molecular simulations. They found that IL containing smaller anions such as [Cl]− and [Br]− presented smaller diffusion coefficients compared to IL with larger anions such as [BF4]− and [NTf2]−, as shown in Table 2. This behavior was explained by Fumino et al.75 noticing that strong and directional hydrogen bonds introduced defects in the IL electrostatic network resulting in large ion mobilities. Since [Cl]− and [Br]− are anions formed by a single atom, their concentrated charge creates strong hydrogen bonds with cations, displaying asymmetry and thus non-directionality towards hydrogen atoms in the cation, causing slow mobility and presenting higher viscosities compared to ILs with large anions.
In order to improve the agreement between calculated and simulated dynamical properties, such as diffusion coefficients13 and viscosities,76 some molecular simulations research groups have scaled the atomic charges of ILs, i.e. from ±1e to ±0.8e, since this mimics both the charge transfer and polarizability.77 Zhang and Maginn77 studied the effect of scaling charges in the calculation of a classical FF and its capability to predict some relevant thermodynamic properties. In their study they found that the reduced-charge scheme improved properties such as the diffusion coefficient and the enthalpy of vaporization in comparison with the full-charge scheme. However, properties such as density were underestimated by about 6%, in addition, properties such as Radial Distribution Function (RDF) and Spatial Distribution Function (SDF) were insensitive to charge scaling.
In a recent contribution, Doherty et al.13 carried a re-parametrization of their previously developed OPLS-2009 IL FF28 validated against current and more reliable available experimental data, such as: densities, heats of vaporization, viscosities, diffusion coefficients, heat capacities, and surface tensions. These authors used a ±0.8e scaled-charge version of their original full-charge FF published in 2009.28 Their results, showed that calculated properties with the scaled-charge FF such as enthalpy of vaporization, surface tension, and self-diffusion coefficients were remarkable improved compared with their previous calculations using the OPLS-2009 IL FF. On the other hand, properties such density, heat capacity at constant pressure, viscosities, and RDF were insensitive to this charge scaling.
The final transport property studied in this work, is the thermal conductivity, estimated by means of NEMD. It is a key property in the design of heat and mass transfer equipment in the chemical industry, metallurgy, fluid flow, etc.78 Recently Zaripov et al.78 indicated the necessity of new and enhanced heat transfers fluids in order to improve product quality, reduce operating costs and its environmental impact in industrial processes. ILs can be used as thermal fluids due to their various physicochemical properties such as negligible vapor pressure, liquid state, density, viscosity, heat capacity and thermal conductivity.55,79 Liu et al.59 calculated the thermal conductivity for a series of ILs based on the [NTf2]− anion, employing Reverse Non-Equilibrium Molecular Dynamics (RNEMD) techniques, by using the Müller-Plathe formalism.80 They calculated a value of 0.107 W m−1 K−1 for thermal conductivity of the [C4mim][NTf2] at 300 K, these authors also reported an experimental value of 0.126 W m−1 K−1 at 298.15 K, presenting an error of 15%. The RNMED technique has also been used by Tenney et al.81 in the determination of reliable thermal conductivities for the [C2mim][OMs] and the [C2mim][CF3COO] ILs. Chen et al.53 also proposed a group contribution method to estimate the thermal conductivities of ILs.
The objective of this work is the determination of thermodynamic, structural and transport properties such as: critical points (ρc, Tc), radial, spatial and combined distribution functions, shear viscosities, self-diffusion coefficients, and thermal conductivities for the [C4mim][CF3COO] and [C4mim][Br] ILs by using molecular simulations. These two ILs have been used experimentally in various condensed phase applications such as: extracting solvents for fluoridated compounds present in alkylated gasoline by a typical liquid–liquid extraction process,41 solvents for the capture of carbon dioxide82,83 as reaction media84,85 and applications in the food and health industry.86
The simulations performed in this work, used AA FF previously developed within the research group,24 validated for the prediction of thermodynamic properties such as: density, heat of vaporization, specific heat at constant pressure, dielectric constant, and surface tension for the [C4mim][PF6], [C4mim][BF4], [C4mim][OMs], [C4mim][NTf2], [C4mim][CF3COO], [C4mim][Br] ILs,24,41 and validated also in the determination of structural properties for the [C4mim][PF6], [C4mim][BF4], and [C4mim][OMs] ILs.24 Experimental evidence was recovered for most of the calculated properties and some new predictions were done where data is not available. These calculated properties are necessary for the development of viscosity and self-diffusivity correlations using, for example, the Vogel–Fulcher–Tamman, VFT equation,45 and the development of new thermodynamic equation-of-states, expanding the possible applications for these ILs studied, as heat transfer fluids, green solvents for the extraction of different substances, solvents as reaction media, condensed phase applications with high importance in the pharmaceutical, chemical and petrochemical industries.
Methodology
Force field development
The information corresponding to the classical FF developed previously within the research group, including their parameters can be found in the ESI section.† Fig. 1 displays a schematic representation of all the ILs studied in this work, along with their corresponding atomic labels.VLE curve
The VLE curve for [C4mim][NTf2], [C4mim][CF3COO] and [C4mim][Br] IL was obtained using well-established methodologies published in the literature.87,88 A liquid configuration was placed in the center of an elongated parallelepiped box in the z-direction surrounded by vacuum, then NVT MD simulations are carried out; as the vapor phase starts to appear, molecules moved from the center of the box into the vacuum space in equilibrium with the liquid. The vapor and liquid densities are calculated by dividing the simulation box along the z-direction into different slabs of fixed length Δz, and then counting the average number of molecules N inside each slab during the MD production step, divided by the volume of each slab as in the following equation:87,88
 | (1) |
The VLE curve was obtained with the GROMACS89 software. The simulations consisted of 200 pair of ILs, Periodic Boundary Conditions (PBC) were applied, and a cutoff of 18 Å was used for all ILs systems for both LJ and electrostatics. Short-range electrostatics interactions were calculated in real-space using the above cutoffs, past this distance the Particle-Mesh-Ewald90,91 (PME) was employed to calculate the long-range electrostatic interactions with an accuracy of 5 × 10−3 by using a Fourier grid spacing of 1.2 Å and a four-order interpolation. The time step for the equilibrium MD simulations was 1 fs. Temperature was maintained constant by means of the V-rescale92 thermostat with a coupling parameter of 1 ps. The size of the parallelepiped box for each IL system along the x, y, and z dimensions were 46 Å × 46 Å × 250 Å, 42 Å × 42 Å × 250 Å and 39 Å × 39 Å × 250 Å for [C4mim][NTf2], [C4mim][CF3COO], and [C4mim][Br], respectively. The NVT simulations were carried out in a temperature range between 300 K to ∼1300 K, simulation times of 10 ns were used for each temperature. The first 3 ns were considered as equilibration stage and the remaining time as production stage, the atomic coordinates were saved every 500 fs during this latter stage. Saved coordinates from a 7 ns, previous NpT simulation at 300 K were used as input for the NVT simulations at 300 K. Rai and Maginn34 calculated the VLE curve for a series of [Cnmim][NTf2] ILs by using molecular simulations with system sizes ranging from 200 to 400 ion pairs, larger systems were used at higher temperatures, 400 ion pairs were used for simulations close to the critical point.
Shear viscosity
The shear viscosity was calculated using the PPM69 technique. In this method an external periodic force is applied in one direction ax(z), affecting only the x component of the velocity vector of the atoms. The Navier–Stokes equation under these conditions and in stationary state, reduces to:11,13,69,93
 | (2) |
ax(z) = a0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kz) cos(kz)
| (3) |
 | (4) |
The solution for this differential equation is as follows:
| vx(z,t) = v0(1 − e−t/τ)cos(kz) | (5) |
vx(z,t) = v0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kz) = a0τ cos(kz) = a0τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(kz) cos(kz)
| (6) |
From eqn (4) and (6), the shear viscosity is obtained as follows:
 | (7) |
The acceleration amplitude a0 needs to be chosen carefully: a small value is needed for the system to remain close to equilibrium, avoiding a large temperature increase affecting the system density. On the other hand, this amplitude value needs to be large enough to avoid large signal to noise ratios.94
The shear viscosities in this work, were calculated using the methodology proposed by Doherty et al.13 employing the same system size for reproducibility purposes, and performed with the GROMACS89 computational package. Simulation boxes containing 500 IL pairs were used for each IL system, the same number of molecules that was used by Doherty et al., PBC and the minima image convention in three directions with a cutoff of 13 Å, were applied. The PME90,91 scheme was applied for electrostatic interactions, and a time step of 1 fs was used for all simulations. The temperature and pressure were kept constant by means of a V-rescale92 thermostat and Berendsen95 barostat, with coupling parameters of 1 ps. Before calculating shear viscosities, EMD simulations were performed with 10 ns of equilibration time followed by 40 ns of production time in the NpT ensemble for each IL. For all ILs studied, the temperature was 300 K with the exception of [C4mim][OMs] IL (358 K). The viscosity of [C4mim][PF6] IL was also evaluated at 350 K. For all systems the pressure was maintained at 1 bar, and all the covalent hydrogen bonds X–H, were constrained using the LINCS96 algorithm. Zhao et al.93 used NEMD simulations with the PPM method to determine the shear viscosities of 1,4-butanediol, 1,3-butanediol, 1,2-butanediol, 2-methyl-1,3-propanediol and 1,2,4-butanetriol, using the OPLS FF and found that the acceleration amplitude value a0, is the most important parameter in the calculation of the shear viscosity, compared with other parameters such as: box size, trajectories length, etc.
Regarding structural properties, Radial Distribution Function (RDF), Spatial Distribution Function (SDF), and Combined distribution Function (CDF), for the [C4mim][CF3COO] and [C4mim][Br] ILs were calculated during the EMD production step by using the VMD97 and TRAVIS98 computational packages.
The coordinates from the NpT EMD production step were fed to the NEMD, using an acceleration amplitude range from 0.04 to 0.12 nm2 ps−1 for each IL. It is important to note that this amplitude range depends on the system size, temperature, and substance. All the NEMD simulations lasted 40 ns; the same simulation parameters as in the EMD simulations such as: temperature, pressure, time step, PBC, cutoff, thermostat, barostat, PME, and LINCS, were used. The last 20 ns were employed to calculate the shear viscosity, temperature, and their standard deviations via the block averaging technique.99
It has been stressed that the dependence of the acceleration amplitude with the shear viscosity is complex, but a limited range of accelerations displays a linear relationship with the shear viscosity of the substance.94 In this work we only consider those accelerations that do not cause an abrupt change in the temperature of the system. To determine the IL viscosity, the acceleration values and shear viscosities for each acceleration amplitude were fitted into a linear relationship by using a weighted least squares technique. These weights were equal to the reciprocal of the square standard deviation for the shear viscosity, those acceleration amplitudes that presented large shear viscosity deviations, contributed slightly to the viscosity calculation by having a very small weight.93 This linear relationship allows the determination of zero shear viscosities by means of an extrapolation with the y-axis.
Self-diffusion coefficients
The self-diffusion coefficients Di, can be calculated through the Einstein relation as follows:59
 | (8) |
In order to assure that we are in the diffusive regime, the β(t) factor was calculated during the simulations by using:70
 | (9) |
Values of β(t) ≈ 1 assure that the IL system is in the diffusive regime, necessary to obtain reliable results, while values of β(t) < 1 indicate a sub-diffusive regime.70
Thermal conductivity
The thermal conductivity λ, for each IL presented in Table 2, were calculated using the RNEMD technique proposed by Müller-Plathe.80 In this method a heat flux is imposed in the system generating a temperature gradient and thus allowing their calculation by means of the following two equations:
 | (10) |
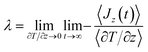 | (11) |
The thermal conductivities were calculated using the LAMMPS103 simulation package, for the reason, that the Müller-Plathe technique is not implemented within the GROMACS simulation package. The FF parameters and the input coordinates from GROMACS were translated into LAMMPS inputs with the aid of the INTERMOL104 software.
The thermal conductivities were obtained after three equilibration steps: first NpT simulations at 300 K for 2 ns, followed by NVT at 300 K for 3 ns, and finally 1 ns in the NVE ensemble. Subsequently, a production period of 1 ns in the NVE ensemble was carried out. The thermal conductivities were computed during this production step. All simulation boxes were orthorhombic, PBC were used in three dimensions with a cutoff of 18 Å, and a time step of 1 fs. To account for long-range electrostatics, the Particle–Particle–Particle–Mesh103 (PPPM) technique was used with a real-space cutoff of 18 Å. The temperature was kept constant at 300 K with the Nosé–Hoover100,101 thermostat with a coupling parameter of 100 fs. The pressure was maintained at 1 bar with the Nosé–Hoover103 barostat with a coupling parameter of 1 ps. In the last two NVE steps the simulation box was divided in 20 blocks or slabs forcing kinetic (velocity) exchanges between hot and cold atoms every 10 fs. The data was saved every 1 ps during the NVE production step, and the thermal conductivity was calculated employing the block averaging technique.99
Results
IL structure
RDFs, SDFs, and CDFs, were calculated in this work for the [C4mim][CF3COO] and [C4mim][Br] ILs at 300 K. RDFs for ion–ion interactions are shown in Fig. 2. The RDF for the [C4mim][CF3COO] IL is shown in Fig. 2a. The [CF3COO]−–[CF3COO]− interaction, red line in Fig. 2a, presents two well defined peaks at 5.15 and 8.65 Å. The [CF3COO]−–[C4mim]+ interaction presents a well-defined peak at 5.05 Å and a second blunt peak at 11.75 Å, with intensities of g(r) ∼2.1 and 1, respectively. Finally, the cation–cation interaction in this IL displays peaks at 8.35 Å and 15.05 Å, with intensities around ∼1. The RDF integration for the [CF3COO]−–[C4mim]+ interaction until the minimum located at ∼8.1 Å, gives a coordination number of 6.68 molecules, this means that in the first solvation layer the cation is surrounded and interacting approximately with 6.7 anions in average. | ||
| Fig. 2 RDFs for [C4mim][CF3COO] and [C4mim][Br] ILs at 300 K. (a) [C4mim][CF3COO] IL. (b) [C4mim][Br] IL. Anion–anion RDFs are colored in blue, anion–cation RDFs are colored in red, and cation–cation RDFs are colored in green. Continuous lines represent the results obtained with our developed FF, dashed lines represent results obtained with the FF by Doherty et al.13 The atomic labels N2, C10 and BR are displayed in Fig. 1, and were used to determine the ion–ion RDFs. | ||
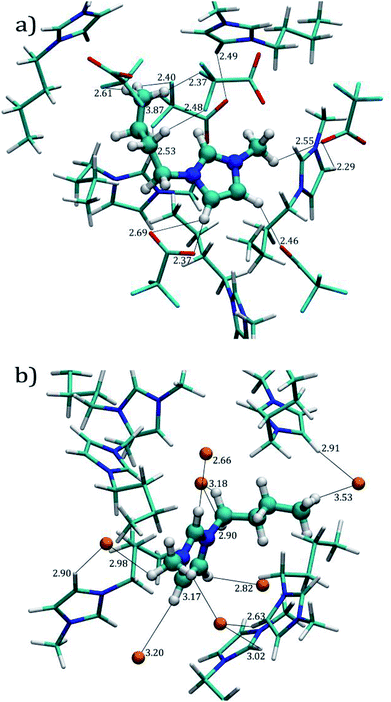
Fig. 3a and b display the molecular environment around ILs (solvation layer and close contacts) obtained from the last MD trajectory frame, for both [C4mim][CF3COO] and [C4mim][Br] ILs, respectively.
The RDFs for the [C4mim][Br] IL are shown in Fig. 2b. The RDFs obtained by employing the FF developed by Doherty et al.,13 labeled as [C4mim][Br]-Doherty, are also plotted in the same figure for comparison purposes as dashed lines. The [Br]−–[Br]− interaction using our developed FF presents a first peak at 7.25 Å, and a second peak at 13.4 Å. The [C4mim][Br]-Doherty FF displays a blunt peak in the 6–8.7 Å range, and a second peak located at 13.05 Å for the same interaction. Furthermore, the [Br]−–[C4mim]+ RDF for both our developed FF and the FF developed by Doherty et al. are very similar to each other, displaying peaks at ∼4.2, 5.85, 10.20 and 16.35 Å, with intensities of 3.5, 1.5 and ∼1, respectively. For the [C4mim]+–[C4mim]+ RDF our FF presents a well-defined peak at 8.05–8.15 Å, with intensity around 1.2, while the [C4mim][Br]-Doherty FF presents a blunt peak located in the 6.55–8.3 Å range with the same intensity. The coordination number for our FF found by integrating the anion–cation RDF gave a value of 5.9 molecules until the minimum located at ∼7.35 Å (Table 3). These integrations were also carried out for the anion–cation by using the [C4mim][Br]-Doherty FF and 5.96 molecules were found until the same first minimum. Despite the RDF differences between [C4mim][Br]-Doherty and the FF developed within the research group, the calculated density values are very similar: 1.277 and 1.271 g cm−3, respectively at 300 K. Comparison for different properties such as: heat of vaporization, heat at constant pressure, and dielectric constant between these FFs can be found in ref. 41.
| LI | RDF | Rcoord | Ncoord |
|---|---|---|---|
| a See Fig. 2 and 5 for RDF graphs. Atoms H13,14,15 are labeled as Hmethyl. See Fig. 1 for atomic labels.b Atoms located at the COM for the ions have been used to calculate the anion–cation RDF. | |||
| [C4mim][CF3COO] | C10–N2b | 7.10 | 6.68 |
| O3–H1 | 3.95 | 1.17 | |
| O3–H2,3 | 3.65 | 1.30 | |
| O3–Hmethyl | 6.65 | 8.02 | |
| F4–H1 | 6.95 | 4.11 | |
| F4–H2,3 | 6.25 | 6.10 | |
| F4–Hmethyl | 7.85 | 18.01 | |
| [C4mim][Br] | BR–N2b | 7.35 | 5.9 |
| BR–H1 | 4.75 | 1.91 | |
| BR–H2,3 | 4.00 | 2.23 | |
| BR–Hmethyl | 5.95 | 10.56 | |
The SDFs display the most probable spatial regions for finding a molecule around a reference molecule in a three dimensional space.98 SDFs were calculated for the [C4mim][CF3COO] and [C4mim][Br] ILs using the TRAVIS98 software and visualized with VMD,97 as shown in Fig. 4; the [C4mim]+ cation was used as reference molecule. In Fig. 4a, the anion isosurfaces for the [C4mim][CF3COO] IL are displayed in red color with a value of 8.1 particles per nm−3, while the cation isosurfaces are displayed in blue color with a value of 3.7 particles per nm−3. The [CF3COO]− anion prefers to occupy the regions close to the H1, H2, and H3 hydrogens in the imidazolium ring as well as the H4 and H5 hydrogens from the butyl chain (see Fig. 1 for atomic labels). On the other hand, the [C4mim]+ cation prefers to be positioned in front of the imidazolium ring favoring π–π interactions. This π–π stacking has been related with the dimer IL stability, since this geometric arrangement increases the interaction energy of the dimer.105
The SDFs for the [C4mim][Br] IL are displayed in Fig. 4b. The isosurface values for the anion and cation are 12 and 4.72 particles per nm−3, respectively. The [Br]− occupies all the top cation region, differing with respect to the [C4mim][CF3COO] IL, and also preferring regions closed to hydrogens in both the imidazolium and in the alkyl chains closed to the ring (H1–5,H13–15). The cation presents the same behavior as in the [C4mim][CF3COO] IL. Kohagen et al.68 reported the SDF for the [C4mim][Br] IL by using the OPLS AA FF, while Ramya et al.74 reported the SDF for the [C6mim][Br] IL by using the AA FF developed by Tsuzuki et al.27 The SDF obtained here using our developed FF displays good agreement with respect to the SDF reported by these same authors.
In a different contribution, Izgorodina and MacFarlane106 studied the [C2mim][Cl] IL by using ab initio and the Symmetry Adapted Perturbation Theory107 (SAPT) calculations, and they found that the anion–cation interactions characterized by placing the anion on top or below the imidazolium ring plane are energetically similar to in plane conformations where the anion forms hydrogen bonds with the hydrogen atom from the imidazolium ring along the C2–H1 direction. These observations are consistent with the behavior displayed by the SDF red isosurfaces obtained in this work for both [C4mim][CF3COO] and [C4mim][Br] ILs. For comparison purposes we have also computed the SDF for the [C4mim][Br] IL by using the FF developed by Doherty et al.13 at 300 K, shown in Fig. 4c. These last results show a good agreement with those SDFs calculated using our developed FF.
Fumino et al.75 indicated that the strong and directional hydrogen bonds in IL can disrupt the Coulombic network, reducing the electric charge effect that any ion feels from other ions, increasing the ions mobility (diffusion coefficients) and decreasing their viscosities.
To elucidate further the hydrogen bonding in [C4mim][CF3COO] and [C4mim][Br] ILs, individual RDFs between negative atoms from anions with hydrogen atoms from the cation, were calculated as shown in Fig. 5.
 | ||
| Fig. 5 Atomic pair RDFs between X−–H for [C4mim][CF3COO] and [C4mim][Br] ILs at 300 K. (a) RDFs between hydrogen atoms (H1, H2,3, Hmethyl and Hterminal) and the O− atom within the [C4mim][CF3COO] IL. (b) RDFs between hydrogen atoms and the F− atom within the [C4mim][CF3COO] IL. (c) RDFs between hydrogens atoms and the [Br]− anion within the [C4mim][Br] IL. H13, H14 and H15 atoms are labeled as Hmethyl. H10, H11, and H12 atoms are labeled as Hterminal, as displayed in Fig. 1a. | ||
Fig. 5a shows the RDFs obtained by pairing O[CF3COO]−− (O3 in Fig. 1c) with H1, H2,3 (also known as HW), Hmethyl (i.e. H13, H14, and H15, see Fig. 1a) and Hterminal, (i.e. H10, H11, and H12). It can be observed that acidic hydrogen atoms from imidazolium ring exhibit the main interaction with oxygen atoms from the [CF3COO]− anion showing a peak at ∼2.45 Å for both H1 and H2,3 atoms, these distances are in agreement with the distances shown in Fig. 3a. The coordination numbers Ncoor, for hydrogen atoms around the oxygen atoms are 1.17 and 1.30 atoms for O3–H1 and O3–H2,3 respectively, as indicated in Table 3. The hydrogen bonds with Hmethyl are also significant, the RDF peak appears at a slightly larger distance than the acidic hydrogen atoms ∼2.65 Å with a coordination number of 8.02 atoms until 6.65 Å. Our results indicate that the RDF for O3–Hterminal presents a weaker intensity of around 2 as compared to intensities of 5.9 for O3–H1, and 3.5 for O3–H2,3 interactions.
The same hydrogen RDFs were calculated for F[CF3COO]−− (F4), and are shown in Fig. 5b. As seen the first peak appears at a similar distance ∼2.8 Å, for all interactions but with a remarkable lower g(r) intensity value compared with O3–H RDFs displayed in Fig. 5a. At distances of ∼2.8 Å, the interactions between F[CF3COO]−− and Hterminal, black line in Fig. 5b, present higher intensities than the O3–Hterminal interactions, as seen in Fig. 3a. The coordination number for these interactions are presented in Table 3.
Fig. 5c presents the [Br]−–H RDF for [C4mim][Br] IL. Unlike O3–H interactions, the RDFs for [Br]− display similar behavior towards H1 and H2,3 hydrogen atoms, presenting higher probabilities of finding bromide atoms around these hydrogens atoms, as seen in Fig. 3b, at average distances of ∼2.85 Å. The coordination number until the first well-defined minimum distance for both interactions were 1.91 and 2.23 hydrogen atoms for H1 and H2,3, respectively as presented in Table 3.
The [Br]−–Hmethyl RDF presents a well-defined peak at ∼3 Å, at similar distances with respect to the hydrogen atoms in the imidazolium ring, but with a lower intensity; in Fig. 3b we can visualize these interactions within the same distances found in the RDFs. The Ncoor for [Br]−–Hmethyl interaction until the first well-defined minimum is 10.56 hydrogen atoms. Finally the [Br]−–Hmethyl RDF shows the same behavior as [C4mim][CF3COO] IL with a blunt peak around 5 Å and a g(r) value close to 1.0 indicating the absence of a specific local arrangement for these interactions.
In order to obtain additional information with respect to the hydrogen bonding behavior in [C4mim][CF3COO] and [C4mim][Br] ILs, CDFs were calculated between acidic hydrogen atoms and negative atoms from anions, by monitoring both the X−–H1 radial and the C1–H1–X− angular distributions (with X− equals O− or [Br]− atoms) for [C4mim][CF3COO] and [C4mim][Br] ILs, as shown in Fig. 6. A higher occurrence for the X−–H1 CDF for both cases is associated with their RDF peaks shown in Fig. 5a and c for [C4mim][CF3COO] and [C4mim][Br] IL, respectively. In the case of [C4mim][CF3COO] IL there is a region of high occurrence located around ∼2.1 to ∼3 Å and in a range of ∼100 to 150°, as displayed in Fig. 6c. A similar behavior is observed in the case of [C4mim][Br] IL displayed in Fig. 6d, however, the distance of high occurrence is slightly larger than [C4mim][CF3COO] IL ∼2.9 Å, and with angles from 90 to 150°. In this same figure we can observe a second region of high occurrence located at 6.3 Å and ∼40° for the [C4mim][Br] IL. Based on the localization of the anion given by CDF, the cation is expected to be placed either above or below the imidazolium ring plane as shown by Doherty et al. for [C2mim]+ cations in [C2mim][DCA] IL, i.e. with an angle of 0 or 180° from their center of rings.
The CDF was also calculated by using the geometric center-of-ring (COR) between two cations in both [C4mim][CF3COO] and [C4mim][Br] ILs. This CDF monitors the distance and the angle formed between the COR–COR vector and a COR-Normalized vector COR-NV, perpendicular to the imidazolium ring plane, as shown in Fig. 7a. Similar agreement with their corresponding SDF shown in Fig. 4 is presented for the cation–cation CDF, where the preferred angle is located around 0 to 40°, corresponding to the underneath position with respect to the imidazolium ring plane, and 140 to 180°, corresponding to the above position in the same plane,105 with distances around of ∼4 Å.
Regarding hydrogen bonds, Tang et al.108 indicated that not only the geometric configurations are important but also their electronic densities. They found by using the theory of Atoms in Molecules that hydrogen bond lengths varied from 1.15 to 3.01 Å and the electronic density at the bond critical point ranged from 0.0033 to 0.168 a.u. In a different contribution, Contreras-García et al.109–111 developed a methodology to map the non-covalent interactions between atoms in a system by analyzing its electronic density (ρ) and its reduced gradient (s).
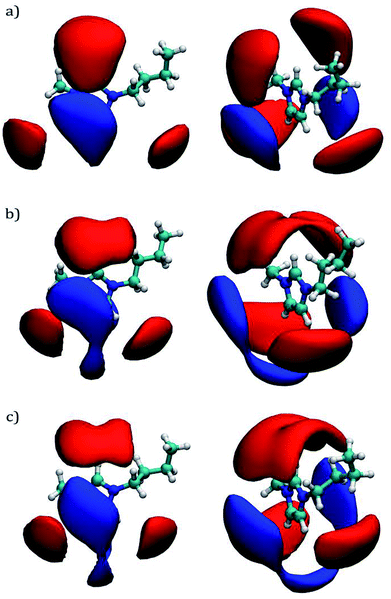
The analysis developed by Contreras-García et al. is called Non-Covalent Interaction (NCI) index, and it can be carried out by using the NCIplot110 program. The analysis is based on a s vs. ρ plot which reveals the magnitude of typical interactions such as hydrogen bonds, weak interactions, and steric clashes.109 To distinguish between attractive and repulsive interactions, it is necessary to resort to the sign of the second eigenvalue (λ2): Sign(λ2), of the electronic density Hessian matrix.111 By plotting Sign(λ2)ρ not only the magnitude of the interaction is reveled but also the nature of such interaction: hydrogen bonds are characterized by negative values of Sign(λ2)ρ, i.e. −0.05 < Sign(λ2)ρ < −0.005 a.u.; weak interactions are related to near zero values of Sign(λ2)ρ, i.e. Sign(λ2)ρ > −0.005 a.u.; and steric repulsions shows positive values for Sign(λ2)ρ.109 The NCI index can be also visualized with the VMD97 package as colored gradient isosurfaces corresponding to the nature of the interaction; blue, green, and red colors are related to hydrogen bonds, weak interactions, and steric repulsions, respectively. The electronic density for the molecular configurations shown in Fig. 3 was calculated by using Density Functional Theory with the M06 (ref. 112)/6-311+G(d,p) functional/basis set employing the Gaussian09 (ref. 113) package. These molecular configurations were obtained from the last saved frame during the EMD production step for the shear viscosity calculations.
Plots of electronic density against its reduced gradient are shown in Fig. 8a and b for [C4mim][CF3COO] and [C4mim][Br] IL, respectively. As can be seen, both IL show weak hydrogen bonds since the peaks are located at Sign(λ2)ρ ≥ −0.015 a.u. Presenting weak hydrogen bonds at ∼ −0.015, −0.014 a.u. and a series of weaker interactions around ∼0.012 a.u along the Sign(λ2)ρ axis. Peaks corresponding to weak hydrogen bonds in Fig. 8a and b are related to isosurfaces colored in blue in Fig. 8c and d for [C4mim][CF3COO] and [C4mim][Br] IL, respectively. The density scale used for the NCI calculations (−0.02 < ρ < 0.02 a.u), displayed in Fig. 8, conceals the visualization of steric repulsions present at density values larger than 0.05 au. By using a larger density scale of −0.10 < ρ < 0.10 a.u., the relevant steric repulsion appeared within the imidazolium ring for both ILs, as displayed in Fig. S2 in the ESI section.†
 | ||
| Fig. 8 Plots of reduced density gradient (s) vs. the electron density multiplied by the sign of the second Hessian eigenvalue Sign(λ2)ρ at 300 K. (a) and (c) Results correspond to the [C4mim][CF3COO] IL; (c) and (d) are results for the [C4mim][Br] IL. Attractive interactions are displayed in blue color, weak interactions in green color, and steric repulsions in red color. The isosurfaces correspond to a cutoff for s of 0.5 a.u. The density color scale varies from −0.020 < ρ < 0.020 a.u. Steric repulsions can only be observed within the ring interactions by incrementing the density color scale to −0.10 < ρ < 0.10 a.u, as displayed in Fig. S2 of the ESI section.† | ||
In the case of [C4mim][CF3COO] IL the weak interactions mentioned above were labeled as A, B, C, and D ranging from (strongest to weakest): darkest blue (A), dark blue (B), light blue (C), to darkest green (D). As can be observed, the main interactions A and B, correspond to hydrogen bonds from hydrogen atoms in symmetric carbons as expected from its RDF, as seen in Fig. 5a.
In the case of [C4mim][Br] IL a weak hydrogen bond for every [Br]− anion labeled as A is displayed, followed by a series of slightly weaker hydrogen bonds labeled as B, for the same [Br]− anion, continuing with weaker hydrogen bonds labeled as C and D. The number of interactions in the [C4mim][Br] IL anion is related with the RDF coordination numbers presented in Table 3. The larger the number of interaction for a single anion, the weaker the interaction strength,114 as observed in Fig. 8d and Ncoord in Table 3. According to the findings by Fumino et al.75 it could be expected, that since the [C4mim][Br] IL shows less localized and directional hydrogen bonds, this IL would present less fluidity in comparison to [C4mim][CF3COO] IL.
VLE curve
The VLE curves for the ILs [C4mim][NTf2], [C4mim][CF3COO], and [C4mim][Br] are shown in Fig. 9. It is important to notice that the gas densities are considered only approximations, since it is difficult to quantify the number of molecules in this phase with the current methodology. It is recommended the use of larger systems and longer simulation times in order to obtain more accurate results for the vapor phase. The calculated critical points in Table 4 and displayed in Fig. 9 were obtained with the law of rectilinear diameters and the density scaling law115 with a critical scaling factor of 0.32. Results from Rane and Errington33 and Rai and Maginn34 for the [C4mim][NTf2] IL were added to Fig. 9a for comparison. For the [C4mim][NTf2] IL the calculated critical temperature is in agreement with the value reported by Rai and Maginn34 and differs only by ∼10 K with respect to the value reported by Rane and Errington,33 as shown in Fig. 8a and Table 4. | ||
| Fig. 9 VLE curve for [C4mim][NTf2], [C4mim][CF3COO], and [C4mim][Br] ILs simulated in this work. (a) Vapor and liquid densities calculated in this work for the [C4mim][NTf2] IL are displayed as black colored circles. Purple squares and orange diamonds are the results obtained from Rane and Errington33 and Rai and Maginn,34 respectively. (b) Vapor and liquid densities obtained in this work for [C4mim][CF3COO] and [C4mim][Br] ILs are displayed as red and blue colored circles, respectively. | ||
| LI | ρc | ρc,sim | ρc,es | Tc | Tc,sim | Tc,es |
|---|---|---|---|---|---|---|
| a ρc, ρc,sim and ρc,es refer to calculated values in this work, simulated values (from literature), and theoretically estimated values (from literature), respectively. Simulated and theoretically estimated values were taken from their corresponding references. Tc, Tc,sim and Tc,es the subindices are the same as those in density. | ||||||
| [C4mim][NTf2] | 0.273 | 0.250 ± 0.003 (ref. 33) | 0.424 (ref. 36) | 1205.4 | 1216 ± 14 (ref. 33) | 1077 (ref. 43) |
| 0.265 ± 0.006 (ref. 34) | 1203 ± 4 (ref. 34) | 1012 (ref. 43) | ||||
| 1269.9 (ref. 36) | ||||||
| [C4mim][CF3COO] | 0.213 | N/A | 0.356 (ref. 36) | 1233.4 | N/A | 1271 (ref. 37) |
| 826.8 (ref. 36) | ||||||
| [C4mim][Br] | 0.234 | N/A | 0.376 (ref. 36) | 1308.2 | N/A | 834.9 (ref. 36) |
The calculated critical temperature for the [C4mim][CF3COO] IL is 1233.4 K, displayed in Fig. 9b, presented a difference of only ∼40 K with respect to the estimated value of 1271 K by Fang et al.37 obtained with a modified Eötvos equation. Finally, the critical temperature for the [C4mim][Br] IL was calculated at 1308.2 K as displayed in Fig. 9b, presenting the highest critical temperature of all the ILs studied in this work. For this IL, Valderrama et al.36 obtained an estimated value of 834.9 K using a group contribution method. The difference between the critical temperatures of [C4mim][CF3COO] and [C4mim][Br] ILs could be related to the number of hydrogen bonds needed to be broken in [C4mim][Br] IL, in order for the system to change its physical phase.
Shear viscosities
The shear viscosities calculated with eqn (7) are presented in Table 5 for all ILs studied in this work. Fig. S3a in the ESI section† displays the shear viscosity against the acceleration amplitude a0, for the [C4mim][OMs] IL. Small a0 values generate large fluctuations in the viscosity presenting large standard deviations, on the other hand, large a0 values increase the temperature considerably. Both of them, small and large amplitude points, were discarded from the viscosity linear relationship adjustment.116 From Fig. S3b,† it can be observed that acceleration amplitude values higher than a0 = 0.11 nm ps−2 do not deviate the temperature considerably from the dotted line, in this same figure only one standard deviation within each viscosity point was plotted.| LI | η | ηexp | ηsim | Δηb (%) |
|---|---|---|---|---|
| a η, ηexp and ηsim refer to calculated values in this work, experimental values (from literature), and simulated values (from literature), respectively. Experimental and simulated values were taken from their corresponding references.b Δη = (η − ηexp)/ηexp.c At 350 K.d At 298 K.e At 353 K.f At 360 K.g At 298.15 K.h At 358.15 K.i At 5.74 mol L−1 IL concentration in aqueous solution. | ||||
| [C4mim][PF6] | 163.86 | 224.74 (ref. 44) | 264.4 (ref. 13)d | −27.09 |
| 228.81 (ref. 45) | −28.39 | |||
| 257.36 (ref. 46) | −36.33 | |||
| 450 (ref. 47) | −63.59 | |||
| 38.4c | 25.51 (ref. 44)c | 39 (ref. 29)e | 50.53 | |
| 27.08 (ref. 48)c | 31.3 (ref. 49)f | 41.08 | ||
| 32.33 (ref. 46)c | 231.3 (ref. 49)f | 18.33 | ||
| [C4mim][BF4] | 84.49 | 90.61 (ref. 44) | 97.8 (ref. 13)d | −6.75 |
| 86.8 (ref. 46) | 111.2 (ref. 31)d | −2.66 | ||
| 107.32 (ref. 48) | −21.27 | |||
| 219 (ref. 47)g | −61.42 | |||
| [C4mim][OMs] | 52.81h | 31.25 (ref. 56)h | N/A | 68.99 |
| [C4mim][NTf2] | 53.67 | 46.24 (ref. 44) | 537.80 (ref. 59) | 16.07 |
| 46.5 (ref. 46) | 45 (ref. 11)g | 15.42 | ||
| 46.44 (ref. 57) | 72.09 (ref. 60)g | 15.57 | ||
| 46.79 (ref. 58) | 49.9 (ref. 13)d | 14.7 | ||
| 69 (ref. 47)g | −22.22 | |||
| [C4mim][CF3COO] | 58.22 | 63.2 (ref. 62) | N/A | −7.88 |
| 70.02 (ref. 44) | −16.85 | |||
| [C4mim][Br] | 160.14 | 200 (ref. 63) | 231.1 (ref. 13)d | −19.93 |
| 230 (ref. 63)d | −30.37 | |||
| 161.05 (ref. 64)d,i | −0.57 | |||
| 1486.49 (ref. 65)d | −89.23 | |||
The calculated standard deviations for the shear viscosity simulations were used as weights (1/σ2) in the linear regression fitting as shown in Fig. S3a.† Extrapolating the y-axis up to a zero amplitude allows the determination of the zero shear viscosity. Zhao et al.93 noticed the existence of a linear correlation between certain acceleration amplitude values and shear viscosities by using a weighted linear regression fitting. The calculated standard deviations for the shear viscosity simulations were used as weights (1/σ2) giving less importance to those points having large standard deviations in the weighted least square fitting. Furthermore, Sprenger et al.11 calculated the shear viscosity for a series of ILs using only a single value for the acceleration amplitude (a0 = 0.03 nm ps−2) and obtained good agreement against experimental values, with a maximum error of 34%.
In this work the obtained shear viscosities are related strongly with an acceleration amplitude value of a0 = 0.5 nm ps−2; for example for the [C4mim][OMs] IL, the shear viscosity evaluated at this amplitude gave a value of 61.26 cP, compared to the value of 52.81 cP obtained with the weighted regression adjustment, both results presented a difference of 16%. With the exception of the [C4mim][OMs] IL, giving the largest deviation against experimental values, our developed FFs predicted shear viscosities in agreement with experimental values presenting errors in the range of 0.5 to 36%. The temperature dependence was also captured in the simulations for the [C4mim][PF6] IL at two different temperatures, i.e., 300 and 350 K, where the zero shear viscosity decreased by a factor of four.
The following trend is observed for the experimental viscosities from higher to lower IL viscosity values: [C4mim][PF6] ∼ [C4mim][Br] > [C4mim][BF4] > [C4mim][CF3COO] > [C4mim][NTf2] > [C4mim][OMs] > [C4mim][PF6](350 K); this same trend was captured using our developed FFs. As indicated previously, the O3–H1 hydrogen bond formed in the [C4mim][CF3COO] corresponds to a coordination number Ncoord, of 1.17 atoms, compared with the BR–H1 hydrogen bond with Ncoord of 1.91 atoms. According to the findings by Fumino et al.75 we could expect a smaller viscosity for [C4mim][CF3COO] IL (higher mobility) compared with [C4mim][Br] IL, due to the existence of more hydrogen bonds.
Self-diffusion coefficients
The self-diffusion coefficients were calculated in this work at 350 K by using the Einstein eqn (8). The calculated self-diffusion coefficients and the calculated β(t) factor are shown in Table 6. From this table it can be observed that the β(t) factor is less than 1 indicating that even after long simulation times, the system is still in the sub-diffusive regime.| LI | Di | β(t) | Di,exp | Di,sim | ΔDib (%) |
|---|---|---|---|---|---|
| a Cation/anion. Di, Di,exp and Di,sim refer to calculated values in this work, experimental values (from literature), and simulated values (from literature), respectively. Experimental and simulated values were taken from their corresponding references.b ΔDi = (Di − Di,exp)/Di,exp for cation/anion.c At 353 K.d At 358.15 K.e Obtained by scaling the atomic partial charges to give ±0.8e. The list of charges can be found in Table S2 of the ESI section.f At 358 K.g At 360 K. | |||||
| [C4mim][PF6] | 1.68/0.71 | 0.90/0.87 | 6.17/5.26 (ref. 44) | 4.7/3.2 (ref. 29)c | −72.77/−86.50 |
| 6.43/5.14 (ref. 45) | −73.87/−86.19 | ||||
| [C4mim][BF4] | 3.57/2.26 | 0.97/0.91 | 10.21/10.20 (ref. 44) | 9.7/8.2 (ref. 29)c | −65.03/−77.84 |
| 9.69/10.10 (ref. 45) | −63.16/−77.62 | ||||
| [C4mim][OMs] | 0.90/0.55d | 0.80/0.84d | 5.48/4.89 (ref. 56)d | N/A | −83.58/−88.75 |
| 3.98/3.40d,e | 0.88/0.94d,e | −27.37/−30.47e | |||
| [C4mim][NTf2] | 4.6/2.46 | 0.88/0.87 | 14.06/11.23 (ref. 44) | 4.91/3.35 (ref. 59) | −67.28/−78.09 |
| 13.80/11.68 (ref. 45) | 10.9/7.8 (ref. 29)c | −66.67/−78.94 | |||
| 8.33/5.32e | 0.95/0.86e | −40.75/−52.63e | |||
| −39.64/−54.45e | |||||
| [C4mim][CF3COO] | 3.59/3.03 | 0.84/0.97 | 11.18/10.23 (ref. 44) | 19.8/17.2 (ref. 29)c | −69.58/−70.38 |
| 11.10/9.76 (ref. 45) | −67.66/−68.95 | ||||
| 9.68/8.23e | 0.97/0.90e | −17.97/−19.55e | |||
| −12.79/−15.68e | |||||
| [C4mim][Br] | 0.51/0.32 | 0.82/1 | 2./N/A (ref. 66) | 22/21.08 (ref. 68)g | −74.50/— |
| 19.8/N/A (ref. 67)c | −97.42/— | ||||
| 9.1/N/A (ref. 68)f | −94.40/— | ||||
| 2.20/1.96e | 0.87/0.95e | 10/—e | |||
| −88.89/—e | |||||
| −75.82/—e | |||||
The self-diffusion coefficients obtained with our developed FF underestimate the experimental values by an average of 77%. Experimental evidence indicates that the cation diffuses faster than the anion, a quality that is captured by our developed FF. The experimental self-diffusion coefficients trend, using the experimental value reported by Seyedlar et al.66 for the [C4mim][Br] IL is: [C4mim][NTf2] > [C4mim][CF3COO] to [C4mim][Br]; this same trend was captured by our simulations.
Doherty et al.13 noticed that by scaling the charges by factor of 0.8, the self-diffusion coefficients increased presenting a better agreement with respect to the experimental values. In their work, for example, the self-diffusion coefficients without scaling charge, i.e. ±1e, for the [C4mim][BF4] IL at 425 K were 7.3 × 10−7 and 6.6 × 10−7 cm2 s−1 for the cation and anion, respectively; after scaling the charges, to give a total charge of ±0.8e, the self-diffusion coefficients increased to 43.1 × 10−7 and 42.9 × 10−7 cm2 s−1, respectively, in agreement with experimental predictions. Under this premise the original charges of the ILs studied in this work, were scaled by employing different scaling factors in order to obtain total charges of ±0.8e for the cation and anion in the [C4mim][OMs], [C4mim][NTf2], [C4mim][CF3COO], and [C4mim][Br] ILs, as indicated in Tables S1 and S2 in the ESI section.† This scaling scheme was used only during the self-diffusion calculations, improving the self-diffusion coefficients considerably with respect to the experimental values, as seen in Table 6, reducing the error from 76% to 36% for this set of ILs. A good agreement with experimental values was obtained for both the [C4mim][CF3COO] and [C4mim][Br] ILs, the latter case is observed when it is compared with the reported value by Seyedlar et al.66 These estimations can be considered reliable since the β(t) factor for each anion in IL is near ∼1.
For comparison purposes, we have also calculated the self-diffusion coefficient for the [C4mim][Br] IL, using the FF developed by Doherty et al.13 This FF labeled as [C4mim][Br]-Doherty, was used at the same simulation conditions employed in this work. This FF gave values of 1.14 × 10−7/1.54 × 10−7 cm2 s−1 for the cation/anion diffusivities, with an error around −43%/— when it was compared against the experimental value of Seyedlar et al.66
Doherty et al.13 showed that some calculated thermodynamic properties are insensitive to the charge scaling scheme, such as: densities, RDFs, SDFs, heat capacities at constant pressure, and viscosities. For example, our calculated densities for [C4mim][OMs], [C4mim][NTf2], [C4mim][CF3COO] and [C4mim][Br] IL change from 1.132, 1.425, 1.161, and 1.232 g cm−3 (with original charges) to 1.110, 1.407, 1.145, and 1.211 g cm−3 (with scaled charges) at the same operating conditions displayed in Table 6, respectively.
Thermal conductivities
The thermal conductivities for the ILs studied in this work were calculated with the aid of eqn (10) and (11) at 300 K. The calculated values are presented in Table 7. Fig. S4a in the ESI section† shows the thermal conductivity for [C4mim][Br] and its fluctuations during the 1 ns production step within the NVE ensemble, plotted every 1 ps, along with a time averaged value. The symmetric temperature profile in the z-direction is displayed in Fig. S4b.† As observed, the average temperature increased during this production step by 40 K, however, it has been reported in the literature that the thermal conductivities for ILs within the temperature range of 294 to 353 K, present a weak temperature dependence.50,51,54,55,59,61 The calculated thermal conductivity value for the [C4mim][Br] IL was 0.115 W m−1 K−1, and to the best of our knowledge there are no experimental values reported in the literature for comparison, only an estimated value could be obtained from the literature that differs around 28%.53| LI | λ | λexp | λsim | λes | Δλb (%) |
|---|---|---|---|---|---|
| a λ, λexp, λsim and λes refer to calculated values in this work, experimental values (from literature), simulated values (from literature), and theoretically estimated values (from literature), respectively. Experimental and simulated values were taken from their corresponding references.b Δλ = (λ − λexp)/λexp.c 298.15 K. | |||||
| [C4mim][PF6] | 0.108 ± 0.004 | 0.145 (ref. 50) | N/A | 0.147 (ref. 53) | −25.52 |
| 0.145 (ref. 51) | −25.52 | ||||
| 0.173 (ref. 52) | −37.57 | ||||
| [C4mim][BF4] | 0.138 ± 0.006 | 0.169 (ref. 54) | N/A | 0.167 (ref. 53) | −18.34 |
| 0.186 (ref. 55) | −25.81 | ||||
| 0.190 (ref. 52) | −27.37 | ||||
| [C4mim][OMs] | 0.161 ± 0.007 | N/A | N/A | 0.171 (ref. 53) | — |
| [C4mim][NTf2] | 0.108 ± 0.003 | 0.126 (ref. 59)c | 0.107 (ref. 59) | 0.123 (ref. 53) | −14.29 |
| 0.127 (ref. 61) | −14.96 | ||||
| [C4mim][CF3COO] | 0.132 ± 0.006 | N/A | N/A | 0.166 (ref. 53) | — |
| [C4mim][Br] | 0.115 ± 0.004 | N/A | N/A | 0.159 (ref. 53) | — |
The values of the thermal conductivities in this work underestimated the experimental values from 14% to 37%. Nevertheless these calculations captured the experimentally available trend, with low thermal conductivities values for the [C4mim][PF6] and [C4mim][NTf2] ILs. The [C4mim][OMs] IL presents the highest thermal conductivity with a value of 0.161 ± 0.007 W m−1 K−1, in agreement with an estimated value obtained with the methodology proposed by Chen et al.53 The thermal conductivity value for the [C4mim][NTf2]IL is in agreement with the simulated value obtained by Liu and Maginn.59 In the case of the [C4mim][CF3COO] IL a value of 0.132 W m−1 K−1 was obtained for the thermal conductivity, differing by 20% with respect to the value estimated using the methodology by Chen et al.53
The exhibiting trend for the calculated thermal conductivities in this work is as follows: [C4mim][OMs] > [C4mim][BF4] ∼ [C4mim][CF3COO] > [C4mim][Br] > [C4mim][PF6] ∼ [C4mim][NTf2], this trend agrees with the values obtained with the methodology proposed by Chen et al., presented in Table 6. Additionally Tenney et al.81 calculated the thermal conductivities for a series of ILs, including [C2mim][OMs] and [C2mim][CF3COO] by using RNEMD simulations with both scaled and non-scaled atomic partial charges. They found that the non-scaled versions of the FF overestimated the experimental values of the thermal conductivities, with values of 0.28 and 0.22 W m−1 K−1 for the [C2mim][OMs] and [C2mim][CF3COO] IL, respectively.
In order to consider ILs for thermal fluid applications,55 it is necessary to understand how the energy is transferred in its bulk. Therefore Prandt numbers  , were calculated for these ILs studied at 300 K, as indicated in Table 8, using previously calculated values for the heat capacity at constant pressure.24,41 The calculated Pr for these ILs are much larger than 1, indicating that the heat transfer mechanism is dominated by convective forces, in similitude with engine oils.81,117
, were calculated for these ILs studied at 300 K, as indicated in Table 8, using previously calculated values for the heat capacity at constant pressure.24,41 The calculated Pr for these ILs are much larger than 1, indicating that the heat transfer mechanism is dominated by convective forces, in similitude with engine oils.81,117
| LI | Pr |
|---|---|
| a The heat capacities at constant pressure were taken from previous works within the research group ref. 24 and 41. | |
| [C4mim][PF6] | 2222.87 |
| [C4mim][BF4] | 1117.68 |
| [C4mim][NTf2] | 769.39 |
| [C4mim][CF3COO] | 871.78 |
| [C4mim][Br] | 2158.48 |
Conclusions
Thermodynamic, structural and dynamics properties for the [C4mim][CF3COO] and [C4mim][Br] ILs such as: VLE, critical points, RDF, SDF, CDF, NCI index analysis, zero shear viscosities, self-diffusion coefficients, and thermal conductivities were calculated in this work by using equilibrium and non-equilibrium MD simulations. These properties were calculated using our previously developed FF focused on condensed phase applications for ILs, such as extracting solvents for toxic substances, solvents for capturing greenhouse gases, as catalysts, or as solvents used for reaction media.Structural information was obtained by using RDF, SDF, CDF, coordination number, and NCI interaction index, evaluating not only the ion–ion interactions but also the hydrogen bonding present in the [C4mim][CF3COO] and [C4mim][Br] ILs. It was found that hydrogen bonds in both IL are formed through interactions mainly with H1 and H2,3 from the imidazolium ring. The hydrogen coordination number for the oxygen atoms in the [C4mim][CF3COO] IL indicate a one-to-one relationship, in contrast with a hydrogen coordination number of two atoms (H1 and H2,3) surrounding the bromide anion in the [C4mim][Br] IL. The NCI analysis revealed that in spite of [C4mim][Br] IL presenting a larger number of hydrogen bond interactions, these interactions have similar strength compared to those found in the [C4mim][CF3COO] IL.
The CDF distributions allowed the monitoring of the hydrogen bonds between the atoms within the anions and the acidic hydrogen from the imidazolium ring, indicating a single preferred region with angles for these interactions of 90–150° and distances from 2–3 Å for the [C4mim][CF3COO] IL; in the case of [C4mim][Br] the CDF showed for these same interactions two preferred regions, the first region is located at angles of 90–150° with distances from 2–3 Å and the second region is located at angles 30–45° and distances from 6–7 Å. On the other hand, the CDF for the geometric center of ring for the cation presented the same behavior in both the [C4mim][CF3COO] and [C4mim][Br] IL.
The calculated critical points presented good agreement in comparison with simulations from other research groups. The [C4mim][Br] IL, possess a higher critical temperature with respect to the [C4mim][NTf2] and [C4mim][CF3COO] ILs.
Zero shear viscosities were calculated for the following five ILs at 300 K: [C4mim][PF6], [C4mim][BF4], [C4mim][NTf2], [C4mim][CF3COO], and [C4mim][Br], at 358.15 K for the [C4mim][OMs] IL, and at 350 K for the [C4mim][PF6] IL. The calculated viscosities presented, in general, good agreement against experimental values. Also our developed FFs were capable of capturing the temperature dependence of the viscosity for the [C4mim][PF6] IL at 300 K and 350 K, with viscosity values decreasing by a factor of four.
The self-diffusion coefficients for the ILs studied were calculated at 350 K, without applying a scaling factor for the atomic charges, these diffusivities under-estimated the experimental values within an average of 77%. After scaling the individual atomic charges into a total of ±0.8e charge for the anion and the cation, the error against the experimental diffusivity values was reduced from 77% till 37% for the [C4mim][NTf2], [C4mim][CF3COO], and [C4mim][Br] ILs.
The experimental thermal conductivities for some of the ILs studied in this work are scarcely available in the literature, nevertheless the calculated thermal conductivities values from our simulations presented a reliable agreement with the experimental values available. We also calculated the Prandt number for the studied ILs in this work and we found the heat transfer mechanism in ILs is dominated by convective forces, in similitude with engine oils. The calculated Prandt number for ILs ranged from 770 to 2223.
Experimental evidence was recovered for most of the calculated properties and some new predictions were done where data is not available. The results obtained in this work, expand the possible applications for the ILs studied, as heat transfer fluids, green solvents for the extraction of contaminated and toxic substances, solvents as reaction media, condensed phase applications with high importance in the pharmaceutical, chemical and petrochemical industries, where the accuracy of the FF is very important.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. S.-B. acknowledges a doctoral fellowship from CONACyT; J. S-B. and M. G. thankfully acknowledge computer resources, technical advice and support provided by Laboratorio Nacional de Supercomputo del Sureste de México (LNS), a member of the CONACYT national laboratories, with project no. 201801051N. M. G. also acknowledges the High Performance Computational Resources provided by ACARUS at the University of Sonora. J. S.-B. and M. G. thankfully acknowledge the help and advice provided by Prof. Orlando Acevedo and his research group regarding the shear viscosity calculations.References
- R. D. Rogers and K. R. Seddon, Science, 2003, 302, 792–793 CrossRef.
- J. L. Anthony, J. F. Brennecke, J. D. Holbrey, E. J. Maginn, R. A. Mantz, R. D. Rogers, P. C. Trulove, A. E. Visser and T. Welton, Physicochemical Properties of Ionic Liquids, in Ionic Liquids in Synthesis, ed. P. Wasserscheid and T. Welton, Wiley-VCH Verlag, Weinheim, 2002, pp. 41–126 Search PubMed.
- T. Welton, Biophys. Rev., 2018, 10, 691–706 CrossRef CAS PubMed.
- F. van Rantwijk and R. A. Sheldon, Chem. Rev., 2007, 107, 2757–2785 CrossRef CAS PubMed.
- T. Welton, Chem. Rev., 1999, 99, 2071–2083 CrossRef CAS.
- M. L. S. Batista, J. A. P. Coutinho and J. R. B. Gomes, Curr. Phys. Chem., 2014, 4, 151–172 CrossRef CAS.
- Z. Lei, C. Dai and B. Chen, Chem. Rev., 2014, 114, 1289–1326 CrossRef CAS PubMed.
- L. C. Branco, G. V. S. M. Carrera, J. Aires-de-Sousa, I. Lopez-Martin, R. Frade and C. A. M. Afonso, Physico-Chemical Properties of Task-Specific Ionic Liquids, in Ionic Liquids: Theory, Properties, New Approaches, ed. A. Kokorin, InTech, Croacia, 2011, pp. 61–94 Search PubMed.
- L. F. Vega, O. Vilaseca, E. Valente, J. S. Andreu, F. Llovell and R. M. Marcos, Using Molecular Modelling Tools to Understand the Thermodynamic Behaviour of Ionic Liquids, in Ionic Liquids: Theory, Properties, New Approaches, ed. A. Kokorin, InTech, Croatia, 2011, pp. 303–328 Search PubMed.
- D. Frenkel and B. Smit, Molecular Dynamics Simulations, in Understanding Molecular Simulation. From Algorithms to Applications, Academic Press, San Diego, 2002, pp. 62–107 Search PubMed.
- K. G. Sprenger, V. W. Jaeger and J. Pfaendtner, J. Phys. Chem. B, 2015, 119, 5882–5895 CrossRef CAS PubMed.
- B. Doherty, X. Zhong and O. Acevedo, J. Phys. Chem. B, 2018, 122, 2962–2974 CrossRef CAS PubMed.
- B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, J. Chem. Theory Comput., 2017, 13, 6131–6145 CrossRef CAS PubMed.
- P. A. Hunt, Mol. Simul., 2006, 32, 1–10 CrossRef CAS.
- T. Méndez-Morales, J. Carrete, O. Cabeza, L. J. Gallego and L. M. Varela, J. Phys. Chem. B, 2011, 115, 6995–7008 CrossRef PubMed.
- A. Pérez de la Luz, G. A. Méndez-Maldonado, E. Núñez-Rojas, F. Bresme and J. Alejandre, J. Chem. Theory Comput., 2015, 11, 2792–2800 CrossRef PubMed.
- N. E. de Jesús-González, A. Pérez de la Luz, J. López-Lemus and J. Alejandre, J. Chem. Eng. Data, 2018, 63, 1170–1179 CrossRef.
- E. J. Maginn, J. Phys.: Condens. Matter, 2009, 21, 373101 CrossRef CAS PubMed.
- V. Kempter and B. Kirchner, J. Mol. Struct., 2010, 972, 22–34 CrossRef CAS.
- C. Krekeler, J. Schmidt, Y. Y. Zhao, B. Qiao, R. Berger, C. Holm and L. D. Site, J. Chem. Phys., 2008, 129, 174503 CrossRef PubMed.
- F. Dommert, J. Schmidt, B. Qiao, Y. Zhao, C. Krekeler, L. D. Site, R. Berger and C. Holm, J. Chem. Phys., 2008, 129, 224501 CrossRef PubMed.
- T. Köddermann, K. Fumino, R. Ludwing, J. N. Canongia Lopes and A. A. H. Pádua, ChemPhysChem, 2009, 10, 1181–1186 CrossRef PubMed.
- J. N. Canongia Lopes and A. A. H. Pádua, Theor. Chem. Acc., 2012, 131, 1129 Search PubMed.
- S. Hernández-Ríos, J. Sánchez-Badillo, M. Gallo, P. López-Albarran, J. Gaspar-Armenta and R. González-García, J. Mol. Liq., 2017, 244, 422–432 CrossRef.
- T. I. Morrow and E. J. Maginn, J. Phys. Chem. B, 2002, 106, 12807–12813 CrossRef CAS.
- Z. Liu, S. Huang and W. Wang, J. Phys. Chem. B, 2004, 108, 12978–12989 CrossRef CAS.
- S. Tsuzuki, W. Shinoda, H. Saito, M. Mikami, H. Tokuda and M. Watanabe, J. Phys. Chem. B, 2009, 113, 10641–10649 CrossRef CAS PubMed.
- S. V. Sambasivarao and O. Avecedo, J. Chem. Theory Comput., 2009, 5, 1038–1050 CrossRef CAS PubMed.
- X. Zhong, Z. Liu and D. Cao, J. Phys. Chem. B, 2011, 115, 10027–10040 CrossRef CAS PubMed.
- S. M. Urahata and M. C. C. Ribeiro, J. Chem. Phys., 2004, 120, 1855–1863 CrossRef CAS PubMed.
- Z. Liu, X. Wu and W. Wang, Phys. Chem. Chem. Phys., 2006, 8, 1096–1104 RSC.
- N. Rai and E. J. Maginn, J. Phys. Chem. Lett., 2011, 2, 1439–1443 CrossRef CAS.
- K. S. Rane and J. R. Errington, J. Phys. Chem. B, 2014, 118, 8734–8743 CrossRef CAS PubMed.
- N. Rai and E. J. Maginn, Faraday Discuss., 2012, 154, 53–69 RSC.
- J. O. Valderrama and R. E. Rojas, Ind. Eng. Chem. Res., 2009, 48, 6890–6900 CrossRef CAS.
- J. O. Valderrama and P. A. Robles, Ind. Eng. Chem. Res., 2007, 46, 1338–1344 CrossRef CAS.
- D.-W. Fang, F. Zhang, R. Jia, W.-J. Shan, L.-X. Xia and J.-Z. Yang, RSC Adv., 2017, 7, 11616–11625 RSC.
- V. H. Jadhav, H.-J. Jeong, S. T. Lim, M.-H. Sohn and D. W. Kim, Org. Lett., 2011, 13, 2502–2505 CrossRef CAS PubMed.
- J. R. Pliego Jr, J. Mol. Liq., 2017, 237, 157–163 CrossRef.
- F. D'Anna, S. La Marca and R. Noto, J. Org. Chem., 2008, 73, 3397–3403 CrossRef PubMed.
- A. D. Miranda, M. Gallo, J. M. Domínguez, J. Sánchez-Badillo and R. Martínez-Palou, J. Mol. Liq., 2019, 779–793 CrossRef CAS.
- V. C. Weiss, J. Mol. Liq., 2015, 209, 745–752 CrossRef CAS.
- L. P. N. Rebelo, J. N. Canongia Lopes, J. M. S. S. Esperanza and E. Filipe, J. Phys. Chem. B, 2005, 109, 6040–6043 CrossRef CAS PubMed.
- H. Tokuda, S. Tsuzuki, M. A. B. H. Susan, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 19593–19600 CrossRef CAS.
- H. Tokuda, K. Hayamizu, K. Ishii, M. A. B. H. Susan and M. Watanabe, J. Phys. Chem. B, 2004, 108, 16593–16600 CrossRef CAS.
- J. Jacquemin, P. Husson, A. A. H. Padua and V. Majer, Green Chem., 2006, 8, 172–180 RSC.
- J. G. Huddleston, A. E. Visser, W. M. Reichert, H. D. Willauer, G. A. Broker and R. D. Rogers, Green Chem., 2001, 3, 156–164 RSC.
- W. Li, Z. Zhang, B. Han, S. Hu, Y. Xie and G. Yang, J. Phys. Chem. B, 2007, 111, 6452–6456 CrossRef CAS.
- J. Picálek and J. Kolafa, Mol. Simul., 2009, 35, 685–690 CrossRef.
- D. Tomida, S. Kenmochi, T. Tsukada, K. Qiao and C. Yokoyama, Int. J. Thermophys., 2007, 28, 1147–1160 CrossRef CAS.
- C. A. Nieto de Castro, M. J. V. Lourenco, A. P. C. Ribeiro, E. Langa and S. I. C. Vieira, J. Chem. Eng. Data, 2010, 55, 653–661 CrossRef CAS.
- Y. Zhao, Y. Zhen, B. P. Jelle and T. Boström, J. Therm. Anal. Calorim., 2017, 128, 279–288 CrossRef CAS.
- Q.-L. Chen, K.-J. Wu and C.-H. He, Ind. Eng. Chem. Res., 2014, 53, 7224–7232 CrossRef CAS.
- D. Tomida, S. Kenmochi, T. Tsukada and C. Yokayama, Heat Tran. Asian Res., 2007, 36, 361–372 CrossRef.
- M. E. van Valkenburg, R. L. Vaughn, M. Williams and J. S. Wilkes, Thermochim. Acta, 2005, 425, 181–188 CrossRef CAS.
- A. Stark, A. W. Zidell, J. W. Russo and M. M. Hoffman, J. Chem. Eng. Data, 2012, 57, 3330–3339 CrossRef CAS.
- M. Vranes, S. Dozic, V. Djeric and S. Gadzuric, J. Chem. Eng. Data, 2012, 57, 1072–1077 CrossRef CAS.
- M. Vranes, N. Zec, A. Tot, S. Papovic, S. Dozic and S. Gadzuric, J. Chem. Thermodyn., 2014, 68, 98–108 CrossRef CAS.
- H. Liu, E. Maginn, A. E. Visser, N. J. Bridges and E. B. Fox, Ind. Eng. Chem. Res., 2012, 51, 7242–7254 CrossRef CAS.
- E. G. Blanco-Díaz, E. O. Castrejón-González, J. F. J. Alvarado, A. Estrada-Baltazar and F. Castillo-Borja, J. Mol. Liq., 2017, 242, 265–271 CrossRef.
- R. Ge, C. Hardacre, P. Nancarrow and D. W. Rooney, J. Chem. Eng. Data, 2007, 52, 1819–1823 CrossRef CAS.
- J. M. Crosthwaite, M. J. Muldoon, J. K. Dixon, J. L. Anderson and J. F. Brennecke, J. Chem. Thermodyn., 2005, 37, 559–568 CrossRef CAS.
- P. N. Tshibangu, S. N. Ndwandwe and E. D. Dikio, Int. J. Electrochem. Sci., 2011, 6, 2201–2213 CAS.
- W. Liu, L. Cheng, Y. Zhang, H. Wang and M. Yu, J. Mol. Liq., 2008, 140, 68–72 CrossRef CAS.
- K.-S. Kim, B.-K. Shin and H. Lee, Korean J. Chem. Eng., 2004, 21, 1010–1014 CrossRef CAS.
- A. O. Seyedlar, S. Stapf and C. Mattea, J. Phys. Chem. B, 2017, 121, 5363–5373 CrossRef PubMed.
- B. Aoun, M. A. González, M. Russina, D. L. Price and M.-L. Saboungi, J. Phys. Soc. Jpn., 2013, 82, SA002 CrossRef.
- M. Kohagen, M. Brehm, Y. Lingscheid, R. Giernoth, J. Sangoro, F. Kremer, S. Naumov, C. Iacob, J. Kärger, R. Valiullin and B. Kirchner, J. Phys. Chem. B, 2011, 115, 15280–15288 CrossRef CAS PubMed.
- B. Hess, J. Chem. Phys., 2002, 116, 209–217 CrossRef CAS.
- E. J. Maginn, Acc. Chem. Res., 2007, 40, 1200–1207 CrossRef CAS PubMed.
- M. H. Kowsari, S. Alavi, M. Ashrafizaadeh and B. Najafi, J. Chem. Phys., 2009, 130, 014703 CrossRef CAS.
- C. Rey-Castro and L. F. Vega, J. Phys. Chem. B, 2006, 110, 14426–14435 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS.
- K. R. Ramya, P. Kumar and A. Venkatnathan, J. Phys. Chem. B, 2015, 119, 14800–14806 CrossRef CAS.
- K. Fumino, A. Wulf and R. Ludwig, Angew. Chem., Int. Ed., 2008, 47, 8731–8734 CrossRef CAS PubMed.
- M. Chen, R. Pendrill, G. Widmalm, J. W. Brady and J. Wohlert, J. Chem. Theory Comput., 2014, 10, 4465–4479 CrossRef CAS PubMed.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. B, 2012, 116, 10036–10048 CrossRef CAS PubMed.
- Z. I. Zaripov, F. M. Gumerov, V. F. Khairutdinov, M. Musial, E. Zorebski, M. Dzida and I. M. Abdulagatov, Fluid Phase Equilib., 2019, 485, 135–145 CrossRef CAS.
- Y. U. Paulechka, J. Phys. Chem. Ref. Data, 2010, 39, 033108 CrossRef.
- F. Müller-Plathe, J. Chem. Phys., 1997, 106, 6082–6085 CrossRef.
- C. M. Tenney, M. Massel, J. M. Mayes, M. Sen, J. F. Brennecke and E. J. Maginn, J. Chem. Eng. Data, 2014, 59, 391–399 CrossRef CAS.
- P. J. Carvhalho, V. H. Álvares, B. Schröder, A. M. Gil, I. M. Marrucho, M. Aznar, L. M. N. B. F. Santos and J. A. P. Coutinho, J. Phys. Chem. B, 2009, 113, 6803–6812 CrossRef PubMed.
- A. Yokozeki, M. B. Shiflett, C. P. Junk, L. M. Grieco and T. Foo, J. Phys. Chem. B, 2008, 112, 16654–16663 CrossRef CAS PubMed.
- X. Hu, C. Ngwa and Q. Zheng, Curr. Org. Synth., 2016, 13, 101–110 CrossRef CAS.
- A. Zare, A. Hasaninejad, A. Parhami, A. R. Moosavi-Zare, F. Khedri, E. Parsaee, M. Abdolalipoor-Saretoli, M. Khedri, M. Roshankar and H. Deisi, J. Serb. Chem. Soc., 2010, 75, 1315–1324 CrossRef CAS.
- C. Li, J. Zhang, C. Zhao, L. Yang, W. Zhao, H. Jiang, X. Ren, W. Su, Y. Li and J. Guan, R. Soc. Open Sci., 2018, 5, 180133 CrossRef.
- J. Alejandre, J. L. Rivera, M. A. Mora and V. de la Garza, J. Phys. Chem. B, 2000, 104, 1332–1337 CrossRef CAS.
- J. Alejandre, D. J. Tildesley and G. A. Chapela, J. Chem. Phys., 1995, 102, 4574–4583 CrossRef CAS.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, Software X, 2015, 1–2, 19–25 Search PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8592 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10090–10092 CrossRef.
- G. Bussi, D. Donadio and M. Parrinnello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- L. Zhao, X. Wang, L. Wang and H. Sun, Fluid Phase Equilib., 2007, 260, 212–217 CrossRef CAS.
- L. Zhao, T. Cheng and H. Sun, J. Chem. Phys., 2008, 129, 144501 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Brehm and B. Kirchner, J. Chem. Inf. Model., 2011, 51, 2007–2023 CrossRef CAS PubMed.
- A. R. Leach, Computer Simulation Methods, in Molecular Modelling Principles and Applications, Prentice Hall, 2nd edn, New York, 2001, pp. 303–352 Search PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef.
- M. Parrinello and A. Rahman, Appl. Phys., 1981, 52, 7182–7190 CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. R. Shirts, C. Klein, J. M. Swails, J. Yin, M. K. Gilson, D. L. Mobley, D. A. Case and E. D. Zhong, J. Comput.-Aided Mol. Des., 2017, 31, 147–161 CrossRef CAS.
- R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2014, 16, 3238–3253 RSC.
- E. I. Izgorodina and D. R. MacFarlane, J. Phys. Chem. B, 2011, 115, 14659–14667 CrossRef CAS PubMed.
- B. Jeziorski, R. Moszynsli and K. Szalewicz, Chem. Rev., 1994, 94, 1887–1930 CrossRef CAS.
- T.-H. Tang, E. Deretey, S. J. K. Jensen and I. G. Csizmadia, Eur. Phys. J. D, 2006, 37, 217–222 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Kainan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
- J. Contreras-García, R. A. Boto, F. Izquierdo-Ruiz, I. Reva, T. Woller and M. Alonso, Theor. Chem. Acc., 2016, 135, 242 Search PubMed.
- Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian09, Wallingford CT, Gaussian, Inc., 2009 Search PubMed.
- J. M. C. Marques, J. L. Llanio-Trujillo, M. Albertí, A. Aguilar and F. Pirani, J. Phys. Chem. A, 2013, 117, 8043–8053 CrossRef CAS PubMed.
- L. Vega, E. de Miguel, L. F. Rull, G. Jackson and I. A. McLure, J. Chem. Phys., 1992, 96, 2296–2305 CrossRef CAS.
- Y. Song and L. L. Dai, Mol. Simul., 2010, 36, 560–567 CrossRef CAS.
- J. Qu, J. J. Truhan, S. Dai, H. Luo and P. J. Blau, Tribol. Lett., 2006, 22, 207–214 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02058f |
| This journal is © The Royal Society of Chemistry 2019 |