Open Access Article
Open Access ArticleMicrowave absorption enhancement by adjusting reactant ratios and filler contents based on 1D K–MnO2@PDA and poly(vinylidene fluoride) matrix†
Shu-Qing Lva,
Wei Xubc,
Wujisiguleng Huanga,
Guo-Cheng Lv*b and
Guang-Sheng Wang *c
*c
aSchool of Civil Engineering, Northeast Dianli University, Jilin 132012, PR China
bSchool of Materials Science and Technology, China University of Geosciences, Beijing, 100083, PR China. E-mail: guochenglv@cugb.edu.cn
cSchool of Chemistry, Beihang University, Beijing 100191, PR China. E-mail: wanggsh@buaa.edu.cn
First published on 29th April 2019
Abstract
One-dimensional K–MnO2 nanorods were prepared by a wet chemical process. Dopamine hydrochloride (PDA) layers with various thicknesses were coated and finally, the composites were filled in a poly(vinylidene fluoride) (PVDF) matrix using the hot-molding procedure. The complex permittivity and permeability of the K–MnO2@PDA/PVDF composites could be adjusted by reactant amount ratios and filler contents. The minimum reflection loss could reach −49.4 dB and an effective absorption bandwidth (<−10 dB) covering 11.12 GHz was achieved with 20% filler content when the reactant amount ratio between K–MnO2 and PDA was 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375, which was derived from effective internal polarization processes. It is expected that these novel composites can be used as high-performance microwave absorbers.
0.375, which was derived from effective internal polarization processes. It is expected that these novel composites can be used as high-performance microwave absorbers.
Introduction
Due to the extensive use of electromagnetic waves in the GHz frequency range employed in electronic instruments and in telecommunication and related technologies in recent years, the materials of electromagnetic (EM) interference attenuation have attracted increasing attention owing to their clear use in eliminating undesirable EM radiation.1,2 Compared to the research on conventional metals, many researches have been devoted to develop high-performance microwave absorption materials in the submicron or nanometer scales with the advantages of strong absorption, a wide absorption bandwidth, thinness, and lightweight to block harmful EM waves and convert EM energy into thermal energy through internal loss.3–6Until now, diverse structures such as hollow,7,8 porous,9 foamed,10 core–shell11 and yolk–shell12 structures have been investigated to achieve high-performance absorption. Among them, the synthesis of one-dimensional (1D) nanomaterials is an effective way to improve electromagnetic performance.13–15 The large anisotropy of 1D nanomaterials may overcome the drawbacks of low permeability values at a high frequency due to the Snoek's limit,16 which can greatly enhance the electromagnetic properties. Recent research has demonstrated that the absorbers with 1D nanostructures can achieve better absorption performance. For instance, Fe nanochains were prepared by Zhan et al. using a chemical route,17 and the products achieved minimum reflection loss of −20.4 dB for a thickness of 2 mm. Yan et al.18 reported Fe3O4 nanowires fabricated via an NaAc-assisted coprecipitation method that achieved a minimum reflection loss of −16.67 dB at 8.32 GHz.
Moreover, MnO2 has gained wide attention in the field of shielding and absorption in the microwave band range due to its distinctive physical and chemical properties.19–22 The structure of K–MnO2 is constructed from edge-sharing double chains of MnO6 octahedra, forming a 2 × 2 tunnel structure that can allow potassium insertion, improving its dielectric properties.23,24
Herein, we report a binary composite synthesized simply by 1D K–MnO2 nanorods and polydopamine (PDA). The microwave absorption properties of the composite were researched systematically and showed a large absorption bandwidth in the GHz range. Therefore, this composite with a unique structure is a promising candidate for high-performance microwave absorption.
Experimental section
Preparation of K–MnO2 nanorods
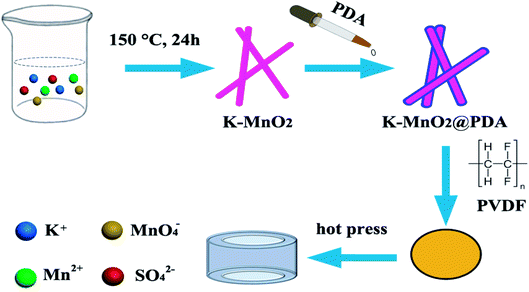
The K–MnO2 nanorods were prepared by a hydrothermal method as outlined in our previous work.25 Briefly, 0.01 mol KMnO4 and 0.015 mol MnSO4·H2O were dissolved in 50 mL water with vigorous stirring at room temperature for 30 min. The dark brown precipitates were transferred into a Teflon-lined stainless autoclave after aging and kept at 150 °C for 24 h. After the reaction, the precipitates were centrifuged, washed, and dried for further characterization.Preparation of K–MnO2@PDA nanofibers
The as-prepared K–MnO2 nanorods (40 mg) were dispersed into 100 mL Tris buffer aqueous solution (2 mg mL−1, pH 8.5) followed by the addition of dopamine hydrochloride (30 mg). After that, the reaction solution was stirred gently at room temperature for 20 min to form a uniform PDA coating. The K–MnO2@PDA nanofibers were obtained by centrifugation and washed with deionized water. Meanwhile, samples were also prepared with 0, 3.75, 7.5, and 15 mg dopamine hydrochloride addition.Preparation of K–MnO2@PDA/PVDF nanocomposites
The desired amount of PVDF was dispersed in 25 mL of N,N-dimethylformamide (DMF) with magnetic stirring at room temperature for 30 min. Various amounts of K–MnO2@PDA nanofibers were added and the solution became transparent. After stirring and ultrasonication for 1 h, the mixture was poured onto a glass plate to form a thin film and dried at 60 °C for 5 h. The dried mixture was pressed into cylinder-shaped samples (Φout = 7.00 mm and Φin = 3.04 mm) by hot pressing at 210 °C (Scheme 1). In the range of 2–18 GHz and with the coaxial wire method, we measured the complex permittivity and permeability values.Physicochemical characterization of samples
The morphology and size of the K–MnO2 nanorods and K–MnO2@PDA nanofibers were examined using field emission scanning electron microscopy (FESEM, JSM-6700F) and high-resolution transmission electron microscopy (HR-TEM, JEOL JEM-2010F). Powder diffraction data were collected using an X-ray diffractometer (XRD, Philips X'Pert Pro Super). Thermogravimetric analysis (TG) was performed in N2 using a Pyris Diamond TG analyzer (PerkinElmer Inc., USA). The samples were heated from 30 °C to 800 °C at a heating rate of 5 °C min−1. The EM parameters were measured using a two-port vector network analyzer (Agilent E5071C).Results and discussion
The structural characterizations of K–MnO2 and K–MnO2@PDA were carried out by SEM and TEM. The typical images of the samples display nanorod and nanofiber morphologies with diameters of about 30–50 nm and lengths of 0.5–5 μm. The typical powder XRD patterns of the as-synthesized products are shown in Fig. 1(e). It can be concluded that the diffraction peaks are uniquely indexed to the pure tetragonal phase of K–MnO2 (JCPDS No. 42-1348) and no characteristic peaks for impurities are observed, suggesting its high purity and crystallinity. The strong diffraction peaks for K–MnO2 and K–MnO2@PDA are almost coincident; however, the intensities decrease due to the outer layer amorphous PDA. As shown in Fig. 1(f), the TG curve of K–MnO2 exhibits three characteristic stepwise weight losses. The slight mass loss below 250 °C results from the loss of absorbed water and surface-related water. The rapid mass loss between 250 °C and 700 °C may be attributed to the loss of the water bound inside the 2 × 2 tunnels, the internal structural water and oxygen atoms on the surfaces; this indicates that the octahedral bond of MnO6 begins to break and the tunnel structure also collapses to a certain extent. The evolution of the lattice oxygen is likely the reason for the final mass loss, which may lead to a phase change. On the basis of the weight loss rate, the amount of PDA in the composites is determined to be about 20 wt%. Moreover, we can observe from Fig. 2 that different PDA coating thicknesses can be achieved by controlling the reactant amount ratios, leading to the adjustment of the impedance matching condition by balancing the complex permittivity and permeability.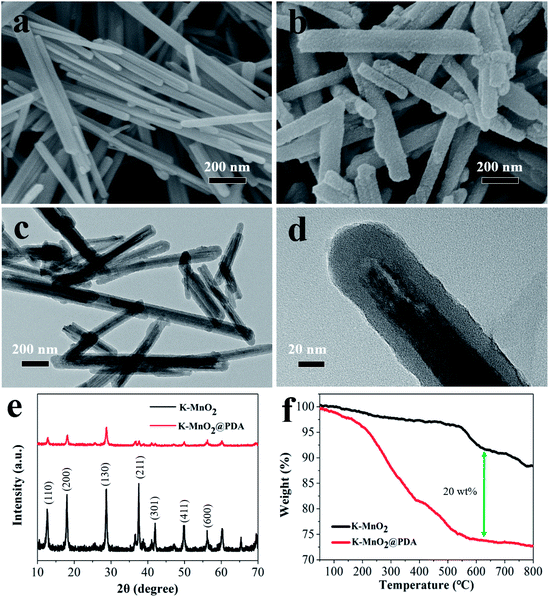 | ||
| Fig. 1 SEM images of (a) K–MnO2 nanorods and (b) K–MnO2@PDA nanofibers. TEM images of (c and d) K–MnO2@PDA, (e) XRD patterns and (f) TG curves. | ||
 | ||
Fig. 2 TEM images of K–MnO2@PDA nanofibers with various reactant amount ratios of (a) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, (b) 4 3, (b) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, (c) 4 1.5, (c) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.75, (d) 4 0.75, (d) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375. 0.375. | ||
To investigate the electromagnetic wave absorption properties of K–MnO2 nanorods and K–MnO2@PDA nanofibers, products with various reactant amount ratios were blended with PVDF to form composites via a hot-press process. The frequency dependences relative permittivity and permeability, dielectric loss, and magnetic loss for several samples are shown in Fig. S1.† The real part of permittivity (ε′) and real permeability (μ′) represent the storage capability of the electric and magnetic energies, whereas imaginary permittivity (ε′′) and imaginary permeability (μ′′) are related to the dissipation of energy and magnetic loss, respectively.26,27 It is worth mentioning that the values of ε′ and ε′′ tend to decrease after gradual increase in the amounts of PDA. Negative values of μ′′ appear in the high frequency range, which may be caused by the electromagnetic field-induced eddy current, suggesting that the magnetic energy is radiated out.28
The reflection loss (RL) values can be calculated according to the measured relative permittivity and permeability for a given frequency range and layer thickness based on the transmission line theory using the following equation:29,30
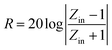 | (1) |
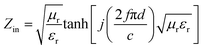 | (2) |
Fig. 3 shows the RL curves and corresponding color versions of the five samples with different ratios at layer thickness of 2.0–5.0 mm in the range of 2–18 GHz. It is well-known that the key factors for measuring the absorption properties of a material are mainly the RL values and effective frequency bandwidth (RL < −10 dB). We can observe that the reactant amount ratios have an important influence on the absorption properties. Compared with other amount ratios, for 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375 of reactants, the minimum RL value can reach −49.4 dB at 12.56 GHz with a low layer thickness of 2.0 mm; the effective frequency bandwidth is from 10.96 to 14.8 GHz (3.84 GHz). Meanwhile, at layer thickness of 2.0–5.0 mm, the bandwidth is from 3.68 to 14.8 GHz (11.12 GHz), which is more than half of the test bandwidth.
0.375 of reactants, the minimum RL value can reach −49.4 dB at 12.56 GHz with a low layer thickness of 2.0 mm; the effective frequency bandwidth is from 10.96 to 14.8 GHz (3.84 GHz). Meanwhile, at layer thickness of 2.0–5.0 mm, the bandwidth is from 3.68 to 14.8 GHz (11.12 GHz), which is more than half of the test bandwidth.
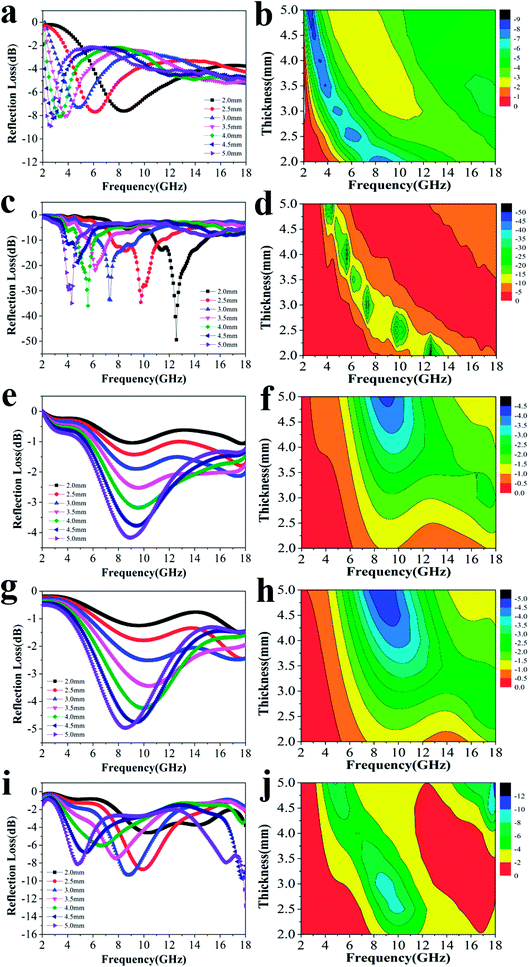 | ||
Fig. 3 The RL curves for nanofibers with various reactant amount ratios of (a) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, (c) 4 0, (c) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375, (e) 4 0.375, (e) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.75, (g) 4 0.75, (g) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, (i) 4 1.5, (i) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 and the corresponding color filled versions of RL (b, d, f, h, j). 3 and the corresponding color filled versions of RL (b, d, f, h, j). | ||
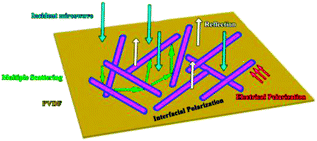
As a typical kind of dielectric and multi-interfacial material, the dielectric loss mechanism of K–MnO2@PDA/PVDF is mainly attributed to polarization processes such as electrical polarization, interfacial polarization, and multiple scattering. Each polarization process results in a profound effect on the loss of energy. At a low frequency, the Debye dipolar relaxation is the main cause of dielectric loss in the composites.31 On the basis of the Debye theory, ε′ and ε′′ can be described as follows:32,33
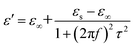 | (3) |
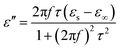 | (4) |
According to the above-mentioned information, the relationship between ε′ and ε′′ can be described as follows:34
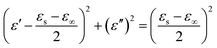 | (5) |
Thus, the plot of ε′ versus ε′′ would be a single semicircle, which is generally denoted as the Cole–Cole semicircle. Each semicircle corresponds to an effective Debye dipolar relaxation process.35 It can be observed that Fig. S2c† exhibits the most semicircles among all. This confirms that K–MnO2@PDA with a reactant ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375 has the most excellent microwave absorption properties.
0.375 has the most excellent microwave absorption properties.
To explore the absorption properties for different loadings, we also tested four samples with 5%, 10%, 20%, and 30% filler contents at a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375, and their RL values are presented in Fig. 4. Except for the observations for 20% filler content, the absorption properties for other three filler contents were also favorable as a whole. The minimum RL values and effective frequency bandwidths for 5%, 10%, and 30% filler contents over 2–18 GHz were −11.4 dB, 4.96 GHz; −18.9 dB, 12.64 GHz and −20.9 dB, 7.76 GHz, respectively. Furthermore, Fig. S4† displays that all the ε′ and ε′′ values increase dramatically after the introduction of more fillers, indicating that the composite can significantly improve the polarization ability and the dielectric-loss capability. Additionally, all the ε′ curves show a decreasing trend with increasing frequency, which is indicative of a frequency dispersion behavior. This can be explained by the increased lag in polarization with respect to the electric-field change at a higher frequency.36 This decreasing trend also occurs in the case of ε′′ (Scheme 2).
0.375, and their RL values are presented in Fig. 4. Except for the observations for 20% filler content, the absorption properties for other three filler contents were also favorable as a whole. The minimum RL values and effective frequency bandwidths for 5%, 10%, and 30% filler contents over 2–18 GHz were −11.4 dB, 4.96 GHz; −18.9 dB, 12.64 GHz and −20.9 dB, 7.76 GHz, respectively. Furthermore, Fig. S4† displays that all the ε′ and ε′′ values increase dramatically after the introduction of more fillers, indicating that the composite can significantly improve the polarization ability and the dielectric-loss capability. Additionally, all the ε′ curves show a decreasing trend with increasing frequency, which is indicative of a frequency dispersion behavior. This can be explained by the increased lag in polarization with respect to the electric-field change at a higher frequency.36 This decreasing trend also occurs in the case of ε′′ (Scheme 2).
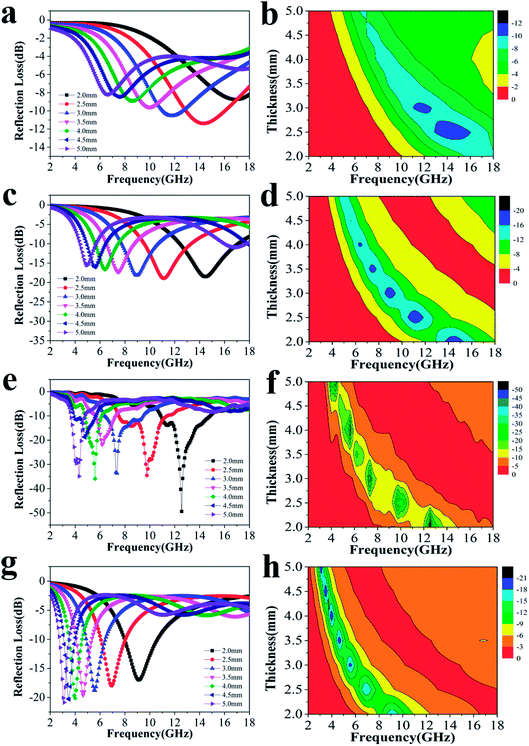 | ||
| Fig. 4 The RL curves for nanofibers with (a) 5%, (c) 10%, (e) 20%, (g) 30% filler contents with thicknesses of 2.0–5.0 mm, and the corresponding color filled versions of RL (b, d, f, h). | ||
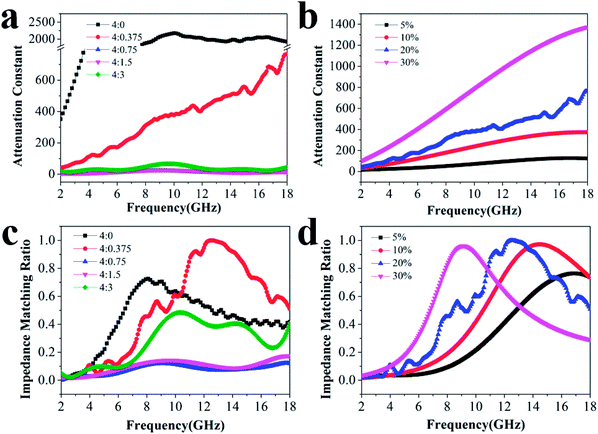
The attenuation constant α determines the attenuation properties of materials and can be expressed as follows:37
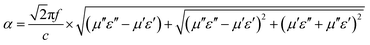 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375 moves closer to 1.0. The sample with 20% filler content also presents a moderate ratio compared to the others, revealing that microwaves are effectively reduced after entering the absorber.
0.375 moves closer to 1.0. The sample with 20% filler content also presents a moderate ratio compared to the others, revealing that microwaves are effectively reduced after entering the absorber.
Conclusions
In summary, K–MnO2@PDA composites with various coating thicknesses were synthesized successfully by adjusting the reactant amount ratios. The hybrid showed excellent absorption strength with a maximum absorption peak of −49.4 dB and an effective absorption bandwidth of 11.12 GHz with 20% filler content when the reactant amount ratio was 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375. The microwave absorption properties of the composites with different filler contents (5%, 10%, 20%, and 30%) at a reactant ratio of 4
0.375. The microwave absorption properties of the composites with different filler contents (5%, 10%, 20%, and 30%) at a reactant ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.375 were also researched in detail. The above results verified that the hybrids can achieve considerable electromagnetic wave absorption performance. This was attributed to the internal polarization process resulting from the successful regulation of reactant amount ratios and filler loading. It is believed that K–MnO2@PDA has great potential for use in the microwave absorption application field.
0.375 were also researched in detail. The above results verified that the hybrids can achieve considerable electromagnetic wave absorption performance. This was attributed to the internal polarization process resulting from the successful regulation of reactant amount ratios and filler loading. It is believed that K–MnO2@PDA has great potential for use in the microwave absorption application field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 51472012), the Fundamental Research Funds for the Central Universities.Notes and references
- X.-M. Meng, X.-J. Zhang, C. Lu, Y.-F. Pan and G.-S. Wang, J. Mater. Chem. A, 2014, 2, 18725–18730 RSC.
- Y.-F. Pan, G.-S. Wang, L. Liu, L. Guo and S.-H. Yu, Nano Res., 2017, 10, 284–294 CrossRef CAS.
- J. Feng, F. Pu, Z. Li, X. Li, X. Hu and J. Bai, Carbon, 2016, 104, 214–225 CrossRef CAS.
- X. Li, J. Feng, H. Zhu, C. Qu, J. Bai and X. Zheng, RSC Adv., 2014, 4, 33619–33625 RSC.
- Y. Sun, J. Zhang, Y. Zong, X. Deng, H. Zhao, J. Feng, M. He, X. Li, Y. Peng and X. Zheng, ACS Appl. Mater. Interfaces, 2019, 11, 6374–6383 CrossRef CAS PubMed.
- X. Zheng, J. Feng, Y. Zong, H. Miao, X. Hu, J. Bai and X. Li, J. Mater. Chem. C, 2015, 3, 4452–4463 RSC.
- X.-J. Zhang, J.-Q. Zhu, P.-G. Yin, A.-P. Guo, A.-P. Huang, L. Guo and G.-S. Wang, Adv. Funct. Mater., 2018, 28, 1800761 CrossRef.
- G. Wang, Z. Gao, S. Tang, C. Chen, F. Duan, S. Zhao, S. Lin, Y. Feng, L. Zhou and Y. Qin, ACS Nano, 2012, 6, 11009–11017 CrossRef CAS PubMed.
- F. Ye, Q. Song, Z. Zhang, W. Li, S. Zhang, X. Yin, Y. Zhou, H. Tao, Y. Liu, L. Cheng, L. Zhang and H. Li, Adv. Funct. Mater., 2018, 28, 1707205 CrossRef.
- Y. Zhang, Y. Huang, T. Zhang, H. Chang, P. Xiao, H. Chen, Z. Huang and Y. Chen, Adv. Mater., 2015, 27, 2049–2053 CrossRef CAS PubMed.
- Q. Liu, Q. Cao, H. Bi, C. Liang, K. Yuan, W. She, Y. Yang and R. Che, Adv. Mater., 2016, 28, 486–490 CrossRef CAS PubMed.
- J. Liu, J. Cheng, R. Che, J. Xu, M. Liu and Z. Liu, J. Phys. Chem. C, 2013, 117, 489–495 CrossRef CAS.
- X. Liu, Y. Chen, X. Cui, M. Zeng, R. Yu and G.-S. Wang, J. Mater. Chem. A, 2015, 3, 12197–12204 RSC.
- S.-Q. Lv, Y.-F. Pan, P.-B. Yang and G.-S. Wang, RSC Adv., 2016, 6, 55546–55551 RSC.
- W. Xu, Y.-F. Pan, W. Wei, G.-S. Wang and P. Qu, Appl. Surf. Sci., 2018, 428, 54–60 CrossRef CAS.
- G. Chai, D. Xue, X. Fan, X. Li and D. Guo, Appl. Phys. Lett., 2008, 93, 152516 CrossRef.
- X. Zhan, H. Tang, Y. Du, A. Talbi, J. Zha and J. He, RSC Adv., 2013, 3, 15966–15970 RSC.
- A. Yan, Y. Liu, Y. Liu, X. Li, Z. Lei and P. Liu, Mater. Lett., 2012, 68, 402–405 CrossRef CAS.
- G.-S. Wang, S. He, X. Luo, B. Wen, M.-M. Lu, L. Guo and M.-S. Cao, RSC Adv., 2013, 3, 18009–18015 RSC.
- R. Koivula, J. Pakarinen, M. Sivenius, K. Sirola, R. Harjula and E. Paatero, Sep. Purif. Technol., 2009, 70, 53–57 CrossRef CAS.
- X. Wang, L. Mei, X. Xing, L. Liao, G. Lv, Z. Li and L. Wu, Appl. Catal., B, 2014, 160–161, 211–216 CrossRef CAS.
- J. Tao, K. Song, G. Lv, L. Mei, Z. Li, L. Liao, X. Wang, X. Xing and B. Xu, Mater. Express, 2014, 4, 539–544 CrossRef CAS.
- L. Athouël, P. Arcidiacono, C. Ramirez-Castro, O. Crosnier, C. Hamel, Y. Dandeville, P. Guillemet, Y. Scudeller, D. Guay, D. Bélanger and T. Brousse, Electrochim. Acta, 2012, 86, 268–276 CrossRef.
- L. Kang, M. Zhang, Z.-H. Liu and K. Ooi, Spectrochim. Acta, Part A, 2007, 67, 864–869 CrossRef PubMed.
- W. Xu, G. Lv, X. Xing, X.-J. Zhang and G.-S. Wang, Sci. Adv. Mater., 2016, 8, 966–971 CrossRef CAS.
- X.-J. Zhang, G.-S. Wang, W.-Q. Cao, Y.-Z. Wei, J.-F. Liang, L. Guo and M.-S. Cao, ACS Appl. Mater. Interfaces, 2014, 6, 7471–7478 CrossRef CAS PubMed.
- C. Tian, Y. Du, P. Xu, R. Qiang, Y. Wang, D. Ding, J. Xue, J. Ma, H. Zhao and X. Han, ACS Appl. Mater. Interfaces, 2015, 7, 20090–20099 CrossRef CAS PubMed.
- M. Zhang, G. Zhangzhu, S. Wen, H. Lu, R. Wang, W. Li, S. Ding, A. Ghulam and P. Zheng, Chem. Eng. J., 2018, 345, 345–352 CrossRef CAS.
- X. Jian, B. Wu, Y. Wei, S. X. Dou, X. Wang, W. He and N. Mahmood, ACS Appl. Mater. Interfaces, 2016, 8, 6101–6109 CrossRef CAS PubMed.
- Y.-F. Pan, G.-S. Wang and Y.-H. Yue, RSC Adv., 2015, 5, 71718–71723 RSC.
- M.-S. Cao, W.-L. Song, Z.-L. Hou, B. Wen and J. Yuan, Carbon, 2010, 48, 788–796 CrossRef CAS.
- W. Xu, G.-S. Wang and P.-G. Yin, Carbon, 2018, 139, 759–767 CrossRef CAS.
- H. Yu, T. Wang, B. Wen, M. Lu, Z. Xu, C. Zhu, Y. Chen, X. Xue, C. Sun and M. Cao, J. Mater. Chem., 2012, 22, 21679–21685 RSC.
- G.-S. Wang, X.-J. Zhang, Y.-Z. Wei, S. He, L. Guo and M.-S. Cao, J. Mater. Chem. A, 2013, 1, 7031–7036 RSC.
- S. He, G.-S. Wang, C. Lu, J. Liu, B. Wen, H. Liu, L. Guo and M.-S. Cao, J. Mater. Chem. A, 2013, 1, 4685–4692 RSC.
- H. Wang, Y. Y. Dai, D. Y. Geng, S. Ma, D. Li, J. An, J. He, W. Liu and Z. D. Zhang, Nanoscale, 2015, 7, 17312–17319 RSC.
- D. Ding, Y. Wang, X. Li, R. Qiang, P. Xu, W. Chu, X. Han and Y. Du, Carbon, 2017, 111, 722–732 CrossRef CAS.
- Z. Li, X. Li, Y. Zong, G. Tan, Y. Sun, Y. Lan, M. He, Z. Ren and X. Zheng, Carbon, 2017, 115, 493–502 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra01248f |
| This journal is © The Royal Society of Chemistry 2019 |