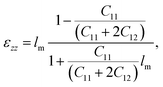Effect of Sb content on anisotropic magnetoresistance in a (Ga, Mn)(As, Sb) ferromagnetic semiconductor thin film

Abstract

The effect of Sb content on the in-plane anisotropic magnetoresistance (AMR) of the quaternary ferromagnetic semiconductor (Ga, Mn)(As, Sb) was investigated. The results showed that the strain increased with Sb content, but the hole density was found to fluctuate. Dominant cubic and uniaxial symmetries were observed for the current along the [110] crystalline direction. The dependence of the symmetry on the Sb content was demonstrated for the longitudinal AMR, which mainly results from the alteration of the local stain relaxation and the hole density. A phenomenological analysis showed that the variation of the AMR coefficients is a good explanation for the observed experimental results.

---

Introduction

The hole-mediated ferromagnetism occurring in the diluted magnetic semiconductor (DMS) (Ga, Mn)As offers the possibility of controlling its magnetic properties, e.g., the magnetic transport properties,^1–4 the magnetic anisotropy (ref. 5–10) and the anisotropic magnetoresistance (AMR).^11–13 In particular, DMSs are suitable materials for the study of AMR due to the sensitivity of AMR to the carrier concentration and strain. The crystalline AMR in (Ga, Mn)As depends on two factors: the current direction and the angle between the magnetization and the crystalline axes.¹³ However, most studies on the AMR of DMS materials mainly focused on ternary alloys. Recent reports have shown that quaternary DMSs, such as (In, Ga, Mn)As and (Ga, Mn)(As, P), offer a new degree of freedom to control the fundamental physical properties due to the incorporation of a fourth element.^14–19 For example, the incorporation of P into (Ga, Mn)As layers might reduce the epitaxial strain or even change its direction, resulting in a strong modification of the magnetic anisotropy, in particular, a switching of the magnetic axis from in-plane along 〈110〉 to out-of-plane along [001] in the case of a sufficiently large P concentration.¹⁷ In a previous study we have demonstrated that the incorporation of Sb affects the effective Mn content x_eff as well as the Curie temperature T_C in the quaternary alloy ferromagnetic semiconductor (Ga, Mn)(As, Sb).²⁰

Recently, Howells et al. (ref. 21) reported a noticeable current direction and an anomalous temperature dependence of the AMR in the quaternary alloy ferromagnetic semiconductor (Ga, Mn)(As, Sb), which was attributed to the interplay between the crystalline and noncrystalline AMR components and a crossed AMR term. Their results further suggested that an accurate control of the AMR may be possible by adjusting the alloy composition in the quaternary alloy DMS. In this study, we investigated the effect of the Sb content on the AMR of (Ga, Mn)(As, Sb) quaternary alloy ferromagnetic semiconductor thin films. The Sb content in the thin films affects the lattice constant and the strain, allowing for the tuning of the AMR features of the samples.

Experimentation

A series of (Ga, Mn)(As, Sb) films with a thickness of 100 nm were grown on epiready semi-insulating GaAs (001) substrates by low-temperature molecular-beam epitaxy (LT-MBE). The entire growth process was monitored by in situ reflection high-energy electron diffraction (RHEED), and the substrate temperature was measured by a thermal couple. A 100 nm thick buffer layer of GaAs was first grown on the substrate at 560 °C to smooth the surface of the substrate. The substrate was then cooled to 260 °C for the growth of a 100 nm thick (Ga, Mn)(As, Sb) layer. The Mn/Ga flux ratio and the excess As₄ flux were the same for all samples. The total Mn mass percentage of the films was estimated to 2.5% according to the Mn/Ga flux ratio, and the Sb/As beam equivalent pressure (BEP) ratio σ was selected to 0% (without Sb incorporation), 0.96%, 1.63% and 2.43%, respectively. The growth process has been previously described in detail elsewhere.²⁰

Results and discussion

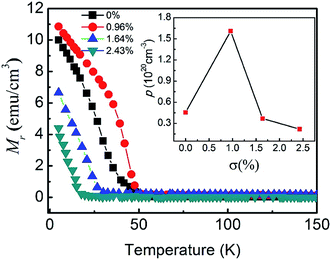
The temperature dependence of the remanent magnetization M_r of the annealed samples after removal of the external magnetic field was measured along the in-plane [11̄0] direction in the range from 5 to 150 K using a superconducting quantum interference device (SQUID), and the results are shown in Fig. 1. The magnetization lies in-plane along a direction determined by a competition between a uniaxial anisotropy favoring the [11̄0] axis and a biaxial anisotropy favoring the in-plane [100] axes, as is typical for III–V DMS films under compressive strain.²² The observed in-plane magnetization can obviously divided into two stages: the first corresponds to uniaxial anisotropy and the second to biaxial anisotropy. The uniaxial and biaxial anisotropy constants vary, respectively, as the square and fourth power of the spontaneous magnetization across the whole temperature range up to T_C, so uniaxial anisotropy is dominant from around 5 K up to the Curie temperature T_C of 50 K, especially for the sample with σ = 0.96%. The hole density p was obtained through conventional Hall measurements at a saturation field above 4 T. The Hall resistances R_xy could be described as the sum of ordinary and anomalous parts as given by R_xy = R₀B_z + R_AM_z, where B_z and M_z are the perpendicular-to-plane components of the magnetic field and the magnetization, respectively. The ordinary Hall coefficient R₀ is given by (1/ped), where e is the elementary electric charge, d is the film thickness, and p is the hole density. We can separate these two parts in high magnetic field because the anomalous Hall resistance will saturate at a certain magnetic field, but the normal Hall resistance has a linear increase. The R₀ is obtained from the slope of the curve when the magnetic field is above 4 T. The values of p can be calculated from R₀, and the results for annealed samples are shown in the inset image in Fig. 1. As the Sb content was increased, the hole density p reached a maximum for the sample with σ = 0.96%, and then drastically decreased. The higher the hole concentration, the higher the amount of substitutional Mn atoms in the film, and the higher the Curie temperature T_C.²³ The observed behavior is consistent with the predictions of the p–d Zener model.⁶

Fig. 1 Temperature dependence of the remanent magnetization M_r after removal of the magnetic field for (Ga, Mn)(As, Sb) films with Sb mass percentages of 0%, 0.96%, 1.64%, and 2.43%, respectively. The inset image shows the hole density p versus the Sb/As BEP ratio σ (in%).

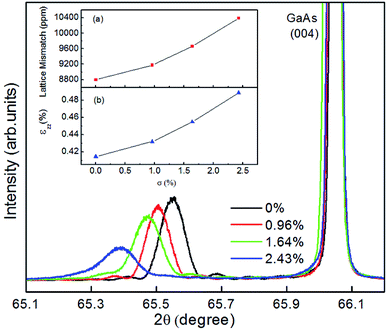
Fig. 2 shows the results of the high-resolution X-ray diffraction (HR-XRD) measurements performed on the four (Ga, Mn)(As, Sb) samples at room temperature. The intensity of the diffraction peak gradually weakens and the half width increases with the increasing of the Sb concentration, which indicates that the crystal quality of the sample is gradually decreasing. The lattice constant was calculated from the position of the (004) peak of the (Ga, Mn)(As, Sb) layer assuming that the layer was fully strained and showed the same elastic constant as GaAs. The strained films are characterized by their substrate-film lattice mismatch l_m = (a_film − a_sub)/a_film,²⁴ where a_sub and a_film are the relaxed lattice constants of the GaAs substrate and the (Ga, Mn)(As, Sb) film, respectively. The results of the calculation are shown in the inset image (a) in Fig. 2. The vertical strain ε_zz can be calculated as follows:¹⁶

where C₁₁ and C₁₂ are the elastic stiffness constants, z is along the direction of growth. As an approximation, the values for GaAs were used for all samples, i.e., C₁₁ = 11.90 × 10¹⁰ Pa and C₁₂ = 5.34 × 10¹⁰ Pa.²⁵ The inset image in Fig. 2(b) shows the variation of ε_zz with the Sb content. Both the lattice mismatch and the vertical strain gradually and monotonically increased. However, a higher Sb content resulted in a significant degradation of the crystal quality, and correspondingly the ferromagnetic behavior of the samples disappeared. In our Sb concentration range, the observed positive ε_zz classifies the annealed (Ga, Mn)(As, Sb) films as typical compressive strain semiconductors. The hole density p, the lattice constants and the strain ε are linked with each other. The variation of the Sb concentration induces competing effects between these properties, which affects the AMR of ferromagnetic (FM) semiconductors.

Fig. 2 Double-crystal XRD patterns obtained for the (Ga, Mn)(As, Sb) films with different values of σ. The inset images (a) and (b) show the lattice mismatch and the vertical strain ε_zz as a function of σ, respectively.

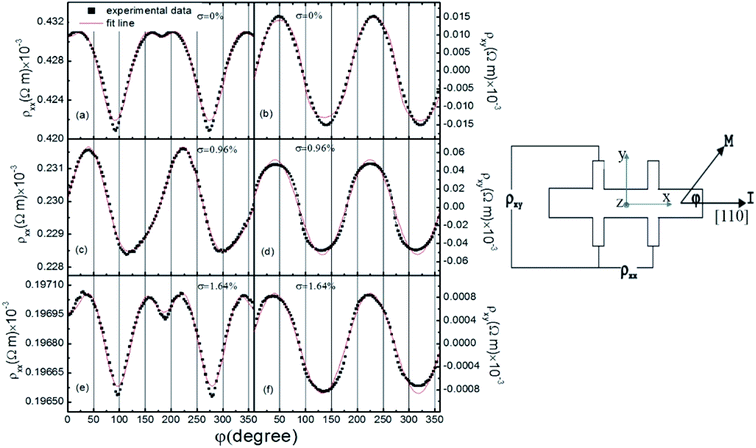
The AMR in the (Ga, Mn)(As, Sb) films with σ = 0%, 0.96% and 1.64% was studied by performing magnetotransport measurements. The sample with σ = 2.43% was not studied because of its poor ferromagnetic behavior. The longitudinal resistance ρ_xx and the transverse or planar Hall DC resistance ρ_xy were recorded by applying the standard four-probe measurement technique using Hall bars at 10 K with a DC current of 10 μA along the [110] direction and a 0.5 T in-plane magnetic field. A schematic diagram of the Hall bar structure is shown in Fig. 3. The angular dependence of the resistance was measured in a superconducting magnet equipped with a rotating sample holder, which allowed to continuously change the angle φ between the magnetic field H and the current I. The sample was rotated around the [001] direction, and thus ρ_xx and ρ_xy varied with φ. The results of the measurements are shown in Fig. 3. Both ρ_xx and ρ_xy were found to oscillate as the sample was rotated, but the observed oscillation periods are different. Whereas the oscillations in ρ_xy can be described using a simple cosine or sine function, which is typical for polycrystalline FM films,¹³ the oscillations in ρ_xx cannot be described this way.

Fig. 3 Dependence of ρ_xx and ρ_xy on the angle φ between H or M and I for an in-plane magnetic field with H = 0.5 T observed for the (Ga, Mn)(As, Sb) samples at T = 10 K. The black and red curves are the measured and fitted results, respectively. And schematic diagram of Hall bar.

Because the 0.5 T magnetic field was large enough to saturate the sample, the magnetization M should be fully aligned with H. The angle between M and I is almost identical to the angle between H and I. Therefore, the AMR of the samples can be described only as a function of the angle φ. The longitudinal and transverse AMR dependence on the angle φ for the (Ga, Mn)(As, Sb) samples with different Sb content are shown in Fig. 4(a) and (b). Usually the longitudinal and transverse AMR is expressed as AMR_xx = (ρ_xx − ρ_av)/ρ_av and AMR_xy = (ρ_xy − ρ_av)/ρ_av, respectively, where ρ_av is the average value of the longitudinal resistivity over 360° in the plane of the film.²¹ In Fig. 4(a), the longitudinal AMR is subject to an oscillation from the obviously dominant cubic to a uniaxial symmetry and then reverts to the cubic symmetry as the Sb content further increases. Unlike the symmetry observed for AMR_xx, the transverse AMR shows a uniaxial symmetry, as shown in Fig. 4(b). However, the greatest AMR_xy was found for the sample with σ = 0.96%. The AMR sharply decreased when σ reached 1.64%. The crystalline terms are generally associated with band warping effects reflecting the underlying crystal symmetry. The cubic symmetry originating from the long-range ferromagnetic phase coincides with the fourfold symmetry of the [001] plane of the zinc blende crystalline structure. The twofold symmetry originates from the alignment of spins with random orientations in single crystals.¹³ Fig. 4(c) shows the longitudinal AMR of the sample with σ = 0.96% for the [110]-oriented Hall bar at various temperatures. Initially, as the temperature increases from 2 K to 10 K, the AMR_xx increases first, and then the AMR_xx is always weakened as the temperature continues to rise from 15 K to 55 K above the T_C temperature, which is due to the reduction in the magnetization on approaching T_C. In the temperature range of 2–55 K, the distribution of Sb in the crystal does not change too much with the increase of temperature, but the mobility of holes will be greatly affected, so the AMR_xx intensity will change accordingly. But its uniaxial symmetry does not change.

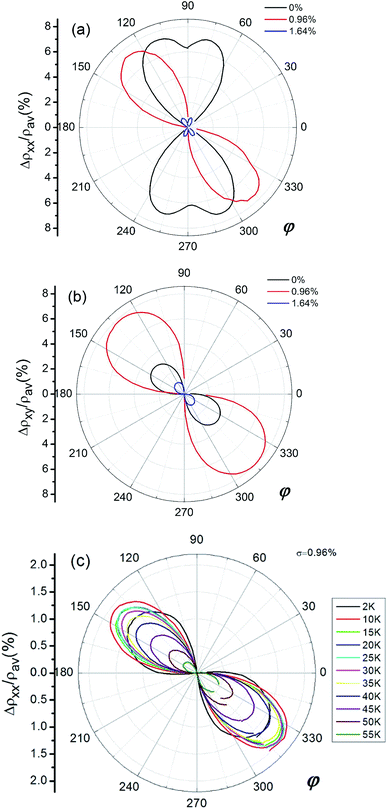Fig. 4 Angle dependence of (a) the longitudinal and (b) the transverse AMR of the (Ga, Mn)(As, Sb) films with different σ. And (c) the temperature dependence of AMR_xx for σ = 0.96%.

The strong sensitivity of the magnetic anisotropy to the epitaxial strain for the (Ga, Mn)As ferromagnetic semiconductor was already pointed out by Ohno et al.¹ Recently, it has been reported that the patterning allows the in-plane compressive strain in the (Ga, Mn)As film to relax in the direction along the width of the bar, which can lead to an additional uniaxial component in the magnetocrystalline anisotropy for bars with widths ≤1 μm.²⁶ In our experiment, the incorporation of Sb results in an increase of the lattice constant and the vertical strain. When the Sb content is increased, both the FM behavior and the crystal quality of the sample decline, and the AMR signal correspondingly weakens. The AMR_xy or the planar Hall resistance show a uniaxial symmetry as previously reported in literature (ref. 13). The strongest AMR signal obtained for the sample with σ = 0.96% corresponds to the sample with the highest hole density. Therefore, the increased strong spin–orbit interaction induced by a homogeneous Sb incorporation may lead to the uniaxial term dominant in AMR_xx for σ = 0.96%.

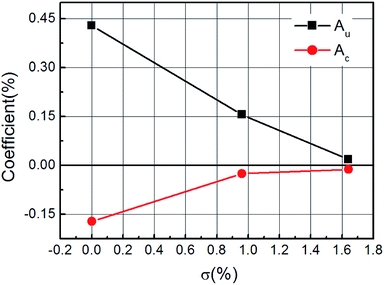
From a phenomenological perspective, the AMR can be written as a sum of a uniaxial term (twofold symmetry) and a cubic crystalline term (fourfold symmetry), and therefore the longitudinal and transverse magnetoresistance can be described by the following equations:¹³

ρ_xx = ρ₀(1 + A_u cos 2φ + A_c cos 4φ) (1)

and

ρ_xy = ρ₁ sin 2φ (2)

where A_u, A_c, ρ₀ and ρ₁ are constants which can be determined by fitting the experimental data. The well-fitted results are presented in Fig. 3, corresponding to the solid lines. The coefficients of the uniaxial term (A_u) and the cubic crystalline term (A_c) were obtained from eqn (1). Fig. 5 shows the variation of the coefficients with σ. For the sample without Sb, A_u = 0.429%, which is about two times the magnitude of A_c (−0.172%). In this case, both components were found to be dominant. In contrast, for σ = 0.96%, A_u = 0.156% and A_c = −0.025%, and therefore AMR_xx is almost exclusively determined by the uniaxial component. As the Sb content increases, all coefficients tend towards zero because of the bad crystal quality of the samples, which is in good agreement with our experimental data.

Fig. 5 The coefficients A_c and A_u of the AMR_xx term versus σ.

In summary, we have investigated the in-plane anisotropic magnetoresistance (AMR) of GaAs-based (Ga, Mn)(As, Sb) quaternary ferromagnetic semiconductor films. With the increase of the Sb content, the lattice constant and the vertical strain in the films were found to increase accordingly. The angle dependence of AMR_xx showed that the cubic component was suppressed, resulting from an increase of the local compressive strain. A suitable Sb concentration can make the uniaxial symmetry dominate the AMR_xx term, and a high hole density causes a strong AMR_xy signal.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank H. L. Wang and J. H. Zhao for providing samples. This work was supported by the National Nature Science Foundation of China under Grant No. 61076117, the Fundamental Research Funds for the Central Universities No. JB2014108 and Beijing Higher Education Young Elite Teacher Project No. GJ2013051.

References

1. F. Matsukura, H. Ohno, A. Shen and Y. Sugawara, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, R2037.
2. T. Omiya, F. Matsukura, T. Dietl, Y. Ohno, T. Sakon, M. Motokawa and H. Ohno, Phys. E, 2000, 7, 976.
3. H. Ohno and F. Matsukura, Solid State Commun., 2001, 117, 179.
4. T. Jungwirth, J. Sinova, K. Y. Wang, K. W. Edmonds, R. P. Campion, B. L. Gallagher, C. T. Foxon, Q. Niu and A. H. Macdonald, Appl. Phys. Lett., 2003, 83, 320.
5. M. Sawicki, F. Matsukura, A. Idziaszek, T. Dietl, G. M. Schott, C. Ruester, C. Gould, G. Karczewski, G. Schmidt and L. W. Molenkamp, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 245325.
6. T. Dietl, H. Ohno, F. Matsukura, J. Cibert and D. Ferrand, Science, 2000, 287, 1019 , http://www.sciencemag.org/search?author1=T.+Dietl%26sortspec=date%26submit=Submit.
7. K. Y. Wang, K. W. Edmonds, R. P. Campion, L. X. Zhao, C. T. Foxon and B. L. Gallagher, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085201.
8. L. Sangyeop, C. Seonghoon, B. Seul-Ki, L. Hakjoon, Y. Taehee, L. Sanghoon, X. Liu and J. K. Furdyna, Solid State Commun., 2016, 244, 7.
9. Y. Yuan, T. Amarouche, C. Xu, A. Rushforth, R. Böttger, K. Edmonds, R. Campion, B. Gallagher, M. Helm, H. J. von Bardeleben and S. Zhou, J. Phys. D: Appl. Phys., 2018, 51, 145001.
10. M. Sawicki, K. Y. Wang, K. W. Edmonds, R. P. Campion, C. R. Staddon, N. R. S. Farley, C. T. Foxon, E. Papis, E. Kamińska, A. Piotrowska, T. Dietl and B. L. Gallagher, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 121302.
11. A. W. Rushforth, K. Výborný, C. S. King, K. W. Edmonds, R. P. Campion, C. T. Foxon, J. Wunderlich, A. C. Irvine, P. Vašek, V. Novák, K. Olejník, S. Jairo, T. Jungwirth and B. L. Gallagher, Phys. Rev. Lett., 2007, 99, 147207.
12. V. D. Baxter, R. Dmitry, S. Julia, Y. Sasaki, X. Liu, J. K. Furdyna and C. H. Mielke, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 212407.
13. D. Wu, W. Peng, E. Johnston-Halperin, D. D. Awschalom and S. Jing, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125320.
14. S. Ohya, I. Muneta, Y. Xin, K. Takata and M. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 094418.
15. S. Ohya, H. Kobayashi and M. Tanaka, Appl. Phys. Lett., 2003, 83, 2175.
16. M. Yahyaoui, K. Boujdaria, M. Cubukcu, C. Testelin and C. Gourdon, J. Phys.: Condens. Matter, 2013, 25, 34600.
17. A. Lemaître, A. Miard, L. Travers, O. Mauguin, L. Largeau, C. Gourdon, V. Jeudy, M. Tran and J.-M. George, Appl. Phys. Lett., 2008, 93, 021123.
18. W. Ouerghui, H. Ben Abdallah and K. Ben Saad, Phys. Status Solidi B, 2017, 1700115.
19. X. Liu, X. Li, S.-N. Dong, M. Dobrowolska and J. K. Furdyna, Phys. C, 2018, 548, 93.
20. J. J. Deng, J. T. Che, J. Chen, W. J. Wang, B. Hu, H. L. Wang and J. H. Zhao, J. Appl. Phys., 2013, 114, 243901.
21. B. Howells, M. Wang, K. W. Edmonds, P. Wadley, R. P. Campion, A. W. Rushforth, C. T. Foxon and B. L. Gallagher, Appl. Phys. Lett., 2013, 102, 052407.
22. K. Y. Wang, M. Sawicki, K. W. Edmonds, R. P. Campion, S. Maat, C. T. Foxon, B. L. Gallagher and T. Dietl, Phys. Rev. Lett., 2005, 95, 217204.
23. T. Jungwirth, K. Y. Wang, J. Mašek, K. W. Edmonds, K. Jürgen, S. Jairo, M. Polini, N. A. Goncharuk, A. H. MacDonald, M. Sawicki, A. W. Rushforth, R. P. Campion, L. X. Zhao, C. T. Foxon and B. L. Gallagher, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165204.
24. W. W. Chow and S. W. Koch, Semiconductor-Laser Fundamentals, Springer-Verlag, Berlin, 1999.
25. M. Glunk, J. Daeubler, L. Dreher, S. Schwaiger, W. Schoch, R. Sauer and W. Limmer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 195206.
26. J. Wunderlich, A. C. Irvine, J. Zemen, V. Holý, A. W. Rushforth, E. De Ranieri, U. Rana, K. Výborný, J. Sinova, C. T. Foxon, R. P. Campion, D. A. Williams, B. L. Gallagher and T. Jungwirth, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054424.

---

Footnote

† PACS: 75.50.Pp; 75.30.Gw; 73.43.Qt.

---