Open Access Article
Open Access ArticleAn accurate ground state potential surface for the scattering reaction F− + F2(v,j) → F2(v′,j′) + F−
Dequan Wang *a,
Deguo Wangb,
Liwei Fu
*a,
Deguo Wangb,
Liwei Fu a,
Jianyu Wangc,
Guang Shi*d,
Yanchun Li
a,
Jianyu Wangc,
Guang Shi*d,
Yanchun Li *a and
Xuri Huanga
*a and
Xuri Huanga
aLaboratory of Theoretical and Computational Chemistry, Institute of Theoretical Chemistry, Jilin University, Changchun, People’s Republic of China. E-mail: dequan_wang@jlu.edu.cn
bDepartment of Assets Logistic Management, Jilin University, Changchun, People’s Republic of China
cState Key Laboratory of Inorganic Synthesis & Preparative Chemistry, Jilin University, Changchun, People’s Republic of China
dHematology and Oncology Department, The Second Hospital, Jilin University, Changchun, People’s Republic of China
First published on 15th January 2019
Abstract
The accuracy of three-dimensional adiabatic potential energies for F3− ions is reduced with higher level ab initio methods. The accurate numerically fitted method, the 3D-spline method, was performed to obtain an accurate adiabatic potential energy surface for the ground state of F3− ions. A linear minimum geometry was found in the present work, and the corresponding parameters were in excellent agreement with those of the optimized structure and those reported in previous work. By comparing the lowest potential energies for different attacking angles one can see that the favorite reaction pathway for the title reaction is F− + F2(v,j) → F3−(C∞) → F− + F2(v′,j′).
1 Introduction
Halogens atoms are known to form hypervalent anions of the type X3−. The most simple hypervalent anion is the trifluoride anion (F3−). A clear understanding of F3− can help us to understand all kinds of hypervalent anions. The first report the existence of F3− was in 1976 (ref. 1). The experimental studies that followed observed F3− in a rare gas matrix2,3 and in the gas phase.4,5 Braïda and Hiberty6 investigated and analyzed F3− with breathing-orbital valence bond methods. The bond strength D(F2–F−) of F3− has been measured using energy-resolved collision-induced dissociation, and the results amount to 21–26 kcal mol−1.5 Theoretical methods7,8 estimated that the F2–F− band energy is about 1.14–1.22 eV. The minima structures for the singlet state of F3− were searched by Czernek and Živný9 with the MRCI/aug-cc-pVQZ method.Since quantum chemical calculations can produce sufficiently reliable data for this system, a careful look at the potential energy surfaces (PESs) can help us guess the likely reaction mechanism. Despite several investigations of the F− + F2 reaction kinetics, an accurate understanding of the reaction mechanism of this system is still quite limited. For the precise dynamical simulation of this system, high-quality electronic structure PESs over a broad range of molecular configurations are the first requisite step.
Up to now, no accurate PES data are presently available for the reaction of F− colliding with F2. To obtain more perfect dynamic study results for this system, a three dimensional PES is constructed in the present work.
In the current study, we carried out high level ab initio calculations for the ground state of a global PES for F3−. Our main goal is to produce a highly accurate potential energy surface for the title reaction system with Jacobi coordinates over a broad range of molecular configurations, so that we can perform further dynamical studies. The outline of the present work is as follows: the second section will introduce the computational methods, the global PES will be presented in the third section and the conclusions and discussions will be shown in the fourth section.
2 Computational methods
The potential energies were calculated at the HF/CCSD(T) level. The higher level basis set, the augmented correlation consistent polarized valence quadruplet-zeta (aug-cc-pVQZ), was employed as implemented in the MOLPRO 2012 package.10As with our previous works,12,13 Jacobi coordinates (R, r, θ) were used to characterize this three-body system, in which R indicates the distance of the fluorine anion (F−) from the center of mass of the two fluorine atoms, r is the distance of the two fluorine atoms, and θ represents the angle between the two vectors R and r. The singlet state of the F3− configurations was sampled over a broad range, i.e. r distances from 0.4 Å to 5.0 Å, R from 0.0 Å to 20.0 Å, and θ from 0.0° to 90.0°.
The scan grids of r, R and θ were set with different steps according to their ranges. The grid details for these ranges are as follows: the angle grid was 10°, for r from r = 0.4 Å to r = 3.0 Å, Δr = 0.1 Å including r = 1.73 Å, 1.74 Å, and 1.75 Å; for r from r = 3.2 Å to r = 5.0 Å, Δr = 0.2 Å; for R from R = 0.0 Å to R = 4.4 Å, ΔR = 0.2 Å, and includes the R = 0.1 Å point; for R from R = 4.8 Å to R = 12.0 Å, ΔR = 0.4 Å; for R from R = 12.5 Å to R = 15.0 Å, ΔR = 0.5 Å; the other grids are fixed in 1.0 Å. The 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 geometries were chosen to generate the ab initio energy points in this region. The large number of points warrant the quality of the following fitted PES. The three dimensional (3D) B-spline method was used in this work.
200 geometries were chosen to generate the ab initio energy points in this region. The large number of points warrant the quality of the following fitted PES. The three dimensional (3D) B-spline method was used in this work.
3 Results
To easily discuss the results, the potential energy of F− + F2 is regarded as 0 eV.3.1 Diatomic atom (F–F) potential energy
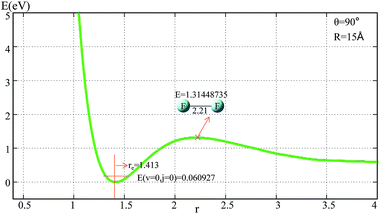
The potential energies of the F2 molecule for our fitted PES are shown in Fig. 1. For the demonstration of this potential, R was fixed at 15 Å, and θ was fixed at 90°.From Fig. 1 one can see that the equilibrium distance of F2 is 1.413 Å, which is in good agreement with the real value of 1.412 Å;6 the electronic energy for the vibrational state v = 0 and the rotational state j = 0 of this equilibrium structure is 0.061 eV. With an increase in r(F–F), the energy increased to a transition state then separated to the two F atoms. The diatomic atom distance and potential energy for the transition state point were 2.21 Å and 1.314 eV, respectively.
For the title reaction, the three atoms are identical and the potential energy surface for the reaction entrance (F− attacking F2 reaction pathway) and exit (the new F− separating from F2 reaction pathway) should be the same. After analyzing the reaction entrance, the whole reaction potential energy surface was clearly shown. In the following two sections, the reaction entrances for the one-dimensional (1D) and two-dimensional (2D) potential energy surface will be discussed.
3.2 The reaction entrances for the 1D potential energy surface
The potential energies of fixed r values for F− attacking the F2 molecule with different angles are plotted in Fig. 2. Panel (a) in Fig. 2 shows the potential energy as a function of R for r fixed at 1.313–1.813 Å. When R > 3.5 Å, r = 1.413 Å, and the lowest potential energy is presented; when R < 3.25 Å, the energies for r = 1.713 and 1.813 Å are lower than the others; when R reaches 2.7 Å, the title system arrives at its global minimum area. For θ = 90° (see panel (b) in Fig. 2) there is no minimum geometry. Panel (c) exhibits the 1D-PES with different angles θ = 0°, 30°, 60°, and 90° and r fixed at 1.413 Å. From this panel, one can see that the minimum geometry can be found only in the θ = 0° channel, so we can make the conclusion that the most important reaction channel is the θ = 0° reaction pathway.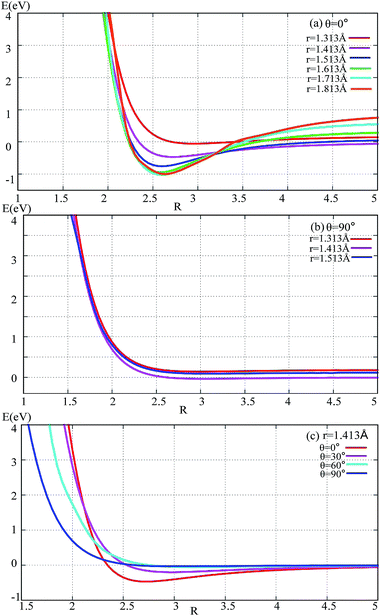 | ||
| Fig. 2 Potential energy surface as a function of distance R (in Å) with different angles and r values. | ||
3.3 Two dimensional (2D) adiabatic potential energy surface
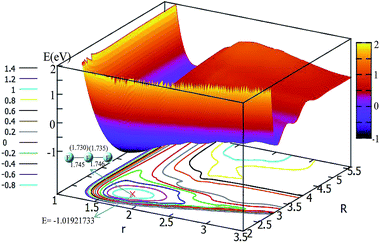
In order to get a more pictorial view of how the F3− potential energy changes with R and r, two dimensional potential energy surfaces (2D-PESs) were drawn with four different angles, i.e. θ = 0°, 30°, 60°, and 90° in Fig. 3–6, respectively. The 2D-PES of F3− is shown in the upper part for every figure, and the contour plot of this 2D-PES is shown in the lower part, in which the energy difference between any two adjacent curves is 0.2 eV. In such a contour, the small distance between two adjacent curves corresponds to the sharp energy changes with distance and vice versa.Fig. 3 shows the F3− potential energy surface for θ = 0°. Fig. 3 shows that when the F− ion is far away from the F2 molecule (3.5 Å < R, and 1.1 Å < r < 1.8 Å), the potential energy is nearly consistent with the change in R value; when R < 3.5, with a decrease in R value, the r value is increased and the minimum geometry is then formed; when R is reduced to 2.6 Å, and r extends to 1.73 Å, the F3− molecule reaches its global minimum area. The bond distances of the minimum structure are 1.730 Å and 1.735 Å in our fitted PES, which are in good agreement with the optimized values (1.745 Å and 1.746 Å) with the b3lyp/6-311++g** calculation level using the Gaussian program.11 The potential energy of the global minimum is −1.02 eV, which is consistent with the results of Artau et al.5 (from −0.911 eV to −1.127 eV).
The potential energy surface for θ = 30° is shown in Fig. 4. By shortening the R distance, the potential energy becomes lower and lower; when the R values reach 2.7 Å, and the r value stretches to 1.78 Å, the system arrives at its minimum energy (−0.445 eV). This minimum is not really the minimum of the structure, if it is optimized the linear minimum geometry will be achieved.
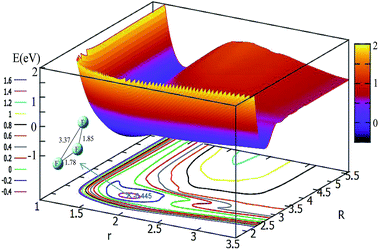 | ||
| Fig. 4 2D and contour plot of the potential energy surface (in eV) as a function of the distances R and r (in Å) at a fixed θ = 30°. | ||
For θ = 60° and 90°, the characteristics of these two PESs are similar to each other (see Fig. 5 and 6). For every fixed r value, the potential energy slightly changed with the transformation of the R values. From these two figures, one can see that a slight minimum may have existed, and its energies were higher than −0.2 eV. We tried to optimize these geometries many times to find them with the Gaussian program, but we failed in the end.
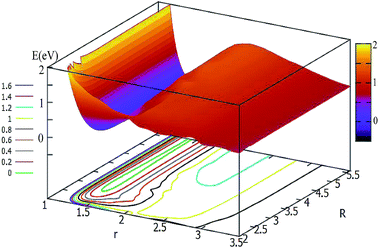 | ||
| Fig. 5 2D and contour plot of the potential energy surface (in eV) as a function of the distances R and r (in Å) at θ = 60°. | ||
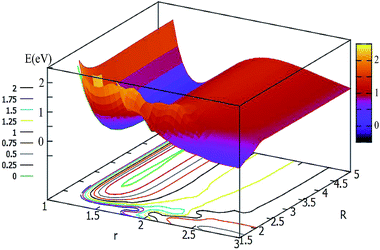 | ||
| Fig. 6 2D and contour plot of the potential energy surface (in eV) as a function of the distances R (in Å) and r at θ = 90°. | ||
From analyzing the globle PESs, the F3− system could overcome the reaction barrier (nearly 3.2 eV) to reach it's three atom area. The r value of this reaction barrier is nearly equal to 2.2 Å. This characteristic is different from the HCC,12 LiHH,13 and OCC14 systems which were investigated in our previous studies.
To easily understand the relationship of the PES with different angles, the lowest potential energy surface is plotted in Fig. 7. From Fig. 7, we can find that the potential energies become lower and lower with decrease the attacking angles; the lowest energy corresponds to the linear geometry, and the potential energies changed from 90° to 0° do not have any reaction barrier. From this PES, we can predict the reaction mechanics. No matter which angle the F− ion attacks the F2 molecule from, the reaction should form the linear F3− ion first, then separate to the new F− ion and F2 products. The accurate trajectory method can be used to confirm the mechanism of this reaction, and we will continue this work in the near future using the present fitted adiabatic PES.
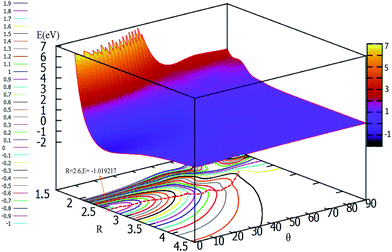 | ||
| Fig. 7 2D and contour plot for the lowest potential energy surface (in eV) as a function of distance R (in Å) and θ (in degree) at a fixed r = 1.73 Å. | ||
4 Conclusions
A high level ab initio method is performed to format an accurate adiabatic potential energy surface for the F− + F2(v,j) → F2(v′,j′) + F− scattering reaction. The MOLPRO quantum chemistry package was used for scanning all geometry points in the Jacobi coordinate; the intermediate was found and optimized with the Gaussian package.. An accurate and much larger region of configuration space for the potential energy surface was produced by a precise three dimensional spline fitting method. A linear symmetry intermediate was found in the present work, the bond distances of the minimum structure were 1.730 Å and 1.735 Å in our fitted PES, and the structure and energy of this minimum were in good agreement with those of the previous work. By analyzing the lowest PES with different attacking angles, we found that there were no reaction barriers from θ = 90° to θ = 0°, furthermore we can come to the conclusion that the favorite reaction pathway is F− + F2(v,j) → F3−(C∞) → F− + F2(v′,j′). Further work with full dynamical studies are worth doing with the present PES.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (No. 21604031, 21373099, 21573090, 21673092), the Jilin Province Science and Technology Development Plan (20150101005JC) and the Ministry of Education of China (20130061110020).References
- B. S. Ault and L. Andrews, J. Am. Chem. Soc., 1976, 98, 1591–1593 CrossRef CAS.
- B. S. Ault and L. Andrews, Inorg. Chem., 1977, 16, 2024–2028 CrossRef CAS.
- R. D. Hunt, C. Thompson, P. Hassanzadeh and L. Andrews, Inorg. Chem., 1994, 33, 388–391 CrossRef CAS.
- A. A. Tuinman, A. A. Gakh, R. J. Hinde and R. N. Compton, J. Am. Chem. Soc., 1999, 121, 8397–8398 CrossRef CAS.
- A. Artau, K. E. Nizzi, B. T. Hill, L. S. Sunderlin and P. G. Wenthold, J. Am. Chem. Soc., 2000, 122, 10667–10670 CrossRef CAS.
- B. Braïda and P. C. Hiberty, J. Am. Chem. Soc., 2004, 126, 14890–14898 CrossRef PubMed.
- G. L. Heard, C. J. Marsden and G. E. Scuseria, J. Phys. Chem., 1992, 96, 4359–4366 CrossRef CAS.
- F. Mota and J. J. Novoa, J. Chem. Phys., 1996, 105, 8777–8785 CrossRef CAS.
- J. Czernek and O. Živný, J. Chem. Phys., 2008, 129, 194305–194309 CrossRef PubMed.
- H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby, M. Schütz and others, MOLPRO, version 2012.1, a package of ab initio programs, http://www.molpro.net Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Revision A. 02, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed.
- D. Q. Wang, L. W. Fu, Z. X. Qu, Y. K. Chen and X. R. Huang, Eur. Phys. J. D, 2017, 71, 252–258 CrossRef.
- L. W. Fu, D. Q. Wang and X. R. Huang, RSC Adv., 2018, 8, 15595–15602 RSC.
- D. Q. Wang, D. G. Wang, L. W. Fu and X. R. Huang, Chem. Phys., 2018, 517, 228–236 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |