Structure evolution of chromium-doped boron clusters: toward the formation of endohedral boron cages

Abstract

The electron-deficient nature of boron endows isolated boron clusters with a variety of interesting structural and bonding properties that can be further enriched through metal doping. In the current work, we report the structural and electronic properties of a series of chromium-doped boron clusters. The global minimum structures for CrB_n clusters with an even number of n ranging from 8 to 22 are proposed through extensive first-principles swarm-intelligence structure searches. Half-sandwich structures are found to be preferred for CrB₈, CrB₁₀, CrB₁₂ and CrB₁₄ clusters and to transform to a drum-like structure at CrB₁₆ cluster. Endohedral cage structures with the Cr atom located at the center are energetically most favorable for CrB₂₀ and CrB₂₂ clusters. Notably, the endohedral CrB₂₀ cage has a high symmetry of D_2d and a large HOMO–LUMO gap of 4.38 eV, whose stability is attributed to geometric fit and formation of an 18-electron closed-shell configuration. The current results advance our understanding of the structure and bonding of metal-doped boron clusters.

---

1. Introduction

Boron is an element of fascinating structural and chemical complexity, leading to topics of considerable interest in chemistry. It has three valence electrons that are deficient compared with the four valence orbitals, and it prefers to share rather than donate the valence electrons. These characteristics make it difficult for B to achieve filled octets through classical 2c–2e bonds, giving rise to a rich variety of structures along with electron-deficient multicentered bonds, both in its elemental form and chemical compounds.¹ Sixteen polymorphs have been discovered for bulk B with B₁₂ icosahedron being a prevalent motif.² 1D nanotubes^3–5 and 2D sheets^6–8 have been fabricated in which triangular planar B lattices with hexagonal holes are found to be energetically favorable.⁹

For 0D B clusters, the situation is even more interesting. Joint photoelectron spectroscopy and theoretical studies carried out over the past decades show that anionic B_n⁻ clusters up to n = 38 are planar or quasi-planar,^10,11 in which delocalized multicentered bonds are responsible for the stabilities.¹² Theoretical calculations suggested a planar-to-tubular structure transition taking place at B₂₀ for neutrals.¹³ Subsequently, combined collision cross section measurements and theoretical calculations confirmed the existence of tubular structures for cationic B_n⁺ clusters with n = 16–25.¹⁴ Most strikingly, the long-sought B fullerene analogue (borospherenes) was first observed at B₄₀ (ref. 15) after extensive theoretical investigations,^16–19 and a series of axially chiral borospherenes were subsequently identified at B₃₉⁻,²⁰ B₄₁⁺ and B₄₂²⁺.²¹ For larger B clusters, recent theoretical studies have suggested quasi-planar,^22,23 tubular,²⁴ cage-like²⁵ and bilayered²³ structures as ground states at certain sizes, and core–shell structures are generally expected to be energetically most favorable for n > ∼68.^26–28

The structural diversity of B clusters can be further enriched through metal doping. Metal-centered monocyclic B rings can be formed by transition metal doping of small B_8–10 anionic clusters²⁹ in which NbB₁₀⁻ (ref. 30) and TaB₁₀⁻ (ref. 30) hold the highest coordination number of 10 in planar molecular species. Interesting half-sandwich structures have been found in Co/Rh doped B₁₂ anionic clusters,³¹ and drum-like structures have been observed in CoB₁₆⁻,³² MnB₁₆⁻ (ref. 33) and TaB₂₀⁻ (ref. 34) clusters, in which the TaB₂₀⁻ cluster possesses the highest coordination number (20) heretofore known in chemistry. Motivated by the discovery of borospherenes in our previous work, we have designed symmetric endohedral B cages, such as MnB₂₀⁺,³⁵ MoB₂₄ (ref. 36) and WB₂₄,³⁶ whose stabilities are attributed to the formation of 18-electron closed-shell configurations, as well as geometric fits between the sizes of the transition metal atoms and the cavities of the B cages. It was further suggested that, by reasonable choice of the transition metal atom and number of B atoms, other-sized boron cages are also likely to be stabilized. Recently, a theoretical study found that even the small B₁₂ cluster can show interesting transitions from quasi-planar to tubular and cage-like structures through interactions with lithium atoms, in which charge transfer plays a critical role.³⁷

Metal doping has been proven to be an effective avenue to achieve intriguing structure motifs in B clusters. Given the large number of possible combinations between metal atoms and the number of B atoms yet to be investigated, it not unreasonable to expect more fascinating phenomena in this group of chemical species. As such, in this paper, we report systematic investigations on the structure and bonding of a series of chromium (Cr) doped B clusters by means of the swarm-intelligent CALYPSO structure searching method and first-principles density functional calculations. Ground-state structures are proposed for CrB_n clusters with an even number of n ranging from 8 to 22, revealing an intriguing transition from half-sandwich to drum-like and then endohedral cage-like structures. In particular, a symmetric D_2h endohedral cage is revealed as the ground-state structure for the CrB₂₀ cluster. The rest of the manuscript is organized as follow. The second section describes the computational details. Section 3 presents the results and discussion, and the conclusions from the present results are given in Section 4.

2. Calculation details

The unbiased structure searches of CrB_n clusters with an even number of n ranging from 8 to 22 are based on the global minimization of the potential energy surfaces, merging ab initio total energy calculations via the CALYPSO (Crystal structure AnaLYsis by Particle Swarm Optimization) package.^38–41 Several major techniques are included in the algorithm to achieve high efficiency, e.g., point group symmetry constraints in structural generation, bond characterization matrix technique for fingerprinting structures, and a local version of the particle swarm optimization algorithm enabling simultaneous search in different energy funnels.³⁹ Its validity has been manifested by successful identification of the ground-state structures for a large number of systems. More than 2000 trial structures were generated for each cluster.

During the structure searches, the underlying energy calculations and structure relaxations are carried out in the framework of density functional theory (DFT) with the PBE functional⁴² implemented in the ABACUS (Atomic-orbital Based Ab initio Computation at USTC) package.⁴³ ABACUS was developed to perform large-scale DFT simulations using linear combinations of atomic orbitals.^44,45 The recently developed systematically improvable optimized numerical atomic orbitals^44,45 were found to be an excellent choice to describe various materials, such as molecules, crystalline solids, surfaces, and defects.⁴³ The atomic orbitals basis set of B includes two s, two p and one polarized d orbitals (2s2p1d), whereas the basis set of Cr includes four s, two p, two d and one polarized f orbitals (4s2p2d1f). The radii of the numerical atomic orbitals are set to 7 bohr for B and 8 bohr for Cr in the first-round local structure optimization, while 8 bohr for B and 9 bohr for Cr are used in the second-round local structure optimization. We adopt the SG15 Optimized Norm-Conserving Vanderbilt pseudopotentials,⁴⁶ and the energy cutoff for charge density is 240 Ry.

The low-lying isomers obtained from the structure searches were reoptimized at different spin states at PBE0/Cr/Stuttgart/B/6-311+G* level of theory using the Gaussian 09 Package.⁴⁷ The calculation of harmonic vibrational frequencies ensures that the cluster geometries are true local minima on the potential energy surface (no imaginary frequencies obtained). At this step, singlet, triplet, quintet and septet states were considered for all of these even-number-electrons clusters. In a previous benchmark calculation, the PBE0 functional was confirmed to be suitable for describing the energy difference of isomers of medium-sized boron clusters (e.g., B₂₀) compared to the high-level CCSD(T) results.²⁸ The natural bond orbital (NBO) and adaptive natural density partitioning (AdNDP) analytical methods were carried out with the Multiwfn package⁴⁸ in order to achieve a better understanding of the bonding mechanism.

3. Results and discussion

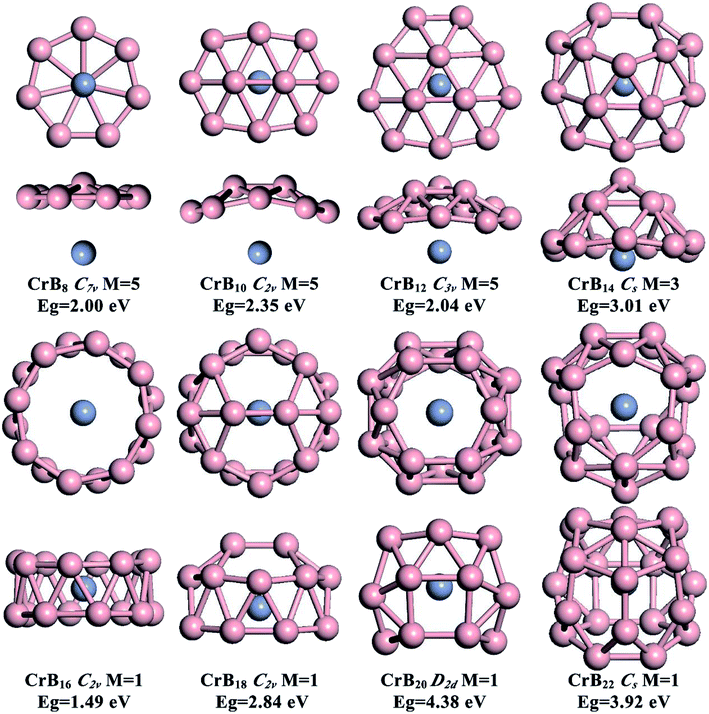
The global minimum structures for CrB_n (n = 8, 10, 12, 14, 16, 18, 20 and 22) clusters obtained from the current structure searches are depicted in Fig. 1. To facilitate understanding of the structures via visualization, top and side views are given along with their point group symmetries, spin multiplicity values (M) and HOMO–LUMO energy gaps (E_g). Other low-lying isomers are shown in the ESI, Fig. S1–S8.† Generally, the effect of Cr doping on the structures of B clusters gradually is enhanced as the number of B atoms increases. For small-sized CrB_n (n = 8, 10 and 12) clusters, the B structures are similar to those in bare B clusters, while larger CrB_n clusters exhibit B structures different from the corresponding bare B clusters. This leads to interesting transitions from half-sandwich to drum-like and then to endohedral cage-like structures as the number of B atoms increases. High spin states (triplet and quintet states) are preferred for small-sized CrB_n clusters with n < 14, and the magnetism is completely quenched for CrB_n clusters with n ≥ 16.

Fig. 1 The lowest-energy ground-state isomers of CrB_n (n = 8, 10, 12, 14, 16, 18, 20 and 22) clusters derived from the global minimum structure search. For each system, two sides of the views are given. For each structure, the point group symmetry, spin multiplicity (M) and LUMO–HOMO gap (E_g) are indicated.

3.1 CrB₈, CrB₁₀, CrB₁₂ and CrB₁₄ clusters with half-sandwich structures

As depicted in Fig. 1, small-sized CrB_n clusters with n = 8, 10, 12 and 14 exhibit half-sandwich structures, whereas quasi-planar or bowl-like B_n moieties are coordinated to the Cr atom. High spin states are found to be the ground states for these global-minimum structures (quintets for CrB₈, CrB₁₀, CrB₁₂, and triplets for CrB₁₄). Other low-lying isomers are given in Fig. S1–S8 in the ESI.† Spin density distributions shown in ESI, Fig. S9† indicates that the magnetism mainly originates from the unpaired 3d electrons of the Cr atom.

The B structures in CrB₈, CrB₁₀ and CrB₁₂ are very similar to those in bare B clusters, which are quasi-planar with one, two and three interior B atoms surrounded by seven-, eight- and nine-membered B rings, respectively. Due to the existence of the Cr atom, the interior B atoms in the B moieties display slight out-of-plane distortions. Note that, although CrB₁₀ is isovalent to NbB₁₀⁻ and TaB₁₀⁻, it does not adopt the metal-centered monocyclic B rings in NbB₁₀⁻ and TaB₁₀⁻ as the ground state. This may be due to the smaller size of the Cr atom (1.39 Å) compared with those of Nb (1.64 Å) and Ta (1.70 Å), which is not optimal for fitting the cavity of the ten-membered B ring. The half-sandwich structure of CrB₁₂ is the same as those in experimental CoB₁₂⁻ and RhB₁₂⁻, further indicating that the double aromatic B₁₂ moiety is a promising inorganic ligand.

Inserting two B atoms into the B₁₂ moiety in the CrB₁₂ cluster leads to the formation of CrB₁₄. The B₁₄ moiety in CrB₁₄ has a bowl-like structure with five interior B atoms surrounded by a nine-membered B ring, which is different from the structures of neutral or charged bare B₁₄ clusters.^10,49 In contrast to CrB₈, CrB₁₀ and CrB₁₂, the Cr atom is half encircled by the bowl-like B₁₄ moiety in CrB₁₄, leading to enhanced Cr–B interactions and partially quenched magnetism. The significant curving of the B moiety in CrB₁₄ indicates the gradually enhanced effect of Cr doping on the structure evolution and onset of structure transition in CrB_n clusters.

3.2 The CrB₁₆ cluster with a drum-like structure

The well-known drum-like structure with the Cr atom located at the center of a B₁₆ double-ring tube occurs with the CrB₁₆ cluster, having a point group of C_2v (Fig. 1). Within this structure, the magnetism is completely quenched due to the strong coordination interactions between the Cr atom and the B₁₆ tube. This type of structure was initially observed in CoB₁₆⁻ (ref. 32) and MnB₁₆⁻ (ref. 33) by joint photoelectron spectroscopy measurement and ab initio calculations. Later, studies found that larger B₁₈ and B₂₀ tubes can be stabilized by doping larger transition metal atoms (Rh and Ta), leading to drum-like RhB₁₈⁻ (ref. 50) and TaB₂₀⁻,³⁴ respectively. Interestingly, recent theoretical studies have found that the smaller B₁₄ tube can be formed by the doping of an Fe atom,⁵¹ though the size of Fe (1.32 Å) is larger than that of Co (1.26 Å). Thus, it seems that whether drum-like structures can be formed in metal-doped B clusters is closely related to the size of the doping atom and the cavity of the B tube, as well as the charge and spin states of the metal-doped B clusters.

The chemical bonding of the current drum-like CrB₁₆ cluster was analyzed using the Adaptive Natural Density Partitioning (AdNDP)⁵² method, which is an extension of the Natural Bond Orbital method.⁵³ AdNDP analyses can display both localized and delocalized bonding in molecules simultaneously, providing relatively simple bonding pictures for complicated molecular structures.³³ The AdNDP analyses revealed a similar bonding character for CrB₁₆ as those of CoB₁₆⁻ and MnB₁₆⁻, where the 54 valence electrons in CrB₁₆ can be divided into four bonding types as shown in Fig. 2. The occupation numbers (ON) of all the identified bonds range from 1.71 to 2.00 |e|. The first type represents localized bonds (Fig. 2a), which can be described in two manners: (1) as sixteen 3c–2e σ bonds on the sixteen B₃ triangles on the drum surface with ON = 1.94 |e| or (2) as sixteen 2c–2e σ bonds within the two B₈ rings with ON = 1.73 |e|. In fact, the sixteen 3c–2e σ bonds can also be represented by sixteen 2c–2e σ bonds on the two B₈ rings on the drum surface are shown in Fig. S10 in ESI.†

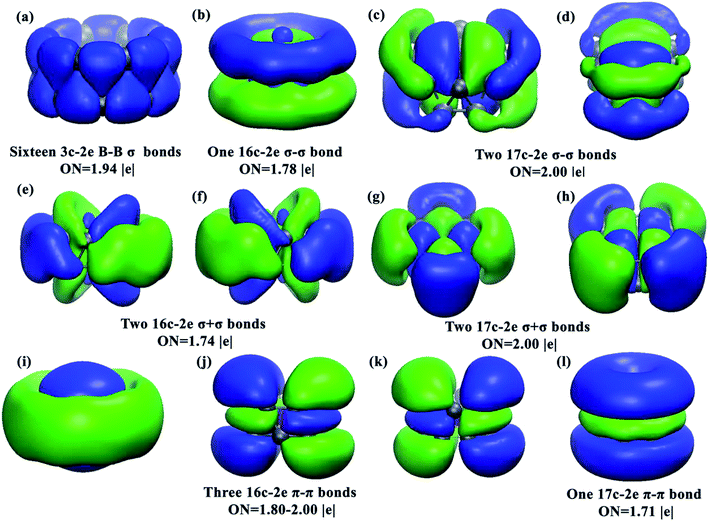Fig. 2 Images of the chemical bonding of CrB₁₆ obtained from AdNDP analyses. ON stands for occupation number.

The remaining three bonding types describe totally delocalized bonds (Fig. 2b–d, e–i and j–m) and account for bonding between the two B₈ rings and between the Cr atom and the B₁₆ tube. Following the previous work on CoB₁₆⁻ and MnB₁₆⁻, the “+” sign is used to denote that the delocalized bonds between the two B₈ rings overlap positively, while the “−” sign means a negative overlap. The second bonding type (Fig. 2b–d) consists of one 16c–2e σ − σ bond with ON = 1.78 |e| and two 17c–2e σ − σ bonds with ON = 2.00 |e|. The one 16c–2e σ − σ bond represents a bonding interaction within each B₈ ring and an antibonding interaction between the two B₈ rings, while the two 17c–2e σ − σ bonds represent mainly covalent bonding between Mn (3d_xz and 3d_yz) and the B₁₆ tube. The third bonding type (Fig. 2e–h) contains two 16c–2e σ + σ bonds with ON = 1.74 |e| and two 17c–2e σ + σ bonds with ONs = 2.00 |e|. The two 16c–2e bonds represent delocalized σ bonding in the B₁₆ frame, and the two 17c–2e σ + σ bonds represent covalent bonding between Cr (3d_xy and 3d_x²−y²) and the B₁₆ tube. The fourth bonding type consists of three 16c–2e π − π bonds and one 17c–2e π − π bond. These four bonds account for π bonding interactions between the two B₈ rings.

3.3 Transition from drum-like to endohedral cage-like structures in CrB₁₈, CrB₂₀ and CrB₂₂ clusters

As depicted in Fig. 1, capping two B atoms on one side of the drum-like CrB₁₆ structure leads to the global minimum structure of the CrB₁₈ cluster, which can be seen as an intermediate structure between drum-like and endohedral cage-like structures. Notably, a symmetric endohedral cage with the Cr atom located at the center emerges as the global minimum structure for the CrB₂₀ cluster. The structure is composed of twenty B triangles, four B quadrangles and two B hexagons in D_2d symmetry. It has the largest HOMO–LUMO gap of 4.38 eV among CrB_n clusters considered in the current work. The high symmetry and large HOMO–LUMO gap imply highly degenerate electronic states and the potentially high chemical stability of the CrB₂₀ cluster. Further addition of two B atoms into the CrB₂₀ cluster also leads to an endohedral cage-like structure in the CrB₂₂ cluster, suggesting that endohedral cage-like motifs may be prevalent for larger CrB_n clusters with n > 20. However, the endohedral CrB₂₂ cage is rather irregular, and its HOMO–LUMO gap (3.92 eV) is smaller than that of CrB_20.

Early theoretical studies have demonstrated metal doping as a viable route for stabilizing cage-like B structures. A series of transition-metal-centered endohedral B cages have been proposed, such as FeB₁₈, FeB₂₀, MnB₂₀⁺, MoB₂₄, and WB₂₄. However, the transition metal should possess both geometric and electronic states that can fit in high symmetric endohedral B cage-like clusters that eventually lead to the high stability structures that can be formed. The current endohedral D_2d CrB₂₀ cage should be one such paradigm. The geometric factor responsible for the stability is straightforward. Our previous calculations have demonstrated that the Cr atom is too small to fit a large B₂₄ cage, indicating smaller B cages are suitable for accommodating one Cr atom.

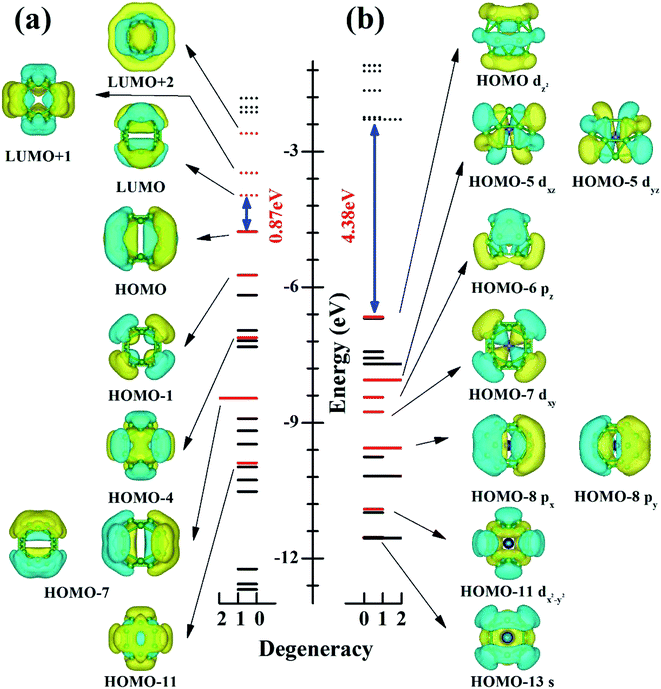
To understand electronic factors responsible for the stability of the endohedral CrB₂₀ cage, the chemical bonding of the bare D_2d B₂₀ cage and endohedral D_2d CrB₂₀ cage were analyzed based on canonical molecular orbitals (CMOs). Fig. 3 shows the comparison of eigenvalue spectra for the D_2d cage without (a) and with (b) Cr encapsulation. One can clearly note that the Cr encapsulation significantly increases the HOMO–LUMO gap from 0.87 eV for the bare D_2d B₂₀ cage to 4.38 eV for the D_2d CrB₂₀. For bare D_2d B₂₀ (Fig. 3a), there are 6 occupied π-orbitals (HOMO, HOMO−1, HOMO−4, two HOMO−7, and HOMO−11) and 3 unoccupied π-orbitals (LUMO, LUMO+1 and LUMO+2). The moderate HOMO–LUMO gap in bare D_2d B₂₀ is attributed to the mid-lying binding energies of these out-of-surface delocalized π-orbitals, and they will interact with the electronic orbitals of Cr atoms in the endohedral CrB₂₀ cages. Cr has an electronic configuration of [Ar]4s¹3d⁵ with 6 valence electrons, adding the 12 π-electrons (from 6 occupied π-orbitals) of bare D_2d B₂₀ gives a total of 18 electrons. This special electron counting number of 18 is favorable for forming a stable 18-electron closed-shell configuration, similar to that of previous MnB₂₀⁺, MoB₂₄ and WB₂₄ clusters. Indeed, nine CMOs involved in the “spd–π interaction” have been identified for the D_2d CrB₂₀ endohedral cage as depicted in Fig. 3b, i.e., HOMO−13 (s-like), HOMO−11 (d_x²−y²-like), HOMO−8 (double degenerate, p_x-like and p_y-like), HOMO−7 (d_xy-like), HOMO−6 (p_z-like), HOMO−5 (double degenerate, d_xz-like and d_yz–π like) and HOMO−1 (3d_z²-like). Thus, the CrB₂₀ cluster represents another example of having a symmetric endohedral cage configuration stabilized by the 18-electron configuration.

Fig. 3 Eigenvalue spectrum vs. electronic state degeneracy of (a) bare D_2d–B₂₀ cage and (b) D_2d–CrB₂₀. For each case, the HOMO–LUMO gap is indicated (in blue). The π-orbitals (red lines) (a) and the orbitals involving the 18-electron closed-shell configuration (b) are shown.

4. Conclusions

In summary, we systematically investigated the structural and electronic properties of CrB_n clusters with n = 8, 10, 12, 14, 16, 18, 20 and 22 through extensive swarm-intelligent structure searches and first-principles calculations. It is found that Cr doping significantly modifies the structural evolution of B clusters. Intriguing transitions from half-sandwich to drum-like and then to endohedral cage-like structures are revealed as the number of B atoms increases. CrB₈, CrB₁₀ and CrB₁₂ clusters exhibit half-sandwich structure with quasi-planar B moieties similar to the bare B cluster, indicating that small-sized B clusters are promising inorganic ligands. A drum-like structure is formed with CrB₁₆ clusters, while endohedral cage structures emerge with the larger CrB₂₀ and CrB₂₂ clusters. The endohedral CrB₂₀ cage has a high symmetry of D_2d and the largest HOMO–LUMO gap among CrB_n in the current work, indicating its high chemical stability, which is attributed to the geometric fit between the size of the Cr atom and the void of the B cage as well as the formation of the 18-electron configuration.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors acknowledge the funding support from National Natural Science Foundation of China (Grants No. 11534003, 11604117, 11404128, 11704151 and 61775081), the Science Challenge Project, No. TZ2016001, National Key Research and Development Program of China (Grant No. 2016YFB0201200), and Program for JLU Science and Technology Innovative Research Team. Part of the calculations were performed in the high performance computing center of Jilin University and Tianhe2-JK in the Beijing Computational Science Research Center.

References

1. X. Sun, X. Liu, J. Yin, J. Yu, Y. Li, Y. Hang, X. Zhou, M. Yu, J. Li, G. Tai and W. Guo, Adv. Funct. Mater., 2017, 27, 1603300.
2. B. Albert and H. Hillebrecht, Angew. Chem., Int. Ed., 2009, 48, 8640–8668.
3. F. Liu, C. Shen, Z. Su, X. Ding, S. Deng, J. Chen, N. Xu and H. Gao, J. Mater. Chem., 2010, 20, 2197.
4. V. Bezugly, J. Kunstmann, B. Grundkötter-Stock, T. Frauenheim, T. Niehaus and G. Cuniberti, ACS Nano, 2011, 5, 4997–5005.
5. J. Kunstmann, V. Bezugly, H. Rabbel, M. H. Rümmeli and G. Cuniberti, Adv. Funct. Mater., 2014, 24, 4127–4134.
6. G. Tai, T. Hu, Y. Zhou, X. Wang, J. Kong, T. Zeng, Y. You and Q. Wang, Angew. Chem., Int. Ed., 2015, 54, 15473–15477.
7. B. Feng, J. Zhang, Q. Zhong, W. Li, S. Li, H. Li, P. Cheng, S. Meng, L. Chen and K. Wu, Nat. Chem., 2016, 8, 563–568.
8. A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516.
9. H. Tang and S. Ismail-Beigi, Phys. Rev. Lett., 2007, 99, 115501.
10. A. N. Alexandrova, A. I. Boldyrev, H. J. Zhai and L. S. Wang, Coord. Chem. Rev., 2006, 250, 2811–2866.
11. Z. Zhang, E. S. Penev and B. I. Yakobson, Chem. Soc. Rev., 2017, 46, 6746–6763.
12. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358.
13. B. Kiran, S. Bulusu, H.-J. Zhai, S. Yoo, X. C. Zeng and L.-S. Wang, Proc. Natl. Acad. Sci., 2005, 102, 961–964.
14. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
15. H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731.
16. J. Lv, Y. Wang, L. Zhu and Y. Ma, Nanoscale, 2014, 6, 11692–11696.
17. T. B. Tai, L. Van Duong, H. T. Pham, D. T. T. Mai and M. T. Nguyen, Chem. Commun., 2014, 50, 1558–1560.
18. N. Gonzalez Szwacki, A. Sadrzadeh and B. I. Yakobson, Phys. Rev. Lett., 2007, 98, 166804.
19. J. T. Muya, G. Gopakumar, M. T. Nguyen and A. Ceulemans, Phys. Chem. Chem. Phys., 2011, 13, 7524.
20. Q. Chen, W.-L. Li, Y.-F. Zhao, S.-Y. Zhang, H.-S. Hu, H. Bai, H.-R. Li, W.-J. Tian, H.-G. Lu, H.-J. Zhai, S.-D. Li, J. Li and L.-S. Wang, ACS Nano, 2015, 9, 754–760.
21. Q. Chen, S. Y. Zhang, H. Bai, W. J. Tian, T. Gao, H. R. Li, C. Q. Miao, Y. W. Mu, H. G. Lu, H. J. Zhai and S. D. Li, Angew. Chem., Int. Ed., 2015, 54, 8160–8164.
22. A. B. Rahane and V. Kumar, Nanoscale, 2015, 7, 4055–4062.
23. L. Sai, X. Wu, N. Gao, J. Zhao and R. B. King, Nanoscale, 2017, 9, 13905–13909.
24. F. Y. Tian and Y. X. Wang, J. Chem. Phys., 2008, 129, 024903.
25. T. B. Tai and M. T. Nguyen, Chem. Commun., 2016, 52, 1653–1656.
26. D. L. V. K. Prasad and E. D. Jemmis, Phys. Rev. Lett., 2008, 100, 100–103.
27. H. Li, N. Shao, B. Shang, L.-F. Yuan, J. Yang and X. C. Zeng, Chem. Commun., 2010, 46, 3878.
28. F. Li, P. Jin, D. E. Jiang, L. Wang, S. B. Zhang, J. Zhao and Z. Chen, J. Chem. Phys., 2012, 136, 074302.
29. C. Romanescu, T. R. Galeev, W. L. Li, A. I. Boldyrev and L. S. Wang, Acc. Chem. Res., 2013, 46, 350–358.
30. T. R. Galeev, C. Romanescu, W. L. Li, L. S. Wang and A. I. Boldyrev, Angew. Chem., Int. Ed., 2012, 51, 2101–2105.
31. I. A. Popov, W.-L. Li, Z. A. Piazza, A. I. Boldyrev and L.-S. Wang, J. Phys. Chem. A, 2014, 118, 8098–8105.
32. I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654.
33. T. Jian, W. L. Li, I. A. Popov, G. V. Lopez, X. Chen, A. I. Boldyrev, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 154310.
34. W.-L. Li, T. Jian, X. Chen, H.-R. Li, T.-T. Chen, X.-M. Luo, S.-D. Li, J. Li and L.-S. Wang, Chem. Commun., 2017, 53, 1587–1590.
35. L. Zhao, X. Qu, Y. Wang, J. Lv, L. Zhang, Z. Hu, G. Gu and Y. Ma, J. Phys. Condens. Matter, 2017, 29, 265401.
36. J. Lv, Y. Wang, L. Zhang, H. Lin, J. Zhao and Y. Ma, Nanoscale, 2015, 7, 10482–10489.
37. X. Dong, S. Jalife, A. Vásquez-Espinal, E. Ravell, S. Pan, J. L. Cabellos, W. Liang, Z. Cui and G. Merino, Angew. Chem., Int. Ed., 2018, 57, 4627–4631.
38. Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B, 2010, 82, 094116.
39. J. Lv, Y. Wang, L. Zhu and Y. Ma, J. Chem. Phys., 2012, 137, 084104.
40. Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070.
41. H. Wang, Y. Wang, J. Lv, Q. Li, L. Zhang and Y. Ma, Comput. Mater. Sci., 2016, 112, 406–415.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. P. Li, X. Liu, M. Chen, P. Lin, X. Ren, L. Lin, C. Yang and L. He, Comput. Mater. Sci., 2016, 112, 503–517.
44. M. Chen, G. C. Guo and L. He, J. Phys. Condens. Matter, 2010, 22, 445501.
45. M. Chen, G. C. Guo and L. He, J. Phys. Condens. Matter, 2011, 23, 325501.
46. D. R. Hamann, Phys. Rev. B, 2013, 88, 085117.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
48. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
49. C. Longjiu, J. Chem. Phys., 2012, 136, 104301.
50. T. Jian, W.-L. Li, X. Chen, T.-T. Chen, G. V. Lopez, J. Li and L.-S. Wang, Chem. Sci., 2016, 7, 7020–7027.
51. N. M. Tam, H. T. Pham, L. Van Duong, M. P. Pham-Ho and M. T. Nguyen, Phys. Chem. Chem. Phys., 2015, 17, 3000–3003.
52. D. Y. Zubarev and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2008, 10, 5207.
53. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09143a

‡ Equally share the first authorship.

---