A theoretical investigation into the first-row transition metal–O₂ adducts

Abstract

An extensive investigation into various M–O₂ species (M = Cr^I, Mn^I, Fe^I, Co^I, Ni^I, Cu^I) has been conducted using a Density Functional Theory (DFT) approach, generating M^I–O₂, M^II–superoxo or M^III–peroxo species. Two different ligands, 12-TMC and 14-TMC, are used to gauge the effects of the ligand ring-size. In general, theory reproduces the experimental results (where available) well enough to give confidence in the calculations. In addition to the usual calculated features of the individual metal complexes, a statistical analysis has been done by comparing the M–O₂ species across the periodical system. It is found that the O₂ binding energy diminishes with higher metal atomic number, while an end-on structure becomes gradually favored. Also, multi-spin state reactivity becomes more likely for metals above Fe. The spin density on O₂ (and with it the formal oxidation state of the metal) is more dependent on the prevailing spin state of the compound rather than the metal type per se, and the higher flexibility of the larger 14-TMC ring has also been verified. The theoretical methods used are also evaluated regarding their accuracy.

---

Introduction

In biochemical systems, evolution has taken advantage of the fact that air (and with it, O₂) is easily accessible.¹ Not only is the O–O bond energy rich which can be utilized to drive the reaction, but the oxygen atoms can be attached to substrates to make them solvable in in vivo systems. The O–O bond break is frequently catalysed by metal centres; thus, an initial metal–dioxygen species is expected to form.² Depending on the external electron and proton donor sources, one could expect the presence of one or more type(s) of such intermediates, e.g. metal–superoxo, –peroxo and –hydroperoxo species.^3–5 It is evident that the initial oxidation state and type of the metal is also a key factor, as for instance both metal(II)- and metal(III)–peroxo species could be plausibly formed.^6,7 In addition to the fact that these species may be en route to form high-valent metal-oxo species⁸ (which are usually the prime candidates to be the oxygenating species^9,10), there are suggestions that these species can act as the oxygenating species themselves as well.¹¹ Thus, the literature is full of studies on both synthetic and biologically occurring metal–dioxygen species, in order to understand the inherent features of these species.^12–16

Our current study is an attempt to contribute to this field by comparing the effects and features of different metals to each other, in an otherwise identical setting. The last condition however, is not easy to achieve. From already published studies, it is sometimes difficult to compare similar species side-by-side due to differences in methods, ligands, metals, solvents etc. used in experiments. This heterogeneity of the studies is probably necessary, as the individual species may not be stable for studies in different experimental conditions. However, much of this problem can be circumvented in theoretical studies, where the stability is not an issue. Even though theoretical methods also have methodological variations between the studies, at least over-the-board homogeneity is possible. The added advantage is that species not yet experimentally isolated could also be studied and compared. Thus, we opted for a theoretical approach in our current study.

In this study, we have calculated [(L)MO₂]⁺ species (Fig. 1), where M is one of the six transition metals (Cr, Mn, Fe, Co, Ni and Cu) with an oxidation state of +1 and O₂ is a neutral species. Hence, any re-distribution of electrons within the complex could result in M^II–superoxo or M^III–peroxo species depending on the precise circumstances. The ligands (L) of both 12-TMC (1,4,7,10-tetramethyl-1,4,7,10-tetraazacyclo-dodecane) and 14-TMC (1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane) were used, enabling us to compare the effects of the ligand ring size. The particular choice of the formal metal(III)-peroxide and TMC ligands for this study is due to the existence of several experimental results for this set of compounds.¹⁷ The existing experimental studies are not a complete set, but enough to allow us to assess the accuracy of our calculations. Therefore, the present work is also a study in how well theoretical methods can match up to and predict experiments. For each of the metal species, we have calculated all the probable spin states, without the O₂ adduct as well as with it in both side-on and end-on fashions. The calculated structures presented here include 97 gas-phase optimized structures and 105 solvent-phase optimized ones. We will denote each species as 1^M for [(12-TMC)MO₂]⁺ species and 2^M for [(14-TMC)MO₂]⁺ species (M = Cr, Mn, Fe, Co, Ni or Cu).

Fig. 1 The models used in this study. [(12-TMC)MO₂]⁺ (upper row) and [(14-TMC)MO₂]⁺ (lower row) with O₂ binding in either a side-on (left column) or an end-on (right column) fashion. M = Cr, Mn, Fe, Co, Ni or Cu. H-Atoms were omitted for clarity.

Methods

Computational details

Calculations were performed using density functional theory (DFT)¹⁸ as implemented in ORCA¹⁹ package. Two functionals, B3LYP^20–24 and BP86,^21,25,26 were used in this study to estimate the energy accuracy of hybrid vs. pure functionals for these systems. The basis set used was CP(PPP)^27,28 for the metal, and Def2-TZVPP²⁹ for the rest. The optimizations were done at the BP86/[CP(PPP)+Def2-TZVPP]/GAS level (where GAS denotes gas-phase), whereby a single-point frequency calculation was carried out at the same level. This also enabled us to calculate the free energy (ΔG) at this level. Also, a single-point B3LYP//BP86/[CP(PPP)+Def2-TZVPP]/GAS calculation was done on that geometry for energy comparisons. The effect of the functional for the geometry optimization itself was investigated only in few cases where it could possibly matter (as detailed in relevant sections). The effects of solvent (acetonitrile) were dealt with separately as a new optimization at the BP86/[CP(PPP)+Def2-TZVPP]/COSMO level, with the solvent being included as a dielectric medium using the COSMO³⁰ scheme as implemented in ORCA. A subsequent single-point B3LYP/[CP(PPP)+Def2-TZVPP]/COSMO calculation was done for the BP86/[CP(PPP)+Def2-TZVPP]/COSMO optimized geometry as well. No frequency calculation has been carried out due to questions of the validity of such calculation on the solvent optimized structures.³¹ Dispersion calculations, where it is suspected to matter, was done by the DFT-D3 program to correct the energies.³² To test its effect on the geometries as well, the representative species (vide infra) were reoptimized at the BP86-D level. The RMSDs were found to be on average at 0.07 Å for 1^M and 0.05 Å for 2^M (see ESI, Table S9†) These values are much smaller than the RMSDs found when comparing the BP86 structures (without dispersion) to the X-ray structures (Table 1); hence the dispersion effect on geometry optimizations were deemed to be of little consequence to our study and not used. To test the sensitivity of the calculations to basis sets, the entire set of calculations were also conducted with CP(PPP) + TZVP^28,33 basis set, without no significant bearing for the current results (data not shown). The data quoted in the text are taken from the BP86/[CP(PPP)+Def2-TZVPP]/COSMO calculations, unless explicitly stated otherwise. A more in-depth look at the electronic structures was done with Natural Bond Orbital (NBO) 6.0 program.³⁴ All the data can be found in the ESI.†

Table 1 Comparison to experiments^a

Metal	12-TMC							14-TMC
	End-on or Side-on		Bond lengths M–O(avg)/O–O (Å)		RMSD^b core/all (Å)	Spin S		End-on or Side-on		Bond lengths M–O(avg)/O–O (Å)		RMSD^b core/all (Å)	Spin S
	DFT	EXP	DFT(solv)	EXP		DFT	EXP	DFT	EXP	DFT(solv)	EXP		DFT	EXP
a The theoretical values presented in this table correspond to the lowest energy spin states. In case there are ambiguities in the theoretical results, the spin state matching experiments are chosen. For the theoretical distances, solvent optimized geometries are given. Values for all spin states are given in ESI.† b Root mean square deviation of the atomic positions between the calculated and the X-ray structures. Core is defined as consisting of the metal, O and N atoms. c The results are ambiguous depending on different functionals as well as the solution phase and/or free energy corrections, that can be chosen to match the experimental values. d EXAFS value. e The distance to the bonding oxygen only, in the spin state matching the DFT column.
Cr	S		1.88/1.47			3/2		S		1.89/1.45			3/2
Mn^37,47	S	S	1.86/1.44	1.85/1.41	0.34/0.98	2	2	S	S	1.86/1.43	1.88/1.40	0.04/0.13	2	2
Fe^36,49	S		1.94/1.44			?^c		S	S	1.95/1.43	1.91/1.46	0.05/0.13	?^c	5/2
Co^38,39,65	S	S	1.88/1.43	1.87/1.44	0.03/0.36	0	0	S	S	1.87/1.38	1.88^d/—	N/A	?^c	1
Ni^35,40	S	S	1.88/1.40	1.89/1.39	0.03/0.11	?^c	1/2	E	E	1.93^e/1.31	1.98^d/—	N/A	3/2	1/2
Cu	E		2.42/1.30			1		E		2.06/1.29			1

---

Models used

When it comes to geometry, TMC is notorious regarding possible variations in the structure. For instance, there may or may not be an axial (solvent) ligand bound to the opposite side of the molecular oxygen. Also, the methyl groups of TMC can be oriented all syn or trans to the bound oxygen, or a mix thereof. The ring structure symmetry is also subject to variations: given a particular C–C bond in the ligand, its corresponding bond on the other side could be either parallel or crossing to it. A full investigation into all these and more possible geometries in combination with all possible spin states would require some resources, with little gain in our understanding of the core metal system. Instead, we have opted to start our calculations from the known X-ray structure for Ni^III–peroxo species for the 12-TMC ligand (1^Ni)³⁵ and Fe^III–peroxo species for the 14-TMC ligand (2^Fe).³⁶ In these structures, the molecular oxygen is bound syn to the methyl groups without any other axial ligands. Also in 2^Fe, for a given C–C bond, the counterpart at the opposite side of the ring is not parallel but crossing. Using the same ligand conformation, we only replace the metal atom. While the ligand conformation may or may not differ for other metal species (not all the species have X-ray structures solved), this gives us the advantage to be able to compare the different metal species with a consistent constant influence from the ligand.

Results

Correlation to experiments

Before discussing new conclusions drawn from the calculations, it is necessary to assess the reliability of the calculations. This is done by comparing two experimentally available criteria: geometry and ground spin state.

Having decided on the ligand conformation (see Methods section), the most obvious geometric feature is whether the dioxygen molecule (O₂) is bound in an end-on or a side-on fashion. There are seven cases in total, where the binding mode of O₂ to the metal is experimentally known: a side-on mode for 1^M (M = Mn, Co, Ni) and 2^M (M = Mn, Fe, Co), and an end-on mode for 2^Ni (Table 1). The calculations are in good agreement with all these seven cases, regardless of the DFT functional or solvent phase used. Moreover, the calculations give the same unanimous answers to the potential structures of the remaining unknown structures. Consequently, the predictive value of the calculations for the binding geometries is high, and should reflect the preferred O₂ binding mode correctly for the unknown structures as well.

To date, there are only five X-ray structures available among the investigated species. For the 1^Ni species, the Ni–O and O–O bond lengths differ by less than 0.01 Å between the calculated and X-ray structures (Table 1). Overlaying only the core section (defined as the metal, O and N atoms), the root-mean square deviation (RMSD) of the atom positions is 0.03 Å, while overlaying the whole atoms results in a RMSD of 0.11 Å. Thus, the calculation seems to be able to reproduce the X-ray structure quite excellently. The RMSD is only marginally larger for 1^Co species (0.36 Å), but this is mostly due to the outlying part of the ligand as the core has the same RMSD as in the Ni case (0.03 Å). Similarly, the calculations on 2^Fe and 2^Mn species show good agreement with experiments as well (Table 1). For the 1^Mn species, the agreement is a little bit worse, with a RMSD of 0.34 Å at the core. In this case, the discrepancy indeed comes from the different C–C bond configurations of the TMC ligand; our use of the 12-TMC ligand configuration from Ni differs slightly from what is experimentally obtained in the Mn case. However, we have shown in our earlier work that a small RMSD of 0.03 Å could be obtained if we were to calculate the 12-TMC configuration corresponding to what has been obtained experimentally for the Mn case.³⁷ As our stated goal is to compare the change of the metal but not the ligand, we keep the 12-TMC structure as calculated in this study, noting that the experimental and theoretical Mn–O and O–O distance differences are still within 0.03 Å (Table 1).

Regarding the spin states, there are six cases where the ground states are experimentally determined. Theory reproduces the experiments unambiguously only in two cases: 2^Mn and 2^Fe (Table 1). If the “right” functional or energy treatment is chosen, theory can match the experiments in three other cases: 1^Co, 1^Ni, and 2^Co. For 1^Co, the electronic energies of both functionals, with or without solvent, predict an S = 0 ground state, in agreement with experiments. Using Gibb's free energy, S = 0 is indeed the ground state at T = 10 K (at which the experiments were done), but not at 298 K. For the 1^Ni case, BP86 prefers the S = 1/2 state, while B3LYP prefers S = 3/2 instead. For 2^Co, BP86 prefers S = 0, while B3LYP prefers S = 2. There are conflicting reports about the preferred spin state of this species,^38,39 but the latest NMR spectra taken at 233 K points to an S = 1 state for this species.³⁹ Indeed, inclusion of thermal effects at 233 K (i.e. obtaining Gibb's free energy) corrects the BP86 energy to an S = 1 preference (see ESI, Table S1†). Only in one case do the current DFT methodologies not match the experimentally determined spin state at all: 2^Ni. The erroneous results on Ni from DFT calculations have been observed before,^40–43 and is discussed in the relevant section below.

The overall conclusion drawn from the above described comparisons of geometry and spin state between the calculated and experimental structures indicates that the accuracy can be fairly good, if some special attention is given to certain cases.

Orbitals

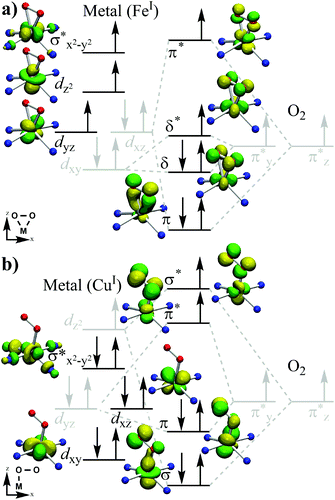
We begin this section by presenting the orbitals involved and the principle of orbital mixings that defines all the species in this study. We define the z-axis as along the normal of the ligand plane (in the case of end-on, this would be along the M–O bond) and the x-axis in the direction of the O–O bond, projected perpendicular to the z-axis (Fig. 2). The five atomic 3d-orbitals on the metal are usually defined as d_xy, d_xz, d_yz, d_z² and d_x²−y². As the last orbital mixes with the ligand nitrogen p_x/y orbitals in a head-to-head fashion, we denote the generated antibonding molecular orbital as σ*_z²−y². On the peroxide side, each of the oxygen atoms contains three p orbitals that can mix with the corresponding p orbitals on the other oxygen atom to form the six classical O₂ bonding π- and anti-bonding π*-orbitals. Of these, only the valence orbitals named π*_y and π*_z are of interest in our study. These π*_y/z orbitals mix with the metal d orbitals in different fashion depending on the structure, and understanding this mixing enables us to correctly describe the electronic configurations of the metal–peroxo species.

Fig. 2 The five metal valence orbitals (d_xy, d_xz, d_yz, d_z² and σ*_x²–y²) combine with two O₂ valence orbitals (π*_y and π*_z) to create a seven valence orbital system of an M–O₂ complex. (a) Side-on system where the d_xy orbital on the metal combines with the π*_y orbital on O₂ to form δ and δ* orbitals. Similarly, the d_xz orbital combines with the π*_z orbital on O₂ to form π and π* orbitals. The actual electron occupation shown is for the S = 5/2 side-on Fe^I + O₂ species. (b) End-on system where the d_yz orbital combines with the π*_y orbital to form π and π* orbitals. The d_z² orbital combines with the π*_z orbital to form δ and δ* orbitals. The electron occupation shown is for the S = 1 end-on Cu^I + O₂ species.

For the side-on bound general M–O₂ species, the five d orbitals of the metal are in Fig. 2a shown to overlap symmetrically with the O₂ π*-orbitals. The lowest lying d orbital, d_xy, mixes with π*_y to form two new orbitals, a bonding δ-orbital and an anti-bonding δ*-orbital. Similarly, d_xz is found to mix with π*_z resulting in a low-energy bonding (π) and a high-energy anti-bonding (π*) orbitals as well. Although d_yz shows some signs of mixing with the bonding π_y-orbital of the oxygen, this mixing is relatively small and not significant for our discussion below; hence, we regard this as a pure d_yz orbital. In the absence of an axial ligand, d_z² does not really mix with other orbitals, and we retain its designation as d_z². Thus, the seven resulting orbitals of the side-on mode species are π, δ, δ*, d_yz, d_z², σ*_x²–y² and π*. Hence, while the metals are usually described to have “five d orbitals” in colloquial language, strictly speaking this may not be the case outside of the isolated metal atom. In our case, molecular interaction creates seven molecular orbitals, which have metal atomic d orbital components. However, usually (and fortunately) only the five valence orbitals are energetically high enough to matter in reactions, thereby supporting the “five d orbitals” notion.

For the end-on species (Fig. 2b), the orbital mixing occurs slightly different. As expected, the O₂ π* orbitals now overlap the metal orbitals asymmetrically, with only the proximal oxygen atom part interacting with the metal. π*_y now mixes heavily with d_yz to form the bonding and anti-bonding pair of orbitals (π and π*). The π*_z orbital on the other hand now overlaps with the d_z² orbital in a head-to-head fashion to create σ/σ* orbital. The seven generated orbitals here are thus denoted as σ, d_xy, π, d_xz, σ*_x²–y², π* and σ*.

Depending on the exact nature of the metal and spin state, the degree of mixing can vary and other alternative descriptions of the involved orbitals are possible. However, we found that significant deviations from the above descriptions only occur in case of high energy spin configurations, where there are some room for alternative orbital mixings. The above description was general and systematic enough for us to apply it to our systems of interest, which are the ground states of each species. Henceforth, we will use the above defined orbital terminology. Table 2 shows the energetically lowest valence orbital occupations found in this study using the above described orbital nomenclature.

Table 2 Valence orbital electronic configuration of the MO₂ species

Side-on	π	δ	δ*	d yz	d z ^2	σ*x^2–y^2	π*
a According to B3LYP, there is a β-electron in this orbital. b According to BP86, there is a β-electron in this orbital.
1 ^Cr, 2^Cr	↑↓	↑↓	↑	↑	↑
1 ^Mn, 2^Mn	↑↓	↑↓	↑	↑	↑	↑
1 ^Fe, 2^Fe	↑↓	↑↓	↑	↑	↑	↑	↑
1^Co	↑↓	↑↓	↑↓	↑↓	↑↓
2 ^Co	↑↓	↑↓	↑(↓)^a	↑↓	↑(↓)^b	↑
1^Ni	↑↓	↑↓	↑↓	↑↓	↑↓	↑
End-on	σ	d xy	π	d xz	σ*x^2–y^2	π*	σ*
2 ^Ni	↑↓	↑↓	↑↓	↑↓	↑	↑	↑
1 ^Cu, 2^Cu	↑↓	↑↓	↑↓	↑↓	↑↓	↑	↑

---

However, an alternate view is available for the end-on 12-TMC species. In the 14-TMC case, the metal–N ligands form a fairly planar plane, which is not the case for 12-TMC. Due to the small ring size, the “plane” is heavily distorted in the 12-TMC case. In fact, it is so distorted that one of the ligand nitrogen atoms forms almost a linear N–M–O direction, which can serve as the x-axis. Together with a perpendicular M–N direction, we can define a new “plane”. Looking at the five d orbitals of the metals, they fit remarkably well to this coordinate system, where the metal orbitals simply switch designations (σ*_x²–y² → σ*_z², d_xy → d_yz, etc.) due to the change of the coordinate axis (x → z, y → y, z → −x). However, in the interest of comparability to the 14-TMC species, we approximate the heavily distorted 12-TMC plane as planar, and designate the orbitals with the same nomenclature as close as possible to the 14-TMC orbitals.

Individual metal–O₂ species

In this section, we detail the individual results obtained for all the metal–O₂ species separately. A statistical analysis over all the species will be presented afterwards based on the designated representative species in each of the subsections below. All the energy values for all the species and computational protocols are presented in the ESI, Table S1.†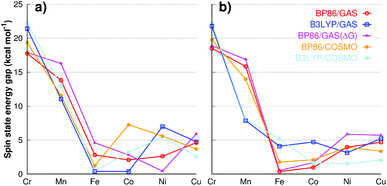

CrO₂. The “Cr^III–peroxo” species has not yet been experimentally synthesized, although the experimental data of both Cr^III–superoxo^44,45 and Cr^IV–peroxo⁴⁶ species are available. Nevertheless, the calculations on our CrO₂ species are uniformly suggesting a side-on structure. This is in contrast to the Cr^III–superoxo species where an end-on crystal structure was obtained with 14-TMC.^44,45 With 12-TMC, however, a side-on Cr^IV–peroxo species was seen instead.⁴⁶ The calculated ground state for the CrO₂ species in our study is a tri-radical side-on S = 3/2 state with singly occupied orbitals of δ*, d_yz and d_z² in both 1^Cr and 2^Cr. This state is around 20 kcal mol⁻¹ more preferable than the next available spin state (Fig. 3), making this theoretical spin state assignment a fairly certain prediction. Based on the low energies, we designate the side-on S = 3/2 states as representative states for 1^Cr and 2^Cr.

Fig. 3 Energy difference between the ground state and the second lowest state, without changing end-on/side-on geometry for (a) 12-TMC and (b) 14-TMC ligand.

The O₂ moiety shows almost zero in Mulliken spin density distribution, a fact that curiously enough occurs in many of the other MO₂ species studied here as well (Table 3). A closer look at the orbitals shows that the relevant electrons are located in the δ, δ* and π orbitals, which are partially delocalized on the O₂ moiety (Fig. 2). Examining δ(β), one finds that this orbital is of significantly less mixed character than δ(α). δ(β) is centred more on O₂ rather than Cr, hence it's β-electron spin density is roughly 1 on the O₂ part and 0 on the Cr part. This cancels out the combined 1 of α-spin from both δ(α) and δ*(α) orbitals; i.e. the contribution of spin density on the O₂ moiety from both δ and δ* orbitals is zero. The π orbital on the other hand is more evenly delocalized between Cr and O₂. Therefore, it contributes partially with its α (0.5) and β (0.4) electrons to the electron count, but largely cancel each other out in terms of spin.

Table 3 Electron count obtained from NBO calculations at the BP86/Def2-TZVPP/COSMO level

	Total electron count						Oxidation state assignment based on
	Metal			O2			Total electron count	Valence orbital analysis
	α	β	Δα–β	α	β	Δα–β
a Round-off error implicates this S = 1 species to appear to be in an S = 1/2 state. Adding spin from the ligand to Cu spin count will imply Cu^II. b Round-off error implicates this S = 1/2 or 3/2 species to appear to be in an S = 1 state. Adding spin from the ligand to Ni spin count will imply Ni^II.
1 ^Cr	12.93	10.06	2.86	8.55	8.39	0.16	^4Cr^I + ^1O2	^4[Cr^III–peroxo]
1 ^Mn	13.64	9.89	3.75	8.51	8.44	0.07	^5Mn^I + ^1O2	^5[Mn^III–peroxo]
1 ^Fe	14.09	10.32	3.78	8.95	8.07	0.88	^5Fe^II + ^2O2˙^−	^6[Fe^II–superoxo]
1 ^Co	12.96	12.96	0.00	8.50	8.50	0.00	^1Co^I + ^1O2	^1[Co^III–peroxo]
1 ^Ni	13.73	12.97	0.76	8.41	8.50	–0.09	^2Ni^I + ^1O2	^2[Ni^III–peroxo]
1 ^Cu	14.09	13.70	0.39	8.96	7.59	1.37	^1Cu^I + ^2O2˙^−^a	^3[Cu^II–superoxo]
2 ^Cr	12.92	10.02	2.90	8.53	8.41	0.12	^4Cr^I + ^1O2	^4[Cr^III–peroxo]
2 ^Mn	13.65	9.86	3.79	8.48	8.46	0.03	^5Mn^I + ^1O2	^5[Mn^III–peroxo]
2 ^Fe	14.09	10.33	3.76	8.95	8.05	0.91	^5Fe^II + ^2O2˙^−	^6[Fe^II–superoxo]
2 ^Co	13.66	12.06	1.59	8.48	8.30	0.18	^3Co^I + ^1O2	^3[Co^III–peroxo]
2 ^Ni	14.05	12.71	1.34	8.96	7.66	1.30	^2Ni^I + ^2O2˙^−^b	^4[Ni^II –superoxo]
2 ^Cu	14.08	13.71	0.37	8.96	7.58	1.38	^1Cu^I + ^2O2˙^−^a	^3[Cu^II–superoxo]

---

To investigate the electron distribution in more detail, we have performed NBO calculations, where the default Lewis structure determined by the program was used on all the representative species in this study. NBO analysis on 1^Cr and 2^Cr yielded a Mulliken natural population of 13 α-electrons and 10 β-electrons on the Cr atom (Table 3). One arrives therefore to the conclusion that the Cr atom has 23 electrons and 3 in spin density, i.e. an S = 3/2 Cr^I species. At the same time, the O₂ moiety has 8.5 α-electrons and 8.4 β-electrons. This would imply almost 17 electrons on O₂ (i.e. superoxo), but as the fractional 0.5 α- and 0.4 β-electrons almost cancel each other out in spin density distribution, these decimals may be best treated here as round-off errors. This would imply 16 electrons on O₂, and the resulting designation should be a singlet O₂ species. Taken together, the spatial distribution of the electrons is thus more consistent with a ⁴Cr^I–¹O₂ designation (the multiplicity number M = 2S + 1 is used as the left superscript), which would not be compatible with the conventional oxidation state designation of these kinds of species. Given that there are some error margins to consider when dealing with Mulliken analysis, and in order to confirm the existing spectroscopic conventions, a better designation would be S = 3/2 Cr^III–peroxo (see Discussion section). This species would produce the same spin density distribution and the same number of electrons in the valence orbitals as ⁴Cr^I–¹O₂.

MnO₂. Experimentally, the “Mn^III–peroxo” species has been found to be in its side-on S = 2 state for 14-TMC⁴⁷ (2^Mn) and 13-TMC⁴⁸ ligands through Evan's method, while the spin state for 1^Mn was determined only indirectly by geometrical comparisons to DFT results.³⁷ The calculations indeed uniformly give an energetically very stable side-on S = 2 state as the ground state for the MnO₂ species (Fig. 3), with singly occupied electrons at δ*, d_yz, d_z² and σ*_x²–y² orbitals (Table 2). Despite its high-spin ground state, no unpaired electron is seen on the O₂ group. This is because the orbital occupation is identical to that of CrO₂ (Table 2), but with an extra electron in the σ*_x²−y² orbital, which does not affect the spin on O₂. Like the CrO₂ case described above, the designated representative state is deduced to be a side-on S = 2 Mn^III–peroxo species, based on the conventional valence electron analysis.

FeO₂. Different from the two previous cases, the energetic differences between different spin states are within 5 kcal mol⁻¹ (Fig. 3). Therefore, one could expect that spin states other than the ground state could be observed or utilized during any substrate reactions. Reflecting these close energies, the ground state designation depends on the calculation protocol. For all B3LYP based calculations, the ground state is an S = 5/2 state for both 1^Fe and 2^Fe, consistent with known bias for the high-spin state preference of the B3LYP functional. BP86 reproduces this result in the case of 2^Fe, except in the gas-phase, which supports an S = 3/2 state by less than 0.4 kcal mol⁻¹. Since more calculations implicate an S = 5/2 rather than S = 3/2 ground state for 2^Fe, we deem the representative structure to be a side-on S = 5/2 structure for 2^Fe, consistent with experimental evidence.^36,49 For 1^Fe, BP86 results in S = 3/2, in total contrast to the B3LYP calculations (including B3LYP optimized structures). In the absence of any experimental results for 1^Fe, we rely on the B3LYP results (i.e. a side-on S = 5/2 species), which in our experience usually renders reliable results for Fe species.^50–52

Assuming the S = 5/2 ground state, Table 3 shows that the Fe structures have one radical on the O₂ moiety and four on Fe, seemingly implicating a Fe^II–superoxo. This stems from the single occupations of the π* and σ* orbitals, which spin-polarizes the O₂ moiety to its superoxo character. As mentioned above, the obtained bond lengths indicate that the calculated geometries match experiments (Table 1) and therefore, the calculation results should warrant a serious consideration. However, a Fe^II–superoxo structure is not (yet) supported experimentally. Based on the Raman spectroscopy and X-ray structure data, this structure has been determined to be a Fe^III–peroxo species.^36,49 As mentioned above, the X-ray geometries are well reproduced by the current calculations, while the Raman vibrations are reasonably close (BP86 gas-phase Fe–O/O–O stretching frequencies: 431/957 cm⁻¹, experimental values: 487/825 cm⁻¹).³⁶ Noteworthy is that if S = 3/2 is assumed in 2^Fe, B3LYP gives that the δ* orbital is doubly occupied (while BP86 reveals that d_z² is doubly occupied instead). The configuration in this case is more akin to Fe^III–peroxo, in a similar pattern to the other MO₂ structures. Hence, depending on the spin state, the O₂ peroxo/superoxo character fluctuates.

CoO₂. Co represents the metal where its ground state remains most difficult to be determined, albeit pure end-on structures can be ruled out. For 1^Co, the calculations generally result in a side-on S = 0 ground state. On the free energy scale however, the preferred spin state is found to be temperature dependent. At our default calculation temperature (298 K), the side-on S = 1 is the ground state. However, the experiments were done at 10 K, where an S = 0 ground state was found. Indeed, changing the calculation settings to 10 K do yield an S = 0 ground state. This state is also in excellent agreement with the crystal structure regarding Co–O and O–O bond lengths. Therefore, the calculations predict temperature effects to be of some importance in experiments. We assign the side-on S = 0 structure as the representative state for 1^Co.

For 2^Co, BP86 gas- and solvent-phase calculations favour a side-on S = 0 state, while B3LYP yields an S = 2 spin state. The BP86 preference for S = 0 was found in earlier calculations as well.³⁹ Again, the temperature effect seems to matter here as well, as the calculated BP86 free energies (at 233 K) yield an S = 1 preference. Indeed, the most recent NMR experiments at 233 K have determined that this structure is in an S = 1 state.³⁹ Examining our computationally obtained S = 1 structure, we find that it exhibits a “half side-on/end-on” structure, where one Co–O bond is longer than the other (1.80 Å/1.94 Å, average 1.87 Å). This is somewhat in contradiction to earlier calculations, where symmetric Co–O₂ distances were obtained, despite a very similar calculation setup (albeit a slightly larger basis sets was applied here).³⁹ However, the average Co–O (1.87 Å) and O–O distances are similar to earlier theoretical results,³⁹ and match the EXAFS Co–O bond distance of 1.88 Å.³⁹ We therefore assign the half side-on/end-on S = 1 structure as the representative state for 2^Co. The earlier calculations assigned this structure as a Co^III–peroxo structure based on the Mulliken spin density distribution analysis for the S = 1 spin state,³⁹ which is about the same as in the current study. An interesting note however is that the electronic structure is different between the functionals: BP86 finds a β-electron in the d_z² orbital, while B3LYP finds this electron in the δ* orbital. The former electron occupation makes the structure slightly ferromagnetically coupled between Co and O₂, while the latter spin distribution makes the structure slightly anti-ferromagnetically coupled (see ESI, Tables S2 vs. S3†).

NiO₂. The spin state preference of the 1^Ni structure is divided along the functional lines. BP86 prefers the S = 1/2 state in accordance with experiments,³⁵ while B3LYP prefers S = 3/2. Both however prefer the side-on species to the end-on one. We have earlier advocated the use of BP86 when calculating Ni species partly because of this and other issues.⁴³ The geometry also supports an S = 1/2 species, as the S = 3/2 Ni–O bond length of 2.05 Å is too long compared to the experimental result of 1.89 Å.³⁵ The side-on S = 1/2 species show virtually no spin density on O₂, and we therefore designate 1^Ni as a side-on S = 1/2 Ni^III–peroxo species, in accordance with experimental findings.

For 2^Ni, the present and previous^40,41 DFT calculations uniformly prefer the S = 3/2 state over S = 1/2, irrespective of functional, solvent or thermal additions.⁵³ Noteworthy is that even ab initio CASSCF calculations yielded an S = 3/2 state for this structure.⁴² While an end-on species is experimentally supported by EXAFS,^35,40 EPR suggest that this species is in an S = 1/2 state.⁴⁰ The reason for this last discrepancy to theoretical results is not known. Both spin states exhibit calculated O–O bond vibrations close to the experimentally obtained values to be of no help in identifying the ground state. Also, in three out of five calculation protocols, the end-on S = 1/2 structure is not even the second favoured structure. In fact, the B3LYP side-on S = 3/2 structure is slightly preferred over even the end-on S = 3/2 structure, let alone the S = 1/2 species (optimizing the geometries with B3LYP did not change this fact). The only support the calculations give to this being an S = 1/2 species is the calculated Ni–O bond distance. This bond was determined by EXAFS to be 1.98 Å,⁴⁰ which is in fact close to the calculated S = 1/2 value (1.96 Å, Table S4 in ESI†). However, the calculated S = 3/2 value is also close (1.93 Å) and therefore also plausible. In terms of spin density distribution, there is 1.2 α-spin density on Ni and 0.5 β-spin density on O₂ in the end-on S = 1/2 state. Rounding off both these values strictly to 1 introduces a round off error, as it will yield an S = 1 ²Ni^III–²O₂˙⁻ species. There is, however, partial significant spin on the 14-TMC ligand (0.3). If we reason that this spin also belongs to Ni as much of it comes from the singly occupied σ*_x²−y² orbital, the round offs yield a ³Ni^II–²O₂˙⁻ species. Thus, the spin distribution seems to imply a borderline case between anti-ferromagnetic coupled ³Ni^II–²O₂˙⁻ and ²Ni^III–¹O₂²⁻. In the S = 3/2 state, the spin density distribution is higher on both Ni (1.3) and O₂ (1.3), which can also be rounded off to ³Ni^II–²O₂˙⁻ with addition of 0.4 spin from the ligand to Ni. Both spin states could thus fit into the description of “Ni^II–superoxo” as described by XAS.⁴⁰

Since the spin state determination was done by EPR comparison to known metal–superoxo S = 3/2 species (and not to S = 3/2 Ni species specifically as this has not been reported before, see footnote 16 of ref. 40), it leaves some room for possible experimental errors. We chose in this publication to designate 2^Ni as an end-on S = 3/2 species since the theoretical values overwhelmingly support this structure, but a final reconciliation between theory and experiment in this issue is pending.

CuO₂. While no TMC CuO₂ structures exist, there are by now a number of literature examples of biological⁵⁴ and synthetic Cu^II–superoxo^55–58 or Cu^III–peroxo^59,60 species. Theoretical treatment of these species have suggested that the Cu^II–superoxo/Cu^III–peroxo assignment is on a sliding scale,⁵ and that DFT may not treat the antiferromagnetically coupled S = 0 Cu^II–superoxo species well in terms of energy, but its geometrical features have been still reproduced satisfactorily.⁶¹ Given the lack of a specific TMC Cu species, the last point cannot be verified for the current species, and we present our DFT results here as obtained.

Both 1^Cu and 2^Cu yield similar results from the calculations. The preferred spin state is S = 1, as was earlier found in a DFT study on 2^Cu with a Cl axial ligand.⁶² The preferred structures obtained here are the end-on species. Hence, these are our representative structures for both 1^Cu and 2^Cu. The O–O bond distances are short, 1.30 Å for 1^Cu and 1.29 Å for 2^Cu. The spin density distribution is ambiguous 1.4 on the O₂ moiety and, in conjunction with the short O–O bond length, would probably be designated as a superoxo species (i.e. Cu^II–superoxo). The NBO calculation reveals 0.3 spin on Cu, which can be raised to 0.6 by adding spin from the ligand to it, being closer to the expected 1 for an S = 1/2 Cu^II species. However, given the weak Cu–O bond strength (under 20 kcal mol⁻¹ depending on the calculation protocol) and the long Cu–O bond lengths of 1.96 Å and 2.06 Å for 1^Cu and 2^Cu, respectively, a borderline case between ²Cu^II–²O₂˙⁻ and a weakly interacting ¹Cu^I–³O₂ species seems to be plausible in this case.

Statistical analysis of the MO₂ structures

In the below section, we aim to utilize our extensive data on the individual MO₂ structures to gain some insights into the trends in metal variations.

Spin state stability. In transition metal systems, multi-spin state reactivity is invoked in many cases, where the reactive spin state is not necessarily the same as the stable ground spin state.⁶³ We have therefore looked into the energy gap between the energetically lowest spin state structure and the second-lowest spin state for each of the species (without changing the side-on/end-on geometry). Here, the energetically lowest structure is not necessarily the representative structure that we have established earlier. We have strictly followed the energetic order given within each of the computational protocol used, enabling us to compare the performance of the computational protocols as well.

As Fig. 3 shows, there is a considerable energy gap (around 20 kcal mol⁻¹) for 1^Cr and 2^Cr to switch its spin state. Therefore, any multi-spin state reactivity here can be ruled out. The massive preference for the ground spin state is clear for any of the computational protocol given; indicating that the spin state preference is very reliable. For 1^Mn and 2^Mn, the energy gap is in the 15 kcal mol⁻¹ range that varies depending on the methods and ligand. This makes multi-spin state reactivity not easy, but still within the theoretically possible range and cannot be ignored. For all the other metals, the gap is typically within 5 kcal mol⁻¹ and thus spin transitions are real and possible, which must be considered in any studies of these species.

Stability of the peroxo adduct. One way of measuring the stability of the MO₂ species is to consider the O₂ binding energy with respect to M^I + O₂ → M^IIIOO. As the energy reference point, the lowest energy M^I state + triplet O₂ within each computational protocol was chosen, and compared to the energetically lowest 1^M and 2^M structure. As can be seen from Fig. 4, there is a clear trend that the binding energy becomes weaker with higher metal atomic number. With a binding energy of 60 kcal mol⁻¹ or more, the 1^Cr and 2^Cr complexes can be seen as “stable” with respect to O₂ dissociation, while 1^Cu and 2^Cu would feature a binding energy of no more than 14 kcal mol⁻¹ (depending on the calculation method). Partial experimental support for this can be inferred as 1^Cu and 2^Cu species has yet to be synthesized, and the current data predict that it would be a somewhat challenging task compared to other metals, at least with respect to O₂ uncoupling. By this logic, 1^Cr and 2^Cr species should be obtained easily.

Fig. 4 The M–O₂ binding energies for (a) 12-TMC and (b) 14-TMC ligand.

Side-on vs. end-on. A related observation in this study is the energy gap between the energetically lowest side-on structure versus the lowest end-on structure. Fig. 5 shows a trend where this energy gap diminishes with higher metal atomic number. The trend however continues beyond the 0 kcal mol⁻¹ line where the end-on structure is out-right preferred in 1^Cu, 2^Ni and 2^Cu. This has an implication for the reaction mechanisms. As the reorganization energy from a side-on to an end-on structure is high for the lower atomic number MO₂ species (M = Cr, Mn and Fe), it is predicted that any O–O bond cleaving reaction would generally not proceed through an end-on M^III–peroxo species containing those metals, although it remains a weak possibility for 1^Fe, 2^Fe and 2^Mn. Indeed, in a theoretical study on cyclohexadiene C–H activation by (14-TMC)Fe^III–superoxo species,⁵² we found that the product of this step, the (14-TMC)Fe^III–hydroperoxo species, essentially kept its side-on configuration in its energetically lowest state despite the protonation. This state was within 1 kcal mol⁻¹ of the corresponding end-on species, showing that in a putative Fe^III–peroxo proton abstraction reaction, protonation with a following reorganization is preferred rather than reorganization followed by protonation. The same side-on structure was also found even for 12-TMC Co^III–hydroperoxo species,⁶⁴ indicating that the reorganization to an end-on M^III–peroxo species may not be all that common, even transiently during reactions.

Fig. 5 Energy differences (E_end-on − E_side-on) for various M–O₂ complexes with (a) 12-TMC and (b) 14-TMC ligand.

Spin on O₂. A common notion is that the spin density distribution on the O₂ group may be proportional to its reactivity. Plotting the spin density distribution on the O₂ group versus metals in the representative state determined above reveals an interesting feature. As can be seen from Fig. 6, 1^Cu, 2^Cu and 2^Ni give the largest spin density distribution on the O₂ moiety, indicating a high reactivity (hence instability) of these species. On the other end of the spectra, Cr and Mn based complexes are unanimously shown to have very small spin on the O₂ moiety, indicating stability. For Fe, due to its unique five-electron high spin preference, large spin density distribution on O₂ is found, and therefore implying a high reactivity. Worth noting is that 1^Ni due to its side-on conformation has lower spin density on O₂ than the end-on 2^Ni, hence lower reactivity is expected and confirmed experimentally.³⁵ However, it should be kept in mind that spin density distribution on O₂ is not necessarily the sole determining factor for the reactivity.

Fig. 6 Spin density distribution on the O₂ moiety for various M–O₂ complexes with (a) 12-TMC and (b) 14-TMC ligand. The spin state chosen for each of the metal structure is corresponding to the representative state for each species, as discussed in the text.

Discussion

Ring size effect

In term of differences between 12-TMC and 14-TMC ligands, the general trends on spin state stability, O₂ binding energies and spin density distribution are similar (Fig. 3, 4 and 6). Looking at the average M–N bond lengths, it is clear that these bonds in 2^M are longer than those in 1^M, due to the larger ring size (Fig. 7a). As a result, this probably causes the σ*_x²−y² orbital energy to be lower and closer to the d_z² orbital in 2^M compared to the corresponding case in 1^M. This may be the cause to why 1^Co prefers to avoid occupying the σ*_x²−y² orbital by switching to an S = 0 state (Table 2), while the more accessible σ*_x²−y² orbital in 2^Co is occupied to form an S = 1 ground state.

Fig. 7 (a) The average M–N distance, showing that the 14-TMC ligand affords larger M–N distances and (b) the smallest N–M–N angle, showing that 14-TMC fluctuates more and therefore is more flexible.

The flexibility of the ligand binding can also be illustrated with the (smallest) N–M–N angle, where the two N atoms oppose each other, and therefore indicate the planarity of the M–(4 × N) plane. In 2^M, this angle deviates from 125° to 149° within the representative species (a span of 24°, Fig. 7b). In 1^M however, this angle is markedly more constrained, ranging from 105° to 114° (a span of 9°). The larger ring size thus generates more flexibility. The smaller N–M–N angle also means that the O₂ binding site is wider and more accessible to O₂. This can be seen from the O₂ binding energies, where the binding is few kcal mol⁻¹ stronger for 1^M than 2^M (Fig. 4). The calculations thus corroborate experimental results,^35,65 that explain the preference of a side-on binding mode for 1^Nivs. an end-on binding mode for 2^Ni as a result of the spatial openness at the O₂ binding site.

Metal oxidation states

The availability of the exact electronic structure enables us to investigate the question of whether a certain structure is in fact an M^I, M^II or M^III state, coupled to O₂, superoxo or peroxo moiety, respectively. This is, however, a challenging task from a computational point of view. One might, naturally, assume that the electron count would have something to do with it. A useful case was discussed in some length above for 1^Cr and 2^Cr, vide supra. Thus, the electron count by NBO generally supports a ^MM^I–¹O₂ designation in our current study (Table 3). However, as M^I–O₂ species are clearly not acceptable in light of current conventions, most computational chemists look at the number of electrons in the valence orbitals only, combined with the spin density distribution. In the current study, most of the species were found to have no spin on the O₂ part and with the number of electrons in the five highest valence orbitals matching the isolated M^III, consistent with a M^III–peroxo designation. Hence, this is the oxidation state we generally present above (with the exception of Fe and Cu based structures, vide supra). Noteworthy is that the excess radical distribution would be the same for ^MM^III–peroxo as for ^MM^I–¹O. There is also a good agreement with the geometries and spin states obtained in comparison to experiments; implying that the calculations and experiments in fact agree but that the oxidation states interpretations may need some further reconciliations between theoreticians and experimentalists.

Comparing with experiments, our calculated oxidation states differ from the experimentally determined ones in the case of Fe. We determine these species to be an Fe^II–superoxo species because of the high-spin S = 5/2 configuration that is only attainable for Fe, yielding a total spin of just below 1 on the O₂ moiety (Table 3). The experiments indicate an Fe^III–peroxo species instead based on both the O–O distance and resonance Raman frequencies, which are both reproduced by our calculations. For Cu based structures, no experimental structure exists, but if attainable, we predict it to be a borderline case to a Cu^I–O₂ species.

Computational protocol dependence

In this study, we have deliberately made use of BP86 geometries only as this functional is generally known to compete with (and even excel over) B3LYP when it comes to the quality of geometries, while being faster to compute.⁶⁶ We have shown here that the obtained BP86 geometries are indeed in agreement with experiments, where available (Table 1). B3LYP is generally thought of as being more accurate in energy evaluations, while BP86 seemed to be a better fit for Ni species specifically.⁴³ This prompted us to consider both energies in our evaluations. We consider both the SCF gas-phase energy and the Gibb's free energy, and we also incorporate acetonitrile solvent effects on both geometries and energies for comparison. There are individual cases where the choice of computational protocol matter (vide supra), but if looking at trends over multiple species (as in Fig. 3–6), the conclusions will most likely be the same. Hence, we do not see any excessive method dependence in our calculations, but there are enough deviations to imply that methodology checks are always warranted in any individual calculation.

Conclusions

We have used five different computational protocols (BP86//BP86/GAS ΔE, B3LYP//BP86/GAS ΔE, BP86//BP86/GAS ΔG, BP86//BP86/COSMO ΔE and B3LYP//BP86/COSMO ΔE) to evaluate the characteristics of six M^I + O₂ compounds (M = Cr, Mn, Fe, Co, Ni and Cu) with two different closely related ligands, 12-TMC and 14-TMC. The geometries, valence orbital electron occupations and oxidation states are either predicted or confirmed (where experiments are available). A statistical comparison over all the metals reveals that as the metal atomic number goes up, (1) O₂ binding energy decreases, (2) spin state preference becomes less clear, (3) end-on structure is gradually being stabilized, and becomes preferred at Ni or Cu. In addition, the spin density distributions on the O₂ group are seen to be more dependent on the individual spin state rather than the metal atomic number, and experimental observations about 14-TMC having a more flexible ring wrapping than 12-TMC have also been confirmed. Determining the most likely structure and spin state, we find that 1^Cr and 2^Cr are side-on S = 3/2 Cr^III–peroxo species, 1^Mn and 2^Mn are side-on S = 2 Mn^III–peroxo species, 1^Fe and 2^Fe are side-on S = 5/2 Fe^II–superoxo species, 1^Co is a side-on S = 0 Co^III–peroxo species, 2^Co is a half side-on/end-on S = 1 Co^III–peroxo species, 1^Ni is a side-on S = 1/2 Ni^III–peroxo species, 2^Ni is an end-on S = 3/2 Ni^II–superoxo species, and finally 1^Cu and 2^Cu are end-on S = 1 Cu^II–superoxo species.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was gratefully supported by the NRF of Korea through CRI (NRF-2012R1A3A2048842 to W. N.), GRL (NRF-2010-00353 to W. N.), and MSIP (NRF-2013R1A1A2062737 to K.-B. C.). Professors Joan S. Valentine and Jaeheung Cho are acknowledged for ideas and consultations.

Notes and references

1. Active Oxygen in Biochemistry, ed. J. S. Valentine, C. S. Foote, A. Greenberg and J. F. Liebman, Springer, Boston, MA, 1995.
2. M. Unno, H. Chen, S. Kusama, S. Shaik and M. Ikeda-Saito, J. Am. Chem. Soc., 2007, 129, 13394.
3. N. Kitajima, H. Komatsuzaki, S. Hikichi, M. Osawa and Y. Moro-oka, J. Am. Chem. Soc., 1994, 116, 11596.
4. D. P. de Sousa, J. O. Bigelow, J. Sundberg, L. Que, Jr. and C. J. McKenzie, Chem. Commun., 2015, 51, 2802.
5. C. J. Cramer and W. B. Tolman, Acc. Chem. Res., 2007, 40, 601.
6. J. Rosenthal and D. G. Nocera, Acc. Chem. Res., 2007, 40, 543.
7. E. E. Chufán, S. C. Puiu and K. D. Karlin, Acc. Chem. Res., 2007, 40, 563.
8. Y.-M. Lee, S. Hong, Y. Morimoto, W. Shin, S. Fukuzumi and W. Nam, J. Am. Chem. Soc., 2010, 132, 10668.
9. S. Shaik, D. Kumar, S. P. de Visser, A. Altun and W. Thiel, Chem. Rev., 2005, 105, 2279.
10. Metal-Oxo and Metal-Peroxo Species in Catalytic Oxidations, ed. B. Meunier, Springer, Berlin Heidelberg, 2000.
11. A. D. Vaz, S. J. Pernecky, G. M. Raner and M. J. Coon, Proc. Natl. Acad. Sci. U. S. A., 1996, 93, 4644.
12. W. Nam, Acc. Chem. Res., 2007, 40, 465.
13. A. J. Jasniewski and L. Que, Jr., Chem. Rev., 2018, 118, 2554.
14. M. Guo, T. Corona, K. Ray and W. Nam, ACS Cent. Sci., 2019, 5, 13.
15. W. Nam, Y.-M. Lee and S. Fukuzumi, Acc. Chem. Res., 2018, 51, 2014.
16. K. Ray, F. F. Pfaff, B. Wang and W. Nam, J. Am. Chem. Soc., 2014, 136, 13942.
17. J. Cho, R. Sarangi and W. Nam, Acc. Chem. Res., 2012, 45, 1321.
18. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
19. F. Neese, ORCA – an ab initio, Density Functional and Semiempirical program package, Version 3.01, University of Bonn, 2010.
20. The B3LYP/G functional as first implemented in the Gaussian packages was used here.
21. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
22. A. D. Becke, J. Chem. Phys., 1993, 98, 1372.
23. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
24. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785.
25. J. P. Perdew, Phys. Rev. B, 1986, 33, 8822.
26. J. P. Perdew, Phys. Rev. B, 1986, 34, 7406.
27. The ORCA basis set ‘CoreProp’ was used. This basis is based on the TurboMole DZ basis developed by Ahlrichs and coworkers and obtained from the basis set library under ftp://ftp.chemie.uni-karlsruhe.de/pub/basen (now defunct).
28. The Ahlrichs (2d2fg,3p2df) polarization functions were obtained from the TurboMole basis set library under ftp://ftp.chemie.uni-karlsruhe.de/pub/basen (now defunct). Sc-Zn: 2p functions from Wachters JCP, 52 (1970), 1033 plus one f-function from the TurboMole library.
29. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
30. S. Sinnecker, A. Rajendran, A. Klamt, M. Diedenhofen and F. Neese, J. Phys. Chem. A, 2006, 110, 2235.
31. J. Ho, A. Klamt and M. L. Coote, J. Phys. Chem. A, 2010, 114, 13442.
32. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
33. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829.
34. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, Theoretical Chemistry Institute, University of Wisconsin-Madison, 2013.
35. J. Cho, R. Sarangi, J. Annaraj, S. Y. Kim, M. Kubo, T. Ogura, E. I. Solomon and W. Nam, Nat. Chem., 2009, 1, 568.
36. J. Cho, S. Jeon, S. A. Wilson, L. V. Liu, E. A. Kang, J. J. Braymer, M. H. Lim, B. Hedman, K. O. Hodgson, J. S. Valentine, E. I. Solomon and W. Nam, Nature, 2011, 478, 502.
37. H. Kang, J. Cho, K.-B. Cho, T. Nomura, T. Ogura and W. Nam, Chem. – Eur. J., 2013, 19, 14119.
38. Y. Jo, J. Annaraj, M. S. Seo, Y.-M. Lee, S. Y. Kim, J. Cho and W. Nam, J. Inorg. Biochem., 2008, 102, 2155.
39. R. Sarangi, J. Cho, W. Nam and E. I. Solomon, Inorg. Chem., 2011, 50, 614.
40. M. T. Kieber-Emmons, J. Annaraj, M. S. Seo, K. M. Van Heuvelen, T. Tosha, T. Kitagawa, T. C. Brunold, W. Nam and C. G. Riordan, J. Am. Chem. Soc., 2006, 128, 14230.
41. R. Latifi, L. Tahsini, D. Kumar, G. N. Sastry, W. Nam and S. P. de Visser, Chem. Commun., 2011, 47, 10674.
42. J. Zapata-Rivera, R. Caballol and C. J. Calzado, J. Comput. Chem., 2012, 33, 1407.
43. K.-B. Cho, J. Cho, S. Shaik and W. Nam, J. Phys. Chem. Lett., 2014, 5, 2437.
44. J. Cho, J. Woo and W. Nam, J. Am. Chem. Soc., 2010, 132, 5958.
45. J. Cho, J. Woo and W. Nam, J. Am. Chem. Soc., 2012, 134, 11112.
46. A. Yokoyama, J. E. Han, J. Cho, M. Kubo, T. Ogura, M. A. Siegler, K. D. Karlin and W. Nam, J. Am. Chem. Soc., 2012, 134, 15269.
47. M. S. Seo, J. Y. Kim, J. Annaraj, Y. Kim, Y.-M. Lee, S.-J. Kim, J. Kim and W. Nam, Angew. Chem., Int. Ed., 2007, 46, 377.
48. J. Annaraj, J. Cho, Y.-M. Lee, S. Y. Kim, R. Latifi, S. P. de Visser and W. Nam, Angew. Chem., Int. Ed., 2009, 48, 4150.
49. J. Annaraj, Y. Suh, M. S. Seo, S. O. Kim and W. Nam, Chem. Commun., 2005, 4529.
50. L. M. Blomberg, M. R. A. Blomberg and P. E. M. Siegbahn, J. Inorg. Biochem., 2005, 99, 949.
51. S. Shaik, S. Cohen, Y. Wang, H. Chen, D. Kumar and W. Thiel, Chem. Rev., 2010, 110, 949.
52. K.-B. Cho, H. Chen, D. Janardanan, S. P. de Visser, S. Shaik and W. Nam, Chem. Commun., 2012, 48, 2189.
53. The side-on S = 3/2 species is predicted to be a TS by BP86 frequency calculation, yielding an imaginary frequency of i143.84 cm⁻¹ and higher in energy than the S = 1/2 species. However, both single-point and optimized B3LYP calculations actually predict this structure to be the energetically lowest structure.
54. S. Itoh, Curr. Opin. Chem. Biol., 2006, 10, 115.
55. K. Fujisawa, M. Tanaka, Y. Moro-oka and N. Kitajima, J. Am. Chem. Soc., 1994, 116, 12079.
56. P. J. Donoghue, A. K. Gupta, D. W. Boyce, C. J. Cramer and W. B. Tolman, J. Am. Chem. Soc., 2010, 132, 15869.
57. J. Y. Lee, R. L. Peterson, K. Ohkubo, I. Garcia-Bosch, R. A. Himes, J. Woertink, C. D. Moore, E. I. Solomon, S. Fukuzumi and K. D. Karlin, J. Am. Chem. Soc., 2014, 136, 9925.
58. S. Kim, J. Y. Lee, R. E. Cowley, J. W. Ginsbach, M. A. Siegler, E. I. Solomon and K. D. Karlin, J. Am. Chem. Soc., 2015, 137, 2796.
59. N. W. Aboelella, E. A. Lewis, A. M. Reynolds, W. W. Brennessel, C. J. Cramer and W. B. Tolman, J. Am. Chem. Soc., 2002, 124, 10660.
60. A. M. Reynolds, B. F. Gherman, C. J. Cramer and W. B. Tolman, Inorg. Chem., 2005, 44, 6989.
61. B. F. Gherman and C. J. Cramer, Inorg. Chem., 2004, 43, 7281.
62. A. Ansari, P. Jayapal and G. Rajaraman, Angew. Chem., Int. Ed., 2015, 54, 564.
63. M. Swart and M. Costas, Spin States in Biochemistry and Inorganic Chemistry, John Wiley & Sons, Ltd, Oxford, UK, 1st edn, 2015.
64. W.-Y. Tcho, B. Wang, Y.-M. Lee, K.-B. Cho, J. Shearer and W. Nam, Dalton Trans., 2016, 45, 14511.
65. J. Cho, R. Sarangi, H. Y. Kang, J. Y. Lee, M. Kubo, T. Ogura, E. I. Solomon and W. Nam, J. Am. Chem. Soc., 2010, 132, 16977.
66. M. Bühl and H. Kabrede, J. Chem. Theory Comput., 2006, 2, 1282.

---

Footnote

† Electronic supplementary information (ESI) available: Energies, NBO results, Mulliken spin density distributions, geometries and coordinates. See DOI: 10.1039/c9qi00407f

---