Development of a quantum chemical descriptor expressing aromatic/quinoidal character for designing narrow-bandgap π-conjugated polymers

Abstract

A new quantum chemical descriptor, quinoid stabilization energy (QSE), is established for the computational design of narrow-bandgap polymers. QSE was constructed based on the energy change of homodesmotic reactions of a dimethylated monomer with oligoacetylene. It can be uniquely defined for heterocyclic and polycyclic monomers, unlike the arbitrary conventional descriptors based on bond length alternation. Density functional theory (DFT) calculations revealed a relationship between QSE and the bandgap of polymers. According to the relationships obtained for 268 homopolymers and 179 alternating copolymers selected from many different families, narrow-bandgap polymers can be designed with QSE = 0, which indicates the intermediate state between aromatic and quinoid forms. Copolymers having QSE = 0 can be achieved by combining a quinoidal monomer with an aromatic one. The main advantage of this approach of designing narrow-bandgap polymers is that it requires only information of the monomers and their linking site. Using this approach, we propose a new candidate of narrow-bandgap alternate copolymers constructed by two monomer units that are both usually categorized as acceptors. The proposed copolymer has a calculated bandgap of 0.76 eV, indicating a potentially high air stability. Since QSE as a simple descriptor is highly compatible with machine learning, this approach should accelerate the development of ultra-narrow-bandgap polymers.

---

Introduction

π-Conjugated polymers are used in organic light emitting diodes,^1–5 organic solar cells,^6–12 and organic field effect transistors.^13–16 Among them, those with narrow bandgaps are of great interest, because their near infrared (NIR) absorption, high conductivity, and ambipolar charge transport properties are useful for those devices. Additionally, NIR absorption has attracted increasing research attention in the field of biomedicine, with applications in optical and electronic biosensors, bioimaging, and anticancer and antimicrobial therapies.^17–25 In general, polymers have excellent moldability, and their various properties can be tuned according to different molecular designs. The tunability enables narrowing of the bandgap of π-conjugated polymers, although the organic matter has an inherently wide bandgap. However, the design of narrow-bandgap polymers remains challenging because the molecular design of π-conjugated polymers can be considered in an extremely large number of possible polymers. Commonly, narrow-bandgap polymers are synthesized by combining two or more monomers. From a selection of only 100 kinds of monomers, 4950 different copolymers can be obtained by combining two monomers. Therefore, an efficient strategy is required to find candidate narrow-bandgap polymers.

Computational design could dramatically speed up the discovery of new narrow-bandgap polymers. The corresponding strategy is usually based on identifying key quantum chemical descriptors that determine the bandgap of π-conjugated polymers. With the rapid recent development in materials informatics, the importance of quantum chemical descriptors continues to grow. The donor–acceptor approach, which is the most popular design strategy for realizing narrow-bandgap π-conjugated polymers using quantum chemical descriptors,^26–28 achieves a narrow bandgap by copolymerizing a monomer having a high highest occupied molecular orbital (HOMO) level as a donor and a monomer having a low lowest unoccupied molecular orbital (LUMO) level as an acceptor.²⁸ Thus, the key quantum chemical descriptors in this approach are the HOMO level of a donor and the LUMO level of an acceptor.

Another strategy that aims for an intermediate structure between the aromatic and quinoidal forms (the aromatic-quinoid approach) has been proposed as a design guideline for realizing narrow-bandgap polymers.^29–33 For example, the bandgap of poly(isothianaphthene) (PITN) is 1.0 eV.³⁴ This molecule is believed to have an intermediate structure between the aromatic and quinoidal forms (Fig. 1). The aromatic-quinoid approach was based on the theoretical investigations reported by Brédas.^35,36 He observed that the minimal bandgap is obtained when the poly(thiophene) lies between those of the quinoidal and aromatic forms upon changing and forcing the bond length between carbon atoms. Thus, a narrow bandgap is obtained when the bond alternation is small.

Fig. 1 Chemical and resonance structures of poly(isothianaphthene).

In 2013, Bérubé and co-workers proposed a quantum chemical descriptor based on bond alternation.³⁰ They indicated theoretically that alternate copolymers composed of aromatic and quinoidal monomer units have an intermediate structure between aromatic and quinoidal forms, and appear to have narrow bandgaps. In addition, they reported that the aromatic-quinoid approach could better predict the bandgap than the donor–acceptor approach. Also, this approach can handle homopolymers and copolymers in a unified way. Therefore, the aromatic-quinoid approach is a promising design guideline for realizing narrow-bandgap polymers.

Recently, narrow-bandgap polymers have been synthesized using the aromatic-quinoid approach.^37–49 For example, a π-conjugated polymer including the thienoquinoid skeleton was synthesized with a bandgap as narrow as 0.88 eV.³⁷ In addition, experimental studies have also used similar approaches based on quinoidal measurements by the bond alternation of copolymers to design narrow-bandgap polymers.^44,45 These narrow-bandgap copolymers were qualitatively designed by the aromatic-quinoid approach. However, the quantum chemical descriptor based on bond alternation is not suitable for designing narrow-bandgap polymers because the conventional descriptor has some problems, as described below.

Our purpose in this study is developing new quantum chemical descriptors that are suitable for the design of narrow-bandgap polymers based on the aromatic-quinoid approach. Specifically, the new descriptor improves the following three issues found in the conventional descriptor.

(1) Calculation of polymers is necessary in the conventional descriptor because it is based on bond alternation for polymers.

(2) Since the conventional descriptor excludes heteroatom-containing bonds from the evaluation of bond alternation, it could not be applied to heterocycles such as 1,3,4-thiadiazole rings that do not contain C–C or C=C bonds.

(3) The conventional descriptor is somewhat arbitrary in the selection of bonds for evaluating bond alternation in the polycyclic monomer unit.

Fundamentally, these three problems arise because the conventional descriptor is based on bond alternation. As a solution, we have developed quinoid stabilization energy (QSE), which is a descriptor based on the stabilization energy of structural change from the aromatic form to the quinoidal form. QSE provides a guideline for combining monomers to create narrow-bandgap copolymers. It can uniformly handle monomers containing heteroatoms, and its value is uniquely determined for every monomer. In addition, it is possible to predict the change in the bandgap depending on the linkage of the monomer. QSE has already been demonstrated as a powerful tool for designing ultra-narrow-bandgap polymers by Hasegawa and co-workers.³⁸ Finally, since the new descriptor can be obtained from simple calculations, it is promising for use in materials informatics. This paper describes details of the development and assessment of QSE for designing narrow-bandgap copolymers.

Definition of QSE

In order to estimate the stabilization energy of the structural change of the monomer unit in the polymers from the aromatic form to the quinoidal form, energy change in the dehydrogenation of the dimethyl form of the monomer was calculated. The case of poly(thiophene) is exemplified in eqn (1).

The energy change of this reaction, described as ΔE_mono, includes not only energy change due to the structural change from the aromatic form to the quinoidal form but also those due to dehydrogenation and the expansion of π conjugation. To compensate for the redundant energy changes, such as dehydrogenation, the energy change associated with hydrogenation to form oligo(acetylene) (eqn (2)) was calculated.

The energy change of this reaction (ΔE_a) converged to 31.4 kcal mol⁻¹ for the oligo(acetylene) with n = 8 (see Fig. S1 of the ESI†). Therefore, 31.4 kcal mol⁻¹ was used for ΔE_a in this work. QSE was defined by eqn (3) from ΔE_mono and ΔE_a,

QSE = ΔE_mono + ΔE_a (3)

That is, QSE is the energy change of the homodesmotic reaction shown in eqn (4).

A positive QSE indicates that the aromatic form is stable for the monomer unit in the polymer, while a negative QSE shows that the quinoidal form is stable.

Computation details

All calculations were carried out using the Gaussian 16 program.⁵⁰ The QSE was calculated using the long-range and dispersion-corrected ωB97X-D⁵¹ functional combined with the 6-311G(d,p)⁵² basis set. The optimized molecular structures were verified by vibrational analysis, as equilibrium structures do not have imaginary frequencies. The zero-point energy was calculated using the unscaled vibrational frequencies. The detailed procedure of the QSE calculation is described in the ESI.† To confirm the accuracy of the QSE calculation, we tested 10 typical monomers by the single-point calculation at the CCSD(T)⁵³/6-311G(d,p) level for the optimized structure obtained at the ωB97X-D/6-311G(d,p) level. The trend of QSE from ωB97X-D was in good agreement with that of CCSD(T), although the former includes a systematic error of about 3 kcal mol⁻¹ compared to the latter, as shown in Fig. S2 of the ESI.†

The geometry of polymers was optimized by the one-dimensional periodic boundary condition (PBC) calculation at the B3LYP/6-31G(d,p) level.^54,55 The bandgap of polymers was obtained by the single-point calculation using 100 k-points along the Brillouin zone at the B3LYP/6-31G(d,p) level. In this study, the “calculated bandgap” was defined as the minimal direct gap between the highest occupied crystal orbital (HOCO) and the lowest unoccupied crystal orbital (LUCO), which was at the Γ-point in almost all polymers. The direct gap is related to the experimental optical bandgap. The functional dependence of the calculated bandgap is discussed in the ESI (Fig. S3 and Table S1†).

Results and discussion

Correlation between QSE and the bandgap of homopolymers

In order to evaluate the correlation between the QSE of the monomers and the bandgap of the polymers, QSE values of 268 monomers and the bandgaps of their homopolymers were calculated.^56,57 The calculated bandgap and QSE are plotted in Fig. 2. The bandgap is the lowest when QSE = 0, and therefore the polymers having an intermediate state between the aromatic form and the quinoidal form have a narrow bandgap.

Fig. 2 Correlation between the QSE and bandgap in 268 homopolymers.

Unfortunately, a range of bandgap values at the same QSE values was 1–2 eV. While the distribution of the bandgap against QSE shows that the narrow-bandgap polymers can be qualitatively predicted by having QSE near 0, the quantitative prediction of bandgap is still difficult.

Based on the values of QSE, representative examples of aromatic, quinoidal, and their intermediate monomer units are shown in Fig. 3. The two intermediate monomer units with the narrowest theoretical bandgaps are thienoisoindigo (TII) and pyrroloisoindigo (PII), and the theoretical bandgaps of their homopolymers are 0.70 and 0.68 eV, respectively. The experimental optical bandgap of poly(thienoisoindigo) is reported as 0.57 eV.⁵⁸ Since bond alternation is not completely eliminated in the TII polymer (Fig. S4†), it is considered that the bandgap does not disappear in the vicinity of QSE = 0 because of the Peierls transition, which is a distortion of the periodic lattice of a one-dimensional system due to the oscillation of atomic positions.

Fig. 3 Chemical structure, QSE in kcal mol⁻¹, and calculated bandgap (E_g) in eV for a few examples of aromatic, quinoidal, and intermediate monomer units.

The QSEs of thiophene (Thi), isothianaphthene (ITN), and isonaphthothiophene (INT) are 12.1, −3.3, and −10.0 kcal mol⁻¹, respectively, and the experimental optical bandgaps of their homopolymers are 2.1,⁵⁹ 1.0,³⁴ and 1.5 eV (ref. 60) (calculated values: 2.05, 1.47, and 1.97 eV). In these three molecules, the smaller the absolute value of QSE, the narrower the homopolymer bandgap. The relationship between the number of condensed benzene rings and the bandgap cannot be handled by the donor–acceptor approach, neither can it be explained by the extension of the π-conjugated system. An advantage of QSE is the ability to evaluate the changes in the bandgap due to the different numbers of annulated rings.

The change in bandgap due to the difference in linkage can also be estimated by QSE. For example, in thieno[3,4-b]thiophene linked at 2,4-position (2,4-TT) and at 4,6-position (4,6-TT), the QSE values are 17.2 and 3.5 kcal mol⁻¹, respectively. So, the QSE values change depending on the linkage for the same monomer unit. The calculated bandgaps of 2,4-TT and 4,6-TT homopolymers are 1.92 and 0.96 eV, respectively. This result indicates that QSE can guide the design of appropriate linkage to achieve a narrow bandgap.

1,3,4-Thiadiazole (TDz) is a monomer unit without any C–C bond in the ring, and so it could not be evaluated by the conventional bond alternation-based indicators. The QSE value of TDz is 25.2 kcal mol⁻¹. The calculated bandgap of the TDz homopolymer is 3.19 eV, which correlates with the QSE value. Thus, QSE could be successfully applied to monomer units that do not have C–C or C=C bonds in the ring.

When adjacent monomer units are considerably twisted, the bandgap could be significantly different from the value predicted from QSE, and this problem is also encountered in the donor–acceptor approach. For example, although thiadiazoloquinoxaline (TDQ) has a QSE value close to 0 (−1.6 kcal mol⁻¹), the calculated bandgap of its homopolymer is 2.52 eV. This wide bandgap can be explained by the fact that poly(TDQ) has a large dihedral angle of 70° between adjacent monomer units due to steric hindrance. In addition, by the twist in the polymers, the larger variation of bandgaps in Fig. 2 in the region of QSE > 0 than in QSE < 0 can be explained as follows. Polymers having the quinoidal form exhibit high planarity due to the double bond between the monomer units. On the other hand, polymers having the aromatic form are often twisted. Thus, neither the QSE nor the donor–acceptor approach can be used to evaluate the bandgap of polymers that are largely twisted due to steric hindrance. To improve the prediction accuracy, it would be necessary to consider not only the QSE but also the twist of polymers.

Applying QSE to alternating copolymers

The number of possible monomer combinations in copolymers is enormous. Just for alternating copolymers, about 5000 copolymers can be created from the combination of 100 kinds of monomers. If the bandgap of the copolymers can be predicted only from the monomer information, then it is possible to design narrow-bandgap polymers without performing a large amount of calculation. Therefore, we assumed the QSE of alternating copolymers (QSE_CO) to be the average QSE of the two constituent monomers, as expressed in eqn (5).

QSE_CO = (QSE₁ + QSE₂)/2 (5)

Here, QSE₁ and QSE₂ are the QSE values of monomer 1 and 2, respectively. The calculated bandgaps of 179 alternating copolymers are plotted against QSE_CO in Fig. 4.⁵⁶ The copolymers with the smallest bandgap have QSE_CO values around 0. This result indicates a guideline: alternating copolymers with narrow bandgaps can be designed by combining two monomers that have an average QSE near 0.

Fig. 4 Correlation between QSE_CO and a bandgap of the 179 alternate copolymers.

Note that the distribution character of the bandgap against QSE_CO was the same as that for homopolymers (Fig. 2). Thus, the use of QSE_CO is also inappropriate for quantitatively predicting the bandgap of copolymers.

A few examples of alternating copolymers with narrow calculated bandgaps are shown in Fig. 5. In the aromatic-quinoid approach using QSE, it is possible to design narrow-bandgap copolymers by combining either two donors or two acceptors. For example, thienopyrroledione⁶¹ (TPD) and thienothiadiazole^62,63 (TTD) are generally used as acceptor units in narrow-bandgap copolymers, and their QSE values are 17.6 and −12.2 kcal mol⁻¹, respectively. Because their alternating copolymer (TPD-TTD) has a QSE_CO close to 0 (2.7 kcal mol⁻¹), it is expected to exhibit a narrow bandgap. Indeed, the calculated bandgap of TPD-TTD was very narrow at 0.76 eV. Furthermore, alternating copolymers combining two acceptor units are expected to have a high ionization potential, which is known to indicate a higher stability in air.^64–72 Therefore, QSE could be used as a new design guideline for narrow-bandgap polymers with high air stability.

Fig. 5 Chemical structures, QSE_CO in kcal mol⁻¹, and calculated bandgap (E_g) in eV for a few examples of narrow-bandgap alternating copolymers.

Applying QSE to periodic copolymers with various monomer ratios

In order to control the bandgap, periodic copolymers with a component monomer ratio different from 1 : 1 are often synthesized.^73–78 Therefore, it is important to predict the appropriate monomer ratio in periodic copolymers for showing a narrow bandgap based on QSE. We tried to extend QSE_CO to periodic copolymers with various monomer ratios, by defining it as the average QSE of two monomers weighted by the mole fraction, as shown in eqn (6).

QSE_CO = QSE₁·w₁ + QSE₂·w₂ (6)

Here, w₁ and w₂ are the mole fractions of monomer 1 and 2, respectively. In the case of alternating copolymers, QSE_CO = (QSE₁ + QSE₂)/2.

As an example, the following two types of periodic copolymers were selected: (1) copolymers of benzo[1,2-b:4,5-c′]dithiophene (BDT) and 3,4-ethylenedioxythiophene (EDOT) and (2) copolymers of benzo[c]furan (BF) and thieno[3,2-b]thiophene (TT). For different monomer ratios in BDT-EDOT and BF-TT, the correlations between the bandgap and QSE_CO are shown in Fig. 6. The bandgap decreases linearly as the absolute value of QSE_CO decreases. The 1 : 1 BDT-EDOT (QSE_CO = 0.9 kcal mol⁻¹) and the 3 : 1 BF-TT (QSE_CO = −0.4 kcal mol⁻¹) have the narrowest bandgap. Therefore, the results show that a narrow bandgap in periodic copolymers can be designed by using a monomer ratio that keeps the mole fraction-weighted average of QSE of the monomers at around 0 kcal mol⁻¹.

Fig. 6 Calculated bandgaps against QSE_CO for (a) BDT-EDOT and (b) BF-TT periodic copolymers with different ratios.

Relationship between the orbital energy level and QSE

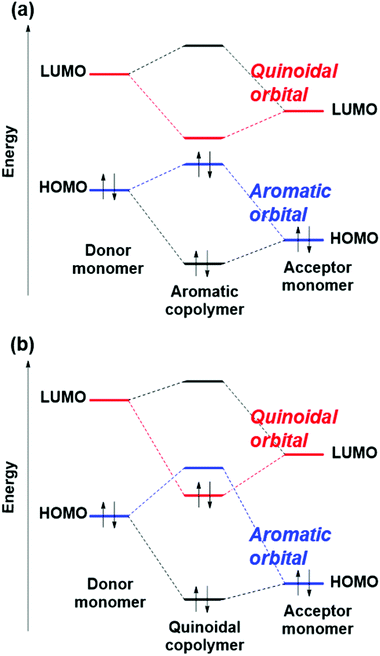
In order to find out why polymers with QSE at around 0 show narrow bandgaps, we investigated HOCO and LUCO of the polymers. Fig. 7(a) plots energy levels of HOCO and LUCO of the alternating copolymers against QSE_CO, where the red and blue symbols indicate aromatic and quinoid type orbitals, respectively. An aromatic type orbital is a π-orbital showing an anti-bonding feature between the monomer units according to Fig. 7(b), and a quinoid type orbital is a π-orbital having a bonding feature between the monomer units, as shown in Fig. 7(c). According to Fig. 7(a), when QSE_CO is positive, HOCO is the aromatic type orbital and LUCO is the quinoid type orbital in most polymers. On the other hand, in the negative QSE_CO region, HOCO is a quinoid type orbital and LUCO is an aromatic type orbital. Thus, the energy levels of the aromatic and quinoid type orbitals are linearly correlated with QSE_CO, and their two approximate straight trend lines intersect at around QSE_CO = 0. This indicates that level crossing of the aromatic and quinoid type orbitals occurs at around QSE_CO = 0. Therefore, the fact that polymers exhibit a narrow bandgap at around QSE = 0 can be explained by that QSE = 0 is near the level crossing of aromatic and quinoidal orbitals. Additionally, the correlation shown in Fig. 7(a) means that the orbital levels of π-conjugated polymers strongly reflect the nature of its monomers, probably resulting in good correlation between the QSE of monomers and the bandgap of polymers.

Fig. 7 (a) Plots of HOCO (filled) and LUCO (empty) energy levels against QSE_CO of the 179 copolymers. Blue and red symbols indicate aromatic and quinoidal orbitals, respectively. (b) The aromatic type orbital (HOCO) and (c) quinoid type orbital (LUCO) of poly(thiophene).

The level crossing of the aromatic and quinoidal type orbitals highlights the problem with the donor–acceptor approach. That approach is also a design guideline for narrow-bandgap copolymers, by combining a donor monomer having a higher HOMO level and an acceptor monomer having a lower LUMO level. The donor–acceptor approach is based on the orbital interaction model, in which the HOMO level of the polymer is somewhat higher than that of the donor by a HOMO–HOMO interaction, and the LUMO level of the polymer is somewhat lower than that of the acceptor by a LUMO–LUMO interaction (not a HOMO–LUMO interaction in the donor–acceptor interactions), as shown in Fig. 8(a).²⁸ In other words, the donor–acceptor approach is established when the HOMO of the polymers is constructed by the HOMO of monomers, and the same with LUMO.

Fig. 8 Schematic orbital interactions in (a) aromatic polymers and (b) quinoidal polymers.

The orbital interaction model in Fig. 8(a) cannot be applied in the quinoidal copolymers (QSE_CO ≲ 0), although it can be applied in the aromatic ones (QSE_CO ≳ 0), as explained by the following three points.

(1) Based on the symmetry of orbitals, the aromatic type orbital of the copolymers is constructed by the aromatic one of the monomers, and the quinoidal type orbital of the copolymers is also constructed by the quinoidal one of the monomers.

(2) In monomers, the aromatic type orbital is HOMO and the quinoidal one is LUMO. To understand the reason, one may consider a 6π ring system. The aromatic type orbital has one node, and the quinoidal type orbital has two nodes. Thus, the former is inevitably more stable than the latter due to the number of nodes, leading to the aromatic type HOMO and the quinoidal type LUMO in the monomers.

(3) In polymers, on the other hand, the aromatic as well as quinoidal type orbitals have two nodes per monomer unit. Therefore, the energy level order of the aromatic and quinoidal type orbitals can change. In other words, the aromatic HOCO and quinoidal LUCO can be replaced by the quinoidal HOCO and aromatic LUCO. Fig. 7(a) clearly shows that the polymers with QSE_CO ≳ 0 have the aromatic HOCO and quinoidal LUCO, and those with QSE_CO ≲ 0 have the quinoidal HOCO and aromatic LUCO.

Based on the above three points, in the aromatic polymers, the aromatic HOMO and quinoidal LUMO of monomers construct the aromatic HOCO and quinoidal LUCO, respectively, as schematically shown in Fig. 8(a). In the quinoidal polymers, the aromatic HOMO and quinoidal LUMO of monomers construct the aromatic LUCO and quinoidal HOCO, respectively, as schematically shown in Fig. 8(b). This means that the donor–acceptor approach cannot be applied in the region of QSE_CO ≲ 0. It also shows that, in the aromatic copolymers, consideration of not only the QSE but also the factor of donor–acceptor can improve the bandgap prediction accuracy.

Now we further demonstrate the problem with the donor–acceptor approach by an approximate scheme. If the donor–acceptor approach is true, the bandgap of copolymers should approximately correlate with the Δε defined below

Δε = ε(lower LUMO) − ε(higher HOMO) (7)

where ε(lower LUMO) is the lower LUMO level between the two monomers, and ε(higher HOMO) is the higher HOMO level between the two. The plot of the bandgap of copolymers against Δε is displayed in Fig. 9. As we expected, the correlation of the bandgap with Δε is not clear in the quinoidal polymers (having quinoidal HOCO and aromatic LUCO) although they are moderately correlated in the aromatic polymers (having aromatic HOCO and quinoidal LUCO). This result shows that the donor–acceptor approach cannot be used in the quinoidal polymers, even though some quinoidal polymers have narrow bandgaps.

Fig. 9 Plots of bandgap of copolymers against the difference in the orbital level between the higher HOMO and the lower LUMO (Δε) in (a) aromatic polymers and (b) quinoidal polymers.

Data mining for finding monomer features influencing QSE

In order to discover monomer features that influence QSE, data mining by the least absolute shrinkage and selection operator (LASSO) regression⁷⁹ was performed. LASSO regression is a linear regression method that includes a penalty term to reduce model complexity and to prevent over-fitting. Since the LASSO regression excludes unnecessary feature values, only features that are truly correlated with QSE can be extracted. In this work, LASSO regression was carried out for QSE and the following 18 monomer features: HOMO level, LUMO level, HOMO–LUMO gap, square of spin operator, ionization potential, electron affinity, electronegativity, chemical hardness, energy gap between the singlet and triplet states (S-T gap), molecular weight, number of N atoms, number of O atoms, number of S atoms, number of rings, number of π-electrons, number of π-electrons in the shortest π-conjugate path between linking sites, and T and y values as diradical indices proposed by Nakano et al.⁸⁰Table 1 shows the coefficients of LASSO regression. Among the monomer features, the S-T gap, number of π-electrons in the shortest path, y value, and HOMO level were extracted, while the coefficients of the other 14 features were zero. The S-T gap and the y value are associated with the diradical character, indicating that the monomers having a high diradical character exhibit a small QSE.

Table 1 LASSO regression coefficients between QSE and extracted features of the monomers

Descriptors	LASSO regression coefficients^a
a The LASSO regression coefficients of the other 14 descriptors were 0. b The π-electron number of the shortest path between the bonding points of the monomer unit.
S-T gap	9.18
Number of π-electrons (short)^b	8.34
HOMO level	−1.08
y value	−0.35

---

The small QSE in the monomers having a diradical character can be explained as follows. If the radicals are localized on the linking sites, then they form π-bonds with each other leading to a quinoidal form, as shown in Fig. 10. Therefore, the QSE value can be reduced by introducing a structure exhibiting diradical character into the monomer and making a structure in which the radicals are localized on the linking sites.

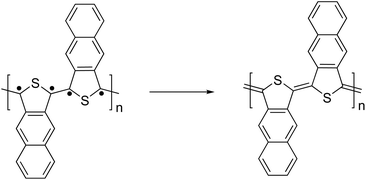Fig. 10 Schematic illustration of quinoidal structure formation in a polymer composed of a diradical monomer unit.

Moreover, the strong correlation of QSE with the number of π-electrons in the shortest path (Table 1) suggests that QSE depends on the monomer size, that is, there is a size effect on the QSE. This effect is currently under investigation. The preliminary results and method to correct the size effect on QSE are described in the ESI.†

Conclusion

For the design of narrow-bandgap polymers, we developed the quinoid stabilization energy (QSE) as a new quantum chemical descriptor based on the stabilization energy of the structural change from the aromatic form to the quinoidal form of the monomer unit. It has the following features. (1) Polymers with narrow bandgaps have QSE = 0. (2) In alternating copolymers, a narrow bandgap in the polymers requires that the averaged QSE of the two monomers is around 0. (3) In periodic copolymers with any monomer ratio, a narrow bandgap in the polymers requires that the averaged QSE of the monomers weighted by their mole fraction is around 0. (4) QSE can be uniquely obtained using simple calculations of only the monomer units and their linking sites. (5) QSE can uniformly treat monomer units with and without heteroatoms. (6) The reason why the polymers show a narrow bandgap around QSE = 0 was shown to be related to level crossing of the aromatic and quinoid type orbitals. (7) Data mining by LASSO regression showed that QSE is strongly influenced by the diradical character of monomers and that QSE has a size effect.

The correlation between QSE and bandgap indicates that the bandgap of polymers strongly reflects the nature of its monomers. The result of HOCO and LUCO levels in polymers shows that the donor–acceptor approach is inapplicable to the quinoidal polymers. The polymer design using QSE will contribute to further narrowing the bandgap of polymers beyond the donor–acceptor approach. Moreover, as a simple quantum chemical descriptor, QSE is highly compatible with machine learning. Therefore, we anticipate that this approach will accelerate the development of ultra-narrow bandgap polymers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The numerical calculations were carried out on the TSUBAME3.0 supercomputer at the Tokyo Institute of Technology, Tokyo, Japan, and on the supercomputer at the Research Center for Computational Science, Okazaki, Japan. We thank Mr Mahiro Iwasaki and Mr Kohta Otsuki for their assistance in a part of DFT calculations. We would like to thank Editage for English language editing. This work was supported by a Grant-in-Aid for Young Scientists (B) (JSPS KAKENHI Grant Number JP17K17720 to Y. H.), a Grant-in-Aid for Specially promoted Research (JSPS KAKENHI Grant Number JP17H06092 to S. K.), and a JST CREST (Grant Number JPMJCR1522 to S. K.).

Notes and references

1. P. Vincett, W. Barlow, R. Hann and G. Roberts, Thin Solid Films, 1982, 94, 171.
2. D. A. Pardo, G. E. Jabbour and N. Peyghambarian, Adv. Mater., 2000, 12, 1249.
3. A. P. Kulkarni, C. J. Tonzola, A. Babel and S. A. Jenekhe, Chem. Mater., 2004, 16, 4556.
4. X. Yang, D. Neher, D. Hertel and T. K. Däubler, Adv. Mater., 2004, 16, 1440.
5. S. Bhadra, D. Khastgir, N. K. Singha and J. H. Lee, Prog. Polym. Sci., 2009, 34, 783.
6. C. W. Tang, Appl. Phys. Lett., 1986, 48, 183.
7. N. S. Sariciftci, L. Smilowitz, A. J. Heeger and F. Wudl, Science, 1992, 258, 1474.
8. G. Yu, J. Gao, J. Hummelen, F. Wudl and A. J. Heeger, Science, 1995, 270, 1789.
9. E. Bundgaard and F. Krebs, Sol. Energy Mater. Sol. Cells, 2007, 91, 954.
10. S. L. Potisek, D. A. Davis, N. R. Sottos, S. R. White and J. S. Moore, J. Am. Chem. Soc., 2007, 129, 13808.
11. F. C. Krebs, M. Jørgensen, K. Norrman, O. Hagemann, J. Alstrup, T. D. Nielsen, J. Fyenbo, K. Larsen and J. Kristensen, Sol. Energy Mater. Sol. Cells, 2009, 93, 422.
12. A. Facchetti, Mater. Today, 2013, 16, 123.
13. H. Koezuka, A. Tsumura and T. Ando, Synth. Met., 1987, 18, 699.
14. G. H. Gelinck, H. E. A. Huitema, E. van Veenendaal, E. Cantatore, L. Schrijnemakers, J. B. P. H. van der Putten, T. C. T. Geuns, M. Beenhakkers, J. B. Giesbers, B.-H. Huisman, E. J. Meijer, E. M. Benito, F. J. Touwslager, A. W. Marsman, B. J. E. van Rens and D. M. de Leeuw, Nat. Mater., 2004, 3, 106.
15. A. Knobloch, A. Manuelli, A. Bernds and W. Clemens, J. Appl. Phys., 2004, 96, 2286.
16. J. Simmons, I. In, V. Campbell, T. Mark, F. Léonard, P. Gopalan and M. Eriksson, Phys. Rev. Lett., 2007, 98, 086802.
17. J. Yang, D. Shen, L. Zhou, W. Li, X. Li, C. Yao, R. Wang, A. M. El-Toni, F. Zhang and D. Zhao, Chem. Mater., 2013, 25, 3030.
18. L. Cheng, C. Wang, L. Feng, K. Yang and Z. Liu, Chem. Rev., 2014, 114, 10869.
19. A. L. Antaris, H. Chen, K. Cheng, Y. Sun, G. Hong, C. Qu, S. Diao, Z. Deng, X. Hu, B. Zhang, X. Zhang, O. K. Yaghi, Z. R. Alamparambil, X. Hong, Z. Cheng and H. Dai, Nat. Mater., 2016, 15, 235.
20. Q. Miao, Y. Lyu, D. Ding and K. Pu, Adv. Mater., 2016, 28, 3662.
21. Y. Lyu, C. Xie, S. A. Chechetka, E. Miyako and K. Pu, J. Am. Ceram. Soc., 2016, 138, 9049.
22. J. Geng, C. Sun, J. Liu, L. Liao, Y. Yuan, N. Thakor, J. Wang and B. Liu, Small, 2014, 11, 1603.
23. Y. Zhang, C. Teh, M. Li, C. Y. Ang, S. Y. Tan, Q. Qu, V. Korzh and Y. Zhao, Chem. Mater., 2016, 28, 7039.
24. Q. Qian, X. Huang, X. Zhang, Z. Xie and Y. Wang, Angew. Chem., Int. Ed., 2013, 52, 10625.
25. Y. Lyu, Y. Fang, Q. Miao, X. Zhen, D. Ding and K. Pu, ACS Nano, 2016, 10, 4472.
26. E. E. Havinga, W. ten Hoeve and H. Wynberg, Polym. Bull., 1992, 29, 119.
27. J. Roncali, Chem. Rev., 1997, 97, 173.
28. H. A. M. van Mullekom, J. A. J. M. Vekemans, E. E. Havinga and E. W. Meijer, Mater. Sci. Eng., 2001, 32, 1.
29. H. Zhou, L. Yang and W. You, Macromolecules, 2012, 45, 607.
30. N. Bérubé, J. Gaudreau and M. Coîté, Macromolecules, 2013, 46, 6873.
31. L. Dou, Y. Liu, Z. Hong, G. Li and Y. Yang, Chem. Rev., 2015, 115, 12633.
32. B. M. Wong and J. G. Cordaro, J. Phys. Chem. C, 2011, 115, 18333.
33. C. Liu, K. Wang, X. Gong and A. J. Heeger, Chem. Soc. Rev., 2016, 45, 4825.
34. F. Wudl, M. Kobayashi and A. Heeger, J. Org. Chem., 1984, 49, 3382.
35. J. Brédas, J. Chem. Phys., 1985, 82, 3808.
36. J. Brédas, Synth. Met., 1987, 17, 115.
37. K. Kawabata, M. Saito, I. Osaka and K. Takimiya, J. Am. Chem. Soc., 2016, 138, 7725.
38. T. Hasegawa, M. Ashizawa, Y. Hayashi, S. Kawauchi, H. Masunaga, T. Hikima, T. Manaka and H. Matsumoto, ACS Appl. Polym. Mater., 2019, 1, 542.
39. Y. Sun, Y. Guo and Y. Liu, Mater. Sci. Eng., R, 2019, 136, 13.
40. J. Huang, S. Lu, P.-A. Chen, K. Wang, Y. Hu, Y. Liang, M. Wang and E. Reichmanis, Macromolecules, 2019, 52, 4749.
41. A. E. London, H. Chen, M. A. Sabuj, J. Tropp, M. Saghayezhian, N. Eedugurala, B. A. Zhang, Y. Liu, X. Gu, B. M. Wong, N. Rai, M. K. Bowman and J. D. Azoulay, Sci. Adv., 2019, 5, eaav2336.
42. M. E. Foster, B. A. Zhang, D. Murtagh, Y. Liu, M. Y. Sfeir, B. M. Wong and J. D. Azoulay, Macromol. Rapid Commun., 2014, 35, 1516.
43. J. D. Douglas, G. Griffini, T. W. Holcombe, E. P. Young, O. P. Lee, M. S. Chen and J. M. J. Fréchet, Macromolecules, 2012, 45, 4069.
44. J. Hou, M. Park, S. Zhang, Y. Yao, L. Chen, J. Li and Y. Yang, Macromolecules, 2008, 41, 6012.
45. N. Kleinhenz, L. Yang, H. Zhou, S. C. Price and W. You, Macromolecules, 2011, 44, 872.
46. Y.-J. Cheng, S.-H. Yang and C.-S. Hsu, Chem. Rev., 2009, 109, 5868.
47. K. B. Vu, V. V. Vu, H. P. Thi Thu, H. N. Giang, N. M. Tam and S. T. Ngo, Synth. Met., 2018, 246, 128.
48. W. Zhang, T. Huang, J. Li, P. Sun, Y. Wang, W. Shi, W. Han, W. Wang, Q. Fan and W. Huang, ACS Appl. Mater. Interfaces, 2019, 11, 16311.
49. H. Xu, Y. Yang, C. Zhong, X. Zhan and X. Chen, J. Mater. Chem. A, 2018, 6, 6393.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016.
51. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
52. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650.
53. J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968.
54. A. D. Becke, J. Chem. Phys., 1993, 98, 5648.
55. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623.
56. The data were partially reported in the conference proceedings: K. Otsuki, Y. Hayashi and S. Kawauchi, J. Comput. Chem., Jpn., 2017, 16, 123.
57. We used calculated bandgaps here in this study because of the following reasons: (1) theoretical calculation could produce a large and homogeneous dataset of bandgaps, (2) there are only very limited experimental data of quinoidal polymers, and (3) the calculated bandgap corresponds to the bandgap of single-chain systems, and this is suitable for our purpose because the aromatic-quinoid approach treats the bandgap of polymers in single-chain systems. Although the experimental bandgap is influenced by the packing of polymer chains in bulk systems, the bandgap of single-chain systems is important for showing a narrow bandgap in bulk systems.
58. T. Hasegawa, M. Ashizawa, J. Hiyoshi, S. Kawauchi, J. Mei, Z. Bao and H. Matsumoto, Polym. Chem., 2016, 7, 1181.
59. M. Kobayashi, J. Chen, T.-C. Chung, F. Moraes, A. J. Heeger and F. Wudl, Synth. Met., 1984, 9, 77.
60. Y. Ikenoue, Synth. Met., 1990, 35, 263.
61. Y. Zhang, S. K. Hau, H. L. Yip, Y. Sun, O. Acton and A. K. Y. Jen, Chem. Mater., 2010, 22, 2696.
62. J. Qi, X. Zhou, D. Yang, W. Qiao, D. Ma and Z. Y. Wang, Adv. Funct. Mater., 2014, 24, 7605.
63. H. Bohra, S. Y. Tan, J. Shao, C. Yang, A. Efrem, Y. Zhao and M. Wang, Polym. Chem., 2016, 7, 6413.
64. J. Locklin, M. M. Ling, A. Sung, M. E. Roberts and Z. Bao, Adv. Mater., 2006, 18, 2989.
65. U. Zschieschang, F. Ante, T. Yamamoto, K. Takimiya, H. Kuwabara, M. Ikeda, T. Sekitani, T. Someya, K. Kern and H. Klauk, Adv. Mater., 2010, 22, 982.
66. T. Ashimine, T. Yasuda, M. Saito, H. Nakamura and T. Tsutsui, Jpn. J. Appl. Phys., 2008, 47, 1760.
67. S. A. Ponomarenko, S. Kirchmeyer, A. Elschner, N. M. Alpatova, M. Halik, H. Klauk, U. Zschieschang and G. Schmid, Chem. Mater., 2006, 18, 579.
68. M. Mamada, J. I. Nishida, D. Kumaki, S. Tokito and Y. Yamashita, J. Mater. Chem., 2008, 18, 3442.
69. H. Meng, Z. Bao, A. J. Lovinger, B. C. Wang and A. M. Mujsce, J. Am. Chem. Soc., 2001, 123, 9214.
70. J. A. Merlo, C. R. Newman, C. P. Gerlach, T. W. Kelley, D. V. Muyres, S. E. Fritz, M. F. Toney and C. D. Frisbie, J. Am. Chem. Soc., 2005, 127, 3997.
71. S. A. Ponomarenko, S. Kirchmeyer, M. Halik, H. Klauk, U. Zschieschang, G. Schmid, A. Karbach, D. Drechsler and N. M. Alpatova, Synth. Met., 2005, 149, 231.
72. M. Koppe, M. Scharber, C. Brabec, W. Duffy, M. Heeney and I. McCulloch, Adv. Funct. Mater., 2007, 17, 1371.
73. X. Guo and M. D. Watson, Org. Lett., 2008, 10, 5333.
74. M. M. Durban, P. D. Kazarinoff and C. K. Luscombe, Macromolecules, 2010, 43, 6348.
75. M. M. Szumilo, E. H. Gann, C. R. McNeill, V. Lemaur, Y. Oliver, L. Thomsen, Y. Vaynzof, M. Sommer and H. Sirringhaus, Chem. Mater., 2014, 26, 6796.
76. Z. Ma, W. Sun, S. Himmelberger, K. Vandewal, Z. Tang, J. Bergqvist, A. Salleo, J. W. Andreasen, O. Inganäs, M. R. Andersson, C. Müller, F. Zhang and E. Wang, Energy Environ. Sci., 2014, 7, 361.
77. X. Liu, P. Cai, Z. Chen, L. Zhang, X. Zhang, J. Sun, H. Wang, J. Chen, J. Peng, H. Chen and Y. Cao, Polymer, 2014, 55, 1707.
78. X. Liu, B. He, C. L. Anderson, J. Kang, T. Chen, J. Chen, S. Feng, L. Zhang, M. A. Kolaczkowski, S. J. Teat, M. A. Brady, C. Zhu, L. W. Wang, J. Chen and Y. Liu, J. Am. Chem. Soc., 2017, 139, 8355.
79. R. Tibshirani, J. R. Stat. Soc. Ser. B, 1996, 58, 267.
80. M. Nakano, R. Kishi, T. Nitta, T. Kubo, K. Nakasuji, K. Kamada, K. Ohta, B. Champagne, E. Botek and K. Yamaguchi, J. Phys. Chem. A, 2005, 109, 885.

---

Footnote

† Electronic supplementary information (ESI) available: Descriptions of determining the degree of oligoacetylene polymerization, benchmark calculation of QSE and the bandgap, recipe of QSE calculation, LASSO regression, C–C bond length of poly(thienoisoindigo), investigation of the size effect and size correction for QSE, and list of QSE. See DOI: 10.1039/c9py00987f

---