Open Access Article
Open Access ArticleTuning and in situ monitoring of surface-initiated, atom-transfer radical polymerization of acrylamide derivatives in water-based solvents†
Joydeb
Mandal
,
Rok
Simic
 and
Nicholas D.
Spencer
and
Nicholas D.
Spencer
 *
*
Laboratory for Surface Science and Technology, Department of Materials, ETH Zurich, Vladimir-Prelog-Weg 5, CH-8093 Zurich, Switzerland. E-mail: nspencer@ethz.ch
First published on 1st July 2019
Abstract
In order to gain better control over the growth and dispersity of surface-tethered poly(acrylamides), the SI-ATRP kinetics of N-isopropylacrylamide (NIPAM), N,N-dimethylacrylamide (DMAM) and N-hydroxyethyl acrylamide (HEAM) have been systematically investigated in situ in an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water mixture by means of the quartz crystal microbalance with dissipation (QCM-D). The addition of tetraethylammonium chloride (tEtAmCl) or tetraethylammonium bromide (tEtAmBr) in association with additional CuIIX2 (X = Cl or Br) resulted in improved control over the polymerization kinetics. Evidence for such improved SI-ATRP kinetics was provided by a slower and more linear decrease in the resonance frequency of the QCM-D sensors, indicating a linear increase in solvated brush mass as a function of polymerization time. This was further validated by carrying out multiple re-initiations and measuring the growth of the polymer brushes upon each initiation, by means of both QCM-D and ellipsometry. An indirect estimation of the effect of improving the living nature of polymer brush growth on their dispersity was performed by carrying out nanoindentation experiments by means of colloidal-probe atomic force microscopy on polymer brushes grown under different reaction conditions. For an identical indentation load, polymer brushes grown in the absence of CuIIX2 and tEtAmX exhibited a much larger indentation depth, indicating a substantially softer structure, presumably as a consequence of the higher degree of chain-length dispersity.
20 ethanol/water mixture by means of the quartz crystal microbalance with dissipation (QCM-D). The addition of tetraethylammonium chloride (tEtAmCl) or tetraethylammonium bromide (tEtAmBr) in association with additional CuIIX2 (X = Cl or Br) resulted in improved control over the polymerization kinetics. Evidence for such improved SI-ATRP kinetics was provided by a slower and more linear decrease in the resonance frequency of the QCM-D sensors, indicating a linear increase in solvated brush mass as a function of polymerization time. This was further validated by carrying out multiple re-initiations and measuring the growth of the polymer brushes upon each initiation, by means of both QCM-D and ellipsometry. An indirect estimation of the effect of improving the living nature of polymer brush growth on their dispersity was performed by carrying out nanoindentation experiments by means of colloidal-probe atomic force microscopy on polymer brushes grown under different reaction conditions. For an identical indentation load, polymer brushes grown in the absence of CuIIX2 and tEtAmX exhibited a much larger indentation depth, indicating a substantially softer structure, presumably as a consequence of the higher degree of chain-length dispersity.
Introduction
A major incentive for the tailoring of the surface chemistry of biomaterials is to improve their biocompatibility. This is achieved by controlling their interactions with active components of living systems, such that they mimic the natural physiological state. Over the past decade, the use of polymer brushes has emerged as one of the most versatile approaches to tailor the surface properties of materials for a wide range of applications, because of the excellent control it offers over both architecture and functionality.1,2 Applications include the design of adaptive interfaces and the modulation of bio-adhesion, friction, and wettability.3–5The biocompatibility of a number of water-soluble acrylamide-based polymers makes them ideal for many biomedical applications,6,7 such as in tissue engineering and drug delivery. However, the suitability of the corresponding polymer brushes for mimicking biological functions, such as the articulating surface of cartilage, have not been studied extensively, in part due to difficulties in growing them with tunable thicknesses. Surface-initiated, atom-transfer radical polymerization (SI-ATRP),8–11 among various other surface-initiated controlled radical polymerization (SI-CRP) techniques, has been proven to be highly versatile for the generation of polymer brushes, because it potentially provides full control over the tunability of brush thickness and grafting density. Other advantages of SI-ATRP for designing tailored surfaces include the readily accessible and inexpensive catalyst systems (normally copper complexes of aliphatic or aromatic amines), initiators (alkyl halides) and a wide range of commercially available suitable monomers.12 Nevertheless, achieving tunability in brush thickness with SI-ATRP of acrylamide derivatives has remained elusive due to their tendency towards uncontrolled growth in water-containing solvents. This can be explained by the very low effective concentration of the ATRP deactivator (CuIIX2Ln; X = Cl or Br, L = ligand), due to the displacement of its halide ligand by water molecules.13–15 Matyjaszewski and co-workers have shown that the effective concentration of CuIIX2Ln can be increased and hence the ATRP kinetics can be modulated by the addition of a halide salt such as tEtAmX (X = Cl or Br) to the reaction medium.14 However, although poly(acrylamide) brushes may be ideal for many biomedical applications, detailed investigation of the SI-ATRP kinetics of water-soluble acrylamides and hence an effort to achieve tunable polymer brush growth has been somewhat neglected, due to difficulties in monitoring the SI-ATRP kinetics in real time. Although the SI-ATRP kinetics of N-isopropylacrylamide (NIPAM) have been studied in recent times by several other groups,16,17 a better understanding of the SI-ATRP kinetics of water-soluble acrylamides can have great potential in designing biologically relevant functional surfaces.
In this study, we have systematically investigated the effect of both CuIIX2 and tEtAmX on the SI-ATRP kinetics of N,N-dimethylacrylamide (DMAM), N-hydroxyethyl acrylamide (HEAM) and N-isopropylacrylamide (NIPAM) both in situ and ex situ using QCM-D and ellipsometry.
A remarkable observation was the transition from uncontrolled to well-controlled SI-ATRP kinetics due to the combined effect of CuIIX2 and tEtAmX. Controlled behavior was reflected as a more moderate and far more linear decrease in the resonance frequency (−ΔF) of the QCM-D-sensor, corresponding to a linear increase in the brush thickness as a function of polymerization time. In a recent report, Luan and coworkers showed that the presence of a thick dissipative film reduces the sensitivity of QCM-D measurements due to attenuation of the acoustic waves, potentially leading to erroneous results. This effect they termed “hearing loss”.18 In order to determine whether this issue is significant in the results reported below, we have also evaluated the SI-ATRP kinetics, in parallel and ex situ by measuring dry brush thickness at different time intervals by means of ellipsometry. While the amount of data collected in this way is, of course, far less than via the in situ approach, the ellipsometric kinetic results precisely mirror those measured by QCM-D.
Special attention was paid to evaluating the effect of improved SI-ATRP kinetics on the polymer-brush dispersities in a nondestructive way. In addition to the commonly used size-exclusion chromatography (SEC) of the detached polymer chains, colloidal-probe AFM indentation was used to indirectly measure the effect of reaction conditions on chain-length dispersity. Comparison of the force–distance curves obtained from the colloidal-probe AFM indentation experiments revealed substantial differences between the swollen states of polymer brushes grown with or without the CuIIX2 and tEtAmX, despite their similar dry thicknesses. The differences presumably originate from the higher degree of chain-length dispersity when the brushes are grown in the absence of CuIIX2 and tEtAmX.
Results and discussion
Because our primary objective was to understand and achieve greater control over the SI-ATRP kinetics of water-soluble monomers, such as DMAM, HEAM and NIPAM in water-based solvents, we chose to study their real-time growth in 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water mixture under different catalytic conditions using a quartz crystal microbalance with dissipation (QCM-D). This technique was chosen because of its exceptional ability to monitor changes in the mass of the polymer films, as they grow in real time.19–21 The polymerization was performed at room temperature from a monolayer of SI-ATRP initiator, immobilized onto the SiO2-coated QCM-D sensors. In brief, a baseline was first established by flowing 80
20 ethanol/water mixture under different catalytic conditions using a quartz crystal microbalance with dissipation (QCM-D). This technique was chosen because of its exceptional ability to monitor changes in the mass of the polymer films, as they grow in real time.19–21 The polymerization was performed at room temperature from a monolayer of SI-ATRP initiator, immobilized onto the SiO2-coated QCM-D sensors. In brief, a baseline was first established by flowing 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water through the QCM-D cells; the medium was then switched to the complete reaction mixture (CRM; i.e. 80
20 ethanol/water through the QCM-D cells; the medium was then switched to the complete reaction mixture (CRM; i.e. 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water + monomer + catalyst + ligand) to initiate the polymerization and finally terminated by switching the flow back to 80
20 ethanol/water + monomer + catalyst + ligand) to initiate the polymerization and finally terminated by switching the flow back to 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water. A schematic illustration of the experimental setup is presented in Scheme 1.
20 ethanol/water. A schematic illustration of the experimental setup is presented in Scheme 1.
 | ||
| Scheme 1 Schematic illustration of the QCM-D-flow system used, to study the in situ SI-ATRP kinetics of N-isopropylacrylamide, N,N-dimethylacrylamide and N-hydroxyethylacrylamide. | ||
The SI-ATRP kinetics were monitored in real time by following the decrease in the resonance frequency (−ΔF) of the QCM-D sensors as a function of polymerization time. The use of QCM-D in studying SI-ATRP kinetics is advantageous over other techniques such as ellipsometry or XPS because of its ability to provide a finer detail of the kinetics in situ and in real time, without the necessity for carrying out individual experiments for each data point. The polymerization of NIPAM, DMAM, and HEAM was first investigated at room temperature in 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
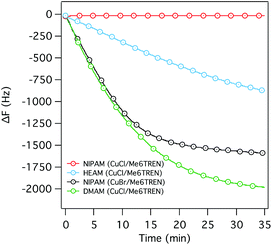
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water as mentioned before, with CuCl as the catalyst and tris[2-(dimethylamino)ethyl]amine (Me6TREN) as the ligand. The ligand was added in excess (twice the molar concentration of CuCl) to ensure the complete dissolution of the catalyst. Although the polymerization worked well with DMAM and HEAM (Fig. 1), as manifested in a decrease in the resonance frequency with polymerization time, NIPAM did not appear to polymerize at all (Fig. 1), notwithstanding literature references to successful ATRP of NIPAM in the presence of CuCl as a catalyst.22–24
20 ethanol/water as mentioned before, with CuCl as the catalyst and tris[2-(dimethylamino)ethyl]amine (Me6TREN) as the ligand. The ligand was added in excess (twice the molar concentration of CuCl) to ensure the complete dissolution of the catalyst. Although the polymerization worked well with DMAM and HEAM (Fig. 1), as manifested in a decrease in the resonance frequency with polymerization time, NIPAM did not appear to polymerize at all (Fig. 1), notwithstanding literature references to successful ATRP of NIPAM in the presence of CuCl as a catalyst.22–24
 | ||
| Fig. 1 In situ SI-ATRP kinetics of NIPAM, DMAM and HEAM studied by measuring the variation in the resonance frequency as a function of polymerization time. | ||
However, we were able to successfully polymerize NIPAM using CuBr as the catalyst (Fig. 1). The ΔF–t curves corresponding to the polymerization of DMAM and NIPAM exhibited nonlinear profiles, with a rapid initial decrease of the resonance frequency (ΔF), saturating within a short period of polymerization, suggesting a very transient reaction profile, which was confirmed by a nonlinear increase in the dry brush thickness measured by ellipsometry at various time intervals (Fig. 2c). Interestingly, SI-ATRP of HEAM, under similar reaction condition, exhibited a steady, linear decrease in the resonance frequency (Fig. 1), again confirmed by a steady increase in the dry brush thickness over a longer period of time (Fig. 2c), indicating reasonably controlled growth of the p(HEAM) brushes.
In ATRP, the termination process is suppressed by the so-called “persistent radical effect”—an equilibrium favouring the dormant polymer chains over the propagating radicals by many orders of magnitude.25 However, in the case of SI-ATRP, this equilibrium can be disturbed by an inadequate supply of the CuIIX2 species resulting from the infinitesimally small number of initiating sites on the surface. The CuIIX2 concentration becomes further diluted due to diffusion into the reaction medium, resulting in a high local concentration of the propagating radicals, favouring termination.26 The inclusion of additional CuIIX2 species or sacrificial initiator (free initiator in the solution) at the onset of polymerization should be able to compensate for this effect, and reduce such termination processes.9 In an exemplary case, we chose to study the effect of the inclusion of additional CuCl2 on the SI-ATRP kinetics of DMAM while maintaining all other parameters constant. CuCl2 was chosen rather than sacrificial initiator, in order to avoid the formation of free polymer chains and the resulting effects associated with increasing viscosity in the medium—an increase in viscosity not only affects the coupling between the QCM-D-sensor surface and the reaction medium27 but also dramatically influences the SI-ATRP kinetics.28–30
Although the overall kinetics slowed down with increasing CuCl2 concentration, as represented by the diminishing slopes of the ΔF–t plots (Fig. 2a), the ΔF–t plots also exhibited a saturation of the resonance frequency within a short period of polymerization, suggesting a transient SI-ATRP lifetime, albeit convoluted with the hearing-loss effect of QCM-D, similar to that observed in the absence of additional CuCl2. Confirming this, the ex situ kinetic study, i.e. measuring the dry thickness of the grafted thin-films at different times by means of ellipsometry, also indicated transient growth in the dry brush thickness. However, the maximum dry thickness obtained in the presence of additional CuCl2 was significantly smaller compared to that obtained in the absence of CuCl2 (Table 1). Since the loss in sensitivity of a QCM-D measurement has a direct dependence on the thickness of the dissipative film, it is reasonable to assume that the contribution of hearing loss to the nonlinearity of the ΔF–t plots is not as significant as the contribution of the transient polymerization kinetics.
Although ATRP is widely employed for its control over the polymerization process and its ability to achieve well-defined polymers, it can struggle when performed in the presence of water because of the dissociation of the ATRP deactivator (CuIILnX2) due to the displacement of the halide ligands from the CuIILnX2 by water molecules, pushing the effective concentration of CuIILnX2 to an extremely low value.14 The effective concentration of the CuIILnX2 species can be elevated by suppressing the dissociation of CuIILnX2 species via the inclusion of halide salts such as tetraethylammonium chloride or bromide (tEtAmX), as suggested by Matyjaszewski and co-workers.14,15 Therefore, in order to achieve further control over the SI-ATRP kinetics, we chose to perform the polymerization in the presence of tEtAmCl. As expected, the ΔF–t curves exhibited a much slower and more linear decrease in the resonance frequency at elevated tEtAmCl concentration, even though the concentration of CuCl2 was kept unchanged (Fig. 2b). Significantly, neither ΔF nor the associated change in dissipation (ΔD) exhibited any overtone dependence (Fig. S2†) when polymerization was performed in the presence of CuCl2 and tEtAmCl. Such overtone independence of the growing polymer film is a primary characteristic of a non-dissipative film, and an indication that hearing loss is not a significant problem in this case.31
Therefore, one can argue that it is the polymerization kinetics rather than the loss of QCM-D sensitivity that determines the nature of the ΔF–t curves for polymer brushes with significantly high grafting density. So, it is reasonable to assume that the result described above demonstrates a slower but more controlled SI-ATRP kinetics because of an elevated effective concentration of the ATRP deactivator (CuIILnX2) in the reaction medium. Similar experiments were also carried out with HEAM and NIPAM and demonstrated controlled growth of both p(NIPAM) and p(HEAM) brushes. Presumably, the SI-ATRP kinetics of both NIPAM and HEAM exhibited a similar dependence on the catalytic composition of the reaction medium (Fig. S3 and S2†).
As expected, ex situ determination of the SI-ATRP kinetics for DMAM, NIPAM and HEAM also exhibited a much more linear increase in dry brush thickness when the polymerizations were carried out in the presence of both CuIIX2 and tEtAmX (Fig. 2c and Table 1). These two extreme polymerization conditions, as well as the samples synthesized in these conditions will be designated as ‘uncontrolled’ and ‘controlled’ in the following sections.
In order to evaluate the livingness of the SI-ATRP kinetics under the controlled polymerization conditions, we carried out a simple experiment with all three monomers following our previously reported procedure19 where the polymerization was interrupted and reinitiated multiple times by switching the IRM (incomplete reaction mixture = monomer + solvent) solution to CRM (complete reaction mixture = IRM + ligand + catalyst + tEtAmX) solution and vice versa, resulting in staircase-like growth profiles in QCM-D as shown in Fig. 3a. Polymerization efficiencies upon each re-initiation were determined by measuring the average slope of the polymerization profiles and normalizing the slope to the first initiation as shown in Fig. 3b. The relative polymerization rate of all three systems decreases upon every re-initiation; however, as expected from our previous observations, SI-ATRP of HEAM exhibited the highest relative rate of 57% at the 4th initiation, compared to 24% and 15% for DMAM and NIPAM, respectively. To rule out the effect of polymerization time on the relative rate, all three monomers were polymerized for the same period of time at each re-initiation. Similar experiments were also carried out ex situ, where the polymerization was interrupted by exposing the samples to air and reinitiated again with fresh CRM solution and continued for 15 minutes of polymerization. The growth of the polymer brushes upon each re-initiation was measured by ellipsometry and is presented in Fig. 3c (Table S1†). As expected, the ex situ SI-ATRP also exhibited the highest growth of 47% at the 4th initiation in case of HEAM compared to 35% and 24% for DMAM and NIPAM, respectively. The obtained values are similar to the efficiencies obtained from the in situ QCM-D data mentioned earlier.
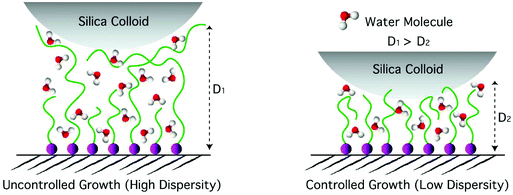
The control of SI-ATRP during polymer-brush growth can also be determined by measuring the dispersity of the grafted polymer chains using size exclusion chromatography (SEC) of chemically detached polymer chains; however, this method requires a substantial area of sample and a specially designed, cleavable initiator for clean and efficient detachment of the tethered polymer chains.32 Here, we report an indirect and non-destructive way of evaluating polymer brush dispersity by measuring force–distance curves, obtained by colloidal-probe nanoindentation of the polymer brushes in water, as shown in Fig. 4. For each of the monomers, averaged indentation curves are shown for a sample synthesized under uncontrolled polymerization conditions as well as for two samples synthesized under controlled polymerization conditions, one with similar dry thickness and one with similar polymerization time to the uncontrolled sample. Fig. 4a shows the three force–distance curves corresponding to three p(DMAM) brushes differing either in polymerization conditions or polymerization time. For all p(DMAM) samples, the indentation depth, at the maximum applied load of about 50 nN, was larger than their dry thickness, meaning that all the samples swelled substantially in water.
The uncontrolled sample with a dry thickness of 98 nm yielded a significantly larger indentation depth at a given applied force compared to the controlled sample with a comparable dry thickness of 82 nm. Such differences in the stiffness of the swollen polymer brushes are the result of a more gradual increase in polymer-chain density upon indentation in the case of the swollen, uncontrolled sample because of a greater degree of chain-length dispersity, as depicted in Scheme 2. Assuming that under the highest applied load the swollen brush was compressed all the way down to its dry thickness, the lower limit of the swelling ratio could be determined by dividing the total indentation depth by the dry thickness. In the case of DMAM, such estimated swelling ratios were in the range of 3.3–4.6.
Fig. 4b and c show similar data for the p(HEAM) and p(NIPAM) brushes, respectively. In a similar way to p(DMAM) brushes, p(HEAM) and p(NIPAM) brushes also swelled in water and qualitatively similar results were obtained. For p(HEAM), the swelling ratios according to the above assumption were in the order of 2.5–4.6. As expected, the thicker controlled sample appeared softer compared to the thinner controlled sample but stiffer than the uncontrolled sample of similar dry thickness; again, due to the greater chain-length dispersity. As expected, the force–distance curves corresponding to the p(NIPAM) brushes (Fig. 4c) showed swelling ratios of 2.5–5.7 and exhibited similar behavior to those of p(HEAM) and p(DMAM) brushes.
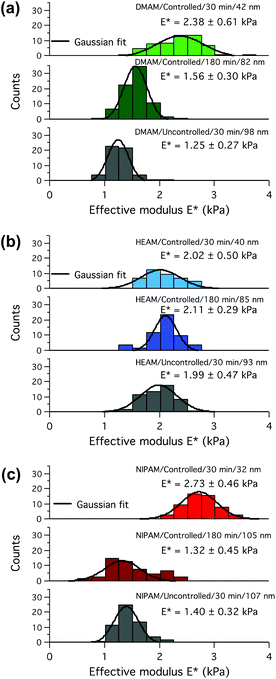
Since the dispersity of the tethered polymer chains should have the highest impact at the outer edge of the polymer brush layer, the magnified force–distance plots for the topmost 20–30% of the indentation depths (insets in Fig. 4), emphasizing the differences in the initial stiffnesses of the samples upon contact, have been examined in detail. Fitting a Hertzian contact model to the very beginning of the indentation data resulted in rather excessive scatter of the contact moduli due to the relatively low measured forces (<40 pN) compared to the noise level (RMS ∼7 pN). To avoid excessive scatter due to the low signal-to-noise ratio, the model had to be fitted to the outermost 20% of the total indentation depths, which corresponds to a maximum of 15% of the total swollen thickness and should therefore avoid substantial substrate effects due to the compression of thin layers. The results are presented as histograms of contact moduli in Fig. 5. As expected, the contact modulus E* of the thin controlled p(DMAM) brush was the highest due to shorter polymerization time, which relates to fewer number of dead chains and hence the lowest chain-length dispersity of all samples (Fig. 5a). The mean modulus of the uncontrolled sample was lower than that of the controlled p(DMAM) brush of comparable dry thickness; again, due to the lower chain-length dispersity of the controlled sample. However, only a negligible difference was observed between the mean moduli of the thick controlled and the uncontrolled brushes of p(NIPAM) and p(HEAM), presumably because of possible interchain H-bonding, as discussed later.
One must note that the width of the moduli distribution does not correspond to the chain-length dispersity, since a great number of polymer chains of different lengths becomes compressed within a single indentation. Hence, chain-length dispersity affects the shape of the force curve rather than the distribution of its initial slopes. The distribution of the slopes and thus the distribution of the moduli are therefore more related to lateral inhomogeneity of the samples as well as to uncertainties when fitting forces over shallow depths. Therefore, larger fitted depth of thicker brush layers often results in reduced modulus scatter.
In general, the p(HEAM) and p(NIPAM) brushes exhibited much smaller differences between the controlled and uncontrolled samples of comparable dry thicknesses when compared to the p(DMAM) analog, which can be seen from the force-indentation plots in Fig. 4 and also from the contact moduli evaluation in Fig. 5. The reduced differences in the stiffness of the controlled and uncontrolled p(HEAM) and p(NIPAM) brushes compared to that of the p(DMAM) brushes could originate from the possible interchain hydrogen bonding in the cases of p(HEAM) and p(NIPAM) brushes because of the presence of H-bonding motifs such as secondary amide and hydroxyl groups, which would rather hinder their swelling and provide a uniform stiffness along the entire depth. However, in the case of p(DMAM) brushes, such H-bonding is not possible because of the presence of tertiary amide groups and hence exhibit a dramatically different swelling behavior.
In order to confirm our hypothesis about the dispersity of the tethered polymer chains and its effect on the polymer-brush stiffness, we also measured the molecular weights and polydispersity index (Mn, Mw and PDI) of the tethered polymer chains by detaching the grafted polymer chains following a previously reported procedure.33 As expected, the PDI values of the controlled and uncontrolled p(DMAM) brushes were 1.5 and 2.5 while in the case of p(NIPAM) brushes the value of PDIs were 1.6 and 2.0 (Fig. S7†). The much higher difference in the PDI values in the case of p(DMAM) also explains why the p(DMAM) system exhibited significantly greater difference in the polymer-brush stiffness compared to its p(NIPAM) analogues.
Conclusions
We have systematically investigated the SI-ATRP kinetics of three acrylamide monomers, NIPAM, DMAM and HEAM, in an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water mixture under different catalytic conditions using QCM-D and ellipsometry. Addition of CuX2 (X = Cl or Br) did not lead to any improvement in the transient lifetime of SI-ATRP, but did reduce the reaction rate. However, inclusion of tEtAmCl or tEtAmBr together with CuX2 exhibited improved control over the SI-ATRP kinetics, associated with an extended transient lifetime, because of an increased effective concentration of the ATRP deactivator (CuIILnX2), resulting from the suppressed dissociation of CuIILnX2. The associated effect of SI-ATRP kinetics on the polymer brush dispersity, as measured by SEC, is also reflected in the results of colloidal-probe AFM indentation experiments; the polymer brushes grown under uncontrolled polymerization conditions appeared significantly softer upon contact compared to those grown under controlled polymerization conditions, despite their comparable dry thicknesses. The softer response observed for polymer brushes grown under uncontrolled polymerization conditions is a result of the tethered polymer chains having higher dispersity compared to their controlled analogues.
20 ethanol/water mixture under different catalytic conditions using QCM-D and ellipsometry. Addition of CuX2 (X = Cl or Br) did not lead to any improvement in the transient lifetime of SI-ATRP, but did reduce the reaction rate. However, inclusion of tEtAmCl or tEtAmBr together with CuX2 exhibited improved control over the SI-ATRP kinetics, associated with an extended transient lifetime, because of an increased effective concentration of the ATRP deactivator (CuIILnX2), resulting from the suppressed dissociation of CuIILnX2. The associated effect of SI-ATRP kinetics on the polymer brush dispersity, as measured by SEC, is also reflected in the results of colloidal-probe AFM indentation experiments; the polymer brushes grown under uncontrolled polymerization conditions appeared significantly softer upon contact compared to those grown under controlled polymerization conditions, despite their comparable dry thicknesses. The softer response observed for polymer brushes grown under uncontrolled polymerization conditions is a result of the tethered polymer chains having higher dispersity compared to their controlled analogues.
Experimental section
Materials
a-Bromoisobutyryl bromide (98%), (3-aminopropyl)triethoxysilane (97%), dichloromethane (99.8%, extra dry), triethylamine (99.5%), copper(II) bromide (99%), copper(II) chloride (99%), and Tris[2-(dimethylamino)ethyl]amine (97%) were purchased from Sigma Aldrich (Germany) and used as received. N-Isopropylacrylamide (97%) and N,N-dimethylacrylamide (99%) were purchased from Sigma Aldrich (Germany), whereas N-hydroxyethylacrylamide (>97%) was purchased from Tokyo Chemical Industries. N-Isopropylacrylamide was purified by crystallizing it from a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 (v/v) toluene/hexane mixture and was dried in vacuum prior to use, while other monomers were used without any purification. Cu(I) chloride (99.99%) and Cu(I) bromide (99.99%) were purchased from Sigma Aldrich and were purified by stirring overnight in glacial acetic acid, filtering, and washing several times with acetone, diethyl ether and finally drying under vacuum. Silicon wafers (P/B h100i) were purchased from Si-Mat Silicon Wafers (Germany) while SiO2-coated QCM-D sensors were purchased from Q-Sense (Sweden).
40 (v/v) toluene/hexane mixture and was dried in vacuum prior to use, while other monomers were used without any purification. Cu(I) chloride (99.99%) and Cu(I) bromide (99.99%) were purchased from Sigma Aldrich and were purified by stirring overnight in glacial acetic acid, filtering, and washing several times with acetone, diethyl ether and finally drying under vacuum. Silicon wafers (P/B h100i) were purchased from Si-Mat Silicon Wafers (Germany) while SiO2-coated QCM-D sensors were purchased from Q-Sense (Sweden).
Methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water mixture was degassed by bubbling nitrogen gas for 45 minutes and subsequently transferred using a degassed syringe to a flask containing the 8 mg (0.08 mmol) Cu(I)Cl, kept under nitrogen. The solution was then stirred for 10 minutes until complete dissolution of the catalyst. The QCM-D flow cells equipped with the initiator-modified, SiO2-coated sensors and the dummy sensor were then charged with an 80
20 ethanol/water mixture was degassed by bubbling nitrogen gas for 45 minutes and subsequently transferred using a degassed syringe to a flask containing the 8 mg (0.08 mmol) Cu(I)Cl, kept under nitrogen. The solution was then stirred for 10 minutes until complete dissolution of the catalyst. The QCM-D flow cells equipped with the initiator-modified, SiO2-coated sensors and the dummy sensor were then charged with an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water mixture at a constant flow rate of 2.5 μL s−1. As soon as a stable baseline was established, the polymerization was initiated by switching the medium to the reaction mixture using a multi-position selection valve. Finally, the polymerization was stopped by switching back to the 80
20 ethanol/water mixture at a constant flow rate of 2.5 μL s−1. As soon as a stable baseline was established, the polymerization was initiated by switching the medium to the reaction mixture using a multi-position selection valve. Finally, the polymerization was stopped by switching back to the 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 ethanol/water mixture. The flow rate was maintained at 2.5 μL s−1 using a piston pump (milliGAT Low Flow pump, Model CP-DSM-GF, Valco Instrument Co. Inc., Houston, Texas, USA). Finally, the sensors and the Si-wafers (dummy sensors) were removed from the cells, washed several times with water and ethanol and finally dried under a nitrogen stream.
20 ethanol/water mixture. The flow rate was maintained at 2.5 μL s−1 using a piston pump (milliGAT Low Flow pump, Model CP-DSM-GF, Valco Instrument Co. Inc., Houston, Texas, USA). Finally, the sensors and the Si-wafers (dummy sensors) were removed from the cells, washed several times with water and ethanol and finally dried under a nitrogen stream.
The polymerization were carried out at CuCl2 concentrations of 0, 10, 30, and 50% with respect to CuCl. To achieve superior control over the SI-ATRP kinetics, concentrations of tetraethylammonium chloride (tEtAmCl), corresponding to 20, 40 and 60 times with respect to the molar CuCl concentration, were used.
For the data analysis, data obtained at an initial acquisition rate of 2000 Hz was filtered using a moving average with a width of 20 and a step of 5 data points to reduce the noise level away from the surface to a standard deviation of σ ≈ 7 pN. After removing the background slope and the offset calculated from the signal away from the surface, the contact point was determined on the approach curve as the last data point lying within 2σ from the zero-force line. Indentation depth was calculated as d = Z − ∂, in order to obtain the force–indentation (F–d) curves. Since the contact-point determination is very sensitive, due to the low S/N ratios at that part of the signal, the F–d curves were further aligned to their average maximum indentation depth; i.e. each indentation curve was shifted in depth such that its maximum indentation depth coincided with the average maximum indentation depth. In this way, substantially better overlap of the indentation curves was obtained with only the originally determined contact points now being somewhat scattered around the average contact point at zero indentation depth. The obtained force values at zero indentation depth were subtracted from the force curves to ensure that each force curve starts at the origin of the F–d coordinate system. Due to the uneven distribution of the data points on the indentation axis, the individual force values from F–d curves were interpolated to a common indentation axis with a step of one nanometer. The interpolated values were used to calculate an average F–d curve and standard deviations at each indentation depth for each sample. Such averaged curves with error-bars representing ± one standard deviation are presented in the Results section.
In order to elucidate the differences in dispersity of the brushes, the contact modulus of the outermost 20% the F–d curves, which corresponds to about 15% of the total swollen thickness, was determined by fitting Hertzian contact mechanics for a spherical indenter to the experimental data using the following equation:37
Here, F is the measured force, E* is the effective contact modulus, R is the probe radius, and d is the indentation depth. The results are presented as histograms of moduli E* for each of the samples. The histograms were also fitted using a Gaussian distribution, where the obtained mean values and standard deviations are listed in the corresponding graphs.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We gratefully acknowledge funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement no. 669562).References
- R. Barbey, L. Lavanant, D. Paripovic, N. Schuwer, C. Sugnaux, S. Tugulu and H.-A. Klok, Chem. Rev., 2009, 109, 5437–5527 CrossRef CAS PubMed.
- S. Edmondson, V. L. Osborne and W. T. Huck, Chem. Soc. Rev., 2004, 33, 14–22 RSC.
- M. A. C. Stuart, W. T. Huck, J. Genzer, M. Müller, C. Ober, M. Stamm, G. B. Sukhorukov, I. Szleifer, V. V. Tsukruk and M. Urban, Nat. Mater., 2010, 9, 101 CrossRef.
- W. Senaratne, L. Andruzzi and C. K. Ober, Biomacromolecules, 2005, 6, 2427–2448 CrossRef CAS PubMed.
- O. Azzaroni, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 3225–3258 CrossRef CAS.
- C. De las Heras Alarcón, S. Pennadam and C. Alexander, Chem. Soc. Rev., 2005, 34, 276–285 RSC.
- R. Duncan, Nat. Rev. Cancer, 2006, 6, 688 CrossRef CAS PubMed.
- R. R. Shah, D. Merreceyes, M. Husemann, I. Rees, N. L. Abbott, C. J. Hawker and J. L. Hedrick, Macromolecules, 2000, 33, 597–605 CrossRef CAS.
- K. Matyjaszewski, P. J. Miller, N. Shukla, B. Immaraporn, A. Gelman, B. B. Luokala, T. M. Siclovan, G. Kickelbick, T. Vallant and H. Hoffmann, Macromolecules, 1999, 32, 8716–8724 CrossRef CAS.
- E. S. Dehghani, S. N. Ramakrishna, N. D. Spencer and E. M. Benetti, Ind. Eng. Chem. Res., 2018, 57, 4600–4606 CrossRef CAS.
- W. Feng, J. L. Brash and S. Zhu, Biomaterials, 2006, 27, 847–855 CrossRef CAS PubMed.
- N. V. Tsarevsky and K. Matyjaszewski, Controlled synthesis of polymers with ionic or ionizable groups using atom transfer radical polymerization, ACS symposium series, Oxford University Press, 2006, pp. 79–94 Search PubMed.
- W. Huang, J.-B. Kim, M. L. Bruening and G. L. Baker, Macromolecules, 2002, 35, 1175–1179 CrossRef CAS.
- N. V. Tsarevsky, T. Pintauer and K. Matyjaszewski, Macromolecules, 2004, 37, 9768–9778 CrossRef CAS.
- M. Fantin, A. A. Isse, A. Gennaro and K. Matyjaszewski, Macromolecules, 2015, 48, 6862–6875 CrossRef CAS.
- A. S. Schulz, H. Gojzewski, J. Huskens, W. L. Vos and G. Julius Vancso, Polym. Adv. Technol., 2018, 29, 806–813 CrossRef CAS.
- A. Pomorska, K. Wolski, A. Puciul-Malinowska and S. Zapotoczny, Polymer, 2016, 97, 380–386 CrossRef CAS.
- Y. Luan, D. Li, T. Wei, M. Wang, Z. Tang, J. L. Brash and H. Chen, Anal. Chem., 2017, 89, 4184–4191 CrossRef CAS.
- J. Mandal, R. Varunprasaath, W. Yan, M. Divandari, N. D. Spencer and M. Dübner, RSC Adv., 2018, 8, 20048–20055 RSC.
- H. Ma, M. Textor, R. L. Clark and A. Chilkoti, Biointerphases, 2006, 1, 35–39 CrossRef CAS PubMed.
- S. E. Moya, A. A. Brown, O. Azzaroni and W. T. Huck, Macromol. Rapid Commun., 2005, 26, 1117–1121 CrossRef CAS.
- Y. Xia, X. Yin, N. A. Burke and H. D. Stöver, Macromolecules, 2005, 38, 5937–5943 CrossRef CAS.
- E. A. Appel, J. Del Barrio, X. J. Loh, J. Dyson and O. A. Scherman, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 181–186 CrossRef CAS.
- T. Wu, Y. Zhang, X. Wang and S. Liu, Chem. Mater., 2007, 20, 101–109 CrossRef.
- K. Matyjaszewski, T. E. Patten and J. Xia, J. Am. Chem. Soc., 1997, 119, 674–680 CrossRef CAS.
- J. B. Kim, W. Huang, M. D. Miller, G. L. Baker and M. L. Bruening, J. Polym. Sci., Part A: Polym. Chem., 2003, 41, 386–394 CrossRef CAS.
- M. Rodahl, F. Höök, A. Krozer, P. Brzezinski and B. Kasemo, Rev. Sci. Instrum., 1995, 66, 3924–3930 CrossRef CAS.
- E. M. Benetti, C. Kang, J. Mandal, M. Divandari and N. D. Spencer, Macromolecules, 2017, 50, 5711–5718 CrossRef CAS.
- A. M. Rabea and S. Zhu, Polymers, 2015, 7, 819–835 CrossRef CAS.
- O. Delgadillo-Velázquez, E. Vivaldo-Lima, I. A. Quintero-Ortega and S. Zhu, AIChE J., 2002, 48, 2597–2608 CrossRef.
- K. Kanazawa and N.-J. Cho, J. Sens., 2009, 2009, 824947 Search PubMed.
- C. Kang, R. Crockett and N. D. Spencer, Polym. Chem., 2016, 7, 302–309 RSC.
- R. R. Patil, S. Turgman-Cohen, J. Í. Šrogl, D. Kiserow and J. Genzer, Langmuir, 2015, 31, 2372–2381 CrossRef PubMed.
- C. Kang, R. M. Crockett and N. D. Spencer, Macromolecules, 2013, 47, 269–275 CrossRef.
- J. E. Sader, J. W. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef CAS.
- R. J. Cannara, M. Eglin and R. W. Carpick, Rev. Sci. Instrum., 2006, 77, 053701 CrossRef.
- H. Hertz, J. Reine. Angew. Math., 1881, 92, 156 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9py00587k |
| This journal is © The Royal Society of Chemistry 2019 |