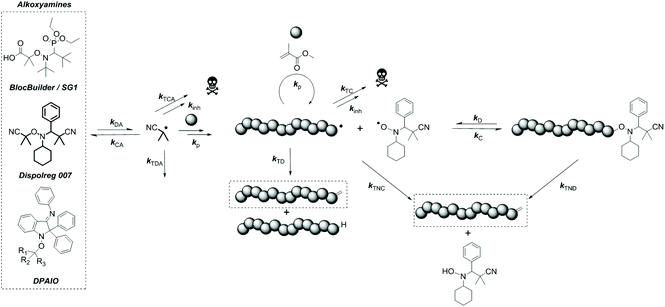
Why can Dispolreg 007 control the nitroxide mediated polymerization of methacrylates?

Abstract

The alkoxyamine 3-(((2-cyanopropan-2-yl)oxy)(cyclohexyl)amino)-2,2-dimethyl-3-phenylpropanenitrile (Dispolreg 007) has recently emerged as a robust regulator for the controlled (co)polymerization of methacrylates and styrene by nitroxide mediated polymerization. However, whilst the successful use of this alkoxyamine in a number of systems has now been demonstrated, the fundamental reason behind its ability to overcome the long-standing issues that normally arise in the nitroxide mediated polymerization of methacrylates has not been conclusively determined. Herein, a combination of quantum chemical calculations, mathematical modelling and experimental data is utilized to compare the behaviour of Dispolreg 007 with alternative nitroxides such as SG1 and DPAIO. The chemical structure of Dispolreg 007 leads to a nitroxide which has a higher rate of combination and a lower rate of β-H transfer with the propagating radical compared to SG1. This is not the case for DPAIO which shows relatively similar rate constants. The comparison between modelled and experimental data allowed for a better understanding of the system, with small amounts of macromonomers being produced mainly by β-H transfer at high monomer conversions (>80%). Finally, the estimation of the rate constants was key to optimize the polymerization conditions to achieve good control and high livingness at high monomer conversions (90%).

---

Introduction

Over the last few decades, the nitroxide mediated polymerization of methacrylates has been regarded as difficult.^1,2 Early attempts of polymerization utilizing 2,2,6,6-tetramethylpiperidine-1-oxyl (TEMPO) derivatives (including alkoxyamines) as regulators showed that the equilibrium between the active and dormant states was shifted towards the active radical species and yielded low monomer conversions (<40%) due to the formation of undesired side-products, notably macromonomers and TEMPO hydroxylamine by β-hydrogen transfer, also referred to as disproportionation.^3,4 Disproportionation can either be intramolecular (from the macroalkoxyamine) or intermolecular (between propagating and persistent radicals) as depicted in Scheme 1 and cannot be distinguished by chemical analysis. However, the structure of the nitroxide and the nature of the substituents around the cleavable C–O bond have been shown to influence which pathway is favoured.^1,5

Scheme 1 Polymerization mechanism and alkoxyamine/nitroxide structures.

Extensive work has been carried out on the development of new nitroxides/alkoxyamines to shift the dormant/active equilibrium and to avoid undesired disproportionation events. The use of α-hydrogen nitroxides/alkoxyamines which include 2,2,5-trimethyl-4-phenyl-3-azahexane-3-nitroxide (TIPNO) and N-tert-butyl-N-[1-diethylphosphono-(2,2-dimethylpropyl)] (SG1) nitroxide has improved the ability to polymerize styrene and acrylate derivatives with good control, though the polymerization of methacrylates is still problematic.^6–8 More specifically for SG1/BlocBuilder, β-hydrogen transfer could be reduced for one monomeric unit, unfortunately not for the polymer, due to a strong penultimate effect.⁹ The penultimate effect also affected the rate constant for recombination (k_C) and decomposition (k_D) of the macroalkoxyamine and as a result did not allow good control and “livingness” according to theoretical calculations, which was confirmed by experimental data.¹⁰ This issue could be overcome through copolymerization of methacrylates with small amounts of co-monomers, as introduced by Charleux et al.^11,12

The development of more complex structures introduced by Grubbs et al. could regulate the polymerization of methacrylates, but their versatility towards other monomers was limited.^13–15 The development of imidazolines and imidazolidines gave rise to various trends as intramolecular and/or intermolecular disproportionation could be favoured depending on the nature of the substituents but could not be avoided.⁵ 2,2-Diphenyl-3-phenylimino-2,3-dihydro-indol-1-yloxyl (DPAIO) and its derivatives yielded the first successful polymerization of methacrylates, obtaining good control and minimal undesired disproportionation.^16,17 Nevertheless, the limited versatility of the nitroxide towards the polymerization of styrene and acrylates is still problematic, though some modifications on the alkoxyamine structures improved the control in the case of styrene.¹⁸ The development of new nitroxide/alkoxyamine structures has also been motivated to reduce the tendency of undesired disproportionation between two nitroxides (self-disproportionation).^19,20 The instability of the nitroxide can be favoured by the presence of hydrogen atoms on the carbon α to the N–O bond, which can affect the control of the polymerization thereafter.^15,19,21,22

Recently, our research group has introduced Dispolreg 007 (3-(((2-cyanopropan-2-yl)oxy)(cyclohexyl)amino)-2,2-dimethyl-3-phenyl-propanenitrile), which proved to be a robust and readily obtainable regulator for the polymerization of methacrylates and styrene.^23,24 In addition, copolymerization (random, gradient and block) could be achieved in both solution and dispersed media.^25–27 Nevertheless, the underlying reasons for the success of Dispolreg 007 in the polymerization of methacrylates remain unclear and little is known about the reactivity of the corresponding nitroxide with itself and the propagating radical. Herein, we seek to gain a deeper insight into the stability of the generated nitroxide, the polymerization of methyl methacrylate (MMA) with Dispolreg 007, and the nature and importance of the β-H transfer reaction between the propagating radical and the nitroxide. A combination of quantum chemical calculations, mathematical modelling and experimental data is utilized to estimate the values of the various rate constants and compare the level of control exerted by Dispolreg 007 with that of other known alkoxyamines/nitroxides, such as BlocBuilder/SG1 and DPAIO.

Results and discussion

At first glance, the chemical structures of the alkoxyamines/nitroxides of SG1, DPAIO and Dispolreg 007 are rather different (Scheme 1), which can have an impact on the stability of the nitroxide fragment during polymerization.^19,28–30 The cyclic nitroxide DPAIO does not have any hydrogen atoms on the C_α bound to the N–O bond that can be abstracted by a propagating radical or by a nitroxide. Conversely, the β-H in SG1 could be prone to H-abstraction, though it appears to display some remarkable kinetic stability due to optimum structural conformation.³¹ In the case of Dispolreg 007, two α-H atoms are present, which in analogy with literature precedents should not yield a significant control of the polymerization.⁸ The stability of the nitroxide towards self-disproportionation was assessed by quantum chemical calculations (see the ESI† for details), wherein the enthalpy of reaction was calculated for the disproportionation of two nitroxides to yield a hydroxylamine and a nitrone. In the case of SG1, the enthalpy of reaction is rather low, ΔH = 0.15 kJ mol⁻¹, though the stability of the nitroxide is enhanced by an optimum structural conformation.³¹ Self-disproportionation between the nitroxide fragments of Dispolreg 007 (D7) involves substantially higher energies with ΔH = 45.69 kJ mol⁻¹, which indicates that the nitroxide is stable. This stability can be related to a preferred structural conformation (Fig. S1†) in which the –CN and N–O groups are almost in the same plane, which could prevent hydrogen abstraction. This is also observed in the dihedral angles between the N–O and C–H groups (157.2°) and between the N–O and –CN groups (27.6°). In comparison, the experimental dihedral angle between the N–O and C–H groups is rather close to that of the SG1 nitroxide (∼180°;³¹ calculated 173.2° in Table S2†). Noteworthily, the nitroxide structures introduced by the groups of Inamoto and Volodarsky respectively are quite similar to that of D7 and display good stability towards self-disproportionation.^32–35

In order to get a deeper insight into the ability of this apparently stable nitroxide to mediate the polymerization of MMA, we first focused on the structural differences between poly(methyl methacrylate) based macroalkoxyamines, with SG1 (PMMA-SG1), DPAIO (PMMA-DPAIO) and D7 (the nitroxide part of Dispolreg 007 – PMMA-D7) as end groups. The presence of various functional groups along the N–O bond greatly influences the stability of the macro-alkoxyamines, which is reflected in the different values of k_D and k_C. The values of k_D estimated from experimental data have been reported for D7 and SG1, with k^PMMA-D7_D = 1.4 × 10⁻² s⁻¹ (at 90 °C), k^PMMA-SG1_D = 1 × 10⁻² s⁻¹ (at 45 °C). In addition, the value for DPAIO has been estimated from the cleavage temperature to be k^PMMA-DPAIO_D = 2.02 × 10⁻⁴ s⁻¹ (at 120 °C).^10,16,24 In order to understand the differences in the values of k_D and estimate the value of k_C for PMMA-D7, quantum chemical calculations were carried out. For this, high level methods are available and have been utilized to determine the dissociation energies of model alkoxyamines.³⁶ However, in spite of their accuracy for relatively small molecules (∼100 electrons),³⁷ these high level methods are extremely time consuming for larger molecules (PMMA-D7 has 292 electrons; the details are given in the ESI†). Therefore, DFT was used in this work, as it gives a relatively good estimation of bond dissociation energies (BDE) and geometrical parameters.^38,39 The molecular model used for the poly(methyl methacrylate) radical contains two MMA units (Fig. S1† and n = 1 in Fig. 1). The geometrical parameters corresponding to the macro-alkoxyamines/nitroxide and the respective Cartesian coordinates are detailed in the ESI (Tables S1 and S2†). The reliability of the level of quantum calculation was tested by comparison with the predictions of higher level calculations (CBS-4 M,⁴⁰ Table S3†) and in the determination of the geometrical parameters of known nitroxides^31,41 and the BDE of known alkoxyamines,³⁹ with minimal error observed (Tables S4–S6†). It should be stressed that while the quantum chemical calculations provide valuable details on the molecular and electronic structures, this can only yield a qualitative insight into the order of magnitude of the rate constants.

Fig. 1 Potential energy surface for the intermolecular disproportionation process between a poly(methyl methacrylate) radical and a persistent radical. (Black) Nitroxide D7 based on Dispolreg 007; (red) SG1; (blue) DPAIO. The corresponding enthalpies are in kJ mol⁻¹.

The analysis of the C–O bond strength and stability of the different macroalkoxyamines can give an estimation of the order of magnitude of k_D for PMMA-D7, PMMA-SG1 and PMMA-DPAIO.³⁹ The results are summarized in Table 1 and show that the bond dissociation energy (BDE) of the C–O bond is slightly higher for PMMA-D7 (142.30 kJ mol⁻¹) compared with that of PMMA-DPAIO (140.61 kJ mol⁻¹) and substantially higher than that for PMMA-SG1 (84.87 kJ mol⁻¹), which might be explained by several features.

Table 1 Bond dissociation energy (BDE), in kJ mol⁻¹, equilibrium C–O bond length (R_e), in Å, and occupation number (η) for the antibonding σ_CO orbital

	BDE	R e(C–O)	η(σCO*)
Dispolreg 007	142.30	1.439	0.041
DPAIO	140.61	1.447	0.043
SG1	84.87	1.454	0.047

---

First, on comparing the C–O bond distance for the macroalkoxyamines, it is observed that C–O is 0.015 Å shorter in PMMA-D7 than in PMMA-SG1 (1.439 vs. 1.454 Å), which may be ascribed to a lower charge transfer to the antibonding sigma (σ_CO*) orbital. This is reflected in a smaller occupation number in that orbital for PMMA-D7 (0.041) compared to that for PMMA-SG1 (0.047), thus strengthening the C–O bond. The slightly lower BDE of PMMA-DPAIO (140.61 kJ mol⁻¹) compared to that of PMMA-D7 (142.30 kJ mol⁻¹) might also be due to a small elongation of the C–O bond (0.008 Å) and a slightly larger population of the antibonding σ_CO* orbital in PMMA-DPAIO (0.043 compared to 0.041 for PMMA-D7). The higher stability of PMMA-D7 compared to that of PMMA-SG1 suggests that the recombination of the nitroxide with the propagating radical is favored; hence k^PMMA-D7_C/k^PMMA-D7_D > k^PMMA-SG1_C/k^PMMA-SG1_D. In addition, the extensive stabilization provided by the aromatic rings in DPAIO should yield k^PMMA-D7_C/k^PMMA-D7_D relatively similar to k^PMMA-DPAIO_C/k^PMMA-DPAIO_D.

There is a discrepancy between the values of BDE obtained herein and the activation energies of the macroalkoxyamines PMMA-D7 (109 kJ mol⁻¹),²⁴ PMMA-SG1 (≈100 kJ mol⁻¹)² and PMMA-DPAIO (126 kJ mol⁻¹)¹⁶ estimated using experimental data. However, comparison is not straightforward because the confidence intervals of the previously reported values were not given and analysis of the procedures used to estimate these activation energies indicate that these intervals may be significant (see the ESI† for details).

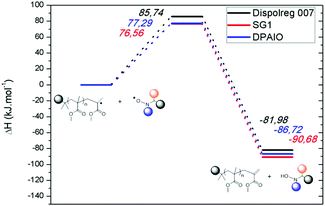
The second set of calculations focused on the undesired disproportionation reaction between a propagating radical and the nitroxide. Disproportionation can either be intermolecular or intramolecular (Scheme 1) with the associated rate constants k_TNC and k_TND respectively. When SG1 and DPAIO are employed, it has been demonstrated that the intramolecular path plays a minor role in the formation of macromonomers.^7,17 Hence, it is important to check if intramolecular disproportionation also plays a minor role with PMMA-D7. It should be noted that the intramolecular disproportionation reaction cannot be predicted by either the structure of the nitroxide/propagating radical or by the geometry of the transition state.⁵ The comparison of the transition state energy of the intra- and intermolecular disproportionation highlighted that for PMMA-D7, the intramolecular path (ΔH^TS_intra = 149.06 kJ mol⁻¹) is kinetically disfavored compared to the intermolecular one (see below, ΔH^TS_inter = 85.74 kJ mol⁻¹). The same behavior is observed for SG1 where values of ΔH^TS_intra = 133.85 kJ mol⁻¹ and ΔH^TS_inter = 76.56 kJ mol⁻¹ were obtained respectively. Overall, the transition states are lower in energy for SG1 than for D7, which suggests that the unlikely intramolecular disproportionation reaction is kinetically easier for SG1.

The predominance of the intermolecular disproportionation process required further calculations. Hence, the potential energy surfaces (PES) were calculated and they are depicted in Fig. 1. The values of the transition states (Fig. 1 and Table S7†) reveal that the intermolecular disproportionation between PMMA and the nitroxide based on Dispolreg 007 (D7) shows a much higher activation energy (ΔH^TS = 85.74 kJ mol⁻¹) compared to DPAIO (77.29 kJ mol⁻¹) and SG1 (76.56 kJ mol⁻¹), which presents the lowest value. Consequently, the β-H transfer is kinetically easier for SG1 and DPAIO compared to D7. Thermodynamically, the reaction is favored with SG1 which shows the most exothermic enthalpy of reaction (ΔH^reac = −90.68 kJ mol⁻¹). This process is thermodynamically less likely to occur with D7, which presents the least negative enthalpy of reaction (ΔH^reac = −81.98 kJ mol⁻¹), whilst an intermediate value is found for DPAIO (ΔH^reac = −86.72 kJ mol⁻¹). Consequently, we should expect the rate constant k^PMMA-D7_TNC to be lower than the recently reported value for PMMA-SG1 of k^PMMA-SG1_TNC = 7.6 × 10³ M⁻¹ s⁻¹ at 90 °C.⁴²

The smaller barrier observed for the intermolecular disproportionation in PMMA-SG1 may be explained in terms of the geometrical structure of the transition state. In the case of PMMA-SG1, the transition state resembles the reactants (early transition state⁴³), thus facilitating the molecular rearrangement to surpass the reaction barrier. For PMMA-D7, the transition state occurs later, with geometrical features of the products more developed, as shown in Table 2 and further displayed in Fig. 2 and S2.†

Fig. 2 Molecular models used in the quantum chemical simulations shown during the transition states of the intermolecular disproportionation reaction. The general molecular structure of the transition state in the intermolecular disproportionation reaction can be found in Fig. S1 and S2 of the ESI.†

Table 2 Geometrical parameters of the transition state in the intermolecular disproportionation. Bond distances in Å and angle in degrees

	R e(C–C)	R e(C–H)	R e(O–H)	α(CHO)
D7	1.412	1.282	1.380	92.7
DPAIO	1.410	1.250	1.431	93.0
SG1	1.421	1.232	1.453	97.1

---

During the formation of the macromonomer, the C–C bond in the transition state is shorter for D7 than for SG1 (R_CC = 1.412 Å vs. 1.421 Å), which means that with D7 the C=C bond is more developed at this stage. Similarly, the hydrogen is farther from the carbon of the incipient double bond of the PMMA–C=CH₂ macromonomer in the case of D7 (R_CH = 1.282 Å) compared to that of SG1 (R_CH = 1.232 Å). The developing hydroxylamine also presents interesting features, with a shorter NO–H bond in the case of D7-H (R_OH = 1.380 Å) than of SG1-H (R_OH = 1.453 Å). DPAIO-H shows geometrical features closer to those of D7-H (see Table 2). This suggests that the transition state for the β-H transfer reaction with DPAIO also occurs later, thus hindering the disproportionation compared to SG1. Nevertheless, the obtained geometrical values are rather similar, which suggests that the electronic distribution might also play a key role in the reactivity of Dispolreg 007.

In summary, three characteristics are likely to influence the control over the polymerization of MMA with Dispolreg 007: (1) the stronger C–ON bond of the macroalkoxyamine PMMA-D7 compared to that of PMMA-SG1, due to a higher BDE. This difference might be the primary cause for control over the polymerization of MMA; (2) the higher energy transition state in the intermolecular disproportionation reaction kinetically disfavors the process compared to that of the PMMA radical and SG1; and (3) thermodynamically, this process is the least exothermic compared with SG1 and DPAIO nitroxides.

Nevertheless, it is important to point out that quantum chemical calculation can only give a hint on the behavior of the system. In order to get a deeper insight into the polymerization and to get a better estimation of the kinetic parameters (e.g. k_C and k_TNC), we relied on experimental data and mathematical modeling. Hence, polymerizations of MMA at 90 °C in the presence of various concentrations of Dispolreg 007 were carried out. The initial monomer concentration was maintained at [M]₀ = 4.35 mol L⁻¹ in toluene, and the initial alkoxyamine concentration [RN]₀ was modified to target various chain lengths, DP_n = [M]₀/[RN]₀ of 50, 100 and 200. The polymerizations were carefully monitored by ¹H NMR (Fig. S3 and S4†) to follow the monomer conversion and the production of the macromonomer (bearing C=CH₂ functionalities, δ = 6.04 and 5.38 ppm) by either radical–radical termination by disproportionation, or β-H transfer (intermolecular disproportionation) to the nitroxide. The influence of intramolecular disproportionation of the macroalkoxyamine is neglected herein; hence k_TND = 0 s⁻¹. This hypothesis is in keeping with our quantum chemical calculations. The evolution of molar mass as a function of monomer conversion was monitored by SEC.

The evolutions of monomer conversion as a function of time, of molar mass as a function of monomer conversion and of the percentage of macromonomers (%MM, calculated as a ratio of the integrals of H₂C=C of the macromonomers at δ = 6.04 and 5.38 ppm and the integral of the polymeric CH₃; ESI†) as a function of monomer conversion were fit using a mathematical model (coded in MATLAB, Scheme S2†), based on the reaction in Scheme 1. The influence of oxygen inhibition is introduced, which affects the radical concentration (and monomer conversion) at the beginning of polymerization. The concentration of the inhibitor selected herein is [O₂]₀ = 1.94 × 10⁻⁴ mol L⁻¹, which is 10 times lower than the highest [O₂]₀ that can be dissolved in toluene, as calculated from the molar fraction of oxygen that can be dissolved in toluene at 25 °C.⁴⁴ The unknown rate constants for alkoxyamine recombination (k_CA), macroalkoxyamine recombination (k_C), disproportionation with nitroxide (k_TNC) and inhibition with oxygen (k_inh) are estimated by fitting the experimental data. Other rate constants and initial values are taken from the literature and are summarized in Table S8.† It is important to note that a better fit was obtained when using a chain length dependent rate constant for termination defined as k^{i, i}_t = k^{1, 1}_t× i^−α_S for i ≤ 100 and α_S = 0.63, hence where radicals of chain lengths CL ≤ 100 are involved.^45–47 The rate constant k^{1, 1}_t corresponds to the monomeric rate constant for termination k^1,1_t = 2.33 × 10¹⁰ × exp(−9000/RT) M⁻¹ s⁻¹.⁴⁷ For radicals with chain lengths CL > 100, the chain length dependent rate constant of termination is expressed as k^{i, i}_t = k^{1, 1}_t × 100^{(−α_S+α_L)}× i^−α_L, with α_L = 0.16.^47,48 Finally, for radicals of chain lengths CL > 1000, the average rate of termination <k_t> was approximated to a singular rate constant of termination k_t = 1.984 × 10⁸ × exp(−5890/RT) M⁻¹ s⁻¹.⁴⁸

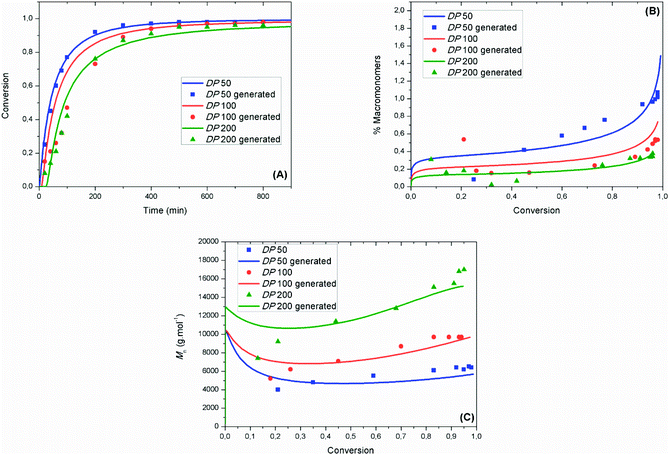
Fig. 3 shows that the experimental evolutions of monomer conversion as a function of time, of molar mass as a function of monomer conversion and of percentage of macromonomers as a function of monomer conversion were well fitted by the mathematical model using the following values (at 90 °C) of k_CA = 3.1 × 10⁶ M⁻¹ s⁻¹ (±4.1 × 10³ M⁻¹ s⁻¹), k_C = 3.7 × 10⁵ M⁻¹ s⁻¹ (±2.0 × 10¹ M⁻¹ s⁻¹), k_TNC = 8.3 × 10² M⁻¹ s⁻¹ (±4.0 × 10⁻² M⁻¹ s⁻¹) and k_inh = 34 × 10⁷ M⁻¹ s⁻¹ (±4.7 × 10⁵ M⁻¹ s⁻¹). The experimental data in Fig. 3A and B are obtained from online NMR measurements, while the experimental data in Fig. 3C are obtained from offline SEC measurements. Offline NMR measurements were also performed (Fig. S5†) and relatively good fitting could be achieved with the mathematical model.

Fig. 3 (A) Experimental (squares, DP₅₀; circles, DP₁₀₀; up triangles, DP₂₀₀; obtained from online NMR measurement) and modeled (lines) evolution of monomer conversion as a function of time. (B) Experimental (squares, DP₅₀; circles, DP₁₀₀; up triangles, DP₂₀₀; obtained from online NMR measurement) and modeled (lines) evolution of percentage of macromonomers (%MM) as a function of monomer conversion. (C) Experimental (squares, DP₅₀; circles, DP₁₀₀; up triangles, DP₂₀₀; obtained from offline SEC measurement) and modeled (lines) evolution of M_n (lines, g mol⁻¹) as a function of conversion.

At low reaction times (<20 min), the fitting of the monomer conversion for high DP_n is not optimum. This might be ascribed to a strong penultimate effect and to side reactions between radicals and oxygen, which might explain the high value obtained for k_inh herein. Both effects do not play a role further on, allowing good fitting between the experimental and modeled data at high monomer conversions (>50%) for all targeted DP_ns. The importance of using chain length dependent rate constants for termination is further highlighted in Fig. S6,† wherein a singular value is selected for k_t. Using the previously utilized value of k_t = 6.07 × 10⁷ M⁻¹ s⁻¹,¹⁶ poorer fitting is obtained for both the evolution of monomer conversion and of macromonomer production. Fig. 3B shows that the %MM increases when DP_n decreases due to a higher nitroxide concentration which is likely to increase the probability of the disproportionation reaction between the nitroxide and a propagating radical. The relative importance of the radical–radical termination by disproportionation vs. nitroxide–radical disproportionation was estimated using the mathematical model. In Fig. S7,† the evolution of the percentage of macromonomers generated by radical–radical termination by disproportionation or nitroxide–radical disproportionation is presented. At DP₅₀, it becomes clear that the disproportionation reaction with a nitroxide is predominant at high conversions, above 80%. In Fig. 3C, the mathematical model could fit the experimental values of molar mass relatively well for all targeted DP_ns. At low conversions the model predicted relatively high molar masses. The reason is that at the beginning of the process the concentration of the nitroxide was very low and the polymer chains grow to high values.

The estimated value of k_CA is in the same order of magnitude as that for an SG1-based alkoxyamine with an initiating tertiary radical (from 24 to 120 °C).^49,50 This is not the case for the macroalkoxyamine, where k^PMMA-D7_C = 3.7 × 10⁵ M⁻¹ s⁻¹ is one order of magnitude higher than k^PMMA-SG1_C = 1.4 × 10⁴ M⁻¹ s⁻¹ (at 45 °C).¹⁰ First, the decrease of an order of magnitude for k_C compared to that of the parent alkoxyamine is expected, due to a penultimate effect.²⁹ Then, the difference in the two macroalkoxyamines coincides with the quantum calculations above, suggesting a higher stability of the Dispolreg 007 based macroalkoxyamine. The estimated value of k^PMMA-D7_C is also lower than k^PMMA-DPAIO_C = 1.45 × 10⁶ M⁻¹ s⁻¹ (at 40 °C).¹⁶

Regarding the β-H transfer reaction, the estimated rate constant for k_TNC = 8.3 × 10² M⁻¹ s⁻¹ (at 90 °C) is lower for Dispolreg 007 than for SG1 (k^PMMA-SG1_TNC = 7.6 × 10³ M⁻¹ s⁻¹ at 90 °C).⁴² This observation is in line with the quantum chemical calculations wherein disproportionation is kinetically less favored in the case of Dispolreg 007. Using this estimated value of k_TNC, it is possible to calculate the theoretical fraction of disproportionation, introduced by Souaille and Fischer, as f_D = k_TNC/(k_TNC + k_C) = 0.22% (at 90 °C).⁵¹ This is indeed far lower than what was calculated for PMMA-SG1 (f_D = 7.8% at 70 °C) as a result of a higher k_C and a lower k_TNC.⁷ The fraction of disproportionation cannot be accurately estimated for DPAIO due to the presence of two breakable bonds C–O and N–O.¹⁷

The maximum monomer conversion C_max one could achieve with Dispolreg 007 can be calculated utilizing the equations derived by Souaille and Fischer (see the ESI† for details).⁵² More specifically, for an initial alkoxyamine concentration [RN]₀ = 2.17 × 10⁻² mol L⁻¹ (corresponding to a targeted DP of 200 using the conditions above), the polymerization of MMA with Dispolreg 007 can reach 98% conversion theoretically, whilst only 90% can be achieved with DPAIO and 69% with SG1.

It is important to stress that the various equations derived by Souaille and Fischer on the features of nitroxide mediated polymerization are obtained assuming chain length independent rate constants.^51–53 Herein, the same assumption clearly cannot be made, due to the importance of the chain length dependency of the rate constant for termination k_t for a more accurate fitting of our experimental data. Therefore, the calculated values of f_D and C_max are given above as approximate indications and should be treated with caution.

The (k_C, k_D) Fischer's diagram often used to predict the features of polymerization is based on chain length independent rate constants and in the absence of β-H transfer between the radicals and the nitroxide. Therefore, this type of diagram is not valid herein.^51,53 Consequently, we relied on mathematical modeling to get an insight into the predictive “livingness” of the polymerization process at high monomer conversions (90%).

Fig. 4 presents the effect of the value of targeted DP_n and the polymerization temperature on the fraction of “living” chains at 90% monomer conversion for the batch solution polymerization of MMA ([M]₀ = 4.35 mol L⁻¹). The simulations were carried out with the parameters in Table S4,† assuming no inhibition. Some inaccuracies are expected due to the unavailability of the activation energies of k_CA, k_C, and k_TNC, which forces us to assume a weak influence of temperature on these rate constants.

Fig. 4 Temperature and targeted DP_n conditions for high “livingness” at high monomer conversion (90%).

Fig. 4 shows that at a reaction temperature of 363 K (90 °C), the percentage of “living” chains at 90% monomer conversion can change dramatically, ranging from 77% to 7% in a range of targeted DP_n of 5 to 595. This is in part due to a difference of the time needed to reach 90% conversion, which will affect the percentage of “dead” chains.⁵⁴ As such, “livingness” can be maximized at lower monomer conversions (and reaction times) during the formation of the PMMA based macro-alkoxyamine thus resulting in good chain extension. This was indeed the strategy utilized in our previous report,²⁴ wherein the polymerization of MMA was stopped at 68% monomer conversion (64% theoretical “livingness”) to yield a well-defined PMMA-b-poly(butyl methacrylate) block copolymer (M_n = 19 800 g mol⁻¹, Đ = 1.46).

Under the batch conditions herein, a decrease of 10 °C of the reaction temperature could significantly increase the “livingness” above 90% conversion, from 84% to 23% for DP_n ranging from 5 to 595. The influence of reaction time is highlighted in Fig. S8,† wherein the percentage of “living” chains is plotted as a function of temperature and time to reach 90% monomer conversion.

In short, high “livingness” can be achieved for the polymerization of MMA in the presence of Dispolreg 007, with minimum macromonomer formation from β-H transfer with the nitroxide. This can be achieved over a range of temperatures and molar masses. However, targeting high “livingness” at high monomer conversion can come at a cost of long reaction time or narrow range of targeted molar masses. It should be emphasized that for shorter reaction times, optimized conditions for “livingness” and control can also be achieved using a slight excess of the nitroxide at the onset of the polymerization or mild reducing agents.^55–57

Conclusions

In this report, we have demonstrated that the reason for the better performance of Dispolreg 007 over SG1 in the polymerization of methyl methacrylate is primarily suitable rate constants for recombination (k_C) for the alkoxyamine and macroalkoxyamine, respectively. This is in combination with a low rate constant for β-H transfer between the propagating radical and the nitroxide (k_TNC). Quantum chemical calculations allowed us to qualitatively predict the influence of the nitroxide fragment, i.e. D7 (the nitroxide part in Dispolreg 007), SG1 and DPAIO, on recombination and disproportionation reactions. As such, the slight influence of the undesired disproportionation reaction (f_D = 0.22% at 90 °C) with the nitroxide fragment of Dispolreg 007 was shown to be due to high enthalpy for the transition state and relatively low enthalpy of reaction compared to SG1. The estimation of the various rate constants was carried out by fitting experimental data with a mathematical model. Finally, this allowed us to get an insight into how to tune the polymerization conditions, e.g. DP_n targeted and polymerization temperature, to maximize the amount of “living” chains at high monomer conversions (90%).

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Dr José Ignacio Miranda from SGIker for his kind assistance on the NMR measurements. Technical and human support provided by IZO-SGI, SGIker (UPV/EHU, MICINN, GV/EJ, ERDF and ESF) is gratefully acknowledged. F. R would like to thank the Diputación Foral de Gipuzkoa (OF 188/2017 (ES)) and the Basque Government (PI2017-11) for financial support. A. S. and N. B. specially acknowledge the financial support obtained through the post-doctoral fellowship Juan de la Cierva en Formación (FJCI-2015-26693) and Incorporación (IJCI-2016-28442), respectively, from the Ministry of Economy and Competitiveness of Spain. The authors would also like to thank the Diputación Foral de Gipuzkoa, University of the Basque Country UPV/EHU (UFI 11/56), Basque Government (GVIT 999-16), MINECO (CTQ2014-59016P) and MICINN (CTQ2016-80886R) for their financial support.

References

1. E. Guégain, Y. Guillaneuf and J. Nicolas, Macromol. Rapid Commun., 2015, 36(13), 1227–1247.
2. J. Nicolas, Y. Guillaneuf, C. Lefay, D. Bertin, D. Gigmes and B. Charleux, Prog. Polym. Sci., 2013, 38(1), 63–235.
3. G. Moad, A. G. Anderson, F. Ercole, C. H. J. Johnson, J. Krstina, C. L. Moad, E. Rizzardo, T. H. Spurling and S. H. Thang, Controlled-Growth Free-Radical Polymerization of Methacrylate Esters: Reversible Chain Transfer versus Reversible Termination, in Controlled Radical Polymerization, American Chemical Society, 1998, vol. 685, pp. 332–360.
4. C. Burguière, M.-A. Dourges, B. Charleux and J.-P. Vairon, Macromolecules, 1999, 32(12), 3883–3890.
5. D. Parkhomenko, E. G. Bagryanskaya, S. R. A. Marque and D. Siri, Phys. Chem. Chem. Phys., 2013, 15(33), 13862–13871.
6. D. Benoit, S. Grimaldi, S. Robin, J.-P. Finet, P. Tordo and Y. Gnanou, J. Am. Chem. Soc., 2000, 122(25), 5929–5939.
7. C. Dire, J. Belleney, J. Nicolas, D. Bertin, S. Magnet and B. Charleux, J. Polym. Sci., Part A: Polym. Chem., 2008, 46(18), 6333–6345.
8. D. Benoit, V. Chaplinski, R. Braslau and C. J. Hawker, J. Am. Chem. Soc., 1999, 121(16), 3904–3920.
9. R. McHale, F. Aldabbagh and P. B. Zetterlund, J. Polym. Sci., Part A: Polym. Chem., 2007, 45(11), 2194–2203.
10. Y. Guillaneuf, D. Gigmes, S. R. A. Marque, P. Tordo and D. Bertin, Macromol. Chem. Phys., 2006, 207(14), 1278–1288.
11. J. Nicolas, L. Mueller, C. Dire, K. Matyjaszewski and B. Charleux, Macromolecules, 2009, 42(13), 4470–4478.
12. J. Nicolas, C. Dire, L. Mueller, J. Belleney, B. Charleux, S. R. A. Marque, D. Bertin, S. Magnet and L. Couvreur, Macromolecules, 2006, 39(24), 8274–8282.
13. A. C. Greene and R. B. Grubbs, Macromolecules, 2010, 43(24), 10320–10325.
14. A. C. Greene and R. B. Grubbs, Macromolecules, 2009, 42(13), 4388–4390.
15. R. B. Grubbs, J. K. Wegrzyn and Q. Xia, Chem. Commun., 2005,(1), 80–82.
16. Y. Guillaneuf, D. Gigmes, S. R. A. Marque, P. Astolfi, L. Greci, P. Tordo and D. Bertin, Macromolecules, 2007, 40(9), 3108–3114.
17. M. Edeleva, S. R. A. Marque, D. Bertin, D. Gigmes, Y. Guillaneuf, S. V. Morozov and E. G. Bagryanskaya, J. Polym. Sci., Part A: Polym. Chem., 2008, 46(20), 6828–6842.
18. P. Astolfi, L. Greci, P. Stipa, C. Rizzoli, C. Ysacco, M. Rollet, L. Autissier, A. Tardy, Y. Guillaneuf and D. Gigmes, Polym. Chem., 2013, 4(13), 3694–3704.
19. A. Nilsen and R. Braslau, J. Polym. Sci., Part A: Polym. Chem., 2006, 44(2), 697–717.
20. C. Detrembleur, C. Jerome, J. De Winter, P. Gerbaux, J.-L. Clement, Y. Guillaneuf and D. Gigmes, Polym. Chem., 2014, 5(2), 335–340.
21. K. Adamic, D. F. Bowman and K. U. Ingold, J. Am. Chem. Soc., 1970, 92(4), 1093–1094.
22. Q. Xia and R. B. Grubbs, J. Polym. Sci., Part A: Polym. Chem., 2006, 44(17), 5128–5136.
23. A. Simula, M. Aguirre, N. Ballard, A. Veloso, J. R. Leiza, S. van Es and J. M. Asua, Polym. Chem., 2017, 8(10), 1728–1736.
24. N. Ballard, M. Aguirre, A. Simula, A. Agirre, J. R. Leiza, J. M. Asua and S. van Es, ACS Macro Lett., 2016, 5(9), 1019–1022.
25. N. Ballard, M. Aguirre, A. Simula, J. R. Leiza, S. van Es and J. M. Asua, Polym. Chem., 2017, 8(10), 1628–1635.
26. N. Ballard, M. Aguirre, A. Simula, J. R. Leiza, S. van Es and J. M. Asua, Chem. Eng. J., 2017, 316, 655–662.
27. N. Ballard, A. Simula, M. Aguirre, J. R. Leiza, S. van Es and J. M. Asua, Polym. Chem., 2016, 7(45), 6964–6972.
28. G. Gryn'ova, C. Y. Lin and M. L. Coote, Polym. Chem., 2013, 4(13), 3744–3754.
29. D. Bertin, D. Gigmes, S. R. A. Marque and P. Tordo, Chem. Soc. Rev., 2011, 40(5), 2189–2198.
30. D. Bertin, D. Gigmes, S. R. A. Marque and P. Tordo, Macromolecules, 2005, 38(7), 2638–2650.
31. S. Grimaldi, D. Siri, J.-P. Finet and P. Tordo, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1998, 54, 1712–1714.
32. M. Iwamura and N. Inamoto, Bull. Chem. Soc. Jpn., 1967, 40(3), 702–702.
33. M. Iwamura and N. Inamoto, Bull. Chem. Soc. Jpn., 1970, 43(3), 860–863.
34. V. A. Reznikov, I. A. Gulorov, Y. V. Gatilov, T. V. Rybalova and L. B. Volodarsky, Russ. Chem. Bull., 1996, 45(2), 384–392.
35. V. A. Reznikov and L. B. Volodarsky, Tetrahedron Lett., 1994, 35(14), 2239–2240.
36. J. L. Hodgson, C. Yeh Lin, M. L. Coote, S. R. A. Marque and K. Matyjaszewski, Macromolecules, 2010, 43(8), 3728–3743.
37. E. I. Izgorodina, D. R. B. Brittain, J. L. Hodgson, E. H. Krenske, C. Y. Lin, M. Namazian and M. L. Coote, J. Phys. Chem. A, 2007, 111(42), 10754–10768.
38. P. Nkolo, G. Audran, R. Bikanga, P. Brémond, S. R. A. Marque and V. Roubaud, Org. Biomol. Chem., 2017, 15(29), 6167–6176.
39. A. Gaudel-Siri, D. Siri and P. Tordo, ChemPhysChem, 2006, 7(2), 430–438.
40. J. A. Montgomery, M. J. Frisch, J. W. Ochterski and G. A. Petersson, J. Chem. Phys., 2000, 112(15), 6532–6542.
41. A. Capiomont and J. Lajzerowicz-Bonneteau, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30(9), 2160–2166.
42. S. K. Fierens, P. H. M. Van Steenberge, F. Vermeire, M.-F. Reyniers, G. B. Marin and D. R. D'Hooge, AIChE J., 2018, 64(7), 2545–2559.
43. G. S. Hammond, J. Am. Chem. Soc., 1955, 77(2), 334–338.
44. T. Sato, Y. Hamada, M. Sumikawa, S. Araki and H. Yamamoto, Ind. Eng. Chem. Res., 2014, 53(49), 19331–19337.
45. C. Barner-Kowollik and G. T. Russell, Prog. Polym. Sci., 2009, 34(11), 1211–1259.
46. G. Johnston-Hall, M. H. Stenzel, T. P. Davis, C. Barner-Kowollik and M. J. Monteiro, Macromolecules, 2007, 40(8), 2730–2736.
47. J. Barth and M. Buback, Macromol. Rapid Commun., 2009, 30(21), 1805–1811.
48. D. R. Taylor, K. Y. v. Berkel, M. M. Alghamdi and G. T. Russell, Macromol. Chem. Phys., 2010, 211(5), 563–579.
49. J. Lalevée, D. Gigmes, D. Bertin, X. Allonas and J. P. Fouassier, Chem. Phys. Lett., 2007, 449(1), 231–235.
50. J. Sobek, R. Martschke and H. Fischer, J. Am. Chem. Soc., 2001, 123(12), 2849–2857.
51. M. Souaille and H. Fischer, Macromolecules, 2000, 33(20), 7378–7394.
52. M. Souaille and H. Fischer, Macromolecules, 2001, 34(9), 2830–2838.
53. H. Fischer, Criteria for Livingness and Control in Nitroxide-Mediated and Related Radical Polymerizations, in Advances in Controlled/Living Radical Polymerization, American Chemical Society, 2003, vol. 854, pp. 10–23.
54. M. Zhong and K. Matyjaszewski, Macromolecules, 2011, 44(8), 2668–2677.
55. M. Souaille and H. Fischer, Macromolecules, 2002, 35(1), 248–261.
56. D. Gigmes, D. Bertin, C. Lefay and Y. Guillaneuf, Macromol. Theory Simul., 2009, 18(7–8), 402–419.
57. E. Malmström, R. D. Miller and C. J. Hawker, Tetrahedron, 1997, 53(45), 15225–15236.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8py00900g

---