Novel flavin-based fluorescent proteins with red-shifted emission bands: a computational study

Abstract

The iLOV protein is a promising member of the class of flavin mononucleotide (FMN) based fluorescent proteins (FbFPs). It is becoming a popular tool for bioanalytical applications and bioimaging as a competitor of the well-known green fluorescent protein and its analogues. The main limitation of FbFPs is that all the members have close values of their absorption and emission band maxima. Therefore the upcoming challenge is to introduce novel variants of FbFPs to extend their color palette. We report the results of computational studies of iLOV variants, introducing point mutations and chromophore analogues. We found that point mutations of the apoprotein and substitution of FMN with either 8-amino-FMN or 8-methylamino-FMN lead to the red shift of emission bands up to 100 nm. Substitution with 1-deaza-FMN and the point mutations of the apoprotein result in a set of novel fluorescent proteins with emission bands in the “transparent” window where light readily penetrates through mammalian tissues. Newly suggested FbFPs can be used for multicolor imaging and also as components of FRET pairs.

---

Introduction

The iLOV fluorescent protein is gradually becoming a popular tool in optogenetics,¹ analytical chemistry² and bioimaging,³ competing with the popular GFP and its analogues. It was engineered on the basis of the LOV2 domain from A. thaliana phototropin 2 upon the addition of six point mutations, which enhanced the fluorescence quantum yield to 0.32.^4,5 In natural LOV domains, photoexcitation leads to a chemical reaction through the triplet state and flavin fluorescence is a side process with a negligible quantum yield.⁶ The iLOV fluorescent protein carries a flavin mononucleotide (FMN) as a chromophore and belongs to the class of flavin mononucleotide based fluorescent proteins (FbFPs). FbFPs have several advantages over GFP variants, for example, a smaller size (being twice lighter than GFP), which makes them promising candidates for viral studies;^4,7,8 and a lack of the obligate post-translational maturation that allows visualization to start immediately after the formation of the protein scaffold; also FbFPs are independent of oxygen that is crucial for studies under anaerobic conditions.¹

The iLOV protein has an absorption band maximum at 447 nm and fluoresces at 493 nm. Notably, all the experimentally obtained FbFPs have similar spectral features.^1,4,5,9–12 First theoretical attempts to add new colors to the palette of FbFPs were made by introducing point mutations to the apoprotein. The most prospective variant is theoretically characterized by a vertical emission energy at ∼530 nm, which is about 40 nm red shifted as compared with the original iLOV.¹³ Still, these spectral properties are far from the “transparent” window (650–900 nm) where light readily penetrates through mammalian tissues.^14,15 Recent experimental studies demonstrated that flavin-containing photoreceptor proteins are also able to form stable complexes with flavin analogues.^16,17 Also, some of the flavin analogues demonstrate absorption and emission band maxima shifted to the longer wavelengths in aqueous solution^18–20 being promising candidates for further investigations (Table 1). These data encourage us to suggest new FbFPs with flavin analogues as a chromophore and point mutations of the apo-iLOV.

Table 1 Spectral properties of riboflavin and its analogues in aqueous solution

	Riboflavin^21	8-Amino-riboflavin^20	8-Methylamino-riboflavin^19	1-Deaza-riboflavin^18
λ a,max, eV (nm)	2.79 (445)	2.62 (473)	2.54 (488)	2.31 (537)
λ F,max, eV (nm)	2.29 (542)	2.33 (533)	2.21 (560)	1.77 (700)
Stokes shift, eV (nm)	0.50 (97)	0.29 (60)	0.34 (72)	0.54 (163)
φ F	0.26	0.19	≈0.4	0.0024

---

The aim of the present study was to suggest novel fluorescent proteins based on iLOV with the absorption and emission bands shifted to the longer wavelength regions. To achieve this goal, we chose two routes: modification of the chromophore group and addition of point mutations to the apoprotein to further alter the spectral properties. Also, we propose that FRET pairs based on the newly suggested FbFPs and sets of FbFPs are applicable for multicolor bioanalytical applications and imaging.

Models and methods

The full-atom 3D structure was obtained from the crystal structure of iLOV (PDB ID: 4EET⁵). Hydrogen atoms were added to the crystal structure considering positively charged side chains of Lys and Arg and negatively charged ones of Glu and Asp. Taking into account the local environment, we suggested neutral side chains with the protonation at the ND atom for all histidine residues. Model systems were solvated by water molecules in a 69 × 76 × 74 ų rectangular water box and neutralized by adding sodium and chloride ions to adjust the ionic strength of the solution to 0.15 M.

For all systems under consideration we performed classical molecular dynamics (MD) simulations using NAMD.²² MD simulations were performed in the NPT ensemble at T = 300 K and p = 1 atm using Langevin dynamics. For the electrostatic calculations the particle mesh Ewald method²³ was employed. Similarly to our previous studies^13,24 the CHARMM27^25–28 force field was applied to the protein macromolecule and TIP3P²⁹ for water molecules. For the chromophores, we used CGenFF³⁰ atom types and parameters, which were created for simulation of drug-like molecules in a biological environment along with CHARMM parameters. However, the partial atomic charges assigned by the CGenFF web server^31,32 showed high penalties. Therefore we recalculated them using a protocol³⁰ designed for the assignment of partial charges in CHARMM and CGenFF force fields. The Force Field Toolkit plugin³³ in VMD program³⁴ was applied. For all the considered systems, we performed 50–100 ns MD runs with a 1 fs integration time step. For the systems supposed to be prospective (the criteria will be discussed in the following section), we performed additional MD runs. These longer trajectories were simulated as a set of ten 100 ns runs, i.e. 1 μs MD trajectory for each model system.

We considered iLOV with FMN analogues: 8-amino-flavin mononucleotide (8-amino-FMN), 8-methylamino-flavin mononucleotide (8-methylamino-FMN) and 1-deaza-flavin mononucleotide (1-deaza-FMN). Next, we modified amino acids at 392 and 489 positions of the apoprotein to positively charged Lys and proposed additional mutations to stabilize the required conformation of lysine side chains.

For prospective mutants, we selected representative frames from MD trajectories as the starting points for combined quantum mechanics/molecular mechanics (QM/MM) geometry optimizations. The NWChem program³⁵ was used for these calculations. QM subsystems contained the isoalloxazine fragment of chromophore, side chains of Gln430, Asn458, Asn468 and the additional Thr394 in model systems containing 8-amino-FMN or 8-methylamino-FMN. For mutated iLOV variants, side chains of Lys392 or Lys489, neighboring amino acid side chains and water molecules that form hydrogen bond with lysines were also included. The QM subsystem was described at the Kohn–Sham DFT level of theory with the hybrid functional PBE0 ³⁶ with the empirical dispersion correction D3 ³⁷ and the cc-pvdz basis set. The hydrogen link atoms and the electronic embedding scheme were applied to connect the QM and MM subsystems. The MM subsystem contained the rest of the chromophore, protein and water molecules within 5 Å of protein or chromophore. The AMBER³⁸ force field was used to describe the MM part. It is technically more convenient to use CHARMM with NAMD, whereas the AMBER force field is better implemented in NWChem. In our previous study of oligopeptide hydrolysis in the active site of MMP-2, we demonstrated that both CHARMM and AMBER force fields led to the same results for the QM/MM energy profiles.³⁹

The following estimates of the vertical electron transition energies (vertical excitation energies S_0,min → S₁ and emission energies S_1,min → S₀) were performed in the molecular clusters obtained from the QM part of the corresponding QM/MM model systems. Vertical transition energies were estimated at the XMCQDPT2 level of theory⁴⁰ provided in the Firefly QC package,⁴¹ partially based on the GAMESS (US)⁴² source code. This method is shown to be reliable for the organic chromophores and flavins, in particular.^13,43–45 First, we performed configuration interaction with single excitations (CIS) calculations. Then, we chose the π-orbitals participating in transitions in CIS to obtain the active space for the complete active space self-consistent field (CASSCF) calculations. The active space was constructed from 12 electrons distributed over 12 orbitals CASSCF(12/12). The corresponding molecular orbitals are presented in the ESI (section S1†). We applied the state-averaging procedure (SA-CASSCF) with averaging over 2 lowest singlet states with equal weights. To choose the number of states to be included in the state averaging, we analyzed the decomposition of the XMCQDPT2 states over the CASSCF states. The criterion to include the state in the averaging procedure was its weight in the XMCQDPT2 state expansion over the CASSCF states. If the weight of the higher state in the expansion of S₀ or S₁ was higher than 0.1, it was included in the state averaging. Additional estimates were performed applying SOS-CIS(D)⁴⁶ (the QChem package⁴⁷) and TD-DFT with the ωB97X-D3 ⁴⁸ functional (the ORCA program⁴⁹) methods. For all transition energy calculations, we used the cc-pVDZ basis set. To estimate S_0,min → S₁ transition energy, we utilized coordinates obtained for the QM part in the QM/MM equilibrium geometry configuration calculations. The S₁ minima were located to estimate vertical S_1,min → S₀ emission energies. To locate minima on the S₁ potential energy surface we performed geometry optimization starting with molecular clusters corresponding to the QM parts of the equilibrium geometry configurations obtained in the QM/MM model systems. During geometry optimization in molecular clusters the coordinates of terminal carbon atoms of all molecular fragments (chromophore and amino acid residues) were fixed. Gradients and forces for the S₁ state were calculated with the SA-CASSCF(4/4) wave function averaged over two lowest singlet states and tracking four lowest singlet states. This active space was suggested following benchmark calculations of small model systems with chromophores in the gas phase and microsolvation models. In CASSCF(4/4) calculations, we chose molecular orbitals from the CASSCF(12/12) active space that mostly contributed to the excitation (with the largest weights in the expansion of the S₁ state over configuration functions). The CASSCF(4/4) approach allowed us to obtain reasonable geometry parameters and energies of the S_1,min → S₀ transition as compared with the experimental values obtained in solution. Molecular orbitals utilized in the CASSCF(4/4) calculations are presented in the ESI (section S2†).

Previous theoretical studies demonstrated that it is challenging to quantitatively describe the spectral properties of 1-deaza-FMN in both water solution and in the LOV domain of YtvA protein.¹⁶ Therefore we performed additional benchmark calculations and tested different protocols, aiming to obtain values that are close to the experimental data taken from ref. 16. We chose SA-CASSCF(2/2) with the state averaging over 2 lowest singlet states with further XMCQDPT2 corrections for vertical excitation energy estimates of the system containing 1-deaza-FMN.

All vertical transition energies were estimated in molecular clusters in vacuo without consideration of the point charges coming from the protein or solvent. This protocol was validated in our previous studies of iLOV variants and another flavin-containing protein, BLUF. In particular, we demonstrated that taking into consideration all the hydrogen bonds formed by the isoalloxazine ring and neighboring residues guaranteed an accuracy of calculated transition wavelengths within several nanometers.^24,44,50

For calculations in small molecular clusters, we truncated phosphate and ribityl parts of the chromophore molecule and considered only the conjugated π-system of the isoalloxazine ring, i.e. analogues of lumiflavin (LF). Calculations in small molecular clusters comprising a chromophore or a chromophore with a water molecule were performed at the PBE0-D3/cc-pvdz level of theory. The S_0,min → S₁ transition energies were calculated similarly to the molecular clusters discussed above.

Molecular docking of chromophores to the chromophore-binding pocket was performed on Autodock4 program package⁵¹ using the local search algorithm with the initial structures corresponding to the equilibrium geometry configurations obtained in QM/MM simulations. To estimate the binding affinities of flavin analogues, we performed rigid docking of the lumiflavin molecule and the corresponding derivatives with truncated ribityl and phosphate parts of the chromophores. For every model system, we performed a local search with 10 runs with the maximum number of Solis and Wets iterations set at 200, the maximum number of consecutive successes or failures both set at 4, the size of the local search space set at 1.0 and the smallest step size set at 0.01.

Results and discussion

Lumiflavin analogues in the gas phase

We analyzed the spectral properties of the lumiflavin (LF) analogues 8-amino-LF, 8-methylamino-LF and 1-deaza-LF in the gas phase. We located equilibrium geometry configurations and estimated the corresponding vertical S_0,min → S₁ transition energies (Fig. 1, Table 2). Similarly to the lumiflavin excitation to the S₁ state the electron density in the considered LF analogues is increased on N5, C4A and O4 atoms and decreased on N1 (C1 in 1-deaza-LF) atom (Fig. 1).²⁴ The calculated vertical excitation energies for all chromophores are about 40 nm blue-shifted compared with the corresponding experimental band maxima in water solution (Tables 1 and 2) similarly to lumiflavin.²⁴

Fig. 1 Electron density difference maps for the S_0,min → S₁ transition of the chromophores under consideration. Salmon-colored isosurfaces correspond to the electron density increase in the S₁ state and violet isosurfaces – to the decrease relative to the S₀ state. Here and in other figures, green, red, blue and white colors correspond to carbon, oxygen, nitrogen and hydrogen atoms, respectively.

Table 2 S_0,min → S₁ transition (local π–π* excitation) energies calculated for small molecular clusters at the XMCQDPT2/CASSCF(12/12)/cc-pvdz level of theory. The energy values are given in eV and the corresponding wavenumbers in nm in parentheses

Model system	S0,min → S1
8-Amino-LF	2.83 (438)
8-Methylamino-LF	2.82 (440)
1-Deaza-LF	2.48 (500)
8-Amino-LF + W1	2.90 (427)
8-Amino-LF + W4	2.74 (452)
8-Amino-LF + W5	2.77 (447)

---

We calculated vertical excitation energies for 8-amino-LF with one water molecule to evaluate the influence of hydrogen bonding with N1, O4 and N5 atoms involved in the electron density redistribution (Fig. 2, Table 2). As was expected from the electron density difference maps (Fig. 1), the hydrogen bond stabilizes the excited state if the electron density is increased in S₁ and stabilizes the ground state if the density is decreased upon the S_0,min → S₁ transition. Thus, the formation of a hydrogen bond with the N1 atom results in the blue shift of the vertical excitation energy compared with the bare chromophore, and red shifts are observed in the model systems with the hydrogen bond with either N5 or O4 atoms.

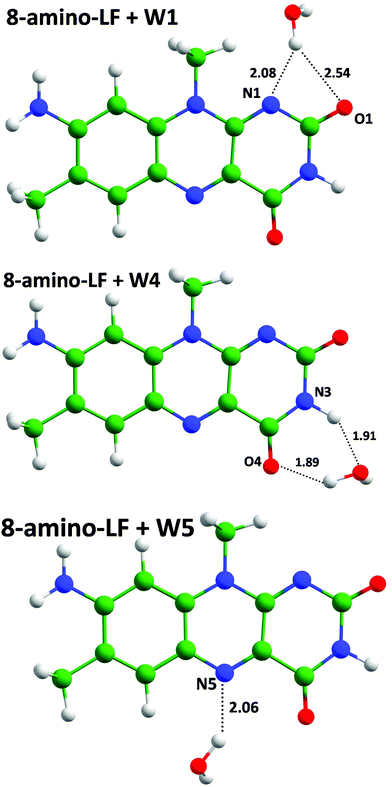Fig. 2 Molecular clusters comprising 8-amino-LF with a water molecule forming hydrogen bonds with heteroatoms of the chromophore. Here and in the next figures distances are shown in Å.

iLOV with FMN analogues

We substitute the chromophore of iLOV with the selected FMN analogues. Here we use the following notations for the considered systems: iLOV-a, iLOV-m and iLOV-d for the systems with 8-amino-FMN, 8-methylamino-FMN and 1-deaza-FMN as cofactors, respectively. The initial set of coordinates was obtained by replacing the isoalloxazine part of FMN in the crystal structure of iLOV (PDB ID: 4EET⁵) with the corresponding part of the FMN analogue.

We performed 50 ns MD simulations for each system with FMN analogues. We intentionally demonstrate in Fig. 3 the distances between N5 or O4 atoms of the chromophores and the side chain of Gln489 for the entire MD trajectories to show both equilibration and production runs. In the iLOV-d model system, hydrogen bonds are formed between the chromophore and side chains of Asn458, Asn468 and Gln430. For iLOV-a and iLOV-m there is an additional hydrogen bond between the N–H fragment of the amino- or methylamino-group, respectively, and the oxygen atom of the side chain of Thr394. Hydrogen bonds in the chromophore-binding pocket of the iLOV with FMN analogues are stable along the trajectory and the corresponding residues keep the conformations close to those in the initial structure observed in the parent iLOV crystals. The only exception is the side chain of Gln489 that is flexible during simulations. We carefully investigate its behavior as it is located close to the O4 and N5 atoms of the chromophore. Hydrogen bonds between Gln489 and N5 atoms are broken in the beginning of the trajectories for all the considered systems. Hydrogen bonds between Gln489 and O4 exist for several nanoseconds in iLOV-a and iLOV-d model systems. In iLOV-m, a hydrogen bond between Gln489 and O4 atoms of the chromophore is formed for the first 5 ns, and also in some frames in the middle of the MD trajectory (Fig. 3). Therefore we compare below the spectral properties of novel FbFPs with the iLOV_out conformer¹³ with the Gln489 side chain being exposed outside the chromophore binding pocket.

Fig. 3 Distances between N5 and O4 atoms of the chromophore and the NE2 atom in Gln489 along the MD trajectories.

For each of these 3 systems, we chose the representative frames with the Gln489 pointing away from the chromophore. We reduced the model system for the QM/MM calculation decreasing the amount of water molecules in the solvation shells around the protein. The equilibrium geometry configurations have the same hydrogen bond network in the chromophore-binding pocket as in MD trajectories (Fig. 4).

Fig. 4 Chromophores and neighboring residues forming hydrogen bonds in the iLOV. The distances correspond to the equilibrium geometry configurations obtained at the QM/MM level; the values in parentheses correspond to the mean value and standard deviation along the MD trajectories.

An important point that should be considered is: how do modifications of the chromophores affect their binding affinity? We performed molecular docking for flavin and its analogues to estimate the corresponding quantities. We intentionally truncated the ribityl and phosphate parts of the chromophores to consider changes of binding affinities attributed to the lumiflavin part. Table 3 summarizes the results and demonstrates that the dissociation constants for all the compounds are in the same order of magnitude with the highest protein affinity being to 1-deaza-LF and the lowest to 8-amino-LF.

Table 3 Dissociation constants and binding energies of lumiflavin and its analogues to apo-iLOV

Cofactor	, kcal mol^−1	K diss, M
LF	−8.35	7.5 × 10^−7
1-Deaza-LF	−8.89	3.0 × 10^−7
8-Methylamino-LF	−8.50	5.8 × 10^−7
8-Amino-LF	−7.57	2.8 × 10^−6

---

Molecular clusters obtained from the QM subsystems of the QM/MM equilibrium geometry configurations were utilized for the calculation of the vertical S_0,min → S₁ transition energies. Minima on the S₁ potential energy surface were located in the same model system, fixing the terminal carbon atoms of all molecular fragments. These calculations were performed at the SA-CASSCF(4/4) level of theory as discussed in the Methods section.

We computed vertical S_0,min → S₁ and S_1,min → S₀ transitions energies using different quantum chemical methods (results are shown in Tables 4 and 5). We mostly relied on the XMCQDPT2/CASSCF(12/12)/cc-pVDZ method, although other results are also considered. The calculated S_0,min → S₁ transition energies are red-shifted compared with the calculated values in the gas phase and blue-shifted compared with the experimental data in solution. These results are in line with our previous calculations of vertical excitation energies in gas phase, iLOV and solvent and the corresponding experimental values.²⁴ Also, our results can be compared with the experimental data on roseoflavin bound to LOV1 His domain¹⁷ as 8-amino-FMN and 8-methylamino-FMN are roseoflavin derivatives. When incorporated into the protein, roseoflavin exhibits a blue shift relative to the absorption in water solution.¹⁷ The results of the SOS-CIS(D) calculations differ from those of the XMCQDPT2/CASSCF(12/12)/cc-pVDZ approach. SOS-CIS(D) reproduces the red shift of iLOV-a species and a slightly larger red shift of the iLOV-m relative to iLOV, whereas the relative position of the iLOV-d is calculated qualitatively wrong. We suppose that this is due to difficulties in the description of the 1-deaza-FMN discussed in earlier theoretical studies.¹⁶

Table 4 Apo-iLOV with FMN analogues: the vertical S_0,min → S₁ excitation energies and the corresponding shifts relative to the iLOV_out. The energy values (eV) and the corresponding wavenumbers (nm) in parentheses are obtained in molecular clusters without external MM charges

System	Method
	XMCQDPT2		TD-DFT		SOS-CIS(D)
	S0,min → S1	Shift	S0,min → S1	Shift	S0,min → S1	Shift
iLOVout	2.82 (439)	0	3.70 (335)	0	3.25 (382)	0
iLOV-a	2.70 (450)	−0.12 (+11)	3.57 (347)	−0.13 (+12)	2.84 (436)	−0.41 (+54)
iLOV-m	2.59 (478)	−0.23 (+39)	3.55 (350)	−0.15 (+15)	2.81 (442)	−0.44 (+60)
iLOV-d	2.36 (526)	−0.46 (+82)	3.34 (371)	−0.36 (+36)	2.95 (420)	−0.30 (+38)

---

Table 5 Apo-iLOV with FMN analogues: Stokes shifts and vertical S_1,min → S₀ emission energies and the corresponding shifts relative to the iLOV_out. The energy values (eV) and the corresponding wavenumbers (nm) in parentheses are obtained in molecular clusters without external MM charges

System	Method
	XMCQDPT2			TD-DFT		SOS-CIS(D)
	Stokes shift	S1,min → S0	Shift	S1,min → S0	Shift	S1,min → S0	Shift
iLOVout	−0.32	2.50 (496)	0	3.34 (372)	0	2.65 (467)	0
iLOV-a	−0.43	2.27 (547)	−0.23 (+51)	3.31 (375)	−0.03 (+3)	2.43 (511)	−0.22 (+44)
iLOV-m	−0.40	2.19 (566)	−0.31 (+70)	3.25 (382)	−0.09 (+10)	2.36 (526)	−0.29 (+59)
iLOV-d	−0.63	1.73 (717)	−0.77 (+221)	2.46 (503)	−0.88 (+131)	1.78 (697)	−0.87 (+230)

---

Mutants of iLOV with FMN analogues

The positively charged amino group of lysine in the close proximity of N5 and O4 atoms of FMN causes the red shift of vertical excitation and emission energies.^13,24 We demonstrate, for small model systems, that in FMN analogues considered in this study the electron density increases mostly on the N5 atom upon excitation to the S₁ state and slightly on the O4 atom similarly to the FMN. Therefore we apply the same approach to propose new fluorescent proteins with the FMN analogues bound to the mutant forms of iLOV with the absorption and emission bands shifted to the longer wavelengths. We mutate two amino acids located close to the N5 atom, i.e. Gln489 or Val392, by lysine. From the experimental studies, we know that the single Q489K mutation is not enough to engineer a new red-shifted FbFP as the lysine side chain tends to be exposed to the solution.¹⁰ Therefore we carefully checked and chose the compensating mutations that stabilize hydrogen bonds between the lysine protonated amino group and N5 and O4 atoms of the chromophore. We replaced hydrophobic amino acids (valine, phenylalanine, leucine and alanine) with polar ones like serine or threonine to introduce hydrogen bonds with the newly introduced lysine. We intentionally did not mutate residues to either glutamate or aspartate as the negative charge of the carboxylate neglects the effects of the positive charge of the protonated amino group of lysine.¹³

We studied the following mutants of apo-iLOV: V392K/A426S, V392K/F410V/A426S, V392K/F410 V/A426S/Q489A, Q489K/L470S/G487S, Q489K/L470T, Q489K/L470S/G487N, Q489K/L470T/L472T, Q489K/L470T/G487T for iLOV-a; V392K/F410V/A426S, Q489K/L470S/G487S, Q489K/L470T, Q489K/L470T/L472T for iLOV-m and V392K/F410V/A426S, Q489K/L470S/G487N, Q489K/L470T, Q489K/L470S/G487S, Q489K/L470T/L472T for iLOV-d.

We performed 50 ns classical MD runs for each model system to select prospective variants. By the latter we assume systems with the major conformation of the lysine protonated amino group located close to the N5 and O4 atoms of the chromophore. Some trajectories were extended up to 100 ns to further check the conformations of residues in the chromophore-binding pocket. From 17 model systems we selected 7 which exhibited the shortest distances between the NZ atom of lysine and either N5 or O4 atoms of the modified FMNs. All the selected mutants are listed in Table 6. Since full specifications of mutants are difficult to perceive, we introduced short names. MD trajectories show that all the selected proteins maintain the “in” conformation in which the lysine side chain does not drift away from the chromophore. At least one of the distances between heavy atoms (N5⋯NZ or O4⋯NZ) fluctuates near the typical hydrogen bond length (Fig. 5).

Fig. 5 Distributions of distances between the N5 and O4 atoms of the chromophore and the nitrogen atom NZ of the lysine side chain in the selected model systems.

Table 6 Notation of promising variants of the mutated iLOV with the FMN analogues

Short name	Chromophore	Full specification
iLOV-aK392	8-Amino-FMN	V392K/F410V/A426S/Q489A
iLOV-aK489ss	8-Amino-FMN	Q489K/L470S/G487S
iLOV-mK392	8-Methylamino-FMN	V392K/F410V/A426S
iLOV-mK489t	8-Methylamino-FMN	Q489K/L470T
iLOV-mK489ss	8-Methylamino-FMN	Q489K/L470S/G487S
iLOV-dK392	1-Deaza-FMN	V392K/F410V/A426S
iLOV-dK489tt	1-Deaza-FMN	Q489K/L470T/L472T

---

To confirm that the selected mutants keep a desired conformation we executed additional 10 × 100 ns MD runs, 1 μs in total, for each system (Fig. 6). We selected initial sets of coordinates for new simulations from the 50 ns trajectory choosing the frames with the highest values of RMSD. The distributions of N5⋯NZ and O4⋯NZ distances in these MD trajectories are shown in Fig. 6. All the selected mutants maintain desired conformations with at least one hydrogen bond between NZ and O4 atoms being stable. The iLOV-dK392 and iLOV-dK489tt variants also have a stable hydrogen bond between NZ and N5 atoms. The occurrence of the NZ⋯N5 hydrogen bond is moderate in iLOV-aK392 and iLOV-aK489ss variants and absent in 8-methylamino-FMN containing variants. Also in iLOV-mK489t and iLOV-mK489ss model systems there is a small population of unfavorable conformations without hydrogen bonds with the chromophore.

Fig. 6 Distributions of distances between the N5 and O4 atoms of the chromophore and the nitrogen atom NZ of the lysine side chain in 1 μs trajectories.

We performed QM/MM optimization for the selected systems starting from the representative frames of the MD trajectories. Equilibrium geometry configurations comprising the part of the chromophore-binding pocket treated at the DFT level are demonstrated in Fig. 7–9. The common feature of mutants of the iLOV-a and iLOV-d series is that hydrogen bonds are formed between the lysine amino group and both N5 and O4 atoms of the chromophore. For the iLOV-m series the lysine amino group is located far from the N5 atom and forms a hydrogen bond only with the O4 atom. For mutants the local surroundings of the chromophore differ from that of systems with the original apo-iLOV. The Lys489 extrudes Asn468 from the chromophore binding pocket concurring to form a hydrogen bond with the O4 atom.

Fig. 7 Chromophores and neighboring residues forming hydrogen bonds in the iLOV mutants with the 8-amino-FMN.

Fig. 8 Chromophores and neighboring residues forming hydrogen bonds in the iLOV mutants with the 8-methylamino-FMN.

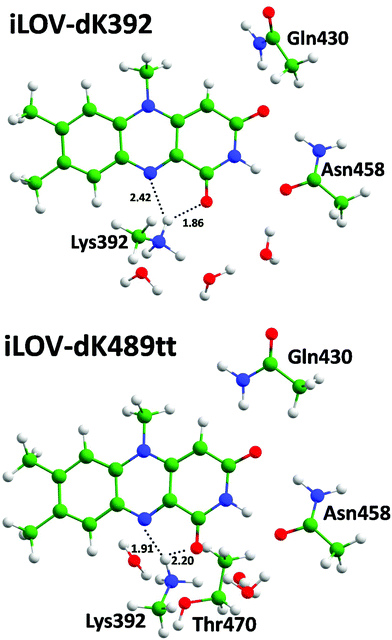Fig. 9 Chromophores and neighboring residues forming hydrogen bonds in the iLOV mutants with the 1-deaza-FMN.

We evaluated vertical transition energies and summarized them in Tables 7 and 8. The largest red shifts of excitation energies relative to the parent iLOV were obtained for the iLOV-dK489tt and iLOV-dK392 systems. These values are more than 150 nm shifted to the longer wavelength region compared with the iLOV_out. These results are expected as the absorption of 1-deaza-FMN is about 100 nm red shifted compared to the FMN (Table 1). Another 50 nm comes from the S₁ state stabilization by the positive charge of the lysine side chain.

Table 7 Mutated apo-iLOV with FMN analogues: vertical S_0,min → S₁ excitation energies and the corresponding shifts relative to the iLOV_out. The energy values (eV) and the corresponding wavenumbers (nm) in parentheses are obtained in molecular clusters without external MM charges

System	Method
	XMCQDPT2		TD-DFT		SOS-CIS(D)
	S0,min → S1	Shift	S0,min → S1	Shift	S0,min → S1	Shift
iLOVout	2.82 (439)	0	3.70 (335)	0	3.25 (382)	0
iLOV-aK392	2.42 (512)	−0.40 (+73)	3.43 (361)	−0.27 (+26)	2.67 (464)	−0.58 (+82)
iLOV-aK489ss	2.36 (525)	−0.46 (+86)	3.42 (363)	−0.28 (+28)	2.69 (461)	−0.56 (+79)
iLOV-mK392	2.49 (499)	−0.33 (+60)	3.46 (359)	−0.24 (+24)	2.68 (462)	−0.57 (+80)
iLOV-mK489t	2.49 (499)	−0.33 (+60)	3.46 (359)	−0.24 (+24)	2.66 (467)	−0.59 (+85)
iLOV-mK489ss	2.54 (488)	−0.28 (+49)	3.44 (361)	−0.26 (+26)	2.65 (468)	−0.60 (+86)
iLOV-dK392	2.09 (592)	−0.73 (+153)	3.08 (402)	−0.62 (+67)	2.61 (476)	−0.64 (+94)
iLOV-dK489tt	2.06 (602)	−0.76 (+163)	3.05 (406)	−0.65 (+71)	2.57 (483)	−0.68 (+101)

---

Table 8 Mutated apo-iLOV with FMN analogues: Stokes shifts and vertical S_1,min → S₀ emission energies and the corresponding shifts relative to the iLOV_out. The energy values (eV) and the corresponding wavenumbers (nm) in parentheses are obtained in molecular clusters without external MM charges

System	Method
	XMCQDPT2			TD-DFT		SOS-CIS(D)
	Stokes shift	S1,min → S0	Shift	S1,min → S0	Shift	S1,min → S0	Shift
iLOVout	−0.32	2.50 (496)	0	3.34 (372)	0	2.65 (467)	0
iLOV-aK392	−0.25	2.17 (570)	−0.33 (+74)	3.17 (391)	−0.17 (+19)	2.29 (542)	−0.36 (+75)
iLOV-aK489ss	−0.28	2.08 (595)	−0.42 (+99)	3.15 (393)	−0.19 (+21)	2.31 (538)	−0.34 (+71)
iLOV-mK392	−0.25	2.24 (553)	−0.26 (+57)	3.25 (381)	−0.09 (+9)	2.37 (524)	−0.28 (+57)
iLOV-mK489t	−0.19	2.30 (539)	−0.20 (+43)	3.30 (376)	−0.04 (+4)	2.40 (516)	−0.25 (+49)
iLOV-mK489ss	−0.32	2.22 (558)	−0.28 (+62)	3.25 (381)	−0.09 (+9)	2.37 (524)	−0.28 (+57)
iLOV-dK392	−0.62	1.47 (843)	−1.03 (+347)	2.24 (554)	−1.10 (+182)	1.42 (873)	−1.23 (+406)
iLOV-dK489tt	−0.62	1.44 (860)	−1.06 (+364)	2.18 (568)	−1.16 (+196)	1.38 (897)	−1.27 (+430)

---

In water solution the maximum of the absorption band of 8-methylamino-FMN is red-shifted relative to the 8-amino-FMN, although iLOV mutants with 8-amino-FMN demonstrate smaller energy gaps between the ground and the first excited singlet states. This can be explained by analyzing the corresponding equilibrium geometry configurations (Fig. 7 and 8). In iLOV mutants with 8-amino-FMN, lysine forms hydrogen bonds with both N5 and O4 atoms whereas in systems with 8-methylamino-FMN the hydrogen bonds are formed only with the O4 atom of the chromophore, resulting in the smaller stabilization effect of the S₁ state.

Table 8 summarizes the results for the vertical S_1,min → S₀ transition energies. The Stokes shifts of the systems containing 1-deaza-FMN are much larger compared with the two other FMN analogues. The emission wavelengths for iLOV-dK392 and iLOV-dK489tt are in the “transparent” window, which makes them promising candidates for in vivo imaging. Also the iLOV-aK489ss emission is close to the 600 nm similarly to the typical red fluorescent proteins (RFP).⁵²

Applications of novel FbFPs

Fluorescent proteins are widely used as individual markers, parts of the FRET pairs or components of multicolor imaging systems. In Fig. 10 we summarize the results for the iLOV-based FbFPs proposed in this study and in ref. 13. Let us consider iLOV, iLOV-a and iLOV-m with the original and mutated apo-protein. First, these proteins cover the spectral region between 500 and 600 nm, making them prospective targets for multicolor imaging as the two emission bands should be separated by 50–60 nm. Second, we propose new FRET pairs composed of the iLOV with the 8-amino-FMN as an energy donor and either iLOV-aK392 or iLOV-a489ss as an energy acceptor. Unfortunately, we cannot recommend the FRET pairs with the 8-methylamino-FMN chromophore as the Stokes shift is reduced with the red shift of the vertical excitation energy in suggested iLOV-m variants. The iLOV-d variants have larger Stokes shifts and the vertical excitation and emission energies are generally shifted to the longer wavelengths. According to our calculations even the original apo-iLOV with the incorporated 1-deaza-FMN should have the fluorescence band maxima in the “transparent” window. Moreover, introduction of the point mutations further shifts the vertical emission energy to a longer wavelength region. The iLOV-d vertical emission energy is separated more than 100 nm from the iLOV-d variants with point mutations, making them applicable for multicolor imaging in the near IR region.

Fig. 10 Vertical excitation and emission energies of the iLOV variants with different point mutations and chromophores. Orange boxes represent the FbFPs that can be utilized as FRET pairs. The data for the iLOV family are taken from ref. 13.

Conclusion

We computationally predicted novel prospective variants of flavin-based fluorescent FbFPs by introducing point mutations into the apo-iLOV and modifying its chromophore. According to the calculation results, a new color palette of these FbFPs covers spectral regions of 500–600 nm in the visible part and 700–860 nm in the near IR. Variation of the spectral properties of the newly suggested FbFPs makes them applicable for multicolor imaging and FRET systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Russian Science Foundation (project no. 17-13-01051). The research was carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University.⁵³

References

1. A. Losi, K. H. Gardner and A. Möglich, Blue-Light Receptors for Optogenetics, Chem. Rev., 2018 DOI:10.1021/acs.chemrev.8b00163.
2. Y. Ravikumar, S. Prabhu Nadarajan, C. Lee and H. Yun, Engineering an FMN-based iLOV protein for the detection of arsenic ions, Anal. Biochem., 2017, 525, 38–43.
3. B. A. Elgamoudi and J. M. Ketley, Lighting up my life: a LOV-based fluorescent reporter for Campylobacter jejuni, Res. Microbiol., 2018, 169, 108–114.
4. S. Chapman, C. Faulkner, E. Kaiserli, C. Garcia-Mata, E. I. Savenkov, A. G. Roberts, K. J. Oparka and J. M. Christie, The photoreversible fluorescent protein iLOV outperforms GFP as a reporter of plant virus infection, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 20038–20043.
5. J. M. Christie, K. Hitomi, A. S. Arvai, K. A. Hartfield, M. Mettlen, A. J. Pratt, J. A. Tainer and E. D. Getzoff, Structural tuning of the fluorescent protein iLOV for improved photostability, J. Biol. Chem., 2012, 287, 22295–22304.
6. R. J. Kutta, K. Magerl, U. Kensy and B. Dick, A search for radical intermediates in the photocycle of LOV domains, Photochem. Photobiol. Sci., 2015, 14, 288–299.
7. X. Dang, S. Chalkias and I. J. Koralnik, JC virus-iLOV fluorescent strains enable the detection of early and late viral protein expression, J. Virol. Methods, 2015, 223, 25–29.
8. J. Röder, C. Dickmeis, R. Fischer and U. Commandeur, Systemic Infection of Nicotiana benthamiana with Potato virus X Nanoparticles Presenting a Fluorescent iLOV Polypeptide Fused Directly to the Coat Protein, Biomed Res. Int., 2018, 2018, 1–12.
9. M. Wingen, J. Potzkei, S. Endres, G. Casini, C. Rupprecht, C. Fahlke, U. Krauss, K.-E. Jaeger, T. Drepper and T. Gensch, The photophysics of LOV-based fluorescent proteins – new tools for cell biology, Photochem. Photobiol. Sci., 2014, 13, 875–883.
10. M. D. Davari, B. Kopka, M. Wingen, M. Bocola, T. Drepper, K.-E. Jaeger, U. Schwaneberg and U. Krauss, Photophysics of the LOV-Based Fluorescent Protein Variant iLOV-Q489 K Determined by Simulation and Experiment, J. Phys. Chem. B, 2016, 120, 3344–3352.
11. M. Wingen, J. Potzkei, S. Endres, G. Casini, C. Rupprecht, C. Fahlke, U. Krauss, K. E. Jaeger, T. Drepper and T. Gensch, The photophysics of LOV-based fluorescent proteins -new tools for cell biology, Photochem. Photobiol. Sci., 2014, 13, 875–883.
12. A. Mukherjee, J. Walker, K. B. Weyant and C. M. Schroeder, Characterization of flavin-based fluorescent proteins: An emerging class of fluorescent reporters, PLoS One, 2013, 8, e64753.
13. M. G. Khrenova, Y. I. Meteleshko and A. V. Nemukhin, Mutants of the Flavoprotein iLOV as Prospective Red-Shifted Fluorescent Markers, J. Phys. Chem. B, 2017, 121, 10018–10025.
14. H. Kobayashi, M. Ogawa, R. Alford, P. L. Choyke and Y. Urano, New Strategies for Fluorescent Probe Design in Medical Diagnostic Imaging, Chem. Rev., 2010, 110, 2620–2640.
15. D. M. Shcherbakova, A. A. Shemetov, A. A. Kaberniuk and V. V. Verkhusha, Natural Photoreceptors as a Source of Fluorescent Proteins, Biosensors, and Optogenetic Tools, Annu. Rev. Biochem., 2015, 84, 519–550.
16. M. R. Silva-Junior, M. Mansurova, W. Gärtner and W. Thiel, Photophysics of Structurally Modified Flavin Derivatives in the Blue-Light Photoreceptor YtvA: A Combined Experimental and Theoretical Study, ChemBioChem, 2013, 14, 1648–1661.
17. A. Tyagi, A. Penzkofer, T. Mathes and P. Hegemann, Photophysical characterisation and photo-cycle dynamics of LOV1-His domain of phototropin from Chlamydomonas reinhardtii with roseoflavin monophosphate cofactor, J. Photochem. Photobiol., B, 2010, 101, 76–88.
18. C. Slavov, M. Mansurova, A. R. Holzwarth and W. Gartner, Excited State Processes in 1-Deazariboflavin Studied by Ultrafast Fluorescence Kinetics, Photochem. Photobiol., 2010, 86, 31–38.
19. A. Tyagi, A. Penzkofer, T. Mathes and P. Hegemann, Photo-degradation behaviour of roseoflavin in some aqueous solutions, Chem. Phys., 2010, 369, 27–36.
20. A. Tyagi, P. Zirak, A. Penzkofer, T. Mathes, P. Hegemann, M. Mack and S. Ghisla, Absorption and emission spectroscopic characterisation of 8-amino-riboflavin, Chem. Phys., 2009, 364, 19–30.
21. P. Zirak, A. Penzkofer, T. Mathes and P. Hegemann, Photo-dynamics of roseoflavin and riboflavin in aqueous and organic solvents, Chem. Phys., 2009, 358, 111–122.
22. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802.
23. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092.
24. M. G. Khrenova, A. V. Nemukhin and T. Domratcheva, Theoretical characterization of the flavin-based fluorescent protein iLOV and its Q489 K mutant, J. Phys. Chem. B, 2015, 119, 5176–5183.
25. A. D. MacKerell, M. Feig and C. L. Brooks, Improved Treatment of the Protein Backbone in Empirical Force Fields, J. Am. Chem. Soc., 2004, 126, 698–699.
26. R. B. Best, X. Zhu, J. Shim, P. E. M. Lopes, J. Mittal, M. Feig and A. D. MacKerell, Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ 1 and χ 2 Dihedral Angles, J. Chem. Theory Comput., 2012, 8, 3257–3273.
27. A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, All-Atom empirical potential for molecular modeling and dynamics studies of proteins, J. Phys. Chem. B, 1998, 102, 3586–3616.
28. A. D. Mackerell, M. Feig and C. L. Brooks, Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations, J. Comput. Chem., 2004, 25, 1400–1415.
29. W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935.
30. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, CHARMM general force field (CGenFF): A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690.
31. K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell, Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges, J. Chem. Inf. Model., 2012, 52, 3155–3168.
32. K. Vanommeslaeghe and A. D. MacKerell, Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing, J. Chem. Inf. Model., 2012, 52, 3144–3154.
33. C. G. Mayne, J. Saam, K. Schulten, E. Tajkhorshid and J. C. Gumbart, Rapid parameterization of small molecules using the force field toolkit, J. Comput. Chem., 2013, 34, 2757–2770.
34. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
35. M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. Van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations, Comput. Phys. Commun., 2010, 181, 1477–1489.
36. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158.
37. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
38. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A second generation force field for the simulation of proteins, nucleic acids, and organic molecules, J. Am. Chem. Soc., 1995, 117, 5179–5197.
39. T. Vasilevskaya, M. G. Khrenova, A. V. Nemukhin, W. Thiel, V. Tatiana, M. G. Khrenova, A. V. Nemukhin and T. Walter, Mechanism of proteolysis in matrix metalloproteinase-2 revealed by QM/MM modeling, J. Comput. Chem., 2015, 36, 1621–1630.
40. A. A. Granovsky, Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory, J. Chem. Phys., 2011, 134, 214113.
41. A. A. Granovsky, http://www.classic.chem.msu.su/gran/firefly/index.html (accessed October 2018).
42. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363.
43. A. Udvarhelyi, M. Olivucci and T. Domratcheva, Role of the Molecular Environment in Flavoprotein Color and Redox Tuning: QM Cluster versus QM/MM Modeling, J. Chem. Theory Comput., 2015, 11, 3878–3894.
44. M. G. Khrenova, A. V. Nemukhin, B. L. Grigorenko, A. I. Krylov and T. M. Domratcheva, Quantum chemistry calculations provide support to the mechanism of the light-induced structural changes in the flavin-binding photoreceptor proteins, J. Chem. Theory Comput., 2010, 6, 2293–2302.
45. T. Domratcheva, B. L. Grigorenko, I. Schlichting and A. V. Nemukhin, Molecular models predict light-induced glutamine tautomerization in BLUF photoreceptors, Biophys. J., 2008, 94, 3872–3879.
46. Y. M. Rhee and M. Head-Gordon, Scaled second-order perturbation corrections to configuration interaction singles: Efficient and reliable excitation energy methods, J. Phys. Chem. A, 2007, 111, 5314–5326.
47. Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. B. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. a. DiStasio, R. C. Lochan, T. Wang, G. J. O. Beran, N. A. Besley, J. M. Herbert, C. Y. Lin, T. Van Voorhis, S. H. Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. M. Rhee, J. Ritchie, E. Rosta, C. D. Sherrill, A. C. Simmonett, J. E. Subotnik, H. L. Woodcock, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in methods and algorithms in a modern quantum chemistry program package, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191.
48. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615.
49. F. Neese, The ORCA program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
50. M. G. Khrenova, Y. I. Meteleshko and A. V. Nemukhin, Mutants of the Flavoprotein iLOV as Prospective Red-Shifted Fluorescent Markers, J. Phys. Chem. B, 2017, 121, 10018–10025.
51. G. M. Morris, R. Huey, W. Lindstrom, M. F. Sanner, R. K. Belew, D. S. Goodsell and A. J. Olson, AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility, J. Comput. Chem., 2009, 30, 2785–2791.
52. K. D. Piatkevich and V. V. Verkhusha, Guide to Red Fluorescent Proteins and Biosensors for Flow Cytometry, Methods Cell Biol., 2011, 102, 431–461.
53. V. Sadovnichy, A. Tikhonravov, V. Voevodin and V. Opanasenko, ‘Lomonosov’: supercomputing at Moscow state university, in Contemp. High Perform. Comput. From Petascale Towar. Exascale, 2013, pp. 283–307.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8pp00361k

---