Open Access Article
Open Access ArticleSequence-dependent mechanical properties of double-stranded RNA†
Alberto
Marin-Gonzalez
 a,
J. G.
Vilhena
a,
J. G.
Vilhena
 bc,
Fernando
Moreno-Herrero
bc,
Fernando
Moreno-Herrero
 *a and
Ruben
Perez
*a and
Ruben
Perez
 *bd
*bd
aDepartment of Macromolecular Structures, Centro Nacional de Biotecnología, Consejo Superior de Investigaciones Científicas, 28049 Cantoblanco, Madrid, Spain. E-mail: fernando.moreno@cnb.csic.es
bDepartamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, E-28049 Madrid, Spain. E-mail: ruben.perez@uam.es
cDepartment of Physics, University of Basel, Klingelbergstrasse 82, CH 4056 Basel, Switzerland
dCondensed Matter Physics Center (IFIMAC), Universidad Autónoma de Madrid, E-28049 Madrid, Spain
First published on 4th November 2019
Abstract
The mechanical properties of double-stranded RNA (dsRNA) are involved in many of its biological functions and are relevant for future nanotechnology applications. DsRNA must tightly bend to fit inside viral capsids or deform upon the interaction with proteins that regulate gene silencing or the immune response against viral attacks. However, the question of how the nucleotide sequence affects the global mechanical properties of dsRNA has so far remained largely unexplored. Here, we have employed state-of-the-art atomistic molecular dynamics simulations to unveil the mechanical response of different RNA duplexes to an external force. Our results reveal that, similarly to dsDNA, the mechanical properties of dsRNA are highly sequence-dependent. However, we find that the nucleotide sequence affects in a strikingly different manner the stretching and twisting response of RNA and DNA duplexes under force. We find that the elastic response of dsRNA is dominated by the local high flexibility of pyrimidine-purine steps. Moreover, the flexibility of pyrimidine-purine steps is independent of the sequence context, and the global flexibility of the duplex reasonably scales with the number of this kind of base-pair dinucleotides. We conclude that disparities of the mechanical response of dinucleotides are responsible for the differences observed in the mechanical properties of RNA and DNA duplexes.
Introduction
Double-stranded RNA (dsRNA) molecules perform a wide variety of functions inside the cell. For example, dsRNA molecules carry the genetic information in some viruses, trigger gene silencing or activate the immune response against viral attacks.1–5 In addition, dsRNA helices are ubiquitous in the 3D structure of regulatory RNAs and in the ribosome.6–9 Indeed, the formation of double-helices is often a prerequisite for the folding of RNA into complex tertiary and quaternary structures.10,11 Not surprisingly, it has been estimated that over one half of the nucleotides in structured RNAs are engaged in canonical Watson–Crick (WC) base pairing.12,13Many of the biological processes involving canonical dsRNA helices interrogate the mechanical properties of the duplex. This occurs both at a global scale – e.g. during packaging of a kilo-base-pair long dsRNA molecule inside the viral capsid – and at a local level – due to proteins that distort the dsRNA structure over distances of a few base pairs.14–16 Furthermore, the formation of tertiary RNA structures involving contacts between canonical dsRNA helices are greatly affected by the sequence-dependent flexibility of these duplexes.13 Therefore, a complete understanding of sequence-dependent dsRNA flexibility might pave the way to designing complex 3D structures from canonical helices with well-characterized mechanical properties. Recent single molecule experiments have assessed the mechanical properties of long dsRNA molecules of random sequence, revealing two striking differences with DNA.17–19 Firstly, dsRNA stretches ∼3 times more under an external force than its DNA counterpart. Namely, dsRNA has an effective stretch modulus of SRNA ∼ 400 pN, much lower than that of dsDNA (SDNA ∼ 1200 pN). Secondly, dsRNA unwinds upon elongating,19 whereas DNA overwinds when stretched.20 Nevertheless, an important aspect of dsRNA flexibility remains elusive: how its mechanical response depends on the nucleotide sequence.
Molecular dynamics (MD) and Monte Carlo (MC) simulations are an excellent complement to single-molecule methods in the study of the mechanical properties of nucleic acids (NA) and allow in depth exploration of sequence effects.21–28 In the case of dsDNA, extensive MD studies have unveiled and characterized a complex scenario of sequence-dependent mechanical properties.21–24 However, in contrast to the vast literature on dsDNA flexibility, much less is known about how sequence affects the mechanical properties of dsRNA. Based on 150 ns long MD simulations, Faustino et al. concluded that sequence patterns of dinucleotide flexibility are reasonably similar for dsRNA and dsDNA.27 Nevertheless, this local approach lacked a systematic analysis of sequence effects on the overall mechanical response of the duplexes. In parallel, a recent MC simulation based on crystallography derived structural parameters explored sequence effects on the global flexibility of long RNA and DNA duplexes.28 Although this work provided insightful predictions of the mechanical properties of these molecules, it was unable to reproduce the characteristic opposite twist-stretch coupling of dsDNA and dsRNA.
In this work we study the sequence-dependent mechanical properties of dsRNA by using constant-force molecular dynamics (CFMD) simulations, which were previously shown to reproduce the experimental mechanical parameters of dsRNA.29 Interestingly, when applied to dsRNA molecules consisting of repeating dinucleotides, our microsecond-long CFMD simulations revealed a strongly sequence-dependent mechanical response. A top-bottom analysis allowed us to identify the high local flexibility of pyrimidine-purine steps as a critical factor in modulating the global elastic response of these duplexes. Consistently, when inserted in dsRNA molecules of random sequences, these pyrimidine-purine steps softened the mechanical response of the entire duplexes. These results motivate the exploration of sequence effects on dsRNA flexibility by means of single-molecule manipulation.
Results
DsRNA mechanical properties are sequence-dependent
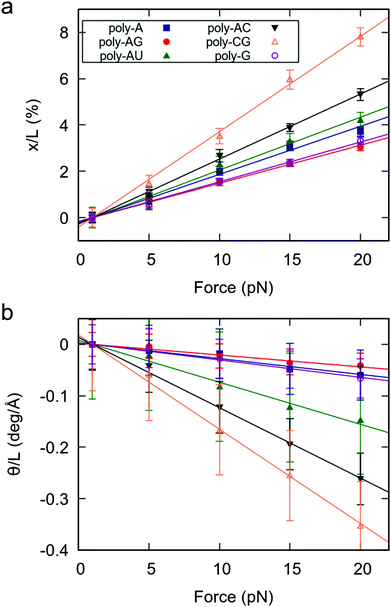
The sequence-dependent mechanical properties of dsRNA were studied using constant-force molecular dynamics (CFMD) simulations following a previously reported protocol.29 We first considered six duplexes with sequences G4(NN)8G4, where NN = AA, AC, AG, AU, CG, GG (see Table 1). Five CFMD simulations were run for each of the sequences at forces F = 1, 5, 10, 15, 20 pN. Further details on simulations and data analysis are provided in the Materials section.| Label | Sequence | % GC | # YR Steps |
|---|---|---|---|
| Benchmark sequences | |||
| Poly-CG | G4(CG)8G4 | 100 | 7 |
| Poly-AC | G4(AC)8G4 | 0 | 7 |
| Poly-AU | G4(AU)8G4 | 0 | 7 |
| Poly-A | G4(AA)8G4 | 0 | 0 |
| Poly-AG | G4(AG)8G4 | 50 | 0 |
| Poly-GG | G4(GG)8G4 | 100 | 0 |
| Random sequences | |||
| Seq-1 | G4CC![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) A A![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) U U![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) AUU AUU![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) CG4 CG4 |
50 | 4 |
| Seq-2 | G4![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) C C![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) C C![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) A A![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) ![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) AG4 AG4 |
50 | 6 |
| Seq-3 | G4C![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) G G![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) GC GC![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) GGC GGC![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) UG4 UG4 |
75 | 4 |
| Seq-4 | G4AUCU![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) A A![[U with combining low line]](https://www.rsc.org/images/entities/char_0055_0332.gif) ![[G with combining low line]](https://www.rsc.org/images/entities/char_0047_0332.gif) AAU AAU![[C with combining low line]](https://www.rsc.org/images/entities/char_0043_0332.gif) ![[A with combining low line]](https://www.rsc.org/images/entities/char_0041_0332.gif) GAG4 GAG4 |
25 | 3 |
As a measure of the mechanical response of RNA duplexes, we obtained the force-induced change in extension and helical twist divided by the extension at F = 1 pN.29 The results, represented in Fig. 1, reveal three important features. Firstly, for all studied sequences, both the elongation and change in helical twist show a linear dependence on the force, as predicted by the widely accepted elastic rod model.19,20,29 Secondly, as evidenced by the negative slopes of Fig. 1b, all sequences show the unwinding-when-stretched behavior characteristic of dsRNA.19 Finally, we found that the mechanical response of dsRNA is strongly affected by the sequence.
Interestingly, a very similar trend is observed in both the extension and twisting response of the RNA duplexes under force. Namely, sequences that are more stretched under an external force (larger slope in Fig. 1a) are more prone to force-induced unwinding (Fig. 1b). This finding is consistent with previous works reporting simple deformability patterns in dsRNA.30,31 According to their force response, the poly-CG is the softest molecule, followed by the poly-AC (see Fig. 1). On the other hand, the poly-A, poly-G and poly-AG are the stiffest, all three showing an approximately similar degree of flexibility. Therefore, in terms of response to an external force, the benchmark sequences consisting of alternating purine-pyrimidine (RY) and pyrimidine-purine (YR) steps are softer than those where all steps are purine–purine (RR). A full quantitative description of the mechanical parameters of these benchmark dsRNA sequences in the context of the elastic rod model can be found in the ESI.†
The local flexibility of pyrimidine-purine steps dominates the elastic response of homogenous RNA duplexes
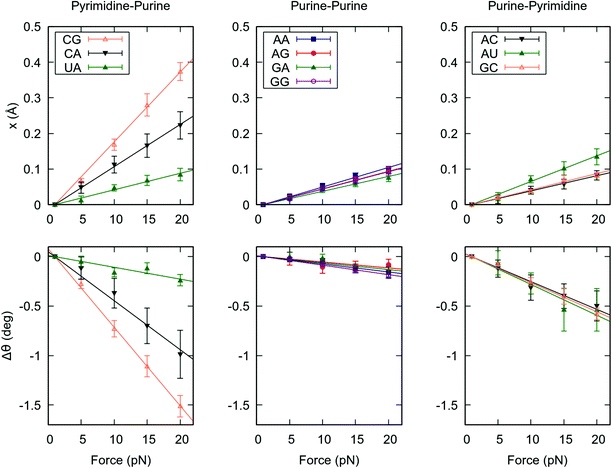
In the previous section we unveiled a significant sequence dependence of the global mechanical properties of the RNA duplex. To gain further insight into how dsRNA sequence affects its global flexibility, we analyzed the force response of the duplexes at a local level. We computed the force-induced variations in helical rise and helical twist for each base pair step, which quantify the contribution of a given dinucleotide to the force response of the entire duplex. We then averaged these quantities over the steps of the same kind, e.g. all the CG dinucleotides, see Fig. 2.Remarkably, the helical rise and helical twist response of each step kind is linear with the force, as occurred for the whole dsRNA helices, see Fig. 1 and 2. More importantly, there is a strong variability among the base pair steps. YR steps (CG, CA and UA) are highly deformable under force, whereas RR and RY steps show a higher stiffness. Among the YR steps a high variability is found, being CG the softest followed by CA and UA in this order. On the contrary, smaller differences are observed among the rest of dinucleotides. Our results suggest that this disparate behaviour at the local level, concretely the high flexibility of the YR steps, is responsible for the differences observed in the global mechanical properties of the benchmark RNA duplexes (Fig. 1). Indeed, the poly-RY duplexes, for which half of the steps are of the kind YR, were systematically more flexible under an external force than their poly-R counterparts, which lack YR steps (Fig. 1).
The enhanced flexibility of pyrimidine-purine steps is independent of the sequence context
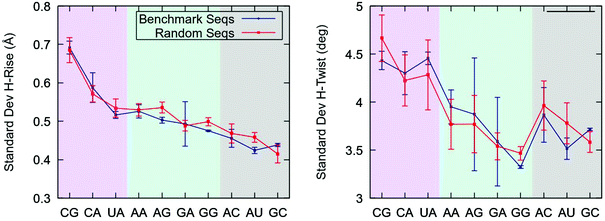
Our finding that pyrimidine-purine steps are highly flexible in the context of the benchmark sequences raises the question of whether this effect is also present in YR-steps of random dsRNA sequences. To address this issue, we considered a set of four randomly generated sequences with different values of fixed GC-content, see Table 1. We performed 1 μs-long unrestrained MD simulations of these random sequences and studied the conformational fluctuations of each base step. In parallel, we simulated the benchmark sequences at zero force and compared the results with the random sequences.Consistent with their softer force response (Fig. 2), YR-steps showed larger helical rise and helical twist fluctuations than the rest of dinucleotides, see Fig. 3. These fluctuations were quantified by computing the standard deviation of these parameters for all the base pair steps and by averaging over the dinucleotides of the same kind, i.e. all the CGs. Importantly, we found that the flexibility trends are similar for both sets of sequences. This result reveals that the large flexibility of YR-steps is not exclusive to the model benchmark sequences and supports the so-called dinucleotide approximation, which assumes that the sequence in which it is embedded has a small effect on the flexibility of an individual dinucleotide. This assumption holds better for helical rise fluctuations, as quantified by the better agreement between the sets of sequences and by the shorter error bars reflecting smaller variations within a given set. An extensive analysis of dsRNA dinucleotide flexibility in the coordinate system of base pair step parameters further supported the dinucleotide approximation, see ESI.‡†
The local flexibility of pyrimidine-purine steps affects the overall elastic response of dsRNA molecules of random sequence
Having proved the high flexibility of YR-steps in random dsRNA sequences, we then turned our attention to the effect of this local flexibility on the global force response of the duplexes. We performed CFMD simulations of the random sequences at F = 1, 5, 10, 15, 20 pN and measured the force-induced changes in extension and helical twist, as done in Fig. 1. Naively, one would expect that the random sequences with larger number of YR-steps will present a softer force response, as happened for the benchmark sequences. Indeed, the degree of elongation and untwisting under force reasonably correlated with the number of YR-steps of the duplexes (Fig. 4 and Table 1). Seq-2, which contains the largest number of YR steps, showed the softest response to an external force; and Seq-4, which has the fewest YR steps, was the most rigid duplex. Seq-3 and Seq-1, which have an intermediate number of YR-steps presented an intermediate force response. Based on these results we propose that the overall mechanical response of a given RNA duplex can be thoroughly tuned by modulating the relative abundance of YR-steps in the nucleotide sequence.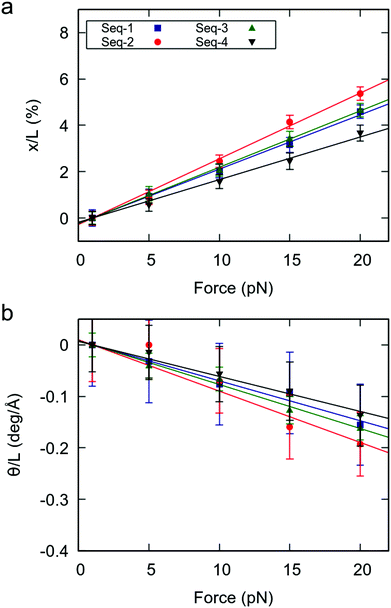 | ||
| Fig. 4 Mechanical force response of the random RNA duplexes. (a) Elongation as function of the applied force. (b) Change in twist as function of the applied force. Elongation and change in twist are divided by the value of the extension at 1 pN. Errors were obtained as described in Fig. 1. | ||
Comparison of sequence effects in dsDNA and dsRNA
The comprehensive study of dsRNA flexibility presented here revealed significant differences with the sequence-dependent dsDNA mechanical properties reported in the literature. Concretely, the nucleotide sequence affects the stretching response of dsDNA and dsRNA to an external force in a strikingly different manner. This can be seen in Fig. 5a, where we compare the values of the effective stretch modulus of our benchmark dsRNA sequences with the ones reported in our previous work for their DNA counterparts.21 Note that the poly-CG RNA duplex is exceptionally flexible, while in the DNA case experiments and simulations show that this sequence is highly stiff;21,22,32 the poly-G DNA is very soft,21,22 but one of the stiffest RNA sequences here studied; and the poly-A DNA is known to be extremely rigid,21,33 whereas the poly-A RNA duplex has a standard mechanical response.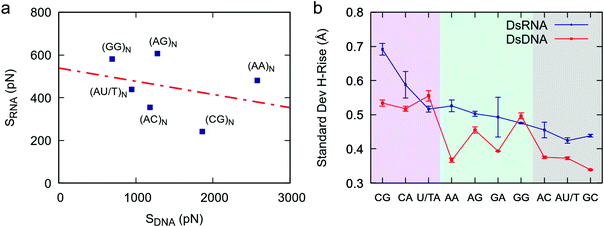 | ||
| Fig. 5 Comparison between dsDNA and dsRNA stretching flexibility. (a) The values obtained in this work for the stretching flexibility of the benchmark dsRNA sequences were compared with the ones reported for the same DNA sequences (changing U by T) in ref. 21. The effective stretch modulus of the dsRNA molecules was obtained as the inverse of the slopes of the force-extension curves (Fig. 1a). The number of dinucleotides comprising the sequences, N, is equal to 8 for dsRNA and 5 for dsDNA. The two data sets, i.e. dsDNA and dsRNA effective stretch moduli, were approximately uncorrelated as quantified by a Pearson correlation factor of r = −0.31. (b) Helical rise fluctuations in DNA and RNA dinucleotides. We analyzed simulations of benchmark DNA sequences (ref. 21) and simulations of benchmark dsRNA sequences (this work) and calculated the helical rise standard deviation of each dinucleotide as described in Fig. 3. | ||
This discrepancy between dsDNA and dsRNA mechanical response can be rationalized by looking at the dinucleotide deformability of both duplexes. We analyzed the DNA helical rise dinucleotide fluctuations of the benchmark sequences from a previous simulation work21 and compared the results with dsRNA (Fig. 5b). Although both nucleic acids share certain features, such as the exceptional flexibility of YR-steps, the patterns of dinucleotide flexibility are indeed quite distinct for dsDNA and dsRNA. For example, the AA dinucleotide is one of the stiffest DNA steps, but is relatively flexible in the dsRNA case; and the opposite occurs for the GG step: it is soft in the DNA duplex, but rigid in dsRNA. We propose that such disparities at the local level are responsible for the differences observed in the mechanical response of the entire duplexes. Importantly, other measurements of dinucleotide flexibility, namely the helical twist fluctuations and the conformational volume, also showed remarkably different sequence-dependence patterns in both nucleic acids (Fig. S1†).
Discussion
A novel difference in the mechanics of dsDNA and dsRNA
Despite their similar chemical composition, dsDNA and dsRNA have been recently shown to exhibit two remarkable differences in their elastic response.18,19 Firstly, dsDNA is around three times stiffer than dsRNA with respect to stretching deformations.18,34,35 Secondly both duplexes possess an opposite twist-stretch coupling.19,20,36 Here we propose a third fundamental difference between dsDNA and dsRNA: the role of the nucleotide sequence on the overall flexibility of the duplex.At first sight, this result might seem controversial: one may argue that because the nucleotide bases are the same in both nucleic acids – excepting uracils/thymine -, their effect on the flexibility of the double-helix should be similar. However, this argument can be rejected in simple terms by resorting to the geometry of the RNA and DNA double-helices, namely the A- and B-forms. In the A-form, consecutive base pairs are highly inclined with respect to each other, whereas in the B-form they are approximately parallel. As a result of these disparate geometries, the chemical interactions between the stacked base pairs are strongly affected, altering their flexibility. For example, the conformations of a given base pair in a highly inclined A-form configuration might be constrained due to steric clashes with its neighbor. Since these steric clashes rely on the geometry of the stacking, they might not be present when this dinucleotide has a B-form planar stacking, which could now explore a broader conformational space. In this case, the dinucleotide would be rigid when found in dsRNA but flexible in dsDNA. Furthermore, even if the local dinucleotide deformability were similar for both molecules, the projection of these deformations on the helical axis would likely differ in the two helical geometries. This idea is introduced in ref. 37. In the case of an RNA A-form helix with inclined base pairs, sliding deformations parallel to the base pairing can substantially elongate the duplex. On the contrary, these very same base pair step deformations can barely stretch the B-form helix, where these sliding movements are practically orthogonal to the helical axis. Consequently, a dinucleotide with high slide flexibility is likely to play a more important role in the force response of dsRNA when compared to dsDNA.
Conclusions
We performed constant-force atomistic molecular dynamics simulations on dsRNA duplexes and found that their global mechanical properties are strongly sequence-dependent. This finding was rationalized from a local perspective: the enhanced flexibility of pyrimidine-purine dinucleotides plays a critical role in the global deformability of the duplex. Consistently, when inserted in dsRNA molecules of random sequences, the number of YR-steps correlated with the overall flexibility of the helix. Our results pave the way towards the design of dsRNA sequences with predefined mechanical properties for biophysical and nanotechnology applications.Methods
Molecular dynamics simulations
Molecular dynamics simulations were performed as described in previous works.21,29 Double-stranded RNA molecules were built using the NAB software.38 The duplexes were neutralized with sodium counterions and no additional salt was added. The neutralized systems were then placed in an approximately cubic box of ∼110 Å of size that was filled with explicit water molecules, totaling ∼120.000 atoms for each system. Energy minimization was then performed in a stage of 5000 steps with restrains on the RNA followed by a second stage of 5000 steps of unrestrained minimization. The systems were then heated up to 300 K and equilibrated for 20 ns in the isobaric-isothermal (NPT) ensemble at P = 1 atm and T = 300 K. Afterwards, starting from the final configuration of the equilibration six production simulations were performed for each sequence: one unrestrained simulation and five constant-force simulations at F = 1, 5, 10, 15 and 20 pN. Each of these production simulations were extended to 1 μs of simulation time.Simulations were run using the AMBER software suite38 with NVIDIA GPU acceleration.39–41 We used parmbs042 with the χOL3 modification43 of the Cornell ff99 force field44 to parameterize the RNA molecules. TIP3P model45 was used to describe water and Joung/Cheatham parameters46 were used for the sodium counterions. We used periodic boundary conditions and Particle Mesh Ewald (with standard defaults and a real-space cutoff of 9 Å) to account for long-range electrostatic interactions. We resorted to the SHAKE algorithm to constrain bonds involving hydrogen. This allowed us to use an integration step of 2 fs. Coordinates were saved every 1000 simulation steps.
Trajectory analysis
Trajectories were analyzed over the entire 1 μs simulation time. The G4 handles were not included in the analysis of all sequences. Helical rise, helical twist and base pair step parameters (shift, slide, rise, tilt, roll and twist) were obtained using the software 3DNA,47 unless otherwise stated.Author contributions
A.M.-G. and J.G.V performed research and analyzed data. A.M.-G., J.G.V, F.M.-H., and R.P. designed research and contributed to discussion of data. A.M.-G. wrote the original draft of the paper and J.G.V, F.M.-H., and R.P. reviewed and edited the manuscript.Conflicts of interest
None declared.Acknowledgements
We thank Urs F. Greber for fruitful discussions, which encouraged us to study the sequence-dependent properties of dsRNA. We thank the financial support from the Spanish MINECO (projects MDM-2014-0377, MAT2017-83273-R (AEI/FEDER, UE), and BFU2017-83794-P (AEI/FEDER, UE)). F. M.-H. acknowledges support from European Research Council (ERC) under the European Union Horizon 2020 research and innovation (grant agreement no. 681299). J. G. V. acknowledges funding from a Marie Sklodowska Curie Fellowship (DLV-795286) within the Horizons 2020 framework. A. M.-G. acknowledges support from the International PhD Program of “La Caixa-Severo Ochoa” as a recipient of a PhD fellowship. The authors acknowledge the computer resources, technical expertise and assistance provided by the Red Española de Supercomputacion at the Minotauro Supercomputer (BSC, Barcelona).References
- A. Fire, et al., Potent and specific genetic interference by double-stranded RNA in Caenorhabditis elegans, Nature, 1998, 391, 806 CrossRef CAS PubMed.
- D. P. Bartel, MicroRNAs: Genomics, Biogenesis, Mechanism, and Function, Cell, 2004, 116(2), 281–297 CrossRef CAS PubMed.
- D. P. Bartel, MicroRNAs: Target Recognition and Regulatory Functions, Cell, 2009, 136(2), 215–233 CrossRef CAS PubMed.
- M. C. Siomi, et al., PIWI-interacting small RNAs: the vanguard of genome defence, Nat. Rev. Mol. Cell Biol., 2011, 12, 246 CrossRef CAS PubMed.
- M. Yoneyama, et al., The RNA helicase RIG-I has an essential function in double-stranded RNA-induced innate antiviral responses, Nat. Immunol., 2004, 5(7), 730–737 CrossRef CAS PubMed.
- L. R. Ganser, et al., The roles of structural dynamics in the cellular functions of RNAs, Nat. Rev. Mol. Cell Biol., 2019, 20(8), 474–489 CrossRef CAS PubMed.
- B. T. Wimberly, et al., Structure of the 30S ribosomal subunit, Nature, 2000, 407(6802), 327–339 CrossRef CAS PubMed.
- P. Nissen, et al., RNA tertiary interactions in the large ribosomal subunit: The A-minor motif, Proc. Natl. Acad. Sci. U. S. A., 2001, 98(9), 4899 CrossRef CAS PubMed.
- J. E. Wilusz, H. Sunwoo and D. L. Spector, Long noncoding RNAs: functional surprises from the RNA world, Genes Dev., 2009, 23(13), 1494–1504 CrossRef CAS PubMed.
- I. Tinoco and C. Bustamante, How RNA folds, J. Mol. Biol., 1999, 293(2), 271–281 CrossRef CAS PubMed.
- P. Brion and E. Westhof, Hierarchy and dynamics of rna folding, Annu. Rev. Biophys. Biomol. Struct., 1997, 26(1), 113–137 CrossRef CAS PubMed.
- J. Stombaugh, et al., Frequency and isostericity of RNA base pairs, Nucleic Acids Res., 2009, 37(7), 2294–2312 CrossRef CAS PubMed.
- J. D. Yesselman, et al., Sequence-dependent RNA helix conformational preferences predictably impact tertiary structure formation, Proc. Natl. Acad. Sci. U. S. A., 2019, 116(34), 16847 CrossRef CAS PubMed.
- G. Lee, et al., Elastic Coupling Between RNA Degradation and Unwinding by an Exoribonuclease, Science, 2012, 336(6089), 1726 CrossRef CAS PubMed.
- G. Masliah, P. Barraud and F. H. T. Allain, RNA recognition by double-stranded RNA binding domains: a matter of shape and sequence, Cell. Mol. Life Sci., 2013, 70(11), 1875–1895 CAS.
- X. Zheng and P. C. Bevilacqua, Straightening of bulged RNA by the double-stranded RNA-binding domain from the protein kinase PKR, Proc. Natl. Acad. Sci. U. S. A., 2000, 97(26), 14162 CrossRef CAS PubMed.
- J. A. Abels, et al., Single-Molecule Measurements of the Persistence Length of Double-Stranded RNA, Biophys. J., 2005, 88(4), 2737–2744 CrossRef CAS PubMed.
- E. Herrero-Galán, et al., Mechanical Identities of RNA and DNA Double Helices Unveiled at the Single-Molecule Level, J. Am. Chem. Soc., 2013, 135(1), 122–131 CrossRef PubMed.
- J. Lipfert, et al., Double-stranded RNA under force and torque: Similarities to and striking differences from double-stranded DNA, Proc. Natl. Acad. Sci. U. S. A., 2014, 111(43), 15408–15413 CrossRef CAS PubMed.
- J. Gore, et al., DNA overwinds when stretched, Nature, 2006, 442(7104), 836–839 CrossRef CAS PubMed.
- A. Marin-Gonzalez, et al., DNA Crookedness Regulates DNA Mechanical Properties at Short Length Scales, Phys. Rev. Lett., 2019, 122(4), 048102 CrossRef PubMed.
- F. Lankaš, et al., Sequence-dependent elastic properties of DNA11Edited by I. Tinoco, J. Mol. Biol., 2000, 299(3), 695–709 CrossRef PubMed.
- F. Lankaš, et al., DNA Basepair Step Deformability Inferred from Molecular Dynamics Simulations, Biophys. J., 2003, 85(5), 2872–2883 CrossRef.
- M. Pasi, et al., μABC: a systematic microsecond molecular dynamics study of tetranucleotide sequence effects in B-DNA, Nucleic Acids Res., 2014, 42(19), 12272–12283 CrossRef CAS PubMed.
- I. Beššeová, et al., Simulations of A-RNA Duplexes. The Effect of Sequence, Solute Force Field, Water Model, and Salt Concentration, J. Phys. Chem. B, 2012, 116(33), 9899–9916 CrossRef PubMed.
- I. Beššeová, et al., Dependence of A-RNA simulations on the choice of the force field and salt strength, Phys. Chem. Chem. Phys., 2009, 11(45), 10701–10711 RSC.
- I. Faustino, A. Pérez and M. Orozco, Toward a Consensus View of Duplex RNA Flexibility, Biophys. J., 2010, 99(6), 1876–1885 CrossRef CAS PubMed.
- F. C. Chou, J. Lipfert and R. Das, Blind Predictions of DNA and RNA Tweezers Experiments with Force and Torque, PLoS Comput. Biol., 2014, 10(8), 37–47 CrossRef PubMed.
- A. Marin-Gonzalez, et al., Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(27), 7049 CrossRef CAS PubMed.
- A. Pérez, et al., The relative flexibility of B-DNA and A-RNA duplexes: database analysis, Nucleic Acids Res., 2004, 32(20), 6144–6151 CrossRef PubMed.
- A. Noy, et al., Relative Flexibility of DNA and RNA: a Molecular Dynamics Study, J. Mol. Biol., 2004, 343(3), 627–638 CrossRef CAS PubMed.
- C. I. Pongor, et al., Optical Trapping Nanometry of Hypermethylated CPG-Island DNA, Biophys. J., 2017, 112(3), 512–522 CrossRef CAS PubMed.
- H. C. M. Nelson, et al., The structure of an oligo(dA)·oligo(dT) tract and its biological implications, Nature, 1987, 330, 221 CrossRef CAS PubMed.
- S. B. Smith, Y. Cui and C. Bustamante, Overstretching B-DNA: The Elastic Response of Individual Double-Stranded and Single-Stranded DNA Molecules, Science, 1996, 271(5250), 795–799 CrossRef CAS PubMed.
- C. G. Baumann, et al., Ionic effects on the elasticity of single DNA molecules, Proc. Natl. Acad. Sci. U. S. A., 1997, 94(12), 6185–6190 CrossRef CAS PubMed.
- T. Lionnet, et al., Wringing out DNA, Phys. Rev. Lett., 2006, 96(17), 1–4 CrossRef PubMed.
- L. Bao, et al., Understanding the Relative Flexibility of RNA and DNA Duplexes: Stretching and Twist-Stretch Coupling, Biophys. J., 2017, 112(6), 1094–1104 CrossRef CAS PubMed.
- D. A. Case, et al., AMBER 14, 2014 Search PubMed.
- A. W. Götz, et al., Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 1. Generalized Born, J. Chem. Theory Comput., 2012, 8(5), 1542–1555 CrossRef PubMed.
- S. L. Grand, A. W. Götz and R. C. Walker, SPFP: Speed without compromise—A mixed precision model for {GPU} accelerated molecular dynamics simulations, Comput. Phys. Commun., 2013, 184(2), 374–380 CrossRef.
- R. Salomon-Ferrer, et al., Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald, J. Chem. Theory Comput., 2013, 9(9), 3878–3888 CrossRef CAS PubMed.
- A. Pérez, et al., Refinement of the AMBER Force Field for Nucleic Acids: Improving the Description of α/γ Conformers, Biophys. J., 2007, 92(11), 3817–3829 CrossRef PubMed.
- M. Zgarbová, et al., Refinement of the Cornell et al. Nucleic Acids Force Field Based on Reference Quantum Chemical Calculations of Glycosidic Torsion Profiles, J. Chem. Theory Comput., 2011, 7(9), 2886–2902 CrossRef PubMed.
- W. D. Cornell, et al., A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules, J. Am. Chem. Soc., 1995, 117(19), 5179–5197 CrossRef CAS.
- W. L. Jorgensen, et al., Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, Molecular Dynamics Simulations of the Dynamic and Energetic Properties of Alkali and Halide Ions Using Water-Model-Specific Ion Parameters, J. Phys. Chem. B, 2009, 113(40), 13279–13290 CrossRef CAS PubMed.
- X. J. Lu and W. K. Olson, 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures, Nucleic Acids Res., 2003, 31(17), 5108–5108 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nr07516j |
| ‡ Our base pair step parameters analysis exposed that, although YR-steps are more generally more flexible, they can be relatively stiff with respect to certain deformations such as slide. Throughout the text, when we describe YR-steps as flexible, we implicitly refer to helical rise and helical twist deformations. |
| This journal is © The Royal Society of Chemistry 2019 |