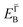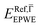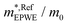Open Access Article
Open Access ArticleSurface state tunable energy and mass renormalization from homothetic quantum dot arrays†
Ignacio
Piquero-Zulaica
 *abc,
Jun
Li
d,
Zakaria M.
Abd El-Fattah
*abc,
Jun
Li
d,
Zakaria M.
Abd El-Fattah
 ef,
Leonid
Solianyk
d,
Iker
Gallardo
a,
Leticia
Monjas
g,
Anna K. H.
Hirsch
ef,
Leonid
Solianyk
d,
Iker
Gallardo
a,
Leticia
Monjas
g,
Anna K. H.
Hirsch
 gh,
Andres
Arnau
gh,
Andres
Arnau
 abi,
J. Enrique
Ortega
abi,
J. Enrique
Ortega
 abj,
Meike
Stöhr
abj,
Meike
Stöhr
 *d and
Jorge
Lobo-Checa
*d and
Jorge
Lobo-Checa
 *kl
*kl
aCentro de Física de Materiales CSIC/UPV-EHU-Materials Physics Center, Manuel Lardizabal 5, E-20018 San Sebastián, Spain. E-mail: ipiquerozulaica@gmail.com
bDonostia International Physics Center, Paseo Manuel Lardizabal 4, E-20018 Donostia-San Sebastián, Spain
cPhysik Department E20, Technische Universität München, 85748 Garching, Germany
dZernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747 AG Groningen, The Netherlands. E-mail: m.a.stohr@rug.nl
ePhysics Department, Faculty of Science, Al-Azhar University, Nasr City E-11884 Cairo, Egypt
fICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Castelldefels, Barcelona, Spain
gStratingh Institute for Chemistry, University of Groningen, Nijenborgh 7, 9747 AG Groningen, The Netherlands
hDepartment for Drug Design and Optimization, Helmholtz Institute for Pharmaceutical Research Saarland (HIPS) – Helmholtz Centre for Infection Research (HZI), Campus Building E8.1, 66123 Saarbrücken, Germany
iDpto. de Física de Materiales, Universidad del País Vasco, E-20018 San Sebastián, Spain
jUniversidad del País Vasco, Dpto. Física Aplicada I, E-20018 San Sebastián, Spain
kInstituto de Ciencia de Materiales de Aragón (ICMA), CSIC-Universidad de Zaragoza, E-50009 Zaragoza, Spain. E-mail: jorge.lobo@csic.es
lDepartamento de Física de la Materia Condensada, Universidad de Zaragoza, E-50009 Zaragoza, Spain
First published on 11th November 2019
Abstract
Quantum dot arrays in the form of molecular nanoporous networks are renowned for modifying the electronic surface properties through quantum confinement. Here we show that, compared to the pristine surface state, the band bottom of the confined states can exhibit downward shifts accompanied by a lowering of the effective masses simultaneous to the appearance of tiny gaps at the Brillouin zone boundaries. We observed these effects by angle resolved photoemission for two self-assembled homothetic (scalable) Co-coordinated metal–organic networks. Complementary scanning tunneling spectroscopy measurements confirmed these findings. Electron plane wave expansion simulations and density functional theory calculations provide insight into the nature of this phenomenon, which we assign to metal–organic overlayer–substrate interactions in the form of adatom–substrate hybridization. To date, the absence of the experimental band structure resulting from single metal adatom coordinated nanoporous networks has precluded the observation of the significant surface state renormalization reported here, which we infer to be general for low interacting and well-defined adatom arrays.
Over the last few decades, the concepts of supramolecular chemistry have been successfully transferred to the construction of two-dimensional (2D) self-assembled molecular arrangements on metallic surfaces.1–4 By selecting the proper tectons (molecular constituents and, if required, metal linkers) and depositing them onto selected substrates, long-range ordered, regular and robust nanoporous networks have been achieved, ranging from hydrogen-5 or halogen-bonded,6 to metal–organic structures.7,8 Such regular structures stand out as ideal templates for nanopatterning organic and inorganic adsorbates by selective adsorption.9–14 Nanoporous networks are also referred to as quantum dot (QD) arrays since they can confine surface state (SS) electrons and provide a vast playground for studying and engineering the electronic properties of new and exotic 2D materials. Indeed, metal–organic networks are known to show novel magnetic properties,15,16 catalytic effects,17 oxidation states,18 and exotic tessellation19–21 and bear the prospect of exhibiting topological electronic bands.22,23
The dominant electronic signature around the Fermi level due to the presence of nanoporous networks comes from the substrate's surface state electrons, which scatter at the molecular array and become confined within individual nanopores.24,25 The tunability of the confined electronic state has so far been achieved by varying the pore dimensions, i.e. the QD size.25,26 However, since the confining potential barriers are not infinite, these QDs are not independent but coupled, as has been shown by angle resolved photoemission spectroscopy (ARPES) through the existence of new dispersive electronic bands24 as well as by Fourier-transform scanning tunneling spectroscopy (FT-STS) data.27 These QD array bands can be modified through the condensation of guest atoms28 or by changing the barrier width.6 The standard fingerprints, whenever the confinement of two-dimensional electron gases (2DEGs) occurs on noble metal surfaces, are in the form of an energy shift of their band bottom towards the Fermi level, an increase of the effective mass, and the appearance of energy gaps at the surface Brillouin zone (BZ) boundaries.6,24,29,30
In this work we show for two homothetic (scalable) metal–organic nanoporous networks (MONNs) grown on Au(111) the first experimental evidence of energy downshifts and reduced effective masses compared to the pristine SS, simultaneous to the opening of zone boundary gaps that suggest electron confinement within the nanocavities. More specifically, these effects are gradual, i.e. they depend on the network dimensions. The interaction between the Au substrate and the MONNs is at the base of these unexpected phenomena and not a consequence of the quantum confinement.
The studied scalable Co-coordinated networks were grown on Au(111) from two related dicarbonitrile-polyphenyl derivatives. Specifically, we used dicarbonitrile-terphenyl (Ph3) and dicarbonitrile-hexaphenyl (Ph6) molecules and Co atoms in a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry to fabricate the MONNs. These tectons were sequentially evaporated (molecules first, then Co) onto Au(111) followed by a mild annealing to 400 K. This resulted in two scalable, periodic, long-range ordered and practically defect free QD arrays [shown in Fig. 1(A and B)] and named hereafter Ph6Co and Ph3Co. In agreement with previous work,25 the networks exhibit sixfold symmetry with unit cell vectors of 3.53 nm (for Ph3Co) and 5.78 nm (for Ph6Co) along the [11
2 stoichiometry to fabricate the MONNs. These tectons were sequentially evaporated (molecules first, then Co) onto Au(111) followed by a mild annealing to 400 K. This resulted in two scalable, periodic, long-range ordered and practically defect free QD arrays [shown in Fig. 1(A and B)] and named hereafter Ph6Co and Ph3Co. In agreement with previous work,25 the networks exhibit sixfold symmetry with unit cell vectors of 3.53 nm (for Ph3Co) and 5.78 nm (for Ph6Co) along the [11![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ] direction and enclose pore areas of 8 nm2 and 24 nm2, respectively. Note that the interaction of both networks with the substrate is assumed to be rather weak since the herringbone reconstruction is neither lifted nor modified in its periodicity (see Fig. S1†).31 We experimentally probed these networks with ARPES [helium I source (h/ν = 21.2 eV) at 150 K] and scanning tunneling microscopy/spectroscopy (STM/STS) at 5 K to obtain both spatially averaged and spatially highly resolved information (ESI†). The experimental data are complemented by Electron Plane Wave Expansion (EPWE) simulations and Density Functional Theory (DFT) calculations (experimental and theoretical methods described in the ESI†).
] direction and enclose pore areas of 8 nm2 and 24 nm2, respectively. Note that the interaction of both networks with the substrate is assumed to be rather weak since the herringbone reconstruction is neither lifted nor modified in its periodicity (see Fig. S1†).31 We experimentally probed these networks with ARPES [helium I source (h/ν = 21.2 eV) at 150 K] and scanning tunneling microscopy/spectroscopy (STM/STS) at 5 K to obtain both spatially averaged and spatially highly resolved information (ESI†). The experimental data are complemented by Electron Plane Wave Expansion (EPWE) simulations and Density Functional Theory (DFT) calculations (experimental and theoretical methods described in the ESI†).
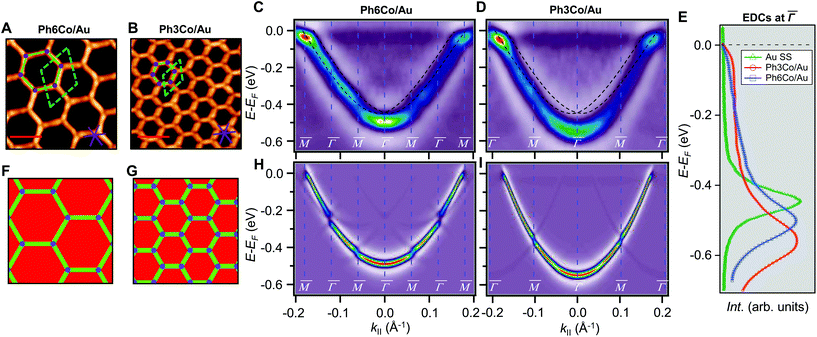 | ||
Fig. 1 STM topographies of the single domain Co-coordinated hexagonal QD arrays using (A) dicarbonitrile-hexaphenyl (Ph6) and (B) dicarbonitrile-terphenyl (Ph3). Scale bar in red corresponds to 5 nm. The high symmetry directions and corresponding unit cells [with unit vectors 5.78 nm (for Ph6Co) and 3.53 nm (for Ph3Co)] are shown in the images (STM parameters: (A) V = −0.50 V, It = 150 pA; (B) V = −0.23 V, It = 250 pA). (C and D) Second derivative of the spectral density obtained by ARPES at 150 K along the  high-symmetry direction for both Ph6Co and Ph3Co nanoporous networks. The band structures exhibit downward shifts of the band bottom and gap openings (clearly visualized in Fig. S2†) at the superstructure symmetry points compared to the pristine Au(111) Shockley state (black dotted lines). (E) Energy distribution curves (EDCs) at normal emission ( high-symmetry direction for both Ph6Co and Ph3Co nanoporous networks. The band structures exhibit downward shifts of the band bottom and gap openings (clearly visualized in Fig. S2†) at the superstructure symmetry points compared to the pristine Au(111) Shockley state (black dotted lines). (E) Energy distribution curves (EDCs) at normal emission ( point) for pristine Au(111) (green), Ph6Co (blue) and Ph3Co (red). A gradual downshift of the band bottom as the pore size is reduced (ΔEPh6Co = 40 meV and ΔEPh3Co = 100 meV with respect to the Au SS) are found. (F and G) 2D potential geometry used for the EPWE modelization, where green stands for the molecular repulsive potentials, purple for slightly repulsive Co regions and red for cavity regions with zero potential. (H and I) Band structure along the point) for pristine Au(111) (green), Ph6Co (blue) and Ph3Co (red). A gradual downshift of the band bottom as the pore size is reduced (ΔEPh6Co = 40 meV and ΔEPh3Co = 100 meV with respect to the Au SS) are found. (F and G) 2D potential geometry used for the EPWE modelization, where green stands for the molecular repulsive potentials, purple for slightly repulsive Co regions and red for cavity regions with zero potential. (H and I) Band structure along the 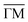 direction of the overlayers simulated by EPWE based on the previous geometry. Matching the experimental ARPES data (gap openings and band-bottom shifts) requires a significant modification of the 2DEG energy reference (see text for details). direction of the overlayers simulated by EPWE based on the previous geometry. Matching the experimental ARPES data (gap openings and band-bottom shifts) requires a significant modification of the 2DEG energy reference (see text for details). | ||
The 2DEG onset of Ph6Co and Ph3Co networks formed on Au(111) is reliably determined by ARPES and only approximately by STS.6 Moreover, ARPES – in contrast to STS – can resolve the QD array band structure from a MONN. However, this can be exceedingly challenging because the networks must be extended, almost defect-free and completely covering the probed surface (in the absence of other coexisting molecular phases).6,24 To achieve these conditions we evaporated the molecules and Co adatoms in orthogonal shallow gradient depositions on the Au(111) substrate, thereby ensuring the existence of an area with optimal coverage and the exact 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometry (cf. ESI†).32Fig. 1(C and D) shows the second derivative of the ARPES spectral density from Ph6Co and Ph3Co along the
2 stoichiometry (cf. ESI†).32Fig. 1(C and D) shows the second derivative of the ARPES spectral density from Ph6Co and Ph3Co along the 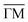 high symmetry direction (see also Fig. S2†). We observed a gradual downshift of the band bottom (
high symmetry direction (see also Fig. S2†). We observed a gradual downshift of the band bottom (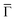 point) towards higher binding energies as the pore size is reduced, which can be quantified from the normal emission energy distribution curves (EDCs) [cf. Fig. 1(E) and Table 1]. Note that this clearly goes in the opposite direction to the energy shift expected from conventional lateral confinement systems (and does not relate to the single components shown in Fig. S3†). Simultaneous to this downshift, we observed a reduction of the effective mass (see Table 1), resembling a Fermi wave-vector pinning (see Fig. S2†). The partial confinement of the substrate's 2DEG is inferred from the presence of small gaps (observed as slight intensity variations) at the symmetry points, which denotes weak scattering from the network barriers. The fact that our experimental dataset does not show spin–orbit splitting for Ph3Co and Ph6Co does not imply its absence, as it might be masked by the ARPES lineshape broadening due to network imperfections and our limited experimental resolution (ESI†).33
point) towards higher binding energies as the pore size is reduced, which can be quantified from the normal emission energy distribution curves (EDCs) [cf. Fig. 1(E) and Table 1]. Note that this clearly goes in the opposite direction to the energy shift expected from conventional lateral confinement systems (and does not relate to the single components shown in Fig. S3†). Simultaneous to this downshift, we observed a reduction of the effective mass (see Table 1), resembling a Fermi wave-vector pinning (see Fig. S2†). The partial confinement of the substrate's 2DEG is inferred from the presence of small gaps (observed as slight intensity variations) at the symmetry points, which denotes weak scattering from the network barriers. The fact that our experimental dataset does not show spin–orbit splitting for Ph3Co and Ph6Co does not imply its absence, as it might be masked by the ARPES lineshape broadening due to network imperfections and our limited experimental resolution (ESI†).33
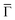 and effective masses (columns
and effective masses (columns 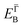 and m*/m0) for the substrate and the two networks. The corresponding 2DEG references (band bottom energy and effective masses) required for matching ARPES with the EPWE simulations are indicated in the last two columns:
and m*/m0) for the substrate and the two networks. The corresponding 2DEG references (band bottom energy and effective masses) required for matching ARPES with the EPWE simulations are indicated in the last two columns: 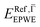 and
and 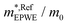
To unravel the potential energy landscapes generated by the molecular networks and their confining properties, we performed EPWE simulations. Such a semi-empirical model has been successfully used for similar systems.6,25,34 The geometries of both systems for the simulations were defined following topographic STM images [see Fig. 1(F and G)]. Assuming repulsive scattering potential sites for molecules (Vmol = 250 meV) and Co atoms (VCo = 50 meV), the experimental data were correctly reproduced. In particular, the ARPES energy gaps (∼25 meV for Ph6Co and ∼30 meV for Ph3Co at ![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) ) reflect the weak scattering strength of the networks [Fig. 1(H and I)]. However, such repulsive scattering is known to shift the 2DEG band bottom (at
) reflect the weak scattering strength of the networks [Fig. 1(H and I)]. However, such repulsive scattering is known to shift the 2DEG band bottom (at 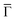 ) upwards, opposite to what is observed here. In this way, the ARPES dispersions can only be matched by EPWE when adopting higher binding energy references and smaller effective masses than the pristine Au(111) SS (see Table 1). In other words, using the original dispersion of the Au(111) SS as a scattering reference cannot correctly reproduce the experimental data.
) upwards, opposite to what is observed here. In this way, the ARPES dispersions can only be matched by EPWE when adopting higher binding energy references and smaller effective masses than the pristine Au(111) SS (see Table 1). In other words, using the original dispersion of the Au(111) SS as a scattering reference cannot correctly reproduce the experimental data.
Such an unexpected scenario questions the confining capabilities of these MONNs. Using STS, we could verify that these networks do confine the Au SS, similar to the ones generated onto Ag(111) by the same family of molecules.25 In the center of Fig. 2(A) we present the Ph6Co STS data acquired at two different positions. The conductance spectra together with the dI/dV maps taken at different voltages [Fig. 2(B–E)] exhibit clear confinement resonances within the pores.6,14,24,25,28,34 Such electron localization mirrors the one observed for the same network on Ag(111).25 In order to directly compare them we adapt the dI/dV spectra in ref. 25 by normalizing the energy axis by the ratio of the respective effective masses  and shifting the onset of the Ag SS to the one of Au (−485 meV at 5 K). The agreement (lineshape and peak energies) between the two datasets is quite reasonable [cf. middle and top of Fig. 2(A)], demonstrating that the confinement properties of Ph6Co are similar for the two substrates.
and shifting the onset of the Ag SS to the one of Au (−485 meV at 5 K). The agreement (lineshape and peak energies) between the two datasets is quite reasonable [cf. middle and top of Fig. 2(A)], demonstrating that the confinement properties of Ph6Co are similar for the two substrates.
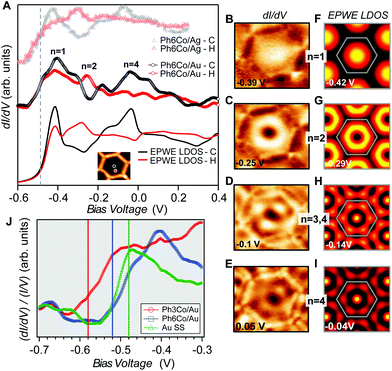 | ||
| Fig. 2 Local confinement and renormalization effects observed by STM/STS. (A) dI/dV spectra at the pore center (black) and halfway (red) for three Ph6Co datasets: Experimental curves of Ph6Co on Au(111) (middle), corresponding EPWE conductance simulation using the ARPES parameters (bottom), and experimental spectra of Ph6Co on Ag(111) adapted from ref. 25 and normalized (see the text) to the Au(111) 2DEG (top). The spectra are made up of the characteristic confined state resonances that alternate depending on the wavefunction spatial distribution, i.e., n = 1 and n = 4 peak at the pore center and n = 2 at halfway.14,35 (B to E) Experimental dI/dV maps reproducing standing wave patterns of the different energy levels n showing excellent agreement with the EPWE simulated ones at similar energies (F to I). The observed deviations for the higher energy conductance maps can be assigned to weak potential alterations stemming from the underlying herringbone reconstruction (see Fig. S1†), which are not considered in the simulations (see text for details). (J) Zoom-in onto the experimental dI/dV onset for the pristine Au(111) SS (green) and Ph6Co (blue) and Ph3Co (red) networks probed at the center of the pores. For comparison, vertical lines marking the bottom energy position found in ARPES (temperature corrected by 30 meV) are included in the panel. The STS onsets are in close proximity to these vertical lines. | ||
We can now address the 2DEG energy downshift with respect to the Au SS upon network formation using local techniques. The overall dI/dV lineshapes at the pore center exhibit broad peak widths (reflecting the ARPES bandwidth) and are quite asymmetric (with maxima being displaced towards higher energy).6,49 Such spectral asymmetry for n = 1 at the pore center can be understood from a band structure perspective: the reduced onset contribution relates to electrons spreading out over the surface given their longer wavelength (λ = 2π/k) at the band bottom (k ∼ 0 around 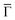 ). Contrarily, STS is maximized at higher energies (close to the
). Contrarily, STS is maximized at higher energies (close to the ![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) point) since the electrons have much shorter wavelengths, thereby becoming much more sensitive to the network barriers and prone to be trapped within the pores. Fig. 2(J) shows the STS spectra of the two networks at the pore center compared to the Au(111) SS. For Ph3Co the onset is clearly shifted away from the Au SS onset, whereas for Ph6Co it is similar but still slightly displaced. This is also the case for these networks on Ag(111) (see Fig. S4†). For Ph6Co, we simulated the STS point spectra and conductance maps [Fig. 2(A and F–I)] using the same scattering parameters and effective mass reduction as described above for the ARPES electron bands. While the experimental and simulated STS spectra match reasonably well, we observe slight discrepancies for the conductance maps obtained at higher energies. This can be ascribed to weak potential variations introduced by the reconstruction of the underlying substrate. Indeed the Ph6Co unit cell is large enough to host both fcc and hcp regions within a single pore (cf. Fig. S1†), which was not accounted for by the EPWE simulations.
point) since the electrons have much shorter wavelengths, thereby becoming much more sensitive to the network barriers and prone to be trapped within the pores. Fig. 2(J) shows the STS spectra of the two networks at the pore center compared to the Au(111) SS. For Ph3Co the onset is clearly shifted away from the Au SS onset, whereas for Ph6Co it is similar but still slightly displaced. This is also the case for these networks on Ag(111) (see Fig. S4†). For Ph6Co, we simulated the STS point spectra and conductance maps [Fig. 2(A and F–I)] using the same scattering parameters and effective mass reduction as described above for the ARPES electron bands. While the experimental and simulated STS spectra match reasonably well, we observe slight discrepancies for the conductance maps obtained at higher energies. This can be ascribed to weak potential variations introduced by the reconstruction of the underlying substrate. Indeed the Ph6Co unit cell is large enough to host both fcc and hcp regions within a single pore (cf. Fig. S1†), which was not accounted for by the EPWE simulations.
In essence, the STS shifts qualitatively agree with the ARPES results, as observed in Fig. 2(J) (vertical lines), supporting a change in the 2DEG reference upon the network presence on the surface. Such subtle downward energy shifts, as is the case of Ph3Co and Ph6Co, also exist for other single atom coordinated MONNs (see Fig. S5†). However, the present effect has not been reported up to now because complementary photoemission experiments are required for determining this 2DEG onset reference.
Different factors might be responsible for these counter-intuitive downward energy shifts of the confined states with respect to the Au SS. This effect can be attributed to the network–substrate interactions in the form of charge transfer (doping effects), localized bound states or hybridization effects of the metal adsorbates that renormalize the 2DEG that is modulated by the network potential landscape. As the shift is gradual, being larger for Ph3Co than for Ph6Co, and the networks are homothetic, it could be induced by charge transfer from the Co adatoms [full surface coverage of Ph3Co/Ph6Co corresponds to 0.015/0.005 monolayers (ML) of Co] to the Au SS, similar to the downshift induced by alkali metals.36 However, the fact that m* decreases and the Fermi wave-vector (kF) is practically pinned suggests the conservation of the 2DEG electron occupancy (the electron density 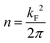 ).37,38 Therefore, the Au SS shift is not driven by electron charge transfer from the Co atom to the Au surface.
).37,38 Therefore, the Au SS shift is not driven by electron charge transfer from the Co atom to the Au surface.
Localized bound states directly below the Co atoms could also be the reason for this downshift. Bound states result from localized attractive perturbations of an atom on a 2DEG39 giving rise to a split resonance with its bonding state shifted to lower energies with respect to the pristine SS band edge.40–42 However, our Co adatom STS spectrum does not show the distinctive feature (peak below the SS onset) in its lineshape, nor the modulation with distance close to the SS onset that are expected for these states (cf. Fig. S6†). The same situation occurs when this MONN family has been grown on Ag(111).25 Moreover, our ARPES band structure (Fig. S2†) is qualitatively similar to the QD array cases for porous networks without coordinating adatoms,6 which clearly differs from the bound state vertically split band structure observed for a random distribution of Au adatoms.38 All these facts discard the bound states of the coordinating atoms as the cause for this effect.
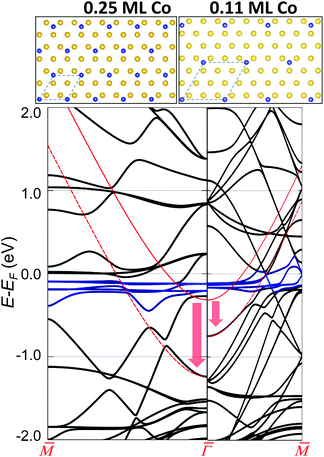
Finally, we consider the Co interaction with the Au substrate, that is, the local Co/Au hybridization.43 For this, we explore the weak Co–Au hybridization by means of DFT calculations of Co atom arrays onto a non-reconstructed Au(111) surface. Fig. 3 shows the calculated band structure from two selected supercells: 2 × 2 (0.25 ML) on the left and 3 × 3 (0.11 ML) on the right. These superstructures introduce an evident difference in the folding of the Au bands (in black), but more importantly, a clear downshift of the pristine Au SS (red arrow). We find that the magnitude of the downshift is directly related to the amount of isolated Co adatoms on the surface (Table S1†). The actual Co coverage within the networks is much lower (by about an order of magnitude), so the expected shift obtained by simple extrapolation to the corresponding Co coverage (of the order of 50 meV) is comparable to the experimental observations (Table S1†). Although geometrical variations (vertical displacements) of the overlayers7,44,45 that could affect the SS reference cannot be completely discarded, the hybridization (coupling) of the Co d-bands (shown in blue in Fig. 3) and folded bulk-bands with the Au(111) SS convincingly explains the observed SS renormalization effect.38,50
This effect turns out to be more general than initially expected. First, because it is likewise observed for this and other families of MONNs grown onto other noble metal substrates (Fig. S5†), and second since additional DFT calculations for homoatomic arrays [Cu/Cu(111) and Au/Au(111)] predict the same effect (Fig. S7†). We deduce that this holds for single (homo- and hetero-) atomic arrays formed onto noble metal substrates whenever the hybridization is weak (physisorption cases), such that the SS character is maintained. Although the modification of the 2DEG does not depend on the network symmetry (see Fig. S5†), the molecule presence is required since it ultimately defines the interaction of the adatom array with the substrate and the adatom concentration defines the energy shift. This scenario commonly applies to MONNs since the adsorption height of adatoms increases due to the coordination with the molecules,7,44–46 effectively reducing their interaction with the substrate.
Interestingly, this surface state energy downshift is not observed for the case of the DPDI-Cu MONN formed on Cu(111).24 We infer that such a difference relates to the number of adatoms at coordinating sites (three for the case of DPDI-Cu) that are prone to be less efficiently uplifted from the surface7 compared to single atom coordinated MONNs. In consequence, the interaction with the underlying substrate would be stronger, leading to higher effective scattering potentials at the coordinating sites, as obtained by EPWE simulations (VCu trimers-DPDI = 390 ± 50 meV vs. VCo-PhXCo = 50 meV).47
In summary, ARPES and STS results reveal a gradual energy and mass renormalization of the Au(111) SS upon the formation of two homothetic single Co coordinated metal–organic networks. EPWE simulations only agree with the experimental data after the 2DEG reference is shifted to higher binding energies. Notably this downshift is gradual with decreasing pore size and is observable in spite of the confining attributes of the nanocavities (that upshifts the states). Our EPWE simulations can satisfactorily match our experimental data using repulsive potentials for both molecules and Co atoms. Overlayer–substrate interactions must be responsible for such counterintuitive effects upon the Au SS reference. Hybridization between the Co adatoms and the folded substrate bands with the Au SS appears as the most plausible cause, as deduced from DFT calculations. We predict that other single atom coordinated MONNs grown on noble metal surfaces should show such subtle counterintuitive 2DEG energy renormalization whenever the SS character is preserved, i.e. for weak coupling cases.
Author contribution
I.P-Z., J.E.O. and J.L-C. conducted the ARPES measurements and data analysis; J.L., L.S. and M.S. performed the STM/STS experiments and analysis; Z.M.A.E-F. performed the EPWE simulations; I.G. and A.A. performed the DFT calculations; L.M. and A.K.H.H. synthesized the molecules; I.P-Z. and J.L-C. wrote the manuscript. All authors contributed to the revision and final discussion of the manuscript; I.P-Z., M.S. and J.L-C. conceived this project.Conflicts of interest
The authors declare that no conflicts of interest exist.Acknowledgements
We acknowledge Prof. J. García de Abajo for providing the EPWE code and the financial support from the Spanish Ministry of Economy, Industry and Competitiveness (MINECO, Grant No. MAT2016-78293-C6 and FIS2016-75862-P), from the Basque Government (Grant No. IT-1255-19 and IT-756-13), from the Regional Government of Aragon (RASMIA project), from the European Regional Development Fund (ERDF) under the program Interreg V-A España-Francia-Andorra (Contract No. EFA 194/16 TNSI) and from the European Research Council (ERC-2012-StG 307760-SURFPRO). The CSIC Open Access Publication Support Initiative through its Unit of Information Resources for Research (URICI) is gratefully acknowledged.References
- J.-M. V. Lehn, Supramolecular Chemistry, Concepts and Perspectives, VCH, Weinheim, 1995 Search PubMed.
- J. L. Atwood, J. E. D. Davies, D. D. MacNicol, F. Vögtle and J.-M. V. Lehn, Comprehensive Supramolecular Chemistry, Pergamon, New York, 1996 Search PubMed.
- S. Stepanow, N. Lin and J. V. Barth, J. Phys.: Condens. Matter, 2008, 20, 184002 CrossRef.
- K. Müller, M. Enache and M. Stöhr, J. Phys.: Condens. Matter, 2016, 28, 153003 CrossRef PubMed.
- G. Pawin, K. L. Wong, K.-Y. Kwon and L. Bartels, Science, 2006, 313, 961 CrossRef CAS PubMed.
- I. Piquero-Zulaica, J. Lobo-Checa, A. Sadeghi, Z. M. Abd El-Fattah, C. Mitsui, T. Okamoto, R. Pawlak, T. Meier, A. Arnau, J. E. Ortega, J. Takeya, S. Goedecker, E. Meyer and S. Kawai, Nat. Commun., 2017, 8, 787 CrossRef PubMed.
- M. Matena, J. Björk, M. Wahl, T.-L. Lee, J. Zegenhagen, L. H. Gade, T. A. Jung, M. Persson and M. Stöhr, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125408 CrossRef.
- L. Dong, Z. Gao and N. Lin, Prog. Surf. Sci., 2016, 91, 101 CrossRef CAS.
- M. Stöhr, M. Wahl, H. Spillmann, L. H. Gade and T. A. Jung, Small, 2007, 3, 1336 CrossRef PubMed.
- Z. Cheng, J. Wyrick, M. Luo, D. Sun, D. Kim, Y. Zhu, W. Lu, K. Kim, T. L. Einstein and L. Bartels, Phys. Rev. Lett., 2010, 105, 066104 CrossRef PubMed.
- J. Wyrick, D.-H. Kim, D. Sun, Z. Cheng, W. Lu, Y. Zhu, K. Berland, Y. S. Kim, E. Rotenberg, M. Luo, P. Hyldgaard, T. L. Einstein and L. Bartels, Nano Lett., 2011, 11, 2944 CrossRef CAS PubMed.
- S. Nowakowska, A. Wäckerlin, S. Kawai, T. Ivas, J. Nowakowski, S. Fatayer, C. Wäckerlin, T. Nijs, E. Meyer, J. Björk, M. Stöhr, L. H. Gade and T. A. Jung, Nat. Commun., 2015, 6, 6071 CrossRef CAS PubMed.
- R. Zhang, G. Lyu, C. Chen, T. Lin, J. Liu, P. N. Liu and N. Lin, ACS Nano, 2015, 9, 8547 CrossRef CAS PubMed.
- M. Pivetta, G. E. Pacchioni, U. Schlickum, J. V. Barth and H. Brune, Phys. Rev. Lett., 2013, 110, 086102 CrossRef PubMed.
- N. Abdurakhmanova, T.-C. Tseng, A. Langner, C. S. Kley, V. Sessi, S. Stepanow and K. Kern, Phys. Rev. Lett., 2013, 110, 027202 CrossRef CAS PubMed.
- T. R. Umbach, M. Bernien, C. F. Hermanns, A. Krüger, V. Sessi, I. Fernandez-Torrente, P. Stoll, J. I. Pascual, K. J. Franke and W. Kuch, Phys. Rev. Lett., 2012, 109, 267207 CrossRef CAS PubMed.
- R. Gutzler, S. Stepanow, D. Grumelli, M. Lingenfelder and K. Kern, Acc. Chem. Res., 2015, 48, 2132 CrossRef CAS PubMed.
- Y. Li, J. Xiao, T. E. Shubina, M. Chen, Z. Shi, M. Schmid, H.-P. Steinrück, J. M. Gottfried and N. Lin, J. Am. Chem. Soc., 2012, 134, 6401 CrossRef CAS PubMed.
- J. I. Urgel, D. Écija, G. Lyu, R. Zhang, C.-A. Palma, W. Auwärter, N. Lin and J. V. Barth, Nat. Chem., 2016, 8, 657 CrossRef CAS PubMed.
- L. Yan, G. Kuang, Q. Zhang, X. Shang, P. N. Liu and N. Lin, Faraday Discuss., 2017, 204, 111 RSC.
- Y.-Q. Zhang, M. Paszkiewicz, P. Du, L. Zhang, T. Lin, Z. Chen, S. Klyatskaya, M. Ruben, A. P. Seitsonen, J. V. Barth and F. Klappenberger, Nat. Chem., 2018, 10, 296 CrossRef CAS PubMed.
- X. Zhang and M. Zhao, Sci. Rep., 2015, 5, 14098 CrossRef CAS PubMed.
- L. Z. Zhang, Z. F. Wang, B. Huang, B. Cui, Z. Wang, S. X. Du, H.-J. Gao and F. Liu, Nano Lett., 2016, 16, 2072 CrossRef CAS PubMed.
- J. Lobo-Checa, M. Matena, K. Müller, J. H. Dil, F. Meier, L. H. Gade, T. A. Jung and M. Stöhr, Science, 2009, 325, 300 CrossRef CAS PubMed.
- F. Klappenberger, D. Kühne, W. Krenner, I. Silanes, A. Arnau, F. J. García de Abajo, S. Klyatskaya, M. Ruben and J. V. Barth, Phys. Rev. Lett., 2011, 106, 026802 CrossRef CAS PubMed.
- A. Shchyrba, S. C. Martens, C. Wäckerlin, M. Matena, T. Ivas, H. Wadepohl, M. Stöhr, T. A. Jung and L. H. Gade, Chem. Commun., 2014, 50, 7628 RSC.
- S. Wang, W. Wang, L. Z. Tan, X. G. Li, Z. Shi, G. Kuang, P. N. Liu, S. G. Louie and N. Lin, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 245430 CrossRef.
- S. Nowakowska, A. Wäckerlin, I. Piquero-Zulaica, J. Nowakowski, S. Kawai, C. Wäckerlin, M. Matena, T. Nijs, S. Fatayer and O. Popova, et al. , Small, 2016, 12, 3757 CrossRef CAS PubMed.
- A. Mugarza, F. Schiller, J. Kuntze, J. Cordón, M. Ruiz-Osés and J. E. Ortega, J. Phys.: Condens. Matter, 2006, 18, S27–S49 CrossRef CAS.
- A. Bendounan, F. Forster, J. Ziroff, F. Schmitt and F. Reinert, Surf. Sci., 2006, 600, 3865 CrossRef CAS.
- M. Ruiz-Osés, D. G. de Oteyza, I. Fernández-Torrente, N. Gonzalez-Lakunza, P. M. Schmidt-Weber, T. Kampen, K. Horn, A. Gourdon, A. Arnau and J. E. Ortega, ChemPhysChem, 2009, 10, 896 CrossRef PubMed.
- I. Piquero-Zulaica, S. Nowakowska, J. E. Ortega, M. Stöhr, L. H. Gade, T. A. Jung and J. Lobo-Checa, Appl. Surf. Sci., 2017, 391, 39 CrossRef CAS.
- J. Lobo-Checa, F. Meier, J. H. Dil, T. Okuda, M. Corso, V. N. Petrov, M. Hengsberger, L. Patthey and J. Osterwalder, Phys. Rev. Lett., 2010, 104, 187602 CrossRef PubMed.
- F. Klappenberger, D. Kühne, W. Krenner, I. Silanes, A. Arnau, F. J. García de Abajo, S. Klyatskaya, M. Ruben and J. V. Barth, Nano Lett., 2009, 9, 3509 CrossRef CAS PubMed.
- J. Li, W.-D. Schneider, S. Crampin and R. Berndt, Surf. Sci., 1999, 422, 95 CrossRef CAS.
- E. Bertel and N. Memmel, Appl. Phys. A: Mater. Sci. Process., 1996, 63, 523 CrossRef CAS.
- F. Forster, A. Bendounan, J. Ziroff and F. Reinert, Surf. Sci., 2006, 600, 3870 CrossRef CAS.
- C. Liu, I. Matsuda, R. Hobara and S. Hasegawa, Phys. Rev. Lett., 2006, 96, 036803 CrossRef PubMed.
- B. Simon, Ann. Phys., 1976, 97, 279 Search PubMed.
- V. Madhavan, W. Chen, T. Jamneala, M. F. Crommie and N. S. Wingreen, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 165412 CrossRef.
- F. E. Olsson, M. Persson, A. G. Borisov, J.-P. Gauyacq, J. Lagoute and S. Fölsch, Phys. Rev. Lett., 2004, 93, 206803 CrossRef CAS PubMed.
- L. Limot, E. Pehlke, J. Kröger and R. Berndt, Phys. Rev. Lett., 2005, 94, 036805 CrossRef CAS PubMed.
- U. Schlickum, R. Decker, F. Klappenberger, G. Zoppellaro, S. Klyatskaya, M. Ruben, I. Silanes, A. Arnau, K. Kern, H. Brune and J. V. Barth, Nano Lett., 2007, 7, 3813 CrossRef CAS PubMed.
- Y.-L. Zhao, W. Wang, F. Qi, J.-F. Li, G. Kuang, R.-Q. Zhang, N. Lin and M. A. Van Hove, Langmuir, 2017, 33, 451 CrossRef CAS PubMed.
- Q. Sun, L. Cai, H. Ma, C. Yuan and W. Xu, ACS Nano, 2016, 10, 7023 CrossRef CAS PubMed.
- M. N. Faraggi, V. N. Golovach, S. Stepanow, T.-C. Tseng, N. Abdurakhmanova, C. S. Kley, A. Langner, V. Sessi, K. Kern and A. Arnau, J. Phys. Chem. C, 2015, 119, 547 CrossRef CAS.
- I. Piquero-Zulaica, Z. M. Abd El-Fattah, O. Popova, S. Kawai, S. Nowakowska, M. Matena, M. Enache, M. Stöhr, A. Tejeda, A. Taleb, E. Meyer, J. E. Ortega, L. H. Gade, T. A. Jung and J. Lobo-Checa, New J. Phys., 2019, 21, 053004 CrossRef CAS.
- K. Seufert, W. Auwärter, F. J. Garcıia de Abajo, D. Ecija, S. Vijayaraghavan, S. Joshi and J. V. Barth, Nano Lett., 2013, 13, 6130 CrossRef CAS PubMed.
- Arrays of coupled QDs give rise to bonding and anti-bonding continuum states. The minimum energy is established by the bonding state and the overall bandwidth (proportional to the QD intercoupling) is defined by the anti-bonding ones.48 The STS technique reveals an enhanced sensitivity to probe the anti-bonding state since the wavefunction shape for the bonding state is more spread out than the anti-bonding one.48 Consequently, the peak lineshapes are generally asymmetric with maxima displaced towards the top of the band, which in ARPES matches the
![[M with combining macron]](https://www.rsc.org/images/entities/char_004d_0304.gif) point energy.
point energy. - The effect of a Co network on the Au Shockley state cannot be tested with ARPES, since at low coverages Co atoms aggregate forming clusters at herring-bone elbows (see Fig. S3†).
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C9NR07365E |
| This journal is © The Royal Society of Chemistry 2019 |