Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Size-dependent exciton substructure in CdSe nanoplatelets and its relation to photoluminescence dynamics†
Judith F.
Specht
a,
Riccardo
Scott
b,
Marta
Corona Castro
a,
Sotirios
Christodoulou
 cd,
Guillaume H. V.
Bertrand
de,
Anatol V.
Prudnikau
cd,
Guillaume H. V.
Bertrand
de,
Anatol V.
Prudnikau
 f,
Artsiom
Antanovich
f,
Artsiom
Antanovich
 f,
Laurens D. A.
Siebbeles
g,
Nina
Owschimikow
b,
Iwan
Moreels
f,
Laurens D. A.
Siebbeles
g,
Nina
Owschimikow
b,
Iwan
Moreels
 dh,
Mikhail
Artemyev
dh,
Mikhail
Artemyev
 f,
Ulrike
Woggon
b,
Alexander W.
Achtstein
f,
Ulrike
Woggon
b,
Alexander W.
Achtstein
 *b and
Marten
Richter
*b and
Marten
Richter
 *a
*a
aInstitut für Theoretische Physik, Nichtlineare Optik und Quantenelektronik, Technische Universität Berlin, Hardenbergstr. 36, 10623 Berlin, Germany. E-mail: marten.richter@tu-berlin.de
bInstitut für Optik und Atomare Physik, Technische Universität Berlin, Strasse des 17 Juni 135, 10623 Berlin, Germany. E-mail: achtstein@tu-berlin.de
cICFO-Institut de Ciencies Fotoniques, 08860 Castelldefels, Barcelona, Spain
dIstituto Italiano di Tecnologia, IT-16163 Genova, Italy
eCEA Saclay, 91191 Gif-sur-Yvette, France
fResearch Institute for Physical Chemical Problems of Belarusian State University, 220006, Minsk, Belarus
gOptoelectronic Materials Section, Delft University of Technology, 2629 HZ Delft, The Netherlands
hDepartment of Chemistry, Ghent University, Krijgslaan 281 - S3, 9000 Gent, Belgium
First published on 12th June 2019
Abstract
CdSe nanoplatelets can be synthesized with different lateral sizes; very small nanoplatelets have almost quantum dot like features (almost discrete exciton states), while very large ones are expected to have properties of colloidal quantum wells (exciton continuum). However, nanoplatelets can be in an intermediate confinement regime with a rich substructure of excitons, which is neither quantum dot like nor an ideal 2D exciton. In this manuscript, we discuss the experimental transition energies and relaxation dynamics of exciton states in CdSe platelets with varying lateral dimensions and compare them with a microscopic theoretical model including exciton–phonon scattering. The model takes special care of the interplay of confinement and Coulomb coupling in the intermediate regime showing strong changes with respect to simple weak or strong confinement models by solving the full four dimensional lateral factorization free exciton wavefunction. Depending on the platelet size broad resonances previously attributed to just ground and excited states are actually composed of a rich substructure of several exciton states in their temporal dynamics. We show that these factorization free exciton states can explain the spectral features observed in photoluminescence experiments. Furthermore we demonstrate that the interplay of exciton bright and dark states provides principle insights into the overall temporal relaxation dynamics, and allows tuning of the exciton cooling via lateral platelet size. Our results and theoretical approach are directly relevant for understanding e.g. the size tuneability of lasing, excitonic cooling dynamics or light harvesting applications in these and similar 2D systems of finite lateral size.
1. Introduction
Recently, semiconductor nanoparticles such as quasi-two-dimensional (2D) CdSe nanoplatelets (NPLs) have been synthesized and characterized1–16 as well as hetero structures of them.17–23 They constitute a novel class of colloidal 2D systems, developed after the synthesis of 0D and 1D systems,24–27 whose unique optoelectronic properties can be controlled by composition, size, and shape and which may provide the colloidal counterpart to epitaxial quantum wells.28–36 In contrast to transition metal dichalcogenides there is a defined control over the finite lateral size of the nanoplatelets. In particular, their lateral size can be tuned by the synthesis duration and proper choice of metal–organic precursors,37 while the thickness is tunable to monolayer precision. Their lateral extent determines the physics between quantum well-like (weak confinement) and quantum dot-like (strong confinement) regimes.38 As a consequence, the exciton properties and dynamics in NPLs interpolate between the Coulomb- and confinement-dominated limits known from ideal quantum wells on the one hand and quantum dots on the other hand. This versatility makes them colloidally grown alternatives to epitaxial quantum wells or dots that are of interest, e.g., for nanoscale light-emitters, efficient lasing or energy harvesting applications.The optical response of these nano-emitters, e.g., in photoluminescence (PL) experiments, is dominated by excitonic effects. The energetic separation between excitons,38 the exciton–phonon interactions,39 the dark–bright splitting of exciton states,11 the oscillator strength and thus the radiative lifetime of excitons39,40 strongly depends on the platelet lateral area. Therefore, varying the lateral size of these nano-objects provides a rich playground for optimizing the optoelectronic properties in terms of internal relaxation dynamics and exciton substructure.
In this article we compare a microscopic theoretical factorization free exciton substructure model to experimental time- and energy-resolved photoluminescence (PL) signals for different platelet sizes. Factorization free exciton eigenstates in this model are obtained from the full four-dimensional Schrödinger equations38 and used to calculate the electron–phonon scattering rates. The full factorization free exciton eigenstates enable us to cover the full range of lateral sizes from weak (quantum well like) to strong confined (quantum dot like) structure, so that the usual approximate factorizations are not applicable. This yields a direct access to the exciton dynamics and the relaxation channels in the system, revealing the interplay of radiative and longitudinal-acoustic (LA) and -optical (LO) phonon scattering processes between the multiple center of mass bright and dark, discrete (small NPLs) and quasi-continuous (large NPLs) exciton states visible in the experimental data.
A direct comparison between theory and experiment at 4 K demonstrates that a large number of (center of mass) bright and dark exciton states contributes to the optical response revealing a substructure of exciton states inside the (double) emission peaks, without substructure so far attributed to ground and excited states for larger platelets.39 In particular for small platelet sizes, phonon bottlenecks can trap the exciton population in higher exciton states, resulting in exciton lifetimes of the order of 100 ps, making these colloidal nanostructures interesting candidates e.g. for quantum-optical applications. The tunability of the cooling and decay dynamics via lateral size gives prospect to tunable excited state lasing or energy harvesting, and further involves the presence of center of mass momentum dark excitons altering the properties, as they provide non emitting exciton storage states, with a density of states controllable by the lateral size. In larger platelets the mentioned phonon bottlenecks are considerably weaker, so that the carrier cooling in the optically active states can be further tuned strongly by the lateral extent of the platelets allowing fast radiative recombination.
2. Experimental and theoretical model
CdSe nanoplatelets were synthesized and characterized by TEM, resulting in a series of nanoplatelets with 4.5 monolayer (ML) thickness and 17 × 6 nm2 to 41 × 13 nm2 lateral size. A dilute platelet solution without aggregates was dispersed in a polymer. The polymer was then deposited on fused silica substrates for low temperature PL measurements. This method avoids any potential stacking of nanoplatelets, thus a proposed excimer mechanism41 for the phenomenological double emission of CdSe platelets does not apply for our experimental situation (see Methods section and ESI† for details).2.1. Theoretical model system
Based on ref. 38, the nanoplatelets are modeled as quantum box like structures with a z confinement of few monolayers and a variable lateral (x, y) confinement chosen according to the experiment (size assessed from TEM measurements). We assume a two-band model in effective-mass approximation for the carriers and focus on exciton states around the band edge by restricting the calculation to the lowest electron and hole subbands. An orthonormal two-particle basis is introduced: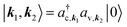 , where a(†)λ,k annihilates (creates) an electron with wave vector k in band λ = c, v and |0〉 denotes the electronic ground state.
, where a(†)λ,k annihilates (creates) an electron with wave vector k in band λ = c, v and |0〉 denotes the electronic ground state.
Introducing an exciton basis |α〉, the wave function Ψα(re, rh) = 〈re, rh|α〉 of exciton state α is factorized into an in-plane part ψα(ρe, ρh) with ρe/h = re/h∥ and a perpendicular part ζ(ze/h):42Ψα(re, rh) = ψα(ρe, ρh)ζ(ze)ζ(zh). The z envelope is approximated by a Gaussian: ζ(z) = 1/(2πσz2)1/4e−z2/4σz2. The standard deviation σz = z0/3 has been determined in a way that ζ2(ze/h) has almost decayed at the boarders of the platelet of width z0 = 0.302 nm × 4.5 monolayers.3ψα(ρe, ρh) solves the four-dimensional factorization free stationary Schrödinger equation for in-plane motion:32,33,43
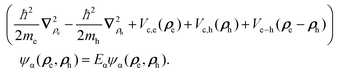 | (1) |
Here, the first two terms describe the free motion of the electron and hole with effective mass me/h and Eα denotes the exciton binding energy. Vc,e(ρe) and Vc,h(ρh) are the lateral confinement potentials of the electron and hole, which are modeled as infinitely deep potential wells. Ve−h(ρe − ρh) represents the attractive Coulomb interaction between the electron and the hole and is given as an effective in-plane potential44
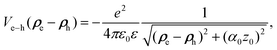 | (2) |
In this study, radiative and phonon-mediated exciton relaxation processes in CdSe nanoplatelets surrounded by oleic acid ligands are studied, therefore the Hamiltonian of the system transformed into the exciton basis introduced above includes:
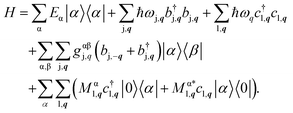 | (3) |
The Hamiltonian includes the electronic part with exciton energy Eα, the free phonon and photon contribution (second and third term), and the coupling to phonons and to the quantized light field (last two terms). b(†)j,q denotes the bosonic annihilation (creation) operator for a phonon mode j with wave vector q and frequency ωj,q. c(†)l,q annihilates (creates) a photon of mode l, wave vector q, and frequency 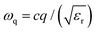 . The coupling elements formulated using the four dimensional exciton wave function are given in the ESI.†
. The coupling elements formulated using the four dimensional exciton wave function are given in the ESI.†
The quantities of interest for the calculation of observables are the expectation values of the exciton density matrix elements. The exciton densities and polarizations are defined as ραβ = trB[〈β|ρ|α〉] and ρα0 = trB[〈ϕ0|ρ|α〉], where trB denotes the trace over the reservoir states. When deriving the equations of motion based on the von Neumann equation iħ∂tρS = [H,ρS] for the system density matrix, the hierarchy problem arising from the many particle coupling is solved by applying a Born–Markov treatment and assuming the phonons to be in thermal equilibrium at the experimental temperature of 4 K: 〈b†j,qbj′,q′〉 = δq,q′δj,j′n(ħωj,q) with n denoting a Bose distribution. Therefore only single phonon scattering processes are included. This limits the validity of the model for acoustic phonon to low temperatures. Furthermore this leads for quantum dots (with large exciton energy spacing) to a phonon bottleneck, which is softened in the experiment by multiphonon effects, surface ligands etc. Especially surface ligands may be able to reduce or remove the phonon bottleneck, as discussed later for the quantum dot like platelet. Here we target larger platelets(more quantum well like with small exciton state energy spacing) for which the single phonon effects are the dominant process,32,42 what can be also seen in the fact that the emission line width at low temperature is consistent with single acoustic phonon deformation potential scattering47 and higher anharmonic terms are not needed to describe the linewidth. Overall this yields the following equations of motion for the exciton densities and polarizations:32
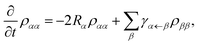 | (4) |
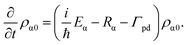 | (5) |
Here Γpd is the phenomenological pure dephasing. The total out-scattering rate 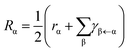 is composed of the spontaneous radiative decay rate
is composed of the spontaneous radiative decay rate
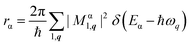 | (6) |
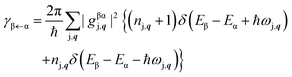 | (7) |
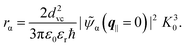 | (8) |
Here, 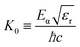 denotes the light cone and
denotes the light cone and 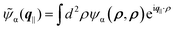 the Fourier transform of the exciton wave function for equally positioned electron and hole with zero center of mass momentum.
the Fourier transform of the exciton wave function for equally positioned electron and hole with zero center of mass momentum.
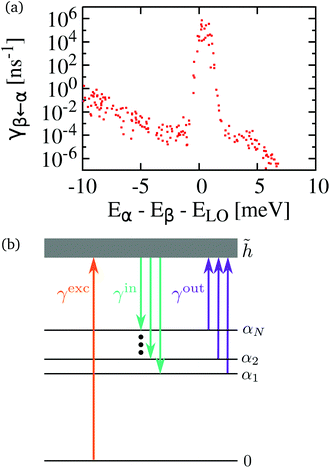
A similar procedure is applied to the phonon scattering rates in order to make them numerically tractable. The strict energy selection rule in the case of optical phonon scattering, the δ function, is replaced by a Gaussian function of width γLO = 0.5 meV to take dephasing due to acoustic phonons into account.40Fig. 1(a) shows the calculated phonon scattering rate γβ←α as a function of the energy difference Eα–Eβ of the involved initial (α) and final exciton states (β). The phonon rate shows a clear resonance at the mean LO phonon energy ELO = 25.5 meV, broadened by the softening parameter γLO. This indicates the existence of a phonon bottleneck since only few exciton states fulfill the required energy match. The asymmetric shape of the curve stems from the LA phonon coupling contribution that increases for decreasing energetic separations between the initial and final state, see eqn (15).
So far, the external photoexcitation of the platelets is not included in the equations of motion. In the considered spectroscopic experiment, the laser excitation takes place at energies far above the band gap. However, the available computational memory restricts the number of calculated exciton states to a limited number of states close to the band gap (40 states). In order to phenomenologically include the incoherent optical pumping, a Lindblad approach is chosen.48,49 Therefore, the Lindblad dissipator ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) is introduced that modifies the von Neumann equation:
is introduced that modifies the von Neumann equation: 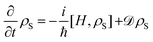 with
with
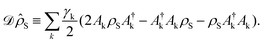 | (9) |
The Lindblad operators A(†)k describe processes that occur at a rate γk in the system. We have furthermore carefully checked, that enough exciton states are included, so that the results converged.
An ensemble of high-energy states in the nanoplatelet is introduced for a phenomenological treatment of the higher energy states above the calculated states. They are assumed to form a quasi-continuous band of high energetic states labeled ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) . At the initial time t0 = 0, a Gaussian-shaped 150 fs laser pulse excites charge carriers from the ground state into the ensemble of high-energy band states modeled using a time-dependent rate γexc. The probability ensemble
. At the initial time t0 = 0, a Gaussian-shaped 150 fs laser pulse excites charge carriers from the ground state into the ensemble of high-energy band states modeled using a time-dependent rate γexc. The probability ensemble ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) itself can interact with the exciton states α in two ways: first, the high-energy band states
itself can interact with the exciton states α in two ways: first, the high-energy band states ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) can decay into the states α under phonon emission at a rate γinα and second, the states α can scatter into the high-energy band states
can decay into the states α under phonon emission at a rate γinα and second, the states α can scatter into the high-energy band states ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) by absorbing a phonon at rate γoutα. All rates are assumed to be mean values and therefore independent of the specific auxiliary state within the high-energy band
by absorbing a phonon at rate γoutα. All rates are assumed to be mean values and therefore independent of the specific auxiliary state within the high-energy band ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) . The three processes, namely the optical pumping from the crystal ground state into the high-energy band and the in- and out-scattering between the high-energy states and the N numerically calculated lowest-energy excitons Xα are schematically depicted in Fig. 1(b).
. The three processes, namely the optical pumping from the crystal ground state into the high-energy band and the in- and out-scattering between the high-energy states and the N numerically calculated lowest-energy excitons Xα are schematically depicted in Fig. 1(b).
The exciton populations ραα couple to the high-energy density ρ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif)
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) , whose equation of motion is given by
, whose equation of motion is given by
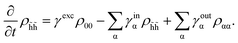 | (10) |
The in-scattering rate is assumed to follow a Gaussian distribution around the mean energy E![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) of the high-energy band: γinα = γLA0 exp[−(Eα − E
of the high-energy band: γinα = γLA0 exp[−(Eα − E![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) )2/σ2
)2/σ2![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) ]. The mean energy E
]. The mean energy E![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) and width σ
and width σ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) characterizing the high-energy band are modeled depending on the energy coverage EαN−Eα1 (with Eα1 and EαN being the energies of the energetically lowest and highest calculated exciton states):
characterizing the high-energy band are modeled depending on the energy coverage EαN−Eα1 (with Eα1 and EαN being the energies of the energetically lowest and highest calculated exciton states):
E![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) = EαN + A(EαN − Eα1) with A = 0.1, = EαN + A(EαN − Eα1) with A = 0.1, | (11) |
σ![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) = BA(EαN − Eα1) with B = 0.7. = BA(EαN − Eα1) with B = 0.7. | (12) |
The parameters A and B are chosen in a way that the phenomenological high-energy band fully decays into the calculated exciton states within few ps (see below). We remark that the experimental observables are insensitive to these parameters. For the out-scattering rate, a detailed-balance expression is chosen: γoutα = γinα exp[Eα − E![[h with combining tilde]](https://www.rsc.org/images/entities/char_0068_0303.gif) /(kBT)].
/(kBT)].
The resulting equation of motion are solved using a time-stepping Runge–Kutta solver from PETSc.50,51 Finally, the time- and frequency-resolved detection signal for incoherent emission is calculated32
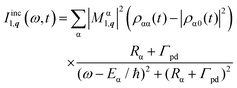 | (13) |
3. Results & discussion
3.1. Time- and energy-resolved photoluminescence
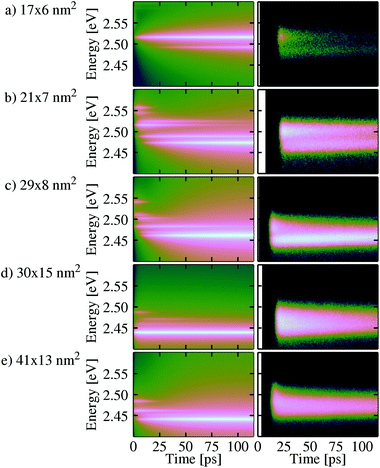
In the following we analyze the experimental data and compare them to the results of our theoretical model to explain the underlying physics. In order to achieve this, the experimental data (right column) and the calculated time- and frequency-resolved PL signal of eqn (13) at 4 K are plotted in Fig. 3 (left column) for five different platelet sizes. An additional minor energy correction was used for each calculated PL signal adjusting the lowest theoretical energy to the experimental data including the z direction confinement. The linewidth of the experimental spectra is larger compared to simulation due to the additional inhomogeneous broadening present in the experiment and finite spectral resolution of the streak camera. Also the deliberately chosen smaller phenomenological pure dephasing in theory (used for plotting only to obtain a better resolution of the underlying exciton structure in Fig. 2) results in slightly smaller simulated line width. | ||
| Fig. 2 Example exciton eigenstates of (a) 17 × 6 nm2 and (b) 30 × 15 nm2. Column E is the energy of the exciton. Column O is a measure for the oscillator strength in arbitary units. r = 0 is a plot of the diagonal wavefunction Ψ(r, r) (electron and hole at the same position r), which gives integrated a measure of the oscillator strength.38 Electron and hole column are the full exciton wavefunction traced out to electron and hole single particle function (useful in strong confinement) and COM and relative are the center of mass and relative mass wavefunction traced out from the full solution (usefull in weak confinement), cf. ref. 38. | ||
The narrow PL lines of the calculated spectra allow to inspect a very important finding: in the experiment, a maximum of two separable exciton signatures is visible in the spectra, which has lead in ref. 39 to a first interpretation, that two exciton states of different energy, e.g. an exciton ground state (GS) and excited state (ES), are visible in PL. As we will see the full four-dimensional exciton calculation will change the picture slightly depending on the platelet size. With increasing platelet size, the GS and ES named signatures are hardly separable any more, but merge into one feature with a fast decaying high-energy shoulder within the first few ps after pulsed excitation (cf.Fig. 3(c–e), right column). However, a comparison to the calculated spectra (left column) reveals immediately that these one or two broadened main lines accessible in the experiment are actually composed of a bunch of different lines resulting from different bright exciton states (cf. the oscillator strength of the different states in Fig. 2) that are gradually populated after the arrival of the incoherent pump pulse. Furthermore the wavefunction diagonal in electron and hole Ψ(r, r) for the different (dark and bright) substructure exciton states does not only enter the oscillator strength via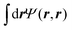 , but also the exchange splitting via
, but also the exchange splitting via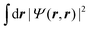 (cf.ref. 25 and 46) and thus may provide an alternative explanation to the magnetic field dependent experimental data in ref. 45 and its trion hypothesis, since the exciton states Fig. 2 in show different symmetries in Ψ(r, r). The energy spacing of the exciton states calculated (cf.Fig. 2) is consistent with other methods using Ansatz wave function with variational principles.23 First, the optical pumping fills the energetically higher exciton states, which are phenomenologically included. With increasing time, they decay into the lower exciton states via phonon-scattering processes until the population resides mainly in the exciton ground state after roughly 100 ps. In the experimental data the behavior is visible in a change of the (shape of the) PL emission bands. This distinct exciton GS line is clearly visible also in the calculated spectra, but only for the smallest platelet only one exciton state contributes to the GS line as expected close to the strong confinement regime. Note, that for the 30 × 15 nm2 platelet higher emitting states exist, but it can be seen that they contribute only very weakly due to fast relaxation into the GS in Fig. 3, both in simulation and experiment.
(cf.ref. 25 and 46) and thus may provide an alternative explanation to the magnetic field dependent experimental data in ref. 45 and its trion hypothesis, since the exciton states Fig. 2 in show different symmetries in Ψ(r, r). The energy spacing of the exciton states calculated (cf.Fig. 2) is consistent with other methods using Ansatz wave function with variational principles.23 First, the optical pumping fills the energetically higher exciton states, which are phenomenologically included. With increasing time, they decay into the lower exciton states via phonon-scattering processes until the population resides mainly in the exciton ground state after roughly 100 ps. In the experimental data the behavior is visible in a change of the (shape of the) PL emission bands. This distinct exciton GS line is clearly visible also in the calculated spectra, but only for the smallest platelet only one exciton state contributes to the GS line as expected close to the strong confinement regime. Note, that for the 30 × 15 nm2 platelet higher emitting states exist, but it can be seen that they contribute only very weakly due to fast relaxation into the GS in Fig. 3, both in simulation and experiment.
The theoretical model is build with the assumption of small exciton energy spacing, since larger platelets are in the focus of this paper, which are more quantum well like than quantum dot like. Therefore it comes with no surprise, that the largest qualitative difference between the experimental and theoretical data is found for the smallest 17 × 6 nm2 platelet (Fig. 3(a)) which is more quantum dot like, where the calculation yields still a substantial population of the higher energy state that remains as long as 2 ns (not shown here), as opposed to a faster decay in the experimental data. So as already expected at the construction of the theoretical model, the typical phonon bottleneck effect is present, since we include only one phonon processes and the efficient transfer process present in the experiment is probably a multi-phonon process, that bridges the high energy spacings in the small platelet (some spacing are in the order of 10 meV). Furthermore in the experiment anharmonicity effects at the surfaces e.g. through ligands might open this decay channel and therefore may explain the qualitative differences in the long time behavior in addition to multiphonon processes. Therefore this behavior is not reflected in the experiment, where indeed in the beginning the intensity of the ES signal is larger compared to the GS, but the overall decay of both lines takes place on a much shorter timescale. However, the behavior is similar to mechanism observed experimentally in ref. 53. Another aspect leading to the slow decay from the higher exciton state can be found in the symmetry of the wave function (cf.Fig. 2(a)). The state shows a p like symmetry so that the relative wavefunction is different to the other states, which may be another reason for temporal storage of the excitation in the simulation. In the experiment deviations from the ideal shape can lift the selection rules, which may open more relaxation channels.
However, also in the experiment, the signal intensity of the higher-energy ES feature relative to the GS line is decreasing with increasing platelet size: for smallest NPLs (Fig. 3(a) and (b)), the ES intensity dominates over the GS intensity, whereas for the intermediate platelet size 29 × 8 nm2 (Fig. 3(c)), the initially weak ES exhibits a fast decay into the GS line that gains intensity very quickly (within few ps). Finally, for the large 30 × 15 nm2 and 41 × 13 nm2 NPLs (Fig. 3(d) and (e)), the intensity of the GS line is very strong right after pulse excitation, whereas the ES lines only appear as very short-lived high-energy shoulder. All trends visible in the measured PL spectra are clearly resembled in the simulations.
3.2. Temporal evolution of exciton populations
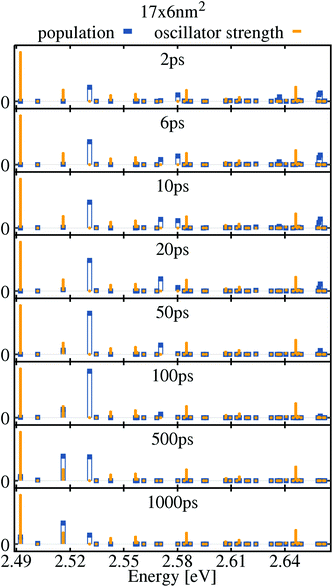
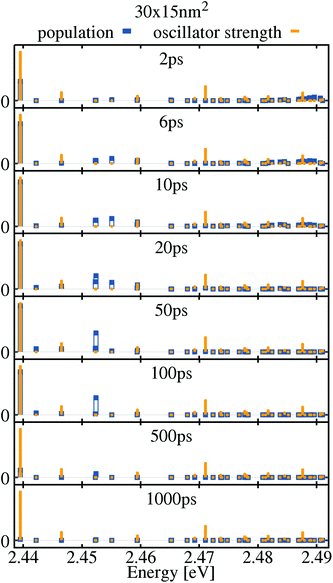
In order to analyze the processes inside the platelet a bit deeper, we have a look at the exciton dynamics used for the calculation of the exciton spectra. Therefore, we inspect snapshots of the populations of the calculated 40 lowest NPL exciton states as plotted over energy. For comparison, Fig. 4 shows the snapshots for the smallest, quantum-dot-like 17 × 6 nm2 platelet and Fig. 6 displays the large 30 × 15 nm2 platelet. We start with the discussion of the smallest platelet, Fig. 4. Eight snapshots are shown, beginning at 2 ps after the initial pulse excitation and ending at 1000 ps. The orange bars represent the oscillator strength of the respective exciton states and the blue bars depict the population. Within the first 20 ps (upper four snapshots), the highest calculated exciton state at 2.656 eV exhibits a significant occupation that is refilled from the initially excited high-energy reservoir (see the center energy of the reservoir in eqn (11)). During the same time, a gradual build-up of some of the lower-energy exciton populations can be observed. In particular the fourth exciton state at 2.662 eV develops a high population. This is particularly interesting since this is a dark exciton state with vanishing oscillator strength (cf.Fig. 2). This means that the phonon scattering into dark states plays a key role in the population distribution within the platelet. As a consequence, population trapping can occur since the dark states cannot decay radiatively. This effect is especially pronounced for the smaller platelets, since the reduced density of exciton states at lower energies removes decay channels due to acoustical phonons (open for larger platelets). Further relaxation due to optical phonons is not possible because of the high energy of optical phonons, which is larger than the exciton state spacing. Also, especially for the smallest, quantum dot like, platelets, where the energetic separation between the low exciton states is rather large due to the strong confinement, phonon scattering becomes inefficient: for example, the energetic distance between the above-mentioned highly populated fourth exciton state and the next lower third exciton state of the 17 × 6 nm2 platelet is 15 meV (cf.Fig. 2). This is not enough to be bridged by LO phonons, however it is too large for LA phonons in single phonon approximation. Therefore, the population of this state can only be reduced by scattering first into higher-energy states and then decay from there towards the ground state, which is very unlikely at the considered low temperature of 4 K. Furthermore it may be reduced by the more p-like symmetry of the state in comparison to other states in this energy range (cf.Fig. 2).This behavior of our theoretical model is expected, since we neglected multi-phonon processes in the model, which may be important for the quantum dot like platelet, since with a combination of multiple phonons the phonon bottleneck can be overcome. Therefore, the phonon bottleneck is less pronounced in the measured spectra since more decay channels are possible. This explains minor deviations between the exciton lifetimes observed in the experimental and calculated PL spectra.
The lower panels of Fig. 4 show that after 50 ps, the high exciton states have almost completely decayed and the population has been transferred to the low-energy excitons. However, for the above-mentioned reasons, even after 1 ns still some bright and dark exciton states are substantially populated. This changes in the case of the large 30 × 15 nm2 platelet shown in Fig. 6: here, the exciton population has completely decayed after 500 ps. Due to the reduced lateral confinement, the exciton states are energetically much closer: whereas for the small 17 × 6 nm2 platelet, the 40 lowest exciton states cover an energy range of 170 meV, this reduces to only 50 meV for the 30 × 15 nm2 platelet. Hence, in the latter phonon scattering is more efficient since more phonon decay channels are allowed. Also for this NPL size, parts of the population are temporarily trapped in dark exciton states at energies of 2.452 meV and 2.455 meV. But the trapping does not prevail as long as in the smaller platelet due to missing phonon bottleneck, but may also be reduced due to similar symmetries visible in the traced out relative wave function (cf.Fig. 2).
Basically the small 17 × 6 nm2 platelet is more quantum dot like, where the disappearance of the phonon bottleneck effect is often assigned to Auger54–56 and also multiphonon effects. At low temperatures the acoustic phonon bottleneck effect was observed for example in ref. 57. However most platelets have more quantum wells like properties with higher exciton state density and the exciton–phonon processes included here are sufficient. For the quantum dot like platelet we remark that most of studies of QDs are at room temperature and thus the temporal dynamic is different to the experiments at low temperatures, presented here.
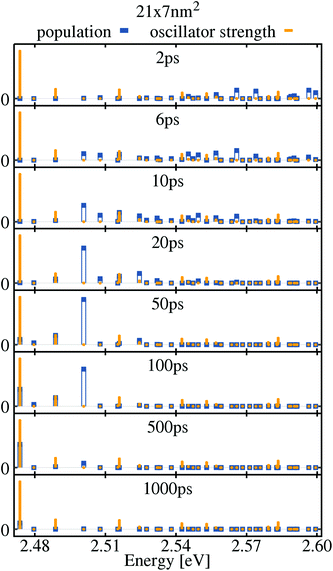
On the other hand the 21 × 7 nm2 platelet as all of the other larger platelets does not show a phonon-bottleneck effect. However as one can see in Fig. 5 a substantial part of the population is stored in a dark state for hundreds of picoseconds and is feeding a bright excited state with lower energy as the dark state. This results in a higher PL emission at excited exciton states (cf.Fig. 3), whereas for the larger platelets the relaxation towards to the lowest exciton states is so efficient due to the increased density of states (e.g. 21 × 7 nm2, 29 × 8 nm2 platelets), that there the PL is dominated by the low energy excitons. We believe that the changes in the distribution of exciton populations due to exciton phonon scattering is also the reason for the predominant emission from the excited state at higher temperatures in experiments.39,58 For example scattering to dark states, which may feed the excited state may be more efficient due to increasing density of states at elevated energies and an increased mean exciton energy in the distribution at elevated temperatures. However we can not explore this, since higher temperatures require multiphonon processes for acoustic phonons, which are not included in our model.
The tunability of recombination dynamics by lateral size, which we demonstrated in this paper can be important for the use of nanoplatelets e.g. in lasing applications, at least for low temperatures, where the excited state lifetime determines the inversion and gain that can be reached in the system. Further a rich sub structure not only of the mentioned exciton states obtained from a factorization free calculation, but also of biexcitons59 and trions is expected in the nanoplatelets and similar 2D systems of finite lateral size.
We demonstrated that the exciton substructure resulting from the factorization free exciton calculation alone could explain the phenomenologically observed double emission of CdSe nanoplatelets and its’ decay dynamics, however we do not exclude a potential additional emission contribution by charged exciton states (trions),45,60e.g. for small, more quantum dot like platelets, but we see qualitative differences in different exciton states, that may lead to different behavior in magnetic fields and not contradicting to the experimental data in ref. 45, however a detailed analysis is beyond the scope of the manuscript, since it is beyond available numerical resources. We would like to emphasis that unlike in ref. 60, where the platelets have been dropcasted directly on fused silica substrates, our nanoplatelets are embedded isolated in polymer. Dropcasting only may have an impact on potential charging of the nanoplatelets by ambient residual charges but also on potential stacking, which both are excluded in our samples using embedding isolated particles in polymer. Hence e.g. trions could contribute in different amount depending on sample preparation. However Diroll et al.41 argue against trion formation that trion formation should be an instantaneous process for nanoplatelets containing an extra charge and that the trion lifetime should be shorter as the exciton lifetime in contrast to the slower rate constant found for the lower state in ref. 39. This is however not necessarily correct, as both exciton and trion state recombination undergo the Giant Oscillator Strength effect,61 which has a different lateral platelet size dependence for both, potentially resulting in regions where the one or the other is the faster process.
Another hypothesis for the phonon replica based genesis58 of the of the phenomenological double emission has already been shown to be unlikely in ref. 39, as the energy spacing varies from 18 to 38 meV by a factor of two with increasing lateral platelet size, much more than a phonon dispersion could allow. In published Raman data,62 a LO-phonon energy of ∼25 meV has been measured for different nanoplatelets, in line with Table 1. Sigle et al.63 have measured the that both confined in- and out of plane LO-phonon modes resemble the bulk dispersion quite well, so given the small energy scale of the dispersion it can be excluded that an LO-phonon replica can cover up to 38 meV energy separation. This is in line with Diroll et al.,41 who showed that the phenomenological energy spacing does not correlate with the Raman determined LO-phonon energy for platelet thickness variation. A potential excimer (charge transfer exciton) hypothesis,41 where two attached platelets allow a charge transfer exciton state seems not applicable to our samples, as first by sample preparation stacking is excluded and secondly in contrast to Tessier et al.58 we do not observe the there discussed characteristic constant energy spacing for varying lateral platelet dimensions. Furthermore since in the preparation stacking is more likely for large platelets, the effect should be strongly size dependent. Another point relates to the strongly extended nature of charge transfer (CT) excitons, the e–h envelope function overlap integrals should be considerably lower for CT exciton, and with them the radiative rates. Due to the reduced wavefunction overlap in a charge transfer state spanning to platelets a much slower exciton relaxation is expected. However that is not observed.47
| Band gap72 | E g | 1.84 eV |
| Mass density | ρ | 5.82 g cm−3 |
| Interband dipole moment | d vc | 0.4 e nm |
| Heavy hole valence band eff. mass73 | m h | 0.41 m0 |
| Conduction band eff. mass73 | m e | 0.22 m0 |
| Sound velocity74 | u | 3.63 km s−1 |
| Static dielectric constant39 | ε stat | 9.4 |
| High-frequency dielectric constant39 | ε ∞ | 7.9 |
| Valence band deformation potential18,75 | D v | −3 eV |
| Conduction band deformation potential18,75 | D c | −6 eV |
| LO phonon frequency at Γ point76 | ω LO Γ | 0.038 fs−1 |
| LO phonon frequency at X point76 | ω LO X | 0.0396 fs−1 |
4. Conclusions
In this manuscript, experimental time and energy resolved photoluminescence spectra were analyzed using a microscopic model for the exciton dynamics in CdSe nanoplatelets including radiative and phonon-assisted scattering processes for center of mass bright and dark states. The PL signals for five different platelet sizes were compared, showing a strong lateral size dependence of the phonon-scattering efficiency and the energy distribution of the exciton states resulting in a LO phonon bottleneck. Therefore, varying the lateral size of these nano-objects provides a rich playground for optimizing the optoelectronic properties in terms of internal relaxation dynamics of the factorization free exciton sub structure.Based on our presented modeling, experimental results and the discussions of alternative explanations of the phenomenological double emission of CdSe nanoplatelets above, we advocate an exciton substructure as reason for the apparent double emission, explaining both energetic position and PL dynamics. Our findings suggest that the experimentally observed, strongly inhomogeneously broadened PL resonances are actually composed of several exciton resonances revealing an exciton substructure, that show strong qualitative difference, which should also result in different magnetic field properties. We argue that trion emission may occur additionally depending on sample preparation and experimental conditions, while excimer formation is unlikely in our isolated nanoplatelets in polymer, but may occur e.g. in concentrated colloidal dispersions.
Although only bright exciton states of the factorization free substructure are visible in the PL signal, the analysis of the temporal evolution of the exciton populations in our samples shows that also the exciton dark states have a major influence on the population dynamics. Population trapping occurs mainly in the small-sized platelets where phonon bottlenecks prevent the occupied dark states from decaying into lower exciton states. This effect is of course overestimated in the simulations since multi-phonon processes are not included in our model. However, all main trends observed in the experiment are reproduced and explained by the theoretical model, which uses the full factorization free four dimensional wavefunction covering weak-, intermediate and strong confinement regimes. The tunability of the dark and bright state dynamics allows to engineer e.g. excited or ground state lasing or the usage of nanoplatelets for solar energy harvesting applications. Further our theoretical model is fully transferrable to other 2D nanostructures, where finite lateral size effects gain increasing attention, like in transition metal dichalcogenides, allowing potentially to tune radiative rates and exciton phonon interaction.
5. Methods
5.1. Samples and setup
CdSe core NPls with the first exciton absorption bands around 512 nm (4.5 ML) were synthesized as described in ref. 6 and 12. Absorption and PL spectra as well as TEM images and details of the preparation avoiding any stacking effects can be found in the ESI.†Our experimental setup allows for the measurement of time-integrated and -resolved fluorescence of a sample with confocal excitation (titanium sapphire laser (Coherent Mira 900F, FWHM 150 fs, 75.4 MHz) SHG at 420 nm) and detection through an objective (N.A. = 0.4). A spectrometer with an attached CCD (Roper Spec10) for time-integrated or a streak camera (Hamamatsu C5680) for time-resolved measurements is used. We applied a moderate CW equivalent 0.2 W cm−2 excitation density leading to <0.1 percent of the platelets to be excited within one laser pulse (average number of excitons per platelet per pulse below 10−3). Details are given in the ESI.†
5.2. Coupling elements of the Hamilton operator
The phonon-coupling matrix element gαβj,q in the exciton basis reads:32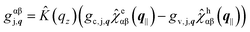 | (14) |
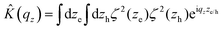 . The Fourier transformed projection of the in-plane wavefunction overlap integral on the electron/hole coordinate is defined as:
. The Fourier transformed projection of the in-plane wavefunction overlap integral on the electron/hole coordinate is defined as: 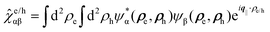 . It is calculated numerically. The matrix element for the deformation-potential coupling to longitudinal-acoustic (LA) phonons reads64,65
. It is calculated numerically. The matrix element for the deformation-potential coupling to longitudinal-acoustic (LA) phonons reads64,65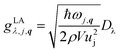 | (15) |
The polar-optical Fröhlich coupling element to longitudinal-optical (LO) phonons is given by65
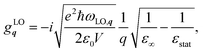 | (16) |
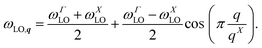 | (17) |
The usage of bulk LO-phonon modes is substantiated, as already mentioned in the main text by results of Sigle et al.,63 showing only very minor deviations in the phonon dispersion of confined modes from bulk so that ligands and polymer matrix around the platelets do not introduce severe alterations. Furthermore Fröhlich coupling already showed reasonable agreement for nanoplatelets in ref. 47, while deviations are probably caused by the way simpler Ansatz for the exciton wavefunction as compared to the Ansatz used here and scatter of data points in ref. 47.
For the exciton–photon coupling the optical matrix element in exciton basis reads:
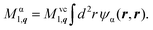 | (18) |
Two polarization modes l = TE, TM of the electric field are distinguished: the transverse electric (TE) and transverse magnetic (TM) mode. The corresponding optical matrix elements are given by32
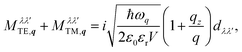 | (19) |
Table 1 lists the CdSe material parameters used for the calculations. Since the radiative loss is emitted into the surrounding medium, the dielectric constant of the oleic acid ligands has been used for the calculation of the optical matrix element:71εr = 2.129.
Author contributions
The manuscript was written by J.F.S., A.W.A. and M.R. A.W.A. initiated the project. R.S., A.W.A. designed the experiments and recorded the experimental spectra. M.R., M.C.C. and J.F.S. developed and performed the theoretical modeling. U.W., N.O., L.D.A.S., I.M., A.W.A. contributed to the discussion. S.C., G.H.V.B., A.V.P., A.A., I.M., M.A. provided samples and their characterization.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support from the Deutsche Forschungsgemeinschaft through SFB 951 B12 (Project No. 182087777), AC290-1/1 (Project No. 265219982), AC290-2/1 (Project No. 324765876) and WO477-32/1 (Project No. 235473865), and well as Belarusian Science Foundation through the CHEMREAGENTS program and BRFFI grant No. X17KIG-004. This project has also received funding from the European Research Council (I.M., grant agreement no. 714876 PHOCONA).Notes and references
- S. Ithurria and B. Dubertret, J. Am. Chem. Soc., 2008, 130, 16504–16505 CrossRef CAS PubMed.
- S. Ithurria, M. D. Tessier, B. Mahler, R. P. S. M. Lobo, B. Dubertret and A. L. Efros, Nat. Mater., 2011, 10, 936 CrossRef CAS PubMed.
- A. W. Achtstein, A. Schliwa, A. Prudnikau, M. Hardzei, M. V. Artemyev, C. Thomsen and U. Woggon, Nano Lett., 2012, 12, 3151–3157 CrossRef CAS PubMed.
- M. Pelton, S. Ithurria, R. D. Schaller, D. S. Dolzhnikov and D. V. Talapin, Nano Lett., 2012, 12, 6158–6163 CrossRef CAS PubMed.
- L. T. Kunneman, M. D. Tessier, H. Heuclin, B. Dubertret, Y. V. Aulin, F. C. Grozema, J. M. Schins and L. D. A. Siebbeles, J. Phys. Chem. Lett., 2013, 4, 3574–3578 CrossRef CAS.
- A. W. Achtstein, A. V. Prudnikau, M. V. Ermolenko, L. I. Gurinovich, S. V. Gaponenko, U. Woggon, A. V. Baranov, M. Y. Leonov, I. D. Rukhlenko, A. V. Fedorov and M. V. Artemyev, ACS Nano, 2014, 8, 7678–7686 CrossRef CAS PubMed.
- C. She, I. Fedin, D. S. Dolzhnikov, A. Demortière, R. D. Schaller, M. Pelton and D. V. Talapin, Nano Lett., 2014, 14, 2772–2777 CrossRef CAS PubMed.
- R. Scott, A. W. Achtstein, A. Prudnikau, A. Antanovich, S. Christodoulou, I. Moreels, M. Artemyev and U. Woggon, Nano Lett., 2015, 15, 4985–4992 CrossRef CAS PubMed.
- A. W. Achtstein, A. Antanovich, A. Prudnikau, R. Scott, U. Woggon and M. Artemyev, J. Phys. Chem. C, 2015, 119, 20156–20161 CrossRef CAS.
- R. Scott, J. Heckmann, A. V. Prudnikau, A. Antanovich, A. Mikhailov, N. Owschimikow, M. Artemyev, J. I. Climente, U. Woggon, N. B. Grosse and A. W. Achtstein, Nat. Nanotechnol., 2017, 12, 1155–1160 CrossRef CAS PubMed.
- L. Biadala, F. Liu, M. D. Tessier, D. R. Yakovlev, B. Dubertret and M. Bayer, Nano Lett., 2014, 14, 1134–1139 CrossRef CAS.
- J. Q. Grim, S. Christodoulou, F. Di Stasio, R. Krahne, R. Cingolani, L. Manna and I. Moreels, Nat. Nanotechnol., 2014, 9, 891–895 CrossRef CAS PubMed.
- S. Dong, J. Lian, M. H. Jhon, Y. Chan and Z.-H. Loh, Nano Lett., 2017, 17, 3312–3319 CrossRef CAS PubMed.
- X. Ma, B. T. Diroll, W. Cho, I. Fedin, R. D. Schaller, D. V. Talapin, S. K. Gray, G. P. Wiederrecht and D. J. Gosztola, ACS Nano, 2017, 11, 9119–9127 CrossRef CAS PubMed.
- S. Christodoulou, J. I. Climente, J. Planelles, R. Brescia, M. Prato, B. Martín-García, A. H. Khan and I. Moreels, Nano Lett., 2018, 18, 6248–6254 CrossRef CAS PubMed.
- J. Planelles, A. W. Achtstein, R. Scott, N. Owschimikow, U. Woggon and J. I. Climente, ACS Photonics, 2018, 5, 3680–3688 CrossRef CAS.
- A. Polovitsyn, Z. Dang, J. L. Movilla, B. Martín-García, A. H. Khan, G. H. V. Bertrand, R. Brescia and I. Moreels, Chem. Mater., 2017, 29, 5671–5680 CrossRef CAS.
- A. Antanovich, A. W. Achtstein, A. Matsukovich, A. Prudnikau, P. Bhaskar, V. Gurin, M. Molinari and M. Artemyev, Nanoscale, 2017, 9, 18042 RSC.
- A. W. Achtstein, O. Marquardt, R. Scott, M. Ibrahim, T. Riedl, A. V. Prudnikau, A. Antanovich, N. Owschimikow, J. K. N. Lindner, M. Artemyev and U. Woggon, ACS Nano, 2018, 12, 9476–9483 CrossRef CAS PubMed.
- R. Scott, S. Kickhofel, O. Schoeps, A. Antanovich, A. Prudnikau, A. Chuvilin, U. Woggon, M. Artemyev and A. W. Achtstein, Phys. Chem. Chem. Phys., 2016, 18, 3197–3203 RSC.
- M. D. Tessier, B. Mahler, B. Nadal, H. Heuclin, S. Pedetti and B. Dubertret, Nano Lett., 2013, 13, 3321–3328 CrossRef CAS PubMed.
- A. Prudnikau, A. Chuvilin and M. Artemyev, J. Am. Chem. Soc., 2013, 135, 14476–14479 CrossRef CAS PubMed.
- F. Rajadell, J. I. Climente and J. Planelles, Phys. Rev. B, 2017, 96, 035307 CrossRef.
- M. G. Bawendi, M. L. Steigerwald and L. E. Brus, Annu. Rev. Phys. Chem., 1990, 41, 477–496 CrossRef CAS.
- A. L. Efros, M. Rosen, M. Kuno, M. Nirmal, D. J. Norris and M. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4843–4856 CrossRef CAS PubMed.
- A. Sitt, A. Salant, G. Menagen and U. Banin, Nano Lett., 2011, 11, 2054–2060 CrossRef CAS PubMed.
- H. Eshet, M. Grünwald and E. Rabani, Nano Lett., 2013, 13, 5880–5885 CrossRef CAS PubMed.
- S. Nakamura, M. Senoh, N. Iwasa and S. ichi Nagahama, Jpn. J. Appl. Phys., 1995, 34, L797 CrossRef CAS.
- S. T. Tan, X. W. Sun, H. V. Demir and S. P. DenBaars, IEEE Photonics J., 2012, 4, 613–619 Search PubMed.
- S. Nakamura, Rev. Mod. Phys., 2015, 87, 1139–1151 CrossRef CAS.
- H. Haug and S. W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, World Scientific, Singapore, 1994 Search PubMed.
- R. Zimmermann, E. Runge and V. Savona, Quantum Coherence Correlation and Decoherence in Semiconductor Nanostructures, 2003, pp. 89–165 Search PubMed.
- R. Zimmermann, F. Grosse and E. Runge, Pure Appl. Chem., 1997, 69, 1179–1186 CAS.
- S. Priyadarshi, A. M. Racu, K. Pierz, U. Siegner, M. Bieler, H. T. Duc, J. Förstner and T. Meier, Phys. Rev. Lett., 2010, 104, 217401 CrossRef CAS PubMed.
- R. Singh, M. Richter, G. Moody, M. E. Siemens, H. Li and S. T. Cundiff, Phys. Rev. B, 2017, 95, 235307 CrossRef.
- M. Richter, R. Singh, M. Siemens and S. T. Cundiff, Sci. Adv., 2018, 4, eaar7697 CrossRef PubMed.
- G. H. V. Bertrand, A. Polovitsyn, S. Christodoulou, A. H. Khan and I. Moreels, Chem. Commun., 2016, 52, 11975–11978 RSC.
- M. Richter, Phys. Rev. Mater., 2017, 1, 016001 CrossRef.
- A. W. Achtstein, R. Scott, S. Kickhöfel, S. T. Jagsch, S. Christodoulou, G. H. V. Bertrand, A. V. Prudnikau, A. Antanovich, M. Artemyev, I. Moreels, A. Schliwa and U. Woggon, Phys. Rev. Lett., 2016, 116, 116802 CrossRef PubMed.
- A. Naeem, F. Masia, S. Christodoulou, I. Moreels, P. Borri and W. Langbein, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121302 CrossRef.
- B. T. Diroll, W. Cho, I. Coropceanu, S. M. Harvey, A. Brumberg, N. Holtgrewe, S. A. Crooker, M. R. Wasielewski, V. B. Prakapenka, D. V. Talapin and R. D. Schaller, Nano Lett., 2018, 18, 6948–6953 CrossRef CAS PubMed.
- R. Zimmermann and E. Runge, Phys. Status Solidi A, 1997, 164, 511–516 CrossRef CAS.
- H. Haug and S. W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, World Scientific, Singapore, 2004 Search PubMed.
- O. Mayrock, H.-J. Wünsche, F. Henneberger, C. Riva, V. A. Schweigert and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 5582–5589 CrossRef CAS.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, V. F. Sapega, Y. G. Kusrayev, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, V. V. Belykh, M. V. Kochiev, N. N. Sibeldin, A. A. Golovatenko, A. V. Rodina, N. A. Gippius, A. Kuntzmann, Y. Jiang, M. Nasilowski, B. Dubertret and M. Bayer, Nanoscale, 2018, 10, 646–656 RSC.
- T. Takagahara, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4569–4584 CrossRef PubMed.
- R. Scott, A. V. Prudnikau, A. Antanovich, S. Christodoulou, T. Riedl, G. H. V. Bertrand, N. Owschimikow, J. K. N. Lindner, Z. Hens, I. Moreels, M. Artemyev, U. Woggon and A. W. Achtstein, Nanoscale, 2019, 11, 3958–3967 RSC.
- H. Carmichael, Statistical Methods in Quantum Optics 1 - Master Equation and Fokker-Planck Equations, Springer, Berlin Heidelberg New York, 1999 Search PubMed.
- H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems, Oxford University Press, Oxford, 2002 Search PubMed.
- S. Balay, S. Abhyankar, M. F. Adams, J. Brown, P. Brune, K. Buschelman, L. Dalcin, V. Eijkhout, W. D. Gropp, D. Kaushik, M. G. Knepley, L. C. McInnes, K. Rupp, B. F. Smith, S. Zampini and H. Zhang, PETSc Web page, 2015, http://www.mcs.anl.gov/petsc, http://www.mcs.anl.gov/petsc.
- S. Balay, S. Abhyankar, M. F. Adams, J. Brown, P. Brune, K. Buschelman, L. Dalcin, V. Eijkhout, W. D. Gropp, D. Kaushik, M. G. Knepley, L. C. McInnes, K. Rupp, B. F. Smith, S. Zampini and H. Zhang, PETSc Users Manual, Argonne National Laboratory Technical Report ANL-95/11 - Revision 3.6, 2015 Search PubMed.
- M. D. Tessier, C. Javaux, I. Maksimovic, V. Loriette and B. Dubertret, ACS Nano, 2012, 6, 6751–6758 CrossRef CAS PubMed.
- F. T. Rabouw, J. C. van der Bok, P. Spinicelli, B. Mahler, M. Nasilowski, S. Pedetti, B. Dubertret and D. Vanmaekelbergh, Nano Lett., 2016, 16, 2047–2053 CrossRef CAS PubMed.
- U. Bockelmann and T. Egeler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 15574–15577 CrossRef CAS.
- P. Guyot-Sionnest, M. Shim, C. Matranga and M. Hines, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, R2181–R2184 CrossRef CAS.
- D. J. Norris and M. G. Bawendi, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 16338–16346 CrossRef CAS PubMed.
- G. Rainò, I. Moreels, A. Hassinen, T. Stöferle, Z. Hens and R. F. Mahrt, Nano Lett., 2012, 12, 5224–5229 CrossRef PubMed.
- M. D. Tessier, L. Biadala, C. Bouet, S. Ithurria, B. Abecassis and B. Dubertret, ACS Nano, 2013, 7, 3332–3340 CrossRef CAS.
- A. Steinhoff, M. Florian, A. Singh, K. Tran, M. Kolarczik, S. Helmrich, A. W. Achtstein, U. Woggon, N. Owschimikow, F. Jahnke and X. Li, Nat. Phys., 2018, 14, 1199 Search PubMed.
- E. V. Shornikova, L. Biadala, D. R. Yakovlev, D. Feng, V. F. Sapega, N. Flipo, A. A. Golovatenko, M. A. Semina, A. V. Rodina, A. A. Mitioglu, M. V. Ballottin, P. C. M. Christianen, Y. G. Kusrayev, M. Nasilowski, B. Dubertret and M. Bayer, Nano Lett., 2018, 18, 373–380 CrossRef CAS PubMed.
- J. Feldmann, G. Peter, E. O. Göbel, P. Dawson, K. Moore, C. Foxon and R. J. Elliott, Phys. Rev. Lett., 1987, 59, 2337–2340 CrossRef CAS.
- S. A. Cherevkov, M. V. Artemyev, A. V. Prudnikau and A. V. Baranov, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 041303 CrossRef.
- D. O. Sigle, J. T. Hugall, S. Ithurria, B. Dubertret and J. J. Baumberg, Phys. Rev. Lett., 2014, 113, 087402 CrossRef.
- T. Takagahara, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 6552–6573 CrossRef CAS PubMed.
- G. D. Mahan, Many-Particle Physics, Kluwer Academic/Plenum Publishers, New York, 2000 Search PubMed.
- B. Krummheuer, V. M. Axt and T. Kuhn, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 195313 CrossRef.
- J. Förstner, C. Weber, J. Danckwerts and A. Knorr, Phys. Rev. Lett., 2003, 91, 127401 CrossRef PubMed.
- I. Waldmüller, J. Förstner, S.-C. Lee, A. Knorr, M. Woerner, K. Reimann, R. Kaindl, T. Elsaesser, R. Hey and K. Ploog, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 205307 CrossRef.
- P. Gartner, J. Seebeck and F. Jahnke, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115307 CrossRef.
- R. Rosati, D. E. Reiter and T. Kuhn, Phys. Rev. B, 2017, 95, 165302 CrossRef.
- The Merck Index - An Encyclopedia of Chemicals, 2006, https://www.rsc.org/Merck-Index Search PubMed.
- D. Katz, T. Wizansky, O. Millo, E. Rothenberg, T. Mokari and U. Banin, Phys. Rev. Lett., 2002, 89, 086801 CrossRef.
- R. Benchamekh, N. A. Gippius, J. Even, M. O. Nestoklon, J.-M. Jancu, S. Ithurria, B. Dubertret, A. L. Efros and P. Voisin, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035307 CrossRef.
- C. F. Cline, H. L. Dunegan and G. W. Henderson, J. Appl. Phys., 1967, 38, 1944–1948 CrossRef CAS.
- J. Li and L.-W. Wang, Appl. Phys. Lett., 2004, 85, 2929–2931 CrossRef CAS.
- Cadmium selenide (CdSe) optical properties, general, refractive index: Datasheet from Landolt-Börnstein - Group III Condensed Matter·Volume 41B: II-VI and I-VII Compounds; Semimagnetic Compounds, 1999, https://materials.springer.com/lb/docs/sm_lbs_978-3-540-31359-5_610.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details for the sample synthesis and characterization. See DOI: 10.1039/C9NR03161H |
| This journal is © The Royal Society of Chemistry 2019 |