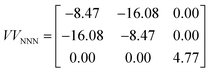Phonon confinement and spin-phonon coupling in tensile-strained ultrathin EuO films

Abstract

Reducing the material sizes to the nanometer length scale leads to drastic modifications of the propagating lattice excitations (phonons) and their interactions with electrons and magnons. In EuO, a promising material for spintronic applications in which a giant spin-phonon interaction is present, this might imply a reduction of the degree of spin polarization in thin films. Therefore, a comprehensive investigation of the lattice dynamics and spin-phonon interaction in EuO films is necessary for practical applications. We report a systematic lattice dynamics study of ultrathin EuO(001) films using nuclear inelastic scattering on the Mössbauer-active isotope ¹⁵¹Eu and first-principles theory. The films were epitaxially grown on YAlO₃(110), which induces a tensile strain of ca. 2%. By reducing the EuO layer thickness from 8 nm to a sub-monolayer coverage, the Eu-partial phonon density of states (PDOS) reveals a gradual enhancement of the number of low-energy phonon states and simultaneous broadening and suppression of the peaks. These deviations from bulk features lead to significant anomalies in the vibrational thermodynamic and elastic properties calculated from the PDOS. The experimental results, supported by first-principles theory, unveil a reduction of the strength of the spin-phonon interaction in the tensile-strained EuO by a factor of four compared to a strain-free lattice.

---

1 Introduction

Known as one of the rare ferromagnetic semiconductors and a model system for the Heisenberg ferromagnet (Curie temperature T_C = 69 K), EuO continues to attract the scientific attention since its discovery in the early 1960s.¹ A rich variety of physical phenomena, such as giant magneto-optic Kerr² and Faraday³ effects, a colossal magnetoresistance,⁴ a metal-to-insulator transition upon doping,^5,6 and an anomalous Hall effect,⁷ have been discovered in this material over the years. The large exchange splitting of 0.6 eV of its conduction band below T_C^8,9 implies a spin polarization of almost 100%.¹⁰ This fact, combined with the integration with Si,^11–13 made EuO an attractive material for spin filters in future Si-based spintronic devices.^14,15

Unlike its electronic and magnetic properties, the lattice dynamics of EuO has only scarcely been investigated. Anomalies in the early Raman and inelastic neutron scattering data obtained across the T_C along with a critical behavior of the thermal conductivity and sound velocity, properties mutually related to the lattice dynamics, indicated a strong interaction between spin waves and lattice vibrations in this material. The advent of the 3^rd generation synchrotron radiation sources combined with the elaborated growth protocol¹⁶ for obtaining strain-free, single crystalline EuO films with outstanding quality and phase purity made it possible to investigate comprehensively the lattice dynamics of this material by inelastic X-ray scattering¹⁷ and nuclear inelastic scattering.^18,19 The experimental results, supported by first-principles theory, uncovered a giant and highly anisotropic spin-phonon coupling induced by the spin dynamics slightly above and well below the T_C in bulk EuO.^20,21

Previous lattice dynamics studies of surfaces, thin films, interfaces, and multilayers revealed drastic modifications of their phonon density of states (PDOS) with respect to the bulk counterparts with the main features being an enhancement of the number of phonon states at low and high energy and suppression and shift of the peaks.^22–27 In EuO, such phonon anomalies, combined with the strong interaction between spins and lattice vibrations could potentially increase the probability for undesired spin flips thus reducing the degree of spin polarization along certain crystallographic directions. This fact, combined with the ongoing efforts for epitaxial strain manipulation of the Curie temperature in thin EuO films^28,29 makes lattice dynamics and spin-phonon interaction investigations in strained EuO films exhibiting thicknesses and configurations similar to those envisaged for tunnel junction applications indispensable.

In this paper we report a systematic lattice dynamics study of ultrathin epitaxial EuO films and buried layers with thicknesses in the range from 8.0 nm to 0.2 nm across the T_C. The derived Eu-partial PDOSs from nuclear inelastic scattering on the Mössbauer-active isotope ¹⁵¹Eu are compared to the results from first-principles theory. To investigate the impact of the tensile epitaxial strain on the lattice dynamics and spin-phonon coupling the films were grown on YAlO₃(110) exhibiting a lattice mismatch of about 2% with EuO(001).³⁰ The results unveil strong size effects that significantly alter the vibrational thermodynamic and elastic properties. The experimental data confirm the presence of spin-phonon interaction in the tensile-strained 8.0 nm thick EuO film being, however, reduced by a factor of four compared to a strain-free lattice.

2 Experimental details

Single-crystalline EuO(001) films with thicknesses of 8.0, 0.4, and 0.2 nm, hereinafter referred to as S1, S2 and S3, were epitaxially grown on YAlO₃(110) applying the protocol described by Ulbricht et al.³⁰ and investigated in situ (under ultrahigh vacuum) at 298 K and 130 K. A second set of EuO(001) films with thicknesses of 8.0, 4.0, and 2.0 nm, hereinafter referred to as S4, S5, and S6, were epitaxially grown on YAlO₃(110) and covered by a 5 nm thick Nb layer (deposited at room temperature) to protect the sensitive EuO from further oxidation, and investigated ex situ at 298 K and 30 K. The capping of the EuO layers was also used to mimic the spatially confined geometry of a tunnel junction.

All samples were prepared in the ultrahigh vacuum system³¹ located at the Nuclear Resonance beamline ID18 ³² of the ESRF-The European Synchrotron in Grenoble. Metallic Eu foil enriched to 97% in the Mössbauer-active isotope ¹⁵¹Eu, supplied by the Oak Ridge National Laboratory (USA), was sublimated from an effusion cell with a molybdenum crucible for producing a steady flux of Eu atoms at a rate of 8.0 Å min⁻¹. High-purity (99.9995%) molecular oxygen was supplied into the growth chamber via a leak valve. Prior to Eu deposition the YAlO₃(110) substrate was annealed at 500 K for 60 minutes followed by annealing at 900 K for 120 minutes in oxygen atmosphere to achieve a clean and smooth surface.

To ensure a complete distillation of the non-oxidized metallic Eu, the substrate was kept at 723 K during Eu deposition. The partial oxygen pressure is critical for achieving films with smooth surfaces. Our systematic reflection high-energy electron diffraction (RHEED) study, see Fig. 1 and 2, showed that for the chosen growth temperature an oxygen pressure of 2 × 10⁻⁹ mbar leads to a streaky pattern with low diffuse background. The rate and amount of the deposited Eu was controlled by a quartz crystal micro balance. In addition, the EuO layer thickness of sample S1 was controlled by X-ray reflectivity measurement and the Eu deposition times for samples S2–S6 were correspondingly adjusted.

Fig. 1 RHEED images obtained with 28 keV energy electrons of the substrate and indicated samples along the [110] (left column) and [100] (right column) azimuths of the EuO(001) surface.

Fig. 2 RHEED images obtained with 28 keV energy electrons of the substrate and indicated samples along the [110] (left column) and [100] (right column) azimuths of the EuO(001) surface.

Electron diffraction images of the clean YAlO₃(110) surface and samples S1–S3 and S4–S6 obtained along two azimuthal directions are depicted in Fig. 1 and 2, respectively. The bright diffraction streaks and relatively low background indicate the formation of epitaxial films with a smooth surface. The streaky patterns visible in Fig. 1 (bottom) confirm the two-dimensional surface morphology also of sample S3 consisting of EuO layer thickness that is just below one monolayer (0.26 nm).

The ¹⁵¹Eu-partial PDOS of all samples was determined from the energy dependence of the probability for nuclear inelastic absorption of X-rays with energy 21.5 keV with an energy resolution of 1.1 meV (full width at half maximum).³³ All samples were illuminated at a grazing angle of about 0.15 degree using a focused X-ray beam with dimensions: vertical × horizontal ≈ 10 μm × 100 μm. Samples S1–S3 were investigated in situ in the UHV system³¹ with a base pressure of 5 × 10⁻¹¹ mbar. The PDOS of samples S1 and S3 was obtained at 130 K, while that of sample S2 was derived from a measurement at 298 K. Samples S4–S6 were measured under vacuum (6 × 10⁻⁷ mbar) at 298 K and at 30 K in a helium-flow cryostat equipped with kapton foil windows for the X-ray beam. In all measurements the X-ray beam was oriented along the EuO[100] direction that revealed the giant spin-phonon interaction in bulk EuO.²⁰ The ¹⁵¹Eu-partial PDOS was obtained from the experimental data in a quasi-harmonic approximation using a formalism described elsewhere.³⁴

3 First-principles calculations

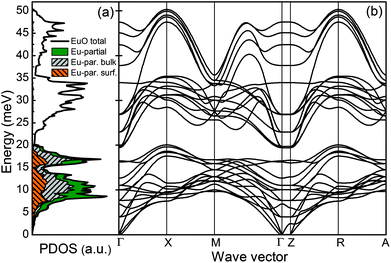
First-principles theory was applied to investigate the lattice dynamics of the EuO(001) surface. The computational model consisted of a five-atomic-layer-thick slab. This structure was fully optimized using the projector augmented-wave method³⁵ and the generalized-gradient approximation³⁶ within the VASP program.³⁷ The strong electron interactions in the 4f states were treated with the GGA+U approach (U = 8.3 eV, J = 0.77 eV). The summation over the reciprocal space was performed on a 4 × 4 × 2 grid. A ferromagnetic order of the spins of the Eu atoms was assumed in the calculations. The phonon dispersions were calculated using the direct method³⁸ implemented in the PHONON software.³⁹ The force constants and dynamical matrices were derived by displacing all non-equivalent atoms from their equilibrium positions and calculating the Hellmann–Feynman forces. The PDOS was obtained by random sampling the k points in the first Brillouin zone.

The calculated total and element-specific PDOS and phonon dispersions along the high-symmetry directions are plotted in Fig. 3(a) and (b). The Eu-partial PDOS dominates below 20 meV and above this energy mainly the O-partial PDOS with the cut-off energy at 50 meV is present. The phonon dispersions corresponding to oxygen vibrations are clearly separated from the europium phonon modes.

Fig. 3 Ab initio calculated lattice dynamics of the relaxed EuO(100) slab: (a) total, Eu-partial and layer-projected PDOS; (b) phonon dispersions along the indicated high symmetry directions in the Brillouin zone.

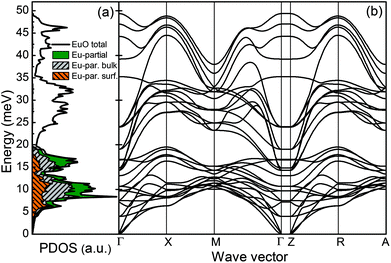
To study the effect of the epitaxial strain on the phonon dispersions and PDOS, calculations were performed using a lattice constant increased by 2% compared to the bulk value. The results are plotted in Fig. 4(a) and (b). The phonon dispersions corresponding to oxygen vibrations are shifted downwards, thus partly overlapping with the Eu modes. The Eu-partial PDOS is enhanced around 7 meV due to phonon softening at the X and R points. We observe also changes in the Eu phonon modes at higher energies and for other wave vectors. The lack of imaginary phonon modes demonstrates that both systems are dynamically stable.

Fig. 4 Ab initio calculated lattice dynamics of the strained EuO(100) slab: (a) total, Eu-partial and layer-projected PDOS; (b) phonon dispersions along the indicated high symmetry directions in the Brillouin zone.

4 Results and discussion

4.1 Lattice dynamics of EuO(001)/YAlO₃(110) films

The experimentally derived Eu-partial PDOS of samples S1–S3 at the indicated temperatures are plotted in Fig. 5(a). This figure demonstrates that the PDOS of sample S1 exhibits the main features of bulk EuO,²⁰ namely two peaks at 11 and 17 meV and a high energy cut-off around 22 meV. The solid/red line marks the calculated PDOS of a strain-free EuO crystal²⁰ convoluted with the damped harmonic oscillator (DHO) function⁴⁰ with a quality factor Q = 8. This function accounts remarkably well for the phonon lifetime broadening that arises from strain-relaxation induced distribution of interatomic distances.^24,41 The relatively low value of Q indicates a residual epitaxial strain in the EuO films on YAlO₃(110), which fully relaxes at a film thickness of about 38 nm.³⁰ In addition, Fig. 5(a) shows that the PDOS of S1 obtained at 298 K closely resembles the one derived at 130 K, which indicates a harmonic nature of the lattice vibrations in the strained EuO lattice.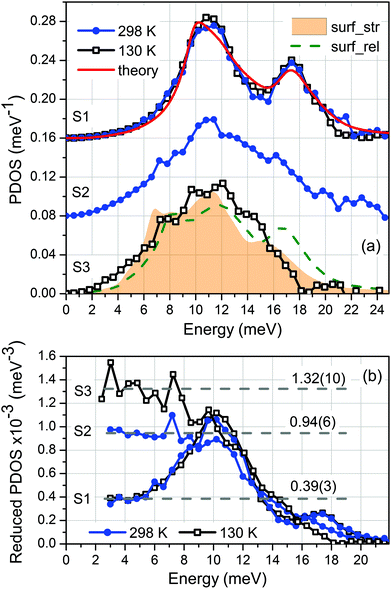

Fig. 5 Experimental results for (a) PDOS and (b) reduced PDOS (PDOS/E²) of samples S1–S3 obtained at the indicated temperatures. The curves in (a) are up-shifted by 0.08 meV⁻¹ for clarity. The solid line, dashed line, and shaded area denote the ab initio calculated Eu-partial PDOS of bulk EuO²⁰ and the xy-projected surface PDOS of the relaxed (surf_rel) and strained (surf_str) EuO slab, respectively, convoluted with the DHO function (Q = 8). The Debye levels in the low-energy limit of PDOS/E² are given in (b).

The reduction of the EuO film thickness (sample S2) leads to well-pronounced deviations of the Eu-partial PDOS from the thick film. The number of phonon states at low energy increases significantly, the peak at 11 meV becomes broader, while the one at 17 meV diminishes on account of the phonon states around 15 meV. Further reduction of the film thickness to a sub-monolayer coverage (sample S3) results in even more pronounced anomalies in the PDOS. These are further enhancement of the low-energy phonon states, broadening of the peak at 11 meV and a high-energy cut-off at 18 meV.

The calculated PDOSs of the relaxed and strained EuO(100) surface convoluted with the DHO function with Q = 8 are plotted in Fig. 5(a) with dashed/green line and shaded area, respectively. A comparison between the calculated PDOS reveals that the tensile epitaxial strain leads to an overall shift of the spectral features to lower energies by about 1 meV and a redistribution of the number of phonon states. Furthermore, this plot demonstrates that the overall shape of the PDOS of sample S3 and the number of phonon states at 7 meV, around 11 and 16 meV are to a large extent reproduced by the PDOS of the native tensile-strained EuO surface. On the other hand, the number of phonon states up to 5 meV and between 12 and 15 meV is underestimated by the theory.

Combined experimental and theoretical studies of strain-free metal/semiconductor heterostructures⁴² and metallic multilayers⁴³ demonstrated that the force constants of the atoms located at the interface are drastically reduced compared to the bulk values. This gives rise to an entirely different PDOS of the interface layers from that of a bulk material. In particular, up to a two-fold enhancement of the number of low-energy states along the interface was measured and theoretically confirmed for the strain-free Fe₃Si/GaAs interface.⁴² Due to the grazing-incidence scattering geometry used in our experiment we determine the in-plane projected PDOS. Therefore, the observed discrepancy between experiment and theory up to 5 meV and between 12 and 15 meV most likely originates from the EuO/YAlO₃ interface-specific PDOS. Phonon calculations for a realistic model of this interface, however, could not be performed due to the low symmetry of the system and the large number of atoms, which have to be included in the supercell. On the other hand, a simple model of a single EuO layer on the YAlO₃ substrate turned out to be dynamically unstable with a high number of imaginary (soft) modes.

Fig. 5(b) presents the reduced PDOS (PDOS/E²) of samples S1–S3 and demonstrates the significant enhancement of the number of low-energy phonon states as the EuO film thickness is reduced. While for S2 the Debye level in the low-energy limit increases by a factor of 2.4 relative to S1, in sample S3 this factor approaches 3.4. As discussed below, this has important implications on the vibrational thermodynamics of ultrathin EuO films.

4.2 Lattice dynamics of Nb/EuO(001)/YAlO₃(110) films

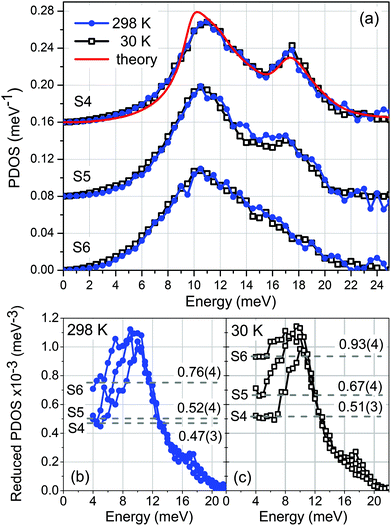
Next we consider EuO(001) films grown on YAlO₃(110) and covered by a 5 nm thick protective Nb layer. Fig. 6(a) shows the Eu-partial PDOS of samples S4–S6 obtained from the experiment performed at 298 K and 30 K. Similarly to the PDOS of S1, the phonon spectrum of S4 exhibits the main features of bulk EuO,²⁰ namely two peaks at 11 and 17 meV and a high energy cut-off around 22 meV. The ab initio calculated PDOS of a strain-free EuO crystal convoluted with the DHO function with Q = 8 (solid line) is fully consistent with the experimental data.

Fig. 6 Experimental results for (a) PDOS and (b)–(c) reduced PDOS (PDOS/E²) of samples S4–S6 obtained at the indicated temperatures. The curves in (a) are up-shifted by 0.08 meV⁻¹ for clarity. The solid line denotes the ab initio calculated Eu-partial PDOS of bulk EuO convoluted with the DHO function (Q = 8). The Debye levels in the low-energy limit of PDOS/E² at the indicated temperatures are given in (b) and (c).

The PDOS of S5 exhibits an enhancement of the low-energy states and a broadening of the peaks that is particularly notable for the peak at 17 meV, Fig. 6(a). By further reduction of the EuO film thickness these anomalies become more pronounced. The peak at 10.5 meV is significantly broader in the PDOS of S6, while the high-energy peak diminishes.

A combined experimental and theoretical lattice dynamics study⁴² of Fe₃Si/GaAs heterostructures disclosed three main sources of vibrational anomalies in thin buried epitaxial layers. The phonon confinement leads to a significant broadening of all peaks, which can satisfactorily be described by the DHO function. The second effect, which is the main source of vibrational anomalies at low energy is the interface-specific PDOS, discussed in the previous section. It arises even at a strain-free interface⁴² due to the reduced force constants of the interface atoms induced by the differences in the first and second coordination spheres compared to the bulk atoms. The third source of deviations of the PDOS from that of the bulk material is the Nb/EuO interface. This interface is characterized with a certain degree of disorder that leads to both low- and high-energy phonon states.⁴⁴ The combination of these three factors leads to the phonon anomalies in samples S5 and S6.

The reduced PDOS (PDOS/E²) of samples S4–S6, plotted in Fig. 6(b) and (c), quantifies the low-energy enhancement of the PDOS derived at 298 K and 30 K, respectively. In S5 the Debye level in the low-energy limit increases only by a factor of 1.1 at 298 K and 1.3 at 30 K relative to S4. In S6 these factors are, respectively, 1.6 and 1.8. The observed difference between the Debye levels at 298 K and 30 K can be attributed to a spin-phonon interaction, as discussed below.

4.3 Spin-phonon coupling in Nb/EuO(001)/YAlO₃(110) films

Employing inelastic X-ray scattering and nuclear inelastic scattering, unusually strong and highly anisotropic spin-phonon coupling has been discovered in a strain-free 100 nm thick EuO(001) film deposited on YSZ(001).^20,21 This effect manifests itself in a five-fold increase of the line-width of the transverse acoustic phonon branch along the Γ–X direction of the Brillouin zone in the vicinity and below the T_C. Although the effect on the PDOS is less pronounced due to the momentum averaging, a broadening reaching 17% of the acoustic peak at 11 meV was measured along the EuO[100] direction at 30 K compared to the room-temperature PDOS.

Fig. 6(a) reveals that the Eu-partial PDOS of samples S4–S6 obtained along EuO[100] at 30 K are seemingly identical to the ones derived at 298 K. In order to estimate the influence of the tensile epitaxial strain, we compare in Fig. 7(a) the PDOS of S4 with that of the 100 nm thick strain-free EuO(001) film grown on YSZ(001), referred to as bulk.²⁰ This comparison demonstrates that the peaks of the PDOS of S4 are broader from those of the bulk sample already at 298 K. To quantify the widths of the peaks, the phonon spectra were approximated by a combination of two Voigt profiles depicted with dashed lines in Fig. 7(a). Fig. 7(b) demonstrates that at 298 K the FWHM of the peaks at 11 and 17 meV in the PDOS of S4 exceed by 32% and 49% the FWHM of the respective peaks in the PDOS of bulk EuO. This is a consequence of the phonon confinement and tensile-strain relaxation in the crystal lattice, which leads to a distribution of interatomic distances along the film thickness. Furthermore, Fig. 7(b) reveals that the FWHM of the peak at 11 meV in the PDOS of S4 increases by ca. 4% upon cooling implying a reduction of the spin-phonon coupling strength by about a factor of 4 compared to a strain-free EuO. The FWHM of the second peak decreases upon cooling in a similar fashion in both samples, which is a typical temperature dependence of the phonon widths resulting from an anharmonic potential.⁴⁵ Although similar analysis (not shown) of the PDOS of S5 and S6 do not show anomalous behavior of the FWHM values upon cooling, the enhanced Debye levels at 30 K compared to the values at 298 K evident in Fig. 6(b) and (c) might originate from spin-phonon interaction in these samples.

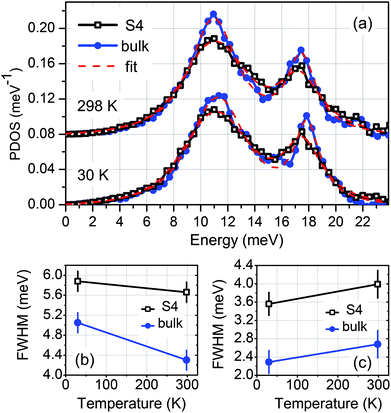Fig. 7 (a) A comparison of the PDOS of sample S4 with that of bulk EuO²⁰ at the indicated temperatures. The spectra are up-shifted by 0.08 meV⁻¹ for clarity. The red/dashed line stands for the fit of the experimental data with a combination of two Voigt profiles. The FWHM as a function of temperature for the peaks at 11 and 17 meV are plotted in (b) and (c), respectively.

Furthermore, we analyse the ab initio calculated force constants between the nearest-neighbor (NN) and next-nearest-neighbor (NNN) in a tensile-strained by 2% lattice of bulk EuO, which play a decisive role for the spin-phonon coupling process.⁴⁶ The force constants between the NN atoms along EuO[010] (between Eu and O atoms) are given by the matrix (in units N m⁻¹):

while those between the NNN atoms along EuO[110] (between two Eu atoms) are:

As demonstrated for the relaxed EuO,²⁰ strong and anisotropic spin-phonon coupling occurs if the values of VV_NNN are comparable to those of VV_NN. Although the given matrix elements demonstrate that this is as well the case in the strained EuO, the values are reduced by about 8% from the relaxed EuO (see ESI to ref.²⁰) due to the increased interatomic distances and the reduced exchange coupling. These effects imply an overall reduction of the spin-phonon coupling strength in the tensile-strained EuO, which is confirmed experimentally (Fig. 7(b)).

4.4 Vibrational thermodynamic and elastic properties

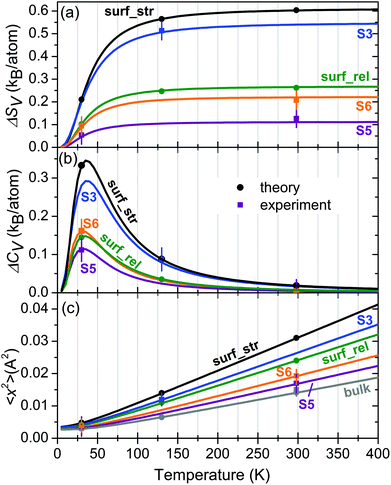
Using the formalism described elsewhere⁴⁷ we calculate and discuss important vibrational thermodynamic and elastic properties of the investigated samples. Table 1 summarizes the experimental and theoretical values of the vibrational entropy S_V, lattice specific heat C_V at constant volume, mean square atomic displacement 〈x²〉, and mean force constant F calculated from the Eu-partial PDOS of samples S1–S6, bulk EuO and the relaxed and strained EuO surface at the indicated temperature T. Furthermore, the temperature evolution of these properties can be calculated from the PDOS in harmonic approximation. Fig. 8 displays the temperature dependence of the excess of vibrational entropy ΔS_V (Fig. 8(a)) and specific heat ΔC_V (Fig. 8(b)) with respect to the bulk EuO, as well as the mean square displacement 〈x²〉 of the Eu atoms (Fig. 8(c)). These plots reveal the drastic deviations of the thermoelastic properties of the ultrathin EuO films from the corresponding bulk values.

Fig. 8 Temperature evolutions of: (a) excess vibrational entropy ΔS_V, (b) excess specific heat ΔC_V, and (c) mean square displacement 〈x²〉 of samples S3, S5 and S6 calculated from the experimental PDOS, as well as of the relaxed (surf_{_}rel) and strained (surf_str) EuO(100) surface and of bulk EuO obtained from the theoretical PDOS. The available experimental and theoretical values are also plotted.

Table 1 Eu-partial and EuO[100]-projected experimental/theoretical values of the vibrational entropy S_V, lattice specific heat C_V, mean square displacement 〈x²〉, and mean force constant F of the investigated samples at the given temperature T. The bulk values are obtained from the PDOS of a strain-free 100 nm thick EuO(001) film deposited on YSZ(001).²⁰ The values of the relaxed and strained EuO surface are calculated from the xy-projected PDOS plotted in Fig. 3(a) and 4(a), respectively

Sample	T (K)	S V (kB per atom)	C V (kB per atom)	〈x^2〉 (Å^2)	F (N m^−1)
S1	298	5.22(4)/5.283	2.93(3)/2.935	0.015(2)/0.0141	109(8)/101
	130	2.93(4)/2.927	2.68(3)/2.682	0.007(2)/0.0065	103(8)/101
S2	298	5.44(4)/—	2.94(3)/—	0.022(2)/—	102(8)/—
S3	130	3.44(4)/—	2.77(3)/—	0.012(2)/—	74(8)/—
S4	298	5.23(4)/5.283	2.93(3)/2.935	0.016(2)/0.0141	109(8)/101
	30	0.26(4)/0.236	0.67(3)/0.686	0.003(2)/0.0030	110(8)/101
S5	298	5.42(4)/—	2.94(3)/—	0.017(2)/—	93(8)/—
	30	0.33(4)/—	0.80(3)/—	0.004(2)/—	93(8)/—
S6	298	5.50(4)/—	2.94(3)/—	0.019(2)/—	92(8)/—
	30	0.37(4)/—	0.85(3)/—	0.004(2)/—	90(8)/—
Bulk	298	5.24(4)/5.283	2.93(3)/2.935	0.015(2)/0.0141	107(8)/101
	30	0.25(4)/0.236	0.67(3)/0.686	0.003(2)/0.0030	106(8)/101
Surface relaxed	298	—/5.546	—/2.943	—/0.0241	—/89
	130	—/3.175	—/2.718	—/0.0111	—/89
	30	—/0.338	—/0.833	—/0.0041	—/89
Surface strained	298	—/5.887	—/2.954	—/0.0311	—/71
	130	—/3.493	—/2.771	—/0.0140	—/71
	30	—/0.447	—/1.021	—/0.0048	—/71

---

At 298 K, S3 exhibits a deviation of S_V from the bulk value of ΔS_V = 0.54 ± 0.04k_B per atom at 298 K. Our first-principles calculations demonstrate that the effect is even stronger for the native, tensile-strained EuO surface, reaching a value of 0.6k_B per atom at 298 K, as depicted in Fig. 8(a). These values exceed the largest reported deviations of 0.43k_B per atom obtained for disordered interfaces in bulk nanocrystalline materials,⁴⁸ 0.50k_B per atom for isolated Fe nanoparticles,⁴⁹ and 0.52k_B per atom for the native Fe(110) surface.²⁵ Furthermore, Fig. 8(a) demonstrates that for the tensile-strained EuO surface ΔS_V exceeds the value of the relaxed EuO surface by more than a factor of two. The corresponding values at 298 K for S5 and S6 are ΔS_V = 0.11k_B per atom and ΔS_V = 0.22k_B per atom, respectively.

Fig. 8(b) and Table 1 show that the largest excess lattice specific heat ΔC_V = 0.34k_B per atom is observed at 36 K for the strained EuO surface, corresponding to an enhancement of 37% relative to the bulk EuO. In samples S3, S5 and S6 the values are 0.29k_B per atom, 0.11k_B per atom and 0.16k_B per atom, respectively, implying deviations of 31%, 12% and 17% from the bulk value at this temperature. At room temperature these deviations amount to a fraction of a percent (see Table 1).

Fig. 8(c) and Table 1 demonstrate that at 298 K the mean square displacement 〈x²〉 of the Eu atoms is enhanced relative to the bulk value by factors of 2.2 and 1.7 at the strained and relaxed EuO surface, respectively, whereas for samples S3, S5, and S6 these factors are 1.8, 1.1 and 1.3, accordingly. They reflect the drastically augmented number of low-energy phonon states and exceed the largest reported deviations of this quantity in ultrathin Fe films on W(110) (factor of 1.5)²⁴ and isolated Fe nanoparticles (factor of 1.6).⁴⁹

The temperature independent, within the harmonic approximation, mean force constants F calculated from the PDOS reflect the lattice softening of the investigated samples and the EuO surface (see Table 1). While the largest deviation of F from the bulk value reaches 30% for the strained surface layer, which is close to that of S3 (27%), in S5 and S6 it is 8% and 10%, respectively.

5 Conclusions

Employing nuclear inelastic scattering on the Mössbauer-active isotope ¹⁵¹Eu and first-principles theory we performed a systematic lattice dynamics study of ultrathin epitaxial EuO(001) films on YAlO₃(110). This substrate induces about 2% lattice expansion of the EuO films. A set of samples with thicknesses of 8.0, 0.4 and 0.2 nm were prepared and studied in situ at 298 K and 130 K. A second set of samples with thicknesses of 8.0, 4.0 and 2.0 nm were covered by a protective Nb layer and investigated ex situ at 298 K and 30 K. The reduction of the film thickness leads to drastic deviations of the Eu-partial PDOS from the bulk crystal.

The PDOS of the uncovered ultrathin EuO(001) films is characterized by a significant enhancement of the number of low-energy states, broadening of the peak at 11 meV and an overall suppression and shift of the peak at 17 meV to lower energy. The main spectral features of the sample with the lowest EuO coverage (just below a monolayer) are satisfactory reproduced by the ab initio calculated PDOS of the native EuO surface assuming 2% lattice expansion. The PDOS of the Nb-covered EuO films is characterized by overall broadening of the phonon peaks, enhancement of the low-energy phonon states and suppression of the high-energy peak. These anomalies originate from phonon confinement in the ultrathin EuO films and the interface-specific PDOS that arise from both EuO/YAlO₃ and Nb/EuO interfaces. The tensile epitaxial strain induces an additional broadening of the phonon peaks compared to a strain-free lattice. Consequently, the vibrational thermodynamic and elastic properties of the investigated samples drastically deviate from those of the strain-free EuO crystal.

Analysis of the PDOSs obtained at 298 K and 30 K unveil a small increase in the FWHM of the peak at 11 meV of the strained 8 nm-thick EuO film upon cooling. This indicates a spin-phonon interaction being, however, reduced by about a factor of 4 compared to a strain-free crystal. This effect is attributed to the reduced mean force constants between the nearest-neighbors and next-nearest-neighbors in a tensile-strained lattice, which reduces the exchange coupling strength compared to a strain-free crystal.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We thank Ilya Sergeev (DESY) for sharing his software for the calculation of temperature dependence of thermodynamic and elastic properties from the phonon density of states. We acknowledge ESRF-The European Synchrotron for provision of synchrotron radiation facilities, the National Isotope Development Center at Oak Ridge National Lab, which is sponsored by the U.S. DOE Basic Energy Sciences, for providing the ¹⁵¹Eu source material, and the Excellence Initiative for the financial support of the UHV-Analysis Lab via the project KIT-Nanolab@ANKA. S. S. acknowledges the financial support by the Helmholtz Association (VH-NG-625) and BMBF (05K16VK4). A. M. O. kindly acknowledges support by Narodowe Centrum Nauki (NCN) under Project No. 2016/23/B/ST3/00839 and the Alexander von Humboldt Fellowship (Humboldt-Forschungspreis). P. P. acknowledges support by Narodowe Centrum Nauki (NCN, National Science Centre) under Project No. 2017/25/B/ST3/02586 and the access to ESRF financed by the Polish Ministry of Science and High Education – decision number: DIR/WK/2016/19.

References

1. B. T. Matthias, R. M. Bozorth and J. H. V. Vleck, Phys. Rev. Lett., 1961, 7, 160–163.
2. J. H. Greiner and G. J. Fan, Appl. Phys. Lett., 1966, 9, 27–29.
3. K. Y. Ahn and M. W. Shafer, J. Appl. Phys., 1970, 41, 1260–1262.
4. M. R. Oliver, J. O. Dimmock, A. L. McWhorter and T. B. Reed, Phys. Rev. B: Solid State, 1972, 5, 1078–1098.
5. G. Petrich, S. von Molnár and T. Penney, Phys. Rev. Lett., 1971, 26, 885–888.
6. M. W. Shafer, J. B. Torrance and T. Penney, J. Phys. Chem. Solids, 1972, 33, 2251–2266.
7. T. Yamasaki, K. Ueno, A. Tsukazaki, T. Fukumura and M. Kawasaki, Appl. Phys. Lett., 2011, 98, 082116.
8. W. Nolting and A. M. Oleś, Phys. Phys. B: Condens. Matter Mater. Phys., 1980, 22, 6184–6195 ; 1982, 23, 4122–4128.
9. P. G. Steeneken, L. H. Tjeng, I. Elfimov, G. A. Sawatzky, G. Ghiringhelli, N. B. Brookes and D.-J. Huang, Phys. Rev. Lett., 2002, 88, 047201.
10. T. S. Santos, J. S. Moodera, K. V. Raman, E. Negusse, J. Holroyd, J. Dvorak, M. Liberati, Y. U. Idzerda and E. Arenholz, Phys. Rev. Lett., 2008, 101, 147201.
11. A. Schmehl, V. Vaithyanathan, A. Herrnberger, S. Thiel, C. Richter, M. Liberati, T. Heeg, M. Röckerath, L. F. Kourkoutis, S. Mühlbauer, P. Böni, D. A. Muller, Y. Barash, J. Schubert, Y. Idzerda, J. Mannhart and D. G. Schlom, Nat. Mater., 2007, 6, 882–887.
12. R. P. Panguluri, T. S. Santos, E. Negusse, J. Dvorak, Y. Idzerda, J. S. Moodera and B. Nadgorny, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125307.
13. C. Caspers, M. Müller, A. X. Gray, A. M. Kaiser, A. Gloskovskii, C. S. Fadley, W. Drube and C. M. Schneider, Phys. Status Solidi RRL, 2011, 5, 441–443.
14. C. Caspers, A. Gloskovskii, M. Gorgoi, C. Besson, M. Luysberg, K. Z. Rushchanskii, M. Lezaić, C. S. Fadley, W. Drube and M. Müller, Sci. Rep., 2016, 6, 22912.
15. L. L. Lev, D. V. Averyanov, A. M. Tokmachev, F. Bisti, V. A. Rogalev, V. N. Strocov and V. G. Storchak, J. Mater. Chem. C, 2017, 5, 192–200.
16. R. Sutarto, S. G. Altendorf, B. Coloru, M. M. Sala, T. Haupricht, C. F. Chang, Z. Hu, C. Schüßler-Langeheine, N. Hollmann, H. Kierspel, H. H. Hsieh, H.-J. Lin, C. T. Chen and L. H. Tjeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 205318.
17. Light Scattering in Solid IX, ed. M. Cardona and R. Merlin, Springer, Berlin, 2007.
18. M. Seto, Y. Yoda, S. Kikuta, X. W. Zhang and M. Ando, Phys. Rev. Lett., 1995, 74, 3828–3831.
19. W. Sturhahn, T. S. Toellner, E. E. Alp, X. Zhang, M. Ando, Y. Yoda, S. Kikuta, M. Seto, C. W. Kimball and B. Dabrowski, Phys. Rev. Lett., 1995, 74, 3832–3835.
20. R. Pradip, P. Piekarz, A. Bosak, D. G. Merkel, O. Waller, A. Seiler, A. I. Chumakov, R. Rüffer, A. M. Oleś, M. Krisch, T. Baumbach and S. Stankov, Phys. Rev. Lett., 2016, 116, 185501.
21. R. Pradip, P. Piekarz, A. Bosak, D. G. Merkel, O. Waller, A. Seiler, A. I. Chumakov, R. Rüffer, A. M. Oleś, M. Krisch, T. Baumbach and S. Stankov, Phys. Rev. Lett., 2017, 119, 079903.
22. R. Röhlsberger, W. Sturhahn, T. S. Toellner, K. W. Quast, P. Hession, M. Hu, J. Sutter and E. E. Alp, J. Appl. Phys., 1999, 86, 584–587.
23. T. Ruckert, W. Keune, W. Sturhahn, M. Y. Hu, J. P. Sutter, T. S. Toellner and E. E. Alp, Hyperfine Interact., 2000, 126, 363–366.
24. S. Stankov, R. Röhlsberger, T. Slezak, M. Sladecek, B. Sepiol, G. Vogl, A. I. Chumakov, R. Rüffer, N. Spiridis, J. Lazewski, K. Parlinski and J. Korecki, Phys. Rev. Lett., 2007, 99, 185501.
25. T. Slezak, J. Lazewski, S. Stankov, K. Parlinski, R. Reitinger, M. Rennhofer, R. Rüffer, B. Sepiol, M. Slezak, N. Spiridis, M. Zajac, A. I. Chumakov and J. Korecki, Phys. Rev. Lett., 2007, 99, 066103.
26. B. R. Cuenya, W. Keune, R. Peters, E. Schuster, B. Sahoo, U. von Hörsten, W. Sturhahn, J. Zhao, T. S. Toellner, E. E. Alp and S. D. Bader, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 165410.
27. N. Spiridis, M. Zajac, P. Piekarz, A. I. Chumakov, K. Freindl, J. Goniakowski, A. Koziol-Rachwal, K. Parlinski, M. Slezak, T. Slezak, U. D. Wdowik, D. Wilgocka-Slezak and J. Korecki, Phys. Rev. Lett., 2015, 115, 186102.
28. N. J. C. Ingle and I. S. Elfimov, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 121202.
29. A. Melville, T. Mairoser, A. Schmehl, T. Birol, T. Heeg, B. Holländer, J. Schubert, C. J. Fennie and D. G. Schlom, Appl. Phys. Lett., 2013, 102, 062404.
30. R. W. Ulbricht, A. Schmehl, T. Heeg, J. Schubert and D. G. Schlom, Appl. Phys. Lett., 2008, 93, 102105.
31. S. Stankov, R. Rüffer, M. Sladecek, M. Rennhofer, B. Sepiol, G. Vogl, N. Spiridis, T. Slezak and J. Korecki, Rev. Sci. Instrum., 2008, 79, 045108.
32. R. Rüffer and A. I. Chumakov, Hyperfine Interact., 1996, 97, 589–604.
33. O. Leupold, J. Pollmann, E. Gerdau, H. D. Rüter, G. Faigel, M. Tegze, G. Bortel, R. Rüffer, A. I. Chumakov and A. Q. R. Baron, Europhys. Lett., 1996, 35, 671–676.
34. V. G. Kohn and A. I. Chumakov, Hyperfine Interact., 2000, 125, 205–221.
35. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
36. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1994, 77, 3865–3868.
37. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
38. K. Parlinski, Z. Q. Li and Y. Kawazoe, Phys. Rev. Lett., 1997, 78, 4063–4066.
39. K. Parlinski, Software Phonon, Cracow, 2011.
40. B. Fåk and B. Dorner, Institute Laue Langevin Technical Report No. 92FA008S, 1992 (unpublished).
41. A. Seiler, P. Piekarz, S. Ibrahimkutty, D. Merkel, O. Waller, R. Pradip, A. Chumakov, R. Rüffer, T. Baumbach, K. Parlinski, M. Fiederle and S. Stankov, Phys. Rev. Lett., 2016, 117, 276101.
42. J. Kalt, M. Sternik, I. Sergueev, J. Herfort, I. Sergueev, B. Jenichen, H.-C. Wille, O. Sikora, P. Piekarz, K. Parlinski, T. Baumbach and S. Stankov, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 121409.
43. W. Keune, S. Hong, M. Y. Hu, J. Zhao, T. S. Toellner, E. E. Alp, W. Sturhahn, T. S. Rahman and B. R. Cuenya, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 98, 024308.
44. S. Stankov, Y. Z. Yue, M. Miglierini, B. Sepiol, I. Sergueev, A. I. Chumakov, L. Hu, P. Svec and R. Rüffer, Phys. Rev. Lett., 2008, 100, 235503.
45. The value of the FWHM at 30 K plotted in Fig. 4(c) of ref. 20 is not correct. The correct value is plotted in Fig. 7(c).
46. T. M. Cheng and L. Li, J. Magn. Magn. Mater., 2008, 320, 1–7.
47. M. Y. Hu, W. Sturhahn, T. S. Toellner, P. D. Mannheim, D. E. Brown, J. Zhao and E. E. Alp, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 094304.
48. S. Stankov, M. Miglierini, A. I. Chumakov, I. Sergueev, Y. Z. Yue, B. Sepiol, P. Svec, L. Hu and R. Rüffer, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 82, 144301.
49. B. R. Cuenya, L. K. Ono, J. R. Croy, K. Paredis, A. Kara, H. Heinrich, J. Zhao, E. E. Alp, A. T. DelaRiva, A. Datye and W. Keune, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 165406.

---

Footnote

† Present address: Department of Engineering Physics, École Polytechnique de Montréal, Montréal-6079, Québec H3C 3A7, Canada.

---