Microtubule self-healing and defect creation investigated by in-line force measurements during high-speed atomic force microscopy imaging†
Christian
Ganser
 *a and
Takayuki
Uchihashi
*ab
*a and
Takayuki
Uchihashi
*ab
aDepartment of Physics, Nagoya University, Chikusa-ku, Furo-cho, 464-8602 Nagoya, Aichi, Japan. E-mail: cganser@d.phys.nagoya-u.ac.jp; uchihast@d.phys.nagoya-u.ac.jp
bExploratory Research Center on Life and Living Systems, Higashiyama, Myodaiji, 444-8787 Okazaki, Aichi, Japan
First published on 19th November 2018
Abstract
Microtubules are biopolymers composed of tubulin and play diverse roles in a wide variety of biological processes such as cell division, migration and intracellular transport in eukaryotic cells. To perform their functions, microtubules are mechanically stressed and, thereby, susceptible to structural defects. Local variations in mechanical properties caused by these defects modulate their biological functions, including binding and transportation of microtubule-associated proteins. Therefore, assessing the local mechanical properties of microtubules and analyzing their dynamic response to mechanical stimuli provide insight into fundamental processes. It is, however, not trivial to control defect formation, gather mechanical information at the same time, and subsequently image the result at a high temporal resolution at the molecular level with minimal delay. In this work, we describe the so-called in-line force curve mode based on high-speed atomic force microscopy. This method is directly applied to create defects in microtubules at the level of tubulin dimers and monitor the following dynamic processes around the defects. Furthermore, force curves obtained during defect formation provide quantitative mechanical information to estimate the bonding energy between tubulin dimers.
Introduction
Microtubules (MTs), prominently found in eukaryotic cells, are self-assembled hollow biopolymer tubes with tubulin dimers as the repeating unit.1,2 The dimers consist of one α-tubulin and one β-tubulin and form a linear chain within an MT, called the protofilament. A typical MT consists of 13 protofilaments. The primary functions of MTs include the structural reinforcement of cilia and flagella, organizing the cell interior as a part of the cytoskeleton and acting as transport pathways for the motor proteins such as kinesin3,4 and dynein.5 In all cases, it is important to resist mechanical damage and minimize defects which soften the MTs6 or hinder the transport of cargo by motor proteins.7–9 Another study suggests that MT breaking is a necessary mechanism to promote wound healing.10 The mechanical properties of MTs are commonly explored theoretically11–13 and experimentally.14–17 Molecular dynamics simulations are often performed in theoretical studies of MT mechanics.12,18 Experiments to study MTs as a whole employ optical tweezers14 to bend the MTs, while a different approach is to analyze thermal fluctuations of MTs.15,16In order to gain information of MT mechanics on the level of single tubulin dimers, a more localized approach is desirable. Such local information can be provided by atomic force microscopy (AFM). The conventional AFM has already proven to be a useful tool for the manipulation of biological samples,19 including membrane proteins.20 With this method, the molecular defects in hexagonally packed bacterial layers could be created by unzipping the protein complex.21 The imaging of MTs was shown to be possible both in air22 and in buffer solution23 using tapping mode. Mechanical properties could also be extracted by deforming an MT by pushing it with the AFM tip and using the cantilever as a force sensor.24 Such studies revealed that the elastic properties of MTs are affected by the stabilizing agents, taxol25 and guanylyl-(α,β)-methylene-diphosphonate (GMPCPP).26 Both the agents reduce MTs’ stiffness.27,28 Furthermore, the finite element simulations of a temperature dependence of MTs’ elastic response during indentation and bending of suspended MTs could also be investigated by AFM.29,30 The observations of the response of MTs during indentation revealed the creation of defects during force application.24,31 Spontaneous healing of defects in MTs was observed within minutes after the damage occurred.24 These conventional AFM studies, however, suffer from a low imaging rate. The healing of a defect, for example, was determined to happen within 4 min and gives no information about the mechanism.24 A faster approach to investigate self-healing of MTs is total internal reflection fluorescence (TIRF) microscopy with an imaging rate of about 7 frames per second,6 but it lacks the spatial resolution to resolve the local structures. Furthermore, the latter study investigated self-healing of MTs with externally provided tubulin,6 whereas the former finds this mechanism even without tubulin in the surrounding buffer solution.24
Another topic that is difficult to study is bond energies between tubulin dimers in MTs. The available investigations are either of a purely theoretical nature32 or were performed by comparing the results of simulations to experimental results.33 Bond energies between tubulin dimers have been estimated by Monte Carlo simulations of the MTs’ dynamic instability as −18.5 kBT to −27.8 kBT for the longitudinal bonds. Lateral bond energies are estimated as −3.2 kBT to −5.7 kBT.33 Molecular dynamics simulations using a hard sphere indenting a microtubule revealed that the longitudinal and lateral bond energies are 25.1 kBT and 11.6 kBT, respectively.32 A direct experimental determination of bond energies and verification of the theoretical studies, however, are still lacking.
In this work, we developed an in-line force curve method based on high-speed AFM (HS-AFM) with a high temporal resolution. This method allows the application of localized forces at a specific site on the sample and the imaging of the following structural dynamics in real time. We applied this technique to create local structural defects on MTs and observed the self-healing events with a temporal resolution of 500 ms. Furthermore, the tubulin bond energies in MTs were determined quantitatively using the in-line force measurements.
Results and discussion
In-line force measurements
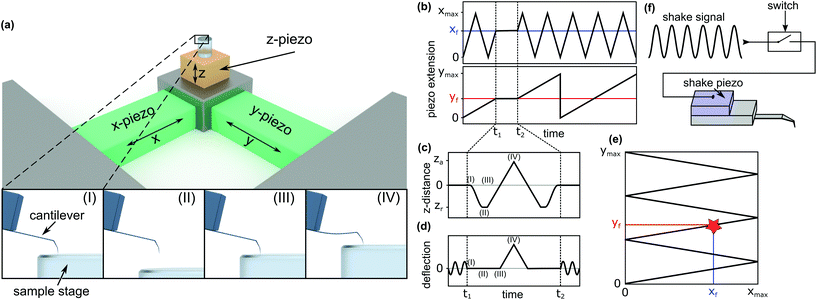
To investigate the local mechanical properties of microtubules, defect creation, and self-healing and to measure tubulin bond energies, the basic imaging function of standard HS-AFM34 is not enough. To enable the quantitative measurement of the in-line force curves during the scanning of an image in tapping mode, extensive modifications in hardware and software of the HS-AFM are required. These modifications resulted in a method where the time between finishing a force curve and resuming the scan is only 40 ms. In the following, the details of the method, called the in-line force curves, are discussed.A schematic explanation of the in-line force measurements is depicted in Fig. 1. The basic setup of the HS-AFM is shown in the upper side of Fig. 1a, while in the lower part, the movement of the z-piezo and the cantilever's reaction during the loading cycle are illustrated. The stopping of the HS-AFM scan at the desired position (indicated xf and yf in Fig. 1b and e) is performed by holding the x- and y-piezo voltages constant when they correspond to xf and yf positions. Then, the feedback is interrupted to directly control the z-piezo. Next, at time t1, the z-piezo is moved according to the schedule shown in Fig. 1c. The cantilever's response is illustrated in Fig. 1d. At time t2 + 40 ms, the feedback is resumed and the scan is continued.
In HS-AFM, the imaging of topography is performed in tapping mode, where the cantilever oscillates close to its resonance frequency. To record a quasi-static force curve, the cantilever's oscillation needs to be switched off between t1 and t2. This process is illustrated in Fig. 1d: at time t1, the oscillation is switched off and the deflection of the cantilever is caused only by applying a force to the sample surface. At time t2, the oscillation is switched on again. The tip trajectory on the sample is sketched in Fig. 1e, where a red star marks the position of force application. In this work, an analogue switch (ADG451, Analog Devices, Norwood, USA) was used to interrupt the voltage of the shake piezo and stop the cantilever's oscillation, as sketched in Fig. 1f.
Between time periods t1 and t2, the z-piezo is first retracted ((I)–(II) in Fig. 1a, c and d). The distance between the AFM tip and the sample surface is the largest at this position. Then, the z-piezo is extended linearly, indicated by positions (II)–(III)–(IV). At position (III), the tip comes into contact with the surface and the approach from position (II) to (III) gives a base line for the zero force. From position (III) to (IV), the extension of the z-piezo causes the AFM tip to press into the sample surface, bending the cantilever proportionally to the applied force. Returning the tip to its initial position is done by repeating the steps in the reverse order. Extending the z-piezo and recording the cantilever deflection can be done in two basic ways: ‘step-by-step’ or ‘at once’.
In the ‘step-by-step’ approach, the z-piezo voltage is incremented stepwise. After each increment, the deflection is read out. This method allows the control of the force by comparing the deflection against a critical value after each step, but it is slow. For example, a force schedule consisting of 600 data points where each point is an average of five measurements will require 80 ms. The acquisition time increases linearly with the number of data points to be recorded.
In the ‘at once’ approach, the application of the z-piezo voltage and the measurement of the deflection is done externally using a digital oscilloscope (PicoScope 5443B, Pico Technology, UK), which is triggered by the AFM's control software. The advantage of this method is a high-speed measurement – force curves can be plotted within 3 ms or less, limited by the z-piezo's maximum speed.35 The time between the two data points can be as low as 8 ns, allowing for a high temporal resolution. The number of data points does not influence the time needed for the measurements. The disadvantage is that the maximum force cannot be controlled, because the implementation of a triggered reaction to a critical deflection values is difficult.
Both the described approaches are distance controlled. Force controlled measurements at the same time scale can be implemented in the future. However, they would require far-reaching modifications as the HS-AFM system was not initially designed to be operated in this way.
Both approaches were compared by evaluating the average dissipated energy from the force curves’ hysteresis on microtubules at the same maximum deformations using the same average loading speed. No differences were found. Furthermore, both methods resulted in force curves on microtubules with similar characteristics. Basically, the main difference between the two approaches is the temporal resolution. If the average loading speeds were selected to be the same for both the methods, no differences would be observed. Because of that the results of both methods are combined in the following.
Defect creation and self-healing processes of MTs
For the purpose of this work, a “defect” shall be defined as a continuous agglomeration of tubulin vacancies in the MT lattice. Fig. 2 shows typical successive images to create a defect with the method described above.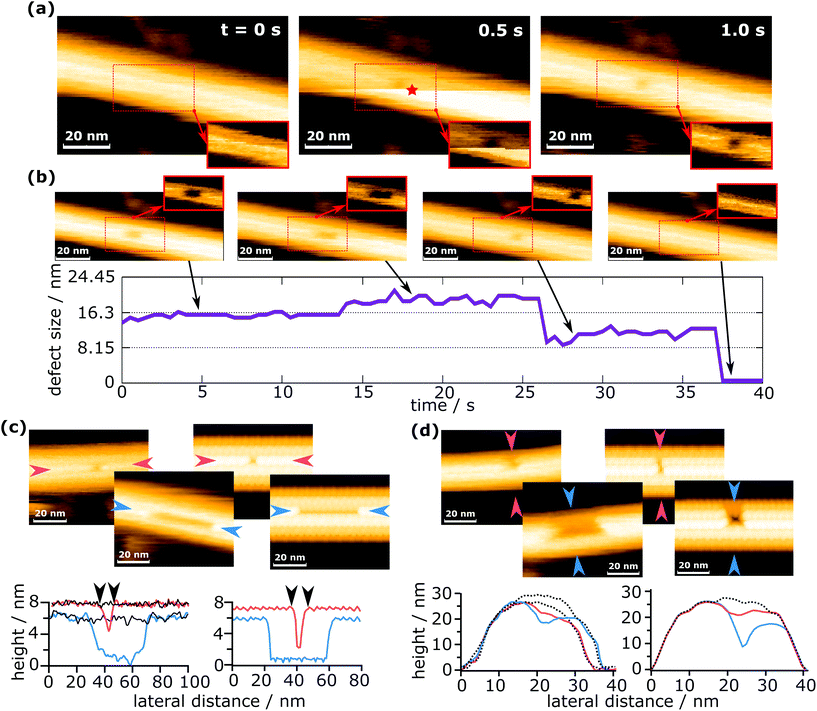 | ||
| Fig. 2 Defect creation and self-healing of a defect. (a) Creation of a defect in an MT and (b) the subsequent growth and complete healing of the defect (see also ESI Movie 1†). The insets in (a) and (b) show the region of the dashed rectangle with a pronounced contrast for the defect. The red star marks the time and the position of force application. (c) Comparison of the defect length from the measurements (left) with the simulated data (right). (d) Comparison of the defect width from the measurements (left) with the simulated data (right). The solid black lines in (c) and dotted black lines in (d) represent the undeformed MT, showing that there is no deformation except defect creation. | ||
In Fig. 2a, a force was applied during imaging at 0.5 s, at the position indicated by a red star. Note that the position of force application is not identical to the position of the defect. The reason for this is that defect creation is not as simple as pushing out one or more dimers with the tip. A possible explanation of this mechanism is given in a later section. Because images are always scanned from bottom to top, the upper part is the one after force application. The horizontally oriented step in Fig. 2a at 0.5 s that separates the two parts (before and after force application) is caused by the z-piezo's hysteresis. When a defect is created during the process, it can be observed in the same frame where a force was applied, if it is located in the upper part (as is the case in Fig. 2a). This immediate recording of topography provides important information to differentiate force curves that measured the creation of a defect from those which did not, e.g., if a defect is created in the following scan by unwanted tip–sample interactions. The defect shown in Fig. 2a is composed of two dimer vacancies along one protofilament. After generating the defect, the HS-AFM images were captured successively to monitor the following dynamics on the MT, as is shown in Fig. 2b. While imaging the MT with the defect, its full recovery was observed. Note that this full recovery was only observed once, whereas isolated healing events were found for about 2% of all defects created. The graph in Fig. 2b indicates the evolution of the defect size over time. The increase of the defect size at around 14 s could be caused by two effects: the first is that the defect could destabilize the protofilament and increase the probability of depolymerization. The second is that the growth of the defect is triggered by scanning. It is not clear which effect is prevalent, but it is likely that both contribute. The increase in the defect's size at 14 s is particularly noteworthy, as it seems to be a half-dimer step. This step might be caused by a partly attached tubulin dimer bending inwards and giving the impression of a half-dimer. In ESI Fig. S1,† a histogram is plotted for the time between defect creation and self-healing events, i.e. tubulin dimer reattachment.
Two scenarios of how this self-healing occurs can be considered: tubulin dimers from the surrounding environment attach to the defect, or the dimers removed by the tip remain in close proximity and reattach to the defect. In both cases, free dimers would perform a random walk, reach the defect site and attach there. The concentration of tubulin in the buffer solution should be negligible, but tubulin dimers and short protofilaments are always adsorbed onto the mica substrate and could migrate to the defect site. In the second case, tubulin dimers could be pushed inside the MT during defect creation. These dimers are considered as confined, because their movement is largely restricted in two dimensions. Such restrained dimers would be more likely to find the closely located defect site than completely free dimers surrounding the MT. Therefore, the most likely scenario is that self-healing is caused by tubulin dimers removed from the MT during indentation and pushed inside the MT.
To demonstrate that the measured defect size corresponds to the number of dimers removed, experimentally determined defect sizes and shapes are compared to sizes extracted from simulated AFM images (Fig. 2c and d). The simulated images are calculated by simple tip–sample dilation36 using the MT protein structure (PDB code: 5SYF).37,38 It should be noted that these simulations are of a purely geometric nature and do not consider deformations caused by scanning forces. The details on the simulation are given in the Experimental section. In Fig. 2c, the defect lengths (measured along a protofilament) are compared, while in Fig. 2d, the widths (measured across protofilaments) are compared. The defect lengths can be easily compared quantitatively, e.g., in Fig. 2c, the experimentally measured defect lengths are 8.7 nm and 43.0 nm, which are close to the values extracted from the simulated images (8.6 nm and 41.1 nm). This allows the identification of the number of dimers removed within a single protofilament. Deciding the number of protofilaments a defect spans can also be done in a similar way to the length determination and is shown in Fig. 2d. This investigation confirms that even with a finite tip radius, it is possible to measure the correct defect size. See ESI Fig. S2† for an additional comparison between simulations and experiments. The determination of the number of dimers removed is hindered by the fact that the edges of the defect are not completely sharp, causing an exact measurement to be difficult. In addition, as is seen in Fig. 2b, apparent sub-dimer steps may occur. From these observations, the error in counting the number of dimers removed is estimated as ±1 dimer per protofilament the defect spans. About 90% of all defects presented in this work span one or two protofilaments, which means that for most cases the error in the number of removed dimers can be considered to be 2 dimers. The maximum error is 5 dimers.
The simulated AFM images in Fig. 2c and d depict a completely undeformed MT except for the removed tubulin dimers. Experiments show the same behavior, which becomes evident when comparing the line profiles from simulated images with experimental images. Please note that the black lines indicate the undeformed MT and coincide with the regions outside the defect. This indicates that the observed deformations are indeed removed dimers and not a lingering buckling of the MT. The buckling of MTs was reported to occur during the elastic part of the loading and should not be permanent.24
Defects and force curves
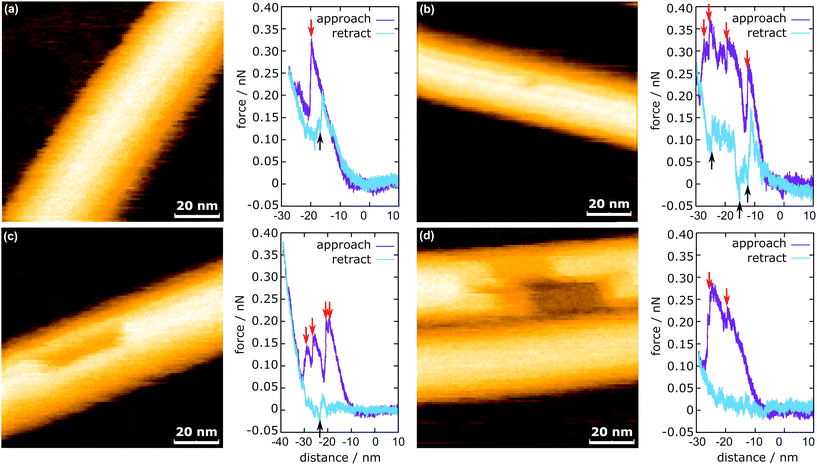
In Fig. 3, the representative HS-AFM images of MTs after force application are presented together with the corresponding force curves. Altogether 2813 force curves were measured. In 83% of the cases (2347 times), the deformation of the MT was completely reversible (Fig. 3a), whereas in the remaining 17% (466 times), observable defects were created (Fig. 3b and c). All four force curves share two characteristics: vertical jumps in the approach curve and a hysteresis. The hysteresis area represents the energy not recovered upon unloading (see ESI Fig. S3†). Schaap et al. identified a horizontal step in the force curve before the onset of the vertical jumps (usually between 0.2 nN and 0.3 nN) to indicate buckling of the microtubule.24 Another study assumed Taxol-stabilized microtubules to be continuous shells and explained the vertical jumps in the force curves with a collapse of the MT and successive indentation of the collapsed tube.31 This model, however, cannot account for the possibility of bond dissociation between the tubulin dimers under stress. In a more recent investigation, Kononova et al. found by using molecular dynamics simulations that the vertical downward jumps in the approach curve (indicated by red arrows in Fig. 3) correspond to tubulin–tubulin bond breaking events.32In the present study, vertical jumps (indicated by the black arrows in Fig. 3a–c) are also observed during the retraction segment of some force curves. See also ESI Fig. S4† for additional examples of force curves. A possible explanation of these jumps is given in the following section.
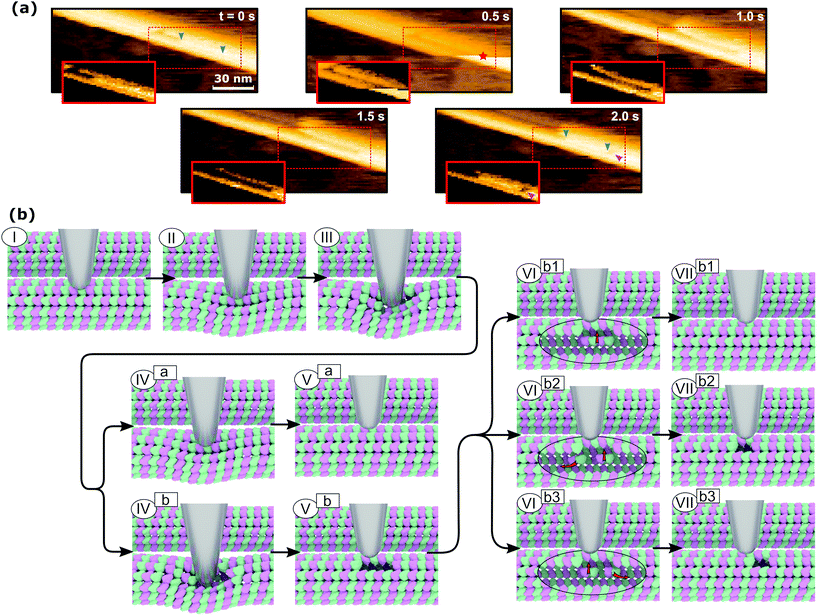
The mechanism of defect creation in MTs by AFM can be explained by considering force curves and the dynamic behavior of the defect directly after its generation. The downward jumps in the approach curve that indicate tubulin–tubulin bond breaking32 are observed even when the overall deformation is reversible, as is seen in Fig. 3a. What has not been explained so far are the upward jumps in the retract curve. These upward jumps bring the retract curve closer to the approach curve and can cause the two curves to overlap completely (Fig. 3a). It has been found that MTs with defects exhibit a reduced stiffness6 and a sudden restoration of the initial stiffness would lead to the MT pushing the cantilever up. This would also explain that the retract curve follows the approach curve from this point on if all or most bonds are restored. Another feature of the force curves is the hysteresis, which is present even if the deformation is fully reversible. Only when no vertical jumps are observed, the hysteresis disappears and the force curves become almost completely elastic. This observation indicates that the hysteresis is caused only by the breaking of tubulin–tubulin bonds and a delayed reformation. This healing of bonds cannot be captured by topography scans as it happens within less than 10 ms after the breaking of the bonds. However, in rare cases, the reattachment of the whole protofilament segments can be found within 2 s after force application. This would be an extreme case of delayed bond reformation and is presented in Fig. 4a. In Fig. 4a, a protofilament segment (5 dimers long) is removed at 0.5 s and most likely pushed inside the MT. Within 1.5 s, a large part (4 dimers long) of that segment reattaches to the MT, leaving a single dimer defect at the right side. See ESI Fig. S5 and S6† for more examples. These observations are indirect evidence for delayed bond reformation.
In order to create the single dimer defect indicated by a magenta arrow in Fig. 4a, the protofilament needed to be broken into two parts. The smaller part does not reattach, which is likely caused by the single dimer diffusing away due to its higher mobility compared to the large segment. The stepwise self-healing depicted in Fig. 2b supports the assumption of a higher mobility for single dimers as it takes a long time to heal the defect. If the single dimer would not diffuse away and stay in close proximity to the defect, the reattachment would happen much faster. Assuming the behavior of MTs during the in-line force measurements is of a similar nature, all observed defects could be created by the same mechanism. This mechanism is illustrated in Fig. 4b. It would also explain why the defects are not always at the exact same position as the point of force application: a protofilament segment is removed and broken and the part farther away from the tip is reattached during the retraction of the AFM tip (VIIb3 in Fig. 4b). Fig. 4b illustrates two different series of events that can lead to reversible deformation: paths (I)⋯(Va) and (I)⋯(VIIb1). Note that between (III) and (IVa) in Fig. 4b, a bond heals and the tip is pushed back up. Three series would lead to defects: (I)⋯(Vb) to obtain a two-dimer defect, (I)⋯(Vb)–(VIb2)–(VIIb2) and (I)⋯(Vb)–(VIb3)–(VIIb3) to create a single-dimer defect from a two-dimer defect by subsequent self-healing during unloading or thereafter.
Bond energy between tubulin dimers
The bond energy between tubulin dimers is ascertained by determining the hysteresis energy of the force curve, ΔG′. This ΔG′ is the free energy for rupturing bonds to create a defect, ΔG, plus the hysteresis of healing bonds during recording of the force curve, ΔG0. ΔG0 is determined by averaging the hysteresis energy from force curves, where no defect is created. Averaging is done only for the same maximum deformation as it increases the hysteresis. ΔG0 is then subtracted from ΔG′ to gain ΔG. This approach is a very simplified way to determine ΔG, as it does not consider the fact that the experiments are conducted under non-equilibrium conditions. A rigorous treatment would require the application39 of Jarzynski's equality (JE)40 or the Crooks fluctuation theorem (CFT)41 if the system is far from equilibrium.42 Both methods would require a large amount of experiments: for each defect shape, about 100 force curves should be recorded, because the number of broken bonds is related to the defect shape, as is explained further below. This is less of a problem for small defect sizes until around three dimers, because they are frequent and their possible configurations are limited. Larger defects are, however, less frequent and can assume a multitude of shapes. As a consequence, the sample size should be increased by a factor of at least 20 to use the JE or the CFT, which would culminate in about 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 force curves. To work with the available 2813 force curves, ΔG is estimated by subtracting ΔG0 from ΔG′ to remove some influence of the dissipated energy on our results. However, as this treatment does not account for non-equilibrium conditions, the results presented in this section should be viewed as estimates.
000 force curves. To work with the available 2813 force curves, ΔG is estimated by subtracting ΔG0 from ΔG′ to remove some influence of the dissipated energy on our results. However, as this treatment does not account for non-equilibrium conditions, the results presented in this section should be viewed as estimates.
To count the number of broken bonds, the shape of the defect and how the tubulin dimers are removed have to be considered. The three fundamental ways of removing the dimers from the MT lattice are sketched in Fig. 5a and are as follows: removing tubulin dimer by dimer, protofilament by protofilament, or all tubulin dimers as one chunk. It is further assumed that one dimer has four bonding sites: two longitudinal ones (i.e., those within one protofilament) and two lateral ones (between two dimers in adjacent protofilaments).32,33 While there should be one lateral bonding site per monomer, it is a common simplification to consider a single lateral bond per dimer.32,33 To account for the shape of the defect, the total energy ΔG is presented below as a function of the number of dimers removed at each protofilament in three equations (one for each of the fundamental ways to remove dimers). The derivation of how to arrive at these equations is described in the ESI.†
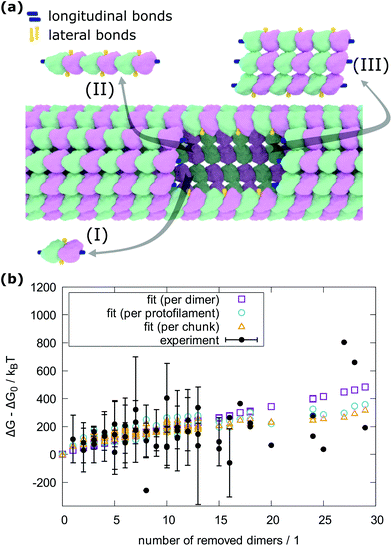 | ||
| Fig. 5 Determination of bond energy between tubulin dimers. (a) Model of an MT with a defect and the three fundamental ways to create the defect. (b) Hysteresis energy of force curves recorded on MTs plotted vs. the number of removed dimers. The experimental results are presented as average and standard deviations and are grouped by the number of protofilaments the resulting defects span for each number of removed dimers. The experimental values that would overlap each other are shifted by 0.2 on the horizontal axis for clarity. The green rectangles, blue circles, and orange triangles are fits with eqn (1), (2) and (3), respectively. Altogether, 2813 force curves were measured and in 466 cases, defects were created. | ||
In the following equations, the number of protofilaments in an MT is M − 1, the number of dimers removed from the i-th protofilament is ni, with nM = 0 always and N is the total number of dimers removed to form the defect. The number m is the number of protofilaments that include a defect. ΔGlo and ΔGla are the longitudinal and lateral free bond energies, respectively. The function H(ni − ni−1) represents the Heaviside step function with H(x) = 0 if x ≤ 0 and H(x) = 1 otherwise.
The total energy ΔG necessary to create a defect dimer by dimer (indicated as (I) in Fig. 5a) can be calculated by the following equation:
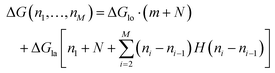 | (1) |
The energy to create a defect protofilament by protofilament ((II) in Fig. 5a) can be calculated by
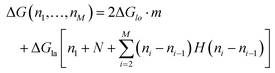 | (2) |
On the other hand, if the dimers are removed as a chunk ((III) in Fig. 5a), then the necessary energy is described by
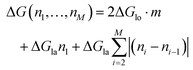 | (3) |
In Fig. 5b, the hysteresis energy from in-line force measurements is plotted versus the number of removed dimers. The values of the measured hysteresis energy are plotted as average and standard deviation at each (N,m) pair. This grouping neglects the summation term in eqn (1)–(3), but it was chosen in favor of a simple representation. To determine the longitudinal and lateral free bond energies, eqn (1)–(3) have to be fitted to the experimental data. These fits are also included in Fig. 5b and their results, ΔGlo and ΔGla, are summarized in Table 1. The result of the dimer-by-dimer fit yields the lowest longitudinal bond energy as 10 kBT. It is unlikely that the defect is created by breaking every single bond between the tubulin dimers. This assumption is supported by Fig. 4a, where an unbroken protofilament segment (4 dimers long) is reattached, and ESI Fig. S5.† However, the self-healing in Fig. 2 occurs as single dimer steps, which indicates that small defects (around 2 dimers in size) could be created by breaking all bonds within. According to ESI Fig. S6†, it is also possible that chunks remain intact during defect creation, although in these cases they might have still been partly attached to the MT, making these special cases. However, according to Table 1, it would not impact the determination of the bond energy considerably if dimers are removed by protofilament or as a chunk.
All results in Table 1 show that longitudinal bonds are stronger than lateral bonds, which is in accordance with theoretically determined values.32,33,43 It is further corroborated by the preferred defect shape: 423 defects are larger than two dimers and 56% of those span only one protofilament. This preference of defects to remain on a single protofilament indicates that it is more likely to break lateral bonds than longitudinal ones. Also, Fig. 4a and ESI Fig. S5† suggest that protofilament segments do not break when removed from the MT, which indicates that ΔGlo > ΔGla. The theoretical values of the longitudinal bond energy reported by VanBuren et al.33 and Kononova et al.32 agree well with our experimental estimates. The lateral bond energy calculated by Kononova et al.,32 however, is two to three times higher than the energy estimated by the other group33 and our experimental estimates. The advantage of the method of Kononova et al. is that it provides access to the exact number of broken bonds during a force experiment. Thus, the method does not rely on statistics to distribute the energy between lateral and longitudinal bonds, as our method does. This could mean that the values reported in this work overestimate the longitudinal bond energy but underestimate the lateral one. A better comparison of our estimates with the bond energies reported by Kononova et al. would be the sum of longitudinal and lateral bond energies. This sum is independent of the assignment to lateral and longitudinal values. By calculating this sum, we find about 61 kBT and 63 kBT for “protofilament” and “chunk” cases, respectively, while Kononova et al.32 report a total energy of about 73 kBT. This is a difference of just about 16%. It is also likely that the simplified method to determine ΔG in this work causes the estimates reported here to deviate from the theoretical values. On considering the simplified approach used to determine the free bond energies, the results reported in Table 1 are good estimates.
Conclusions
In this work, we presented the first application of in-line force measurements, a functional extension of HS-AFM, to gain insight into MT defect creation and self-healing and provided experimental support for so far only theoretically determined tubulin–tubulin bond energies. Using this method, structural defects could be successfully introduced to MTs and the following dynamic events after defect creation were monitored in real time. This investigation revealed that MTs can recover sustained damage by the attachment of single tubulin dimers at a small defect site step by step. Larger defects, however, can be healed by reattaching protofilament segments that were pushed inside the MT. Based on these observations, we introduced a model to explain how the defects are created when an AFM tip locally pushes the MT and the subsequent self-healing process. In short, it is possible that a large amount of bonds break when the AFM indents an MT, and if a protofilament segment is removed in the process, a defect remains. If the removed protofilament segment remains in the proximity of the defect, then there is a chance that the defect is healed completely or partially. Furthermore, by analyzing force curves obtained during the indentation of MTs, the bond energies between tubulin dimers in MTs were estimated to be around 25 kBT for longitudinal bonds and around 5 kBT for lateral bonds.HS-AFM in-line force measurements show great potential for studying processes triggered by deformation on a molecular level. Such processes are not easily accessible due to their dynamic nature. Possible applications include studying defect creation and immediate response to the deformation of cell membranes, inducing conformational changes in proteins and observing the follow-up reaction, and investigation of the time-dependent behavior of biopolymers, such as cellulose and chitin, after deformation. The applications are, however, not limited to biophysical research: polymer science and materials science could also benefit from HS-AFM in-line force measurements, in a similar way.
Experimental
High-speed AFM
The HS-AFM in use was laboratory-built and was operated in tapping mode to record the topography images.34 The cantilevers used for all measurements were BL-AC10DS-A2 (Olympus, Tokyo, Japan), 9 μm long, 2 μm wide and 130 nm thick, according to the manufacturer's specifications. To measure forces, the cantilevers were calibrated using the thermal sweep method.44 For comparability, we give the averages of the spring constant, the Q factor, and the resonance frequency of the cantilevers in use.45 Please note, however, that the Q factor is close to 1, while in order to apply Sader's method and, thus, to take advantage of the Global Calibration Initiative,45Q ≫ 1 is necessary.46 The following values are averages ± standard deviations from altogether 41 measurements of 24 different cantilevers: spring constant k = (0.08 ± 0.02) N m−1, resonance frequency in buffer solution fr = (499 ± 45) kHz, quality factor Q = 1.4 ± 0.1, and inverse sensitivity Si = (30 ± 9) nm V−1. Si was determined by recording a force curve on the mica substrate and measuring the resulting slope of the curve. The reciprocal value of the slope is then Si. At the end of the cantilever, an amorphous carbon tip was grown by electron beam deposition, and the tip apex radius is typically <5 nm. For the tapping mode, the cantilever's free oscillation amplitude was set to be about 1.5 nm, with a set-point of about 80% of the free amplitude during scanning.Force curves were recorded with a frequency of 12.5 Hz (80 ms to approach the sample with the AFM tip from the fully retracted state and fully retract again). This relatively low speed has the advantage that hydrodynamic and inertial effects during force measurement can be neglected.47
2 μL of MT solution was placed on the circular sample stage and left to adsorb onto the freshly cleaved mica surface for 15 min to 30 min. After that the sample stage was thoroughly washed with 20 μL to 40 μL of the observation buffer without letting the surface dry. The observation buffer, in which the MTs were measured, had the following composition: 80 mM piperazine-N,N′-bis(2-ethanesulfonic acid) (PIPES) adjusted to pH 6.9 with KOH, 2 mM MgCl2, and 1 mM ethylene glycol-bis(β-aminoethyl ether)-N,N,N′,N′-tetraacetic acid (EGTA) in Milli-Q water.
For recording force curves, the time of a force curve cycle (the path (I)–(II)–(III)–(IV) followed by the repetition of these steps in reverse, as shown in Fig. 1) was set to be 100 ms (t2 − t1, in Fig. 1). The time of contact between the AFM tip and the sample was usually about 20 ms, leading to about 80 ms between removing the tip from the surface and scanning the first pixel after the force curve. The force curves presented here were all smoothed by a Savitzky–Golay filter of order 4, applied to 31 data points at a time. From all force curves, a quadratic background was removed and was determined from the approach segment (path (II)–(III) in Fig. 1). The calculation of hysteresis energy was affected by neither the filtering nor the background removal.
Simulation of AFM images
The atom coordinates of tubulin dimers were extracted from a CIF file (PDB code: 5SYF),37,38 including the information of how the dimers are assembled to form an MT. During the assembly of the MT, certain dimers are skipped so that a defect of the desired shape is created. A modeled hard tip (cone with 15° half opening angle and a smoothly connected spherical cap with a 2 nm radius) is brought into contact with the atoms of the MT, whose vertical distance is the closest. The vertical position of the tip is saved in a matrix. This process is repeated for a uniform grid across the MT and its surrounding area. Note that these simulations are purely geometric and the shape of the MT is considered to be not deformable. The result is a matrix of height values that represent the topography of an MT with a defect measured by using an AFM tip.Microtubule preparation
MTs are polymerized from tubulin purified from porcine brain.48 The tubulin solution (70 μM), which was stored at −80 °C, was thawed on ice and heated to 37 °C. 4 mM GTP was added, mixed with the tubulin solution and incubated for 30 min at 37 °C. Then, 1 mM Taxol25 was added and again incubated for 15 min at 37 °C. The MTs were then suspended in a buffer with the composition of 80 mM PIPES (pH = 6.9), 2 mM MgCl2, 1 mM EGTA, 1 mM GTP, 50 μM Taxol, and 2.74 M glycerol (20 vol%). Note that the MTs are Taxol-stabilized and during observation by HS-AFM no additional Taxol is provided.Conflicts of interest
There are no conflicts to declare.Acknowledgements
C. G. is an international research fellow of the Japan Society for the Promotion of Science. This work was supported by the JSPS KAKENHI Grant Numbers JP17F17701, JP18H01837 and JP18H04512. Tubulin was kindly gifted by S. Nishikawa and Prof. A. Kakugo, Hokkaido University.Notes and references
- E. Nogales, S. G. Wolf and K. H. Downing, Nature, 1998, 391, 199–203 CrossRef CAS PubMed.
- E. Nogales, M. Whittaker, R. A. Milligan and K. H. Downing, Cell, 1999, 96, 79–88 CrossRef CAS PubMed.
- J. Howard, Annu. Rev. Physiol., 1996, 58, 703–729 CrossRef CAS PubMed.
- D. Inoue, B. Mahmot, A. M. R. Kabir, T. I. Farhana, K. Tokuraku, K. Sada, A. Konagaya and A. Kakugo, Nanoscale, 2015, 7, 18054–18061 RSC.
- R. B. Vallee, J. C. Williams, D. Varma and L. E. Barnhart, J. Neurobiol., 2004, 58, 189–200 CrossRef CAS PubMed.
- L. Schaedel, K. John, J. Gaillard, M. V. Nachury, L. Blanchoin and M. Thery, Nat. Mater., 2015, 14, 1156–1163 CrossRef CAS PubMed.
- Z. X. Wang, L. Tan and J. T. Yu, Mol. Neurobiol., 2015, 51, 1309–1321 CrossRef CAS PubMed.
- W. H. Liang, Q. Li, K. M. R. Faysal, S. J. King, A. Gopinathan and J. Xu, Biophys. J., 2016, 110, 2229–2240 CrossRef CAS PubMed.
- M. W. Gramlich, L. Conway, W. H. Liang, J. A. Labastide, S. J. King, J. Xu and J. L. Ross, Sci. Rep., 2017, 7 CAS , 44290.
- D. J. Odde, L. Ma, A. H. Briggs, A. DeMarco and M. W. Kirschner, J. Cell Sci., 1999, 112, 3283–3288 CAS.
- J. A. Tuszyński, T. Luchko, S. Portet and J. M. Dixon, Eur. Phys. J. E, 2005, 17, 29–35 CrossRef PubMed.
- D. B. Wells and A. Aksimentiev, Biophys. J., 2010, 99, 629–637 CrossRef CAS PubMed.
- Z. J. Donhauser, W. B. Jobs and E. C. Binka, Biophys. J., 2010, 99, 1668–1675 CrossRef CAS PubMed.
- H. Felgner, R. Frank and M. Schliwa, J. Cell Sci., 1996, 109, 509–516 CAS.
- B. Mickey and J. Howard, J. Cell Biol., 1995, 130, 909–917 CrossRef CAS PubMed.
- F. Gittes, B. Mickey, J. Nettleton and J. Howard, J. Cell Biol., 1993, 120, 923–934 CrossRef CAS.
- T. Hawkins, M. Mirigian, M. S. Yasar and J. L. Ross, J. Biomech., 2010, 43, 23–30 CrossRef PubMed.
- N. Jiang, M. E. Bailey, J. Burke, J. L. Ross and R. I. Dima, Cytoskeleton, 2017, 74, 3–17 CrossRef CAS PubMed.
- F. Iwata, K. Ohara, Y. Ishizu, A. Sasaki, H. Aoyama and T. Ushiki, Jpn. J. Appl. Phys., 2008, 47, 6181–6185 CrossRef CAS.
- R. P. Gonçalves and S. Scheuring, Surf. Interface Anal., 2006, 38, 1413–1418 CrossRef.
- D. J. Müller, W. Baumeister and A. Engel, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 13170–13174 CrossRef.
- D. C. Turner, C. Chang, K. Fang, S. L. Brandow and D. B. Murphy, Biophys. J., 1995, 69, 2782–2789 CrossRef CAS PubMed.
- A. Vinckier, I. Heyvaert, A. D'Hoore, T. McKittrick, C. Van Haesendonck, Y. Engelborghs and L. Hellemans, Ultramicroscopy, 1995, 57, 337–343 CrossRef CAS PubMed.
- I. A. T. Schaap, C. Carrasco, P. J. de Pablo, F. C. MacKintosh and C. F. Schmidt, Biophys. J., 2006, 91, 1521–1531 CrossRef CAS PubMed.
- L. A. Amos and J. Löwe, Chem. Biol., 1999, 6, R65–R69 CrossRef CAS PubMed.
- A. A. Hyman, S. Salser, D. N. Drechsel, N. Unwin and T. J. Mitchison, Mol. Biol. Cell, 1992, 3, 1155–1167 CrossRef CAS PubMed.
- A. Vinckier, C. Dumortier, Y. Engelborghs and L. Hellemans, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.–Process., Meas., Phenom., 1996, 14, 1427–1431 CrossRef CAS.
- K. M. Munson, P. G. Mulugeta and Z. J. Donhauser, J. Phys. Chem. B, 2007, 111, 5053–5057 CrossRef CAS PubMed.
- A. Kis, S. Kasas, B. Babić, A. J. Kulik, W. Benoît, G. A. D. Briggs, C. Schönenberger, S. Catsicas and L. Forró, Phys. Rev. Lett., 2002, 89, 248101 CrossRef CAS PubMed.
- A. Kis, S. Kasas, A. J. Kulik, S. Catsicas and L. Forró, Langmuir, 2008, 24, 6176–6181 CrossRef CAS PubMed.
- P. J. de Pablo, I. A. T. Schaap, F. C. MacKintosh and C. F. Schmidt, Phys. Rev. Lett., 2003, 91, 098101 CrossRef CAS PubMed.
- O. Kononova, Y. Kholodov, K. E. Theisen, K. A. Marx, R. I. Dima, F. I. Ataullakhanov, E. L. Grishchuk and V. Barsegov, J. Am. Chem. Soc., 2014, 136, 17036–17045 CrossRef CAS PubMed.
- V. VanBuren, D. J. Odde and L. Cassimeris, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6035–6040 CrossRef CAS PubMed.
- T. Ando, N. Kodera, E. Takai, D. Maruyama, K. Saito and A. Toda, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 12468–12472 CrossRef CAS PubMed.
- F. Rico, L. Gonzalez, I. Casuso, M. Puig-Vidal and S. Scheuring, Science, 2013, 342, 741–743 CrossRef CAS PubMed.
- J. S. Villarrubia, Surf. Sci., 1994, 321, 287–300 CrossRef CAS.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- E. H. Kellogg, N. M. A. Hejab, S. Howes, P. Northcote, J. H. Miller, J. F. Díaz, K. H. Downing and E. Nogales, J. Mol. Biol., 2017, 429, 633–646 CrossRef CAS PubMed.
- G. Hummer and A. Szabo, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 3658–3661 CrossRef CAS PubMed.
- C. Jarzynski, Phys. Rev. Lett., 1997, 78, 2690–2693 CrossRef CAS.
- G. E. Crooks, Phys. Rev. E, 1999, 60, 2721–2726 CrossRef CAS.
- D. Collin, F. Ritort, C. Jarzynski, S. B. Smith, I. Tinoco and C. Bustamante, Nature, 2005, 437, 231–234 CrossRef CAS PubMed.
- D. Sept, N. A. Baker and J. A. McCammon, Protein Sci., 2009, 12, 2257–2261 CrossRef PubMed.
- J. L. Hutter and J. Bechhoefer, Rev. Sci. Instrum., 1993, 64, 1868–1873 CrossRef CAS.
- J. E. Sader, R. Borgani, C. T. Gibson, D. B. Haviland, M. J. Higgins, J. I. Kilpatrick, J. Lu, P. Mulvaney, C. J. Shearer, A. D. Slattery, P. A. Thorén, J. Tran, H. Zhang, H. Zhang and T. Zheng, Rev. Sci. Instrum., 2016, 87, 093711 CrossRef PubMed.
- J. E. Sader, J. W. M. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967 CrossRef CAS.
- C. A. Amo and R. Garcia, ACS Nano, 2016, 10, 7117–7124 CrossRef CAS PubMed.
- M. Castoldi and A. V. Popov, Protein Expression Purif., 2003, 32, 83–88 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nr07392a |
| This journal is © The Royal Society of Chemistry 2019 |