Nonsolvent induced reconfigurable bonding configurations of ligands in nanoparticle purification†
Jun
Zhang‡
a,
Falin
Tian‡
b,
Min
Zhang
c,
Tiefeng
Li
d,
Xueqian
Kong
*a,
Yunlong
Zhou
 *bc and
Nicholas A.
Kotov
*bc and
Nicholas A.
Kotov
 e
e
aCenter for Chemistry of High-Performance & Novel Materials, Department of Chemistry, Zhejiang University, Hangzhou, Zhejiang 310027, China. E-mail: kxq@zju.edu.cn
bEngineering Research Center of Clinical Functional Materials and Diagnosis & Treatment Devices of Zhejiang Province, Wenzhou Institute, University of Chinese Academy of Sciences, Wenzhou, Zhejiang 325000, China. E-mail: zhouyl@wibe.ac.cn
cSchool of Biomedical Engineering, School of Ophthalmology and Optometry and Eye Hospital, Wenzhou Medical University, Wenzhou, Zhejiang 325011, China
dInstitute of Applied Mechanics, Zhejiang University, Hangzhou, Zhejiang 310027, China
eDepartment of Chemical Engineering, and Biointerfaces Institute, University of Michigan, Ann Arbor, Michigan 48109, USA
First published on 16th July 2019
Abstract
The geometry of the organic ligands on colloidal nanoparticles (NPs) is central for understanding the self-assembly behavior and many properties of NP-based soft matter. However, the current models of the NP–media interface give incomplete and often incorrect representations of its structure, especially for aqueous systems. Here, we show that NPs capped with 3-mercaptopropionic acid (MPA) serve as a convenient model for elucidation of surface ligand geometry and its effect on collective noncovalent forces of highly concentrated NPs. Contrary to expectations, MPA was found to form surface layers with different thicknesses varying from monolayer to multilayers depending on the ratio of isopropanol to the as-made NP dispersions in the purification. Solution-state nuclear magnetic resonance (NMR) and theoretical simulations uncovered that the monolayer includes strongly coordinated ligands and adsorbed ligands interacting with the NP surface non-covalently. Increased density of the non-covalently attached ligands results in a multilayered ligand shell. Consequentially, we demonstrate that the viscoelasticity of concentrated NP dispersions carrying a monolayer of MPA is higher than those of multilayered NPs. These observations enable a better understanding of the complexity of water-soluble NP dispersions and collective non-covalent forces of supramolecular NPs.
New conceptsEnumeration of forces between nanoparticles is a difficult but much needed task for the design of numerous soft matter and self-assembling systems. Current models developed for macroscale colloids are not applicable to nanoparticles due to them losing sight of the reconfigurability of the nanoparticle surface layer. In this work, we elucidate the surface ligand geometry and its effect on the collective noncovalent forces using a typical carboxy-thiol bifunctional ligand capped nanoparticle that serves as a convenient model. The conceptual novelty of this work includes several innovative aspects. (1) The introduction of low and high volume ratio of isopropanol to crude nanoparticle dispersions in the purification results in the different thickness of the surface ligand varying from monolayer to multilayer. (2) Nuclear magnetic resonance and theoretical simulations uncover that the monolayer includes bound ligands and strongly adsorbed ligands inserted, while the multilayer is composed of the bound ligand layer entangled with strongly and weakly adsorbed ligands. (3) The ligand can have both monolayered and multilayered configuration that represent a completely unexpected fact not accounted for in any current NP models. (4) The viscoelasticity of nanoparticle assemblies carrying a monolayer of thiol ligand is higher than those of multilayered nanoparticles. This work provides clear evidence for the ligand binding model in colloidal nanoparticles and lays the foundation of multiscale computational models adequately applying to many assembly systems and macroscale biomaterial designs. |
Introduction
The spectrum of interactions between inorganic nanoparticles (NPs) coated with organic surface ligands includes van der Waals and electrostatic interactions, hydrogen bonds, coordination bridges, and other interactions.1–3 This benefits from the nanoparticle ligands with chemical bonding and/or physical adsorption, which is different from the model of polymer adsorption mainly driven by the high conformational entropy.4 Their accurate enumeration and prediction of organic surface ligand-coated inorganic NPs are currently unattainable building on the obscure ligand structures, such as the organic shells on metal NPs and quantum dots.5,6 However, current knowledge about the molecular configurations of surface ligands for the wide variety of NPs with short hydrophilic ligands is limited, let alone how the NPs self-assemble into superstructures via non-covalent forces.2,7–9 Furthermore, derivations made from existing knowledge of microscale colloids10,11 or other NPs lead to conclusions about their structure and the different forces between the NPs that are uncertain at best. Consequently, deciphering the connections between the molecular structure at Ångström and nanometer levels and macroscale properties represents one of the most pressing scientific problems today.Highly concentrated NP dispersions as a convenient research model elucidate the structure of nanoscale interfaces including the complex case of aqueous media.12,13 Here, we show that NPs capped with 3-mercaptopropionic acid (MPA) form hydrogels with dramatically different viscoelasticity when prepared using slight changes in the purification of their as-made NP dispersions. The properties of the viscoelastic gels translate the interparticle interactions from the nanoscale to macroscale implying intrinsic differences in the structure of the NP surface. We performed nuclear magnetic resonance (NMR) spectroscopy on the NP colloids and revealed different bonding configurations of the MPA ligands. Combined with simulations, it was also found that NP assembly may have a widely variable surface ligand configuration from monolayer to multilayers depending on the preparation procedure. The viscoelasticity of hydrogels assembled from monolayered NPs is higher than those of multilayered NPs. Our investigation uncovered structure–property relationships for NP assemblies and illustrated the possibility to engineer ligands with two or more functional groups to form superstructures with tailored properties originating from collective interactions in the surface ligands on NPs.14–17
Results and discussion
Properties of highly concentrated MPA–CdTe dispersions
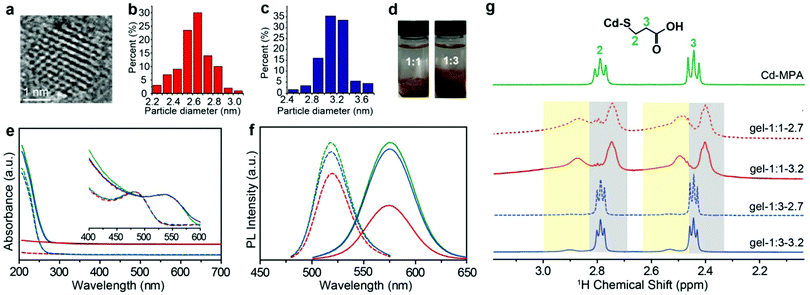
MPA-stabilized CdTe NPs (MPA–CdTe) were synthesized with an average diameter of ∼2.7 nm and ∼3.2 nm in aqueous solution (Fig. 1a–c and Fig. S1, S2, ESI†).18–20 The charged NPs with an average diameter of ∼2.7 and ∼3.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) nm were synthesized by controlling the time of the reflux stage and remained stable for several days. The sizes of NPs differ from each other by one additional atomic layer of CdTe. The as-made dispersions of MPA-stabilized NPs usually contain many salts and free Cd–MPA complexes, which form dynamically balanced concentrations of each species through adsorption and desorption with NPs.21 These unbound complexes, formed through the non-covalent forces between NPs, keep the superficial configuration of NPs stable and thus enrich the physical and chemical properties of the NPs.22
nm were synthesized by controlling the time of the reflux stage and remained stable for several days. The sizes of NPs differ from each other by one additional atomic layer of CdTe. The as-made dispersions of MPA-stabilized NPs usually contain many salts and free Cd–MPA complexes, which form dynamically balanced concentrations of each species through adsorption and desorption with NPs.21 These unbound complexes, formed through the non-covalent forces between NPs, keep the superficial configuration of NPs stable and thus enrich the physical and chemical properties of the NPs.22
Here we used a strategy based on judicious control of attractive interactions between NPs. The typical method to purify the as-made NP solution is to remove excessive unbound molecules by nonsolvent (i.e., methanol, ethanol, and IPA) to vary solution polarity.3,23–25 Considering the ligand configuration and similar size for the core and ligand, the nonsolvent dosage plays a dominant role to ligands for the surface ligand adsorption. Here, we added different volume ratios of IPA (or other nonsolvents, see Fig. S3 and S4, ESI†) to the as-made NP dispersions to partially remove free complexes and subsequently control the amount of ligand adsorption on the NP surface (i.e. vNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vIPA = 1
vIPA = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and νNP
1 and νNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) νIPA = 1
νIPA = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, here vNP is the volume of NP dispersion and vIPA is the volume of IPA). We noticed that phase separation occurred and the two groups of IPA-enriched NP dispersion exhibited different viscosities in the fluid phase. The NP enriched phase was separated by the centrifugal speed at 5000 rpm for 5 minutes and then dried for 24 hours under vacuum. The dried NP solid was hydrated by deionized water into gel-like concentrated NP dispersions with a high-quantum yield of about ∼31%. Optical images show that there is an obvious difference between the two hydrogels: the morphology of the one formed with 1
3, here vNP is the volume of NP dispersion and vIPA is the volume of IPA). We noticed that phase separation occurred and the two groups of IPA-enriched NP dispersion exhibited different viscosities in the fluid phase. The NP enriched phase was separated by the centrifugal speed at 5000 rpm for 5 minutes and then dried for 24 hours under vacuum. The dried NP solid was hydrated by deionized water into gel-like concentrated NP dispersions with a high-quantum yield of about ∼31%. Optical images show that there is an obvious difference between the two hydrogels: the morphology of the one formed with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 NP
1 NP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) IPA is dry and brittle, and that of 1
IPA is dry and brittle, and that of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 is dense and sticky (Fig. 1d). High resolution transmission electron microscopy (HRTEM) images show structural similarities for both NP hydrogels in that they are composed of densely packed CdTe NPs. Scanning electron microscopy (SEM) images show slight differences; the morphology of the 1
3 is dense and sticky (Fig. 1d). High resolution transmission electron microscopy (HRTEM) images show structural similarities for both NP hydrogels in that they are composed of densely packed CdTe NPs. Scanning electron microscopy (SEM) images show slight differences; the morphology of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 sample is more like a brittle solid compared to the NP gels from the 1
1 sample is more like a brittle solid compared to the NP gels from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 sample (Fig. S1, ESI†). The SAXS measurements for both hydrogels show zero-characteristic peaks, meaning that nanoparticles in hydrogels have similarly random structures (Fig. S5, ESI†). In this paper, to differentiate the as-made MPA–CdTe dispersions that have not been purified by isopropanol (IPA), we shall refer to the concentrated MPA–CdTe dispersions as: gel-1
3 sample (Fig. S1, ESI†). The SAXS measurements for both hydrogels show zero-characteristic peaks, meaning that nanoparticles in hydrogels have similarly random structures (Fig. S5, ESI†). In this paper, to differentiate the as-made MPA–CdTe dispersions that have not been purified by isopropanol (IPA), we shall refer to the concentrated MPA–CdTe dispersions as: gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x-NP size (i.e., gel-1
x-NP size (i.e., gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-2.7, gel-1: 3-2.7, gel-1
1-2.7, gel-1: 3-2.7, gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1–3.2, and gel-1
1–3.2, and gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2), where x is the volume ratio of the IPA.
3-3.2), where x is the volume ratio of the IPA.
Ultraviolet and visible (UV-vis) spectra and photoluminescence (PL) spectra provide a preliminary evaluation of the IPA–NP ratio effect in solution, for example, the relative intensity of the absorption spectra below 300 nm for gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is much lower than that of gel-1
1 is much lower than that of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 under the same NP concentrations,26 showing that a higher content of free Cd–MPA complexes was retained in gel-1
3 under the same NP concentrations,26 showing that a higher content of free Cd–MPA complexes was retained in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Fig. 1e and Fig. S3, ESI†). Meanwhile, the aqueous dispersion of negatively charged NPs with sizes 2.7 and 3.2 nm displayed PL peaks at 519 and 575 nm, respectively, whereas PL peaks of the corresponding hydrogels were positioned at 544 and 590 nm, respectively. The quantitative intensity of PL spectra of gel-1
3 (Fig. 1e and Fig. S3, ESI†). Meanwhile, the aqueous dispersion of negatively charged NPs with sizes 2.7 and 3.2 nm displayed PL peaks at 519 and 575 nm, respectively, whereas PL peaks of the corresponding hydrogels were positioned at 544 and 590 nm, respectively. The quantitative intensity of PL spectra of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is lower than that of gel-1
1 is lower than that of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (Fig. 1f), meaning that the low IPA ratio is more efficient at removing Cd–MPA complexes for purification.
3 (Fig. 1f), meaning that the low IPA ratio is more efficient at removing Cd–MPA complexes for purification.
The effect of IPA on the ligands and morphology
The addition of nonsolvent alcohol to crude NP dispersion not only removes extra free complexes but also potentially strips adsorbed ligands coating the NP core.23 Surface ligands enable control of NP colloidal stability and self-assembly. IPA was used as the purification nonsolvent because it prevents chemical damage of surface ligands and etching of the CdTe surface. When exposed to deionized water, MPA–NPs retain uniform dispersity. Adding IPA reduces the electrostatic repulsion of NPs in solution and removes free Cd–MPA complexes from NP dispersion by changing the polarity. Thus, the MPA–CdTe coated surface ligands and even part of the free complexes can be precipitated, and most of the extra free salts and complexes were effectively removed.21 Herein, we tentatively compare the number of ligands by thermogravimetric analysis (TGA). The ligand ratio of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with sizes of 2.7 nm or 3.2 nm is about 10% w/w, which is significantly lower than that of gel-1
1 with sizes of 2.7 nm or 3.2 nm is about 10% w/w, which is significantly lower than that of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (∼26% w/w), indicating that more complexes were retained in the gel-1
3 (∼26% w/w), indicating that more complexes were retained in the gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 NP dispersion (Fig. S6, ESI†).
3 NP dispersion (Fig. S6, ESI†).
Bound and unbound surface ligands
1H NMR spectroscopy is able to quantify and differentiate the bound and unbound ligands in the NP dispersions.5,27,28 The bound ligands on NPs are usually broadened due to reduced tumbling rates29,30 compared with the free Cd–MPA complexes (Fig. S7, ESI†). The methylene signals of the MPA–CdTe dispersion appear at two different chemical shifts (Fig. 1g). The broadened peaks with larger chemical shifts belong to bound ligands (designated as (MPA)S–NP) with positions at δH ∼ 2.5 ppm and ∼2.9 ppm (with yellow background). The resonances positioned at δH ∼ 2.4 ppm and ∼2.8 ppm (with gray background) belong to unbound Cd–MPA complexes which are mostly interacting with NPs. Notably, in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the integral area of Cd–MPA complexes is ∼6 times that of the bound ligands; while in gel-1
3, the integral area of Cd–MPA complexes is ∼6 times that of the bound ligands; while in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the adsorbed Cd–MPA complex is only ∼0.6 times that of the bound ligands. More Cd–MPA complexes are retained in gel-1
1, the adsorbed Cd–MPA complex is only ∼0.6 times that of the bound ligands. More Cd–MPA complexes are retained in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 than in gel-1
3 than in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is in line with the UV-vis and TGA results. In addition, gel-1
1, which is in line with the UV-vis and TGA results. In addition, gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 contains ∼5% IPA (the residual nonsolvent) resonating at 1.5 and 4.0 ppm (Fig. S8, ESI†). And gel-1
3 contains ∼5% IPA (the residual nonsolvent) resonating at 1.5 and 4.0 ppm (Fig. S8, ESI†). And gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 exhibits small triplets at 2.5 and 2.8 ppm (Fig. S8, ESI†) corresponding to ∼2% dithiodipropionic acid (DTDPA), the by-product produced in the synthetic process of Cd–MPA complexes.31
1 exhibits small triplets at 2.5 and 2.8 ppm (Fig. S8, ESI†) corresponding to ∼2% dithiodipropionic acid (DTDPA), the by-product produced in the synthetic process of Cd–MPA complexes.31
Composition and content
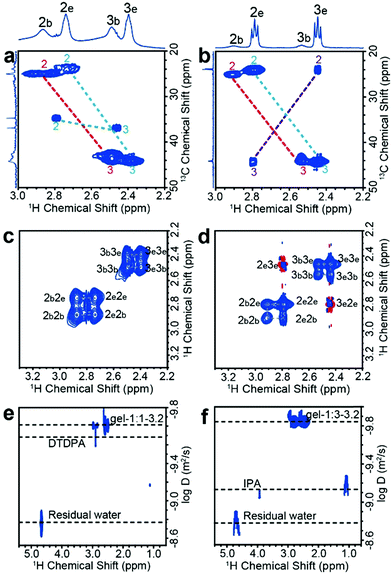
The one-dimensional NMR spectra can only monitor substances whose chemical shifts are distinguishable, while 1H–13C HSQC (heteronuclear single quantum coherence) experiments are used to distinguish signals with superimposed 1H chemical shifts. The use of HSQC experiments is necessary because either the thiol or the carboxylate group of MPA can bond to metals, which, in principle, could lead to a variety of coordination structures. For free MPA in solution, the 13C chemical shift of the alpha-methylene carbon (position no. 2) is ∼23 ppm, and that of the beta-methylene carbon (position no. 3) is ∼42 ppm. These resonances shift slightly downfield when MPA is bound to the Cd2+ or CdTe NPs (Fig. S8, ESI†). We first tested the reaction precursor (Cd–MPA complexes) by HSQC (Fig. S9, ESI†). The result shows that the Cd–MPA solution contains both (MPA)COO–Cd in which Cd2+ binds to the carboxylate group and (MPA)S–Cd complexes in which Cd2+ binds to the thiol group. The (MPA)S–Cd complexes are the dominant component in the mixture because the bonding strength of the thiol group with cadmium is greater than that of a carboxylate group. The gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 dispersion contains three components, including 63% (MPA)S–NP (MPA binds to NP surface), 37% (MPA)S–Cd complexes, and 2% free DTDPA (Fig. 2a). The gel-1
1-3.2 dispersion contains three components, including 63% (MPA)S–NP (MPA binds to NP surface), 37% (MPA)S–Cd complexes, and 2% free DTDPA (Fig. 2a). The gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 dispersion contains 14% (MPA)S-NP, 65% (MPA)S–Cd complexes, 16% (MPA)COO–Cd complexes and 5% free IPA (Fig. 2b and Fig. S10, ESI†). Later, we will show that the (MPA)S–Cd complexes are not free in the NP gel dispersion and they are closely associated with NPs forming a multicomponent structure as a whole. In addition, we found that the thiolate alpha-methylene protons appear at δH ∼ 2.9 ppm, indicating that the sulfhydryl group of the bound ligands forms a terminal bond to single cadmium ions (S–Cd) in the NP hydrogels.31
3-3.2 dispersion contains 14% (MPA)S-NP, 65% (MPA)S–Cd complexes, 16% (MPA)COO–Cd complexes and 5% free IPA (Fig. 2b and Fig. S10, ESI†). Later, we will show that the (MPA)S–Cd complexes are not free in the NP gel dispersion and they are closely associated with NPs forming a multicomponent structure as a whole. In addition, we found that the thiolate alpha-methylene protons appear at δH ∼ 2.9 ppm, indicating that the sulfhydryl group of the bound ligands forms a terminal bond to single cadmium ions (S–Cd) in the NP hydrogels.31
Using the elemental analysis results (Table S2, ESI†) and the quantification results by NMR as described in the previous paragraphs (Table S3, ESI†), we calculated the mass ratios of bound ligands with respect to the inorganic core of CdTe NPs (Table S4, ESI†) and finally obtained the average number of bound ligands and adsorbed ligands per nanoparticle as shown in Table 1.
| NP gels | Bound ligands (MPA)S-NP | Adsorbed ligands (MPA)S–Cd |
|---|---|---|
gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 1-3.2 |
160 | 95 |
gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 3-3.2 |
240 | 1120 |
NP–surface ligand interactions
NOESY (nuclear Overhauser effect spectroscopy) experiments can be used to understand NP–ligand and ligand–ligand interactions in the liquid state. The bound ligands and the inorganic cores of NPs move together with slowed tumbling rates like macromolecules. As a result, their 1H signals have negative cross relaxation rate constants and generate NOE cross-peaks with the same sign as their diagonal peaks (Fig. 2c and d, blue contour). In contrast, the cross peaks of free Cd–MPA complexes have a red contour (with positive cross relaxation rate constants, Fig. S11a, ESI†).32 The interaction and exchange between bound and free ligands will also generate transfer NOE (trNOE) signals which have the same sign as their diagonal peaks. The trNOE signals appeared at frequencies of the free ligands because those NOE signals were generated in the bound state and transferred to the free state.32 Molecules that had no interaction with the NP surface generated zero trNOE cross-peaks. The strong NOE cross-peaks with the same sign (in blue contours) at 2b2e, 2e2b, 3b3e, and 3e3b in Fig. 2c and d demonstrate that the (MPA)S–Cd complexes are adsorbed and desorbed from the NP surface dynamically by exchanging between the two states. In the gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 spectrum (Fig. 2d), the cross peaks with the opposite sign (red contour) at 2e3e and 3e2e actually arise from the (MPA)COO–Cd complexes, which tumble freely without interacting with the NP surfaces. Therefore, (MPA)S–Cd complexes interact strongly with NPs probably due to the hydrogen bonds between the carboxylate group themselves and those of bound ligands on the NP surface, while (MPA)COO–Cd complexes behave more like free molecules because the thiol groups have no significant hydrogen bond. The gel-1
3-3.2 spectrum (Fig. 2d), the cross peaks with the opposite sign (red contour) at 2e3e and 3e2e actually arise from the (MPA)COO–Cd complexes, which tumble freely without interacting with the NP surfaces. Therefore, (MPA)S–Cd complexes interact strongly with NPs probably due to the hydrogen bonds between the carboxylate group themselves and those of bound ligands on the NP surface, while (MPA)COO–Cd complexes behave more like free molecules because the thiol groups have no significant hydrogen bond. The gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 and gel-1
1-3.2 and gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 contain different amounts of these species and therefore lead to different macroscopic properties. Although trNOE spectroscopy is the more robust technique for detecting chemical exchange signals, they can also be verified by rotating-frame nuclear Overhauser effect correlation spectroscopy (ROESY).33 The ROESY experiment also shows that 2b2e, 2e2b, 3b3e, and 3e3b signals originate mainly from the exchange of adsorbed and desorbed (MPA)S–Cd complexes (Fig. S12a and b, ESI†).
3-3.2 contain different amounts of these species and therefore lead to different macroscopic properties. Although trNOE spectroscopy is the more robust technique for detecting chemical exchange signals, they can also be verified by rotating-frame nuclear Overhauser effect correlation spectroscopy (ROESY).33 The ROESY experiment also shows that 2b2e, 2e2b, 3b3e, and 3e3b signals originate mainly from the exchange of adsorbed and desorbed (MPA)S–Cd complexes (Fig. S12a and b, ESI†).
Diffusion speed
DOSY (diffusion ordered NMR spectroscopy) can differentiate species based on their diffusivity and reveal interactions and dispersity in solution. As shown in Fig. 2e and f, DTDPA (2.1 × 10−10 m2 s−1) and IPA (7.6 × 10−10 m2 s−1) have a much smaller diffusion coefficient than that of the nanoparticles (∼1.4 × 10−10 m2 s−1) which indicates that these species move freely and interact little with the NPs. Their small molecule-like movement can be verified by COSY (Fig. S11, ESI†). In gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 and gel-1
1-3.2 and gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2, water has the same diffusion coefficient as 1.7 × 10−9 m2 s−1, which is consistent with the diffusion coefficient of deionized water (Fig. S13, ESI†). However, the (MPA)S–Cd complexes have the same diffusion coefficient as the bound ligands (MPA)S–NP, suggesting the formation of a larger complex. The hydrodynamic diameter, d, of the complex can be derived from the diffusion coefficient, D, by the Stokes–Einstein equation (eqn (1)).34
3-3.2, water has the same diffusion coefficient as 1.7 × 10−9 m2 s−1, which is consistent with the diffusion coefficient of deionized water (Fig. S13, ESI†). However, the (MPA)S–Cd complexes have the same diffusion coefficient as the bound ligands (MPA)S–NP, suggesting the formation of a larger complex. The hydrodynamic diameter, d, of the complex can be derived from the diffusion coefficient, D, by the Stokes–Einstein equation (eqn (1)).34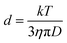 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 has a hydrodynamic diameter of 3.2 ± 0.1 nm based on the diffusion coefficients of (1.5 ± 0.1) × 10−10 m2 s−1, and that in NP-1
1-3.2 has a hydrodynamic diameter of 3.2 ± 0.1 nm based on the diffusion coefficients of (1.5 ± 0.1) × 10−10 m2 s−1, and that in NP-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 has a hydrodynamic diameter of 3.6 ± 0.1 nm based on the diffusion coefficient of (1.3 ± 0.1) × 10−10 m2 s−1. For gel-1
3-3.2 has a hydrodynamic diameter of 3.6 ± 0.1 nm based on the diffusion coefficient of (1.3 ± 0.1) × 10−10 m2 s−1. For gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2, the hydrodynamic diameter is almost the same as that of the core size of NPs and we expect that the bound ligands and adsorbed (MPA)S–Cd form a monolayered structure. In gel-1
1-3.2, the hydrodynamic diameter is almost the same as that of the core size of NPs and we expect that the bound ligands and adsorbed (MPA)S–Cd form a monolayered structure. In gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2, most of the (MPA)S–Cd also interact strongly with the NPs in the aqueous solution and form a multilayered structure with a considerably larger hydrodynamic diameter.
3-3.2, most of the (MPA)S–Cd also interact strongly with the NPs in the aqueous solution and form a multilayered structure with a considerably larger hydrodynamic diameter.
Computational modeling of the binding configurations
To complement experimental NMR observations, density functional theory (DFT) simulation was performed to analyze the binding structure of MPA surface ligands on the CdTe NP surface. In the simulation, the models were constructed with one MPA anion and different CdTe NP surfaces, including CdTe(100) and CdTe(111), the two main facets of the CdTe NP (see the ESI† for the detailed description of the simulation methods). From a series of simulations, we concluded that when the MPA anion is placed on the CdTe(100) facet, the most stable geometry of optimized MPA is that each thiol–sulfur bridges with two Cd atoms (Ebind = 1.30 eV, Fig. 3a). The top binding structure (i.e. each thiol–sulfur interacting with one Cd atoms) is also a stable geometry, although the binding energy (Ebind = 0.92 eV, Fig. 3b) is smaller than the bridge binding structure. When the MPA anion is at the CdTe(111) facet, the only stable configuration is the top binding (Ebind = 0.70 eV, Fig. 3c). This result points out that there exist two binding structures of MPA on the CdTe(100) facet including the bridge and the top binding structures, and one binding structure on CdTe(111). Moreover, the stronger binding energy of MPA on CdTe(100) reflects that the (100) facet is the dominant component of the CdTe NP surface, which is in general accordance with the earlier study of CdSe NPs.35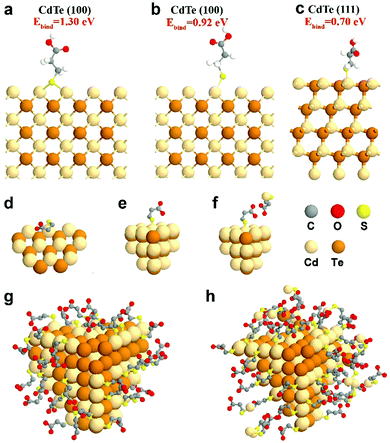 | ||
Fig. 3 Simulation results of MPA on CdTe NPs. DFT-optimized MPA geometries on the CdTe(100) surface with MPA bonded in (a) the bridge fashion or (b) the top fashion, and on CdTe(111) surfaces with MPA bonded in (c) the top fashion. Please see ESI† for the calculation method and binding energies. Schematic diagrams of (d) MPA bound to the edge of the NPs, (e) MPA coated on the facet of the NPs, and (f) the interaction of free and bound ligands. Schematic representations of a CdTe NP in (g) gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 with a monolayer of ligands and (h) gel-1 1-3.2 with a monolayer of ligands and (h) gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 with multiple layers of ligands. 3-3.2 with multiple layers of ligands. | ||
We also simulated the interaction between free MPA–Cd and the MPA coated on CdTe(100) or (111) facets (Fig. 3f and Fig. S14, ESI†). The results showed that when free MPA–Cd is close to the bound MPA on CdTe, hydrogen bonding exists between the carboxylate groups of each MPA molecule. The energy of hydrogen bonding ranges from 0.18 eV to 0.38 eV. These results confirm that strong interactions exist between the CdTe NPs and free MPA–Cd complexes, which agrees with our experimental results.
Furthermore, some free ligands may adsorb onto the NPs by van der Waals forces. In gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2, the nanoparticles retain a monolayer structure, indicating that the bound ligand layer contains some free ligands (Fig. 3g). But in gel-1
1-3.2, the nanoparticles retain a monolayer structure, indicating that the bound ligand layer contains some free ligands (Fig. 3g). But in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2, the surface is a multilayered structure which includes a bound ligand layer entangled with adsorbed ligands and an additional layer of adsorbed ligands. As shown in Fig. 3h, the adsorbed ligands could be further divided into strongly-associated ligands and loosely-associated ligands (via van der Waals forces).
3-3.2, the surface is a multilayered structure which includes a bound ligand layer entangled with adsorbed ligands and an additional layer of adsorbed ligands. As shown in Fig. 3h, the adsorbed ligands could be further divided into strongly-associated ligands and loosely-associated ligands (via van der Waals forces).
Collective non-covalent forces of NP dispersions
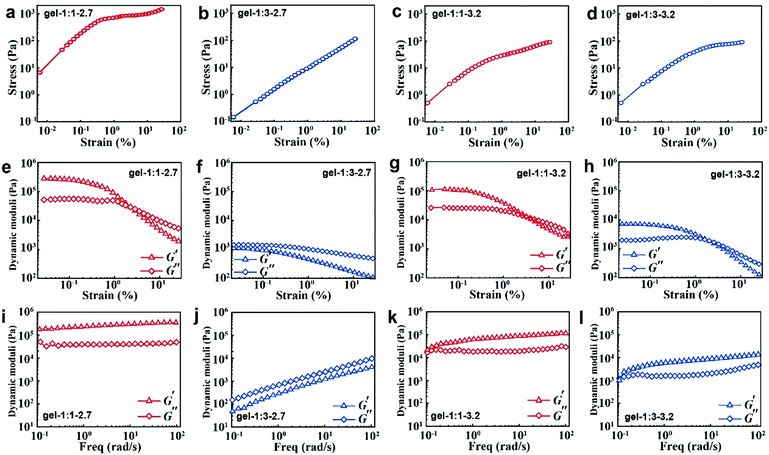
When the NPs are formed into hydrogels, their surface ligand layer affects their collective forces in terms of their viscoelastic properties. Typically, the noncovalent bond in accordance with loss modulus results revealed that the stress increases linearly with the strain amplitude applied to the gels in the initial stage; then the stress deviates from linearity at high strains (Fig. 4a–d). Moreover, the less free MPA–Cd complexes in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 would always induce high shear modulus for all strains (Fig. 4e and g), and in particular, small particles easily contribute to the formation of that behaviour. When more free MPA-Cd complexes are retained in gel-1
1 would always induce high shear modulus for all strains (Fig. 4e and g), and in particular, small particles easily contribute to the formation of that behaviour. When more free MPA-Cd complexes are retained in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, the test result is the opposite (Fig. 4f and h). Frequency responses of gel-1
3, the test result is the opposite (Fig. 4f and h). Frequency responses of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-2.7 (Fig. 4j) are remarkably different from the other three gels, and the latter three gels (Fig. 4i, k and l) revealed G′ > G′′ over the entire range of frequencies, while the former showed that G′ < G′′. This result indicated that more free MPA–Cd complexes may transform the properties of the gel made by small nanoparticles from elastic to viscous behaviour. As mentioned above, the low volume fraction of IPA (νNP
3-2.7 (Fig. 4j) are remarkably different from the other three gels, and the latter three gels (Fig. 4i, k and l) revealed G′ > G′′ over the entire range of frequencies, while the former showed that G′ < G′′. This result indicated that more free MPA–Cd complexes may transform the properties of the gel made by small nanoparticles from elastic to viscous behaviour. As mentioned above, the low volume fraction of IPA (νNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) νIPA = 1
νIPA = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with less free complexes has higher purification efficiency for the MPA–CdTe and facilitates the formation of a gel of high stiffness. However, MPA–CdTe purified by the high volume fraction of IPA (νNP
1) with less free complexes has higher purification efficiency for the MPA–CdTe and facilitates the formation of a gel of high stiffness. However, MPA–CdTe purified by the high volume fraction of IPA (νNP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) νIPA = 1
νIPA = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) contains more free complexes, which leads to viscous behaviour.
3) contains more free complexes, which leads to viscous behaviour.
Similar to van der Waals forces driving the polymer coated microspheres into a highly flocculated state,11 the rheology observations of CdTe NPs are essentially caused by the difference in composition and thickness of surface ligands. In gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2, bound ligands and strongly adsorbed ligands form the monolayer ligand structure, which strengthens the dipole–dipole interaction between the NPs.36 The collective properties of gel-1
1-3.2, bound ligands and strongly adsorbed ligands form the monolayer ligand structure, which strengthens the dipole–dipole interaction between the NPs.36 The collective properties of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-3.2 are close to the rigidity of the inorganic “hard” core due to the thin ligand layer. However, in gel-1
1-3.2 are close to the rigidity of the inorganic “hard” core due to the thin ligand layer. However, in gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2, the bound ligand and its adsorbed ligand entangled with both strongly and weakly form the multilayered ligand structure, which weakens the dipole–dipole interactions because of the large separation between NPs. When these NPs are made into hydrogels, due to the thick ligand layer, the collective property of gel-1
3-3.2, the bound ligand and its adsorbed ligand entangled with both strongly and weakly form the multilayered ligand structure, which weakens the dipole–dipole interactions because of the large separation between NPs. When these NPs are made into hydrogels, due to the thick ligand layer, the collective property of gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-3.2 is close to the viscosity and softness of organic ligands.
3-3.2 is close to the viscosity and softness of organic ligands.
Conclusions
This work demonstrates that the binding patterns of bifunctional ligands on the NP surface have a strong influence on NP–NP interactions, making it possible to better understand non-additivity of various nanoscale non-covalent interactions and create multiscale computational models adequately describing their macroscale behavior.37 The understanding of binding models between ligands and NPs leads to inorganic–organic hydrogels with high viscoelasticity and many applications such as biosensors.38 Similar relationships between surface layer structures can also be generalized to the hierarchical assembly of NPs1,9,13 and other nanoscale components such as clay, graphene, nanocellulose and other nanoscale components using different self-assembly techniques.39–41 This study also enables the establishment of a parallel with the design of the nanoscale components for hydrogels in biology. The knowledge about the surface chemistry of inorganic NPs makes possible not only replication of the best viscoelastic materials found in nature,12,42,43 but actually improving upon them by exploiting the collective supramolecular bonds between surface ligands on their surface. This study also enlightens the pathway to quantitative biomimetics when the design of such materials may not only use the structural blueprint from biological analogs but also the computational algorithms for predictions of their functionalities.Methods
Experimental methods
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (IPA
1 (IPA![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NP) or 3
NP) or 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 volume ratio, and centrifuged at 5000 rpm/5 min. After the supernatant was removed quickly, the viscous transparent NP drops were directly obtained. Residual IPA was removed in a vacuum desiccator for 24 h at room temperature.
1 volume ratio, and centrifuged at 5000 rpm/5 min. After the supernatant was removed quickly, the viscous transparent NP drops were directly obtained. Residual IPA was removed in a vacuum desiccator for 24 h at room temperature.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and gel-1
1 and gel-1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3) were diluted in equal proportions to fulfill the solution test, including solution-state NMR, UV-vis, and PL measurement.
3) were diluted in equal proportions to fulfill the solution test, including solution-state NMR, UV-vis, and PL measurement.
 | (2) |
| ΔEg = ΔEg,NP − ΔEg,0 = a1e−d/b1 + a2e−d/b2 | (3) |
Calculation methods
In this work, the first principle density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP).46–48 The PAW method49 implemented by Kresse et al. was used to calculate the electronic and atomic structures of all the systems studied here. Exchange–correlation effects were treated in generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) potential.50 The kinetic energy cutoff was chosen to be 400 eV. Brillouin zone integration was sampled with 3 × 3 × 1 Monkhorst–Pack mesh K-points for CdTe(100) and CdTe(111) surface system relaxation, and 5 × 5 × 5 K-points for the relaxation of the bulk CdTe. The Gaussian smearing method51 with a width of 0.05 eV was employed to determine electron occupancies. The energy and force convergence criteria are set to be 10−5 eV and 0.03 eV Å−1, respectively.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Natural Science Foundation of China (no. 21773172, no. 21603166 and 21573162 to Y. L. Z.), WIBEZD 2014001-02 to Y. L. Z., the Natural Science Foundation of Zhejiang Province (LQ17B030003) and S20170014 to F. L. T., J. Z. and X. K. acknowledge the National Key Research and Development Program of China 2016YFA0203600, Zhejiang Provincial Natural Science Foundation R19B050003, Zhejiang University K. P. Chao's High Technology Development Foundation.Notes and references
- M. Boles, M. Engel and D. V. Talapin, Self-Assembly of Colloidal Nanocrystals: From Intricate Structures to Functional Materials, Chem. Rev., 2016, 116, 11220 CrossRef CAS PubMed.
- K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Nanoscale Forces and Their Uses in Self-Assembly, Small, 2009, 55, 1600–1630 CrossRef PubMed.
- Z. Tang, N. A. Kotov and M. Giersig, Spontaneous Organization of Single CdTe Nanoparticles into Luminescent Nanowires, Science, 2002, 297, 237–240 CrossRef CAS PubMed.
- Y. J. Harry and G. Steve, Absorbed Polymer Multilayers in A Bad Solvent, Macromolecules, 1991, 24, 3023–3026 CrossRef.
- H. Al-Johani, E. Abou-Hamad, A. Jedidi, C. M. Widdifield, J. Viger-Gravel, S. S. Sangaru, D. Gajan, D. H. Anjum, S. Ould-Chikh and M. N. Hedhili, et al., The Structure and Binding Mode of Citrate in the Stabilization of Gold Nanoparticles, Nat. Chem., 2017, 9, 890–895 CrossRef CAS PubMed.
- W. R. Algar, T. Jeen, M. Massey, W. J. Peveler and J. Asselin, Small Surface, Big Effects, and Big Challenges: Toward Understanding Enzymatic Activity at the Inorganic Nanoparticle–Substrate Interface, Langmuir, 2019, 35, 7067–7091 CrossRef CAS PubMed.
- J. C. Love, L. A. Estroff, J. K. Kriebel, R. G. Nuzzo and G. M. Whitesides, Self-Assembled Monolayers of Thiolates on Metals As A Form of Nanotechnology, Chem. Rev., 2005, 105, 1103–1169 CrossRef CAS PubMed.
- C. T. Yip, T. W. Lo, S.-C. Zhu, G. Y. Jia, H. Sun, C.-H. Lam and D. Lei, Tight-Binding Modeling of Excitonic Response In Van der Waals Stacked 2D Semiconductors Nanoscale Horiz., 2019, 4, 969–974 CAS.
- N. A. Kotov, Nanoparticle Assemblies and Superstructures, Boca Raton, New York, London, Tokyo, CRC Press, 2005, p. 648 Search PubMed.
- S. Buzzaccaro, R. Rusconi and R. Piazza, “Sticky” hard spheres: Equation of state, phase diagram, and metastable gels, Phy. Rev. Lett., 2007, 99, 098301 CrossRef PubMed.
- J. E. Smay, G. M. Gratson, R. F. Shepherd, J. Cesarano III and J. A. Lewis, Directed Colloidal Assembly of 3D Periodic Structures, Adv. Mater., 2002, 14, 1279–1283 CrossRef CAS.
- M. Yang, H. Chan, G. Zhao, J. H. Bahng, P. Zhang, P. Král and N. A. Kotov, Self-Assembly of Nanoparticles into Biomimetic Capsid-like Nanoshells, Nat. Chem., 2017, 9, 287–294 CrossRef CAS PubMed.
- S. Bhattacharya and S. K. Samanta, Soft-Nanocomposites of Nanoparticles and Nanocarbons with Supramolecular and Polymer Gels and Their Applications, Chem. Rev., 2016, 116, 11967–12028 CrossRef CAS PubMed.
- K. Skakuj, S. Wang, L. Qin, A. Lee, B. Zhang and C. A. Mirkin, Conjugation Chemistry-Dependent T-Cell Activation with Spherical Nucleic Acids, J. Am. Chem. Soc., 2018, 140, 1227–1230 CrossRef CAS PubMed.
- N. A. Kotov, Inorganic Nanoparticles as Protein Mimics, Science, 2010, 330, 188–189 CrossRef CAS PubMed.
- R. Klajn, K. J. M. Bishop and B. A. Grzybowski, Light-Controlled Self-Assembly of Reversible and Irreversible Nanoparticle Suprastructures, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 10305–10309 CrossRef CAS PubMed.
- F. Rechberger and M. Niederberger, Synthesis of aerogels: from molecular routes to 3-dimensional nanoparticle assembly, Nanoscale Horiz., 2017, 2, 6–30 RSC.
- A. L. Rogach, T. Franzl, T. A. Klar, J. Feldmann, N. Gaponik, V. Lesnyak, A. Shavel, A. Eychmüller, Y. P. Rakovich and J. F. Donegan, Aqueous Synthesis of Thiol-Capped CdTe Nanocrystals:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) State-of-the-Art, J. Phys. Chem. C, 2007, 111, 14628–14637 CrossRef CAS.
State-of-the-Art, J. Phys. Chem. C, 2007, 111, 14628–14637 CrossRef CAS. - A. L. Rogach, L. Katsikas, A. Kornowski, D. Su, A. Eychmüller and H. Weller, Synthesis and Characterization of Thiol-Stabilized CdTe Nanocrystals, Ber. Bunsen-Ges., 1996, 100, 1772–1778 CrossRef CAS.
- Y. Li, L. Jing, R. Qiao and M. Gao, Aqueous synthesis of CdTe nanocrystals: progresses and perspectives, Chem. Commun., 2011, 47, 9293–9311 RSC.
- A. Shavel, N. Gaponik and A. Eychmüller, Factors Governing the Quality of Aqueous CdTe Nanocrystals:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Calculations and Experiment, J. Phys. Chem. B, 2006, 110, 19280–19284 CrossRef CAS PubMed.
Calculations and Experiment, J. Phys. Chem. B, 2006, 110, 19280–19284 CrossRef CAS PubMed. - Y. Min, M. Akbulut, K. Kristiansen, Y. Golan and J. Israelachvili, The Role of Interparticle and External Forces in Nanoparticle Assembly, Nat. Mater., 2008, 7, 527–538 CrossRef CAS PubMed.
- E. Scalise, V. Srivastava, E. Janke, D. Talapin, G. Galli and S. Wippermann, Surface Chemistry and Buried Interfaces in All-Inorganic Nanocrystalline Solids, Nat. Nanotechnol., 2018, 13, 841–848 CrossRef CAS PubMed.
- Z. Chu, Y. Han, P. Král and R. Klajn, “Precipitation on Nanoparticles”: Attractive Intermolecular Interactions Stabilize Specific Ligand Ratios on the Surfaces of Nanoparticles, Angew. Chem., Int. Ed., 2018, 57, 7023–7027 CrossRef CAS PubMed.
- C. Wang, M. Fang, J. Han, H. Zhang, Y. Cui and B. Yang, Two Opposite Effects of Alcohols in the Precipitation of Aqueous Nanocrystals, J. Phys. Chem. C, 2009, 113, 19445–19451 CrossRef CAS.
- W. W. Yu, L. Qu, W. Guo and X. Peng, Experimental Determination of the Extinction Coefficient of CdTe, CdSe, and CdS Nanocrystals, Chem. Mater., 2003, 15, 2854–2860 CrossRef CAS.
- A. Ceccon, V. Tugarinov and G. M. Clore, TiO2 Nanoparticles Catalyze Oxidation of Huntingtin Exon 1-Derived Peptides Impeding Aggregation: A Quantitative NMR Study of Binding and Kinetics, J. Am. Chem. Soc., 2018, 141, 94–97 CrossRef PubMed.
- L. Piveteau, T.-C. Ong, B. J. Walder, D. N. Dirin, D. Moscheni, B. Schneider, J. Bär, L. Protesescu, N. Masciocchi and A. Guagliardi, et al., Resolving the Core and the Surface of CdSe Quantum Dots and Nanoplatelets Using Dynamic Nuclear Polarization Enhanced PASS–PIETA NMR Spectroscopy, ACS Cent. Sci., 2018, 4, 1113–1125 CrossRef CAS PubMed.
- D. K. Nagesha, X. Liang, A. A. Mamedov, G. Gainer, M. A. Eastman, M. Giersig, J.-J. Song, T. Ni and N. A. Kotov, In2S3 Nanocolloids with Excitonic Emission: In2S3 vs CdS Comparative Study of Optical and Structural Characteristics, J. Phys. Chem. B, 2001, 105, 7490–7498 CrossRef CAS.
- D. Diaz, M. Rivera, T. Ni, J.-C. Rodriguez, S.-E. Castillo-Blum, D. Nagesha, J. Robles, O.-J. Alvarez-Fregoso and N. A. Kotov, Conformation of Ethylhexanoate Stabilizer on the Surface of Cds Nanoparticles, J. Phys. Chem. B, 1999, 103, 9854–9858 CrossRef CAS.
- S. A. Majetich, A. C. Carter, J. Belot and R. D. McCullough, lH NMR Characterization of the CdSe Nanocrystallite Surface, J. Phys. Chem., 1994, 98, 13705–13710 CrossRef CAS.
- B. Fritzinger, I. Moreels, P. Lommens, R. Koole, Z. Hens and J. C. Martins, In Situ Observation of Rapid Ligand Exchange in Colloidal Nanocrystal Suspensions Using Transfer NOE Nuclear Magnetic Resonance Spectroscopy, J. Am. Chem. Soc., 2009, 131, 3024–3032 CrossRef CAS PubMed.
- Z. Hens and J. C. Martins, A Solution NMR Toolbox for Characterizing the Surface Chemistry of Colloidal Nanocrystals, Chem. Mater., 2013, 25, 1211–1221 CrossRef CAS.
- B. Fritzinger, R. K. Capek, K. Lambert, J. C. Martins and Z. Hens, Utilizing Self-Exchange To Address the Binding of Carboxylic Acid Ligands to CdSe Quantum Dots, J. Am. Chem. Soc., 2010, 132(29), 10195–10201 CrossRef CAS PubMed.
- J. Zhou, C. Pu, T. Jiao, X. Hou and X. Peng, A Two-Step Synthetic Strategy toward Monodisperse Colloidal CdSe and CdSe/CdS Core/Shell Nanocrystals, J. Am. Chem. Soc., 2016, 138, 6475–6483 CrossRef CAS PubMed.
- Z. Zhang, Z. Tang, N. A. Kotov and S. C. Glotzer, Simulations and Analysis of Self-Assembly of CdTe Nanoparticles into Wires and Sheets, Nano Lett., 2007, 7(6), 1670–1675 CrossRef CAS PubMed.
- C. Batista-Silvera, R. Larson and N. A. Kotov, Non-Additivity of Nanoparticle Interactions, Science, 2015, 350(6257), 1242477 CrossRef PubMed.
- T. Hu, J. Xu, Y. Ye, Y. Han, X. Li, Z. Wang, D. K. Sun, Y. L. Zhou and Z. H. Ni, Visual Detection of Mixed Organophosphorous Pesticide Using QD-AChE Aerogel Based Microfluidic Arrays Sensor, Biosens. Bioelectron., 2019, 136, 112–117 CrossRef CAS PubMed.
- L.-B. Mao, H.-L. Gao, H.-B. Yao, L. Liu, H. Cölfen, G. Liu, S.-M. Chen, S.-K. Li, Y.-X. Yan, Y.-Y. Liu and S.-H. Yu, Synthetic Nacre by Predesigned Matrix-Directed Mineralization, Science, 2016, 354, 107–110 CrossRef CAS PubMed.
- Y. Zhang, F. Zhang, Z. Yan, Q. Ma, X. Li, Y. Huang and J. A. Rogers, Printing, Folding and Assembly Methods for Forming 3D Mesostructures in Advanced Materials, Nat. Rev. Mater., 2017, 2, 17019 CrossRef CAS.
- S. E. Wolf, J. Leiterer, M. Kappl, F. Emmerling and W. Tremel, Early Homogenous Amorphous Precursor Stages of Calcium Carbonate and Subsequent Crystal Growth in Levitated Droplets, J. Am. Chem. Soc., 2008, 130(37), 12342–12347 CrossRef CAS PubMed.
- Y. Zhou, P. F. Damasceno, B. S. Somashekar, M. Engel, F. Tian, J. Zhu, R. Huang, K. Johnson, C. McIntyre, K. Sun, M. Yang, P. F. Green, A. Ramamoorthy, S. C. Glotzer and N. A. Kotov, Unusual Multiscale Mechanics of Biomimetic Nanoparticle Hydrogels, Nature Commun., 2018, 9, 181 CrossRef PubMed.
- Z. Nie, A. Petukhova and E. Kumacheva, Properties and Emerging Applications of Self-Assembled Structures Made from Inorganic Nanoparticles, Nat. Nanotechnol., 2010, 5, 15–25 CrossRef CAS PubMed.
- Z. Yuan, A. Zhang, Y. Cao, J. Yang, Y. Zhu and P. Yang, Effect of Mercaptocarboxylic Acids on Luminescent Properties of CdTe Quantum Dots, J. Fluoresc., 2012, 22, 121–127 CrossRef CAS PubMed.
- S. Sapra and D. D. Sarma, Evolution of the Electronic Structure with Size in II–VI Semiconductor Nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 125304 CrossRef.
- G. Kresse and J. Hafner, Ab initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Hafner, Ab initio Molecular-Dynamics Simulation of The Liquid-Metal–Amorphous-Semiconductor Transition in Germanium, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00397e |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |