Top-down fabrication of small carbon nanotubes

Abstract

The control of diameter and chirality of carbon nanotubes (CNTs) has long been extremely challenging and critical for various CNT applications. Here, we report a top-down method that allows for reliable control of the diameter of individual few-walled carbon nanotubes (CNTs), thereby producing nanotubes with a desired diameter, including the smallest ones. This method involves the use of electron irradiation assisted by concurrent thermal annealing, which enables carbon removal from a CNT in a rather organized fashion, leading the nanotube to shrink uniformly and flawlessly. The smallest nanotubes can be routinely obtained by this self-contracting process of any few-walled nanotubes (1–4 shells) to reach their diameter limits, that is, 4.1 Å for single-walled CNTs (likely indexed as (5, 0) or (3, 3)), and 1.01, 1.66 and 2.41 nm for 2–4 walled CNTs, respectively (with their innermost tubes of ∼3.2 Å presumably indexed as (4, 0)). A new scenario based solely on the climb movements of 5|7 dislocations is proposed to well explain the observed nanotube shrinking processes, which are associated with the motions of atomic-scale kinks in different pathways. Due to the unique ability to dictate the exact CNT diameter, this facile method may open up a new avenue toward the ultimate strategy for bulk production of monosized and even chirality-specific small CNTs.

---

New concepts

Size and chirality control of carbon nanotubes (CNTs) is a prerequisite for their many high-tech applications. Currently, producing the structural-specific CNTs through the controlled growth approaches via e.g. catalyst design etc., still remains a challenge. CNT growth is essentially an orderly mass-addition process. We propose here that there could be a strategy to produce CNTs through the opposite process, i.e., the continuous atom removal from a given CNT. However, a key question remains: can this mass-reduction process proceed in a controlled way, so as to obtain the desired well-defined CNTs? In this work, we demonstrate a facile diameter-control method that enables carbon removal from a CNT in a rather organized fashion, thus routinely producing nanotubes with any wanted smaller diameter while maintaining their structural perfection. The smallest nanotubes reaching their theoretical diameter limits can thus be easily obtained for any few-walled CNTs (1–4 shells), which even makes bulk production of chirality-specific CNTs possible. Importantly, we also propose a scenario based solely on the climb movements of 5|7 dislocations to well explain the frequently-observed motions of atomic-scale kinks in different pathways, which is critical for the CNT shrinking process in a seamless pattern.

Introduction

The extraordinary properties of carbon nanotubes (CNTs) are strongly dependent upon their size and atomic-scale structure. A slight change in the CNT diameter and helicity, as defined by the chirality indices (n, m), can drastically modify its band structure and electronic properties. Therefore, CNTs with precisely-defined diameter and chirality are critical for many high-tech applications, such as CNT transistors and photoelectric devices, etc.^1–4 Over the past two decades, substantial progress has been made toward the bulk production of single-wall CNTs (SWNTs) within a narrow structural range by e.g. developing selective growth approaches via catalyst design and kinetics optimization, etc.^5–10 Nevertheless, the ultimate goal of producing a certain type of CNT with any desired diameter or chirality still remains tremendously challenging.

CNT growth is essentially an orderly mass-addition process. Accordingly, there might be a strategy to produce structural-specific CNTs through the opposite process, that is, continuous atom removal from a given CNT. Such a substractive (or top-down) process, however, may probably result in poorly-defined CNT structures if it proceeds in a random manner. In this work, we present a facile top-down approach that enables carbon removal from any few-walled CNT (1–4 walls) in a rather organized fashion, so as to routinely produce nanotubes with any wanted smaller diameter while maintaining their structural perfection. This post-synthesis top-down approach involves the use of electron irradiation assisted by concurrent thermal annealing, as demonstrated inside a transmission electron microscope (TEM). We also propose a new scenario based solely on dislocation climb motion to explain all the observed phenomena during the CNT seamless shrinking process, including the organized atom removal and associated kink motion behaviors.

In particular, this CNT self-contracting process provides us with a rare opportunity to study the issue in terms of how small a nanotube can be, which has aroused the great interest of the CNT and electronics communities. Because most of the unique properties of CNTs originate from the quantum confinement along the circumferential direction, the extremely thin CNTs can possess many exotic electronic properties, such as the superconducting behavior found in 4.2 Å SWNTs.¹¹ Numerous efforts have been focused on experimentally exploring the CNT diameter limit.^11–17 To date, the smallest self-stabilized SWNTs ever reported are around 4 Å in diameter,¹⁵ and even thinner tubes in the range of 3–4 Å can be occasionally found in the spatially confined environments (such as the innermost shell encapsulated in a multi-walled CNT (MWNT)).^16,17 Then, what exactly is the smallest SWNT diameter? Does it have any certain chirality? More generally, what are the smallest diameters for double-walled CNTs (DWNTs), triple-walled CNTs (TWNTs) and other few-walled CNTs? These crucial and interesting issues, however, remain elusive due to the lack of experimental attempts to clarify them. We herein also try to give our own answer to these questions based on the present technique.

Results and discussion

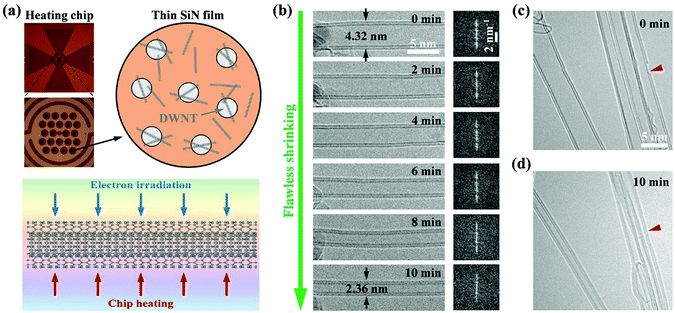
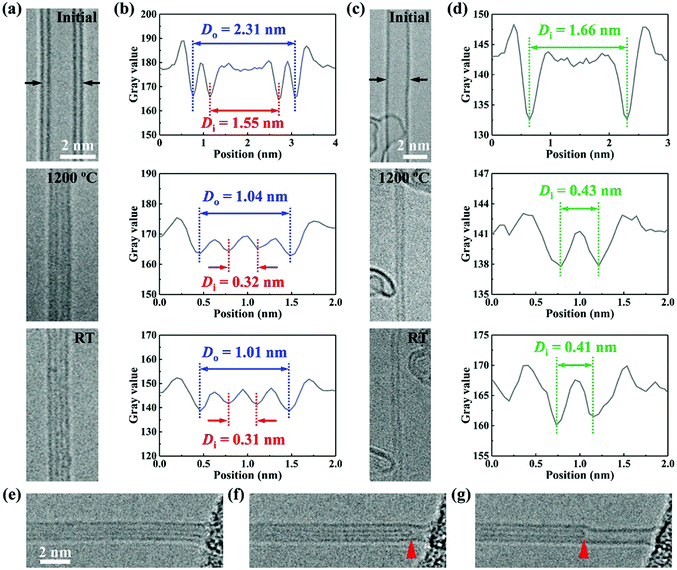
We performed the experiments by using double-walled CNTs synthesized by an arc-discharge method (a small amount of 1-, 3-, and 4-walled CNTs can also be found in this sample). The choice of DWNTs relies on the fact that they are the simplest MWNT objects to study the inter-layer coupling and synergy effects involved in the tube shrinking process. The CNT shrinking experiments were conducted inside a TEM (FEI Talos F200s) by using an MEMS-based heating holder (FEI-NanoEx) with an accurate temperature control up to 1200 °C.¹⁸Fig. 1a illustrates schematically the experimental method: a number of DWNTs, randomly distributed on a thin SiN film of the MEMS heating chip, were exposed to a 200 kV electron beam at increased temperature. The series of high-resolution TEM (HRTEM) images in Fig. 1b shows a representative shrinking process of a single DWNT under irradiation/annealing. The pristine DWNT had an initial outer diameter of 4.32 nm. When irradiated with a beam dose of 20 A cm⁻² at 1200 °C, this DWNT began to shrink seamlessly without introducing visible disorder to the tube lattice, as also evident from the corresponding fast Fourier transform (FFT) patterns (Fig. 1b). After 10 min irradiation, the DWNT shrank uniformly down to 2.36 nm, reduced by ∼45% compared with the initial diameter (see Movie S1, ESI† for more details).

Fig. 1 Uniform and flawless shrinking of the double-walled CNTs. (a) Schematic illustration of the in situ TEM experimental setup. The randomly distributed DWNTs on a thin SiN film of the MEMS heating chip are exposed to electron irradiation under elevated temperature for tailoring the tube diameter. (b) Structural evolution of a shrinking DWNT under irradiation/annealing (with a beam dose of 20 A cm⁻² at 1200 °C) and the corresponding fast Fourier transform (FFT) patterns. (c and d) Multiple DWNTs before and after the 10 min irradiation/annealing respectively. The red arrowheads indicate the hole in the outer wall of a DWNT that is repaired after the shrinking process.

In some cases, we deliberately prolonged the irradiation to explore the thinnest CNT possible. Strikingly, as shown in the case of Fig. 2a, this process can lead the DWNT to shrink until reaching an extremely small outer diameter of only ∼1.04 nm (by examining the image intensity profile in Fig. 2b). Meanwhile, the inner shell of the DWNT also evolves into an ultrathin nanotube of only ∼3.2 Å. When cooled down to ambient temperature, the DWNT contracted a little further, accompanied by a slight reduction of the outer and inner diameters down to 1.01 and 0.31 nm, respectively, with a wall spacing of 3.5 Å in between. Here, as far as we know, we have produced the smallest self-stabilized DWNT, because the diameter of the inner tube already approaches the theoretical limit, i.e. ∼3 Å, which was scarcely observed and only possible under confined conditions.^16,17 With further irradiation, the inner tube broke and shrank in length due to the continuous atom evaporation from the closed cap, as presented in Fig. 2e–g and Movie S2 (ESI†). The localized carbon removal can be primarily attributed to the extremely curved surface at the CNT apex constructed with pentagons and tetragons, which may significantly reduce the displacement threshold energy (i.e. the minimum energy to cause atoms to be permanently displaced from its lattice site).^19,20 This actually implies that with the confinement from the outside wall, the inner tube at this stage should be at its diameter and stability limit, since further carbon loss would only lead the nanotube to break or shrink in length. A nanotube of 3.1–3.2 Å can be most likely indexed as a zigzag (4, 0) (3.3 Å) tube, capped with half a C₁₆ cage that comprises one tetragon at the top, surrounded by four pentagons.¹⁶ The less probable structure is the armchair (2, 2) (2.8 Å) nanotubes, which can be capped by half of a C₁₂ cage, as proposed by Zhao et al.¹⁷

Fig. 2 Thinnest DWNT and SWNT obtained by the shrinking process. (a) HRTEM images showing a DWNT before and after the self-contracting process, as well as its final state at room temperature. (b) The corresponding image intensity profiles across the DWNT diameter at the different stages. (c and d) Similar case showing the diameter changes of a SWNT. A representative case of a DWNT at its dimeter and stability limit (e), after the breakage (f) and further axial shrinkage of its inner shell (g). The arrows in (f and g) indicate the cap of the inner tube.

Obviously, one of the most fascinating advantages of this top-down approach is the ability to produce ultrathin nanotubes in a completely controlled manner, which can be practically applied for engineering nearly all the few-walled CNTs. Using this method, we also created SWNTs as thin as 4.1 Å, which is about 1 Å larger than the smallest nanotube of ∼3 Å due to the lack of confinement effect. Nevertheless, this should be at least among the smallest free-standing SWNTs. In fact, the smallest SWNTs ever synthetized are 4.2 ± 0.2 Å in diameter.¹² Thus, through this self-contracting process, our experiments confirm the earlier prediction that the self-stabilized CNTs should be at least 4 Å in diameter.²¹ Theoretically, a 4 Å nanotube likely has a zigzag (5, 0) (4.0 Å) or armchair (3, 3) (4.1 Å) structure,^14,15 and both can be capped by half a C₂₀ cage.

Furthermore, the thinnest triple- and four-walled CNTs of only 1.66 and 2.41 nm in diameter can also be routinely created in a similar way (see Fig. S1, ESI†). These two CNTs both have an innermost shell as small as 3.2 Å, making the entire nanotubes approach the theoretical limits for 3- and 4-walled CNTs, respectively. Since the diameter of the innermost shell is close to the wall spacing (3.4–3.5 Å), we suggest that the smallest diameter of n-walled CNTs (n ≥ 2) can be practically approximated as: D_min (nm) = 0.34 × (2n − 1).

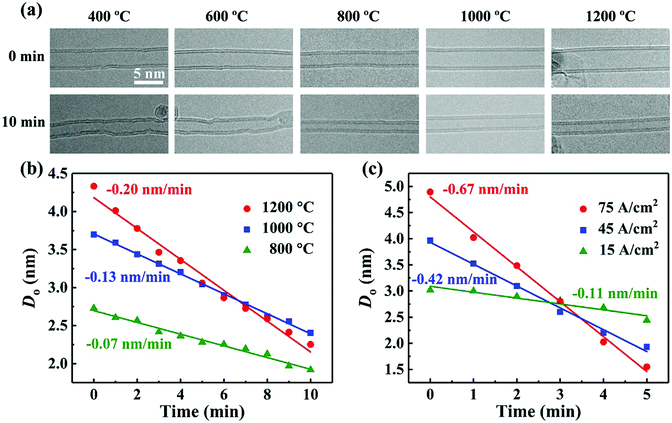
Since the annealing temperature is far below the sublimation point of CNTs (>2000 °C),²² the irradiation should dominate the mass loss process through the “knock on” collision. This can be further confirmed by a comparative experiment: the CNT annealing at 1200 °C without irradiation for 1 hour caused no visible size reduction of the nanotube (Fig. S2, ESI†). Nevertheless, the concurrent annealing may somewhat influence the progress of CNT shrinking. We then experimentally evaluated these two factors, i.e. the irradiation dose and annealing temperature, as they are the two key variables for precise control of nanotube diameter. Fig. 3a shows a series of HRTEM images of the DWNTs irradiated with the same electron dose of 20 A cm⁻² but at different temperatures (T = 400, 600, 800, 1000 and 1200 °C, respectively). All the DWNTs shrank considerably under 10 min irradiation. However, with the decrease in temperature (below 800 °C), the originally straight tube walls became increasingly disordered. Actually, when irradiated at room temperature, the DWNTs become even more defective (Fig. S3, ESI†), proving the importance of the high annealing temperature (better above 1000 °C) for retaining the high structural quality of the irradiated DWNTs.^18,19,23 Along with the graphitic layer disordering, the decreased temperature also leads to a lower CNT shrinking rate, as is evident from the tube size changes at different annealing temperatures (Fig. 3a). A more quantitative evaluation of this issue can be found in Fig. 3b. The DWNT diameter decreases linearly with the irradiation time, and from the slope of the data points in Fig. 3b, we calculate the diameter shrinking rates at 800, 1000, and 1200 °C to be 0.07, 0.13 and 0.20 nm min⁻¹, respectively.

Fig. 3 Dependence of the DWNT shrinking process on annealing temperature and irradiation intensity. (a) HRTEM images showing the dimensional and morphological changes of the DWNTs under irradiation (with the same dose of 20 A cm⁻²) at different annealing temperatures. Outer diameter (D_o) as a function of time during the DWNT shrinking processes at different annealing temperatures (b), or at 1200 °C with different irradiation doses (c).

The temperature dependence of the DWNT shrinking rate can be understood by evaluating the displacement threshold energy (T_d).^19,24,25 We determine T_d by relating it to the atom displacement rate p (it can be experimentally obtained by measuring the size reduction). p is given by the product of the beam current density j and the displacement cross section σ, where σ can be related to T_d using the analytical approximation proposed by McKinley and Feshbach.²⁴ Thus, the T_d values for the DWNTs irradiated at 800, 1000, and 1200 °C are estimated to be 34, 32 and 30 eV, respectively. As expected, the calculated T_d decreases with increasing temperature, indicating that carbon atoms are more easily displaced as interstitial atoms or evaporated into the vacuum under irradiation due to thermal agitation. However, these values are significantly larger than the reported T_d for MWNTs irradiated at room temperature (15–20 eV).²⁶ Considering these hot DWNTs and their small diameter, the discrepancy between the calculated and actual values should be even larger. We reckon that this discrepancy may be accounted for by the following two reasons. First, the displaced atoms as interstitials would immediately recombine with the irradiation-induced vacancies at high temperature, causing an underestimated p through measuring the tube size reduction. Second, the atom evaporation, i.e. the complete loss of carbon from the lattice, occurs only at certain locations (i.e. the kinks in the nanotubes, as discussed below) instead of the entire tube walls,¹⁸ which also reduces the nominal atom displacement rate p. The above two factors can both cause a reduced σ and accordingly an over-calculated T_d.

Besides, the relationship between p and j also implies that the CNT shrinking rate depends positively on the irradiation dose. As clearly demonstrated in Fig. 3c, for the irradiation experiments at the same temperature of 1200 °C, the increased beam intensity can remarkably accelerate the shrinking process of DWNTs. This, along with the temperature adjustment, can provide a precise control for tailoring the nanotube diameter.

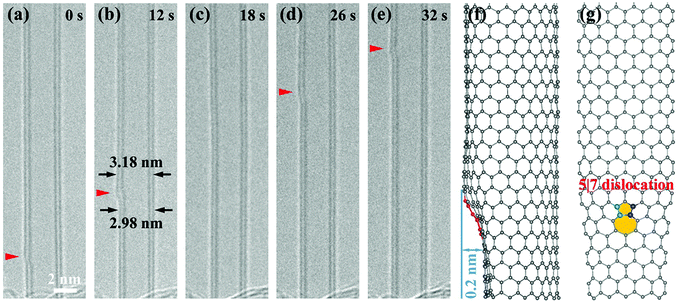
The most notable feature of the CNT self-contracting process is that it proceeds in a nearly flawless fashion or, in other words, the substantial loss of mass does not destroy the nanotube perfection. Closer examination shows that instead of the random removal of atoms from the lattice, the CNT actually shrinks in a rather organized way associated with the kink nucleation and motion, which was frequently observed in our experiments. As depicted in Fig. 4a–e, a kink first appeared at the bottom of the left wall and propagated upward along the DWNT with a velocity of ∼0.54 nm s⁻¹. Once the kink was swept by, the tube diameter was reduced instantly (see Movie S3, ESI†). This kink structure, as previously visualized,^27,28 indicates the existence of a 5|7 dislocation core. As schematically illustrated in Fig. 4f and g, the warping of a graphene lattice containing a 5|7 topological defect can result in a visible kink, i.e. a 0.2 nm-tall step on the side wall, in agreement with our observation and the previous structural simulations.²⁰ From the dislocation theory viewpoint, the observed kink movement in the longitudinal direction should originate from dislocation climb.^29,30 As pointed out by Ding et al., an atomistic step of the climb process involves the removal of two atoms from the 5|7 dislocation core, followed by the immediate bond reconstruction that restores the lattice seamlessly, thus leading the 5|7 defect to shift by one lattice parameter.³⁰ More precisely, the C₂ dimers depart preferably from the side of the pentagon due to its lowest sublimation energy (as illustrated in Fig. 5g and 6), and the continuous emission of C₂ dimers from these particular sites causes the kink to move in a specific path, leading to the seamless CNT shrinkage.²⁰

Fig. 4 Kink motion along a DWNT in the roughly longitudinal direction. (a–e) Time-lapsed HRTEM images showing the kink propagating upward along a DWNT, with an estimated velocity of 0.54 nm s⁻¹. The red arrowheads point to the location of the kink that, however, disappears in (c) due to its changes in the advancing direction. (f and g) Atomic structural model of the kink containing the 5|7 topological defect in the hexagonal lattice of a nanotube. The kink structure of about 0.2 nm tall is evident in the side view of the model (f). The green and blue atoms in (g) denote the C₂ dimers at the left and right sides of the pentagon that can be preferentially removed under irradiation.

Fig. 5 Spiral kink motion along a DWNT. (a) A pristine DWNT with it end protruding out of the substrate. (b–g) Time-lapsed HRTEM images showing the kink propagation in a spiral path that results in the size reduction of the DWNT. As marked with the blue arrows, the kink appears alternately on the two sidewalls, indicating a spiral path along the tube surface. Note that the kink vanished at the closed cap of the tube, resulting in the shrinkage of DWNT in both the radial and axial directions (g). (h) Further length reduction of the DWNT after another kink was swept by.

Fig. 6 Climb paths of 5|7 dislocation (for zigzag CNT). (a) Longitudinal path. The red atoms in an armchair chain denote the C₂ dimers that are sequentially removed from the tube lattice, resulting in the longitudinal kink motion. (b and c) Right- and left-handed spiral paths. The blue and green atoms denote the sequential removal of C₂ dimers in the two zigzag chains during the spiral kink motion. (d) Combined path: a longitudinal path mixed with spiral motions of the kink.

In addition to the longitudinal motion, the kink was also found to move in a spiral path along the nanotube walls, similar to Huang's observation in the nanotubes under tensile loading at high temperature.²⁹ Such a screw motion is usually attributed to the stress-induced dislocation glide along the glide plane (i.e. the close-packed planes) inclined to the tube axis.^29–31 In our case, however, all the nanotubes are lying freely on the substrate without a strain intentionally applied along the tube. There might be a possibility that the CNT can be slightly stressed if the tube length decreases upon atom evaporation, with its ends being clamped due to their bonding with the substrate. We then chose a DWNT with its end protruding out of the substrate, as shown in Fig. 5. In this freestanding configuration, we still observed the spiral motion of the kink toward the tube end that switched from the right (Fig. 5b) to the left wall (Fig. 5d), and then back to the right wall (Fig. 5f). Once the kink vanished at the closed cap (Fig. 5g), the nanotube shrank immediately in both radial and axial directions (see Movie S4, ESI†). We therefore conclude that the spiral kink motion, as well as the tube shrinkage, should not arise from the plastic elongation based on dislocation glide that was proposed to explain Huang's observation of the superplastic CNTs.^29,32,33

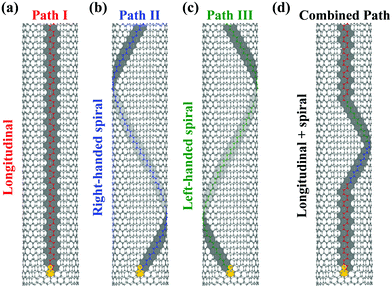
We propose here that all the observed kink motions can be well understood in terms of the dislocation climb without involving the glide mechanism. As seen in Fig. 6, for a given 5|7 dislocation core (take here the lattice of a zigzag nanotube for example, with the 5|7 core orientated in the tube axis direction, i.e. its glide plane along the circumferential direction), the removal of C₂ dimers can occur at the left or right side of the pentagon (also see Fig. 5g),²⁰ which allows the kink to advance in typically three directions, denoted as paths I–III respectively. In path I, the edge dislocations climb vertically, shortening the extra plane by sequential removal of the atoms in an armchair chain (marked as red atoms in Fig. 6a), leading to the longitudinal motion of the kink. In path II or III, the 5|7 dislocation core climbs along a close-packed plane with the removed atoms in a zigzag chain (as marked in blue and green in Fig. 6b and c, denoted as right-handed and left-handed helicities, respectively), thus exhibiting a spiral path along the tube axis. Furthermore, the mixture of the three paths permits a more complicated trajectory for kink motion. As shown in the combined path in Fig. 6d, a vertically-climbing kink can change its advancing direction sequentially into spiral paths II and III, and eventually back to its original path I. This can account for the disappearance of a propagating kink from the field of view as seen in Fig. 4c (the kink should now sit on the top or bottom side of the tube and therefore be hardly visible under TEM lattice imaging) and its reappearance on the same side of the nanotube (Fig. 4d). We suggest that the changes in the kink advancing direction can be ascribed to the irradiation/thermally induced local stress variation, interlayer coupling around the kink, or the interaction of the 5|7 core with the lattice point defects like vacancies or interstitials.²⁰

According to this pure dislocation climb scenario, the kink motion is expected to be chirality dependent. Besides the zigzag-type nanotubes, armchair CNTs also allow both longitudinal and spiral kink motions (see Fig. S4, ESI†). Theoretically, due to the chiral symmetry, a pure longitudinal kink motion is only possible for zigzag and armchair nanotubes, along an armchair or zigzag chain, respectively. A pure spiral trajectory, instead, can be allowed for all the nanotubes irrespective of their chirality (the exact spiral angle, i.e. its inclination angle with respect to the circumferential direction, is dependent on the tube chirality and 5|7 core orientation). It is worth noting that for a chiral nanotube, the kink can propagate roughly along the longitudinal direction. Such a quasi-longitudinal motion, at the atomic scale, should combine the different climb paths through the removal of C₂ dimers from either the left or right side of the pentagon for each step (see Fig. S5, ESI†). In fact, the mixture of climb paths can also explain how the 5|7 kinks of different tube walls can migrate as a group, regardless of the possible divergence of their close-packed planes due to the different chiralities of the walls. The present dislocation dynamics thus differs from the previous explanation of the kink collaborative motion based on both dislocation glide and climb movements, which involves the contribution from the mechanical stress in the system.³⁰

After the vanishing of the kinks at the tube ends (see e.g.Fig. 5e), a fresh kink source is required for maintaining the following shrinking process. Such defects can form through the C–C bond rotation known as the Stone–Wales (SW) transformation.³⁴ Besides, they can also nucleate from a di-vacancy under sublimation conditions (under irradiation or at high temperature) through bond reconstruction, producing a pair of head-to-head edge dislocations, as proposed by Ding et al.³⁰ The two freshly-formed kinks then move in opposite directions simultaneously along the nanotube, which is consistent with our observation (see Fig. S6, ESI†). Interestingly, we also observed that small holes in the broken shells can be repaired when interacting with the propagating kinks (see Fig. 1c, d, Fig. S7 and Movie S5, ESI†). This seems to agree with the theoretical prediction that the 5|7 dislocation core can serve as a scavenger for vacancy defects on the tube lattice,²⁰ and shows the potential use of this post-synthesis method to improve the CNT structural quality.

Also of great interest would be the chirality evolution of a CNT during its diameter reduction process.^35,36 As pointed out by the previous studies, apart from the size shrinking, kink propagation can lead the nanotube chirality to change from (n, m) to (n − 1, m) or (n, m − 1) for each transition step.^29,31 The final tube chirality relies on the starting chirality and its evolution path during the CNT shrinking process (the experimental analysis of this issue is now under way). Importantly, with the tube getting thinner, especially when approaching its diameter limit, the possible chiralities of the final tube become very limited (such as the cases in 4 Å and 3 Å nanotubes). Thus, by self-contracting each n-shell nanotube to the same diameter limit (e.g. 4 Å for SWNTs), we can not only produce the monosized small CNTs, but possibly achieve the chirality-limited or even chirality-specific production of nanotubes.

The last but not the least important, multiple DWNTs exposed to the same e-beam can be controlled to shrink simultaneously (as shown in Fig. 1c and d). This is different from the previous CNT shrinking processes assisted with tensile loading and/or Joule heating that allows only one single nanotube to be manipulated each time and usually leads to a non-uniform shape.^25,29 Moreover, if we further increase the irradiation area with a broader high-current electron beam, hundreds and even thousands of CNTs can shrink simultaneously under the irradiation (see e.g. Fig. S8, ESI†), thus demonstrating the potential of this method for the diameter control of CNTs on a large scale.

Conclusions

To sum up, we have demonstrated, as far as we know, the first top-down approach for reliable manipulation of CNT diameter. Few-walled CNTs in this highly controllable process can shrink in a uniform and flawless fashion by irradiating them at high temperature. This CNT self-contracting technique allow us to readily produce ultrathin 1–4 walled nanotubes approaching their diameter limits, which roughly follow the simplified expression D_min (nm) = 0.34 × (2n − 1) for n-shell CNTs (n ≥ 2). The carbon loss from the shrinking CNT proceeds in an organized fashion mediated by the atomic-scale kink motion along the nearly perfect tube lattice. Without involving the dislocation glide mechanism, we propose a scenario based solely on the climb movements of 5|7 dislocation cores, which can well explain all the observed kink motion behaviors. The CNT-shrinking rate depends highly on the irradiation dose or annealing temperature, thus exhibiting its unique ability to dictate the exact CNT diameter. Besides, this facile method also possesses great potential for CNT batch processing, during which multiple nanotubes can shrink in diameter simultaneously with a controlled rate. We anticipate that this post-synthesis method may pave the way toward the ultimate strategy for complete control of nanotube diameter, as well as the bulk production of chirality-specific CNTs.

Methods

In situ TEM irradiation/heating experiments: the DWNTs used in this work were synthesized by an arc-discharge method. The DWNT sample was first ultrasonically dispersed in glycol, and a tiny drop of sample liquid was subsequently loaded on an MEMS chip used for a heating TEM holder. This heating stage allows the samples to be locally heated up to 1200 °C with a temperature accuracy <4% (with 0.1 °C readout accuracy). In situ TEM heating experiments were conducted inside an FEI Talos-F200s TEM with this heating stage. An accelerating voltage of 200 keV was chosen for the irradiation experiments to ensure the CNT-shrinking process induced by knock-on collision. Experimental videos were obtained by recording sequential TEM images using a CMOS camera.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank Prof. Daiming Tang of the National Institute for Materials Science (NIMS) in Japan for the helpful discussion, and thank Prof. Da Zhan and Jinming Wang of Xiamen University in China for technical support in the course of this work. This work was financially supported by the Natural Science Foundation of China (No. 61471307), the Specialized Research Fund for the Doctoral Program of Higher Education (No. 20130121120009), the Fundamental Research Funds for the Central Universities, the National Program for Thousand Young Talents of China, and the “Double-First Class” Foundation of Materials and Intelligent Manufacturing Discipline of Xiamen University.

References

1. P. Avouris, Z. Chen and V. Perebeinos, Nat. Nanotechnol., 2007, 2, 605.
2. L. J. Yang, S. Wang, Q. S. Zeng, Z. Y. Zhang, T. Pei, Y. Li and L. M. Peng, Nat. Photonics, 2011, 5, 673.
3. M. M. Shulaker, G. Hills, N. Patil, H. Wei, H. Y. Chen, H. S. Wong and S. Mitra, Nature, 2013, 501, 526.
4. C. Qiu, Z. Zhang, M. Xiao, Y. Yang, D. Zhong and L. M. Peng, Science, 2017, 355, 271.
5. C. L. Cheung, A. Kurtz, H. Park and C. M. Lieber, J. Phys. Chem. B, 2002, 106, 2429.
6. G. Zhang, P. Qi, X. Wang, Y. Lu, X. Li, R. Tu, S. Bangsaruntip, D. Mann, L. Zhang and H. Dai, Science, 2006, 314, 974.
7. A. Nish, J.-Y. Hwang, J. Doig and R. J. Nicholas, Nat. Nanotechnol., 2007, 2, 640.
8. M. C. Hersam, Nat. Nanotechnol., 2008, 3, 387.
9. F. Yang, X. Wang, D. Zhang, J. Yang, D. Luo, Z. Xu, J. Wei, J. Q. Wang, Z. Xu, F. Peng, X. Li, R. Li, Y. Li, M. Li, X. Bai, F. Ding and Y. Li, Nature, 2014, 510, 522.
10. S. Zhang, L. Kang, X. Wang, L. Tong, L. Yang, Z. Wang, K. Qi, S. Deng, Q. Li, X. Bai, F. Ding and J. Zhang, Nature, 2017, 543, 234.
11. Z. K. Tang, L. Zhang, N. Wang, X. X. Zhang, G. H. Wen, G. D. Li, J. N. Wang, C. T. Chan and P. Sheng, Science, 2001, 292, 2462.
12. P. M. Ajayan, V. Ravikumar and J. C. Charlier, Phys. Rev. Lett., 1998, 81, 1437.
13. L. F. Sun, S. S. Xie, W. Liu, W. Y. Zhou, Z. Q. Liu, D. S. Tang, G. Wang and L. X. Qian, Nature, 2000, 403, 384.
14. L. C. Qin, X. Zhao, K. Hirahara, Y. Miyamoto, Y. Ando and S. Iijima, Nature, 2000, 408, 50.
15. N. Wang, Z. K. Tang, G. D. Li and J. S. Chen, Nature, 2000, 408, 50.
16. L. M. Peng, Z. L. Zhang, Z. Q. Xue, Q. D. Wu, Z. N. Gu and D. G. Pettifor, Phys. Rev. Lett., 2000, 85, 3249.
17. X. Zhao, Y. Liu, S. Inoue, T. Suzuki, R. O. Jones and Y. Ando, Phys. Rev. Lett., 2004, 92, 125502.
18. X. Li, Y. Cheng, L. Z. Zhao, Q. B. Zhang and M. S. Wang, Carbon, 2018, 133, 186.
19. B. Florian, Rep. Prog. Phys., 1999, 62, 1181.
20. F. Ding, K. Jiao, Y. Lin and B. I. Yakobson, Nano Lett., 2007, 7, 681.
21. S.-i. Sawada and N. Hamada, Solid State Commun., 1992, 83, 917.
22. J. Y. Huang, S. Chen, S. H. Jo, Z. Wang, D. X. Han, G. Chen, M. S. Dresselhaus and Z. F. Ren, Phys. Rev. Lett., 2005, 94, 236802.
23. B. Zhang, L. Zhao, Y. Cheng, D. Golberg and M. S. Wang, Nano Lett., 2016, 16, 5221.
24. W. A. McKinley and H. Feshbach, Phys. Rev., 1948, 74, 1759.
25. T. D. Yuzvinsky, W. Mickelson, S. Aloni, G. E. Begtrup, A. Kis and A. Zettl, Nano Lett., 2006, 6, 2718.
26. A. V. Krasheninnikov and F. Banhart, Nat. Mater., 2007, 6, 723.
27. A. Hashimoto, K. Suenaga, A. Gloter, K. Urita and S. Iijima, Nature, 2004, 430, 870.
28. K. Suenaga, H. Wakabayashi, M. Koshino, Y. Sato, K. Urita and S. Iijima, Nat. Nanotechnol., 2007, 2, 358.
29. J. Y. Huang, S. Chen, Z. F. Ren, Z. Q. Wang, D. Z. Wang, M. Vaziri, Z. Suo, G. Chen and M. S. Dresselhaus, Phys. Rev. Lett., 2006, 97, 075501.
30. F. Ding, K. Jiao, M. Wu and B. I. Yakobson, Phys. Rev. Lett., 2007, 98, 075503.
31. B. I. Yakobson, Appl. Phys. Lett., 1998, 72, 918.
32. J. Y. Huang, S. Chen, Z. Q. Wang, K. Kempa, Y. M. Wang, S. H. Jo, G. Chen, M. S. Dresselhaus and Z. F. Ren, Nature, 2006, 439, 281.
33. J. Y. Huang, S. Chen, Z. F. Ren, Z. Wang, K. Kempa, M. J. Naughton, G. Chen and M. S. Dresselhaus, Phys. Rev. Lett., 2007, 98, 185501.
34. A. J. Stone and D. J. Wales, Chem. Phys. Lett., 1986, 128, 501.
35. K. Hirahara, K. Inose and Y. Nakayama, Appl. Phys. Lett., 2010, 97, 051905.
36. D. M. Tang, D. G. Kvashnin, O. Cretu, Y. Nemoto, F. Uesugi, M. Takeguchi, X. Zhou, F. C. Hsia, C. Liu, P. B. Sorokin, N. Kawamoto, M. Mitome, H. M. Cheng, D. Golberg and Y. Bando, Ultramicroscopy, 2018, 194, 108.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00285e

---