Quantum-confined superfluid
Yuwei
Hao
a,
Xiqi
Zhang
 *b and
Lei
Jiang
*b and
Lei
Jiang
 *ab
*ab
aKey Laboratory of Bio-Inspired Smart Interfacial Science and Technology of Ministry of Education, School of Chemistry, Beijing Advanced Innovation Center for Biomedical Engineering, Beihang University, Beijing, 100191, P. R. China
bCAS Key Laboratory of Bio-Inspired Materials and Interfacial Science, Technical Institute of Physics and Chemistry, Chinese Academy of Sciences, Beijing, 100190, P. R. China. E-mail: xqzhang@mail.ipc.ac.cn; jianglei@iccas.ac.cn
First published on 15th May 2019
Abstract
The quantum-confined superfluid (QSF) concept has been proposed for ultrafast mass transport, which is mainly related to the orderly flow of fluid in a nanoconfined space. Besides biological ionic channels, artificial nanochannels have also demonstrated the QSF phenomenon. Here, the authors’ insight into QSF is introduced, followed by exploring the extended applications to diverse fields, such as QSF-based chemistry and QSF-based biology. For chemistry, the orderly arranged molecules in nanoconfined space will greatly reduce the reaction barrier and achieve highly efficient and selective chemical synthesis. Additionally, the QSF-based biology is of great significance for the deep understanding of ultrafast signal transmission in the nerves and brain, with implications for information systems and medical sciences.
1. Introduction
The quantum-confined superfluid (QSF) concept describes new phenomena with the characteristics of high order, ultrafast transport, and low or even no energy loss.1 These new systems include not only biological ionic channels, such as the potassium channel,2 but also artificial nanospaces, such as 1D ionic channels3 and 2D nanochannels.4 Although QSF was proposed recently, superfluidity can be traced back to 1930s, when it was originally proposed by Kapitsa and Allen in 4He below 2.17 K.5,6 Kapitsa measured the viscosity of 4He when flowing it through a confined channel of 500 nm between two glass disks. In comparison with the viscosity at normal pressure, it decreased almost 1500 times and was even lower than that of hydrogen gas by 104 times.5 The nearly zero viscosity demonstrates that flowing 4He superfluid in confined space is without the loss of kinetic energy. Additionally, Allen found that the velocity of 4He superfluid through capillaries with different diameters increased rapidly as the channel diameter decreased.7 Furthermore, once the intrinsic diameter of the capillary was below 100 nm, the fluid velocity only depended on the temperature rather than the pressure and channel length.Notably, a similar phenomenon with ultrafast ion transport also exists in biological ionic channels, in which ∼107 ions are allowed across a single channel in 1 s.8 The ultrafast ion transport of biological ion channels originates from their special characteristics, such as small size, unique structure and charge distribution on the surface. Therefore, the ions and molecules exist as single ions or molecular strands in the nanoconfined channels, leading to ultrafast transport. Artificial systems also demonstrated ultrafast mass transport like biological nanochannels, such as 1D carbon nanotubes and 2D graphene. The classic Hagen–Poiseuille equation cannot describe the ultrafast mass transport since a nearly zero fluid velocity at the pore wall was assumed regarding conventional laminar flow.9 Therefore, it is still a large challenge to theoretically explain and further extend ultrafast mass transport to diverse fields.
Here, we introduce the concept of QSF to deepen the understanding of ultrafast mass transport in biological and artificial systems. In the following Section 2, we introduce the QSF in detail with regards to biological ionic channels, 1D carbon nanotubes (CNTs) and 2D graphene nanospaces for ion and molecule transport with ultrafast transition. Furthermore, the existing QSF-type transport behaviours as well as molecular dynamic (MD) simulations are surveyed. In Section 3, we exhibit the QSF-chemistry reactions, which arrange the reactant molecules in a certain order, reducing the reaction barrier and achieving highly efficient and selective chemical synthesis. Section 4 presents QSF-biology, especially ultrafast signal transmission in the nerves and brain. Finally, we present our summary and perspectives in the field.
2. Concept of quantum-confined superfluid
According to the theory of classical thermodynamics, the velocity of mass transport would be very slow through nanochannels with ionic selectivity. However, the transport of ions and molecules in the real-life system is in an ultrafast fluid state, which taps into a precisely quantized flow. For example, there is an arranged particle in the potassium nanochannel of Streptomyces lividans, which is comprised of two K+ ions with a distance of 7.5 angstroms and a single H2O molecule in between (Fig. 1a);2,10 the NaK nonselective nanochannel is able to hold only one fully hydrated Na+ in it;11 for calmodulin, each Ca2+ channel also simultaneously binds two Ca2+ ions;12 and the H2O channel allows the transport of water molecules as ordered molecular chains (Fig. 1b), etc. These phenomena in biological systems demonstrate that the ultrafast transport is realized in a quantum manner in that single ionic or molecular chains consist of a certain number of ions or molecules. Thus, we have defined a QSF concept to understand the ultrafast fluid.1 The expression of “quantum-confined” represents the ions or molecules are confined in the channels in a quantum way. It is frictionless and there is no kinetic energy loss between QSF and channels. If the interaction between fluid and nanochannels is strong and there is kinetic energy loss, it is difficult to form QSF. In addition, the artificial ionic channels also exhibit QSF phenomena, which can realize tremendous rectification with an increased critical cylindrical region.3 As shown in Fig. 1c, the asymmetric rectifying behaviour was attributed to the quantized flow, which suggests an artificial QSF system.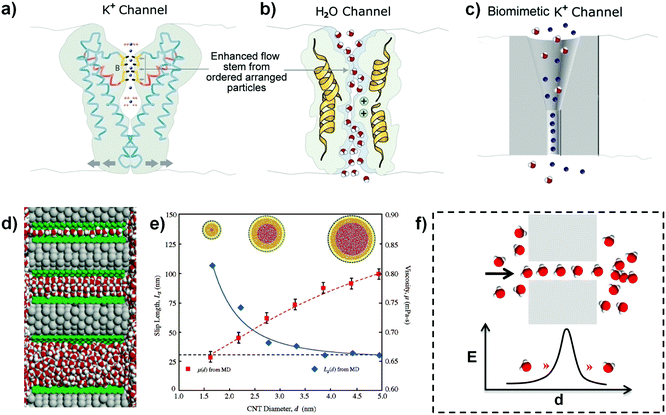 | ||
| Fig. 1 (a) The biological K+ channel from a side view contains two K+ ions with a H2O in the middle. (b) Biological water channel with a strand of ordered H2O molecules illustrating the ultrafast transport in a quantum manner as QSF. Reproduced with permission from ref. 2. (c) Artificial K+ nanochannels containing a cylindrical segment with a rectification feature in the critical region. The asymmetric rectifying behaviour is attributed to the gradual structure by the method of quantized flow, which demonstrated the possibility of artificial QSF systems. Reproduced with permission from ref. 3. (d) Water molecules confined in a 3.1 angstroms channel (top) show the single-file arrangement. Water molecules confined in an 8.6 angstroms channel (middle) arrange into a highly ordered array, while water molecules confined in an 18.1 angstroms channel (bottom) are disordered similarly to the bulk water. Reproduced with permission from ref. 16. (e) The effect of the CNT diameter on the water viscosity and slip length. When confined in narrower CNTs, water exhibits a smaller viscosity and larger slip length. Reproduced with permission from ref. 17. (f) Schematic illustration of ultrafast water transport through a nanochannel in the manner of an ordered water molecular strand and the proposed “quantum tunneling fluid effect”. E represents for the energy of water molecules to transport through the nanochannel. Reproduced with permission from ref. 1. | ||
With regard to an artificial 1D CNT channel, the velocity of ultrafast water flow is 4–5 orders of magnitude higher than that predicted according to conventional fluid mechanics theory.9,13,14 It is revealed that a small change in nanochannel size has a significant influence on the water flow inside the nanochannel, especially for a nanochannel whose diameter is under 10 nm. Based on the MD simulation, the enthalpy, entropy, and free energy of water confined in CNTs with diameters from 0.8 nm to 2.7 nm were discovered.15 It is demonstrated that the confinement effect varied dramatically with the CNT diameter. For CNTs with diameters of 0.8–1.0 nm, the water inside was vapour-like and had the largest entropic gain; for CNTs with diameters of 1.1–1.2 nm, the water was ice-like and had a lower entropy; for CNTs with diameters of more than 1.4 nm, the water was bulk-like. Additionally, water orientations and motions confined inside nanochannels are qualitatively modified.16 The water can arrange spontaneously in an ordered manner when confined in the nanospace of a CNT with a diameter below 8.6 angstroms, whereas in the wider CNT, water molecules were in a disordered state just as bulk water (Fig. 1d). The MD simulation for water transport in CNTs with diameters from 1.66 nm to 4.99 nm demonstrated that the water flow velocity enhancement increased from 47 to 433 as the CNT internal diameter decreased (Fig. 1e).17 In addition to the arranged water strand of approximately five water molecules in one dimension, the pulse-like transmission of water was also observed through a hydrophobic CNT.18 Furthermore, osmotically transporting water molecules through aligned CNT membranes by MD simulation showed several interesting features of confined nanoscale water flow, such as stochastic water flow due to significant thermal fluctuations and frictionless water flow in the nanospace (bound by the nanochannel's entry and exit).19 Accordingly, the observed ultrahigh water flow rate (almost 5 molecules per ns) was comparable to biological water channels. This phenomenon cannot be predicted by macroscopic hydrodynamics. Meanwhile, a 1D ordered water chain of five molecules and pulse-like water transmission through the CNT nanochannel provided theoretical proof for the QSF concept. From the classical hydrodynamics, the penetration barrier in such a small channel in both biological and artificial systems is high, and the ordered ultrafast water flow in the confined nanochannel thus can be acknowledged as “quantum tunneling fluid effect” (Fig. 1f). At the same time, the “tunneling distance” should correspond to the QSF period. For potassium ions channel, the length of the tunneling distance is two potassium ions with a single H2O molecule in between. Meanwhile, for the water channel, the length of the tunneling distance is a water molecule chain.
Moreover, ultrafast transport of organic solvent and water also existed in the 2D nanochannels in GO membranes with a width of 1 nm.20 Compared to the bulk system, the liquid properties were changed when confined in 2D nanochannels.21 For example, enhanced effective shear viscosity, extended relaxation times and nonlinear responses at much lower shear rates were found. Additionally, the dielectric constant (almost 2) of water confined in 2D nanochannels is much smaller than that of bulk water (almost 80).22 In particular, it has been proven that the channel size between two graphene layers can influence the structure, shear viscosity and flow rate of water when the nanochannels decreased below 2 nm.23 Importantly, the water viscosity oscillated with the change of the nanoconfined distance, which should have an important effect on the slip length and further water flow rate. MD simulations revealed that the water formed a highly ordered monolayer when confined inside graphene 2D nanospace. The frictionless flow of the water monolayer resulted in ultrafast water transport. This research is important proof of the QSF concept. By fabricating narrow and smooth capillaries between graphene layers, unexpectedly fast flow (up to 1 m s−1) has been achieved through the nanochannels, which is attributed to the high capillary pressure and large slip lengths.24 The marked enhancement of the water flow is associated with an increased ordered structure of nanoconfined water when the channels accommodate only a few layers of water. Moreover, two-dimensional water flow in angstrom-scale channels can also be enhanced in principle due to rearranging one or two water layers with strongly suppressed dielectric permittivity22,25 or ice-phase formation at room temperature.26 Unlikely, ionic transport in such a confined channel is influenced by the interaction between the hydration shells of ions and the channel wall.27 Measurements of ionic fluid through angstrom-sized 2D channels driven by pressure and an electric field revealed a transistor-like electrohydrodynamic effect.28 The gating performance of water and ions flowing in 2D nanochannels under an applied electric field demonstrated QSF characteristic and played an important role for controlling molecular and ion transport. Furthermore, we have designed a superamphiphilic silicon wafer with a hydrophilic/hydrophobic nanodomain-integrated network to provide proof of the QSF concept.29 Based on the design, both water and oil (hexane) can spread rapidly on the surface.
It should be noted that the wettability significantly impacts the ultrafast water flow in both 1D and 2D nanochannels.30 Through experiments and MD simulation, it has been revealed that the water viscosity is larger in hydrophilic 1D nanochannels than that in hydrophobic 1D nanochannels.31 This result further suggests that the confined water flow is faster in a hydrophobic 1D nanochannel. The water flux in a hydrophilic nanochannel could be reduced by 1 order of magnitude; nevertheless, it can increase by 7 orders of magnitude in hydrophobic nanochannels in comparison with that of bulk water. The MD simulation also revealed that the hydrogen group modified at the edge of the graphene gaps facilitated the diffusion of water molecules into the nanochannel without energy barriers.32 By modification with temperature-responsive poly(N-isopropylacrylamide), a GO membrane can achieve nanogating between hydrophobic and hydrophilic sides.33 The water permeation of the smart GO membrane can be regulated reversibly with a high gating ratio (almost 7) when the temperature changed. Meanwhile, in the case of MD simulation, the CNTs can be designed with a hydrophilic inlet (modified with hydrophilic –COOH end groups) and hydrophobic outlet (modified with hydrophobic –CF3 end groups).34 Attributed to the variation of the dipole orientation of the nanoconfined ordered water molecules in the CNTs with an internal diameter of 0.81 nm, it has been observed that the water density was enhanced on the hydrophobic sides. This result indicated that the asymmetric wettability of nanochannels should be important for the study and application of water transport.
3. QSF-based ordered-assembly reaction
Based on the QSF concept, QSF-chemistry has been proposed, including organic, inorganic, polymer, analytical etc. Specifically, in molecular synthesis, the reactants are first orderly arranged in a sequence in a well-defined confined channel. In QSF catalysis, the reaction could be launched with a low reaction barrier and high efficiency under mild conditions. QSF catalysis is a widespread phenomenon with high-activity in biosystems, such as enzyme synthesis35 and DNA synthesis.36Generally, QSF-type reactions exhibit enhanced performance compared to the bulk system due to the nanoconfinement. For CNTs with internally confined catalyst, such as Rh-based particles, enhanced catalytic ethanol synthesis from syngas can be achieved.37 It has also been proven that Fe nanoparticles as a catalyst inside CNTs led to higher activity and yield compared to those loaded outside CNTs for Fischer–Tropsch synthesis.38 In addition to the nanoconfinement, the hydrogenation of unsaturated organics catalysed by chirally modified Pt inside CNTs exhibited higher enantioselectivity than that loaded outside CNTs due to the catalyst enrichment.39 Additionally, in the polymer field, the high molecular weight of polyethylene nanomaterials with a crystalline fibrous structure can be achieved when adopting a mesoporous silica fibre as a template.40 Additionally, considering the smaller linear channel diameter of a silica fibre (27 angstroms) compared to that of the ordinary lamellar length of polyethylene crystals (almost 100 angstroms), the obtained polymer nanofibres here were inclined to form extended chain crystals. Therefore, the nanoconfinement can improve the activity, selectivity and crystallization, which is important for the chemical reaction. However, the nanoconfinement-enhanced performance still has challenges, such as the unclear mechanism and problems to be solved in nanoconfined chemical reactions.
It should be noted that reactant molecules deposited on specific metal surfaces, such as Au(110) and Cu(110) surfaces, can be preassembled into highly ordered structures. Nanoconfined chemical reactions can also be performed on these surfaces after the structure was ordered along a specific lattice direction, which reacted in situ and yielded the desired products or nanomaterials. Therefore, those specific surfaces with atom row construction can provide a geometrical confinement for molecules and subsequently alter the reaction pathway.41,42 Furthermore, the confinement surfaces also played the role of efficient catalysts, which can lower the energy barriers,43,44 inducing high activity and selectivity in reaction processes. Once the molecules are deposited on the anisotropic Au(110) surface, the surface would undergo a phase transition to (1 × 3) reconstruction, followed by annealing, which resulted in 1D atomic grooves for geometrical nanoconfinement.42,45 These nanosized grooves served as efficient templates to direct the deposited molecules in the terms of diffusion, orientation and surface-confined chemical reactions. For example, the alkyl chains of 1,4-di(eicosyl)benzene confined in the nanochannels of the reconstructed Au(110)-(1 × 3) surface showed an ordered arrangement (Fig. 2a).42 Due to the physical confinement of reactants, the dehydrogenative coupling reaction of these molecules reacted at specific sites with high selectivity, such as terminal CH3 groups or penultimate CH2 groups. The polymer chains were then formed in parallel within the Au(110)-(1 × 3) reconstructed nanosized grooves. Due to the spatial confinement, the C–C coupling reaction of p-sexiphenyl molecules selectively took place at the meta-sites and then yielded linear molecular structures that were in the trans conformation.46 In particular, the branched polymerization was efficiently inhibited resulting from the nanoconfinement. In addition, the linear fatty acid (C30H60O2) with a relatively higher molecular weight can also preassemble into an ordered structure under the confinement of reconstructed grooves along the lattice direction.47 Similarly, through the relatively high catalytic activity and the nanosized templating effect, the 1,4-diiodobenzene dosed on Cu substrates with a [1![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0] lattice direction could arrange into continuous lines and then transform into aligned polyphenylene chains.48 In nanoconfined-preassembled reactions, the reaction efficiency and selectivity could be improved at the same time, due to the geometrical confinement. For the QSF-chemistry, this would improve the performance of nanoconfined chemical reactions, the orientation of the molecular structure and the fabrication of carbon nanomaterials.
0] lattice direction could arrange into continuous lines and then transform into aligned polyphenylene chains.48 In nanoconfined-preassembled reactions, the reaction efficiency and selectivity could be improved at the same time, due to the geometrical confinement. For the QSF-chemistry, this would improve the performance of nanoconfined chemical reactions, the orientation of the molecular structure and the fabrication of carbon nanomaterials.
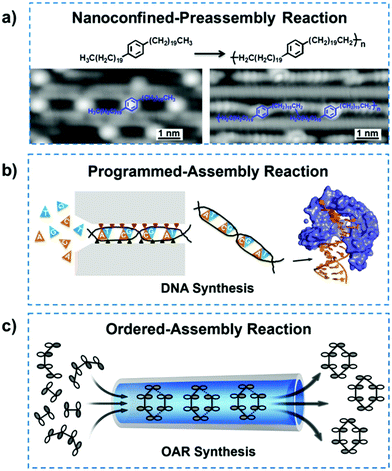 | ||
| Fig. 2 (a) Nanoconfined-preassembly reaction of the C–C coupling of 1,4-di(eicosyl)benzene on reconstructed Au(110)-(1 × 3) atomic grooves and the relevant scanning tunneling microscopy images. Reproduced with permission from ref. 42. (b) Programmed-assembly reaction of DNA synthesis, in which the four kinds of deoxynucleotides are inserted precisely into complementary strands with specific positions and orientations. Reproduced with permission from ref. 52. (c) Ordered-assembly reaction in chemical synthesis. In the OAR process, reactant molecules arrange in an orderly manner and react according to the FMO theory, which exhibits ultrafast directional flow as well as high efficiency and selectivity. Reproduced with permission from ref. 53. | ||
Programmed-assembly reactions such as photosynthesis,49 ATP synthesis,50 cellular respiration51 and DNA replication,52 have inspired us to explore innovative theory and new materials. The common characteristics in these phenomena are highly ordered programmed processes, high efficiency and high yield. For a case study of DNA replication, four kinds of deoxynucleotides can individually insert into the complementary chains, thus presenting accurate positions and conformations due to the base pairing rules, as shown in Fig. 2b. In the replication process, enzymes, such as DNA polymerase and exonuclease, are involved for sequencing, proofreading and error-checking.52 Thousands of deoxynucleotides polymerize to form the targeted DNA double helix, whose sequence and structure are remarkably precise. Such chemical reactions with accurate orientation and high efficiency can be regarded as programmed-assembly reactions, which will inspire us to explore the high-performance QSF-based chemical reactions.
Inspired by the programmed-assembly reactions of physiological behaviours in life, the concept of “ordered-assembly reaction” (OAR) has been proposed based on the QSF concept and frontier molecular orbital (FMO) theory (Fig. 2c).53 FMO theory is a well-known method that can explain the reaction mechanism, enhance the understanding of the reaction process, and predict the reactivity and stereoselectivity of organics where the lowest unoccupied molecular orbital (LUMO) and highest occupied molecular orbital (HOMO) are regarded as the frontier orbitals.54,55 Generally, the HOMO–LUMO pairing of two reactants in an organic reaction should be orbital symmetry-matched and close in energy. If so, electron transfer can occur from the one molecule's HOMO to the other molecule's LUMO or vice versa. Such a reaction can be regarded as thermally feasible.56,57 Based on the proposed OAR concept, the reactant molecules should pass through nanoconfined channels fast with a certain directional flow and properly ordered molecular configurations. On one hand, reactant molecules should arrange in order with a configuration transformed under nanoconfinement to satisfy the symmetry-matching principle of FMO theory. In this way, the energy barrier of the reaction could be lowered and the activity as well as stereoselectivity could be improved. On the other hand, reactant fluid in the nanochannel can achieve a QSF-type ultrafast flow, which would reduce the reaction time. Meanwhile, the reduced reaction time can also inhibit the side reactions and the increase the product selectivity. Additionally, the lower contact time between the reactant and catalyst can reduce the possibility of deactivation and poisoning of the catalyst to improve the catalyst's lifetime. Therefore, in the OAR process, the performance of nanoconfined chemical reactions can be further improved, including but not limited to the efficiency, yield and selectivity.
4. QSF-based nerve signal transmission
Conventionally, the action potentials in neurons play a central role in the communication between cells by the propagation of nerve signals along the neuronal axon, as is well-known according to the Hodgkin–Huxley model.58 In this model, various ion channel proteins are assumed to allow nerves to conduct signals through the selective transport of K+ and Na+ions.59 The voltage-gated ion channels embedded in the plasma membranes of cells can generate action potential, and the specific axon's membrane potential rapidly rises and falls.60 This means that the nerve signal transmission based on action potential is generated by ion diffusion and that the ion fluid is disordered fluid driven by entropy. In Fig. 3a, Na+ ions can enter the cell as the Na+ channels open, and thus, the electrochemical gradient changes, leading to a rise in the potential of the membrane. After that, the ion channels are inactivated, and then, the K+ channels are activated, followed by an outward current of K+ ions. As the K+ ions leave the cell continually, the membrane potential decreases due to the efflux of K+ ions, which results in the entrance of Na+ ions nearby. During the process, the conduction of the action potential is at a relatively slow speed of ∼1 m s−1, and the ion diffusion during the conduction consumes a large amount of energy. Therefore, the traditional action potential mechanism based on ion diffusion cannot sufficiently explain the rapid nerve signal transmission between the nerves and brain.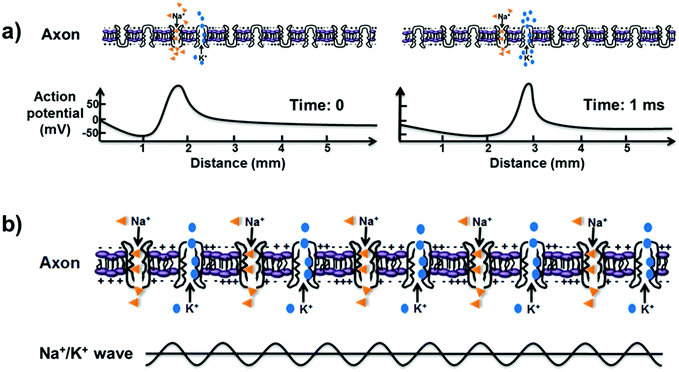 | ||
| Fig. 3 (a) Nerve signal transmission based on the conventional theory of action potential through ion diffusion, which precipitates a domino-like propagation with slow transmission. (b) QISF process in nerve signal transmission. The ultrafast ion transport through all sodium–potassium nanochannels happens simultaneously without energy loss and results in a Na+ and K+ density wave along the neuronal axon. The bottom scheme represents the Na+ and K+ density wave, which serves as an information medium in nerve signal transmission. Reproduced with permission from ref. 63. | ||
The question regarding how the nerves send signals stimulates us to explore a new theory for deep understanding of nerve signal transmission. It has been found that the minimum velocity and maximum amplitude of the solitons is close to the propagation velocity of myelinated nerves, and the nerve signal is transmitted as a mechanical wave that travels down the axon instead of action potential.61 Furthermore, from the perspective of physics, the transmission of electromagnetic signals in nerves should conform to quantum theory.62 The quantum energy states of molecules and ions are key factors for signal generation, amplification and coupling in the nervous system. For decades, emerging new theories have inspired suitable explanations for nerve signal transmission in nature.
Considering the essential ultrafast ion transport in nerve signal transmission, a process of quantum-confined ion superfluid (QISF) has been proposed based on the QSF concept.63 The QISF is confined ordered fluid driven by enthalpy, which is different from the conventional entropy-driven ion diffusion. In the QSIF process, Na+ and K+ ion transport in the sodium–potassium pumps is ultrafast without energy loss. Na+ ions enter the cell through opened Na+ ion channels, and then, the K+ ion channels open to allow the exit of K+ ions outside the cell. In the membrane, all sodium–potassium pumps simultaneously realize the ultrafast ion transport, leading to a Na+ and K+ density wave along the neuronal axon, which plays an important role in the ultrafast nerve signal transmission, as shown in Fig. 3b. Velocity and frequency are distinguishing factors between conventional action potential and QISF mechanism. Similar to the water surface soliton wave and the sound wave in water, the action potential cannot affect the transmission of the Na+ and K+ density wave. The QISF process provides a new perspective for reasonable understanding of ultrafast signal transmission in the nerves and brain. It not only challenges the conventional theory about signal transmission but also inspires the promising development of biochemistry, bioinformatics and biophysics.
5. Conclusion and perspectives
In conclusion, the concept of QSF is introduced with respect to ultrafast ion and water transport in biological channels and artificial 1D and 2D nanochannels. This is demonstrated by experiment and MD simulation. Furthermore, the perspectives of QSF-chemistry and QSF-biology are provided. QSF-chemistry refers to the chemical reaction with assembled reactants, leading to enhanced activity, selectivity, and lowered reaction barrier under mild fields. Additionally, QSF-biology, especially the ultrafast signal transmission between nerves and the brain, is of great significance and promising in information systems and medical sciences.Focusing on the artificial nanoconfined space for ultrafast water transport, the dimension effect and wettability are intriguing. As the channel dimension decreases to the nanoscale (especially lower than 10 nm and even on the angstrom scale), molecular properties, such as the dielectricity and viscosity may be altered. Importantly, these molecules rearrange to form a highly ordered strand or layer formed by a unique number of molecules. The arranged molecular structure could play an important role in the quantum transport of molecules and ions as well as high-efficiency chemical reactions. This has been shown by the high efficiency and selectivity of nanoconfined catalysts and nanoconfined-preassembled reactions. Meanwhile, the wettability of nanochannels is of great significance to water transport and metal melt wetting. A hydrophilic inlet favors the facilitation of water entry and a hydrophobic inside channel wall is preferred for ultrafast water transport. In addition, the melt wetting of metal and polymer into the nanochannel can be regulated by the wettability, which is a key factor for the fabrication of advanced nanomaterials such as the Li+ battery. By combining nanoconfined ultrafast molecule transport and proper wettability, highly efficient separation of water and oil or organic solvents can be realized.
The QSF concept also sheds light on the exploration of a new theory for nerve transmission. Following the development of biology, the mechanism of signal transmission between the nerves and brain has been challenged, and a new mechanism is urgently needed. Introducing the QISF concept into nerve signal transmission may inspire a new mechanism to explain the ultrafast ion transport in biological ionic channels and simultaneous response between the nerves and brain.
Despite the extraordinary performance, there are still many challenging problems and the mechanism is unclear. An obstacle in understanding the physical source of QSF phenomena under nanoconfinement is the lack of the development of nanotechnology for characterization. Additionally, more useful experimental research is required. It should be noted that QSF cannot be applied to all confined conditions. In principle, the special features of the channels, e.g., small size (angstrom-scale), unique chemical structure (superhydrophobic surface) and surface charge distribution, will lead to QSF feature. In addition, the QSF concept has some disadvantages. QSF-based chemical reaction has short contact time with the catalyst inside the channel, which is not conducive to some reactions with slow reaction rates. It is also difficult to quantify ion velocity and characterize of ion density wave in the QSF-based nerve signal transmission. In this situation, the proposed QSF concept, as a challenge to the conventional theory, will greatly promote the development of the synthesis of nanomaterials, application of nanochannels and understanding of nerve signal transmission.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (no. 51603211 and 51673107), the National Key R&D program of China (no. 2016YFA0200803), and the 111 Project (no. B14009).Notes and references
- L. Wen, X. Zhang, Y. Tian and L. Jiang, Sci. China Mater., 2018, 61, 1027–1032 CrossRef CAS.
- R. MacKinnon, Angew. Chem., Int. Ed., 2004, 43, 4265–4277 CrossRef CAS PubMed.
- K. Xiao, G. Xie, Z. Zhang, X.-Y. Kong, Q. Liu, P. Li, L. Wen and L. Jiang, Adv. Mater., 2016, 28, 3345–3350 CrossRef CAS PubMed.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197–200 CrossRef CAS PubMed.
- P. Kapitza, Nature, 1938, 141, 74 CrossRef CAS.
- J. F. Allen and A. D. Misener, Nature, 1938, 141, 75 CrossRef CAS.
- F. Allen John, A. D. Misener and D. Cockcroft John, Proc. R. Soc. London, Ser. A, 1939, 172, 467–491 Search PubMed.
- M. S. P. Sansom, I. H. Shrivastava, J. N. Bright, J. Tate, C. E. Capener and P. C. Biggin, Biochim. Biophys. Acta, Biomembr., 2002, 1565, 294–307 CrossRef CAS.
- M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Nature, 2005, 438, 44 CrossRef CAS PubMed.
- D. A. Doyle, J. M. Cabral, R. A. Pfuetzner, A. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait and R. MacKinnon, Science, 1998, 280, 69–77 CrossRef CAS PubMed.
- C. Shi, Y. He, K. Hendriks, B. L. de Groot, X. Cai, C. Tian, A. Lange and H. Sun, Nat. Commun., 2018, 9, 717–724 CrossRef PubMed.
- M. R. Tadross, I. E. Dick and D. T. Yue, Cell, 2008, 133, 1228–1240 CrossRef CAS PubMed.
- J. K. Holt, H. G. Park, Y. Wang, M. Stadermann, A. B. Artyukhin, C. P. Grigoropoulos, A. Noy and O. Bakajin, Science, 2006, 312, 1034–1037 CrossRef CAS PubMed.
- E. Secchi, S. Marbach, A. Niguès, D. Stein, A. Siria and L. Bocquet, Nature, 2016, 537, 210–213 CrossRef CAS PubMed.
- T. A. Pascal, W. A. Goddard and Y. Jung, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11794–11798 CrossRef CAS PubMed.
- R. J. Mashl, S. Joseph, N. R. Aluru and E. Jakobsson, Nano Lett., 2003, 3, 589–592 CrossRef CAS.
- J. A. Thomas and A. J. H. McGaughey, Nano Lett., 2008, 8, 2788–2793 CrossRef CAS PubMed.
- G. Hummer, J. C. Rasaiah and J. P. Noworyta, Nature, 2001, 414, 188–190 CrossRef CAS PubMed.
- A. Kalra, S. Garde and G. Hummer, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10175–10180 CrossRef CAS.
- Q. Yang, Y. Su, C. Chi, C. T. Cherian, K. Huang, V. G. Kravets, F. C. Wang, J. C. Zhang, A. Pratt, A. N. Grigorenko, F. Guinea, A. K. Geim and R. R. Nair, Nat. Mater., 2017, 16, 1198–1202 CrossRef CAS PubMed.
- S. Granick, Science, 1991, 253, 1374–1379 CrossRef CAS PubMed.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed.
- M. Neek-Amal, F. M. Peeters, I. V. Grigorieva and A. K. Geim, ACS Nano, 2016, 10, 3685–3692 CrossRef CAS PubMed.
- B. Radha, A. Esfandiar, F. C. Wang, A. P. Rooney, K. Gopinadhan, A. Keerthi, A. Mishchenko, A. Janardanan, P. Blake, L. Fumagalli, M. Lozada-Hidalgo, S. Garaj, S. J. Haigh, I. V. Grigorieva, H. A. Wu and A. K. Geim, Nature, 2016, 538, 222–225 CrossRef CAS PubMed.
- A. Schlaich, E. W. Knapp and R. R. Netz, Phys. Rev. Lett., 2016, 117, 048001 CrossRef PubMed.
- G. Algara-Siller, O. Lehtinen, F. C. Wang, R. R. Nair, U. Kaiser, H. A. Wu, A. K. Geim and I. V. Grigorieva, Nature, 2015, 519, 443–445 CrossRef CAS PubMed.
- G. Tocci, L. Joly and A. Michaelides, Nano Lett., 2014, 14, 6872–6877 CrossRef CAS PubMed.
- T. Mouterde, A. Keerthi, A. R. Poggioli, S. A. Dar, A. Siria, A. K. Geim, L. Bocquet and B. Radha, Nature, 2019, 567, 87–90 CrossRef CAS PubMed.
- Z. Zhu, Y. Tian, Y. Chen, Z. Gu, S. Wang and L. Jiang, Angew. Chem., Int. Ed., 2017, 56, 5720–5724 CrossRef CAS PubMed.
- X. Zhang, H. Liu and L. Jiang, Adv. Mater., 2019, 31, 1804508 CrossRef PubMed.
- K. Wu, Z. Chen, J. Li, X. Li, J. Xu and X. Dong, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3358–3363 CrossRef CAS PubMed.
- H. T. Kieu, B. Liu, K. Zhou and A. W. K. Law, Phys. Status Solidi B, 2017, 254, 1700074 CrossRef.
- J. Liu, N. Wang, L.-J. Yu, A. Karton, W. Li, W. Zhang, F. Guo, L. Hou, Q. Cheng, L. Jiang, D. A. Weitz and Y. Zhao, Nat. Commun., 2017, 8, 2011–2019 CrossRef PubMed.
- Q. Chen, L. Meng, Q. Li, D. Wang, W. Guo, Z. Shuai and L. Jiang, Small, 2011, 7, 2225–2231 CrossRef CAS PubMed.
- R. M. Vabulas and F. U. Hartl, Science, 2005, 310, 1960–1963 CrossRef CAS.
- S. Kosuri and G. M. Church, Nat. Methods, 2014, 11, 499–507 CrossRef CAS PubMed.
- X. Pan, Z. Fan, W. Chen, Y. Ding, H. Luo and X. Bao, Nat. Mater., 2007, 6, 507–511 CrossRef CAS PubMed.
- W. Chen, Z. L. Fan, X. L. Pan and X. H. Bao, J. Am. Chem. Soc., 2008, 130, 9414–9419 CrossRef CAS PubMed.
- Z. Chen, Z. Guan, M. Li, Q. Yang and C. Li, Angew. Chem., Int. Ed., 2011, 50, 4913–4917 CrossRef CAS.
- K. Kageyama, J.-I. Tamazawa and T. Aida, Science, 1999, 285, 2113–2115 CrossRef CAS PubMed.
- Q. Sun, L. Cai, S. Wang, R. Widmer, H. Ju, J. Zhu, L. Li, Y. He, P. Ruffieux, R. Fasel and W. Xu, J. Am. Chem. Soc., 2016, 138, 1106–1109 CrossRef CAS PubMed.
- D. Zhong, J.-H. Franke, S. K. Podiyanachari, T. Blömker, H. Zhang, G. Kehr, G. Erker, H. Fuchs and L. Chi, Science, 2011, 334, 213–216 CrossRef CAS PubMed.
- Q. Sun, C. Zhang, H. Kong, Q. Tan and W. Xu, Chem. Commun., 2014, 50, 11825–11828 RSC.
- Z. Cai, R. Pang, M. Liu, H. Qin, S. Chen, J. Zhong and D. Zhong, J. Phys. Chem. C, 2018, 122, 24209–24214 CrossRef CAS.
- K. Sun, A. Chen, M. Liu, H. Zhang, R. Duan, P. Ji, L. Li, Q. Li, C. Li, D. Zhong, K. Müllen and L. Chi, J. Am. Chem. Soc., 2018, 140, 4820–4825 CrossRef CAS PubMed.
- Z. Cai, L. She, L. Wu and D. Zhong, J. Phys. Chem. C, 2016, 120, 6619–6624 CrossRef CAS.
- L. Wu, Z. Cai, M. Liu, W. Ye, H. Ju, J. Zhu and D. Zhong, J. Phys. Chem. C, 2018, 122, 9075–9080 CrossRef CAS.
- J. A. Lipton-Duffin, O. Ivasenko, D. F. Perepichka and F. Rosei, Small, 2009, 5, 592–597 CrossRef CAS PubMed.
- J. Yano and V. Yachandra, Chem. Rev., 2014, 114, 4175–4205 CrossRef CAS PubMed.
- A. Hahn, J. Vonck, D. J. Mills, T. Meier and W. Kühlbrandt, Science, 2018, 360, eaat4318 CrossRef PubMed.
- A. R. Fernie, F. Carrari and L. J. Sweetlove, Curr. Opin. Plant Biol., 2004, 7, 254–261 CrossRef CAS PubMed.
- M. Hogg, P. Osterman, G. O. Bylund, R. A. Ganai, E.-B. Lundström, A. E. Sauer-Eriksson and E. Johansson, Nat. Struct. Mol. Biol., 2014, 21, 49–56 CrossRef CAS PubMed.
- S. Liu, X. Zhang and L. Jiang, Adv. Mater. Interfaces, 2019, 6, 1900104 CrossRef.
- K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- K. Fukui, T. Yonezawa, C. Nagata and H. Shingu, J. Chem. Phys., 1954, 22, 1433–1442 CrossRef CAS.
- K. Fukui, Acc. Chem. Res., 1971, 4, 57–64 CrossRef CAS.
- K. N. Houk, Acc. Chem. Res., 1975, 8, 361–369 CrossRef CAS.
- A. L. Hodgkin and A. F. Huxley, J. Physiol., 1952, 117, 500–544 CrossRef CAS PubMed.
- S. S. L. Andersen, A. D. Jackson and T. Heimburg, Prog. Neurobiol., 2009, 88, 104–113 CrossRef PubMed.
- M. W. Barnett and P. M. Larkman, Pract. Neurol., 2007, 7, 192–197 Search PubMed.
- T. Heimburg and A. D. Jackson, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 9790–9795 CrossRef CAS PubMed.
- G. Liu, Chin. Sci. Bull., 2018, 63, 3864–3866 CrossRef.
- X. Zhang and L. Jiang, Nano Res., 2019 DOI:10.1007/s12274-019-2281-3.
| This journal is © The Royal Society of Chemistry 2019 |



