Photon avalanche in lanthanide doped nanoparticles for biomedical applications: super-resolution imaging†
Artur
Bednarkiewicz
 *ab,
Emory M.
Chan
*ab,
Emory M.
Chan
 c,
Agata
Kotulska
c,
Agata
Kotulska
 ab,
Lukasz
Marciniak
ab,
Lukasz
Marciniak
 a and
Katarzyna
Prorok
a and
Katarzyna
Prorok
 ab
ab
aInstitute of Low Temperature and Structure Research, Polish Academy of Sciences, Wroclaw, Poland. E-mail: a.bednarkiewicz@intibs.pl
bPORT Polish Center for Technology Development, Wroclaw, Poland
cThe Molecular Foundry, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 21st March 2019
Abstract
Confocal fluorescence microscopy is a powerful tool for visualizing biological processes, but conventional laser scanning confocal microscopy cannot resolve structures below the diffraction limit of light. Although numerous sub-diffraction imaging techniques have been developed over the last decade, they are still limited by the photobleaching of fluorescent probes and by their complex instrumentation and alignment procedures. To address these issues, we propose a novel concept that relies on using photon avalanche (PA) anti-Stokes emission nanoparticles as luminescent labels. This technique leverages the highly non-linear relationship between photoluminescence intensity and excitation intensity observed with PA, which narrows the point spread function below 50 nm when the non-linearity exceeds 50. Using theoretical modelling, we evaluate the feasibility of obtaining PA in Nd3+ doped nanoparticles under non-resonant 1064 nm photoexcitation and study the impact of phenomenological parameters, such as photoexcitation intensity, concentration of dopants or features of the host matrix, on the theoretical PA behavior. Using these optimized parameters, our simulations resolved 20-nm features using non-linear orders of 80. These predictions require experimental proof of concept, which must be preceded by development of appropriate PA nanomaterials and experimental conditions to observe PA in nanoparticles at room temperature. When successful, the PA phenomenon in bio-functionalized nanoparticles shall radically simplify the technical means for super-resolution imaging.
Conceptual insightsThe photon avalanche phenomenon in lanthanides has been studied in bulk materials towards up-converting lasers, but little is known about the properties and possible applications of this unusual phenomenon at the nanoscale. Scarce literature reports suggest the capability of photon avalanche to improve the brightness and deep tissue imaging of extremely photo-stable luminescent nano-labels for biomedical imaging, by diminishing concentration quenching between lanthanide dopants.Based on theoretical modelling, a new concept of sub-diffraction imaging has been proposed, which exploits the highly nonlinear luminescent properties of photon avalanche in nanomaterials under non-resonant photoexcitation. The predicted properties support the assertion that single photoexcitation beam (no depletion beam, as opposed to standard STED) raster imaging at near infrared photoexcitation will enable below 50 nm optical resolution to be reached. These features shall be achievable in a simple optical scheme of widespread conventional or Nipkow disk confocal microscopes, which potentially offers wider adoption of super-resolution imaging in biomedical sciences. The consequences of our studies are much broader and other potential target applications include bio-sensing, optical computing and optical thermometry. The current challenge is to experimentally verify the concept by searching for appropriate luminescent materials showing photon avalanche at room temperature at the nanoscale. |
1. Introduction
Optical microscopy is the most enlightening and intuitive technique for visualizing dynamic processes in biology or revealing cellular function, but the resolution of conventional optical microscopes is limited by the diffraction of light. For visible light, the diffraction limit is approximately one-half of the photoexcitation wavelength along the lateral (X–Y) plane and three times larger along the optical axis (Z).1 For many biological applications such resolution is insufficient to resolve molecular constructs such as antibodies labelled with fluorescent proteins (e.g. IgG-AlexaFluor 488 has a hydrodynamic size of 12 nm)2 or such subcellular structures as ribosomes, dendritic spines or the cytoskeleton in neurons.3 The resolution suffers in particular when NIR excitation, with its reduced scattering and lower propensity to excite autofluorescence, is used to penetrate through thick layers of tissue. Two-photon microscopy (Fig. 1a) offers increased penetration depths, better point spread function (PSF) confinement and spatial resolution improvement under NIR photoexcitation, but powerful, costly and cumbersome femtosecond lasers must be used due to the low 2- or 3- photon absorption cross-sections of fluorophores (both endogenously or exogenously administrated).4,5 Recent advances in far-field super-resolution techniques (e.g., stimulated emission depletion (STED) microscopy, photo activated localisation microscopy (PALM), stochastic optical reconstruction microscopy (STORM), 4Pi microscopy, and structured illumination)6,7 have demonstrated that diffraction limits can be overcome through a combination of smart optical design, novel photon excitation and detection schemes, the selection of specialized fluorescent labels and dedicated data processing.6 For example, the concept underlying STED is straightforward and outputs raw data analogous to confocal micrographs. However, this technique is technically challenging, requiring the synchronization of femtosecond pulses, specialized probes with high stimulated emission (SE) cross section, high depletion excitation intensities leading to fast photobleaching and bio-incompatibility. Despite great progress in these areas in the last ten years1 (e.g. CW STED,8 time-gated9 or multi-colour STED10,11), alternative techniques and labels are continuously sought.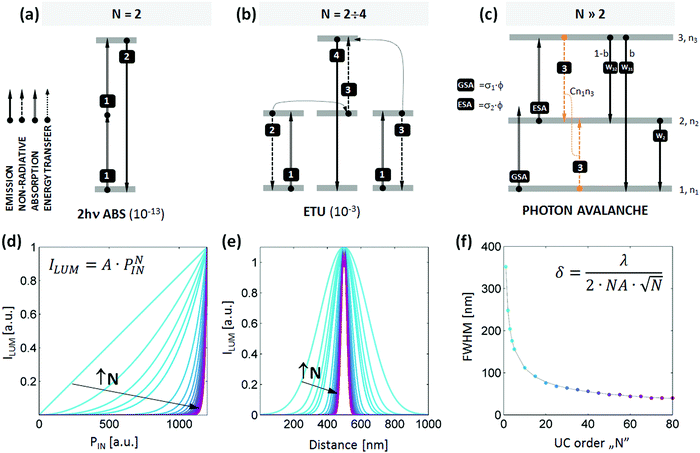 | ||
| Fig. 1 Introduction to photon avalanche emission and multi-photon super-resolution imaging. Schematic comparison of (a) two-photon absorption, (b) energy transfer upconvesion (fr.Addition de Photons par Transferts d'Energie, APTE) and (c) photon avalanche emission. The emission cross sections for given transitions are shown in parentheses.22 Photon avalanche or looping requires negligible ground state absorption (GSA), significant excited state absorption (ESA), i.e. ESA ≫ GSA, and efficient cross-relaxation (process 3) to promote ESA. (d–f) The impact of non-linearity of the luminescent label on (d) the photo-excitation power density dependence of emission, (e) the cross section of emission intensity ILUM(x) and (f) spatial resolution FWHM(N). The data were achieved by scanning a δ0 wide diffraction-limited Gaussian beam (eqn (1), λ = 1064 nm, NA = 1.4) across a single, non-linear, 10 nm diameter NP, as a function of non-linearity strength (defined by N value) (colours on d–f correspond). | ||
Luminescent inorganic nanoparticles12 have been proposed to counter the photobleaching of conventional fluorescent labels.13 Of particular interest, lanthanide doped nanoparticles have been recently proposed for STED,14–16 saturation17 or fluorescence difference microscopy (FED)18 super-resolution imaging. Tm3+ and Yb3+ co-doped NaYF4 “upconverting” nanoparticles (UCNPs) were used as STED probes to image the subcellular cytoskeleton of HeLa cancer cells with 28 nm imaging resolution with 980 nm photoexcitation and 810 nm depletion beams.15 The combination of STED with UCNPs is advantageous because they can be imaged in the absence of background (no absorption or emission of endogenous chromophores) and without photo-bleaching at biologically safe excitation/depletion power ranges in the NIR/visible spectral range. However, the gap between currently available super-resolution techniques and the requirements of life-scientists is still large, and numerous aspects have to be addressed, such as deep-tissue penetration, prolonged observation times, high frame rates, and bio-compatibility. Therefore, to decipher the mechanisms and kinetics of bio-related processes at the molecular level, widespread adoption of super-resolution and multiphoton microscopy requires more straightforward and inexpensive approaches for manipulating light below the diffraction limit.
2. Results and discussion
Here, we propose a simple method for sub-diffraction imaging based on the phenomenon known as photon avalanche.19,20 Unlike STED, this method uses a single excitation beam (obviating the need for a second depletion beam) and eliminates the aforementioned issues by exploiting highly nonlinear optical nanomaterials that up-convert the frequency of light. Multi-photon imaging increases the resolution of light according to the equation: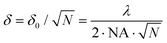 | (1) |
To overcome the intrinsic limitations of multiphoton imaging with up-converting nanoparticles, we reasoned that an alternate up-conversion mechanism, photon avalanche (PA, schematically presented in Fig. 1c), could be exploited to achieve higher nonlinearities than what UCNPs exhibit and thus accomplish finer resolution. Photon avalanche is a highly nonlinear process with a very steep power dependence (e.g. N = 22)23 that should shrink the Gaussian excitation spot profile of a laser scanning confocal microscope below the diffraction limit. The PA process occurs in materials that have strong excited state absorption (ESA) but very weak ground state absorption (GSA). This combination is usually found when the excitation radiation is not resonant with the ground state transition but is resonant with ESA (see mechanism in Fig. 1c). PA also requires the electronic structure of the luminophore to facilitate “looping” of energy. This looping usually occurs through cross-relaxation (CR – process 3 in Fig. 1c), in which a pair of single excited and single ground state ions produce two intermediately excited ions by donating part of the excited state energy to a ground state ion. If these intermediately excited ions can each absorb additional photons via ESA, the looping cycle can repeat, doubling the intermediate state population after every iteration of the loop. This produces a highly non-linear amplification of the light emitted by that state and other related states.
PA has been studied in Nd3+,23,24 Pr3+,25–27 Er3+,28 and Tm3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 29–31 ions doped in bulk materials intended for solid-state lasers. The assignment of the PA mechanisms is typically supported by a characteristic “S”-shape emission intensity power dependence as well as the critical slowing down and power dependence of PA rise-times,32,33 exactly as has been numerically modelled in Fig. 2. PA has mostly been observed at cryogenic temperatures, with only a few reports of PA at room temperature.19,32,33 There are even fewer studies of PA in nanoscale materials. In lanthanide-doped nanomaterials, looping and PA-like behaviour in Tm3+ doped materials have led to an expanded library of excitation wavelengths (e.g., 1064 nm, rather than the more typical ∼800, 915 and 980 nm) that can be used for up-conversion imaging, which have enabled super-resolution stimulated emission depletion based imaging16 and deep-tissue imaging.34 It is still debatable whether these “energy looping nanoparticles” exhibit PA since the strict definition of PA requires that R = σESA/σGSA < 10−4, where σESA and σGSA are the absorption cross sections of ESA and GSA, respectively. Unfortunately, due to these strict requirements, complex electronic structure of lanthanide ions and large surface to volume ratio in nanomaterials, it is challenging to identify lanthanide dopant compositions that can host PA at biologically relevant temperatures.
29–31 ions doped in bulk materials intended for solid-state lasers. The assignment of the PA mechanisms is typically supported by a characteristic “S”-shape emission intensity power dependence as well as the critical slowing down and power dependence of PA rise-times,32,33 exactly as has been numerically modelled in Fig. 2. PA has mostly been observed at cryogenic temperatures, with only a few reports of PA at room temperature.19,32,33 There are even fewer studies of PA in nanoscale materials. In lanthanide-doped nanomaterials, looping and PA-like behaviour in Tm3+ doped materials have led to an expanded library of excitation wavelengths (e.g., 1064 nm, rather than the more typical ∼800, 915 and 980 nm) that can be used for up-conversion imaging, which have enabled super-resolution stimulated emission depletion based imaging16 and deep-tissue imaging.34 It is still debatable whether these “energy looping nanoparticles” exhibit PA since the strict definition of PA requires that R = σESA/σGSA < 10−4, where σESA and σGSA are the absorption cross sections of ESA and GSA, respectively. Unfortunately, due to these strict requirements, complex electronic structure of lanthanide ions and large surface to volume ratio in nanomaterials, it is challenging to identify lanthanide dopant compositions that can host PA at biologically relevant temperatures.
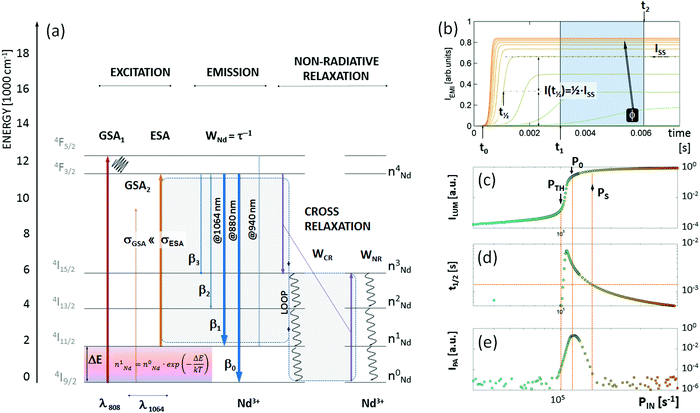
We therefore used numerical solutions to coupled rate equations (eqn (S1)–(S5), ESI†) to investigate whether Nd3+-doped materials35–37 could be potentially used as PA sub-diffraction probes under physiologically relevant 1064 nm photoexcitation. The 1064 nm photons are, to a first approximation, not absorbed by Nd3+ ions from the ground 4I9/2 state to the first metastable 4F3/2 level due to significant E(4F3/2) − E(4I9/2) − hc/λ ∼ 2000 cm−1 energy mismatch. Nevertheless, the 1064 nm photons match the energy gap between the first excited state 4I11/2 and the first metastable 4F3/2 manifold. At increased temperatures, due to Boltzmann population, the 4I11/2 level becomes occupied sufficiently to facilitate 1064 nm photoexcitation of the 4F3/2 level in Nd3+ ions, which has been shown to enable luminescent nanothermometry.38 There are a few other reports of Nd3+ PA behaviour, e.g. lasing at 413 and 730 nm at temperatures <40 K under 603.6 nm in LiYF4 single crystals.39 Nevertheless, the use of Nd3+-doped nanomaterials as PA labels shall be considered as a representative case, with similar conclusions remaining valid for other dopant compositions that potentially host PA.
To understand the features and possible advantages of photon avalanche in Nd3+, we studied the non-GSA-resonant excitation of Nd3+ ions, whose electronic structure is schematically presented in Fig. 2a. Excitation at λexc = 1064 nm is resonant with the ESA 4I11/2 → 4F3/2 transition, while σGSA ≪ σESA (R = 0.98 × 10−4, see ESI†) at this wavelength for the NaYF4 host. The 4I11/2 level population can be achieved either by sideband absorption or thermal population of this state. Upon rising excitation intensity, ESA may occur, and every absorbed photon can undergo either emission, or non-radiative de-excitation or may transfer energy to other Nd3+ ions in the process of cross-relaxation. The emission follows the branching ratio characteristic (Fig. S1, ESI†) for a given host; the 1064 nm and 880 nm emission lines correspond to 4F3/2 → 4I11/2 and 4F3/2 → 4I9/2, which populate the first excited state or the ground state, respectively. However, by increasing the number of Nd3+ ions, faster cross-relaxation (WCR) between the excited and ground states (4F3/2;4I9/2) → (4I15/2;4I15/2) of neighbor Nd3+ ions leads to doubling of the 4I15/2 population. Aided by subsequent non-radiative processes (WNR), the 4I11/2 level population is doubled on every iteration of the loop. It is important to mention that some of these non-radiative processes (i.e.4I11/2 → 4I9/2) may compete with the looping process, but this competition is already considered in the rate equation modelling by including non-radiative losses of 4I11/2 population to the ground state. This sequence, in favourable host matrices (which define non-radiative rates) as well as dopant type and dopant concentration (which define looping strength), should in principle lead to a very steep relationship of emission intensity versus excitation intensity – i.e. high order nonlinearity, which is prerequisite for single excitation beam sub-diffraction imaging approaches.
Using the energy levels and possible transitions in Nd3+ activators shown in Fig. 2a, we assembled a set of rate equations that describe the change in population for each of the energy levels in Nd3+ in time, after an excitation pulse was applied at time t0. The rates of radiative and nonradiative transitions in Nd3+ (eqn (S1)–(S5), ESI†) are phenomenological factors (WNR, WCR, WNd, and β explained above) included in the modelling as parameters. Next, these equations were numerically solved upon 1064 nm PA photoexcitation; kinetic profiles of the populations of the n4Nd level (Fig. 2b) were calculated from solutions of calculations performed with different excitation intensities (i.e. ILUM (PIN, t) = n4Nd). Using in silico screening of these phenomenological parameters and excitation intensities, we identified conditions that are characteristic for photon avalanche. The first characteristic feature is the “S”-shaped relationship between excitation (PIN) and emission (ILUM) intensity with a very steep photon avalanche region (Fig. 2c) above the PA threshold (PIN > PTH) and below the saturation region (PIN < PS). The second feature is the slowing down of the rise-time (t1/2) close to the PA threshold (Fig. 2d). The time-dependent intensity profiles (Fig. 2b) enabled us to determine steady-state up-conversion intensity (Fig. 2b and c, ISS = ILUM(PIN,t → ∞)), half-rise-time (Fig. 2b and c, t1/2 = t(ILUM(PIN,t) = 0.5·ISS)) and the “pure” photon avalanche emission intensity (Fig. 2d), IPA = ILUM(PIN,t2) − ILUM(PIN,t1), t2 > t1, where t1 and t2 are selected time points (explained below in more details), whose selection provides the largest intensity contrast at the kinetic profile of PA emission (Fig. 2b). The steady-state photon avalanche emission (PAS) is achieved very slowly, because building a stable, steady-state population of emitting 4F3/2 level (ISS) requires tens of milliseconds when the excitation power is close to the PA photoexcitation intensity threshold (i.e. PTH < PIN < PS). These values are over 10-fold longer when the excitation intensity (PIN) is lower than the PA photo-excitation intensity threshold (linear or quadratic obsolete absorption) or higher than the PA photo-excitation intensity saturation (efficient ESA). One may therefore find a time window (confined by t1 and t2 time points in Fig. 2b), which discriminates PA photons from conventional luminescence. The t2 is the shortest time after switching on the PA threshold photoexcitation intensity (PIN = PTH) necessary to establish steady state emission, i.e. time t2 at which ILUM(PTH, t2) = ILUM(PTH, t2 + δt) for δt > 0. The t1 (0 < t1 < t2) is the time required to reach steady-state emission using excitation intensities close to the saturation region, i.e. time t1 at which ILUM(PS, t1) = ILUM(PS, t1 + δt) for δt > 0. In our simulations, both t1 and t2 were arbitrarily selected and kept fixed to 3 ms and 6 ms, respectively, for all data in all further experiments. Nevertheless t1 and t2 may be defined experimentally, by measuring half-rise-times (Fig. 2d) to extract “pure” PA photons (Fig. 2e). Once selected for given PA-NPs, t1 and t2 may be used for all further experiments. The difference between time-gated photon avalanche intensity (PAG) counts at t1 and t2 quantifies the number of photons occurring exclusively due to the photon avalanche phenomenon. This metric enables us to determine the origin of emitted photons and assign them as originating from either the PA or ESA phenomenon. Consequently, the IPA (Fig. 2e) not only can be used to get rid of sample autofluorescence, but most of all enables the determination of the optimal P0 to avoid saturation and is of pivotal importance for extreme non-linearities and thus for single beam super-resolution imaging.
We next sought to determine whether Nd3+ could exhibit PA with sufficient non-linearity to increase imaging resolution. A steep power dependence in principle should shrink the width of the diffraction limited Gaussian excitation spot down to tens of nanometers if the critical excitation intensity P0 (Fig. 1d–f) is fixed properly below the saturation region (P0 < PS). To test the resolution of a PA-enabled scanning microscope, we calculated spatially resolved intensity profiles of a single 10 nm diameter NP (Fig. 3a, dark grey) scanned with a diffraction limited Gaussian beam, which based on eqn (1) has a full width at half maximum, FWHM = λ/2·NA = 1064 nm/2 × 1.45 = 367 nm. At excitation intensities under which the optical response of the NP is linear (i.e. ILUM ∼ PIN), the emission intensity profile retains the Gaussian shape of the excitation spot (Fig. 3a, red). When the response is quadratic, as in up-conversion or 2-photon absorption (i.e. ILUM ∼ PNIN, N = 2), the intensity profile narrows by N0.5, or by ca. 1.4-fold (Fig. 3a, orange). If one further increases the power factor N, as is the case with e.g. 3rd or 4th order of Tm3+ blue or violet up-conversion, respectively,31 the resulting intensity profile further narrows down to a ∼1.7 and 2-fold reduced sub-diffraction spot. Up to N = 4, photon up-conversion can be relatively efficiently generated in known UC materials, but higher orders are beyond the reach of the typical UCNP phenomenon. Interestingly, we proposed and demonstrated in silico that N can be further increased without going to the UV spectral range, using photon avalanche (Fig. S3d and f, ESI†) to further narrow the emission spot cross-section size (Fig. 1d–f). Based on eqn (1) (with λ = 1064 an NA = 1.4), a high non-linearity of N = 10 improves the optical resolution by over 3 times down to ∼116 nm and N = 80 results in enhancements as large as 9-fold to reach ∼ 41 nm optical resolution (Fig. 1f and Fig. S2, ESI†).
 | ||
| Fig. 3 The impact of PA parameters on spatial resolution enhancement. (a) Comparison of the cross section of a single ϕ = 10 nm PA NP (dark grey) measured with a diffraction limited Gauss spot (light grey) Gauss profile FWHM ∼ 330 nm and under different conditions of power dependent relationship (linear ILUM ∼ PIN – red, quadratic ILUM ∼ (PIN)2 – orange), and photon avalanche S-shaped in-out relationships (ACR = 1 × 10−5; Io = 1.07 × 105, 1.8 × 105, 3 × 105 – thin, medium and thick blue curves respectively). (b) Comparison of the full width half maximum (FWHM) of the intensity profiles of 10 nm PA NPs for linear (red) and quadratic (orange) in-out emission–excitation dependence (eqn (1)) and at different PA excitation intensities and CR rates, using different S-shaped in-out curves obtained at (c) different concentrations of Nd3+ dopants ACR (ACR = 1, 2, 5, 10 and 20 × 10−5 s−1) and (e) for different non-radiative rates. Panels (d) and (f) present non-linear factors N for data presented on panel (c) and (e) as calculated based on the algorithm available in the ESI.† | ||
Notably, we found that to achieve such improvement in resolution, one must carefully select the excitation beam intensity. Because the S-shaped photon avalanche power dependence (Fig. 2c) contains a steep, power-dependent region between PTH and PS (PTH < PIN < PS) ‘surrounded’ by a relatively flat (N < 3) in-out dependence, the ultimate spatial resolution will depend on the selection of P0 (Fig. 2c and Fig. 3a (blue lines)) as well as the composition and type of the host material (Fig. 3b–f). Selecting an excitation intensity outside these optimal Po value results in the 10 nm NPs being imaged as a much larger object (Fig. 3a, medium and thick navy blue curve). However, as discussed below in greater detail, the optimal P0 narrows the cross-section profile far below the diffraction limit (Fig. 3a, thin line). Such photon avalanche single beam super-resolution imaging (PASSI) therefore has the potential to realize single-excitation-beam, sub-diffraction limited imaging. This in turn should significantly simplify the apparatus for super-resolution imaging by eliminating the need to spatially align the beams and the need to synchronize the excitation or depletion pulses (in non-CW mode).
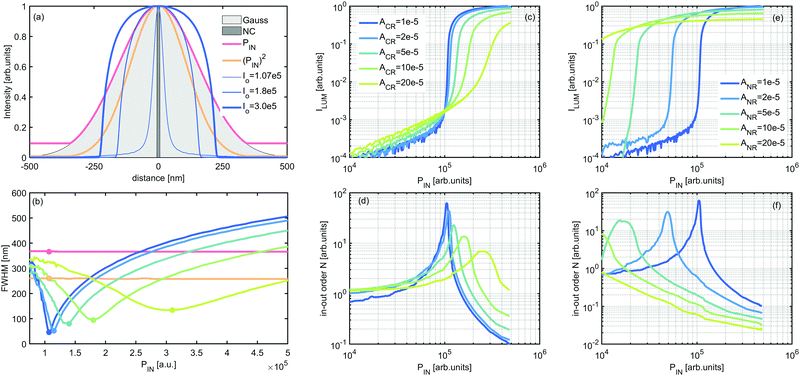
The performance of PA nanomaterials depends on a few phenomenological parameters defined in the model. For example the cross-relaxation rate (WCR) depends on the distance between doping ions and thus should depend on dopant concentration as well as host type (Fig. 3c and d). The non-radiative de-excitation rate (WNR) is a host-dependent factor, which should be lower in e.g. fluorides than in oxides, and also depends on the energy gap ΔE between respective levels (Fig. 3e and f). The variability of the looping strength (WCR, green to blue on Fig. 3c and d) and excitation intensity not only impacts the emission intensity but also affects the full width half maximum (FWHM) of the cross section of the emission profile from a single 10 nm nanoparticle. Raising the dopant concentration (increasing WCR) flattens the power dependence of the S-shaped curve (Fig. 3c), which degrades the spatial resolution (enlarges the FWHM, Fig. 3b), but also widens the acceptable range of I0 required for sub-diffraction limited imaging. The radiative rate (WNd = 1/τR) can be easily determined by experimental measurement (at low temperature and low dopants concentration) of luminescence decay. WNd, as well as the branching ratio (β0..3) from the 4F3/2 level are host dependent parameters (see Fig. S1, ESI†). For example, the β0..3 parameter defines the statistical distribution of emitted photons between 4F3/2 → 4IJ (J = 9/2, 11/2, 13/2, and 15/2, correspondingly) multiplets and may be estimated based on Judd–Ofelt theory for a given host matrix.40,41 Therefore, we hypothesize that selecting appropriate host materials, dopants and dopant concentrations will enable the optimization of lanthanide doped nanoparticles aiming to achieve photon avalanche in nanomaterials. Due to numerous differences in the optical properties of nanoparticles relative to bulk crystals, this may be a challenging task. However, as soon as the PA phenomenon is demonstrated in nanomaterials, sub-diffraction imaging can potentially be demonstrated in a simple and affordable way.
To determine the optical resolution of the proposed system, we used our model to simulate the imaging of a phantom composed of three PA NPs of 10 nm diameter with variable distances between them (Fig. 4a, cross sections at fixed distances – Fig. 4b). The three NPs are indistinguishable when separated by less than 30 nm, but for distances larger than 40 nm (Fig. 4b) the NPs become easily resolvable. These results depend on the host material parameters (Fig. S3, ESI†) and excitation intensity (Fig. S3 and S4, ESI†). Next, we employed a Gaussian excitation beam to image a 2D phantom in silico (Fig. 4c), simulating images produced by conventional linear confocal microscopy (Fig. 4d), and images produced by the steady state (Fig. 4e) and time-gated photon avalanche (Fig. 4f) imaging of 10 nm Nd3+-doped nanoparticles. Optimal parameters of excitation beam and NP composition were taken from the above described in silico studies (i.e. intensity Po = 1.075 × 105; WCR = 1 × 105) and from the time-gated data (t1 = 3 ms, t2 = 6 ms) defined in Fig. 1b.
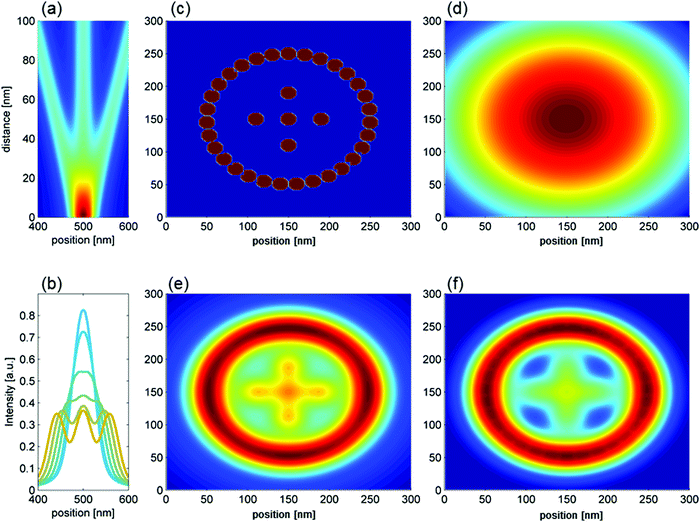 | ||
| Fig. 4 Spatial resolution enhancement using photon avalanche labels. (a) Phantoms composed of 3 NPs (ϕ = 10 nm PA NPs) placed at different distances (y axis) are reconstructed using optimal conditions (ACR = 1 × 10−5, I0 = 1.07 × 105), and (b) respective cross sections of graphs (b) for distances of 5, 10, 20, 30, 40 and 50 nm between the Nd3+-doped NPs. (c) Phantoms composed of 10 nm PA NPs reconstructed with (d) linear, (e) steady state avalanche and (f) time-gated avalanche models (graphs d, e, and f are normalized to their local maxima, cross sections across e and f are presented in Fig. S4, ESI†). | ||
Based on the qualitative information from Fig. 4 and more detailed analysis of cross sections along the centre of the simulated images (Fig. S5 and S6, ESI†) one may conclude that the steady state photon avalanche imaging is better-suited to distinguish the closely spaced NPs (Fig. S5 and S6 – top, ESI†), while the time-gated photon avalanche photons (PAG) approach provides lower background signal, but also lower contrast of closely spaced NPs (Fig. S5 and S6 – bottom, ESI†). The obvious drawback of the postulated PA in super-resolution applications comes from the absolute intensity, which is at least an order of magnitude weaker than the up-conversion itself, but the simulations clearly demonstrated that linear “confocal-like” imaging (Fig. 4d) cannot distinguish individual NPs on the same phantom. Therefore, although weaker, the signal to background of PA imaging should be beneficial in terms of its spatial resolving power and imaging contrast. Another great advantage of PASSI imaging is the fact that no pinhole is required. This is because PA emission occurs only at the exact center of the focal volume, which makes the out-of-focus background signal very low and thus not detectable, either in the X–Y or in the axial Z plane (Fig. S7, ESI†). For this reason, the optical system does not require complex or costly solutions, either in the excitation or detection path, and eventually conventional confocal laser scanning microscopes (LSM) shall prove to be effective systems easily adoptable to PASSI imaging mode.
The advantage of PASSI is that it is a simple solution to technical challenges that currently limit the wide adoption of existing super-resolution methods. First, it enables operation with only one photoexcitation beam, enabling parallel excitation over multiple spots or the simultaneous detection of multiple colors. The long rise-times of intensities in the PA process will enable, through time-gated detection, elimination of the background and sample autofluorescence signals. All these features will enable radical improvements in the signal to noise ratio while also increasing the penetration depth into scattering or heterogeneous media, which are important for ultrasensitive detection in complex biological samples. Although PA in nanomaterials has been rarely reported, lanthanide doped nanoparticles have been extensively studied for over a decade, and their synthesis, characterization and on-demand design are reproducible and relatively well-understood. The major advantages of PA labels with respect to biological applications stem from fundamental properties of lanthanide ions, which include extreme photo-stability, narrowband and multiple absorption/emission as well as large Stokes shift, efficient anti-Stokes emission and ultimately photoexcitation at a single line from robust and affordable laser diodes. Moreover, long wavelength photoexcitation (e.g. 1064 nm for Nd, Tm etc.), where organic molecules neither absorb nor emit photons, provides low background auto fluorescence signal and low scattering of exciting photons. This feature is extremely important for the safety in imaging of biological samples – i.e. no excessive exposure of living samples to photon flux occurs, and thus no thermal or photobleaching side effects are expected. The discussed PA model revealed that finding the most appropriate excitation intensity to enhance the sub-diffraction resolution can be done experimentally, because the PA threshold correlates well with the longest PA rise-time. Importantly, PA based super-resolution imaging is compatible with existing and widely available fluorescent microscopy techniques – in particular, any laser scanning confocal microscope (LSCM) can easily perform PASSI by employing PA nanoparticles and adopting precise control over excitation intensity.
3. Conclusion
The in silico modelling of the photon avalanche phenomenon in Nd3+-doped dielectric NPs demonstrates that their steep power-dependence and slow rise-times, which are characteristic for PA emission, may become key enabling elements of a simple and affordable method for photon avalanche assisted single beam super-resolution imaging (PASSI). The critical parameter to make the proposed system useful is the knowledge of excitation intensity at which saturation begins (Fig. 2c, Po), which can be easily derived experimentally due to the exceptional slowdown of the rise-time in the PA regime (Fig. 2). It is important to note that the Po will be lower than the typically used one in other lanthanide-doped NPs, which is advantageous in light of the laser safety exposure thresholds for living cells. These features make PA interesting not only in terms of its fundamental physics, but also because of its technical simplicity and ability to parallelize the actions by multi-spot sub-diffraction imaging (e.g. as known from Nipkov confocal discs).According to our modelling, PASSI confines the emission point spread function (PSF) to 3–8 times lower volume than conventional confocal PSF without using a depleting beam, without complicated beam overlap adjustments, and without temporal synchronization of the pump and depletion beams. Sub-diffraction limited imaging is an obvious application for this technology and any confocal microscope with appropriate excitation wavelength and spectral filters can perform super-resolution imaging with PASSI without extensive modification. The use of 1064 nm photoexcitation has been shown to be advantageous for biomedical applications due to reduced scattering and autofluorescence under such excitation. Increased observation depths, prolonged observation times, and multi-colour labels under single excitation are also possible with lanthanide-doped nanomaterials.
Future effort is needed to synthesize optimized nanoparticles and provide experimental evidence for the validity of our predictions as well as to evaluate the sensitivity and master the working conditions for the proposed phenomena to occur. Typically, UCNPs are synthesized with diameters around ∼25 nm, but relatively brighter sub 10 nm Ln3+ highly doped UCNPs have been already demonstrated.42 Despite intense research, the surface bio-functionalization of UCNPs still requires reliable protocols to make the UCNPs suitable for bio-specific labeling. The overall size of such constructs should be therefore similar to conventional fluorescently labelled antibodies. The PA phenomenon in nanomaterials may be difficult to observe due to large surface quenching (to be potentially diminished by NP surface passivation) and the requirement for room temperature operation. But little effort has been exerted so far to optimize the Ln3+ nanomaterials for room-temperature PA operation. Fortunately, the physical model relates the in silico variables to the phenomenological parameters, such as radiative and non-radiative rates of cross-relaxation and emission. These suggested parameters should guide experimental explorations into the most appropriate host matrix, dopants and concentrations. As soon as photon avalanche is achieved in nanomaterials, their unique photo-physics will lead to an extraordinary array of applications – including sub-diffraction imaging, sensing, multi-functional labeling and theranostics for biomedical applications, as well as photonic applications such as optical computing, optical switching, and data storage – all of which will benefit from such high optical nonlinearities.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Work at the Molecular Foundry was supported by the Office of Science, Office of Basic Energy Sciences, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. KP acknowledges the support from Foundation for Polish Science (FNP) under the START programme. L. M. acknowledges the support from NCN OPUS 14 under grant UMO-2017/27/B/ST5/02557.References
- G. Vicidomini, P. Bianchini and A. Diaspro, Nat. Methods, 2018, 15, 173 CrossRef CAS PubMed.
- C. Wu, T. Schneider, M. Zeigler, J. Yu, P. G. Schiro, D. R. Burnham, J. D. McNeill and D. T. Chiu, J. Am. Chem. Soc., 2010, 132, 15410 CrossRef CAS PubMed.
- E. D’Este, D. Kamin, F. Göttfert, A. El-Hady and S. W. Hell, Cell Rep., 2015, 10, 1246 CrossRef PubMed.
- F. Helmchen and W. Denk, Nat. Methods, 2005, 2, 932 CrossRef CAS PubMed.
- N. G. Horton, K. Wang, D. Kobat, C. G. Clark, F. W. Wise, C. B. Schaffer and C. Xu, Nat. Photonics, 2013, 7, 205 CrossRef CAS PubMed.
- L. Schermelleh, R. Heintzmann and H. Leonhardt, J. Cell Biol., 2010, 190, 165 CrossRef CAS PubMed.
- B. Huang, H. Babcock and X. Zhuang, Cell, 2010, 143, 1047 CrossRef CAS PubMed.
- K. I. Willig, B. Harke, R. Medda and S. W. Hell, Nat. Methods, 2007, 4, 915 CrossRef CAS PubMed.
- G. Vicidomini, G. Moneron, K. Y. Han, V. Westphal, H. Ta, M. Reuss, J. Engelhardt, C. Eggeling and S. W. Hell, Nat. Methods, 2011, 8, 571 CrossRef CAS PubMed.
- A. Schönle and S. W. Hell, Nat. Biotechnol., 2007, 25, 1234 CrossRef PubMed.
- H. Bock, C. Geisler, C. A. Wurm, C. von Middendorff, S. Jakobs, A. Schönle, A. Egner, S. W. Hell and C. Eggeling, Appl. Phys. B: Lasers Opt., 2007, 88, 161 CrossRef CAS.
- D. Jin, P. Xi, B. Wang, L. Zhang, J. Enderlein and A. M. van Oijen, Nat. Methods, 2018, 15, 1 CrossRef PubMed.
- T. Ha and P. Tinnefeld, Annu. Rev. Phys. Chem., 2012, 63, 595 CrossRef CAS PubMed.
- R. Kolesov, R. Reuter, K. Xia, R. Stöhr, A. Zappe and J. Wrachtrup, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 1 CrossRef.
- Q. Zhan, H. Liu, B. Wang, Q. Wu, R. Pu, C. Zhou, B. Huang, X. Peng, H. Ågren and S. He, Nat. Commun., 2017, 8, 1058 CrossRef PubMed.
- Y. Liu, Y. Lu, X. Yang, X. Zheng, S. Wen, F. Wang, X. Vidal, J. Zhao, D. Liu, Z. Zhou, C. Ma, J. Zhou, J. A. Piper, P. Xi and D. Jin, Nature, 2017, 543, 229 CrossRef CAS PubMed.
- C. Chen, F. Wang, S. Wen, Q. P. Su, M. C. L. Wu, Y. Liu, B. Wang, D. Li, X. Shan, M. Kianinia, I. Aharonovich, M. Toth, S. P. Jackson, P. Xi and D. Jin, Nat. Commun., 2018, 9, 4 CrossRef PubMed.
- Q. Wu, B. Huang, X. Peng, S. He and Q. Zhan, Opt. Express, 2017, 25, 30885 CrossRef CAS PubMed.
- M. F. Joubert, S. Guy and B. Jacquier, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10031 CrossRef CAS.
- R. Scheps, Prog. Quantum Electron., 1996, 20, 271 CrossRef CAS.
- L. Caillat, F. Pellé, B. Hajj, V. Shynkar, D. Chauvat and J. Zyss, Conference on Lasers and Electro-Optics Europe and International Quantum Electronics Conference, CLEO/Europe-IQEC, 2013.
- F. Auzel, Chem. Rev., 2004, 104, 139 CrossRef CAS PubMed.
- H. Deng, S. Yang, S. Xiao, H. M. Gong and Q. Q. Wang, J. Am. Chem. Soc., 2008, 130, 2032 CrossRef CAS PubMed.
- M. F. Joubert, S. Guy and B. Jacquier, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 10031 CrossRef CAS.
- S. Kück, A. Diening, E. Heumann, E. Mix, T. Sandrock, K. Sebald and G. Huber, J. Alloys Compd., 2000, 300, 65 CrossRef.
- M. E. Koch, A. W. Kueny and W. E. Case, Appl. Phys. Lett., 1990, 56, 1083 CrossRef CAS.
- J. S. Chivian, W. E. Case and D. D. Eden, Appl. Phys. Lett., 1979, 35, 124 CrossRef CAS.
- A. Brenier and A. M. Jurdyc, J. Lumin., 1996, 69, 131 CrossRef CAS.
- R. M. Macfarlane, R. Wannemacher, T. Hebert and W. Lenth, Upconversion laser action at 450.2 and 483.0 nm in Tm:YLiF4, Optical Society of America, Baltimore, Maryland United States, 1990.
- V. François, F. Pellé, P. Goldner and D. Simkin, J. Lumin., 1995, 65, 57 CrossRef.
- T. Hebert, R. Wannemacher, R. M. MacFarlane and W. Lenth, Appl. Phys. Lett., 1992, 60, 2592 CrossRef CAS.
- M. F. Joubert, Opt. Mater., 1999, 11, 181 CrossRef CAS.
- M. F. Joubert, S. Guy, S. Cuerq and P. A. Tanner, J. Lumin., 1997, 75, 287 CrossRef CAS.
- E. S. Levy, C. A. Tajon, T. S. Bischof, J. Iafrati, A. Fernandez-Bravo, D. J. Garfield, M. Chamanzar, M. M. Maharbiz, V. S. Sohal, P. J. Schuck, B. E. Cohen and E. M. Chan, ACS Nano, 2016, 10, 8423 CrossRef CAS PubMed.
- A. Bednarkiewicz, D. Wawrzynczyk, M. Nyk and W. Strek, Opt. Mater., 2011, 33, 1481 CrossRef CAS.
- D. Wawrzynczyk, A. Bednarkiewicz, M. Nyk, W. Strek and M. Samoc, Nanoscale, 2012, 4, 6959 RSC.
- A. Bednarkiewicz, D. Wawrzynczyk, M. Nyk and W. Strek, Appl. Phys. B: Lasers Opt., 2011, 103, 847 CrossRef CAS.
- L. Marciniak, A. Bednarkiewicz and K. Elzbieciak, J. Mater. Chem. C, 2018, 6, 7568 RSC.
- W. Lenth and R. M. M. Macfarlane, J. Lumin., 1990, 45, 346 CrossRef CAS.
- G. S. Ofelt, J. Chem. Phys., 1962, 37, 511 CrossRef CAS.
- B. R. Judd, Phys. Rev., 1962, 127, 750 CrossRef CAS.
- D. J. Gargas, E. M. Chan, A. D. Ostrowski, S. Aloni, M. Virginia, P. Altoe, E. S. Barnard, B. Sanii, J. J. Urban, D. J. Milliron, B. E. Cohen and P. J. Schuck, Nat. Nanotechnol., 2014, 9, 300 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00089e |
| This journal is © The Royal Society of Chemistry 2019 |