High Curie temperature and intrinsic ferromagnetic half-metallicity in two-dimensional Cr3X4 (X = S, Se, Te) nanosheets†
Xiwen
Zhang‡
a,
Bing
Wang‡
b,
Yilv
Guo
b,
Yehui
Zhang
b,
Yunfei
Chen
*c and
Jinlan
Wang
 *b
*b
aSchool of Mechanism Engineering & School of Physics, Southeast University, Nanjing 211189, China
bSchool of Physics, Southeast University, Nanjing 211189, China. E-mail: jlwang@seu.edu.cn
cSchool of Mechanism Engineering, Southeast University, Nanjing 211189, China. E-mail: yunfeichen@seu.edu.cn
First published on 25th February 2019
Abstract
Two-dimensional (2D) intrinsic magnetic materials with room temperature ferromagnetism and complete spin-polarization are highly desirable for realizing advanced spintronic devices. However owing to the weak d–p–d super-exchange interaction, many recently realized 2D ferromagnetic (FM) materials present a very low Curie temperature (TC). Here, based on first principles calculations, we report a series of Cr3X4 (X = S, Se, Te) monolayers, in which the coexistence of two oxidation states of Cr atoms results in double-exchange interaction and thereby enhances FM coupling greatly and improves TC up to 370 K for Cr3Se4 and 460 K for Cr3Te4, respectively. Spin-polarized calculations further demonstrate that Cr3Se4 and Cr3Te4 monolayers are FM half-metals, which ideally could achieve 100% spin-polarized currents. Meanwhile, excellent dynamical and thermal stabilities are identified, and a possible synthetic strategy is proposed. Our work not only provides two competitive ferromagnetic candidate materials for nanoscale spintronic applications, but also shows that double-exchange interaction may be a way to realize 2D room temperature FM half-metals.
Conceptual insightsRecently realized two-dimensional (2D) intrinsic ferromagnetic (FM) materials open the door for nanoscale spintronic applications. However, the development is highly limited by the incomplete spin-polarization and low Curie temperature (TC) originating from the weak d–p–d super-exchange interaction. In this article, we present a series of 2D magnetic materials, namely, Cr3X4 (X = S, Se, Te) monolayers with two different oxidation-state Cr ions. A delocalized unpaired electron tends to hop from one Cr ion to another neighboring different oxidation-state Cr ion to effectively save energy, i.e. a double-exchange mechanism, which leads to enhanced FM coupling and high TC (370 K for Cr3Se4 and 460 K for Cr3Te4). The new insights into strong FM coupling being attainable in monolayers via double-exchange interaction provide a feasible way for experiments to realize 2D room temperature ferromagnetism. More than that, Cr3Se4 and Cr3Te4 monolayers are found to be FM half-metals with relatively large spin gaps and 100% spin-polarization at the Fermi level. The thermal and mechanical stabilities have been further confirmed and a possible synthesis route is also proposed. The coexistence of these unique properties in one 2D material is rarely reported but crucial for advanced electronic and spintronic applications. |
Introduction
Spintronics or spin-based electronics, using the spin of electrons, offers great opportunities for next generation information technology.1,2 Two-dimensional (2D) ferromagnetic (FM) materials, as one of the most promising candidates for nanoscale spintronic devices, have been highly sought out.3–5 While much effort has been made for inducing magnetism in 2D non-magnetic systems, success is still limited due to the induced magnetism lacking long-range FM coupling.6–10 Very recently, ferromagnetic Cr2Ge2Te6 bilayers,11 CrI3 monolayers,12 and Fe3GeTe2 monolayers13 have been successfully synthesized, and open the door for achieving long-range FM order in 2D intrinsic ferromagnetic materials. However, the TC of these intrinsic 2D FM materials is far below room temperature because of the weak ferromagnetic super-exchange interaction, which cannot meet most technology applications. In fact, to date, experimental observation of 2D intrinsic room temperature FM materials has never been reported.Half-metals exhibit a metallic density of states at the Fermi level for one spin channel and a band gap for the other spin channel, showing enormous potential for an ideal electrode in spintronic devices. Half-metal electrodes not only can provide fully spin-polarized currents and large magnetoresistance (MR) in giant MR and tunneling MR devices, but also can realize efficient spin injection into semiconductors, opening the way for more applications, including spin-based transistors and spin Seebeck devices. Although numerous half-metallic bulk compounds have been identified,14–19 and spintronic devices based on these materials have been realized,20,21 experimental evidence for 2D half-metallic behavior is still rather scarce. Several recent studies showed that an applied electric field22 and edge modification23–25 can make graphene nanoribbons create 100% spin-polarized currents. Nevertheless, device operation without an electric field is a fundamental objective of spintronics, and edge modifications will add additional challenges to the synthesis process. Therefore, 2D FM materials with high TC and intrinsic half-metallicity remain an important frontier for discovery.
In this paper, for the first time, we propose a family of Cr3X4 (X = S, Se, Te) monolayers; in particular, the Cr3Se4 and Cr3Te4 monolayers exhibit large perpendicular magnetic moments, high-temperature ferromagnetism, 100% spin-polarization ratio, and sizable magnetocrystalline anisotropy energy (MAE), suitable for nanoscale spintronics applications. Notably, the Cr3Se4 and Cr3Te4 monolayers possess two different oxidation-state Cr atoms, which is different from many other 2D Cr-based FM materials, such as CrY3 (Y = Cl, Br, I)26,27 and CrMTe3 (M = Si, Sn, Ge).28,29 The coexistence of two oxidation states of Cr atoms results in a dominant interlayer double-exchange interaction and hence a strong interlayer FM coupling. Meanwhile, the intralayer nearest-neighboring Cr atoms also exhibit FM coupling behaviors because of Cr–X–Cr super-exchange interaction. As a result, the TC values of the Cr3Se4 and Cr3Te4 monolayers estimated with Monte Carlo (MC) simulation based on the 2D Heisenberg Hamiltonian model are as high as 370 K and 460 K, respectively. In addition, our calculation results reveal that Cr3Se4 and Cr3Te4 monolayers exhibit intrinsic FM half-metallicity with relatively large spin gaps and have an out-of-plane easy axis. Their MAEs can be comparable to those of the Fe and Co monolayers deposited on Rh (111) and Rt (111) substrates.30 Phonon dispersion curves and ab initio molecular dynamics (AIMD) simulation further demonstrate their dynamical and thermal stabilities. Experimentally, Cr3Se4 and Cr3Te4 monolayers are possibly obtained by reducing the thickness of CrSe and CrTe thin films recently synthesized31–34 at the nanoscale.
Results and discussion
Magnetic coupling and electronic properties
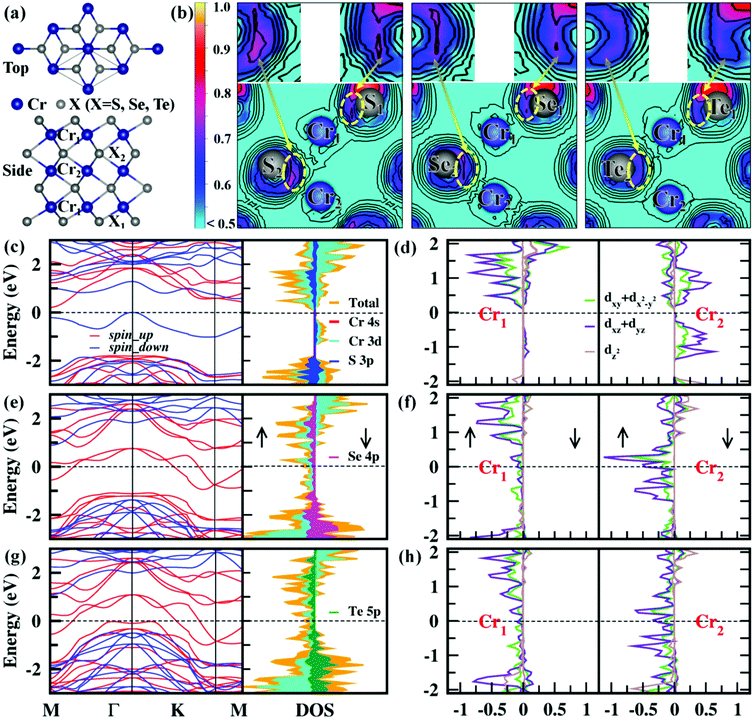
Cr3X4 (X = S, Se, Te) monolayers are isostructural with each Fe3S4 sheet from the layered Fe3S4 bulk35 (Fig. S1, ESI†). The top and side views of the Cr3X4 (X = S, Se, Te) monolayers are given in Fig. 1a, belonging to the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 space group. Similar to double-transition-metal MXene monolayers (e.g. Hf2MnC2O2, Hf2VC2O2 and Hf2VC2F2),36,37 the Cr3X4 (X = S, Se, Te) monolayers are also composed of seven hexagonal layers, with X1–Cr1–X2–Cr2–X2–Cr1–X1 atomic layers stacking along the z-direction. To study the magnetic properties of the Cr3X4 monolayers, we first study the magnetic coupling between the Cr atoms by considering six different spin orderings in a 2 × 2 × 1 supercell (Fig. S2, ESI†). The total energies of the ferromagnetic (FM), antiferromagnetic (AFM), and ferrimagnetic (FIM) configurations are calculated with the HSE06 functional and the relative energies between the FM and AFM/FIM configurations are listed in Table S1, ESI.† The results indicate that the Cr3S4 monolayer exhibits an FIM ground state, while the ground-states of the Cr3Se4 and Cr3Te4 monolayers are FM. The net ground-state magnetic moments are 2.00, 10.00 and 10.00 μB f.u.−1 for Cr3S4, Cr3Se4, and Cr3Te4 respectively, indicating large spin polarization in these 2D Cr3X4 sheets. The major magnetisms in 2D Cr3X4 crystals are mainly located on the Cr atoms as illustrated by the spin charge density distribution in Fig. S2, ESI,† and the magnetic moments carried on the Cr1 and Cr2 atoms are listed in Table 1. From Table 1, we can find that the Cr atoms in Cr3Te4 have a slightly larger magnetic moment than those in Cr3S4 and Cr3Se4, which is likely due to the relatively weak Cr–Te bonds driving localization of the electrons (Fig. 1b).
m1 space group. Similar to double-transition-metal MXene monolayers (e.g. Hf2MnC2O2, Hf2VC2O2 and Hf2VC2F2),36,37 the Cr3X4 (X = S, Se, Te) monolayers are also composed of seven hexagonal layers, with X1–Cr1–X2–Cr2–X2–Cr1–X1 atomic layers stacking along the z-direction. To study the magnetic properties of the Cr3X4 monolayers, we first study the magnetic coupling between the Cr atoms by considering six different spin orderings in a 2 × 2 × 1 supercell (Fig. S2, ESI†). The total energies of the ferromagnetic (FM), antiferromagnetic (AFM), and ferrimagnetic (FIM) configurations are calculated with the HSE06 functional and the relative energies between the FM and AFM/FIM configurations are listed in Table S1, ESI.† The results indicate that the Cr3S4 monolayer exhibits an FIM ground state, while the ground-states of the Cr3Se4 and Cr3Te4 monolayers are FM. The net ground-state magnetic moments are 2.00, 10.00 and 10.00 μB f.u.−1 for Cr3S4, Cr3Se4, and Cr3Te4 respectively, indicating large spin polarization in these 2D Cr3X4 sheets. The major magnetisms in 2D Cr3X4 crystals are mainly located on the Cr atoms as illustrated by the spin charge density distribution in Fig. S2, ESI,† and the magnetic moments carried on the Cr1 and Cr2 atoms are listed in Table 1. From Table 1, we can find that the Cr atoms in Cr3Te4 have a slightly larger magnetic moment than those in Cr3S4 and Cr3Se4, which is likely due to the relatively weak Cr–Te bonds driving localization of the electrons (Fig. 1b).
| Materials | M Cr1 (μB) | M Cr2 (μB) | M tot (μB f.u.−1) | E FM–AFM (meV f.u.−1) | J 1 (meV) | J 2 (meV) | J 3 (meV) | T C (K) |
|---|---|---|---|---|---|---|---|---|
| Cr3S4 | 2.94 | −3.53 | 2.00 | 146.6 | — | — | — | — |
| Cr3Se4 | 3.24 | 3.66 | 10.00 | −58.6 | 12.12 | 10.89 | −0.88 | 370 |
| Cr3Te4 | 3.45 | 3.80 | 10.00 | −218.6 | 30.60 | 9.24 | 2.18 | 460 |
The fundamental character of the FM ordering in Cr3X4 monolayers at low temperature can be further understood by the MAE, which is directly related to the thermal stability of magnetic data storage. Here, spin orbit coupling (SOC) calculations at the HSE06 level are performed to accurately obtain the relative magnetization stability in-plane and out-of-plane. As summarized in Table S2, ESI,† the easy magnetization axes of the Cr3X4 monolayers are along the out-of-plane (001) direction. The calculated MAE of the Cr3Se4 and Cr3Te4 monolayers are 0.10 and 0.15 meV per Cr, respectively, which are comparable to the values of the Fe and Co monolayers deposited on Rh (111) and Rt (111) substrates.30 These sizable MAEs make Cr3Se4 and Cr3Te4 monolayers good candidates for magnetic devices. Having studied the magnetic properties of the Cr3X4 monolayers, we further turn to their ground-state electronic structures. The calculated ground-state spin-dependent electronic structures and corresponding ground-state spin configurations of 2D Cr3X4 unit cells are displayed in Fig. 1 and Fig. S3, ESI.† Obviously, the Cr3S4 monolayer is an FIM semiconductor with a band gap of 0.25 eV, while the Cr3Se4 and Cr3Te4 monolayers exhibit FM half-metallicity, i.e., metallic character for the majority-spin electrons while semiconducting nature for the minority-spin electrons. This means that the majority-spin electrons make a dominant contribution to the charge transport, and the electric current is 100% spin-polarized. As shown in Fig. 1, the spin gaps between the bottommost unoccupied and topmost occupied minority-spin bands are 2.27 eV for the Cr3Se4 monolayer and 1.59 eV for the Cr3Te4 monolayer, respectively, which are relatively large to effectively block the thermally induced spin–flip transition. The total and partial density of states shows a predominant contribution of Cr-d and X-p orbitals to the majority-spin channel and a strong hybridization between the Cr-d and X-p states. This confirms that the important indirect exchange interactions between the two Cr 3d orbitals are mediated by the neighboring X np (n = 3/4/5) orbitals. In addition, the Cr atom in 2D Cr3X4 crystals is under D3d symmetry, and therefore its five Cr 3d orbitals split into a single a (dz2) orbital and two 2-fold degenerate e1 (dxz + dyz) and e2 (dxy + dx2−y2) orbitals, which is in good agreement with the calculated results displayed in Fig. 1d, f, and h and Fig. S4, ESI.† Besides, we find that the PDOS of Cr2 atoms shows a much larger peak near the Fermi level than that of Cr1 atoms, indicating that the Cr2 atoms make a main contribution to the half-metallicity in Cr3X4 monolayers.
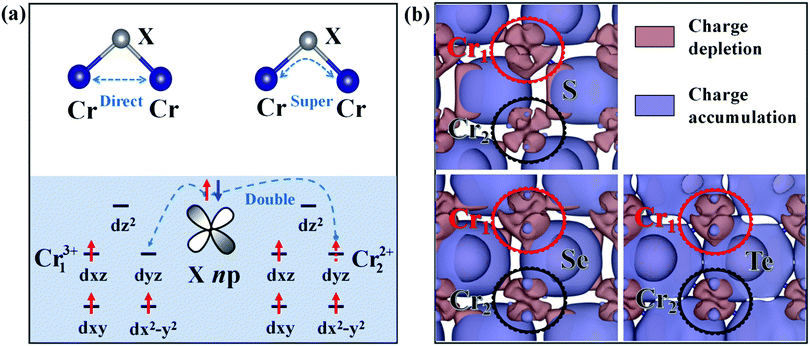
As studied above, the ground-state of the Cr3Se4 and Cr3Te4 monolayers both exhibit FM coupling between the two nearest-neighboring intralayer Cr atoms and interlayer Cr atoms, while that of the Cr3S4 monolayer shows interlayer AFM coupling (Fig. S3, ESI†). Actually, these ground-state intralayer and interlayer coupling behaviors in Cr3X4 can be understood by the competition between the direct-exchange and super-exchange/double-exchange interaction. The distances between the two intralayer nearest-neighboring Cr1 atoms (Table S3, ESI†) are relatively large, therefore, the direct-exchange interaction (usually favoring an AFM arrangement, Fig. 2a) between these intralayer Cr1 atoms in 2D Cr3X4 crystals is weak. Meanwhile, we notice from Table S3, ESI,† that the θ1 (Cr1–X1–Cr1) of 2D Cr3X4 crystals are all close to 90°. As explained by the well-known Goodenough–Kanamori–Anderson (GKA) rule, the super-exchange interaction (Fig. 2a) usually favors FM ordering for the systems with a Cr–X–Cr bond angle of 90°. As a result, the ground-state FM coupling behavior between the two nearest-neighboring intralayer Cr1 atoms can be easily understood. Furthermore, the two nearest-neighboring Cr atoms along the z-direction, unlike the intralayer Cr atoms, are not equivalent. The deformation charge density (Fig. 2b) shows that the Cr1 atom loses more electrons than the Cr2 atom, which leads to the two Cr atoms presenting different valence states. Under an ionic model, each Cr1 (or Cr2) atom will donate 3e (or 2e) to neighboring X. X anions belong to relatively weak ligands, resulting in a high-spin configuration, and therefore the arrangement of electrons are localized on the Cr13+ and Cr22+ ions as displayed in Fig. 2a.
The double-exchange model is superficially similar to the super-exchange model. However, super-exchange interaction generally occurs between two metal atoms with the same valence, while double-exchange interaction occurs only when one metal atom has an extra electron compared to the other.38,39 The interlayer coupling in the Cr3X4 monolayers belongs to the latter case. The X atom connecting the nearest-neighboring Cr13+ and Cr22+ ions, gives up its spin-up or spin-down electron to Cr13+, and then its vacant orbital can be filled by an electron from Cr22+. At the end of the double-exchange process, the electron moves between the neighboring Cr ions retaining its spin. This electron movement from one to another will be facilitated more easily if the electron does not have to change spin direction. The ability to hop (to delocalize) reduces the kinetic energy, and thus leads to FM alignment of the nearest-neighboring Cr ions along the z-direction. Moreover, we notice that the magnetic moments on Cr1 and Cr2 atoms, shown in Table 1, slightly deviate from the ionic picture (Cr13+, 3 μB; Cr22+, 4 μB). It is also likely due to the delocalized hopping electron shared by the two nearest-neighboring Cr ions along the z-direction during the double-exchange process. In addition, the distances of the interlayer nearest-neighboring Cr ions in 2D Cr3S4 are only 3.02 Å and much smaller than those in 2D Cr3Se4 (3.19 Å) and 2D Cr3Te4 (3.26 Å). This suggests that the interlayer direct-exchange interaction in 2D Cr3S4 is much stronger than that in 2D Cr3Se4 and 2D Cr3Te4. Meanwhile, Cr–S bonds are stronger than Cr–Se/Te bonds (see Fig. 1 and Fig. 4), which makes the electron hopping process (interlayer double-exchange process) in a Cr3S4 monolayer more easily hindered than that in Cr3Se4 and Cr3Te4 monolayers. As a result, direct-exchange interaction plays a major role in the interlayer magnetic coupling behaviors in a Cr3S4 monolayer, and thus the interlayer nearest-neighboring Cr ions exhibit AFM ordering. By contrast, a stronger interlayer double-exchange interaction leads to the interlayer FM coupling in Cr3Se4 and Cr3Te4 monolayers.
Curie temperatures of the single-layer FM Cr3Se4 and Cr3Te4
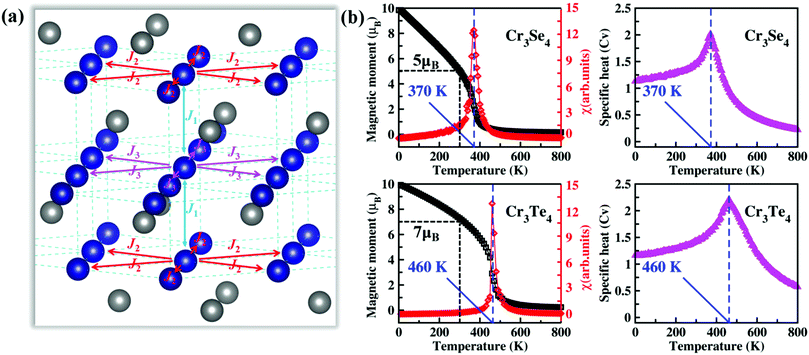
Next, we calculate exchange interaction parameters and then use these exchange parameters to predict the TC of single-layer Cr3Se4 and Cr3Te4. Based on the Heisenberg model, the spin Hamiltonian of Cr3X4 monolayers can be considered as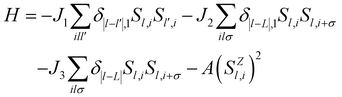 , where J1 and J2/J3 are defined as interlayer and intralayer exchange coupling parameters (Fig. 3a), A is anisotropy energy parameter, and Szl,i is the spin vector of each atom (more details see Fig. S5, ESI†). The interlayer (J1) and intralayer (J2, J3) exchange coupling parameters for Cr3X4 monolayers are estimated by computing the energy differences between FM configurations and different AFM/FIM configurations at the HSE06 functional level. The large and positive interlayer exchange coupling parameter J1 and intralayer exchange coupling parameter J2 fail to make the AFM coupling occur, and thus lead to a robust FM order in Cr3Se4 and Cr3Te4 monolayers (Table 1). Furthermore, it is important to note that their J1 originated from double-exchange interaction is larger than the J2 derived from super-exchange interaction. This indicates that double-exchange interaction makes a dominant contribution to the robust FM arrangement of 2D Cr3Se4 and Cr3Te4 crystals.
, where J1 and J2/J3 are defined as interlayer and intralayer exchange coupling parameters (Fig. 3a), A is anisotropy energy parameter, and Szl,i is the spin vector of each atom (more details see Fig. S5, ESI†). The interlayer (J1) and intralayer (J2, J3) exchange coupling parameters for Cr3X4 monolayers are estimated by computing the energy differences between FM configurations and different AFM/FIM configurations at the HSE06 functional level. The large and positive interlayer exchange coupling parameter J1 and intralayer exchange coupling parameter J2 fail to make the AFM coupling occur, and thus lead to a robust FM order in Cr3Se4 and Cr3Te4 monolayers (Table 1). Furthermore, it is important to note that their J1 originated from double-exchange interaction is larger than the J2 derived from super-exchange interaction. This indicates that double-exchange interaction makes a dominant contribution to the robust FM arrangement of 2D Cr3Se4 and Cr3Te4 crystals.
The TC of FM Cr3Se4 and Cr3Te4 monolayers are computed by carrying out MC simulations with a 50 × 50 × 1 supercell. In the MC simulations, 2 × 105 MC steps for each temperature are employed and spins on all magnetic sites flip randomly. The calculated magnetic moments, magnetic susceptibility (χ), and specific heat capacity (Cv) as functions of temperature for Cr3Se4 and Cr3Te4 monolayers are illustrated in Fig. 3b. We notice that the FM orderings with large magnetic moments (∼5 μB f.u.−1 for Cr3Se4 monolayer; ∼7 μB f.u.−1 for Cr3Te4 monolayer) could be preserved at room temperature (300 K). Furthermore, under the exact solution to the spin Hamiltonians, the TC can be accurately obtained from the peak positions of χ and Cv, and is 370 K for the Cr3Se4 monolayer and 460 K for the Cr3Te4 monolayer. These values are significantly higher than those of bilayer Cr2Ge2Te6 (20 K),11 monolayer CrI3 (45 K),12 and even monolayer VSe2/van der Waals heterostructures.40 Meanwhile, we have estimated the TC (∼43 K) of monolayer CrI3 using the same approach (Fig. S6, ESI†), which agrees well with the experimental measurement one.12 We further calculate the relative energies of the FM/AFM/FIM states as a function of strain and carrier concentration. The FM states are always lower than the AFM/FIM states and the relative energies change little under different strain conditions and carrier concentrations (see Fig. S7, ESI†), indicating that the FM states are quite robust under external perturbations. This indicates that the Cr3Se4 and Cr3Te4 monolayers are potential candidates for spintronic applications.
Stability and practical synthesis approaches
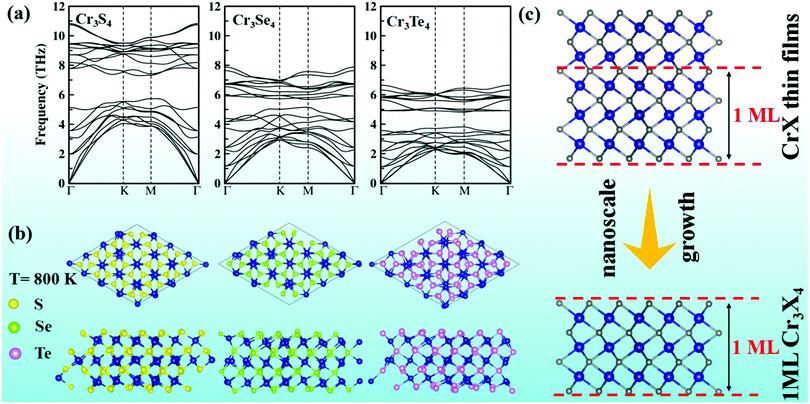
To assess the structural stability of Cr3X4 (X = S, Se, Te) monolayers, we first calculate their cohesive energies by the definition of Ecoh = (ECr3X4 − 3 × ECr − 4 × EX)/7, where ECr3X4 is the total energy of ECr3X4 monolayers, ECr is the energy of an isolated Cr atom, and EX is the energy of the isolated X atom. The calculated cohesive energies are −7.78, −6.65, and −5.96 eV per atom for Cr3S4, Cr3Se4, and Cr3Te4 monolayers, respectively. These values are comparable to that of graphene (−7.85 eV per atom), which suggests their possible stability. Phonon spectra computed by density functional perturbation theory (DFPT) implemented in the Phonopy program41 indicate that the Cr3X4 monolayers are dynamically stable since no imaginary phonon mode appears in the whole Brillouin zone (Fig. 4a). Meanwhile, the acoustic vibration modes become softer from Cr3S4 to Cr3Te4 due to the gradually weakening bond strength from Cr–S to Cr–Te (Fig. 4a and Fig. S2b, ESI†). We further perform ab initio molecular dynamics (AIMD) simulations to assess the thermal stability by employing a 4 × 4 × 1 supercell containing 112 atoms to reduce lattice translational constraints. Fig. 4b displays the structural snapshots of Cr3X4 monolayers at 5 ps at 800 K. Neither geometric reconstruction nor broken bonds have been discovered during the entire process, suggesting that MXenes-like Cr3X4 monolayers have high thermal stability.Considering that Cr3Se4 and Cr3Te4 monolayers exhibit a promising spintronic application and excellent stability, practical synthetic methods are expected to be attractive to experiments. Note that the crystal structures of Cr3X4 monolayers are similar to the layers produced by periodically interrupting the basic CrX framework (Fig. 4c). Moreover, CrSe and CrTe thin films have been successfully produced via chemical bath deposition on substrates (commercial glass) and molecular beam epitaxy on SrTiO3 (111) substrates, respectively.31–34 Therefore, it is possible to obtain 2D Cr3Se4 and Cr3Te4 sheets by reducing the thickness of CrSe and CrTe thin films to the nanoscale (Fig. 4c), which has recently been used to obtain a MnSe2 monolayer.42 Alternatively, it is also possible to obtain 2D Cr3Se4 and Cr3Te4 sheets by the method of chemical vapor deposition, which has been extensively used for obtaining 2D materials on selected substrates.43
In summary, we have predicted a series of stable 2D Cr3X4 (X = S, Se, Te) crystals with novel electronic and magnetic properties utilizing first-principles calculations. A Cr3S4 monolayer is found to be a ferrimagnetic semiconductor while Cr3Se4 and Cr3Te4 monolayers are ferromagnetic half-metals with relatively large spin gaps. Importantly, 2D Cr3Se4 and Cr3Te4 crystals also exhibit large magnetic moments at room temperature and high TC (370 K for Cr3Se4 and 460 K for Cr3Te4). The further analysis shows that the Cr atoms in Cr3Se4 and Cr3Te4 monolayers present two different oxidation states and a delocalized unpaired electron tends to hop between the two neighboring different oxidation-state Cr ions to retain its spin. This magnetic coupling mechanism (double-exchange process) can effectively save energy, and thus facilitates the realization of high-temperature ferromagnetism. Moreover, phonon spectrum calculations and AIMD simulations confirm that the Cr3Se4 and Cr3Te4 monolayers have excellent dynamic and thermal stabilities. Thus, 2D Cr3Se4 and Cr3Te4 crystals are ideal candidates for nanoscale spintronic devices. Additionally, our study suggests that strong FM coupling is attainable via a double-exchange process and perhaps experiments should pay more attention to the double-exchange systems for achieving 2D intrinsic room temperature FM half-metals.
Computational methods
All calculations were performed on the basis of spin-polarized density functional theory (DFT) as implemented in the Vienna ab initio simulation (VASP) package44 with projector-augmented wave (PAW) potentials.45 To exactly deal with the strongly correlated effect on 3d electrons of Cr atoms and give accurate electronic structures, the HSE06 hybrid functional46 was employed. The plane-wave cutoff energy of 400 eV for basis and a vacuum of 15 Å for eliminating adjacent layer interactions were used. The total-energy convergence criterion of 1 × 10−6 eV and the force convergence criterion of −10−2 eV Å−1 were chosen in the complete relaxations including the lattice constants and atomic positions.Phonon dispersion was calculated on the basis of DFPT as embedded in the Phonopy program.41 AIMD simulations were carried out to evaluate the thermal stability of Cr3X4 (X = S, Se, Te) monolayers at the temperature of 800 K. AIMD simulation in the NVT ensemble lasts for 5 ps with a time step of 1 fs. The temperature is controlled by using the Nose–Hoover method.47
Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
This work was supported by the National Key Research and Development Program of China (2017YFA0204800), the Natural Science Funds of China (21525311, 21773027, and 51435003), the Jiangsu 333 project (BRA2016353), the Scientific Research Foundation of Graduate School of Southeast University (YBJJ1773), and the Fundamental Research Funds for the Central Universities of China. The authors are thankful for the computational resources at the SEU and National Supercomputing Center in Tianjin.Notes and references
- C. Felser, G. H. Fecher and B. Balke, Angew. Chem., Int. Ed., 2007, 46, 668–699 CrossRef CAS PubMed.
- H. Kabbour, R. David, A. Pautrat, H. J. Koo, M. H. Whangbo, G. Andre and O. Mentre, Angew. Chem., Int. Ed., 2012, 51, 11745–11749 CrossRef CAS PubMed.
- Z. Jiang, P. Wang, X. Jiang and J. Zhao, Nanoscale Horiz., 2018, 3, 335–341 RSC.
- B. Wang, Q. Wu, Y. Zhang, Y. Guo, X. Zhang, Q. Zhou, S. Dong and J. Wang, Nanoscale Horiz., 2018, 3, 551–555 RSC.
- B. Cai, X. Chen, M. Xie, S. Zhang, X. Liu, J. Yang, W. Zhou, S. Guo and H. Zeng, Mater. Horiz., 2018, 5, 961–968 RSC.
- Y. Tong, Y. Guo, K. Mu, H. Shan, J. Dai, Y. Liu, Z. Sun, A. Zhao, X. Zeng, C. Wu and Y. Xie, Adv. Mater., 2017, 29, 1703123 CrossRef PubMed.
- B. Li, T. Xing, M. Zhong, L. Huang, N. Lei, J. Zhang, J. Li and Z. Wei, Nat. Commun., 2017, 8, 1958 CrossRef PubMed.
- G. Z. Magda, X. Jin, I. Hagymasi, P. Vancso, Z. Osvath, P. Nemes-Incze, C. Hwang, L. P. Biro and L. Tapaszto, Nature, 2014, 514, 608–611 CrossRef CAS PubMed.
- S. Radhakrishnan, D. D. A. Samanta, C. A. d. l. Reyes, L. Deng, L. B. Alemany, T. K. Weldeghiorghis, V. N. Khabashesku, V. Kochat, Z. Jin, P. M. Sudeep, A. A. Martí, C. W. Chu, A. Roy, C. S. Tiwary, A. K. Singh and P. M. Ajayan, Sci. Adv., 2017, 3, 7–14 Search PubMed.
- H. González-Herrero, J. M. Gómez-Rodríguez, P. Mallet, M. Moaied, J. J. Palacios, C. Salgado, M. M. Ugeda, J. Y. Veuillen, F. Yndurain and I. Brihuega, Science, 2016, 352, 437–441 CrossRef PubMed.
- C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265–269 CrossRef CAS PubMed.
- B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-Herrero and X. Xu, Nature, 2017, 546, 270–273 CrossRef CAS PubMed.
- Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, W. Wu, D. H. Cobden, J. H. Chu and X. Xu, Nat. Mater., 2018, 17, 778–782 CrossRef CAS PubMed.
- K. Schwar, J. Phys. F: Met. Phys., 1986, 16, L211–L215 CrossRef.
- K. I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677–680 CrossRef CAS.
- P. J. Brown, K. U. Neumann, P. J. Webster and K. R. A. Ziebeck, J. Phys.: Condens. Matter, 2000, 12, 1827–1835 CrossRef CAS.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 174429 CrossRef.
- M. S. Miao and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 064407 CrossRef.
- J. J. Versluijs, M. A. Bari and J. M. D. Coey, Phys. Rev. Lett., 2001, 87, 026601 CrossRef.
- M. R. Li, M. Retuerto, Z. Deng, P. W. Stephens, M. Croft, Q. Huang, H. Wu, X. Deng, G. Kotliar, J. Sanchez-Benitez, J. Hadermann, D. Walker and M. Greenblatt, Angew. Chem., Int. Ed., 2015, 54, 12069–12073 CrossRef CAS PubMed.
- J. B. Philipp, P. Majewski, L. Alff, A. Erb, R. Gross, T. Graf, M. S. Brandt, J. Simon, T. Walther, W. Mader, D. Topwal and D. D. Sarma, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 144431 CrossRef.
- Y. W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- S. Dutta, A. K. Manna and S. K. Pati, Phys. Rev. Lett., 2009, 102, 096601 CrossRef PubMed.
- Y. Li, Z. Zhou, P. Shen and Z. Chen, ACS Nano, 1953, 1952–1958 Search PubMed.
- O. Hod, V. N. Barone, J. E. Peralta and G. E. Scuseria, Nano Lett., 2007, 7, 2295–2299 CrossRef CAS PubMed.
- L. Pan, L. Huang, M. Zhong, X. W. Jiang, H. X. Deng, J. Li, J. B. Xia and Z. Wei, Nanoscale, 2018, 10, 22196–22202 RSC.
- L. Webster and J. A. Yan, Phys. Rev. B, 2018, 98, 144411 CrossRef.
- H. L. Zhuang, Y. Xie, P. R. C. Kent and P. Ganesh, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035407 CrossRef.
- G. T. Lin, H. L. Zhuang, X. Luo, B. J. Liu, F. C. Chen, J. Yan, Y. Sun, J. Zhou, W. J. Lu, P. Tong, Z. G. Sheng, Z. Qu, W. H. Song, X. B. Zhu and Y. P. Sun, Phys. Rev. B, 2017, 95, 245212 CrossRef.
- A. Lehnert, S. Dennler, P. Blonski, S. Rusponi, M. Etzkorn, G. Moulas, P. Bencok, P. Gambardella, H. Brune and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 094409 CrossRef.
- I. A. Kariper, Opt. Rev., 2017, 24, 139–146 CrossRef CAS.
- I. A. Kariper, J. Non-Oxide Glasses, 2015, 7, 37–44 Search PubMed.
- A. Goswami and P. S. Nikam, Thin Solid Films, 1972, 11, 353–364 CrossRef CAS.
- D. Zhao, L. Zhang, I. A. Malik, M. Liao, W. Cui, X. Cai, C. Zheng, L. Li, X. Hu, D. Zhang, J. Zhang, X. Chen, W. Jiang and Q. Xue, Nano Res., 2018, 11, 3116–3121 CrossRef CAS.
- R. M. Spaxswick, Nature, 1968, 218, 356–357 CrossRef.
- L. Dong, H. Kumar, B. Anasori, Y. Gogotsi and V. B. Shenoy, J. Phys. Chem. Lett., 2017, 8, 422–428 CrossRef CAS PubMed.
- J. J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, J. Am. Chem. Soc., 2018, 140, 9768–9773 CrossRef CAS PubMed.
- P. Friš, D. Munzar, O. Caha and A. Dubroka, Phys. Rev. B, 2018, 97, 045137 CrossRef.
- B. Zhang, C. Cao, G. Li, F. Li, W. Ji, S. Zhang, M. Ren, H. Zhang, R. Q. Zhang, Z. Zhong, Z. Yuan, S. Yuan and G. R. Blake, Phys. Rev. B, 2018, 97, 045137 CrossRef.
- M. Bonilla, S. Kolekar, Y. Ma, H. C. Diaz, V. Kalappattil, R. Das, T. Eggers, H. R. Gutierrez, M. H. Phan and M. Batzill, Nat. Nanotechnol., 2018, 13, 289–293 CrossRef CAS PubMed.
- S. Baroni, S. D. Gironcoli and A. D. Corso, Rev. Mod. Phys., 2001, 73, 515–560 CrossRef CAS.
- D. J. O'Hara, T. Zhu, A. H. Trout, A. S. Ahmed, Y. K. Luo, C. H. Lee, M. R. Brenner, S. Rajan, J. A. Gupta, D. W. McComb and R. K. Kawakami, Nano Lett., 2018, 18, 3125–3131 CrossRef PubMed.
- Z. Cai, B. Liu, X. Zou and H. M. Cheng, Chem. Rev., 2018, 118, 6091–6133 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11185 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- G. J. Martyna, M. L. Klein and M. Tuckerman, J. Chem. Phys., 1992, 97, 2635–2643 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9nh00038k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |