Open Access Article
Open Access ArticleVibration assisted electron tunneling through nano-gaps in graphene nano-ribbons for amino-acid and peptide bond recognition†
Giuseppe
Zollo
 * and
Aldo Eugenio
Rossini
* and
Aldo Eugenio
Rossini
Dipartimento di Scienze di Base e Applicate per l'Ingegneria (Sezione di Fisica), Università di Roma “La Sapienza”, Via A. Scarpa 14-16, 00161 Rome, Italy. E-mail: giuseppe.zollo@uniroma1.it
First published on 18th July 2019
Abstract
Peptide bond and amino-acid recognition by tunneling current flowing across nano-gaps of graphene nano-ribbons has been recently discussed. Theoretical predictions of the tunneling current signals were used in the elastic regime showing peculiar fingerprints. However, inelastic scattering due to vibrations is expected to play an important role. Then, the proposed strategy for peptide sequencing and amino-acid recognition is revised in the light of such inelastic scattering phenomena. Phonon and local vibrational mode assisted current tunneling is calculated by treating electron–phonon scattering in the context of the lowest order expansion of the self-consistent Born approximation. We study Gly and Ala homo-peptides as an example of very similar, small and neutral amino-acids that would be indistinguishable by means of standard techniques, such as the ionic blockade current, in real peptides. We show that all the inelastic contributions to the tunneling current are in the bias range 0 V ≤ V ≤ 0.5 V and that they can be classified, from an atomistic point of view, in terms of energy sub-ranges that they belong to. Peculiar fingerprints can be found for the typical configurations that have been recently found for peptide bond recognition by tunneling current.
1 Introduction
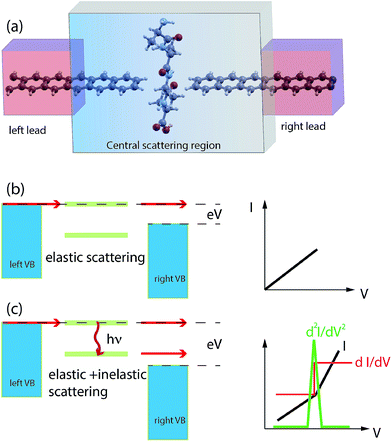
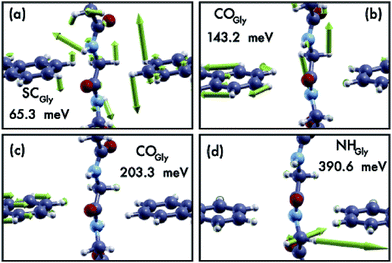
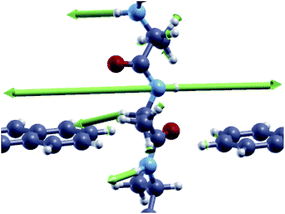
Nano-science and physical phenomena at the nanoscale are being considered for a variety of applications including bio-molecule recognition and sequencing.1–5 Proteins are challenging and the setup of newly conceived methods for fast and reliable amino-acid recognition is highly desirable to face the huge size of the human proteome.3–12 Compared to other schemes, the measurement of the transversal tunneling current across a gap seems to be particularly promising and suitable. Amino-acid (AA) recognition can be attained, at least in principle, by measuring the tunneling current flowing through the gap during peptide translocation, provided a bias is applied between the electrodes:11,13 indeed, the tunneling current measured should reflect the chemical and physical nature of the piece of molecule that occupies the nano-gap. This scheme, however, requires a controlled translocation dynamics of the peptide or the protein (in its primary structure state) which is still an open technological issue. Several proposals to employ nano-gaps for biomolecule sensing have been found in recent literature.13,14 In this context, nano-gaps in “2D materials” are particularly appealing because of the expected sub-molecular resolution of the tunneling current. The applications of 2D materials are even more pronounced in the case of graphene due to its exceptional conduction properties and its ideal 2D character that, in principle, paves the way toward atomistic resolution sensing of biomolecules. Hence graphene nano-gap devices have been proposed as well.15–19 The authors of this work have recently proposed a nano-gap device based on an array of semi-infinite graphene nano-ribbons (GNRs) where the central gap should be devoted to the detection of peptide bonds (PBs) along the peptide back-bone.19 It was shown that using such kinds of GNR based devices (see Fig. 1(a)), it is possible to attain specific signals from single PBs that could be used as a trigger signal for recognition. It is important to emphasize that this proof of principle result is intimately related to the physics that involves the pseudo-π and pseudo-π* orbitals of the GNR leads and the PB molecular orbitals (MOs). Indeed the crucial role played by the N atom involved in the PBs and its pz orbital aligned along the GNR direction in the formation of hybrids allowing the current to flow through the electrodes was also evidenced. The above results have been obtained, for simple glycine (Gly) and alanine (Ala) template peptides, using the non equilibrium Green function approach on the density functional theory basis (DFT-NEGF) and the well-known Landauer–Büttiker formula20–24 (see Section 4). However there are several approximations at this level of theory: among them, one of the most important is that only elastic scattering is considered and one might wonder how molecular vibrations and GNR phonons affect the tunneling current. The inelastic tunneling current across the gap is expected to carry a larger amount of information related to the peculiar vibrational modes, the chemical formula and the charge states of the amino-acid side chains involved. Indeed, while elastic transport gives direct access to the electronic properties of the system (position and broadening of molecular levels for example), the study of the inelastic processes gives a deeper insight into the structure and dynamics of the molecule in the gap. Electrons can exchange energy with the vibrational modes of the molecule thus increasing or reducing the conductance of the junction (Fig. 1(b) and (c)). In the as-prepared ideal sensing device the electrodes are made of two semi-infinite hydrogenated zig-zag GNRs (ZGNRs) of an even type lying in the z direction (see Fig. 1(a)). The nano-gap has a hydrogenated armchair pattern at the border and the distance between two semi-infinite ZGNRs is 5.0 Å (distance between H atoms). Although hydrogenated ZGNRs are expected to have a gap in their ground state due to spin interactions,25,26 it has been reported that metallic unpolarized configurations are stable when a bias is applied and in the presence of ballistic conduction.27,28 Moreover it is known that the spin polarized ground state undergoes a transition to semi-metallic conduction properties when the ZGNR is doped with N atoms29 or when a transverse electric field is applied.30 Then we have chosen the unpolarized metallic phase of the hydrogenated ZGNR as a paradigmatic case of metallic or half-metallic ideal 2D graphene based electrodes.2 Results
We have focussed our attention on Ala and Gly homo-peptides because of the similarity of these two AAs that are small, neutral and have simple hydrophobic side chains. The configurations they assume in the ZGNR nano-gap have been obtained as follows: first we have performed a classical non-equilibrium steered molecular dynamics (SMD) simulation31 at constant velocity and T = 300 K in water and several passages across the nano-gap have been simulated to analyze and collect the most recurring configurations. Then, NVT classical MD simulations at T = 300 K in water have been performed to relax part of the peptide strain due to the previous SMD stage. Then, the most probable configurations have been further relaxed at T = 0 K in the context of density functional theory (DFT) and with a large energy threshold in order to approach a local energy minimum. In this third stage water has been removed. With the above protocol we retain thermal fluctuations of the configurations occurring during the translocation at T = 300 K in water (first and second stages) and correct them in the third stage for the wrong interactions, arising from the classical model potential employed during the classical MD simulations, between the GNR electrodes and the peptide. The final configurations have been employed to calculate the quantum transport and inelastic scattering at low temperature (T = 4.2 K).
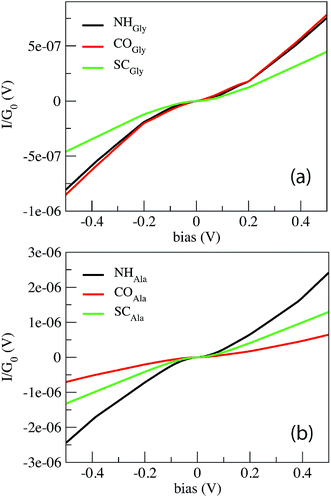
Fig. 2 shows the current in 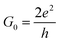 units calculated for the Gly and Ala homo-peptides. We have considered the reference positions corresponding to the characteristic signals obtained from the elastic current as found and extensively discussed recently.19 In a linear case, indeed, we have found that current signals from translocating peptides are related to the NH, CO and SC configurations, i.e. to the configurations with NH, CO and side chain groups in the middle of the gap, the first two being representative of the peptide bond (PB) between adjacent residues.
units calculated for the Gly and Ala homo-peptides. We have considered the reference positions corresponding to the characteristic signals obtained from the elastic current as found and extensively discussed recently.19 In a linear case, indeed, we have found that current signals from translocating peptides are related to the NH, CO and SC configurations, i.e. to the configurations with NH, CO and side chain groups in the middle of the gap, the first two being representative of the peptide bond (PB) between adjacent residues.
From Fig. 1 one can appreciate that inelastic scattering events are important contributions to the tunneling current of both Gly and Ala homo-peptides. For Gly one can observe localized abrupt slope changes while the non linear behavior seems more continuous for Ala. The different current values measured for NH and CO for Ala are due to the amount of overlap between the side chain and the pseudo-π and pseudo-π* orbitals of the nano-ribbons19 which depends on the localization of the peptide in the gap along the y direction in the GNR plane, i.e. along the GNR width. Hence the difference of the current level is not meaningful in terms of the inelastic scattering processes.
We start by analyzing the Gly case.
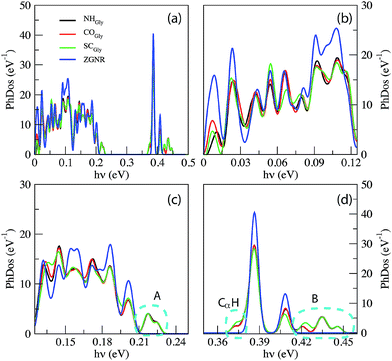
Comparing the phonon density of states (PhDoS) of the three configurations to the one of the ZGNR gap (without the peptide), we find three energy ranges where the PhDoS of the systems does not overlap with the one of the electrodes. Scattering events in these regions, therefore, are due to contributions arising just from the local vibrational modes of the peptide (see Fig. 3). The range 0.42 eV ≤ hν ≤ 0.45 eV (region “B”) contains vibrational modes of the C- and the N-terminals of the homo-peptide and stretching modes of the NH bonds along the peptide backbone. The region “A”, 0.21 eV ≤ hν ≤ 0.23 eV, contains stretching modes of the CO bonds along the peptide backbone and contributions from the C and N-terminals. These modes differ a little between the three configurations but just for the minor contributions from the side chains, CαH and NH groups. Finally we have another region, labeled CαH, due to vibrational modes from the –CH2 group closest to, or in, the gap. In all the other regions of the PhDoS spectra, vibrational modes involve also the ZGNR in the device regions.
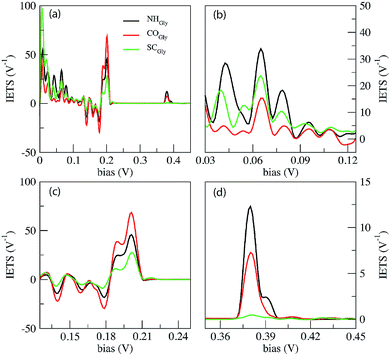
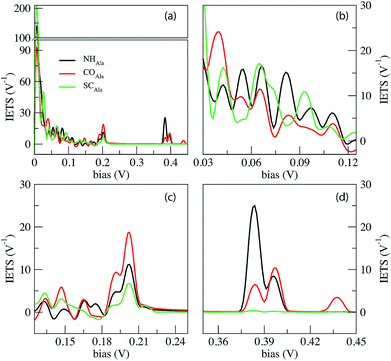
In Fig. 4 we report the IETS signals 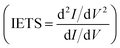 for the three reference configurations mentioned. Three regions are expanded in the same figure for V ≥ 0.03 V because, except for the large peak close to zero occurring in the SC case, the region close to V = 0 does not show marked differences among the three cases.
for the three reference configurations mentioned. Three regions are expanded in the same figure for V ≥ 0.03 V because, except for the large peak close to zero occurring in the SC case, the region close to V = 0 does not show marked differences among the three cases.
Comparing the IETS signals with the corresponding PhDoS and the values of the γ and κ coefficients (see Section 4), four main regions of the IETS spectra can be defined depending on the features of the IETS spectra and the properties of the relevant vibrational modes causing the inelastic scattering. With reference to Fig. 4 we can observe the high energy “side chain” region in the bias range 0.36 V ≤ V ≤ 0.42 V (Fig. 4(d)), the “ZGNR” region in the range 0.19 V ≤ V ≤ 0.21 V (Fig. 4(c)), the “dips” region in the range 0.13 V ≤ V ≤ 0.19 V range (Fig. 4(c)) and, finally, the “low energy” region in the range 0.03 V ≤ V ≤ 0.13 V (Fig. 4(b) and (c)). The energy values of the most important vibrational modes in various regions of the spectra are reported in Table 1 (a complete list of all the important modes can be found in the ESI†). The peaks observed in the high energy “side chain region” are related to the inelastic scattering, the scattering due to local vibrational modes of the closest side chain and CαH. We observe such features for NH and CO but not for the SC (see Fig. 5(d)). The “ZGNR” region instead is characterized by the scattering occurring at the pieces of the ZGNR in the device region with vibrational modes in the ZGNR plane (Fig. 5(c)). The “dips” region shows a complex scenario where both the phonons from the ZGNR and local vibrations from the peptide contribute; the occurrence of the dips in the IETS signals is due to reflection scattering events (with γλ < 0), but also important contributions from the elastic asymmetric term are found. ZGNR phonons mostly involve the hydrogens at the gap border which vibrate perpendicular to the CH bonds (Fig. 5(b)). In the “low energy” region the inelastic scattering is contributed by both peptide vibrational modes and ZGNR phonons with eigenvectors orthogonal to the ZGNR plane (Fig. 5(a)) and only positive differential conductivity coming from symmetric terms (γλ > 0) is measured.
| Region | NH | CO | SC |
|---|---|---|---|
| Low energy | 65.15 (γ+λ) | 65.52 (γ+λ) | 64.95 (γ+λ) |
| 78.2 (γ+λ) | |||
| 79.2 (γ+λ) | |||
| Dips | 132.55 (γ+λκ−λ) | ||
| 139.5 (γ−λ) | 139.7 (γ−λ) | 139.68 (γ−λκ−λ) | |
| 163 (κ+λ) | 162.5 (γ+λκ+λ) | ||
| 178.9 (κ−λ) | 179.16 (γ−λ) | ||
| ZGNR | 199.5 (γ+λ) | 200 (γ+λ) | 200 (γ+λ) |
| 203.25 (γ+λ) | 203 (γ+λ) | 203.17 (γ+λ) | |
| 203.3 (γ+λκ−λ) | 203.42 (γ+λκ−λ) | 203.46 (γ+λκ−λ) | |
| Side chain | 379.28 (γ+λ) | 379.45 (γ+λ) | |
| 380.34 (γ+λ) | 384.6 (γ+λ) | ||
| 390.65 (γ+λ) |
The three reference configurations NH, CO and SC, that result in the double peak signal of the PB in the elastic regime,19 have different IETS features. The SC configuration is characterized by the absence of the scattering processes in the “side chain” region, the existence of an enhanced peak at very low energy (hν ≈ 7 meV) (see Fig. 4(a)) and the lowest IETS signal among the three cases in the ZGNR region. The first of the three feature is related to the lower coupling between the orbitals of the vibrating side chain and the pseudo-π and pseudo-π* orbitals of the left and right electrodes. The large peak at a very low energy is caused by enhanced transmission from the central side chain due to long wavelength vibrational modes orthogonal to the ZGNR plane: these modes, indeed, enhance the current through the side chains which stay out of the ZGNR plane for a part of the oscillation period. Finally, because the modes in the ZGNR region are mainly characterized by in-plane vibrations of the left/right ZGNR, the increase in the conductance is less effective for the SC due to the location of the side chain in the middle of the gap and the lower transmission across the peptide.19
Also the CO and NH configurations can be distinguished from each other: in the “side chain” region the IETS signal for NH is characterized by a satellite of the main peak that is not observed for CO. Moreover the scattering features in the “low energy” region for CO shows just one well-evidenced peak (hν ≈ 65.52 meV) while the remaining part of this region is relatively insensitive to large inelastic processes, different from the NH case. It is worth noting that in the ZGNR region, the differential conductivity in the CO case is the largest due to the enhanced transport related to the off-plane side chain and NH groups.19
The IETS signals from the same relevant configurations of the Ala homo-peptide are shown in Fig. 6. Comparing the PhDoS of the NH, CO and SC configurations to the one of the ZGNR alone (reported in the ESI†) we again obtain three energy regions where just the peptide vibrational modes occur: the first two (regions “A” and “B”) show the same features and energy ranges as the corresponding ones in the Gly case. A difference emerges for the CαH region which now is in the range 0.39 eV ≤ hν ≤ 0.4 eV as a right-hand side satellite of the main PhDoS peak. This shift is related to the larger vibrational energy of the Ala side chain, a methyl group, with respect to that of the Gly one.
We can appreciate the quite larger scattering peaks in the very low energy range with respect to the Gly case. Moreover the peak heights in the ZGNR region here appear much smaller than those for Gly which means that peptide transmission is lower than that in the Gly case as evidenced in the ESI†.19
Similarly to the Gly case, the SC configuration differs from the other two mainly because of three aspects: the lack of IETS signals in the “side chain” region, the large peak at a very low energy (almost twice the ones for NH and CO) and finally the less pronounced oscillation in the “dips” region. The last one reflects the more complex behavior in the dips region with a larger number of modes, with both symmetric and anti-symmetric contributions and close energy values, affecting the inelastic scattering (see the ESI†). Distinction between NH and CO is quite easy because of the additional peak for CO at hν = 438 meV that does not appear in the NH configuration.
Some IETS features can be considered as peculiar of the two cases treated: one of them is the relative importance of the vibrational scattering at a very low bias with respect to the ZGNR region: in the Gly case, the IETS peaks in these two regions are of the same order of magnitude while in the Ala case the IETS peaks in the ZGNR region is about one order of magnitude lower than the one at a very low energy. This circumstance is due to the larger peptide transmission for Gly than for Ala in the ZGNR region. Moreover at a very low energy, where the ZGNRs oscillate perpendicular to their plane, Ala vibrational modes are more in number due to the larger side chain thus enhancing the transmission through the side chains and CαH group. A second feature is the relative importance of the ZGNR and side chain regions: in the Gly case the first one prevails while in the Ala case they are almost comparable. This is related to the different side chain sizes and the larger elastic transport across the “frozen” peptide in the Gly case, typical of the ZGNR region (see the transport properties reported in the ESI†).
Looking at the fine details in the region of interests in Fig. 4 and 6, it is worth emphasizing that the “side chain” region is shifted to a larger energy for Ala where a well separated double peak feature emerges for CO and NH (see Tables 1 and 2). This energy shift is related to the different vibrational modes of the side chain with stretching and alternating stretching modes of the CαH2 group for Gly, while the peak above 390 meV for Ala is related to stretching and alternating stretching modes of the methyl side chain and CαH group. Moreover, it is important to focus the reader's attention to the additional peak at hν = 438 meV for COAla that makes this case quite peculiar. We see from Fig. 7 that this mode involves large stretching of the second nearest NH group and smaller vibrations of the hydrogen bonded to the closest Cα atom and those of the closest (lower) NH group. However, because the second nearest NH group does not contribute to the current (see the ESI†), we attribute this inelastic peak, and the relative increase of the differential conductivity, to the vibrations of the closest CαH and NH groups that, indeed, contribute to the current. Similar modes observed for COGly are not effective in terms of scattering due to the different orientation of the CαH group. The absence of a similar peak for NHAla tells us that this peak originates from the tunneling current flowing across both the CαH and NH groups that are out of the ZGNR plane: this circumstance just occurs for COAla.
| Region | NH | CO | SC |
|---|---|---|---|
| Low energy | 9 (γ+λ) | 11.4 (γ+λ) | 8.7 (γ+λ) |
| 14.3 (γ+λ) | 28.23 (γ+λ) | ||
| 39.38 (γ+λ) | 43.7 (γ+λ) | ||
| 55.14 (γ+λ) | 55.78 (γ+λ) | ||
| 65.63 (γ+λ) | 65.72 (γ+λ) | 64.17 (γ+λ) | |
| 80.55 (γ+λ) | 93.25 (γ+λ) | ||
| Dips | 133.22 (γ+λ) | 136.22 (γ−λκ+λ) | |
| 146.03 (γ+λκ+λ) | 146.5 (γ+λ) | ||
| 162.64 (κ+λ) | 162.67 (κ+λ) | ||
| 172 (γ−λ) | 179.4 (γ−λ) | ||
| ZGNR | 191.46 (γ+λκ+λ) | ||
| 199.97 (γ+λ) | 199.98 (γ+λ) | 200 (γ+λ) | |
| 202.9 (γ+λκ+λ) | 202.8 (γ+λκ+λ) | 202.9 (γ+λ) | |
| 203.44 (γ+λκ−λ) | 203.47 (γ+λκ−λ) | 203.45 (γ+λκ−λ) | |
| Side chain | 384.5 (γ+λ) | 384.3 (γ+λ) | |
| 394.8 (γ+λ) | |||
| 397.7 (γ+λ) | 397.4 (γ+λ) | ||
| 438 (γ+λ) |
 | ||
| Fig. 7 Vibrational mode corresponding to the inelastic scattering peak at hν = 438 meV for the CO configuration of the Ala homo-peptide. | ||
Therefore we can state that although Gly and Ala have similar sizes and equal charge states, which represent a serious difficulty in sequencing and recognition through standard nanotechnological methods (such as ionic blockade current measurements), vibrational scattering phenomena observed through IETS signals appear rather different in terms of the relative importance of the various contributions to the inelastic scattering thus giving a large set of observables that are, in principle, useful to monitor and recognize at the atomistic level the relevant atomic groups of the PBs and side chains in the two cases treated.
There are, however, some interesting similarities in the cases treated: in both Gly and Ala cases the region “A”, namely one of the three energy regions containing just vibrational modes arising from the peptide, does not contribute to the inelastic scattering while the other two make the difference, both of them being at high or very high energy. Therefore tunneling current measurements with bias V ≤ 0.35 V are affected only by vibrational modes that involve both the graphene nano-ribbons and the peptide. Interestingly there exists a bias range 0.203 V ≤ V ≤ 0.35 V where the current shows a local linear behavior, with no additional inelastic events, for all the cases studied. By measuring the tunneling current with two different bias values in this range, slope values could be obtained and employed as a reference for differential tunneling current measurements with a larger bias V ≥ 0.45 V; these differential measurements would be affected, as already shown, just by the peptide vibrational modes, more specifically by the side chain and the CαH modes and, for the COAla case, also by the closest NH stretching mode. Then, three measurement points in the I–V characteristics are supposed to be sufficient to obtain tunneling current signals affected just by the vibrational properties of the side chains and the CαH bond: in this way it would be possible to obtain specific fingerprints for side chain recognition also in the case of narrow electrodes.
3 Conclusions
Previous results shed some light on the inelastic scattering events taking place during tunneling current measurements across the gap of a graphene nano-ribbon when a peptide translocates across it. It is evidenced how, as expected, the amount of the inelastic scattering contribution depends on the applied bias and the corresponding atomic groups and vibrational modes involved in the scattering. The low energy scattering peaks are affected by both peptide local vibrations and ZGNR phonon modes orthogonal to the GNR plane. Therefore, the current measured by applying small bias values is just affected by these modes that increase the differential conductivity (γλ > 0). However these modes are rather dense and no straightforward dependence on the configuration considered arises. Nevertheless, in this bias region the increase of the differential conductivity is much larger for Ala than for Gly indicating the “richer” content of the vibrational modes due to the larger side chain. If the bias is in the “dips” region, then a very complex scenario arises where modes may cause reflection (γλ > 0) or contribute to the inelastic scattering through asymmetric terms with dips and peaks (κλ ≠ 0). This behavior is caused by in-plane vibrational modes of the ZGNR hydrogen atoms in conjunction with local vibrations of relevant groups in the peptide close to the gap. A non monotonic behavior of the conductivity is expected in this region. The important findings are mostly related to the existence of two bias ranges for V ≥ 0.19 meV. In the first one (the ZGNR region) the scattering is induced just by the in-plane ZGNR vibrational modes: here C and H atomic vibrations cause distortion of the pseudo-π and pseudo-π* ZGNR orbitals which results in an enhanced transmission through the peptide thus following the conductivity hierarchy already found in the elastic modeling at low temperature.19 Then a hypothetical measurement of the differential conductance in this region is expected to follow the same curve as the one found in the elastic regime.Finally the “high energy” bias region 0.35 V ≤ V ≤ 0.45 V preserves unique pieces of information on the side chain together with additional high energy peaks related to the vibrational modes of the NH and CαH atomic groups and could be employed, in principle, as a source of observables for side chain recognition also with such narrow ZGNR electrodes.
4 Methods
The elastic approximation of the current tunneling calculated in the context of the DFT-NEGF method is based on the Landauer–Büttiker formula: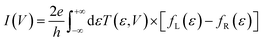 | (1) |
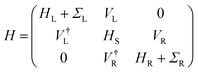 | (2) |
| T(ε) = Tr[G(ε)ΓL(ε)G†(ε)ΓR(ε)] | (3) |
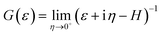 is the Green's function of the system and ΓL(R)(ε) = i[ΣL(R)(ε) − Σ†L(R)(ε)] is the left(right) coupling function.20–24 At this stage, we have employed a 1 × 1 × 30 k-point mesh to calculate the electronically relevant quantities. Due to the narrow ZGNR being used as electrodes, the k-point mesh in the orthogonal plane has not been increased.
is the Green's function of the system and ΓL(R)(ε) = i[ΣL(R)(ε) − Σ†L(R)(ε)] is the left(right) coupling function.20–24 At this stage, we have employed a 1 × 1 × 30 k-point mesh to calculate the electronically relevant quantities. Due to the narrow ZGNR being used as electrodes, the k-point mesh in the orthogonal plane has not been increased.
Following the literature,32,33 the phenomenology of the vibration assisted tunneling, which is schematically drawn in Fig. 1(b) and (c), is described by the Hamiltonian
| H = He + Hph + He–ph | (4) |
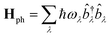 | (5) |
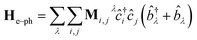 | (6) |
![[b with combining circumflex]](https://www.rsc.org/images/entities/i_char_0062_0302.gif) ) is the electron (phonon) annihilation operator, λ is a phonon label and i and j are electron labels. The electron–phonon coupling matrix Mλ is:
) is the electron (phonon) annihilation operator, λ is a phonon label and i and j are electron labels. The electron–phonon coupling matrix Mλ is: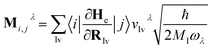 | (7) |
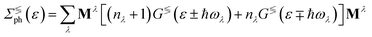 | (8) |
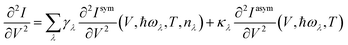 | (9) |
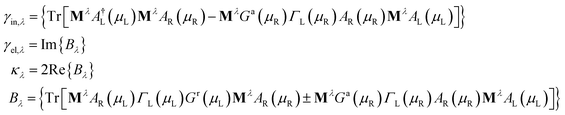 | (10) |
In the previous formulas we have Ga(r)(ε) as the advanced(retarded) electron Green function and AL(R)(ε) = Gr(ε)ΓL(R)(ε)Ga(ε).
The symmetric and asymmetric current universal functions are:
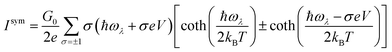 | (11) |
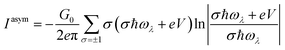 | (12) |
In the system used in this study, all the atoms of the central scattering region, which also contains part of the left and right ZGNR electrodes, have been allowed to vibrate. Transport and inelastic tunneling analyses have been performed using the Transiesta24 and Inelastica32 packages.
Conflicts of interest
There are no conflicts to declare.References
- M. Jain, I. T. Fiddes, K. H. Miga, H. E. Olsen, B. Paten and M. Akeson, Nat. Methods, 2015, 12(4), 351 CrossRef CAS PubMed.
- G. F. Schneider and C. Dekker, Nat. Biotechnol., 2012, 30, 326–328 CrossRef CAS PubMed.
- E. Kennedy, Z. Dong, C. Tennant and G. Timp, Nat. Nanotechnol., 2016, 11, 968–976 CrossRef CAS PubMed.
- J. Wilson, L. Sloman, Z. He and A. Aksimentiev, Adv. Funct. Mater., 2016, 26, 4830–4838 CrossRef CAS PubMed.
- G. Di Muccio, A. E. Rossini, D. Di Marino, G. Zollo and M. Chinappi, Sci. Rep., 2019, 9, 6440 CrossRef PubMed.
- A. Oukhaled, L. Bacri, M. Pastoriza-Gallego, J.-M. Betton and J. Pelta, ACS Chem. Biol., 2012, 7, 1935–1949 CrossRef CAS PubMed.
- D. Di Marino, E. L. Bonome, A. Tramontano and M. Chinappi, J. Phys. Chem. Lett., 2015, 6, 2963–2968 CrossRef CAS PubMed.
- L. Mereuta, M. Roy, A. Asandei, J. K. Lee, Y. Park, I. Andricioaei and T. Luchian, Sci. Rep., 2014, 4, 3885 CrossRef PubMed.
- O. Tavassoly, S. Nokhrin, O. Y. Dmitriev and J. S. Lee, FEBS J., 2014, 281, 2738–2753 CrossRef CAS PubMed.
- D. Rodriguez-Larrea and H. Bayley, Nat. Nanotechnol., 2013, 8, 288–295 CrossRef CAS PubMed.
- T. Ohshiro, M. Tsutsui, K. Yokota, M. Furuhashi, M. Taniguchi and T. Kawai, Nat. Nanotechnol., 2014, 9, 835–840 CrossRef CAS PubMed.
- C. B. Rosen, D. Rodriguez-Larrea and H. Bayley, Nat. Biotechnol., 2014, 32(2), 179–181 CrossRef CAS PubMed.
- S. J. Heerema and C. Dekker, Nat. Nanotechnol., 2016, 11, 127 CrossRef CAS PubMed.
- M. Di Ventra and M. Taniguchi, Nat. Nanotechnol., 2016, 11, 117–126 CrossRef CAS PubMed.
- F. Traversi, C. Raillon, S. Benameur, K. Liu, S. Khlybov, M. Tosun, D. Krasnozhon, A. Kis and A. Radenovic, Nat. Nanotechnol., 2013, 8, 939–945 CrossRef CAS PubMed.
- E. Paulechka, T. A. Wassenaar, K. Kroenlein, A. Kazakov and A. Smolyanitsky, Nanoscale, 2016, 8, 1861–1867 RSC.
- R. G. Amorim, A. R. Rocha and R. H. Scheicher, J. Phys. Chem. C, 2016, 120, 19384–19388 CrossRef CAS.
- J. Prasongkit, G. T. Feliciano, A. R. Rocha, Y. He, T. Osotchan, R. Ahuja and R. H. Scheicher, Sci. Rep., 2015, 5, 17560 CrossRef CAS PubMed.
- A. E. Rossini, F. Gala, M. Chinappi and G. Zollo, Nanoscale, 2018, 10, 5928–5937 RSC.
- K. Stokbro, J. Taylor, M. Brandbyge, J.-L. Mozos and P. Ordejón, Comput. Mater. Sci., 2002, 27, 151–160 CrossRef.
- S. Datta, Electronic Transport in Mesoscopic Systems, Cambridge University Press, 1995 Search PubMed.
- T. N. Todorov, J. Phys.: Condens. Matter, 2002, 14, 3049 CrossRef CAS.
- K. Stokbro, J. Taylor, M. Brandbyge and P. Ordejón, Ann. N. Y. Acad. Sci., 2003, 1006(1), 212–226 CrossRef CAS PubMed.
- N. Papior, N. Lorente, T. Frederiksen, A. Garca and M. Brandbyge, Comput. Phys. Commun., 2017, 212, 8–24 CrossRef CAS.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Phys. Rev. Lett., 2006, 97, 216803 CrossRef PubMed.
- Y. Y. Li, M. X. Chen, M. Weinert and L. Li, Nat. Commun., 2014, 5, 4311 CrossRef CAS PubMed.
- D. Gunlycke, D. A. Areshkin, J. Li, J. W. Mintmire and C. T. White, Nano Lett., 2007, 7, 3608–3611 CrossRef CAS PubMed.
- Z. Li, H. Qian, J. Wu, B.-L. Gu and W. Duan, Phys. Rev. Lett., 2008, 100, 206802 CrossRef PubMed.
- Y. Li, Z. Zhou, P. Shen and Z. Chen, ACS Nano, 2009, 3, 1952–1958 CrossRef CAS PubMed.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Nature, 2006, 444, 347–349 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26(16), 1781–1802 CrossRef CAS PubMed.
- T. Frederiksen, M. Paulsson, M. Brandbyge and A.-P. Jauho, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 205413 CrossRef.
- J.-T. Lü, R. B. Christensen, G. Foti, T. Frederiksen, T. Gunst and M. Brandbyge, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 081405 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9na00396g |
| This journal is © The Royal Society of Chemistry 2019 |