Open Access Article
Open Access ArticleA comparative study of mechanisms of the adsorption of CO2 confined within graphene–MoS2 nanosheets: a DFT trend study†
Francis M.
Enujekwu
 ab,
Collins I.
Ezeh
ab,
Collins I.
Ezeh
 a,
Michael W.
George
ac,
Mengxia
Xu
a,
Michael W.
George
ac,
Mengxia
Xu
 ab,
Hainam
Do
ab,
Yue
Zhang
ab,
Hainam
Do
ab,
Yue
Zhang
 d,
Haitao
Zhao
d,
Haitao
Zhao
 b and
Tao
Wu
b and
Tao
Wu
 *ab
*ab
aDepartment of Chemical and Environmental Engineering, University of Nottingham Ningbo China, Ningbo 315100, China. E-mail: tao.wu@nottingham.ac.uk; tao.wu@hotmail.com
bNew Material Institute, University of Nottingham Ningbo China, Ningbo 315042, China
cSchool of Chemistry, University of Nottingham, Nottingham NG72RD, UK
dInstitute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China
First published on 14th January 2019
Abstract
The space within the interlayer of 2-dimensional (2D) nanosheets provides new and intriguing confined environments for molecular interactions. However, atomic level understanding of the adsorption mechanism of CO2 confined within the interlayer of 2D nanosheets is still limited. Herein, we present a comparative study of the adsorption mechanisms of CO2 confined within graphene–molybdenum disulfide (MoS2) nanosheets using density functional theory (DFT). A comprehensive analysis of CO2 adsorption energies (EAE) at various interlayer spacings of different multilayer structures comprising graphene/graphene (GrapheneB) and MoS2/MoS2 (MoS2B) bilayers as well as graphene/MoS2 (GMoS2) and MoS2/graphene (MoS2G) hybrids is performed to obtain the most stable adsorption configurations. It was found that 7.5 Å and 8.5 Å interlayer spacings are the most stable conformations for CO2 adsorption on the bilayer and hybrid structures, respectively. Adsorption energies of the multilayer structures decreased in the following trend: MoS2B > GrapheneB > MoS2G > GMoS2. By incorporating van der Waals (vdW) interactions between the CO2 molecule and the surfaces, we find that CO2 binds more strongly on these multilayer structures. Furthermore, there is a slight discrepancy in the binding energies of CO2 adsorption on the heterostructures (GMoS2, MoS2G) due to the modality of the atom arrangement (C–Mo–S–O and Mo–S–O–C) in both structures, indicating that conformational anisotropy determines to a certain degree its CO2 adsorption energy. Meanwhile, Bader charge analysis shows that the interaction between CO2 and these surfaces causes charge transfer and redistributions. By contrast, the density of states (DOS) plots show that CO2 physisorption does not have a substantial effect on the electronic properties of graphene and MoS2. In summary, the results obtained in this study could serve as useful guidance in the preparation of graphene–MoS2 nanosheets for the improved adsorption efficiency of CO2.
1 Introduction
Identifying stable systems with improved CO2 capture has become an essential goal for carbon capture and storage technologies.1,2 In recent years, gas-adsorbent materials (GAMs) have received significant attention from many researchers across the globe due to the increased rate of effluent gases (for example, COx, NOx, SOx, Hg0, etc.) from industries.3 Among all these, carbon dioxide (CO2) concentration in the atmosphere has been found to be increasing rapidly (313 ppm, 1960 to 407 ppm, 2017),4 and this has been linked to the increased reliance on fossil fuels within the past century. Accordingly, reduction and capture of green-house gases have been among the most challenging issues in environmental protection.5 In the past decades, the use of capturing and separation techniques like absorption, adsorption, use of membranes and the ilk was widespread, however, the efficiencies of these processes seem to pose a serious challenge.6 In the bid to tackle the issue of global warming, energy-efficient capture of CO2 and other green-house gases through industrially proven and simple processes like adsorption is of critical importance. Although a large number of gas-adsorbent materials have been computationally and experimentally developed in the past, nanostructured GAMs are at the cutting-edge of potentially revolutionary advancements in fast growing technological fields such as molecular sensing, energy storage and harvesting, environmental and sustainability engineering, etc.1–3,7,8 This has led to the rapid increase in the development of novel nanostructured GAMs. Their properties, which include high surface to volume ratio, regular atomic composition, tunable reactivity, effective transport properties and assembling affinity to form supramolecular systems, have warranted their applications in CO2 capture technologies.3Among these nanostructured materials, two-dimensional (2D) nanomaterials like graphene and hexagonal-BN (hBN) sheets have attracted greater interest because of their extraordinary properties attributed to their ultrathin thickness, which is related to quantum effects.9–11 These 2D nanomaterials vary in terms of their electronic properties and functionality. For instance, graphene is a low-work function metallic electrode, hBN is an insulator, and MoS2 is generally an n-type semiconductor (very active potential site for CO2 capture). However, their synergetic function is more attractive for technological application. Recently, several new classes of 2D nanostructures like transition metal dichalcogenides (TMDs) have been studied with more emphasis on molybdenum disulfide (MoS2), which exhibits a number of interesting properties such as high catalytic activity,12 bandgap variation with number of layers,13,14 high carrier mobility15,16 and gas sensing capability that have made it widely used in the adsorption of gas molecules especially toxic gases.17–19 In parallel with the efforts on graphene-like materials, recent studies have focused on the advantage of merging individual properties of different 2D materials. To this end, multilayer heterostructure materials are produced by stacking 2D-crystals of each nanomaterial,20 bonded by relatively weak van der Waals (vdW)-like forces. For example, the possibility of making a graphene/MoS2 bilayer heterostructure has been demonstrated experimentally. Experimental findings show that synthesized materials are more thermally stable with high adsorption capacity.8 Moreover, the space within the interlayer separation of these 2D nanosheets has often provided new and intriguing confined environments for molecular interactions due to the nanoconfinement effect.21–24 The confined space between layers of these nanosheets has provided lower loss and stronger localization of active sites. In addition, the tunability of this spacing can enhance the physico-chemical properties of these nanostructures. Examples of these properties include surface area, penetration depth, adsorption capacity and catalytic activity. Therefore, understanding the underlying principles of CO2 adsorption mechanisms within this nanoconfinement will provide in-depth knowledge into the materials science involving stacking routes of 2D nanomaterials.
The motivation to carry out this present study stems from the impact of interlayer orientation on the electronic properties and binding energy of substrate-grown monolayers25,26 and multi-layered structures of the same material.27 Also, experiments have shown that combining MoS2 and graphene provides tremendous active sites for molecular adsorption that could responsibly remove smoke particles, CO and other toxic volatiles.8 Therefore, it is possible to attune the structural parameters of these sites to facilitate CO2 adsorption. Moreover, experimental and theoretical studies have shown that this nano-space presents new and extraordinary behaviours for molecular intercalations21 and catalytic activities.22–24 In this work, the effect of interlayer distance between 2D materials, graphene/graphene (GrapheneB) and MoS2/MoS2 (MoS2B) bilayers as well as graphene/MoS2 (GMoS2) and MoS2/graphene (MoS2G) hybrids, on CO2 adsorption mechanisms from first principles was investigated, with the aim of finding the most stable conformation for CO2 adsorptions. The orientations and binding energies of CO2 molecule on these surfaces are determined as well.
2 Computational methods and models
All calculations are carried out using DFT28 in conjunction with the projector-augmented wave (PAW)29,30 method, as implemented in Vienna ab initio simulation package (VASP).31,32 The exchange and correlation potentials are treated with the generalized gradient approximation (GGA) functional of Perdew, Burke and Ernzerhof (PBE).33 Valence electrons for Mo and S are generated in 4p65s14d5 and 3s23p4 respectively, while the valence electron for C is generated in 2s22p2. Different dispersion schemes are employed to understand the effects of vdW forces on the adsorption of CO2. Firstly, we include Grimme's34 DFT-D2 method, which adds a semiempirical pairwise force field to conventional DFT calculations. Then, we employ the vdW-DF functional of Langreth and Lundqvist et al., which adds a non-local correlation functional that approximately accounts for dispersion interaction.35–37 The vdW-DFT methods with exchange-correlation energy given by revPBE,35 the opt functionals (optPBE and optB88)38 for accurate exchange functionals for vdW correlation, and vdW-DF2 of Langreth and Lundqvist groups39,40 are considered.Calculations are performed with a 4 × 4 × 1 supercell of monolayer MoS2 (1H-MoS2) containing 16 Mo atoms and 32 S atoms, and a 5 × 5 × 1 supercell of monolayer graphene containing 50 C atoms for the monolayers. The MoS2 bilayer contains two 4 × 4 × 1 supercells of monolayer MoS2 (32 Mo atoms and 64 S atoms) while the graphene bilayer contains two 5 × 5 × 1 supercell monolayers of graphene (100 C atoms). For the hybrid structure, a supercell containing 5 × 5 × 1 lateral periodicity of graphene and 4 × 4 × 1 lateral periodicity of MoS2 monolayer (16 Mo atoms, 32 S atoms and 50 C atoms) were employed which includes 1.9% lattice mismatch41 in order to impose a commensurability condition between the graphene and MoS2 monolayer. To illustrate the fundamental properties of the graphene–MoS2 hybrid, we chose a lateral lattice parameter for the triangular lattice a = 12.34 Å that was optimized for isolated graphene, which is in agreement with graphene-based hybrid systems investigated previously41 to ensure a smaller lattice mismatch. A large vacuum layer of 15 Å is used in the direction to the interface as an isolated slab boundary condition to avoid interlayer interactions. The test for cutoff energy and k-point grid is required for convergence and the result is summarized in the ESI.† The Gaussian smearing width was set to 0.2 eV. The total energy was converged to <10 meV for a plane-wave cutoff of 500 eV and 5 × 5 × 1 Monkhorst–Pack (MP)42k-point sampling for the Brillouin zone. Because of the large quasiparticle dynamics of graphene, the Brillouin zone sampling of electronic states was performed using a finer MP mesh with size 40 × 40 × 1 per unit cell.43 The tetrahedron method with Blöchl corrections for a pure graphene monolayer and bilayer DOS was also adopted. Finer MP mesh and Fermi smearing width of 0 eV was used to ensure accurate prediction of the DOS of semiconductors like graphene. For geometry relaxation, we used the method of conjugate gradient energy minimization. The convergence criterion for energy is chosen to be 10−4 eVbetween two consecutive steps, and the maximum Hellmann–Feynman force exerting on each atom is less than 0.03 eV Å−1 upon ionic relaxation. Using Bader charge analysis, charge transfer between the substrate and the adsorbate is obtained.44
The adsorption energy of a CO2 molecule on multilayer and monolayer structures is investigated. Adsorption energy is calculated as:
| EAE = Esurf+CO2 − (Esurf + ECO2) | (1) |
3 Results and discussion
3.1 Bulk structure parameters
Graphene and MoS2 have hexagonal structures consisting of C–C and S–Mo–S layers respectively. Bulk graphene has two layers and each layer known as a unit cell consists of a central carbon atom connected to three carbon atoms with an adjacent carbon atom on both sides of the layers. Bulk MoS2 also has two such layers, with molybdenum (Mo) atoms of one layer directly above the sulphur (S) atoms of the other layer and vice versa. The lattice constant of pristine graphene and MoS2 sheets using a unit cell were calculated and compared with the literature in order to validate this method and its pseudopotentials. Calculated values are 2.468 Å and 3.186 Å for graphene and MoS2 respectively, which are in excellent agreement with previous theoretical results of 2.463 Å and 3.20 Å.45 Based on this agreement, all other calculations were carried out, which are discussed in the subsequent sections.3.2 Effects of interlayer distance on CO2 adsorption
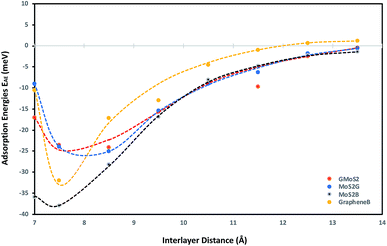
To obtain a clear understanding of the effect of the multilayer structures on CO2 adsorption, the adsorption energies of CO2 (EAE) at various interlayer distances of multilayer structures comprising graphene/graphene bilayer (GrapheneB), MoS2/MoS2 bilayer (MoS2B), graphene/MoS2 hybrid (GMoS2) and MoS2/graphene (MoS2G) hybrid were computed and the results are reported in Table 1. At the start of each geometry optimisation procedure, CO2 molecule is placed horizontally along the z-axis, at the middle distance between the two surface layers. This is assumed in order to avoid the repulsive effect between the electrons of the surface atoms and the lower oxygen atom of the CO2 molecule. Such a repulsive effect was commonly encountered in a configuration where the CO2 molecule is perpendicularly oriented to the surface. This was one of the initial configurations proposed for CO2 physisorption on pristine graphene46 and graphene sheets with (0001) defects.47| Interlayer distance (Å) | Adsorption energies EAE (meV) | |||
|---|---|---|---|---|
| GMoS2 | MoS2G | MoS2B | GrapheneB | |
| a NA: not adsorbed. | ||||
| 3.5 | 237.20 | 27.98 | (NA) | 179.98 |
| 6.0 | 61.10 | 44.87 | (NA) | 67.54 |
| 7.0 | −17.10 | −9.01 | −36.00 | −10.50 |
| 7.5 | −23.55 | −24.00 | −38.00 | −32.00 |
| 8.5 | −24.11 | −25.09 | −28.25 | −17.15 |
| 9.5 | −15.76 | −15.45 | −16.90 | −12.99 |
| 10.5 | −8.90 | −9.00 | −8.13 | −4.57 |
| 11.5 | −9.76 | −6.28 | −4.76 | −1.03 |
| 12.5 | −2.54 | −1.84 | −2.30 | 0.68 |
| 13.5 | −0.49 | −0.55 | −1.36 | 1.17 |
As shown in Table 1, a more negative value means stronger CO2 adsorption. The positive values at separations below 6.0 Å indicate that the spacing between layers is so small that overlapping with CO2 occurred. Hence, energy is required to promote CO2 adsorption. According to Ataca et al.,45 an interlayer spacing of 6.145 Å was estimated via DFT to be the suitable spacing for molecular interaction in the MoS2 interlayer. Below this, no adsorption (NA) will be observed, which corresponds to the results for MoS2B in Table 1. Similarly, the most-suitable interlayer distance that permits molecular adsorption in GrapheneB has been determined to be between 7 Å and 10 Å.48 However, unlike MoS2B, energy is required to facilitate adsorption below this interlayer distance. This is attributed to the structural flexibility of graphene, in contrast to MoS2. Furthermore, it can be stipulated that the required interlayer distance for CO2 adsorption in the GMoS2 hybrid should be the sum of the equilibrium distance between the GMoS2 substrate and the kinetic diameter of CO2 (3.30 Å49). The equilibrium distance between the GMoS2 substrate in different arrangements was measured to be around 3.32 Å.41,50 Hence, energy is demanded for CO2 adsorption at interlayer distances less than 6.62 Å for the GMoS2 hybrid. Considering that CO2 molecule has a kinetic diameter of 3.30 Å,49 it is expected that CO2 intercalation should enlarge the distance between graphene sheets and MoS2 surface and that of the bilayer surfaces. By expanding the vdW gap between the two sheets, a charge transfer between the guest and the host surface is expected to occur with a very large repulsive energy.51
Fig. 1 demonstrates the variation of interlayer spacing with CO2 adsorption energies. This figure shows that 7.5 Å and 8.5 Å interlayer spacings are the most stable conformations for CO2 adsorption on the bilayer and hybrid structures respectively. Also, as the interlayer distance increases, the CO2 binding energy increases as well, but comes to a local minimum at 7.5 Å and 8.5 Å for the bilayer and hybrid structures respectively. It is estimated that GrapheneB has the least total adsorption capacity given the considered range of interlayer distance. It can be assumed that the presence of MoS2 in the hybrid buttressed CO2 adsorption beyond interlayer spacing greater than 8.0 Å. The plot for the GMoS2 hybrid structure is in good agreement with the work of Ma et al.,41 although only graphene adhesion on MoS2 was considered. The peak binding energies per C atom for GMoS2, MoS2G, MoS2B and GrapheneB are −24.11 meV, −25.09 meV, −38.00 meV and −32.00 meV, respectively. Moreover, the adsorption energies of these multilayer structures seem to be a simple sum of the contributions from the constituents with decreasing binding energies in the order: MoS2B > GrapheneB > MoS2G > GMoS2. These values are low which correspond to weak interactions between the layers and CO2 molecule. This is due to the inability of conventional DFT approaches to describe dispersion force in adsorption systems. These values were improved when factors like CO2 orientation and addition of vdW interactions between the CO2 molecule and the surfaces were considered. Furthermore, two different configurations of the bilayer heterostructure were considered. This is to explain the effect of structural anisotropy on the adsorption energies of heterostructures. In the first structure graphene is the substrate (GMoS2) while in the second case MoS2 is the substrate (MoS2G). Optimization results depict that there is discrepancy in the binding energies of CO2 adsorption on these hybrid structures (GMoS2 and MoS2G). This can be ascribed to the modality of the atom arrangement (C–Mo–S–O and Mo–S–O–C) just like in the case of zigzag and armchair arrangements of bilayer graphene27 and the interlayer orientation effect on bilayer heterostructures. This indicates that the conformational anisotropy of this structure determines to a certain degree its CO2 adsorption energy. The most appropriate orientation of this hybrid for optimal adsorption performance is subject to further investigation.
3.3 Effects of CO2 orientation and position
To further understand the interaction of CO2 within these multilayer structures, we calculated CO2 adsorption energy at different CO2 orientations and positions using the same optimum interlayer distance presented earlier. Table 2 summarizes the calculated adsorption energies per carbon atom for the most stable adsorption configuration of the multilayer structures in comparison with the most stable monolayers. In all calculations, CO2 was placed at the mid-point of the interlayer distance for the multilayer structure and the same value was chosen for the monolayers for proper comparison. Also, since the test for cutoff energy and k-point grid is required for convergence, we calculated total energies using different cutoffs and k-points and the results are summarized in the ESI.† The total energy was converged to <10 meV for a plane wave cutoff of 500 eV and 5 × 5 × 1 Monkhorst–Pack42k-point sampling for the Brillouin zone. The adsorption energies of the multilayer structures also seem to be a simple sum of the contributions from the constituents. The structures displayed low energies, which explains the difficulty of conventional DFT approaches to accurately reflect the vdW force in adsorption systems. Our goal here is to gain insight into the surface most active site, which is the CO2 adsorption energies with respect to its positions and orientation on the surface. From the obtained results, it is evident that CO2 molecule prefers to interact with a parallel or inclined orientation with the adsorbent surface than the perpendicular orientation. For instance, considering the edge position of GrapheneB bilayer, the adsorption energy for parallel and 30° parallel-rotation are −27.05 and −23.62 meV respectively, but the value is −5.65 meV for perpendicular attack of CO2 at the same position. This is due to the repulsive effect between the electrons in C-atoms (graphene) and the lower O-atom (CO2 molecule). Consequently, the molecule stays less bounded to the surface compared to the optimum adsorption site. The same effect was addressed by Cabrera-Sanfelix, when CO2 was placed initially perpendicular on graphene sheets with defects.47 Parallel attack of CO2 at the edge position is observed to be the most favourite adsorption site for GMoS2, MoS2B and MoS2G composites with stable adsorption energies of −27.16, −40.37 and −27.07 meV respectively, while the centre position was the most favourable adsorption site for GrapheneB (−32.37 meV). GMoS2 and MoS2G retained this position as their active site for CO2 inclined (30° and 45° respectively) attack on the surface, in contrast to GrapheneB, which favoured the centre position as the favourite adsorption site. These differences can be attributed to changes of the electronic environment causing charge redistribution culminating to variation in adsorption capabilities. In addition, the adsorption capacity derived from the edge site of MoS2 (ref. 52 and 53) can contribute to these changes. For instance, MoS2 monolayer (M4 × 4) favoured the edge position as the favourite adsorption site while graphene monolayer (G5 × 5) favoured the centre position as the favourite adsorption site. Therefore, it is expected that the edge position will be the most favourite adsorption site for the GMoS2 and MoS2G due to the inclusion of the MoS2 layer, whose catalytic activity occurs at the edge sites. Also, since M4 × 4 has higher adsorption energy (−20.33 meV) than G5 × 5 (−16.38 meV), it is expected that M4 × 4 will determine to a certain extent the adsorption properties of the hybrid structures (GMoS2 and MoS2G).| Position/orientation to the surface | Adsorption energies EAE (meV) | |||||
|---|---|---|---|---|---|---|
| GMoS2 | MoS2G | MoS2B | GrapheneB | G5 × 5 | M4 × 4 | |
| a G5 × 5 and M4 × 4 are 5 × 5 and 4 × 4 supercells of graphene and MoS2 monolayers respectively. | ||||||
| Centre/parallel | −25.49 | −26.98 | −27.99 | −26.47 | −15.15 | −17.13 |
| Edge/parallel | −26.48 | −26.54 | −40.37 | −27.05 | −13.21 | −20.33 |
| Centre/perpendicular | 11.27 | 11.77 | 100.02 | −25.64 | −3.10 | −9.92 |
| Edge/perpendicular | 38.00 | 47.97 | −27.31 | −5.65 | −3.90 | −4.23 |
| Centre/parallel (rotated 30°) | −23.27 | −26.73 | −37.44 | −26.04 | −16.38 | −16.60 |
| Edge/parallel (rotated 30°) | −27.16 | −26.60 | −35.98 | −23.62 | −13.94 | −19.37 |
| Centre/parallel (rotated 45°) | −24.03 | −25.05 | −37.75 | −32.37 | −14.07 | −17.47 |
| Edge/parallel (rotated 45°) | −26.16 | −27.07 | −35.98 | −28.23 | −14.41 | −19.23 |
Improved adsorption energies were obtained when the dispersion correction to DFT is considered. To take dispersion force into account, we carried out a spin-polarized calculation using different dispersion force methods and compared the results with conventional DFT approaches. The adsorption energies significantly improved by incorporating vdW interactions between the CO2 molecule and the surfaces as shown in Table 3. However, there are no detailed experimental or computational data for CO2 adsorption on hybrid and bilayer structures so far. Based on previous calculations of CO2 adsorption on pristine monolayer graphene46,54 and MoS2,55 the results obtained using optPBE functional for the monolayers should be reliable. Also, we find that CO2 binds strongly on these multilayer structures. In fact, graphene bilayer gives the highest CO2 adsorption energy among the multilayer structures when vdW-DF2 interactions are included, in contrast to conventional PBE results. This is in contrast to the previous suggestion from conventional PBE results that the adsorption energy of the bilayers is approximately a simple sum of the contributions from the constituents. In addition, it is expected that adsorption energy of CO2 on perfect graphene and MoS2 sheets should be lower because of lack of dispersive interactions in DFT. Due to the addition of vdW interactions, there is a tendency for overestimation of molecular adsorption.56,57 For instance, vdW-DF2 correlation overestimates the adsorption energy of graphene bilayer, while revPBE and optPBE correlations overestimate the adsorption energy of MoS2 bilayer. Furthermore, it is observed that CO2 adsorption energies obtained when revPBE and optPBE correlations are included are similar. Likewise, there are similarities in the adsorption energies calculated using DFT-D2 and vdW-DF2 correlations except for the adsorption energy of bilayer graphene which is overestimated by vdW-DF2 correlation. Also, the results of these correlations for the MoS2 monolayer are in good agreement with the previous calculation.55 On the other hand, the stronger binding between CO2 and graphene monolayer when using DFT-D2 correlation is in agreement with reported values given for CO2 adsorption on perfect monolayer graphene, ∼147–151meV.56,57 Generally, the increase in CO2 adsorption energy with the introduction of vdW interactions indicates that vdW interaction dominates during the adsorption process. This is comparable with previous theoretical results that incorporated vdW interaction.1,55
| Structures | This work | Referencea | ||||||
|---|---|---|---|---|---|---|---|---|
| PBE | DFT-D2 | revPBE | optPBE | optB88 | vdW-DF2 | PBE | DFT-D2 | |
| a The corresponding values of previous calculations for monolayer graphene and MoS2 are given for the sake of comparison. The PBE adsorption energy of ref. 55 for MoS2 monolayer appears to be too small, this is because ref. 55 did not consider CO2 orientation, a similar value was obtained when we considered CO2 orientation (Table 2). Similarly, the DFT-D2 adsorption energy of ref. 1 for graphene monolayer is too small due to the same reason. But the revPBE and optPBE adsorption energies of MoS2 monolayer are in good agreement with the adsorption energy of ref. 55. | ||||||||
| GMoS2 | −27.16 | −145.17 | −321.73 | −333.01 | −242.13 | −161.31 | — | — |
| MoS2G | −27.07 | −169.14 | −300.47 | −313.54 | −254.74 | −186.46 | — | — |
| MoS2B | −40.37 | −195.33 | −1157.28 | −1069.94 | −829.09 | −232.65 | — | — |
| GrapheneB | −32.37 | −241.34 | −405.23 | −450.26 | −368.47 | −1694.0 | — | — |
| G5 × 5 | −16.38 | −153.30 | −209.58 | −249.98 | −224.41 | −160.21 | −17.10(ref. 46) | −60(ref. 1) |
| M4 × 4 | −20.33 | −126.30 | −201.25 (−210 (ref. 55)) | −232.40 (−253 (ref. 55)) | −204.50 | −152.38 | −4.00 (ref. 55) | −139.0 (ref. 55) |
3.4 Structural parameters
The optimized adsorption configuration of CO2 on most stable multi-layered structures determined by PBE calculations and the stacking type of the structures are shown in Fig. 2. The bond length (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), angle of CO2 molecule, interlayer distances, C
O), angle of CO2 molecule, interlayer distances, C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, Mo
C, Mo![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond lengths and the molecular distance are presented in this figure. To further understand the interaction between CO2 and the surface, several structural parameters are calculated and compared with previous studies. The calculated bond length and angle for free CO2 molecule are 1.177 Å and 179.87° respectively, which is in line with 1.16 Å and 180° from experiments,58 and 1.175 Å and 178° from previous theoretical calculation.46 Based on experimental values, bond angles of adsorbed CO2 decreased by about 0.05–0.13°, depending on the structures of the nanocomposite (Table 4). There is no chemical bonding observed, and interactions are dominated by weak vdW forces. In other words, the entire adsorption is purely physisorption due to the small adsorption energy and large separation height (molecular distance). Moreover, only the stable configurations obtained from PBE calculations are presented. This is because the inclusion of vdW interactions slightly changes the stable configurations.
S bond lengths and the molecular distance are presented in this figure. To further understand the interaction between CO2 and the surface, several structural parameters are calculated and compared with previous studies. The calculated bond length and angle for free CO2 molecule are 1.177 Å and 179.87° respectively, which is in line with 1.16 Å and 180° from experiments,58 and 1.175 Å and 178° from previous theoretical calculation.46 Based on experimental values, bond angles of adsorbed CO2 decreased by about 0.05–0.13°, depending on the structures of the nanocomposite (Table 4). There is no chemical bonding observed, and interactions are dominated by weak vdW forces. In other words, the entire adsorption is purely physisorption due to the small adsorption energy and large separation height (molecular distance). Moreover, only the stable configurations obtained from PBE calculations are presented. This is because the inclusion of vdW interactions slightly changes the stable configurations.
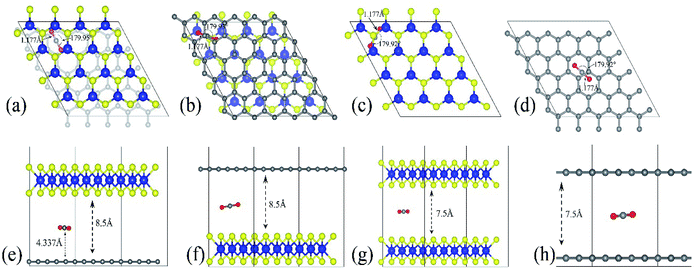 | ||
| Fig. 2 The most stable configuration of the multilayered structures with adsorbed CO2. (a–d) are the top views of GMoS2, MoS2G, MoS2B and GrapheneB and (e and f) are side views of the same structures respectively. Color code: Mo, blue, S, yellow, C, grey, and O, red. The lines define the interlayer distances, bond lengths, and molecular distance while the curved lines define the bond angle. AA stacking type is chosen for both MoS2B and GrapheneB. This is because AA stacking of graphene has been shown to be more preferable for intercalation of molecules according to ref. 59 and ref. 60. Although the binding energy of AB stacking of graphene bilayer is lower than that of AA stacking, which makes AB stacking more stable than AA stacking, AA stacking intercalation structures are more favorable than AB stacking ones, ref. 60. For the hybrid structures, the stacking type is chosen according to ref. 50, where one C atom in the unit cell of graphene sits exactly below a Mo atom. It is reported in ref. 41 that another configuration called TS, where the stacking is such that C atom sits below an S atom, is equivalent in both the binding and electronic properties. | ||
| Structures | Amount of charge transferred (e) | Bond length (Å) angle (deg) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| O1 | C | O2 | CO2 | Mo | S | Cg | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
|
| a Bader charge analysis is used for the charge transfer calculations. Cg is the adjacent carbon atom of graphene surface that is nearer to the adsorbed CO2 molecule, while Mo and S are adjacent molybdenum and sulphur atoms of the MoS2 surface that are nearer to the adsorbed CO2 molecule. The adjacent atoms were chosen arbitrarily based on their proximity to the adsorbed CO2 molecule. Negative charge denotes electron gain. | |||||||||
| GMoS2 | −0.001 | −0.018 | −0.009 | −0.028 | 0.001 | −0.002 | −0.001 | 1.18 | 179.95 (0.05) |
| MoS2G | 0.804 | 0.036 | −0.030 | 0.810 | 0.000 | 0.000 | −0.003 | 1.18 | 179.93 (0.07) |
| MoS2B | 0.035 | −0.033 | 0.015 | 0.017 | 0.000 | 0.000 | N/A | 1.18 | 179.92 (0.08) |
| GrapheneB | 0.021 | −0.012 | −0.016 | −0.007 | N/A | N/A | −0.004 | 1.18 | 179.92 (0.08) |
| G5 × 5 | 0.001 | 0.020 | −0.015 | 0.006 | N/A | N/A | −0.004 | 1.18 | 179.89 (0.11) |
| M4 × 4 | 0.035 | −0.047 | 0.002 | −0.010 | 0.000 | 0.084 | N/A | 1.18 | 179.87 (0.13) |
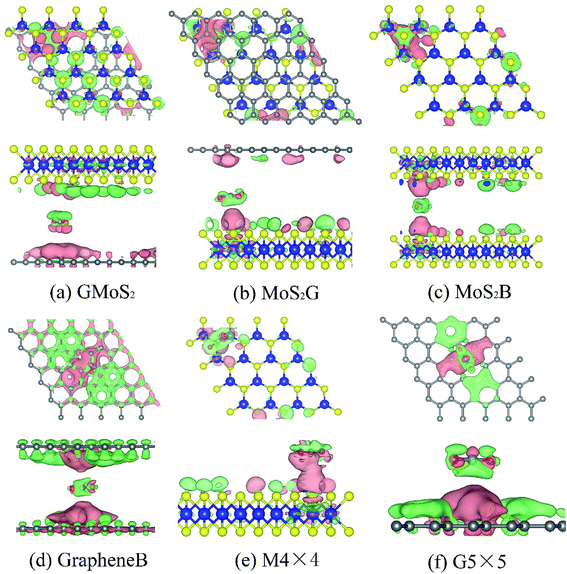
Bader charge analysis shows that the interaction between CO2 and these surfaces causes charge transfer and redistributions (Fig. 3). The amount of charge transferred from Bader charge analysis is summarized in Table 4. It can be seen that while 0.028e of charge is transferred to CO2 on the GMoS2 surface where graphene is the bottommost layer, 0.810e of charge is transferred from CO2 to MoS2 where MoS2 is the topmost layer. This could indicate that the modality of the atom arrangement (C–Mo–S–O and Mo–S–O–C) in both structures affects the charge transfer between the molecule and surface atoms. In order words, the conformational anisotropy of this structure determines to a certain point the charge transfer and redistribution just like in its CO2 adsorption energy. Meanwhile, in some cases, the adjacent S atom of MoS2 and C atom of graphene nearer to the adsorbed CO2 gain electrons, while Mo atom loses an electron in all cases. This is because of the higher electronegativity of S and C atoms compared to the Mo atom. Fig. 3 presents the charge density difference plots for CO2 molecule-surfaces obtained using the formula:
| Δρ = ρmole+surf − (ρmole + ρsurf) | (2) |
The pink region shows the charge accumulation (electron excess) while the green region indicates the charge depletion (electron loss). In all the structures, it can be shown that there is a noticeable polarization of the surfaces upon CO2 adsorption, and electrostatic interaction plays a role in the attractive interaction. Moreover, there is charge accumulation on GMoS2, MoS2G, MoS2B, GrapheneB, G5 × 5 and M4 × 4 upon CO2 adsorption, which suggests that CO2 also has a charge-donor characteristic. In addition, polarization in GrapheneB and MoS2B structures showed to be stronger than in MoS2G, G5 × 5, GMoS2 and MoS2 structures, which gives rise to larger adsorption energies. This explains why GrapheneB and MoS2B displayed larger adsorption energies (−241 and −195 meV, respectively) than MoS2G, G5 × 5, GMoS2 and MoS2 (−169, −153, −145, and −126 meV, respectively) after spin-polarized DFT-D2 calculations mentioned earlier.
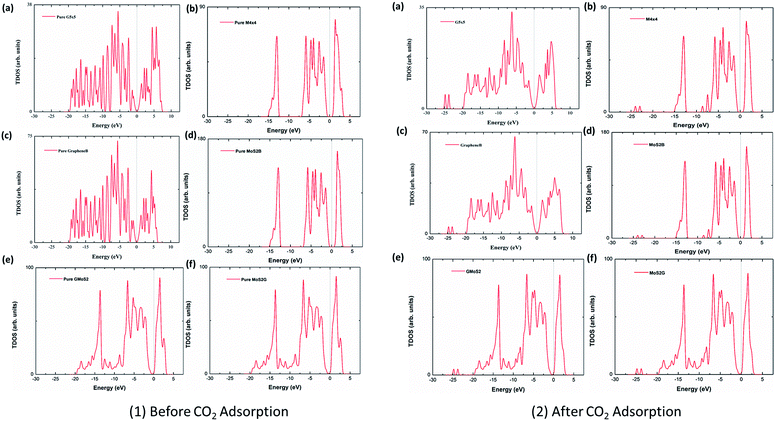
3.5 Density of states (DOS) plots
To analyse the electronic properties of the adsorbed CO2 interaction on the multilayer structures, the total electronic density of states (DOS) was studied for graphene and MoS2 monolayer and bilayer surfaces before and after CO2 adsorption. Fig. 4 shows that the DOS spectra for either the valence or conduction band of the monolayer and bilayer surfaces do not show significant changes before and after adsorption. This indicates that the CO2 interaction with these surfaces is purely physisorption, involving weak interaction forces such as vdW and Lewis acid–base interaction. Subsequently, this will not affect the electronic structure of surface atoms significantly. Although it is observed that the adsorption of CO2 introduces several distinct states at the lower-lying valence bands within the energy level of −22 eV to −25 eV, and offsets some peaks at the conduction bands within energy levels 2.5–5.0 eV, there is no noticeable modification of the DOS near the Fermi level, which also concludes that CO2 physisorption does not have a substantial effect on the electronic properties of graphene and MoS2. DOS spectra of graphene (G5 × 5) and MoS2 (M4 × 4) monolayer, bilayers (GrapheneB and MoS2B) and hybrid (GMoS2 and MoS2G) structures were compared. It is observed that the DOS spectra of the monolayer and bilayer structures are nearly the same. MoS2 (monolayer and bilayer) displayed a spectrum of an intrinsic semiconductor with direct bandgap of 1.66 eV before and after CO2 adsorption, which fairly correspond to both previous experimental (1.80 eV) and computational (1.58 eV) results obtained for pure MoS2 monolayer, whereas graphene (monolayer and bilayer) exhibited a semi-metal spectrum with a small overlap between the valence and conduction band (zero bandgap material).61,62 However, it is noted here that 5 × 5 × 1 k-point mesh produced an un-converged sampling of Brillouin zone for pure graphene, and introduced small peaks around the Fermi level. This is attributed to the large quasiparticle dynamics of graphene,43 particularly at fewer k-point meshes like 5 × 5 × 1. To correct this anomaly, a very fine k-point mesh without increasing the computational cost was proposed. Accordingly, a finer MP mesh of size 40 × 40 × 1 in the unit cell and the tetrahedron method with Blöchl corrections was used to reproduce the Brillouin zone sampling of electronic states. The 40 × 40 × 1 k-point mesh centered at Г gave a faster convergence and accurately predicted the DOS of pure graphene. It also eliminated the small peaks around the Fermi level. As shown in Fig. 4, the Dirac cone was obtained in pure graphene monolayer and bilayer, which is unaffected after CO2 adsorption. The plots are in good agreement with the work of ref. 63, which tested different k-point meshes to generate the DOS of graphene monolayer and bilayer structures. However, the DOS spectra of the bilayer heterostructure seem to be a simple sum of those of each constituent with a shift of the valence and conduction bands. The conduction band shifted closer to the Fermi level, a characteristic of an n-type semiconductor. There is a noticeable modification of DOS spectra near the Fermi level, as the conduction band shifted closer to the Fermi level. This indicates a small band gap opening due to the variation of on-site energy induced by MoS2 that is found in graphene/MoS2 bilayer heterostructures.41 As shown in Fig. 4 (1 and 2), the calculated bandgap is 0.04 eV irrespective of the modality of the atom arrangement in both structures. This specifies that the graphene monolayer in the heterostructure loses its metallic nature, and massless electron characteristics and becomes more semiconducting with a direct narrow bandgap, while significantly increasing the conductivity of the MoS2 monolayer. This is comparable with other hybrid structures.41 It is also observed that the DOS spectra of the hybrid structures are the same, which indicates that the conformational anisotropy does not have any effect on the DOS spectra bilayer heterostructures unlike in its CO2 adsorption energy.4 Conclusion
In this work, a comprehensive first-principles study of the CO2 adsorption mechanism on graphene/graphene, MoS2/MoS2 bilayers and graphene/MoS2, MoS2/graphene hybrids using GGA-PBE is presented. CO2 adsorption energies, indicative of adsorption capacity, were calculated at various interlayer spacings. 7.5 Å and 8.5 Å interlayer spacings are the most stable conformations for CO2 adsorption on the bilayer and hybrid structures respectively, with the bilayers displaying higher adsorption capacities. Beyond an interlayer spacing of 8.0 Å, CO2 adsorption was promoted by the presence of MoS2 in the hybrid. However, this varied with the configuration of the bilayer structure. Moreover, the most active adsorption site was determined by varying CO2 molecule orientation. A parallel CO2 attack at the edge position of the surface exhibited the highest adsorption energies. Parallely inclined orientations also showed promising adsorption potential, however this varied in attack positions for each nanocomposite. The total electronic density of states analysis reveals that CO2 interaction with these surfaces is purely physisorption, which mainly involves weak interaction forces. The Bader charge analysis indicates that there is charge transfer and redistribution between the substrate and the adsorbate. In addition, it was demonstrated that conformational anisotropy could affect CO2 adsorption and other properties due to the modality of the atom arrangement (C–Mo–S–O and Mo–S–O–C) in both heterostructures. In general, the modification of interlayer spacing and structural configuration during the synthesis route is the key to enhancing the adsorption performance of these nanocomposites. This is attainable given the improving successes in atomic level studies and combination of the design of experiments like nanoparticle tracking analysis. Finally, the incorporation of vdW interactions boosted the adsorption energies, thus portraying the importance of doping and functionalization in improving the adsorption performance of these composites.Conflicts of interest
There is no conflicts to declare.Acknowledgements
Following funding bodies are acknowledged for partially sponsoring this research: National Key Research and Development Projects (2017YFC0210400 and 2017YFB0603202), National Natural Science Foundation of China (51706114). Special thanks to the Advanced Energy and Environmental Materials Technology (AEEMT) research group at the University of Nottingham Ningbo China. The computational resources are fully provided by the High-Performance Computer (HPC) System of UNNC. The author (Francis Enujekwu) thanks Bamidele Akinwolemiwa for his helpful discussions.References
- J. Li, et al., Enhanced CO2 capture on graphene via N, S dual-doping, Appl. Surf. Sci., 2017, 399, 420–425 CrossRef CAS.
- S. A. Tawfik, et al., Multiple CO2 capture in stable metal-doped graphene: a theoretical trend study, RSC Adv., 2015, 5(63), 50975–50982 RSC.
- C. Cazorla, The role of density functional theory methods in the prediction of nanostructured gas-adsorbent materials, Coord. Chem. Rev., 2015, 300, 142–163 CrossRef CAS.
- NOAA, Trends in Carbon Dioxide: Globally averaged marine surface monthly mean data, Earth System Research Laboratory (ESRL), ftp://aftp.cmdl.noaa.gov/products/trends/co2/co2_mm_gl.txt, www.esrl.noaa.gov/gmd/ccgg/trends/, 2017 Search PubMed.
- R. F. Service, The Carbon Conundrum, Science, 2004, 305(5686), 962–963 CrossRef CAS PubMed.
- A. B. Rao and A. R. Rubin, A Technical, Economic, and Environmental Assessment of Amine-Based CO2 Capture Technology for Power Plant Greenhouse Gas Control, Environ. Sci. Technol., 2002, 36(20), 4467–4475 CrossRef CAS PubMed.
- L. Ci, et al., Atomic layers of hybridized boron nitride and graphene domains, Nat. Mater., 2010, 9(5), 430 CrossRef CAS PubMed.
- D. Wang, et al., Space-Confined Growth of Defect-Rich Molybdenum Disulfide Nanosheets Within Graphene: Application in The Removal of Smoke Particles and Toxic Volatiles, ACS Appl. Mater. Interfaces, 2016, 8(50), 34735–34743 CrossRef PubMed.
- L. Ci, et al., Atomic layers of hybridized boron nitride and graphene domains, Nat. Mater., 2010, 9, 430 CrossRef CAS PubMed.
- C. Lee, et al., Frictional Characteristics of Atomically Thin Sheets, Science, 2010, 328(5974), 76–80 CrossRef CAS PubMed.
- K. S. Novoselov, et al., Two-dimensional atomic crystals, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(30), 10451–10453 CrossRef CAS PubMed.
- B. K. Miremadi and S. R. Morrison, Highactivity catalyst from exfoliated MoS2, J. Catal., 1987, 103(2), 334–345 CrossRef CAS.
- C. Lee, et al., Anomalous Lattice Vibrations of Single- and Few-Layer MoS2, ACS Nano, 2010, 4(5), 2695–2700 CrossRef CAS PubMed.
- K. F. Mak, et al., Atomically Thin MoS2: A New Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105(13), 136805 CrossRef PubMed.
- B. Radisavljevic, et al., Single-layer MoS2 transistors, Nat. Nanotechnol., 2011, 6, 147 CrossRef CAS PubMed.
- Y. Zhang, et al., Ambipolar MoS2 Thin Flake Transistors, Nano Lett., 2012, 12(3), 1136–1140 CrossRef CAS PubMed.
- L. Hai, et al., Fabrication of Single- and Multilayer MoS2 Film-Based Field-Effect Transistors for Sensing NO at Room Temperature, Small, 2012, 8(1), 63–67 CrossRef PubMed.
- Q. He, et al., Fabrication of Flexible MoS2 Thin-Film Transistor Arrays for Practical Gas-Sensing Applications, Small, 2012, 8(19), 2994–2999 CrossRef CAS PubMed.
- H. Zhao, et al., Structural defects in 2D MoS2 nanosheets and their roles in the adsorption of airborne elemental mercury, J. Hazard. Mater., 2019, 366, 240–249 CrossRef CAS PubMed.
- A. K. Geim and I. V. Grigorieva, Van der Waals heterostructures, Nature, 2013, 499, 419 CrossRef CAS PubMed.
- R. Mu, et al., Visualizing chemical reactions confined under graphene, Angew. Chem., Int. Ed., 2012, 51(20), 4856–4859 CrossRef CAS PubMed.
- X. Pan and X. Bao, The Effects of Confinement inside Carbon Nanotubes on Catalysis, Acc. Chem. Res., 2011, 44(8), 553–562 CrossRef CAS PubMed.
- B. Smit and T. L. M. Maesen, Towards a molecular understanding of shape selectivity, Nature, 2008, 451, 671 CrossRef CAS PubMed.
- J. M. Thomas and R. Raja, Exploiting Nanospace for Asymmetric Catalysis: Confinement of Immobilized, Single-Site Chiral Catalysts Enhances Enantioselectivity, Acc. Chem. Res., 2008, 41(6), 708–720 CrossRef CAS PubMed.
- B. B. Kappes, et al., Orientation-dependent binding energy of graphene on palladium, Appl. Phys. Lett., 2013, 102(5), 051606 CrossRef.
- Y. Murata, et al., Orientation-dependent work function of graphene on Pd(111), Appl. Phys. Lett., 2010, 97(14), 143114 CrossRef.
- Y. Murata, et al., Growth structure and work function of bilayer graphene on Pd(111), Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(20), 205443 CrossRef.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136(3B), B864–B871 CrossRef.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Fromultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- S. Grimme, SemiempiricalGGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- M. Dion, et al., Van der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92(24), 246401 CrossRef CAS PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Van der Waals density functionals applied to solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(19), 195131 CrossRef.
- G. Román-Pérez and J. M. Soler, Efficient Implementation of a van der Waals Density Functional: Application to Double-Wall Carbon Nanotubes, Phys. Rev. Lett., 2009, 103(9), 096102 CrossRef PubMed.
- K. Jiří, R. B. David and M. Angelos, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22(2), 022201 CrossRef PubMed.
- I. Hamada, van der Waals density functional made accurate, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(12), 121103 CrossRef.
- K. Lee, et al., Higher-accuracy van der Waals density functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(8), 081101 CrossRef.
- Y. Ma, et al., Graphene adhesion on MoS(2) monolayer: anab initiostudy, Nanoscale, 2011, 3(9), 3883–3887 RSC.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192 CrossRef.
- A. Bostwick, et al., Quasiparticle dynamics in graphene, Nat. Phys., 2006, 3, 36 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A fast and robust algorithm for Bader decomposition of charge density, Comput. Mater. Sci., 2006, 36(3), 354–360 CrossRef.
- C. Ataca, et al., A Comparative Study of Lattice Dynamics of Three- and Two-Dimensional MoS2, J. Phys. Chem. C, 2011, 115(33), 16354–16361 CrossRef CAS.
- Y. Liu and J. Wilcox, CO2 Adsorption on Carbon Models of Organic Constituents of Gas Shale and Coal, Environ. Sci. Technol., 2011, 45(2), 809–814 CrossRef CAS PubMed.
- P. Cabrera-Sanfelix, Adsorption and Reactivity of CO2 on Defective Graphene Sheets, J. Phys. Chem. A, 2009, 113(2), 493–498 CrossRef CAS PubMed.
- I. A. Baburin, et al., Hydrogen adsorption by perforated graphene, Int. J. Hydrogen Energy, 2015, 40(20), 6594–6599 CrossRef CAS.
- A. F. Ismail, K. Khulbe and T. Matsuura, Gas Separation Membranes: Polymeric and Inorganic, in Membrane Technology and Applications, Springer, 2015,p. 14 Search PubMed.
- B. Sachs, et al., Doping mechanisms in graphene–MoS2 hybrids, Appl. Phys. Lett., 2013, 103(25), 251607 CrossRef.
- A. F. Holleman and E. Wiberg, Inorganic Chemistry,ed. N. Wiberg, Academic Press, San Diego, CA, USA, 2001 Search PubMed.
- J. Deng, et al., Triggering the electrocatalytic hydrogen evolution activity of the inert two-dimensional MoS2 surface via single-atom metal doping, Energy Environ. Sci., 2015, 8(5), 1594–1601 RSC.
- T. F. Jaramillo, et al., Identification of Active Edge Sites for Electrochemical H2 Evolution from MoS2Nanocatalysts, Science, 2007, 317(5834), 100–102 CrossRef CAS PubMed.
- J. Li, et al., Enhanced CO2 capture on graphene via N, S dual-doping, Appl. Surf. Sci., 2017, 399, 420–425 CrossRef CAS.
- S. Zhao, J. Xue and W. Kang, Gas adsorption on MoS2 monolayer from first-principles calculations, Chem. Phys. Lett., 2014, 595–596, 35–42 CrossRef CAS.
- Z. Jijun, et al., Gas molecule adsorption in carbon nanotubes and nanotube bundles, Nanotechnology, 2002, 13(2), 195 CrossRef.
- W.-L. Yim, et al., Vibrational behavior of adsorbed CO2 on single-walled carbon nanotubes, J. Chem. Phys., 2004, 120(11), 5377–5386 CrossRef CAS PubMed.
- CRC, CRC Handbook of Chemistry and Physics,CRC Press, Boca Raton, FL, 90th edn, 2009–2010 Search PubMed.
- C. Tayran, et al., Structural and electronic properties of AB- and AA-stacking bilayer-graphene intercalated by Li, Na, Ca, B, Al, Si, Ge, Ag, and Au atoms, Solid State Commun., 2016, 231–232, 57–63 CrossRef CAS.
- S. Yang, et al., Sodium adsorption and intercalation in bilayer graphene from density functional theory calculations, Theor. Chem. Acc., 2016, 135(7), 164 Search PubMed.
- C. Ataca and S. Ciraci, Functionalization of Single-Layer MoS2 Honeycomb Structures, J. Phys. Chem. C, 2011, 115(27), 13303–13311 CrossRef CAS.
- K. F. Mak, et al., Atomically Thin ${\mathrm{MoS}}_{2}$: A New Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105(13), 136805 CrossRef PubMed.
- A. M. Ukpong, First principles study of van der Waals heterobilayers, Computational Condensed Matter, 2015, 2, 1–10 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00314a |
| This journal is © The Royal Society of Chemistry 2019 |