Impact resistance of nanocellulose films with bioinspired Bouligand microstructures

Abstract

The Bouligand structure features a helicoidal (twisted plywood) layup of fibers that are uniaxially arranged in-plane and is a hallmark of biomaterials that exhibit outstanding impact resistance. Despite its performance advantage, the underlying mechanisms for its outstanding impact resistance remain poorly understood, posing challenges for optimizing the design and development of bio-inspired materials with Bouligand microstructures. Interestingly, many bio-sourced nanomaterials, such as cellulose nanocrystals (CNCs), readily self-assemble into helicoidal thin films with inter-layer (pitch) angles tunable via solvent processing. Taking CNC films as a model Bouligand system, we present atomistically-informed coarse-grained molecular dynamics simulations to measure the ballistic performance of thin films with helicoidally assembled nanocrystals by subjecting them to loading similar to laser-induced projectile impact tests. The effect of pitch angle on the impact performance of CNC films was quantified in the context of their specific ballistic limit velocity and energy absorption. Bouligand structures with low pitch angles (18–42°) were found to display the highest ballistic resistance, significantly outperforming other pitch angle and quasi-isotropic baseline structures. Improved energy dissipation through greater interfacial sliding, larger in-plane crack openings, and through-thickness twisting cracks resulted in improved impact performance of optimal pitch angle Bouligand CNC films. Intriguingly, decreasing interfacial interactions enhanced the impact performance by readily admitting dissipative inter-fibril and inter-layer sliding events without severe fibril fragmentation. This work helps reveal structural and chemical factors that govern the optimal mechanical design of Bouligand microstructures made from high aspect ratio nanocrystals, paving the way for sustainable, impact resistant, and multi-functional films.

---

Introduction

The Bouligand (or twisted plywood) structure¹ is a prevalent architecture found in numerous biological materials, including crustacean and beetle exoskeletons,^2–4 fish scales,^5,6 and mantis shrimp dactyl clubs.⁷ It is a vivid illustration of how nature employs efficient design principles to construct tough, lightweight materials.^8,9 The Bouligand microstructure is composed of uniaxially aligned nanofibers organized into planar sheets, which are stacked to form a helicoid. This structure is believed to offer a combination of high impact tolerance and strength, rivaling tough brick-and-mortar materials, such as nacre.^10–12 Understanding the underlying physics that govern the impact resistance of helicoidal microstructures is very timely given the growing interest in developing bioinspired, impact resistant, and lightweight materials and structures.^13,14 Potential applications of these materials include protective shields for vehicles, body armor, eyewear, packaging, and stretchable and wearable electronics.^14–16

While numerous experimental and computational investigations have attempted to explain the structure–property relationships of Bouligand microstructures that give rise to its impact tolerance, no consensus has emerged regarding the dominant deformation mechanisms associated with this microstructure. Bouligand lamellae in fish scales have been shown to reorient towards external tensile loads during mechanical testing using X-ray scattering, leading to enhanced toughness through stretching and sliding mechanisms.⁵ The mantis shrimp dactyl club also exhibits impressive damage tolerance originating from its Bouligand microstructure, where helicoidally twisted fracture paths formed upon impact improve energy dissipation by creating new surfaces.^7,17 Inspired by these natural materials, both conventional, fiber-reinforced composite pre-pregs and 3D printed materials have been employed to study the underlying deformation and damage mechanisms associated with Bouligand microstructures.^18–24 Experiments and finite element analyses of Bouligand structured composites have demonstrated improved impact resistance and higher residual strength (as much as 80%) compared to quasi-isotropic structures by effectively spreading impact energy in-plane.^14,15,20 Ballistic impact tests have revealed that Bouligand structures (Fig. 1b) with smaller inter-ply, or pitch (γ), angles (22.5 ≤ γ ≤ 45°) lead to higher ballistic limits and can absorb up to 15% more energy during ballistic impacts with larger delamination areas and lower degrees of internal damage.^16,25,26 Fiber orientation has also been found to effectively influence the toughness and strength of bio-inspired composites through changes in the prominent damage and deformation propagation mechanisms when subjected to dynamic strain rates on the order of 1000 s⁻¹.^27–30 Additionally, inter-laminar and inter-fiber interactions of layered structures, including shear strength and interfacial adhesion energy, have been shown to greatly influence the crack propagation and deflection during impact events.^11,21,31,32

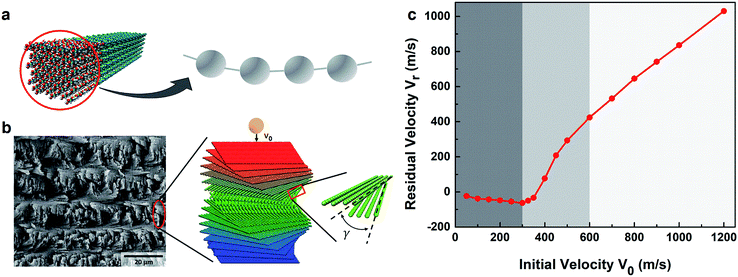Fig. 1 (a) Coarse-graining scheme showing the mapping between the all-atom model of CNCs (left) and the corresponding bead-spring representation (right); (b) a representative SEM image of the helicoidal microstructure of a mantis shrimp dactyl club (left, reprinted with permission Elsevier¹⁴), with a schematic showing the ballistic impact simulations of a bioinspired CNC film with a Bouligand structure with a constant pitch angle of γ (right); (c) typical residual velocity vs. initial velocity relationship for a free standing CNC Bouligand film with an in-plane radius of 500 nm, clamped boundaries, and a projectile radius 80 nm.

Although these experimental and computational efforts begin to show the mechanical and structural features that contribute to the impact resistance of materials with Bouligand structures, they still fall short of revealing the necessary mechanisms and features for optimal impact performance. Due to the challenges associated with Bouligand structure fabrication with nanoscopic features and extracting the mechanical response of materials through ballistic impact experimentation, most prior experimental efforts have been limited to the macroscopic scale with macroscopic elements. Additionally, continuum approaches, like the finite element method, have some disadvantages in modeling micromechanical and molecular systems. These include an inability to accurately describe and probe the effects of intrinsic microstructural and chemistry-dependent features with respect to important deformation mechanisms like interfacial sliding. Consequently, a direct link is still missing between Bouligand microstructures and their impact tolerance, as seen across different materials and length scales. In particular, a nanoscopic understanding of the roles of internal structuring and interfacial properties is critically important for predicting the mechanical properties directly from their constituents. Where experiments and continuum computational approaches have proved inadequate in unraveling key structure–property relationships for materials with Bouligand microstructures, molecular dynamics (MD) simulations can excel by providing meaningful insights into the highly dynamic deformation processes of nano- and microscale systems. In particular, MD failure criteria can be embedded directly in interatomic potentials, chemistry specific alterations can be readily considered by modifying potentials, and its discrete formulation can enable accurate descriptions of covalent rupture and non-covalent sliding events.

In this work, neat, helicoidal cellulose nanocrystal (CNC) films were investigated as a model Bouligand system using MD simulations. CNCs, a polysaccharide analogue of chitin, readily self-assemble into a stable, chiral nematic (or helicoidal) liquid crystalline phase in suspension,^33–35 which can be dried to produce nanoscale films with internal Bouligand structures and emergent photonic features.^36–39 In addition to being optically transparent, CNCs are the building blocks of many naturally hierarchical materials, including plants, bacteria, and tunicates.^40,41 They possess outstanding mechanical properties, such as stiffness and strength that rival Kevlar or functionalized graphene.^42–44 The combination of superior mechanical properties and propensity for self-assembled Bouligand structures makes CNCs a promising candidate for future protective materials and structures.⁴⁵ MD simulations have been successfully used to study CNC-based materials, which not only corroborate experimental findings,^46,47 but have also revealed important structural and interfacial mechanisms that contribute to their superior mechanical performance, offering guidance for experimental material design.^48–50 Recently, we established an atomistically informed coarse-grained modeling approach to extend analyses of CNCs to larger length and time scales, which has been instrumental in explaining the influence of overlap length and interfacial interactions on the mechanical properties of neat CNC nanopapers up to micrometer sizes.⁵¹ With the advent of small-scale ballistic experiments, such as laser-induced projectile impact tests (LIPIT),^52,53 MD simulations have successfully been used to explain the failure mechanisms of nanomaterials subjected to ballistic impacts. MD simulations have also quantified the dependence of ballistic properties on specimen dimensions and projectile geometries,^54–56 complementing experimental studies at the microscopic scales.⁵³ In particular, they have elucidated mechanisms associated with cone wave reflections and spalling effects in graphene membranes.^55–57

Methods

With a validated CG model of CNCs, representative films were constructed with left-handed helicoidal structures typical of chitin-rich shells of crustaceans and self-assembled CNCs.^3,7,34 Specifically, the principal aim of this work was to understand the influence of helicoidal pitch angle, γ, and interfacial energy, on the ballistic resistance and energy absorption of CNC films. The mesoscale computational framework developed herein accurately incorporates representative interfacial and intermolecular interactions of CNCs, while allowing access to micrometer length scales. The CG CNC model also enables a comprehensive evaluation of the full range of Bouligand pitch angles efficiently, which is critical for revealing the optimal design parameters of bio-inspired, ballistic resistant materials built with Bouligand microstructures.

All CG simulations were conducted using Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS),⁵⁸ and visualizations of the Bouligand structures and ballistic impact process were computed with Visual Molecular Dynamics (VMD).⁵⁹ Our previously developed bead-spring mesoscopic model for CNCs is shown in Fig. 1a. Within this model, each CG bead represents all the atoms (4536 total) within 3 repeat-units of the 36-chain structured (110) surface of CNCs. A series of atomistic mechanical characterizations, including uniaxial tension, 3-point bending, and adhesion energy calculations, were carried out to establish the CG force field parameters according to the strain energy conservation principle (see ESI† and our prior work⁵¹ for details). Nonbonded interactions were modeled using a Morse potential to match the interfacial shear properties of CNCs, with D₀ = 240 kcal mol⁻¹ corresponding to the interaction between (110) surfaces of native CNCs without chemical or structural modifications. A failure criterion for the bonds within CNCs to break was set at ε_cut = 5% (b_cut = 32.7 Å) based on previous MD studies with reactive force fields.⁶⁰ Bonds stretched over this distance were considered broken and deleted from the simulation; the bond topology was updated every 50 femtoseconds to facilitate bond rupture during the impact process.⁵¹

As shown in Fig. 1b, CNC films with Bouligand structures were built to investigate structure–property relationships during ballistic impacts. Aligned CNCs were assembled into layers and then stacked on top of each other with constant pitch angles to construct the various Bouligand structures (see inset of Fig. 1b). The projectile was built using CG beads assuming a diamond cubic lattice structure (3.48 g cm⁻³). The projectile was treated as a rigid body since projectiles tend to show no obvious deformation during micro-ballistic impact tests.⁵³ The interactions between the projectile and CNC film were represented with a 12–6 Lennard Jones potential (ε_LJ = 20 kcal mol⁻¹ and σ_LJ = 40 Å). Specific ε_LJ values had a negligible influence on the ballistic response, including projectile reaction force and velocity histories. Higher cohesive energies between the projectile and film tended to increase noise in the force response and frictional losses at high impact velocities, but the mean values were similar, consistent with previous studies (see Fig. S1 in ESI†).⁵⁵ Prior to impact, the CNC film was relaxed using a conjugate gradient energy minimization without any constraints until the change in energy between successive minimization steps divided by the energy magnitude was less than 10⁻¹⁰. Next, CNC CG beads beyond a circular region in the center of the film were constrained to remain in their original positions to create a free-standing, circular film, matching the clamped geometries of previous experiments.⁶¹ The energy minimized, free-standing film was equilibrated at 10 K under an NVT (canonical) ensemble for 20 ns, while the system energy was monitored to ensure convergence. The low temperature was selected to minimize thermal noise during simulations. At the strain-rates studied, thermal contributions to failure were considered to be negligible, with no significant differences in equilibrated film structures (density, interlayer energy, etc.) or impact tolerances observed using equilibrating temperatures up to 300 K. During film equilibration, the position of the projectile was fixed 10 nm above the geometric center of the CNC film to avoid any possible interactions. Following equilibration, under an NVE (microcanonical) ensemble, an initial velocity towards the film was assigned to the projectile to simulate the impact process. The projectile kinetic energy and reaction force histories were recorded to assess the ballistic performance of the various Bouligand films. As a result of the efficiency of the CG CNC model (Fig. 1), it was possible to construct Bouligand films and projectiles that were sufficiently large to provide meaningful comparisons with real micro-ballistic tests.⁵³ During the simulations, the radii of free-standing CNC films were set to be 500 nm, with a thickness of 11 layers (approximately 37 nm); the spherical projectile radius was chosen to be 80 nm. Other film sizes were also tested and no qualitative differences in the deformation mechanisms were found in films with larger radii, although geometric effects should play a role when the span to projectile radius ratio becomes sufficiently small.⁵⁵ In addition, the ratio between projectile radius and film thickness is relatively small compared to standard thin film LIPIT.^53,62,63 The small ratio in this work was purposely chosen to investigate and highlight the frictional effects in the thickness direction on the impact response of films, similar to a previous experimental study on high strain rate deformation of layered nanocomposites using LIPIT.⁵² This is because when the projectile radius is orders of magnitude larger than the film thickness, the deformation in the thickness direction of the film can be usually treated as uniform and the interlayer friction inside the film would be negligible. Furthermore, our recent study shows that, for impact responses that involve a larger area of deformation than projected area through cone wave propagation, the size of the total deformation area depends on the ratio between the projectile radius and film thickness.⁶⁴ More specifically, with a large ratio between projectile radius and film thickness, the deformation zone is much greater than the projected area, resulting in significant energy absorption through elastic in-plane deformation of the film. In these cases, the in-plane properties of the film would influence the penetration energy more than the interlayer properties in the thickness direction.

Results and discussion

Understanding the relationship between initial (V₀) and residual velocity (V_r) during microballistic impacts, as shown in Fig. 1b, is critical for designing high impact tolerance nanostructures. The ballistic limit velocity (V₅₀) and energy absorption (ΔE_k) are two key material design parameters associated with this relationship. V₅₀ corresponds to the projectile V₀ that reliably (at least 50% of the time) penetrates the material, while ΔE_k is the kinetic energy lost from the projectile during the penetration process; both of these quantities are directly obtainable from MD simulations. The relationship between V₀ and V_r can be categorized into three distinct regions based on V_r. In region I, a negative V_r corresponds to a reflecting projectile, meaning no penetration has occurred. With increasing V₀, V_r shows a sudden change from negative to positive (region II), indicating the transition from projectile rebound to penetration. In region II, deformation propagation phenomena, like cone wave formation and interference in graphitic barriers, can be important drivers for overall impact resistance.^53,55 With still greater initial velocities (region III), V_r linearly depends on V₀, with films experiencing immediate, local perforation and fiber fragmentation at the impact site.

Effect of film structure on ballistic performance

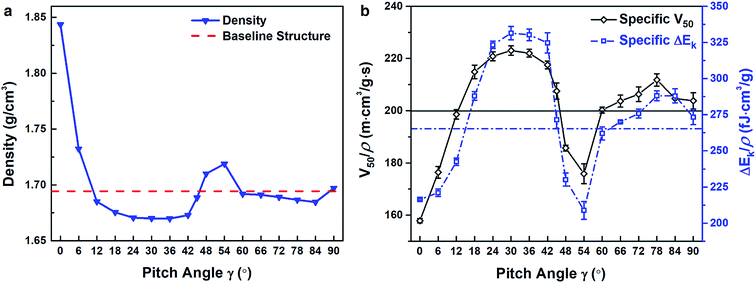
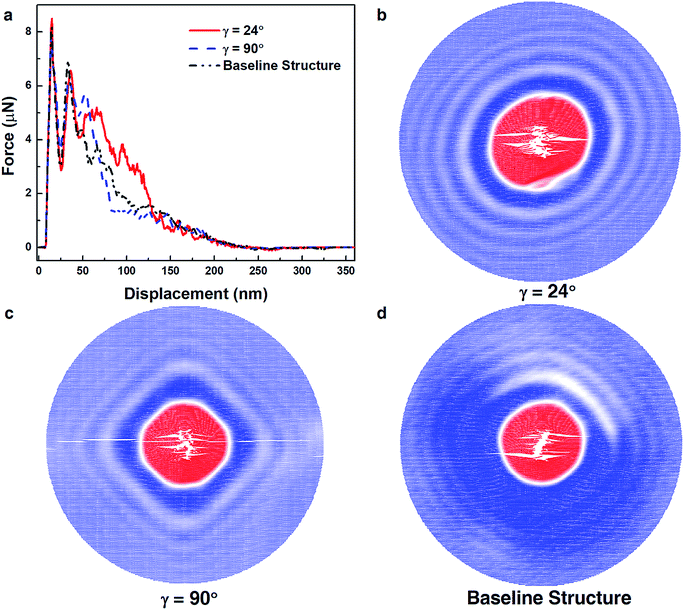
The effect of pitch angle (γ) on film density (ρ) was first characterized. The densities of CNC films following equilibration simulations exhibited a dependence on γ. As shown in Fig. 2a, film densities initially show a sharp decrease with increasing γ, then saturate, notwithstanding a small, local increase between γ = 48° and γ = 60°. For the pure aligned films (γ = 0°), given the bead-spring construction of the CG model, the structure achieved optimal packing. Increasing γ up to 20° compromised this close packing, decreasing the film density. At larger pitch angles, the film density was less sensitive to γ, except for pitch angles around 60°, where the bead-spring CG CNC model preferred a hexagonal close packed structure. Due to the different densities of the Bouligand films, the specific ballistic limit velocity (V₅₀/ρ) and energy absorption (ΔE_k/ρ) for each film were determined to assess the effects of γ on ballistic performance. V₅₀/ρ and ΔE_k/ρ as a function of γ are shown in Fig. 2b. An initial velocity of 400 m s⁻¹ (region II) was used to calculate ΔE_k/ρ. A quasi-isotropic layup ([0/45°/90°/−45]_s), commonly employed in structural composites, was also considered as a baseline reference to compare the impact performance of Bouligand structures. The density of the quasi-isotropic layup was slightly higher than the γ = 45° film due to its midplane symmetry admitting higher packing between certain layers (Fig. 2b). The solid black and dashed blue lines denote its V₅₀/ρ and ΔE_k/ρ in Fig. 2b, respectively. Fig. 2b illustrates a clear improvement in V₅₀/ρ with increasing γ up to approximately 42°, which drops sharply around γ = 60°. A similar trend is also observed for ΔE_k/ρ. Comparing V₅₀/ρ and ΔE_k/ρ values of Bouligand and quasi-isotropic structures, an optimal pitch angle range (from 18–42°) exists where Bouligand structures outperform quasi-isotropic structures both in terms of impact resistance (a 7.5–12% increase) and energy absorption (an 8.6–26% increase). This optimal range, which features relatively small pitch angles, is remarkably similar to the pitch angles adopted by natural Bouligand structures.^4,29 Previously, experiments with bio-inspired, fiber-reinforced composites that contain Bouligand structures have shown that their damage tolerance during impact increases with decreasing γ.^14,15 However, this is the first time that an optimal pitch angle range has been described for the Bouligand structures that maximizes their ballistic performance, which offers guidance for how 1D nanostructures should be arranged layer-by-layer to produce damage tolerant films.

Fig. 2 (a) Density (ρ) profile for Bouligand microstructures with different pitch angles; and (b) specific ballistic limit velocity (V₅₀/ρ) and specific energy absorption (ΔE_k/ρ) as a function of pitch angle. The solid black line and dashed blue line correspond to the specific ballistic limit velocity and specific energy absorption of the quasi-isotropic baseline structure, respectively. The ΔE_k/ρ values are calculated with V₀ = 400 m s⁻¹ for all pitch angles. Data points represent the average of 8 independent simulation series, with error bars corresponding to the standard deviation. Data points without observable error bars have standard deviations smaller than the height of the data point marker.

The discrete nature of the CG model and its ability to incorporate representative interfacial and intermolecular descriptions affords a unique opportunity to examine how specific nanostructures, with their associated failure and energy dissipating mechanisms, contribute to the superior performance of Bouligand structures compared to commonly used composite layups. Structural variation manifested as differences between projectile force histories, as shown by the responses for three representative structures (Bouligand structures with γ = 24°/90° and the quasi-isotropic layup) during a penetrating impact (V₀ = 400 m s⁻¹) in Fig. 3a. The Bouligand structure with γ = 24° exhibited multiple force peaks and a gradual force decay after impact, while the Bouligand structure with γ = 90° exhibited a smaller max force and quicker force decay; the quasi-isotropic structure also showed inferior force response to dissipate energy during impact.

Fig. 3 (a) Force vs. displacement relationship for Bouligand structures of different pitch angles with V₀ = 400 m s⁻¹; corresponding top views showing the vertical displacement for the first layer of films with (b) γ = 24°, (c) γ = 90°, and (d) quasi-isotropic baseline structures.

These differences in projectile force response (Fig. 3a) can be attributed, at least in part, to the deformation and failure within the films during the impact process. Top views of the films (Fig. 3b–d) during impact illustrate the variety of dominant failure and deformation propagation mechanisms present given the same initial velocity. Here, 400 m s⁻¹ was selected because it is slightly greater than the V₅₀ for all structures and in region II, where the influence of internal structure is most likely to drive impact resistance. For γ = 24° (Fig. 3b), CNCs fractured near the impact site due to a large amount of energy transferred directly into the membrane during impact. In addition to the drastic and localized deformation, large surface creation via fiber splitting and minimal CNC rupture further away from the impact were observed (Fig. 3b). However, with γ = 90° (Fig. 3c), fiber splitting events parallel to the direction of CNCs formed sharper, elongated cracks and occurred primarily away from impact site. The combination of these two features provides a possible explanation for the quicker force decay following impact for γ = 90° (Fig. 3a). Fig. 3d corresponds to the quasi-isotropic structure, where an intermediate amount of CNCs rupture and fiber splitting was observed. The extent to which structural damage was closely related to the ballistic resistance of Bouligand microstructures is supported by the observation that films with higher V₅₀ tended to contain fewer broken CNCs bonds (Fig. S2†). In particular, during low velocity impacts (V₀ = 250 m s⁻¹), films in the optimal pitch angle range (18 < γ < 42°) exhibited substantially lower numbers of total bonds broken (<100 bonds) compared to lower performing films (>500 bonds). The top layer vertical displacements of films with different γ (Fig. 3b–d) highlight that film deformation during impact was closely tied to film microstructure. Bouligand films with optimal pitch angles, like γ = 24° in Fig. 3b, tended to exhibit more radially symmetric deformation due to smaller inter-layer rotation angles. A similar deformation pattern was also observed for the quasi-isotropic layup. However, for large pitch angles, like γ = 90° (Fig. 3c), vertical displacements were radially anisotropic, with more pronounced deflection along fiber directions. Therefore, Bouligand structures with optimal pitch angles (illustrated by 24° in Fig. 3b) not only had the least permanent structural damage during impact, but also displayed more radially symmetric vertical deflections. These two features combine to enhance the impact resistance of films with Bouligand microstructures.

Effect of film quasi-static mechanical properties on ballistic performance

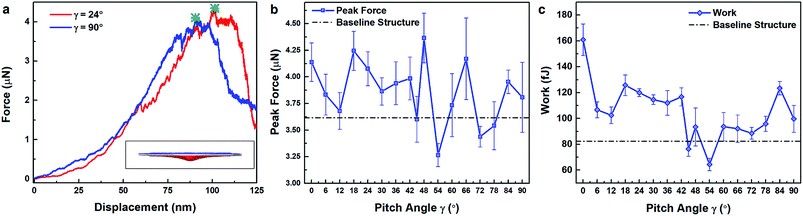
One possible explanation for the dependence of ballistic resistance of Bouligand microstructures on their pitch angle is that there may exist inherent differences in their apparent mechanical properties. Quasi-static loading experiments have shown that materials with Bouligand microstructures may possess improved mechanical properties, including stiffness and peak load, compared to conventional quasi-isotropic or cross-ply structures.^16,18,20 Not only may the mechanical properties of Bouligand thin films depend on their pitch angle, these differences may be correlated with their ballistic performance. To explore the possibility of a connection between material properties and ballistic resistance, nanoindentation simulations were conducted on the Bouligand films (a schematic is shown in the inset of Fig. 4a; details of the nanoindentation procedure can be found in the ESI†). Representative indentation force–displacement curves for γ = 24° and γ = 90° pitch angle films are shown in Fig. 4a. Fig. 4b and c illustrate the peak force and elastic work prior to yielding associated with the indentation process of the Bouligand films as a function of pitch angle, respectively. From Fig. 4b and c, it should be noted that the peak force and nanoindentation work of Bouligand structures are generally greater than those of the quasi-isotropic baseline structures, which corroborate earlier experimental findings.^16,18,20 However, there is insufficient evidence to suggest a significant relationship between either of these quasi-static mechanical properties and V₅₀/ρ (see Fig. S3 in ESI†). Based on these observations, it is possible to conclude that quasi-static material properties do not alone explain the observed dependence of impact resistance on pitch angle in Bouligand films.

Fig. 4 (a) Representative force–displacement curves of Bouligand films during nanoindentation, with the inset showing a schematic of the nanoindentation simulation and peak force highlighted with an *; (b) peak force for different pitch angle films and quasi-isotropic layup (baseline structure); (c) nanoindentation work for different pitch angles and the quasi-isotropic layup. Data points in (b) and (c) correspond to the mean from 5 independent simulations, with the error bars corresponding to the standard deviation.

Effect of film interfacial properties on ballistic performance

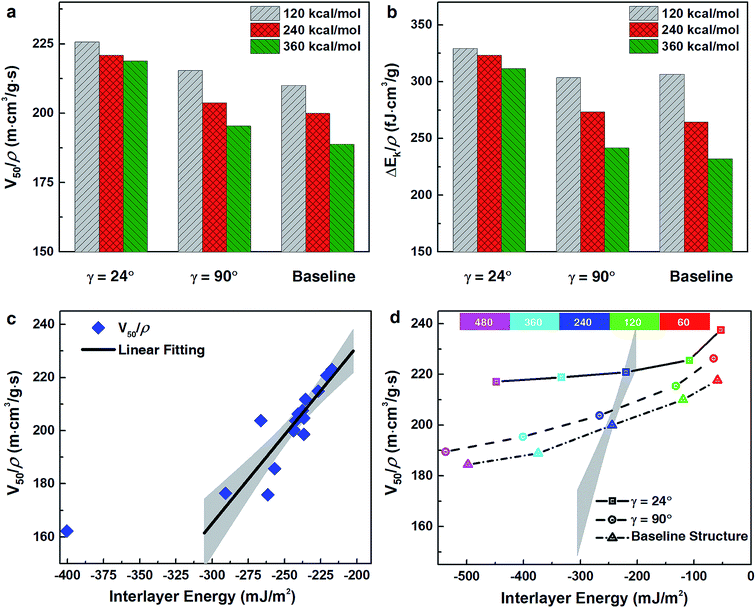
Taken together, these impact and nanoindentation simulations highlight that the influence of pitch angle is much less pronounced for dynamic loading compared to quasi-static deformations. It is plausible that inter-layer interactions affect energy propagation during dynamic deformation and may be largely influenced by fiber orientations. The dependence of inter-layer energy on pitch angle was calculated through a direct summation of nonbonded interactions across adjacent layers. Films containing pitch angles in the optimal performance range (18 < γ < 42°) exhibited smaller inter-layer interactions (see Fig. S4 in ESI†). Importantly, as seen in Fig. 5c, there exists a strong correlation between inter-layer interactions and V₅₀/ρ (P_slope < 0.001).

Fig. 5 Influence of interfacial adhesion energy on (a) V₅₀/ρ and (b) ΔE_k/ρ with D₀ = 240 kcal mol⁻¹ (native CNCs). (c) Relationship between V₅₀/ρ and inter-layer energy for native CNCs; solid black represents a linear regression between the inter-layer energy and V₅₀/ρ (ignoring γ = 0°) of native CNCs, with the gray region corresponding to the 95% mean confidence interval. (d) The sensitivities of various pitch angles (denoted by different shapes and line styles) to changes in interfacial energy; each point along the curves colored according to its specific D₀ value (see color code at the top of (d)) and the 95% mean prediction confidence interval from (c) is also shown in gray.

Understanding this relationship is critical because the interfacial adhesion energy of CNCs can be readily tuned through surface modifications, such as hydrogen bonds or ions exchanged onto the nanocrystals.^40,41,65 In the context of the CG CNC model, varying the depth of the Morse potential energy well, D₀, directly corresponds to changes in the interfacial adhesion energy of CNCs and, thus, inter-layer interactions. Three representative structures (i.e., Bouligand films with γ = 24°/90° and the quasi-isotropic baseline structure) were chosen to illustrate the influence of D₀ on both V₅₀/ρ and ΔE_k/ρ (shown in Fig. 5a and b, respectively). As shown in Fig. 5a and b, both V₅₀/ρ and ΔE_k/ρ were reduced with increasing D₀ due to increased interfacial shear strength. This leads to a reduction in the energy dissipated through fiber fragmentation, crack opening, and inter-layer sliding mechanisms (Fig. S8†). Despite this performance degradation, Bouligand structures with optimal pitch angles (represented by γ = 24° in Fig. 5a and b), still outperformed the quasi-isotropic structure throughout the D₀ range examined. Furthermore, decreases in V₅₀/ρ and ΔE_k/ρ occurred more gradually in the optimal pitch angle (γ = 24°) film compared to the quasi-isotropic and suboptimal pitch angle films (γ = 90°) with increasing interfacial adhesion energy (Fig. 5a and b, respectively). This trend was supported by the lower sensitivity of the total number of bonds broken to variation in D₀ during high velocity impacts for γ = 24° films compared to quasi-isotropic and suboptimal pitch angle films (Fig. S7†). These findings confirm the important role of interfacial interactions in dissipating impact energy; namely, that smaller pitch angles correspond to smaller interfacial shear strength and improved performance. They also highlight that Bouligand structures with relatively small pitch angles better maintain impact resistance for different interfacial energies.

If inter-layer interaction is the key factor that dictates ballistic resistance, then modifying the interfacial adhesion of CNCs should be an effective tool for controlling their impact properties according to the relationship shown in Fig. 5c. The existence of this relationship implies that interfacial energy, not internal microstructure, may drive the ballistic response of Bouligand films. It also suggests the possibility of improving impact resistance through surface modification. That is, given a particular microstructure, it may be possible to control the ballistic performance purely through changing the interfacial adhesion. However, even though altering D₀ values effectively modulates the V₅₀/ρ and ΔE_k/ρ (Fig. 5a and b, respectively), the corresponding relationships (black lines in Fig. 5d) do not follow the predicted linear dependence on inter-layer interactions (the solid black line in Fig. 5c). In fact, isolated modifications to interfacial adhesion indicate that the structural influence of pitch angle alone is substantially greater than the effect of interfacial interactions.

These ballistic simulations also provide valuable insights into the deformation and failure mechanisms that correspond to the improved impact tolerance of Bouligand films. The difference between in-plane mechanical properties of adjacent layers of Bouligand structures becomes smaller with decreasing pitch angle, leading to a smaller interfacial shear strength that facilitates energy dissipation through inter-layer sliding events.¹⁸ Also, helicoidal structures with optimal pitch angles allow for larger in-plane crack openings between fibers, improving energy dissipation and promoting crack twisting through the film thickness as cracks are deflected by the underlying secondary fibers. This reduces the strain energy release rate and leads to an overall enhanced impact resistance,^16,17 which is clearly seen in simulation trajectories (see Fig. S5 in ESI†). On the other hand, unidirectional and Bouligand structures with very small pitch angles (<6°) tend to undergo splitting events during penetrating impacts (see Fig. S6 in ESI†). In this failure mode, projectiles penetrate the film by locally separating fibers through the thickness with minimal permanent film damage. Alternatively, the impact energy impulse can be carried by the fibers directly under the projectile, causing the film to fail by bond rupture at the impact site or clamped boundaries (Fig. S6†). For films with large pitch angles, adjacent layers have drastically different fiber orientations and in-plane mechanical properties, resulting in a larger radial dependence of deformation wave speeds (Fig. 3d). This hinders energy transfer between layers, which may explain the sharp decay of the force response following initial impact (Fig. 3a). Anisotropic in-plane mechanical properties may also compromise energy dissipation by limiting interfacial sliding.

Conclusions

In this study, ballistic impact simulations of CNC films with Bouligand microstructures were carried out using a previously validated, CG model of CNCs to investigate the influence of both the structural (i.e., γ) and mechanical (i.e., D₀) features on their impact resistance. The role of pitch angle on the film densities was identified. V₅₀/ρ and ΔE_k/ρ were determined as a function of pitch angle in an effort to quantify the ballistic performance advantage of Bouligand films compared to a quasi-isotropic baseline control. Bouligand structures exhibited optimal impact resistance at relatively small pitch angles (18 < γ < 42°), which can be further improved by decreasing CNC interfacial interactions. This work shows the unique nanoscale mechanics that allow for impact energy in small pitch angle films to be effectively dissipated through large in-plane cracks, through-thickness twisting cracks, and interfacial sliding events. Meanwhile, new insights into the importance of uniform wave propagation with minimal CNC rupture have been shown to help maintain film integrity during impact. Furthermore, decreasing the interfacial adhesion energy of CNCs effectively enhances their impact resistance and energy absorption, and this effect is more pronounced for Bouligand microstructures with optimal pitch angles. This study has a number of important limitations. In particular, only Bouligand structures with relatively long, pure CNCs (approximately 1 micrometer) that spanned the whole specimen were considered. This was done to illustrate the relationship between two key designing factors, γ and D₀, and the impact resistance of Bouligand thin films at the microscale. Moreover, fiber-reinforced composites in experiments more often incorporate short fibers to construct helicoidal structures⁶⁶ and use mid-plane symmetry^14,15 to exclude any potential extension-bending coupling behavior. Additionally, the effect of polymer matrices on the ballistic impact response is neglected here. These features will likely introduce more complex fiber and matrix failure mechanisms during impact, meaning that the effects of fiber length, in-plane arrangements, and the nanoconfinement on matrix may also be important in determining the optimal ballistic performance of materials with Bouligand microstructures. These factors could be further studied with CG models of CNCs and polymers in the future. Another important limitation relates to the representation of CNCs with a bead-spring CG strategy. Geometries of real CNCs tend to be rod-like, with planar cross-sections and atomic roughness.⁴⁰ While the mechanical and interfacial properties of CNCs are well captured by our CG model,⁵¹ the physical geometries of CNCs may affect interlayer interactions and, therefore, film density. However, given the important role internal structure plays in dictating the impact tolerance of CNC films (Fig. 5d), any changes resulting from the interlayer interactions of more physically representative CNCs are not likely to alter the ballistic performance trends observed herein. Furthermore, while modifying D₀ does not affect the mechanical properties of individual CNC fibers, it may manifest as differences in the apparent mechanical properties of structures assembled from those CNCs. This is especially true for the non-fiber aligned in-plane and out-of-plane directions, where nonbonded interactions primarily dictate the structural response. Increasing D₀ may also lead to a transition in the film failure mechanisms from inter-fiber and inter-layer sliding to CNC rupture, which may bound the impact resistance of CNC films with Bouligand microstructures. Finally, the methodology and findings here are not limited to CNC films, but are generally applicable to the design and development of 1D materials with Bouligand microstructures.

Conflicts of interest

The authors have no conflicts of interest to declare.

Acknowledgements

The authors acknowledge funding from the Army Research Office (award #W911NF1710430), Office of Naval Research (PECASE Award, grant no. N00014-16-1-3175), and the Center for Hierarchical Materials Design (CHiMaD) funded by National Institute of Standards and Technology (award #70NANB14H012). Authors acknowledge support from the Dept. of Civil and Environmental Engineering and Dept. of Mechanical Engineering at Northwestern University, as well as supercomputing grants from Northwestern University High Performance Computing Center, Department of Defense High Performance Computing Modernization Program, and Argonne Leadership Computing Facility Director's Discretionary Program.

References

1. Y. Bouligand, Twisted Fibrous Arrangements in Biological Materials and Cholesteric Mesophases, Tissue Cell, 1972, 4, 189–217.
2. P.-Y. Chen, A. Y.-M. Lin, J. McKittrick and M. A. Meyers, Structure and Mechanical Properties of Crab Exoskeletons, Acta Biomater., 2008, 4, 587–596.
3. S. Nikolov, M. Petrov, L. Lymperakis, M. Friák, C. Sachs, H.-O. Fabritius, D. Raabe and J. Neugebauer, Revealing the Design Principles of High-Performance Biological Composites Using Ab Initio and Multiscale Simulations: The Example of Lobster Cuticle, Adv. Mater., 2010, 22, 519–526.
4. R. Yang, A. Zaheri, W. Gao, C. Hayashi and H. D. Espinosa, AFM Identification of Beetle Exocuticle: Bouligand Structure and Nanofiber Anisotropic Elastic Properties, Adv. Funct. Mater., 2016, 1603993.
5. E. A. Zimmermann, B. Gludovatz, E. Schaible, N. K. Dave, W. Yang, M. A. Meyers and R. O. Ritchie, Mechanical Adaptability of the Bouligand-Type Structure in Natural Dermal Armour, Nat. Commun., 2013, 4, 2634.
6. W. Yang, V. R. Sherman, B. Gludovatz, M. Mackey, E. A. Zimmermann, E. H. Chang, E. Schaible, Z. Qin, M. J. Buehler and R. O. Ritchie, et al., Protective Role of Arapaima Gigas Fish Scales: Structure and Mechanical Behavior, Acta Biomater., 2014, 10, 3599–3614.
7. J. C. Weaver, G. W. Milliron, A. Miserez, K. Evans-Lutterodt, S. Herrera, I. Gallana, W. J. Mershon, B. Swanson, P. Zavattieri and E. DiMasi, et al., The Stomatopod Dactyl Club: A Formidable Damage-Tolerant Biological Hammer, Science, 2012, 336, 1275–1280.
8. H. D. Espinosa, J. E. Rim, F. Barthelat and M. J. Buehler, Merger of Structure and Material in Nacre and Bone – Perspectives on De Novo Biomimetic Materials, Prog. Mater. Sci., 2009, 54, 1059–1100.
9. P. Fratzl, Biomimetic Materials Research: What Can We Really Learn from Nature's Structural Materials?, J. R. Soc., Interface, 2007, 4, 637–642.
10. X. Li, J. Wang, J. Du, M. Cao, K. Liu, Q. Li, X.-Q. Feng and L. Jiang, Spear and Shield: Survival War between Mantis Shrimps and Abalones, Adv. Mater. Interfaces, 2015, 2, 1500250–n/a.
11. K. Wu, Z. Zheng, S. Zhang, L. He, H. Yao, X. Gong and Y. Ni, Interfacial Strength-Controlled Energy Dissipation Mechanism and Optimization in Impact-Resistant Nacreous Structure, Mater. Des., 2018, 163, 107532.
12. W. Xia, J. Song, Z. Meng, C. Shao and S. Keten, Designing Multi-Layer Graphene-Based Assemblies for Enhanced Toughness in Nacre-Inspired Nanocomposites, Mol. Syst. Des. Eng., 2016, 1, 40–47.
13. G. X. Gu, M. Takaffoli and M. J. Buehler, Hierarchically Enhanced Impact Resistance of Bioinspired Composites, Adv. Mater., 2017, 29, 1700060.
14. L. K. Grunenfelder, N. Suksangpanya, C. Salinas, G. Milliron, N. Yaraghi, S. Herrera, K. Evans-Lutterodt, S. R. Nutt, P. Zavattieri and D. Kisailus, Bio-Inspired Impact-Resistant Composites, Acta Biomater., 2014, 10, 3997–4008.
15. D. Ginzburg, F. Pinto, O. Iervolino and M. Meo, Damage Tolerance of Bio-Inspired Helicoidal Composites under Low Velocity Impact, Compos. Struct., 2017, 161, 187–203.
16. J. S. Shang, N. H. H. Ngern and V. B. C. Tan, Crustacean-Inspired Helicoidal Laminates, Compos. Sci. Technol., 2016, 128, 222–232.
17. N. Suksangpanya, N. A. Yaraghi, D. Kisailus and P. Zavattieri, Twisting Cracks in Bouligand Structures, J. Mech. Behav. Biomed. Mater., 2017, 76, 38–57.
18. T. Apichattrabrut and K. Ravi-Chandar, Helicoidal Composites, Mech. Adv. Mater. Struct., 2006, 13, 61–76.
19. Q. Chen and N. M. Pugno, Bio-Mimetic Mechanisms of Natural Hierarchical Materials: A Review, J. Mech. Behav. Biomed. Mater., 2013, 19, 3–33.
20. L. Cheng, A. Thomas, J. L. Glancey and A. M. Karlsson, Mechanical Behavior of Bio-Inspired Laminated Composites, Composites, Part A, 2011, 42, 211–220.
21. B. Ribbans, Y. Li and T. Tan, A Bioinspired Study on the Interlaminar Shear Resistance of Helicoidal Fiber Structures, J. Mech. Behav. Biomed. Mater., 2016, 56, 57–67.
22. U. G. K. Wegst, H. Bai, E. Saiz, A. P. Tomsia and R. O. Ritchie, Bioinspired Structural Materials, Nat. Mater., 2015, 14, 23–36.
23. G. X. Gu, I. Su, S. Sharma, J. L. Voros, Z. Qin and M. J. Buehler, Three-Dimensional-Printing of Bio-Inspired Composites, J. Biomech. Eng., 2016, 138, 021006–021016.
24. Y. Yang, Z. Chen, X. Song, Z. Zhang, J. Zhang, K. K. Shung, Q. Zhou and Y. Chen, Biomimetic Anisotropic Reinforcement Architectures by Electrically Assisted Nanocomposite 3D Printing, Adv. Mater., 2017, 29, 1605750–n/a.
25. Y. Wang, X. Chen, R. Young, I. Kinloch and G. Wells, A Numerical Study of Ply Orientation on Ballistic Impact Resistance of Multi-Ply Fabric Panels, Composites, Part B, 2015, 68, 259–265.
26. Y. Wang, X. Chen, R. Young, I. Kinloch and G. Wells, An Experimental Study of the Effect of Ply Orientation on Ballistic Impact Performance of Multi-Ply Fabric Panels, Text. Res. J., 2015, 86, 34–43.
27. J. Andersons and M. König, Dependence of Fracture Toughness of Composite Laminates on Interface Ply Orientations and Delamination Growth Direction, Compos. Sci. Technol., 2004, 64, 2139–2152.
28. F. D. Fischer, O. Kolednik, J. Predan, H. Razi and P. Fratzl, Crack Driving Force in Twisted Plywood Structures, Acta Biomater., 2017, 55, 349–359.
29. N. Guarin-Zapata, J. Gomez, N. Yaraghi, D. Kisailus and P. D. Zavattieri, Shear Wave Filtering in Naturally-Occurring Bouligand Structures, Acta Biomater., 2015, 23, 11–20.
30. R. S. Sikarwar, R. Velmurugan and N. K. Gupta, Influence of Fiber Orientation and Thickness on the Response of Glass/Epoxy Composites Subjected to Impact Loading, Composites, Part B, 2014, 60, 627–636.
31. A. Gargano, K. Pingkarawat, V. L. Pickerd, M. E. Ibrahim and A. P. Mouritz, Effect of Fibre-Matrix Interfacial Strength on the Explosive Blast Resistance of Carbon Fibre Laminates, Compos. Sci. Technol., 2017, 138, 68–79.
32. K. K, S. Kazemahvazi and B. P. Russell, Optimal Fibre Architecture of Soft-Matrix Ballistic Laminates, Int. J. Impact Eng., 2016, 88, 227–237.
33. K. J. De France, K. G. Yager, T. Hoare and E. D. Cranston, Cooperative Ordering and Kinetics of Cellulose Nanocrystal Alignment in a Magnetic Field, Langmuir, 2016, 32, 7564–7571.
34. J. P. F. Lagerwall, C. Schutz, M. Salajkova, J. Noh, J. Hyun Park, G. Scalia and L. Bergstrom, Cellulose Nanocrystal-Based Materials: From Liquid Crystal Self-Assembly and Glass Formation to Multifunctional Thin Films, NPG Asia Mater., 2014, 6, e80.
35. I. Usov, G. Nystrom, J. Adamcik, S. Handschin, C. Schutz, A. Fall, L. Bergstrom and R. Mezzenga, Understanding Nanocellulose Chirality and Structure-Properties Relationship at the Single Fibril Level, Nat. Commun., 2015, 6, 7564.
36. B. Natarajan, C. Emiroglu, J. Obrzut, D. M. Fox, B. Pazmino, J. F. Douglas and J. W. Gilman, Dielectric Characterization of Confined Water in Chiral Cellulose Nanocrystal Films, ACS Appl. Mater. Interfaces, 2017, 9, 14222–14231.
37. C. Schütz, M. Agthe, A. B. Fall, K. Gordeyeva, V. Guccini, M. Salajková, T. S. Plivelic, J. P. F. Lagerwall, G. Salazar-Alvarez and L. Bergström, Rod Packing in Chiral Nematic Cellulose Nanocrystal Dispersions Studied by Small-Angle X-Ray Scattering and Laser Diffraction, Langmuir, 2015, 31, 6507–6513.
38. K. E. Shopsowitz, H. Qi, W. Y. Hamad and M. J. MacLachlan, Free-Standing Mesoporous Silica Films with Tunable Chiral Nematic Structures, Nature, 2010, 468, 422–425.
39. B. Wang and A. Walther, Self-Assembled, Iridescent, Crustacean-Mimetic Nanocomposites with Tailored Periodicity and Layered Cuticular Structure, ACS Nano, 2015, 9, 10637–10646.
40. R. J. Moon, A. Martini, J. Nairn, J. Simonsen and J. Youngblood, Cellulose Nanomaterials Review: Structure, Properties and Nanocomposites, Chem. Soc. Rev., 2011, 40, 3941–3994.
41. R. Sinko, X. Qin and S. Keten, Interfacial Mechanics of Cellulose Nanocrystals, MRS Bull., 2015, 40, 340–348.
42. I. Diddens, B. Murphy, M. Krisch and M. Müller, Anisotropic Elastic Properties of Cellulose Measured Using Inelastic X-Ray Scattering, Macromolecules, 2008, 41, 9755–9759.
43. T. Ramanathan, A. A. Abdala, S. Stankovich, D. A. Dikin, M. Herrera-Alonso, R. D. Piner, D. H. Adamson, H. C. Schniepp, X. Chen and R. S. Ruoff, et al., Functionalized Graphene Sheets for Polymer Nanocomposites, Nat. Nanotechnol., 2008, 3, 327–331.
44. R. Sinko, S. Mishra, L. Ruiz, N. Brandis and S. Keten, Dimensions of Biological Cellulose Nanocrystals Maximize Fracture Strength, ACS Macro Lett., 2013, 3, 64–69.
45. B. Natarajan and J. W. Gilman, Bioinspired Bouligand Cellulose Nanocrystal Composites: A Review of Mechanical Properties, Philos. Trans. R. Soc., A, 2017, 376, 20170050.
46. R. Sinko and S. Keten, Effect of Moisture on the Traction-Separation Behavior of Cellulose Nanocrystal Interfaces, Appl. Phys. Lett., 2014, 105, 243702.
47. R. Sinko and S. Keten, Traction–Separation Laws and Stick–Slip Shear Phenomenon of Interfaces between Cellulose Nanocrystals, J. Mech. Phys. Solids, 2015, 78, 526–539.
48. D. M. Fox, R. S. Rodriguez, M. N. Devilbiss, J. Woodcock, C. S. Davis, R. Sinko, S. Keten and J. W. Gilman, Simultaneously Tailoring Surface Energies and Thermal Stabilities of Cellulose Nanocrystals Using Ion Exchange: Effects on Polymer Composite Properties for Transportation, Infrastructure, and Renewable Energy Applications, ACS Appl. Mater. Interfaces, 2016, 8, 27270–27281.
49. X. Qin, W. Xia, R. Sinko and S. Keten, Tuning Glass Transition in Polymer Nanocomposites with Functionalized Cellulose Nanocrystals through Nanoconfinement, Nano Lett., 2015, 15, 6738–6744.
50. M. Shishehbor and P. D. Zavattieri, Effects of Interface Properties on the Mechanical Properties of Bio-Inspired Cellulose Nanocrystal (CNC)-Based Materials, J. Mech. Phys. Solids, 2018, 124, 871–896.
51. X. Qin, S. Feng, Z. Meng and S. Keten, Optimizing the Mechanical Properties of Cellulose Nanopaper through Surface Energy and Critical Length Scale Considerations, Cellulose, 2017, 24, 3289–3299.
52. J. H. Lee, D. Veysset, J. P. Singer, M. Retsch, G. Saini, T. Pezeril, K. A. Nelson and E. L. Thomas, High Strain Rate Deformation of Layered Nanocomposites, Nat. Commun., 2012, 3, 1164.
53. J.-H. Lee, P. E. Loya, J. Lou and E. L. Thomas, Dynamic Mechanical Behavior of Multilayer Graphene Via Supersonic Projectile Penetration, Science, 2014, 346, 1092–1096.
54. Y. Zhang, Z. Meng, X. Qin and S. Keten, Ballistic Impact Response of Lipid Membranes, Nanoscale, 2018, 10, 4761–4770.
55. Z. Meng, A. Singh, X. Qin and S. Keten, Reduced Ballistic Limit Velocity of Graphene Membranes Due to Cone Wave Reflection, Extreme Mech. Lett., 2017, 15, 70–77.
56. Z. Meng, J. Han, X. Qin, Y. Zhang, O. Balogun and S. Keten, Spalling-Like Failure by Cylindrical Projectiles Deteriorates the Ballistic Performance of Multi-Layer Graphene Plates, Carbon, 2018, 126, 611–619.
57. B. Z. Haque, S. C. Chowdhury and J. W. Gillespie, Molecular Simulations of Stress Wave Propagation and Perforation of Graphene Sheets under Transverse Impact, Carbon, 2016, 102, 126–140.
58. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117, 1–19.
59. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38.
60. X. Wu, R. Moon and A. Martini, Tensile Strength of Iβ Crystalline Cellulose Predicted by Molecular Dynamics Simulation, Cellulose, 2014, 21, 2233–2245.
61. M. K. Hazzard, S. Hallett, P. T. Curtis, L. Iannucci and R. S. Trask, Effect of Fibre Orientation on the Low Velocity Impact Response of Thin Dyneema® Composite Laminates, Int. J. Impact Eng., 2017, 100, 35–45.
62. W. Xie, S. Tadepalli, S. H. Park, A. Kazemi-Moridani, Q. Jiang, S. Singamaneni and J.-H. Lee, Extreme Mechanical Behavior of Nacre-Mimetic Graphene-Oxide and Silk Nanocomposites, Nano Lett., 2018, 18, 987–993.
63. J. Hyon, O. Lawal, O. Fried, R. Thevamaran, S. Yazdi, M. Zhou, D. Veysset, S. E. Kooi, Y. Jiao and M.-S. Hsiao, et al., Extreme Energy Absorption in Glassy Polymer Thin Films by Supersonic Micro-Projectile Impact, Mater. Today, 2018, 21, 817–824.
64. Z. Meng and S. Keten, Unraveling the Effect of Material Properties and Geometrical Factors on Ballistic Penetration Energy of Nanoscale Thin Films, J. Appl. Mech., 2018, 85, 121004.
65. Z. Wei, R. Sinko, S. Keten and E. Luijten, Effect of Surface Modification on Water Adsorption and Interfacial Mechanics of Cellulose Nanocrystals, ACS Appl. Mater. Interfaces, 2018, 10, 8349–8358.
66. B. Natarajan, A. Krishnamurthy, X. Qin, C. D. Emiroglu, A. Forster, E. J. Foster, C. Weder, D. M. Fox, S. Keten and J. Obrzut, et al., Binary Cellulose Nanocrystal Blends for Bioinspired Damage Tolerant Photonic Films, Adv. Funct. Mater., 2018, 0, 1800032.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00232k

---