Open Access Article
Open Access ArticleNoble metal supported hexagonal boron nitride for the oxygen reduction reaction: a DFT study†
Seoin
Back
a and
Samira
Siahrostami
 *b
*b
aSUNCAT Center for Interface Science and Catalysis, Department of Chemical Engineering, Stanford University, Stanford, CA 94305, USA
bDepartment of Chemistry, University of Calgary, 2500 University Drive NW, Calgary, Alberta, Canada T2N 1N4. E-mail: samiras.siahrostami@ucalgary.ca
First published on 26th October 2018
Abstract
Discovering active, stable and cost-effective catalysts for the oxygen reduction reaction (ORR) is of utmost interest for commercialization of fuel cells. Scarce and expensive noble metals such as Pt and Pd are the state-of-the-art active ORR catalysts but suffer from low stability against CO poisoning. Hexagonal boron nitride (h-BN) is a particularly attractive material due to its low cost and stability; however, it suffers from intrinsic low activity toward the ORR in the pristine form as a result of its inherently low conductivity with a large band gap of ∼5.5 electron volts. During the past few years, several strategies such as using metal supports, metal doping and atomic vacancies have been reported to significantly increase the conductivity, thereby promoting the ORR activity. Herein we use density functional theory calculations to systematically study these strategies for activating inert h-BN and further examine the stability against CO poisoning. We show that noble metals, such as Ag, Pd, and Pt, require boron (B) or nitrogen (N) vacancies to reasonably activate h-BN toward the ORR. For example, Pd supported h-BN with B-vacancies exhibits significantly high ORR activity. All three examined metal supported h-BNs are predicted to be stable against CO poisoning. These results demonstrate that supporting h-BN on noble metals is a promising strategy to increase the stability against CO poisoning while maintaining high ORR activity.
1. Introduction
Fuel cells, converting the chemical energy of fuels such as H2 into electricity, are the most promising clean energy technology for replacing fossil fuels in the transport sector.1 However, the sluggish oxygen reduction reaction (ORR) at the fuel cell cathode remains the main drawback to overcome. Generally, Pt catalysts are the state-of-the-art ORR catalysts. Nevertheless, the commercialization of Pt catalysts is limited due to the scarcity of Pt, time-dependent drift and CO poisoning.1,2 These issues have triggered academic and industrial research studies toward discovering cost-effective, active and stable ORR catalysts.3,4 Several approaches have been proposed to enhance the catalytic activity and reduce the amount of Pt usage, including alloying with non-precious metals5–7 and using core–shell structures8,9 and nanostructures.10–12 Recently, graphene and isoelectronic hexagonal boron-nitride (h-BN) sheets have been widely investigated as alternative cost-effective ORR catalysts.13–17 Unlike graphene, the pristine h-BN sheet is a semiconductor with an intrinsically large band gap of ∼5.5 eV with no states at the Fermi level. This makes the pristine h-BN sheet completely inert toward the ORR. However, its ORR catalytic activity can be significantly improved by surfactant exfoliation, hetero-atom or metal doping, and deposition on metal supports.18–26 Gao et al. investigated the role of different defects for Cu supported BN and found that a boron vacancy helps in binding ORR intermediates more strongly.27On the other hand, h-BN exhibits other unique properties such as high stability which is favorable for the ORR. In fact, the h-BN sheet could serve as a protective layer for the underneath metal substrate and enhance the stability under ORR conditions.13,28,29 Recently, Zhang et al. reported that CO binding energy becomes much weaker on Pt supported boron nitride compared to that on the Pt surface, thereby alleviating the CO poisoning effect.28 Zuo et al. observed that Pd supported boron nitride retained its ORR activity after 4000 cycles, while the half-wave potential of commercial Pt/C decreased by 33 mV.22 These experiments indicate that depositing h-BN on metal supports is a promising technique to enhance the stability of noble metal supports while maintaining the activity.
Herein, we systematically analyze the ORR catalytic activity of h-BN sheets supported on different noble metals (h-BN@M (M: Ag, Pd and Pt)) using density functional theory (DFT) calculations. For comparison, we also calculate the ORR activity of h-BN@Cu which has been reported to be as active as a Pt catalyst for the ORR.17 We show that all the examined h-BNs supported on noble metals require nitrogen (N) or boron (B) vacancies to show reasonable ORR activity. Particularly, h-BN@Pd with B vacancies has similar ORR activity to a Pt catalyst, which is in very good agreement with recently reported experimental results.22 We also show that the stability of h-BN@M against CO poisoning is much improved compared to that of a Pt catalyst. Finally, we also discuss the calculated ORR activity and stability of transition metals doped in single and double vacancies of the two-dimensional h-BN and show that Cu-doped and Ag-doped at single B-vacancy is significantly active and stable for the ORR.
2. Computational details
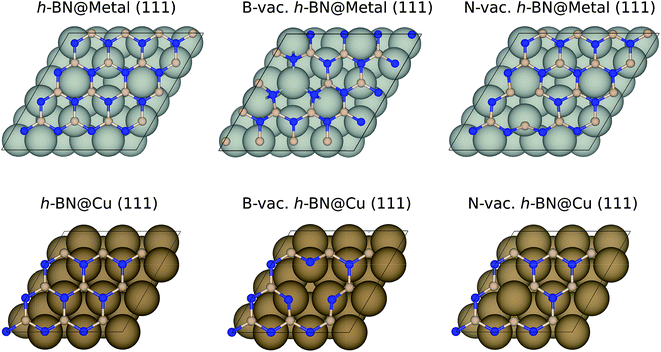
We performed geometry optimizations and calculated electronic energies using the Vienna Ab Initio Simulation Package (VASP)30,31 and projector augmented wave (PAW) pseudopotentials.32 We chose to use the BEEF-vdW33 exchange–correlation functional, which was shown to accurately describe both chemisorption and physisorption.34 The energy cutoff was set to 500 eV, and the convergence criteria for energy (self-consistent iteration) and force (ionic relaxation) were set to 10−4 eV and 0.05 eV Å−1, respectively. The bulk geometry of BN was optimized using a (12 × 12 × 4) Monkhorst–Pack k-point mesh, resulting in a B–N distance of 1.45 Å, in agreement with the previous calculations and experiments.35,36 A (3 × 3 × 1) k-point mesh was utilized to calculate the energetics of metal-supported boron nitride. Note that we utilized the Quantum Espresso code37 with the BEEF-vdW functional33 and ultrasoft pseudopotentials38 for h-BN based single atom catalyst calculations. More details can be found in the previous publication.39Among the four metal supports (Ag, Cu, Pd, and Pt), we modeled (4 × 4) BN supported on three-layered (111) surfaces of Ag, Pd and Pt using a 2(√3 × √3) supercell, while we modeled (3 × 3) BN supported on Cu (111) using a (3 × 3) supercell to minimize the lattice mismatches (Fig. 1). The resulting lattice mismatches were 2.48, 3.86, 2.07 and 1.79% for Ag, Cu, Pd and Pt, respectively. We note that the previous theoretical investigation showed that influence of strain effect on the binding energies of ORR intermediates was less than 0.10 eV for 4% strain of BN.40 During the structural optimizations, atoms in the bottom two layers were kept fixed, while other atoms including adsorbates were fully relaxed. To avoid an artificial interaction between periodic images along the z-direction, we included a vacuum spacing of 15 Å.
The calculated electronic energies were converted into free energies by adding free energy corrections for adsorbates (zero-point energy, enthalpy and entropy corrections). The free energy correction was obtained from a harmonic oscillator approximation at 300 K as implemented in the Atomic Simulation Environment (ASE), and the correction values for *O, *OH and *OOH were 0.06 eV, 0.35 eV and 0.42 eV, respectively. We also studied the effect of solvation on the adsorption energies of oxygen intermediates on h-BN@Pd as an example. We included an explicit solvation model containing eight H2O molecules in the supercell derived from the minima-hopping method (Fig. S1†).41 The calculated solvation stabilization effects for *OH and *OOH were found to be negligible (−0.09 and −0.01 eV, respectively), compared to the −0.5 and −0.25 eV on metal surfaces.42
3. Results and discussion
We begin by considering the adhesion energies of h-BN supported on metals, calculated as Eh-BN@M − EM − Eh-BN, where Eh-BN@M, EM and Eh-BN are electronic energies of the h-BN@M complex, clean metal slabs and h-BN with/without vacancies, respectively. Among the various possibilities, the most stable geometries are chosen for further investigations. For example, a B-vac. prefers to sit on top of the metal atom rather than on the bridge site. Table 1 summarizes the adhesion energies of metal supported h-BN. Although the perfect h-BN binds weakly on metal supports, the interaction becomes stronger when atomic vacancies are introduced. Particularly, adhesion energies of h-BN with B-vacancies are the strongest since N atoms tend to move toward the metal supports. This is not observed for the case of N-vacancies. We further analyzed the bonding character of h-BN and metal supports using the electron localization function (ELF),43 where we found that van der Waals interactions are dominant (Fig. S2†).| Adhesion energies per BN pair (eV) | Without vac. | B-vac. | N-vac. |
|---|---|---|---|
| Ag | −0.07 | −0.20 | −0.11 |
| Pd | −0.08 | −0.34 | −0.29 |
| Pt | −0.10 | −0.34 | −0.29 |
| Cu | −0.07 | −0.46 | −0.15 |
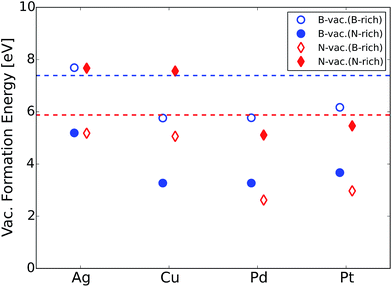
Next, we calculated the formation energies for B- or N-vacancies (ΔEvac.) for all the h-BN@M complexes using eqn (1).
| ΔEvac. = EB/N-vac. h-BN@Metal − Eh-BN@Metal + μB/N | (1) |
| Electrons per BN pair | Without vac. | B-vac. | N-vac. |
|---|---|---|---|
| Ag | 0.00 | −0.09 | 0.03 |
| Pd | 0.00 | −0.05 | 0.02 |
| Pt | 0.00 | −0.03 | 0.04 |
| Cu | 0.00 | −0.14 | 0.03 |
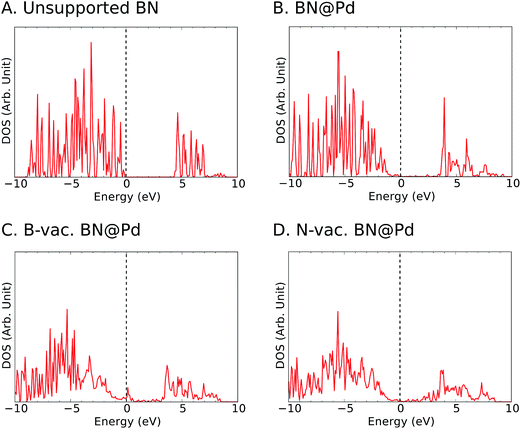
To gain insights into the electronic structure in the presence of vacancies and supports, we calculated the density of states (DOS) projected onto B and N atoms (Fig. 4 and S3–S5†). In agreement with previous reports in the literature,44 we observed ∼4 eV bandgap for the freestanding h-BN. It is known that metal-induced gap states are formed near the Fermi level for metal supported h-BN, and they significantly influence the catalytic activities.45,46 We note that such gap states were observed for all supports particularly with B vacancies (Fig. 4 and S3–S5†).
To investigate the ORR activity, we assume an associative mechanism47 and utilize the computational hydrogen electrode (CHE) to include the effect of potential described in detail elsewhere.47,48 We calculate the adsorption free energies of ORR intermediates, namely, *OOH, *O, and *OH, relative to gas phase H2 and liquid phase H2O.
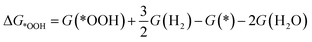 | (2a) |
| ΔG*O = G(*O) + G(H2) − G(*) − G(H2O) | (2b) |
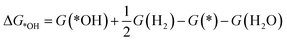 | (2c) |
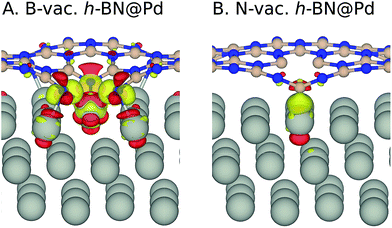
We note that it is crucial to take a surface coverage under reaction conditions into consideration, which could provide more realistic information rather than assuming a low coverage limit. For example, a catalyst surface with strong *OH adsorption energy is expected to be covered with *OH. For the h-BN@M with/without a B-vac., we found that ΔG*OH is rather weak, so we expected that the low coverage limit provides beneficial insights. However, the binding free energies of the oxygen intermediates on h-BN@M with a N-vac. are significantly strong (up to −2.0 eV ΔG*OH) and adsorbed *O spontaneously fills the N-vac. during the geometry optimization (Fig. 5B). Therefore, we constructed a surface Pourbaix diagram (more details are in ESI Note 1†) for all h-BN@M systems with a N-vac. and determined the most stable surface coverage at 0.80 VRHE, the potential at which ORR current densities are measured (Fig. 5 and S6–S8†).7
 | ||
| Fig. 5 (A) Surface Pourbaix diagram of N-vac. BN@Pd. (B) The most stable *O and *OH coadsorbed surface termination of N-vac. BN@Pd at 0.8 VRHE. | ||
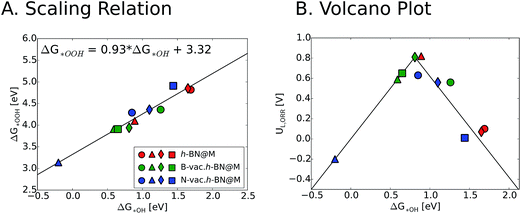
We now turn our focus on the correlation between binding free energies of *OH and *OOH. Previous theoretical calculations have revealed a universal scaling relation between ΔG*OOH and ΔG*OH on various types of catalyst surfaces including transition metals, transition metal oxides and two dimensional materials, resulting in an inherent overpotential (∼0.4 V) for the oxygen reduction and evolution reactions.17,48–50 For metal supported h-BN, we also observed a linear scaling behavior between ΔG*OH and ΔG*OOH, which is similar to the general scaling relation (ΔG*OOH = ΔG*OH + 3.2 (±0.2)). We note that introducing vacancies generally strengthens the binding free energies of reaction intermediates. This in turn improves the ORR activity of h-BN@M systems with weak oxygen binding (such as h-BN@Ag, h-BN@Pd and h-BN@Pt) but adversely affects that of moderate binding h-BN@M catalysts (such as h-BN@Cu) (Fig. 6).
To measure the activity, we take into account the maximum potential at which all the reaction steps are energetically downhill, known as the limiting potential (UL). The calculated overpotential is defined as the difference between the limiting potential and the equilibrium potential (1.23 V). Fig. 6B displays the UL as a function of ΔG*OH. In agreement with previous theoretical results, h-BN@Cu is expected to catalyze the ORR with an UL of 0.82 V.40 On the other hand, other metal supports are inactive toward the ORR due to the weak interaction with oxygen intermediates. Once the vacancies are formed, however, all h-BN@M become active for the ORR (Fig. 7). Interestingly, h-BN@Pd with a B-vac. shows a similar activity to Pt (111). Our calculations agree well with a recently published experiment on BN@Pd composites which revealed an ORR activity comparable to that of the commercial Pt/C catalyst.22
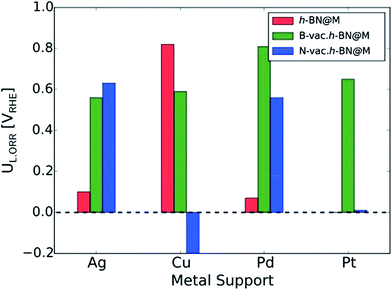 | ||
| Fig. 7 The calculated ORR limiting potentials (UL,ORR) for metal supported h-BN with/without atomic vacancies. The h-BN@Pt is not presented since it does not bind *OOH. | ||
The calculated CO adsorption energies are −0.62 eV and −0.01 eV for h-BN@Cu and h-BN@Pd with B-vac., respectively. These energies are significantly weaker than the CO adsorption energy on Pt (111), −1.65 eV, indicating less CO poisoning on h-BN@M compared to Pt (111).
We would like to mention that several experimental efforts have been made to synthesize metal supported BN. For example, the chemical vapor deposition (CVD) technique using borazine (B3N3H6) gas has been applied to deposit h-BN sheets on different metal supports.51,52 In addition, an exfoliated BN dispersion can be spin-coated on the metal electrodes.53 Vacancies are naturally formed during the synthesis procedure or can be purposely generated using low energy argon or nitrogen ion-bombardment.54 Vacancies in h-BN sheets have been successfully observed using an aberration corrected high-resolution transmission electron microscope with exit-wave reconstruction.55 Given that vacancy formation energies of metal supported BN are notably lower compared to that of the freestanding counterpart (Fig. 2), we expect that atomic vacancies in metal supported BN are highly probable to form and contribute to the ORR.
Lastly, we would like to emphasize that an alternative strategy to activate pristine two-dimensional materials such as h-BN is to embed single atoms of transition metals in the vacancies. We have recently examined this approach for a wide range of metal atoms implanted in various two-dimensional materials (SACs, single atom catalysts).39 Transition metals can be embedded in the single and double vacancies of h-BN (Fig. 8A). By calculating the formation energies (ΔEform) of the metal-doped h-BN systems relative to the bulk metal and h-BN with vacancies, we found strong stabilization between a wide range of transition metal atoms and the h-BN supports with metals doped in the single boron vacancy (B-vac.) being the most stable structures. We also examined the stability of these systems against dissolution under electrochemical ORR conditions. Fig. 8B displays the calculated dissolution potentials of metals as a function of formation energies of metal doped h-BN systems. The horizontal dashed line at U = 0.8 VRHE takes into account the potential at which the current density is measured for the ORR. The vertical dashed line represents ΔEform = 0.0 eV, which is the upper bound to the stability of the systems. The left side of the vertical dashed line indicates a favorable formation of the metal-doped h-BN system, while the upper side of the horizontal dashed line indicates electrochemical stability of the system under ORR conditions. Therefore, catalysts in the pink region are expected to survive under the ORR potential (Fig. 8B). Based on the calculated limiting potentials, doping Ag and Cu in the B-vac. of the h-BN sheet provides promising platforms for efficient ORR catalysis with UL of 0.74 V and 0.89 V, respectively. This compares very well with those of the two most active ORR systems in the current study, i.e., h-BN@Cu and h-BN@Pd with a B-vac.
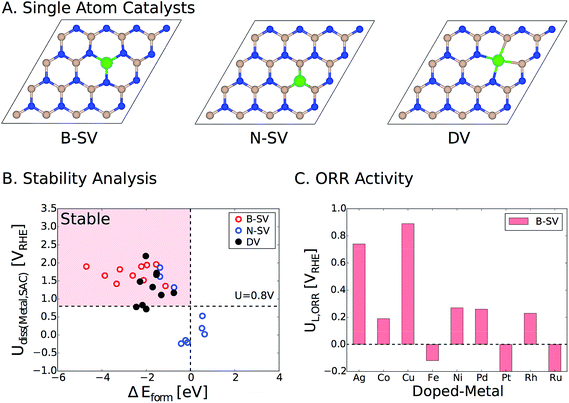 | ||
| Fig. 8 (A) Top view of h-BN based single atom catalysts. B-SV, N-SV, and DV indicate a boron and a nitrogen single vacancy and a double vacancy, respectively. (B) Dissolution potentials vs. formation energies of metal atoms doped in the vacancies of h-BN. Catalysts in the pink region are stable in terms of both formation energy and dissolution potential. The details of the calculations can be found in the previous publication.39 (C) The calculated ORR limiting potentials (UL) for several examined transition metals doped in the B-vac. of h-BN. Note that we only considered B-SV, since it is the most stable configuration. Color code: boron (pink), nitrogen (blue), and metal (green). | ||
4. Conclusion
In summary, we have systematically investigated the ORR activity of Ag, Pt and Pd supported h-BNs with/without B and N vacancies. We found that noble metal supports stabilize the h-BN sheet through charge transfer and activate it for the ORR, which is inert otherwise. Due to the metal supports and vacancies in the h-BN sheet, additional electronic states appear between occupied and unoccupied states, which are known to be responsible for activating the h-BN sheet. We found that h-BN@Ag, h-BN@Pd, and h-BN@Pt become active only if a B- or N-vac. is introduced. We demonstrated that the h-BN@Cu does not require vacancies and even without vacancies it is a highly active ORR catalytic system with UL = 0.82 V. This is in agreement with a previous report on the ORR activity of h-BN@Cu.17 Our calculated limiting potential for h-BN@Pd with a B-vac. agrees well with the recently reported experimental ORR onset potential of h-BN supported on Pd.22 We also found very weak CO binding energy on h-BN@Pd, in agreement with reported enhanced durability for the ORR.22 Lastly, by examining the stability and activity of a wide range of transition metals doped in single and double vacancies of h-BN, we showed that both Ag- and Cu-doped h-BN can be highly active and stable toward the ORR.Conflicts of interest
There are no conflicts to declare.References
- J. Baschuk and X. Li, Int. J. Energy Res., 2001, 25, 695–713 CrossRef CAS
.
- E. Antolini, J. R. Salgado and E. R. Gonzalez, J. Power Sources, 2006, 160, 957–968 CrossRef CAS
.
- M. K. Debe, Nature, 2012, 486, 43 CrossRef CAS PubMed
.
- H. A. Gasteiger, S. S. Kocha, B. Sompalli and F. T. Wagner, Appl. Catal., B, 2005, 56, 9–35 CrossRef CAS
.
- V. R. Stamenkovic, B. S. Mun, K. J. Mayrhofer, P. N. Ross and N. M. Markovic, J. Am. Chem. Soc., 2006, 128, 8813–8819 CrossRef CAS PubMed
.
- V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Marković, Science, 2007, 315, 493–497 CrossRef CAS PubMed
.
- J. Greeley, I. Stephens, A. Bondarenko, T. P. Johansson, H. A. Hansen, T. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552 CrossRef CAS PubMed
.
- S. Back and Y. Jung, ChemCatChem, 2017, 9, 3173–3179 CrossRef CAS
.
- A. L. Strickler, A. Jackson and T. F. Jaramillo, ACS Energy Lett., 2016, 2, 244–249 CrossRef
.
- D. Wang, Y. Yu, H. L. Xin, R. Hovden, P. Ercius, J. A. Mundy, H. Chen, J. H. Richard, D. A. Muller and F. J. DiSalvo, Nano Lett., 2012, 12, 5230–5238 CrossRef CAS PubMed
.
- K. Jiang, Q. Shao, D. Zhao, L. Bu, J. Guo and X. Huang, Adv. Funct. Mater., 2017, 26, 1700830 CrossRef
.
- R. Chattot, T. Asset, P. Bordet, J. Drnec, L. Dubau and F. Maillard, ACS Catal., 2016, 7, 398–408 CrossRef
.
- K. Gong, F. Du, Z. Xia, M. Durstock and L. Dai, Science, 2009, 323, 760–764 CrossRef CAS PubMed
.
- Y. Zheng, Y. Jiao, L. Ge, M. Jaroniec and S. Z. Qiao, Angew. Chem., 2013, 125, 3192–3198 CrossRef
.
- L. Qu, Y. Liu, J.-B. Baek and L. Dai, ACS Nano, 2010, 4, 1321–1326 CrossRef CAS PubMed
.
- J. W. To, J. W. D. Ng, S. Siahrostami, A. L. Koh, Y. Lee, Z. Chen, K. D. Fong, S. Chen, J. He and W.-G. Bae, Nano Res., 2017, 10, 1163–1177 CrossRef CAS
.
- S. Siahrostami, C. Tsai, M. Karamad, R. Koitz, M. García-Melchor, M. Bajdich, A. Vojvodic, F. Abild-Pedersen, J. K. Nørskov and F. Studt, Catal. Lett., 2016, 146, 1917–1921 CrossRef CAS
.
- Y. Li, M. Li, L. Jiang, L. Lin, L. Cui and X. He, Phys. Chem. Chem. Phys., 2014, 16, 23196–23205 RSC
.
- W. Yang, T.-P. Fellinger and M. Antonietti, J. Am. Chem. Soc., 2010, 133, 206–209 CrossRef PubMed
.
- D. S. Su, S. Perathoner and G. Centi, Chem. Rev., 2013, 113, 5782–5816 CrossRef CAS PubMed
.
- Z. W. Liu, F. Peng, H. J. Wang, H. Yu, W. X. Zheng and J. Yang, Angew. Chem., 2011, 123, 3315–3319 CrossRef
.
- L.-X. Zuo and L.-P. Jiang, J. Electrochem. Soc., 2017, 164, H805–H811 CrossRef CAS
.
- R. He, D. Wen, W. Shen and M. Li, Phys. Chem. Chem. Phys., 2018, 20, 10240–10246 RSC
.
- A. F. Khan, M. P. Down, G. C. Smith, C. W. Foster and C. E. Banks, J. Mater. Chem. A, 2017, 5, 4103–4113 RSC
.
- D. Shin, S. Sinthika, M. Choi, R. Thapa and N. Park, ACS Catal., 2014, 4, 4074–4080 CrossRef CAS
.
- G. Elumalai, H. Noguchi and K. Uosaki, Phys. Chem. Chem. Phys., 2014, 16, 13755–13761 RSC
.
- X. Gao, S. Wang and S. Lin, ACS Appl. Mater. Interfaces, 2016, 8, 24238–24247 CrossRef PubMed
.
- Y. Zhang, X. Weng, H. Li, H. Li, M. Wei, J. Xiao, Z. Liu, M. Chen, Q. Fu and X. Bao, Nano Lett., 2015, 15, 3616–3623 CrossRef CAS PubMed
.
- Y. Tang, B. L. Allen, D. R. Kauffman and A. Star, J. Am. Chem. Soc., 2009, 131, 13200–13201 CrossRef CAS PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef
.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef
.
- J. Wellendorff, T. L. Silbaugh, D. Garcia-Pintos, J. K. Nørskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS
.
- A. Du, Y. Chen, Z. Zhu, R. Amal, G. Q. Lu and S. C. Smith, J. Am. Chem. Soc., 2009, 131, 17354–17359 CrossRef CAS PubMed
.
- W. Paszkowicz, J. Pelka, M. Knapp, T. Szyszko and S. Podsiadlo, Appl. Phys. A, 2002, 75, 431–435 CrossRef CAS
.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed
.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892 CrossRef
.
- S. Back, A. Kulkarni and S. Siahrostami, ChemCatChem, 2018, 10, 1–7 CrossRef
.
- R. Koitz, J. K. Nørskov and F. Studt, Phys. Chem. Chem. Phys., 2015, 17, 12722–12727 RSC
.
- A. A. Peterson, Top. Catal., 2014, 57, 40–53 CrossRef CAS
.
- Z.-D. He, S. Hanselman, Y.-X. Chen, M. T. Koper and F. Calle-Vallejo, J. Phys. Chem. Lett., 2017, 8, 2243–2246 CrossRef CAS PubMed
.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS
.
- V. Solozhenko, A. Lazarenko, J.-P. Petitet and A. Kanaev, J. Phys. Chem. Solids, 2001, 62, 1331–1334 CrossRef CAS
.
- S. Lin, J. Huang and X. Gao, Phys. Chem. Chem. Phys., 2015, 17, 22097–22105 RSC
.
- A. Lyalin, A. Nakayama, K. Uosaki and T. Taketsugu, J. Phys. Chem. C, 2013, 117, 21359–21370 CrossRef CAS
.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef
.
- A. Kulkarni, S. Siahrostami, A. Patel and J. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed
.
- I. C. Man, H. Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS
.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS
.
- C. Oshima and A. Nagashima, J. Phys.: Condens. Matter, 1997, 9, 1 CrossRef CAS
.
- A. Preobrajenski, A. Vinogradov and N. Mårtensson, Surf. Sci., 2005, 582, 21–30 CrossRef CAS
.
- K. Uosaki, G. Elumalai, H. Noguchi, T. Masuda, A. Lyalin, A. Nakayama and T. Taketsugu, J. Am. Chem. Soc., 2014, 136, 6542–6545 CrossRef CAS PubMed
.
- R. Peter, A. Bozanic, M. Petravic, Y. Chen, L.-J. Fan and Y.-W. Yang, J. Appl. Phys., 2009, 106, 083523 CrossRef
.
- C. Jin, F. Lin, K. Suenaga and S. Iijima, Phys. Rev. Lett., 2009, 102, 195505 CrossRef PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8na00059j |
| This journal is © The Royal Society of Chemistry 2019 |